Time-Domain Near-Infrared Spectroscopy and Imaging: A Review
Abstract
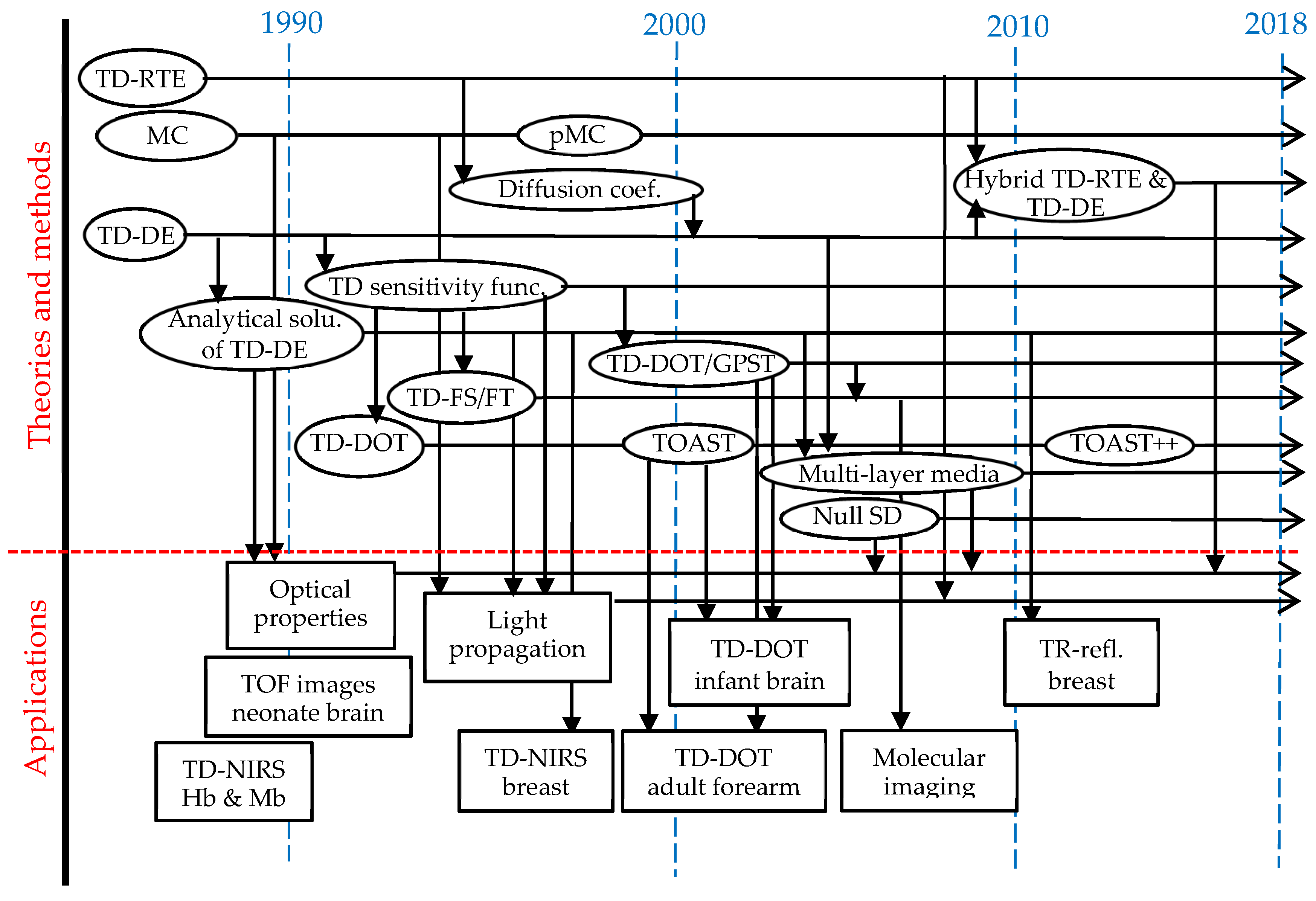
:1. Introduction
2. Theoretical Background of TD-NIRS
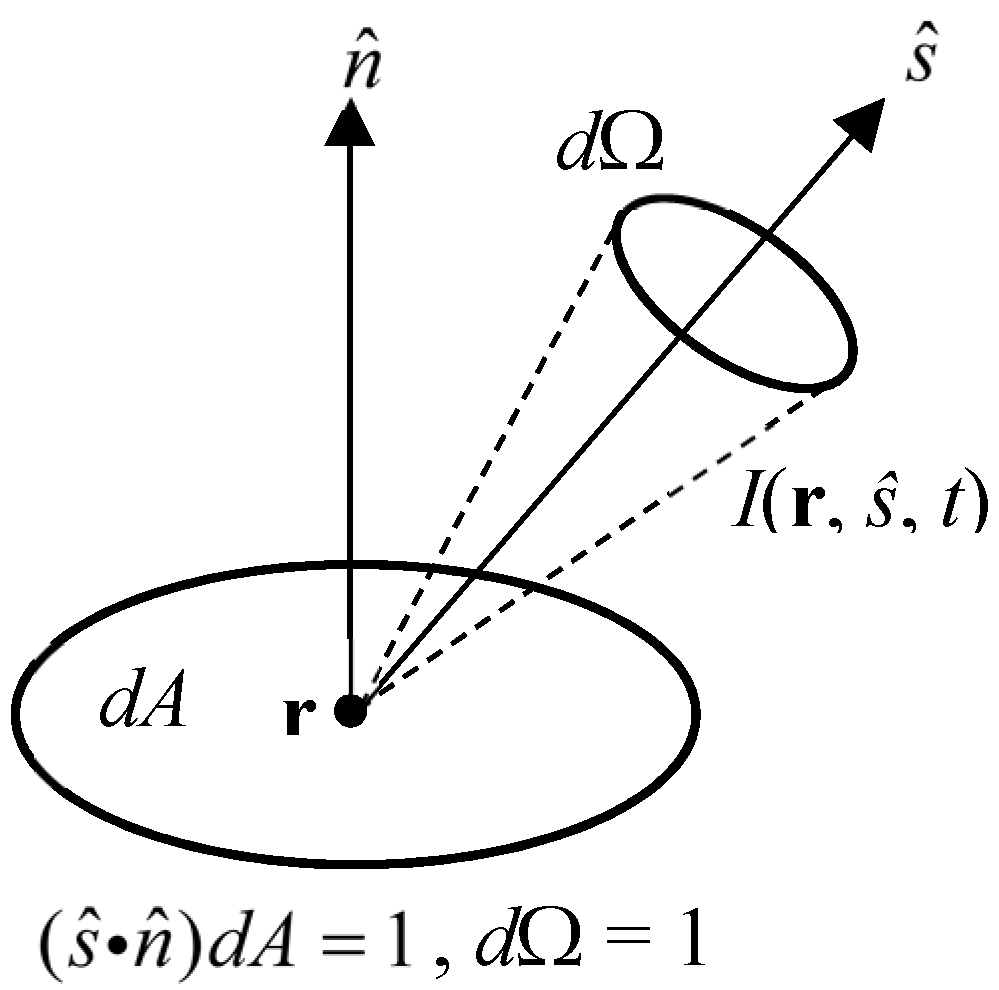
2.1. Radiative Transfer Equation (RTE)
2.2. Expansion of the RTE by Spherical Harmonics and the PN Approximations
2.3. The P1 Approximation
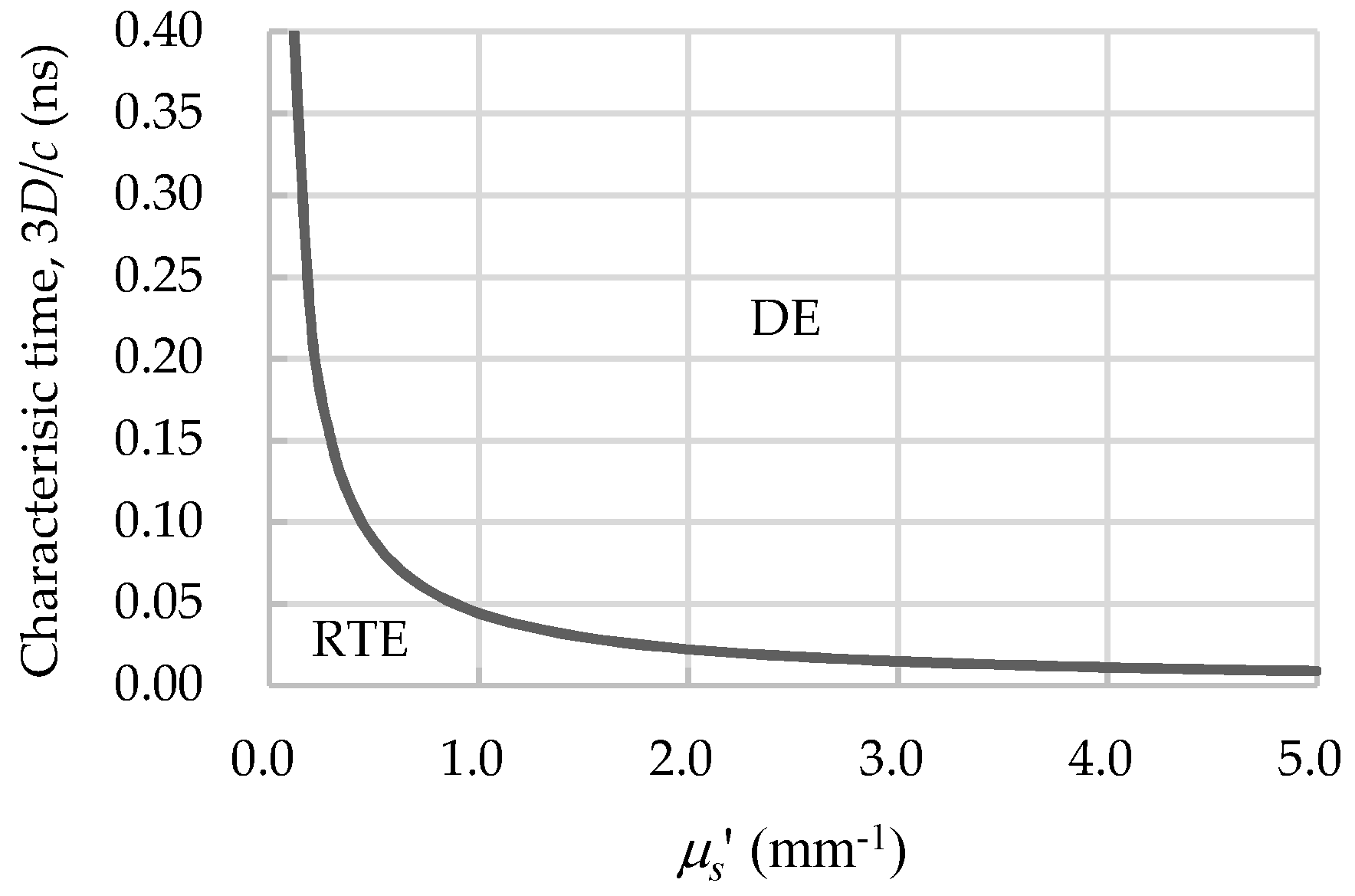
2.4. Diffusion Approximation and Diffusion Equation (DE)
2.5. Diffusion Coefficient Independent of the Absorption Coefficient in TD-DE
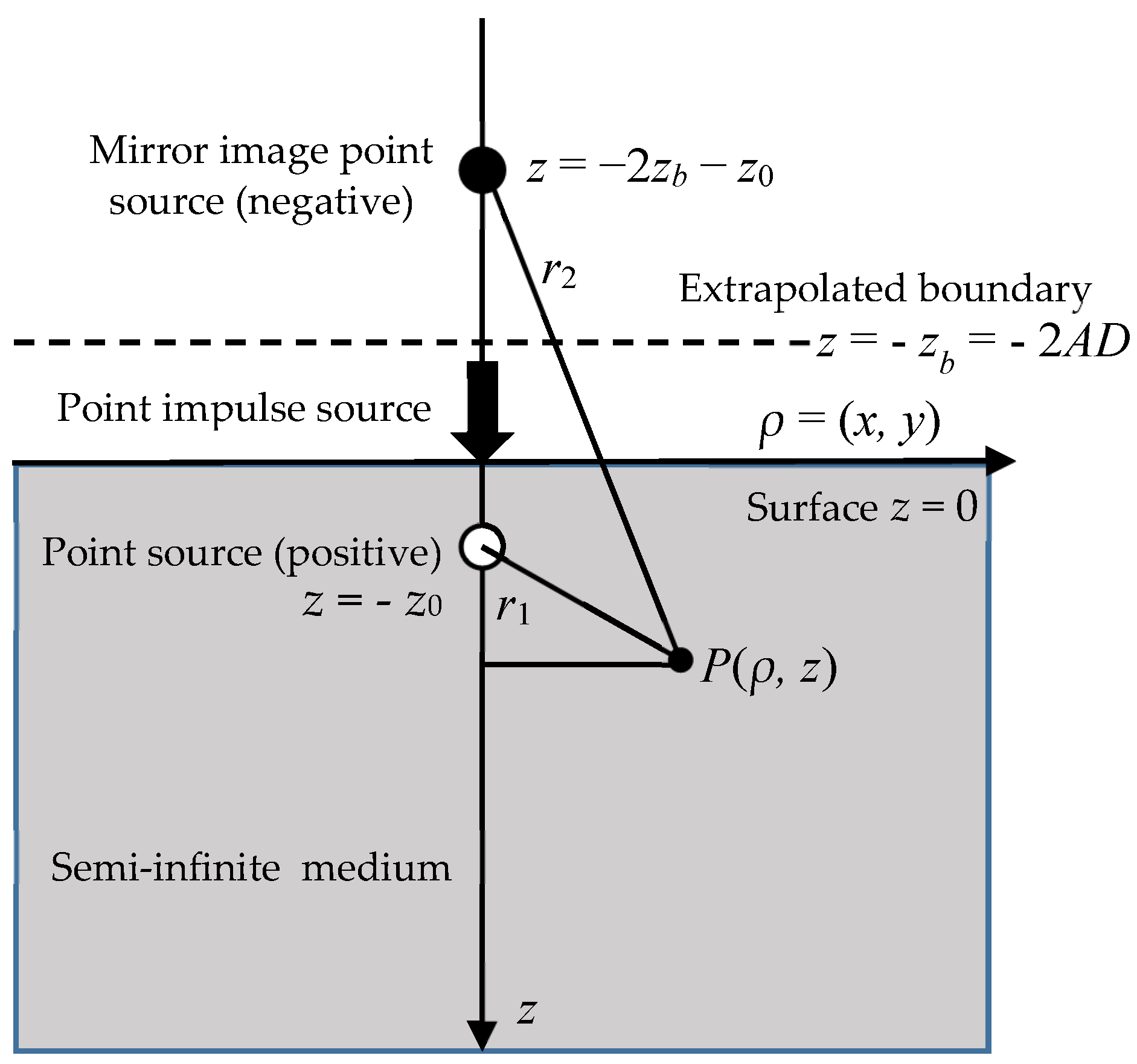
2.6. Boundary Condition for DE
2.7. Analytical Solutions for TD-DE
2.8. Monte Carlo Simulations
2.9. Time-Domain Sensitivity Functions of Optical Signals
2.10. Time-Resolved (TR) Mean Depth of Light Propagation
2.11. Time-Resolved (TR) Pathlength
2.12. Physiological Information and Optical Properties
3. Instruments for TD-NIRS
3.1. Overview of TD-NIRS Instruments
3.2. Time-Correlated Single Photon Counting (TCSPC) Technique
3.2.1. Principle, Components, Characteristics, and Operation of the TCSPC Technique
3.2.2. Single- and Dual-Channel TD-NIRS Systems Based on the TCSPC Technique
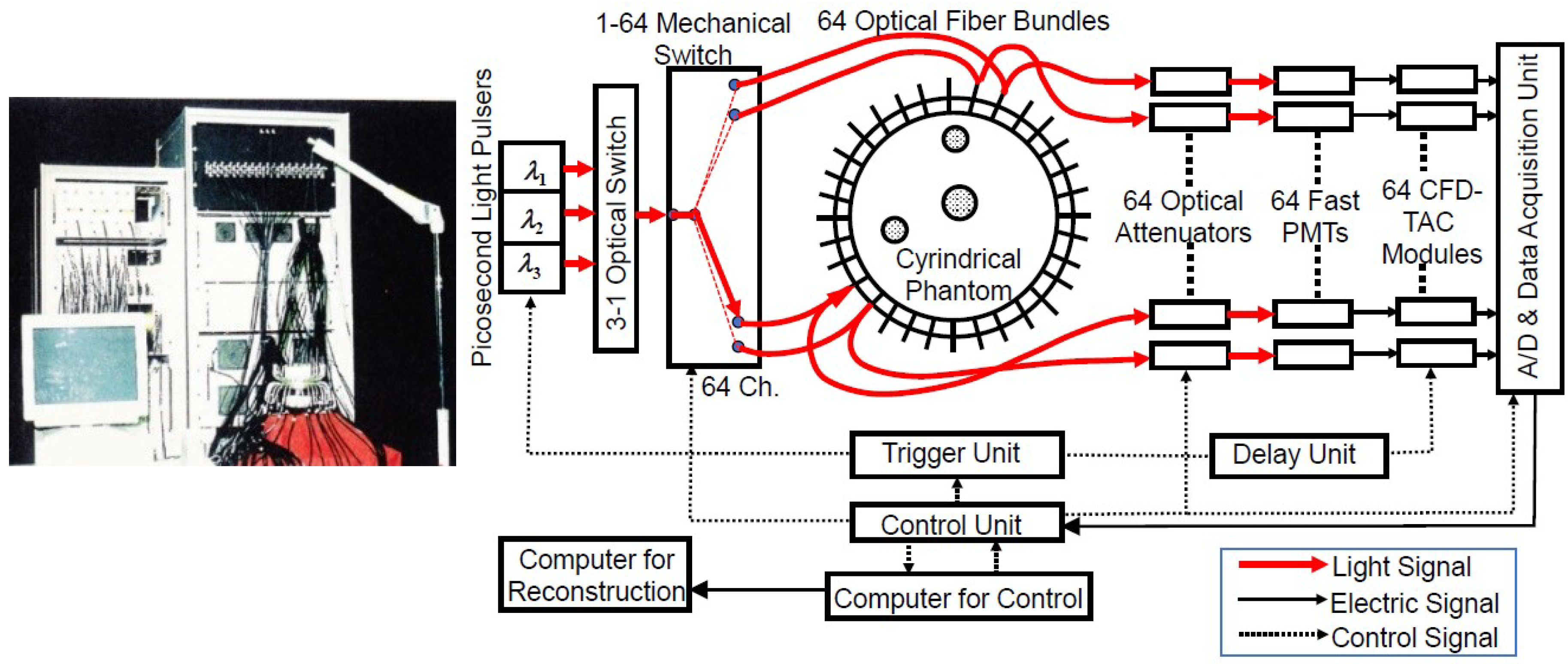
3.2.3. Multi-Channel TD-NIRS Systems Based on TCSPC for DOT
3.3. Other New TD-NIRS Systems
3.3.1. MONSTIR II
3.3.2. TD-DOT and TD-NIRS Systems for Optical Mammography
3.3.3. Compact TD-NIRS Systems Using MPPCs (or SiPMs)
3.3.4. TD-NIRS Systems Using SPADs
3.3.5. TD-NIRS Systems Using Pseudo-Random Bit Sequences
3.3.6. TD-NIRS Systems Using ICCD
3.3.7. Compact TD-NIRS System Incorporating Devices Used in Telecommunications
3.3.8. TD-NIRS Systems for Measurement of Water, Lipid, and Collagen Contents
3.4. Future Trend of TD-NIRS Instruments
4. Advanced Theories and Methods for TD-NIRS
4.1. Solving the TD-RTE and TD-DE Numerically
4.2. Analytical Solutions for the TD-RTE
4.3. The TD-RTE with Spatially Varying Refractive Index
4.4. Solutions of the Telegraph Equation (TE)
4.5. Perturbation Theory
4.5.1. Formulation of the TD-Perturbation Based on the TD-DE
4.5.2. First Order TD-Perturbation Using the TD-DE
4.5.3. Higher Order TD Perturbation Using the TD-DE
4.5.4. TD-Perturbation Using the TD-RTE
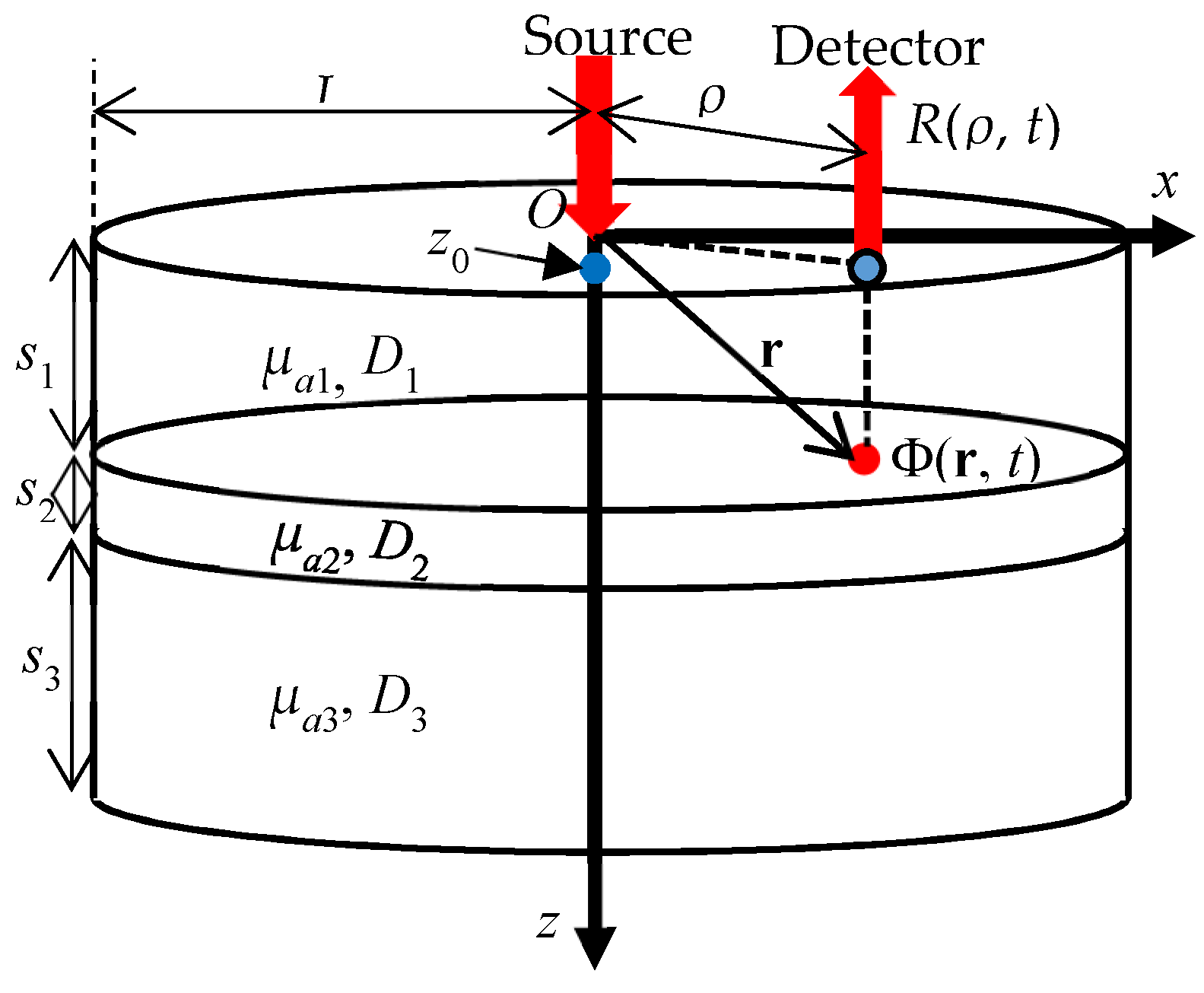
4.6. Multi-Layered Media
4.7. Advanced Monte Carlo Simulations
4.8. Hybrid RTE and DE Models
4.9. Anisotropic Light Propagation in TD
5. Studies toward Clinical Applications of TD-NIRS
5.1. Features of TD-Light Propagation Including Penetration Depth, Optical Pathlength, etc.
5.1.1. Light Propagation Based on the Microscopic Beer–Lambert Law
5.1.2. Mean-TOF, Partial Pathlength, and Sensitivity for the Head Model
5.1.3. Use of Null SD Distance
5.1.4. Measurement of Mean Pathlength
5.2. Measuring Optical Properties
5.2.1. Homogenous Semi-Infinite Media or Infinite Slab
5.2.2. Multi-Layered Media
5.3. Time-Domain Diffuse Optical Tomography (TD-DOT)
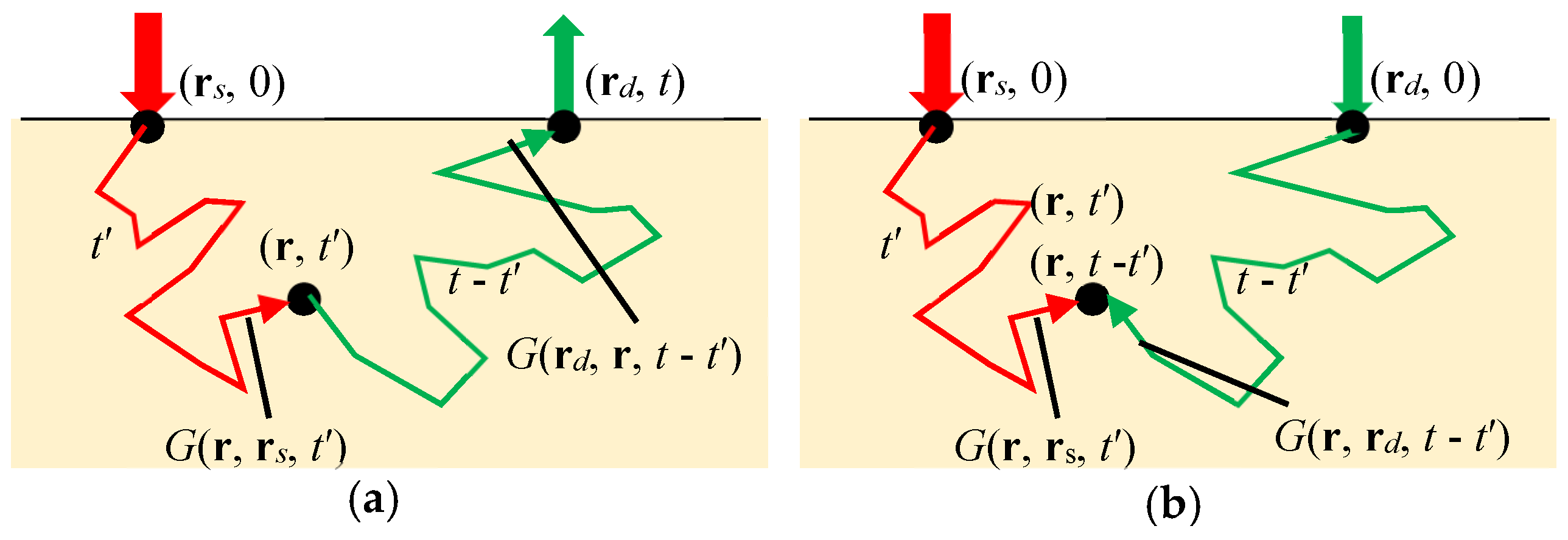
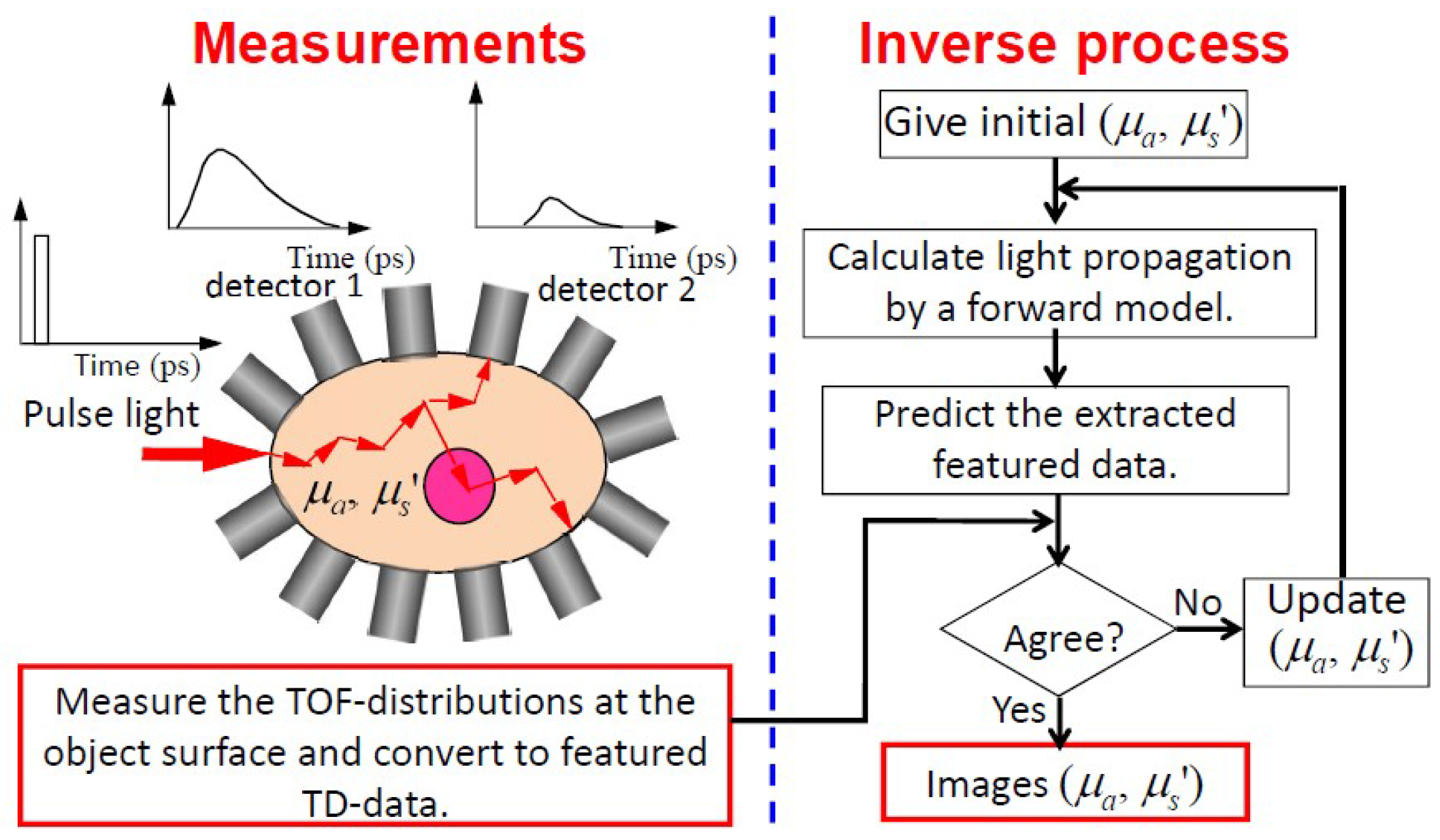
5.3.1. General Concept of TD-DOT
5.3.2. Modified Generalized Pulse Spectrum Technique for TD-DOT
5.3.3. Other Techniques for TD-DOT
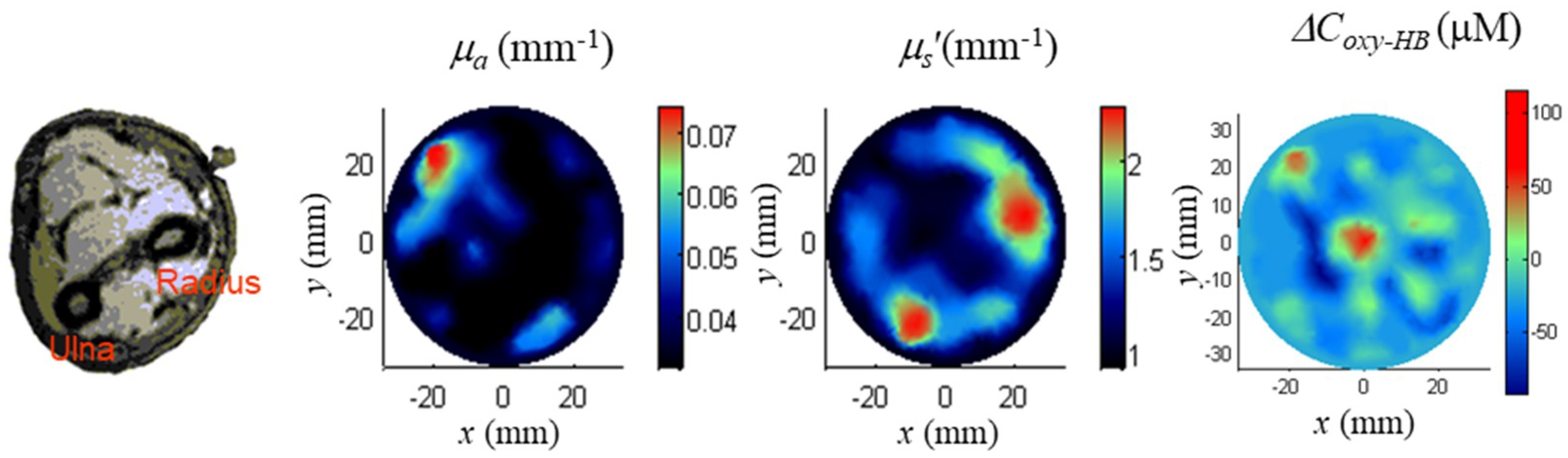
5.3.4. Brain Imaging
5.3.5. Breast Imaging
5.3.6. Muscle Imaging
5.4. Time-Domain Fluorescence Diffuse Optical Spectroscopy (TD-FS) and Tomography (TD-FT)
5.4.1. Fundamental Equations for TD-FS and TD-FT
5.4.2. Analytical Solutions of the Equations for TD-FS
5.4.3. Clinical Applications of TD-FS
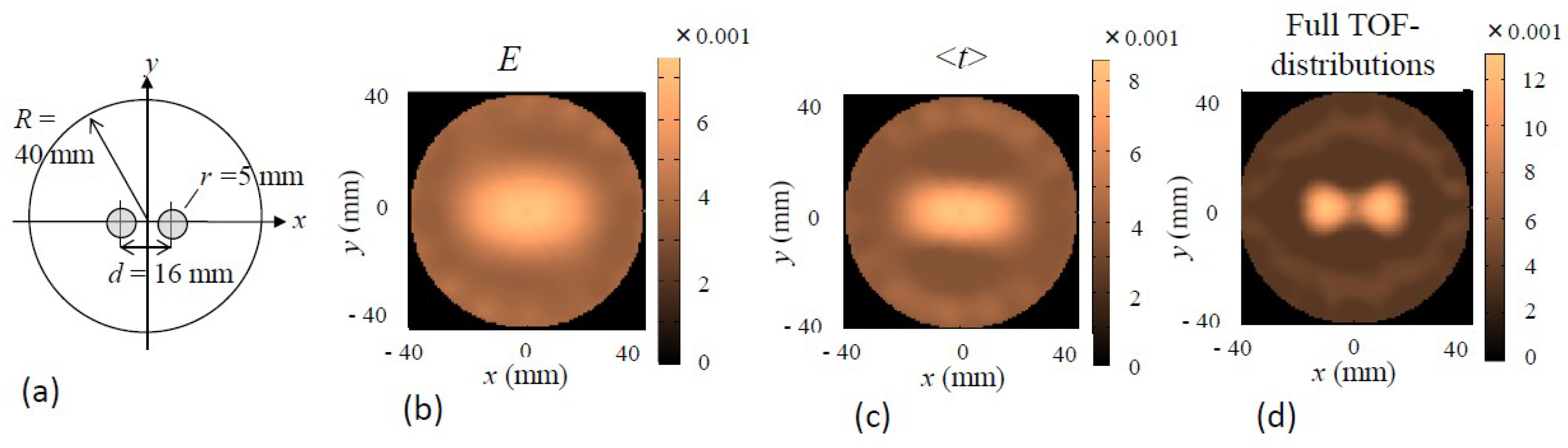
5.4.4. TD-FT Using Full TOF-Distributions and Effects of Featured Data Types
5.4.5. TD-FT Using Early Arriving Photons
5.4.6. TD-FT Using the GPST Algorithm
5.4.7. Total Light Approach in TD-FS and TD-FT
5.4.8. Transformation of TD-FT to FD-FT
5.4.9. Application of MC Method for TD-FT
6. Clinical Applications of Commercially Available TD-NIRS Systems by Japanese Researchers
6.1. Group from Kagawa Medical University
6.2. Group from Kagoshima University Hospital
6.3. Group from Nihon University School of Medicine
6.4. Group of Professor Hamaoka (Tokyo Medical University)
6.5. Other Groups in Japan
7. Summary
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Ferrari, M.; Quaresima, V. Near infrared brain and muscle oximetry: From the discovery to current applications. J. Near Infrared Spectrosc. 2012, 20, 1–14. [Google Scholar] [CrossRef]
- Torricelli, A.; Contini, D.; Pifferi, A.; Caffini, M.; Re, R.; Zucchelli, L.; Spinelli, L. Time domain functional NIRS imaging for human brain mapping. NeuroImage 2014, 85, 28–50. [Google Scholar] [CrossRef]
- Papadimitriou, K.I.; Dempsey, L.A.; Hebden, J.C.; Arridge, S.R.; Powell, S. A spread spectrum approach to time-domain near-infrared diffuse optical imaging using inexpensive optical transceiver modules. Biomed. Opt. Express 2018, 9, 2648–2663. [Google Scholar] [CrossRef] [PubMed]
- Arridge, S.R. Optical tomography in medical imaging. Inverse Prob. 1999, 15, R41–R93. [Google Scholar] [CrossRef]
- Duderstadt, J.J.; Hamilton, L.J. Nuclear Reactor Analysis; Wiley: New York, NY, USA, 1976; ISBN 978-0-471-22363-4. [Google Scholar]
- Kaltenbach, J.M.; Kascheke, M. Frequency- and time-domain modelling of light transport in random media. In Medical Optical Tomography: Functional Imaging and Monitoring; Muller, G.J., Ed.; SPIE Optical Engineering Press: Bellingham, WA, USA, 1993; pp. 65–86. ISBN 0819413801, 0819413798. [Google Scholar]
- Bigio, I.J.; Fantini, S. Quantitative Biomedical Optics; Theory, Methods, and Applications; Cambridge University Press: Cambridge, UK, 2016; ISBN 978-0-521-87656-8. [Google Scholar]
- Furutsu, K.; Yamada, Y. Diffusion approximation for a dissipative random media and the applications. Phys. Rev. E 1994, 50, 3634–3640. [Google Scholar]
- Tsuchiya, Y. Photon path distribution and optical responses of turbid media: Theoretical analysis based on the microscopic Beer–Lambert law. Phys. Med. Biol. 2001, 46, 2067–2084. [Google Scholar] [CrossRef] [PubMed]
- Graaff, R.; Ten Bosch, J.J. Diffusion coefficient in photon diffusion theory. Opt. Lett. 2000, 25, 43–45. [Google Scholar] [CrossRef] [PubMed]
- Aronson, R.; Corngold, N. Photon diffusion coefficient in an absorbing medium. J. Opt. Soc. Am. A 1999, 16, 1066–1071. [Google Scholar] [CrossRef]
- Elaloufi, R.; Carminati, R.; Greffet, J.-J. Definition of the diffusion coefficient in scattering and absorbing media. J. Opt. Soc. Am. A 2003, 20, 678–685. [Google Scholar] [CrossRef]
- Bassani, M.; Martelli, F.; Zaccanti, G.; Contini, D. Independence of the diffusion coefficient from absorption: Experimental and numerical evidence. Opt. Lett. 1997, 22, 853–855. [Google Scholar] [CrossRef]
- Nakai, T.; Nishimura, G.; Yamamoto, K. Tamura, Expression of the optical diffusion coefficient in high-absorption turbid media. Phys. Med. Biol. 1997, 42, 2541–2549. [Google Scholar] [CrossRef]
- Durduran, T.; Chance, B.; Yodh, A.G.; Boas, D.A. Does the photon diffusion coefficient depend on absorption? J. Opt. Soc. Am. A 1997, 14, 3358–3365. [Google Scholar] [CrossRef]
- Furutsu, K. Pulse wave scattering by an absorber and integrated attenuation in the diffusion approximation. J. Opt. Soc. Am. A 1997, 14, 267–274. [Google Scholar] [CrossRef]
- Pierrat, R.; Greffet, J.-J.; Carminati, R. Photon diffusion coefficient in scattering and absorbing media. J. Opt. Soc. Am. A 2006, 23, 1106–1110. [Google Scholar] [CrossRef]
- Patterson, M.S.; Chance, B.; Wilson, B.C. Time resolved reflectance and transmittance for the noninvasive measurement of tissue optical properties. Appl. Opt. 1989, 28, 2331–2336. [Google Scholar] [CrossRef] [PubMed]
- Arridge, S.R.; Cope, M.; Delpy, D.T. The theoretical basis for the determination of optical pathlengths in tissue: Temporal and frequency analysis. Phys. Med. Biol. 1992, 37, 1531–1560. [Google Scholar] [CrossRef]
- Kienle, A.; Foschum, F.; Hohmann, A. Light propagation in structural anisotropic media in the steady-state and time domains. Phys. Med. Biol. 2013, 58, 6205–6223. [Google Scholar] [CrossRef]
- Bonner, R.F.; Nossal, R.; Havlin, S.; Weiss, G.H. Model for photon migration in turbid biological media. J. Opt. Soc. Am. A 1987, 4, 423–432. [Google Scholar] [CrossRef]
- Wilson, B.C.; Adam, G. A Monte Carlo model for the absorption and flux distributions of light in tissue. Med. Phys. 1983, 10, 824–830. [Google Scholar] [CrossRef]
- Wang, L.; Jacques, S.L.; Zeng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Method. Prog. Biomed. 1992, 47, 131–146. [Google Scholar] [CrossRef]
- Monte Carlo Light Scattering Programs. Available online: https://omlc.org/software/mc/ (accessed on 26 August 2018).
- Boas, D.A.; Culver, J.P.; Stott, J.J.; Dunn, A.K. Three dimensional Monte Carlo code for photon migration through complex heterogeneous media including the adult human head. Opt. Express 2002, 10, 159–170. [Google Scholar] [CrossRef] [PubMed]
- Cui, W.; Wang, N.; Chance, B. Study of photon migration depths with time-resolved spectroscopy. Opt. Lett. 1991, 16, 1632–1634. [Google Scholar] [CrossRef] [PubMed]
- Schotland, J.C.; Haselgrove, J.C.; Leigh, J.S. Photon hitting density. Appl. Opt. 1993, 32, 448–453. [Google Scholar] [CrossRef] [PubMed]
- Arridge, S.R. Photon-measurement density functions. Part I: Analytical forms. Appl. Opt. 1995, 34, 7395–7409. [Google Scholar] [CrossRef] [PubMed]
- Patterson, M.S.; Andersson-Engels, S.; Wilson, B.C.; Osei, E.K. Absorption spectroscopy in tissue-simulating materials: A theoretical and experimental study of photon paths. Appl. Opt. 1995, 34, 22–30. [Google Scholar] [CrossRef]
- Sawosz, P.; Kacprzak, M.; Weigl, W.; Borowska-Solonynko, A.; Krajewski, P.; Zolek, N.; Ciszek, B.; Maniewski, R.; Liebert, A. Experimental estimation of the photons visiting probability profiles in time-resolved diffuse reflectance measurement. Phys. Med. Biol. 2012, 57, 7973–7981. [Google Scholar] [CrossRef]
- Choi, J.H.; Wolf, M.; Toronov, V.; Wolf, U.; Polzonetti, C.; Hueber, D.; Safonova, L.P.; Gupta, R.; Michalos, A.; Mantulin, W.; et al. Noninvasive determination of the optical properties of adult brain: Near-infrared spectroscopy approach. J. Biomed. Opt. 2004, 9, 221–229. [Google Scholar] [CrossRef]
- Martelli, F.; Del Bianco, S.; Ismaelli, A.; Zaccanti, G. Light Propagation through BIOLOGICAL Tissue and Other Diffusive Media; SPIE Press: Bellingham, WA, USA, 2010; ISBN 978-0-8194-7658-6. [Google Scholar]
- Brazy, J.E.; Lewis, D.V.; Mitnick, M.H.; Jöbsis vander Vliet, F.F. Noninvasive Monitoring of Cerebral Oxygenation in Preterm Infants: Preliminary Observations. Pediatrics 1985, 75, 217–225. [Google Scholar]
- Delpy, D.T.; Cope, M.; van der Zee, P.; Arridge, S.R.; Wray, S.; Wyatt, J. Estimation of optical pathlength through tissue from direct time of flight measurement. Phys. Med. Biol. 1988, 33, 1433–1442. [Google Scholar] [CrossRef]
- van der Zee, P.; Cope, M.; Arridge, S.R.; Essenpreis, M.; Potter, L.A.; Edwards, A.D.; Wyatt, J.S.; McCormick, D.C.; Roth, S.C.; Reynolds, E.O.R.; et al. Experimentally measured optical pathlengths for the adult head, calf and forearm and the head of the newborn infant as a function of inter optode spacing. Adv. Exp. Med. Biol. 1992, 316, 143–153. [Google Scholar]
- Chance, B.; Nioka, S.; Kent, J.; McCully, K.; Fountain, M.; Greenfeld, R.; Holtom, G. Time-resolved spectroscopy of hemoglobin and myoglobin in resting and ischemic muscle. Anal. Biochem. 1988, 174, 698–707. [Google Scholar] [CrossRef]
- O’connor, D.V.; Phillips, D. Time Correlated Single Photon Counting; Academic Press: London, UK, 1984; ISBN 9780323141444. [Google Scholar]
- Nomura, Y.; Hazeki, O.; Tamura, M. Exponential attenuation of light along nonlinear path through the biological model. Adv. Exp. Med. Biol. 1989, 248, 77–80. [Google Scholar] [PubMed]
- Cubeddu, R.; Pifferi, A.; Taroni, P.; Torricelli, A.; Valentini, G. Compact tissue oximeter based on dual-wavelength multichannel time-resolved reflectance. Appl. Opt. 1999, 38, 3670–3680. [Google Scholar] [CrossRef] [PubMed]
- Oda, M.; Yamashita, Y.; Nakano, T.; Suzuki, A.; Shimizu, K.; Hirano, I.; Shimomura, F.; Ohmae, E.; Suzuki, T.; Tsuchiya, Y. Near infrared time-resolved spectroscopy system for tissue oxygenation monitor. Proc. SPIE 1999, 3597, 611–617. [Google Scholar]
- Grosenick, D.; Wabnitz, H.; Rinneberg, H.H.; Moesta, K.T.; Schlag, P.M. Development of a time-domain optical mammograph and first in vivo applications. Appl. Opt. 1999, 38, 2927–2943. [Google Scholar] [CrossRef]
- Ida, T.; Iwata, Y. Correction for counting losses in X-ray diffractometry. J. Appl. Cryst. 2005, 38, 426–432. [Google Scholar] [CrossRef]
- Oda, M.; Ohmae-Yamaki, E.; Suzuki, H.; Suzuki, T.; Yamashita, Y. Tissue oxygenation measurements using near-infrared time-resolved spectroscopy. J. Jpn. Coll. Angiol. 2009, 49, 131–137. (In Japanese) [Google Scholar]
- Oda, M.; Yamashita, Y.; Nakano, T.; Suzuki, A.; Shimizu, K.; Hirano, I.; Shimomura, F.; Ohmae, E.; Suzuki, T.; Tsuchiya, Y. Near-infrared time-resolved spectroscopy system for tissue oxygenation monitor. Proc. SPIE 2000, 4160, 204–210. [Google Scholar]
- Eda, H.; Oda, I.; Ito, Y.; Wada, Y.; Oikawa, Y.; Tsunazawa, Y.; Takada, M.; Tsuchiya, Y.; Yamashita, Y.; Oda, M.; et al. Multichannel time-resolved optical tomographic imaging system. Rev. Sci. Instrum. 1999, 70, 3595–3602. [Google Scholar] [CrossRef]
- Fukuzawa, R.; Okawa, S.; Matsuhashi, S.; Kusaka, T.; Tanikawa, Y.; Hoshi, Y.; Gao, F.; Yamada, Y. Reduction of image artifacts induced by change in the optode coupling in time-resolved diffuse optical tomography. J. Biomed. Opt. 2011, 16, 116022. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, F.; Tanikawa, Y.; Yamada, Y. Time-resolved diffuse optical tomography and its application to in vitro and in vivo imaging. J. Biomed. Opt. 2007, 12, 062107. [Google Scholar] [CrossRef] [PubMed]
- Ueno, M.; Fukuzawa, R.; Okawa, S.; Yamada, Y.; Kusaka, T.; Nishida, T.; Isobe, K.; Tanikawa, Y.; Gao, F.; Sato, C.; et al. In vivo measurement of premature neonate head using diffuse optical tomography. Book of Abstracts, 3rd Asian and Pacific Rim Symp. In Proceedings of the Biophotonics (APBP2007), Cairns, Australia, 9–11 July 2007; pp. 43–44. [Google Scholar]
- Schmidt, F.E.W.; Fry, M.E.; Hillman, E.M.C.; Hebden, J.C.; Delpy, D.T. A 32-channel time-resolved instrument for medical optical tomography. Rev. Sci. Instrum. 2000, 71, 256–265. [Google Scholar] [CrossRef]
- Ueda, Y.; Yamanaka, T.; Yamashita, D.; Suzuki, T.; Ohmae, E.; Oda, M.; Yamashita, Y. Reflectance Diffuse Optical Tomography: Its Application to Human Brain Mapping. Jpn. J. Appl. Phys. 2005, 44, L1203–L1206. [Google Scholar] [CrossRef]
- Cooper, R.J.; Magee, E.; Everdell, N.; Magazov, S.; Varela, M.; Airantzis, D.; Gibson, A.P.; Hebden, J.C. MONSTIR II: A 32-channel, multispectral, time-resolved optical tomography system for neonatal brain imaging. Rev. Sci. Instrum. 2014, 85, 053105. [Google Scholar] [CrossRef] [PubMed]
- Ueda, Y.; Yoshimoto, K.; Ohmae, E.; Suzuki, T.; Yamanaka, T.; Yamashita, D.; Ogura, H.; Teruya, C.; Nasu, H.; Imi, E.; et al. Time-Resolved Optical Mammography and Its Preliminary Clinical Results. Tech. Cancer Res. Treat. 2011, 10, 393–401. [Google Scholar] [CrossRef]
- Yoshimoto, K.; Ohmae, E.; Yamashita, D.; Suzuki, H.; Homma, S.; Mimura, T.; Wada, H.; Suzuki, T.; Yoshizawa, N.; Nasu, H.; et al. Development of time-resolved reflectance diffuse optical tomography for breast cancer monitoring. Proc. Spie 2017, 10059, 100590M. [Google Scholar]
- Taroni, P.; Paganoni, A.M.; Ieva, F.; Pifferi, A.; Quarto, G.; Abbate, F.; Cassano, E.; Cubeddu, R. Non-invasive optical estimate of tissue composition to differentiate malignant from benign breast lesions: A pilot study. Sci. Rep. 2016, 7, 40683. [Google Scholar] [CrossRef]
- Fujisaka, S.; Ozaki, T.; Suzuki, T.; Kamada, T.; Kitazawa, K.; Nishizawa, M.; Takahashi, A.; Suzuki, S. A clinical tissue oximeter using NIR time-resolved spectroscopy. Adv. Exp. Med. Biol. 2016, 876, 427–433. [Google Scholar]
- Buttafava, M.; Martinenghi, E.; Tamborini, D.; Contini, D.; Dalla Mora, A.; Renna, M.; Torricelli, A.; Pifferi, A.; Zappa, F.; Tosi, A. A Compact Two-Wavelength Time-Domain NIRS System Based on SiPM and Pulsed Diode Lasers. IEEE Photonics J. 2016, 9, 7800114. [Google Scholar] [CrossRef]
- Re, R.; Martinenghi, E.; Dalla Mora, A.; Contini, D.; Pifferi, A.; Torricellia, A. Probe-hosted silicon photomultipliers for time-domain functional near-infrared spectroscopy: Phantom and in vivo tests. Neurophotonics 2016, 3, 045004. [Google Scholar] [CrossRef]
- Puszka, A.; Di Sieno, L.; Dalla Mora, A.; Pifferi, A.; Contini, D.; Boso, G.; Tosi, A.; Hervé, L.; Planat-Chrétien, A.; Koenig, A.; et al. Time-resolved diffuse optical tomography using fast-gated single-photon avalanche diodes. Biomed. Opt. Express 2013, 4, 1351–1365. [Google Scholar] [CrossRef]
- Dalla Mora, A.; Contini, D.; Arridge, S.; Martelli, F.; Tosi, A.; Boso, G.; Farina, A.; Durduran, T.; Martinenghi, E.; Torricelli, A.; et al. Towards next-generation time-domain diffuse optics for extreme depth penetration and sensitivity. Biomed. Opt. Express 2015, 6, 1749–1760. [Google Scholar] [CrossRef] [PubMed]
- Di Sieno, L.; Wabnitz, H.; Pifferi, A.; Mazurenka, M.; Hoshi, Y.; Dalla Mora, A.; Contini, D.; Boso, G.; Becker, W.; Martelli, F.; et al. Characterization of a time-resolved non-contact scanning diffuse optical imaging system exploiting fast-gated single-photon avalanche diode detection. Rev. Sci. Instrum. 2016, 87, 035118. [Google Scholar] [CrossRef]
- Sinha, L.; Brankov, J.G.; Tichauer, K.M. Enhanced detection of early photons in time-domain optical imaging by running in the “dead-time” regime. Opt. Lett. 2016, 41, 3225–3228. [Google Scholar] [CrossRef] [PubMed]
- Kalyanov, A.; Jiang, J.-J.; Lindner, S.; Ahnen, L.; di Costanzo, A.; Mata Pavia, J.; Sanchez Majos, S.; Wolf, M. Time Domain Near-Infrared Optical Tomography with Time-of-Flight SPAD Camera: The New Generation. In Proceedings of the Optical Tomography and Spectroscopy, Biophotonics Congress: Biomedical Optics Congress 2018, OSA, FL, USA, 3–6 April 2018. [Google Scholar]
- Chen, N.G.; Zhu, Q. Time-resolved diffusive optical imaging using pseudo-random bit sequences. Opt. Express 2003, 11, 3445–3454. [Google Scholar] [CrossRef] [PubMed]
- Mo, W.R.; Chen, N.G. Fast time-domain diffuse optical tomography using pseudorandom bit sequences. Opt. Express 2008, 16, 13643–13650. [Google Scholar] [CrossRef]
- Selb, J.; Stott, J.J.; Franceschini, M.A.; Sorensen, A.G.; Boas, D.A. Improved sensitivity to cerebral hemodynamics during brain activation with a time-gated optical system: Analytical model and experimental validation. J. Biomed. Opt. 2005, 10, 011013. [Google Scholar] [CrossRef]
- Zhao, Q.; Spinelli, L.; Bassi, A.; Valentini, G.; Contini, D.; Torricelli, A.; Cubeddu, R.; Zaccanti, G.; Martelli, F.; Pifferi, A. Functional tomography using a time-gated ICCD camera. Biomed. Opt. Express 2011, 2, 705–716. [Google Scholar] [CrossRef] [PubMed]
- Lange, F.; Peyrin, F.; Montcel, B. Broadband time-resolved multi-channel functional near-infrared spectroscopy system to monitor in vivo physiological changes of human brain activity. Appl. Opt. 2018, 57, 6417–6429. [Google Scholar] [CrossRef] [PubMed]
- Ohmae, E.; Yoshizawa, N.; Yoshimoto, K.; Hayashi, M.; Wada, H.; Mimura, T.; Suzuki, H.; Homma, S.; Suzuki, N.; Ogura, H.; et al. Stable tissue-simulating phantoms with various water and lipid contents for diffuse optical spectroscopy. Biomed. Opt. Exp. 2018, 9, 5792–5808. [Google Scholar] [CrossRef]
- Schweiger, M.; Arridge, S.R.; Delpy, D.T. Application of the Finite-Element Method for the Forward and Inverse Models in Optical Tomography. J. Math. Imag. Vis. 1993, 3, 263–283. [Google Scholar] [CrossRef]
- Lewis, E.E.; Miller, W.F., Jr. Computational Methods of Neutron Transport; American Nuclear Society, Inc.: La Grande Park, IL, USA, 1993; ISBN 0-89448-452-4. [Google Scholar]
- Das, C.; Trivedi, A.; Mitra, K.; Vo-Dinh, T. Experimental and numerical analysis of short-pulse laser interaction with tissue phantoms containing inhomogeneities. Appl. Opt. 2003, 42, 5173–5180. [Google Scholar] [CrossRef] [PubMed]
- Pal, G.; Basu, S.; Mitra, K.; Vo-Dinh, T. Time-resolved optical tomography using short-pulse laser for tumor detection. Appl. Opt. 2006, 45, 6270–6282. [Google Scholar] [CrossRef] [PubMed]
- Fujii, H.; Yamada, Y.; Kobayashi, K.; Watanabe, M.; Hoshi, Y. Modeling of light propagation in the human neck for diagnoses of thyroid cancers by diffuse optical tomography. Int. J. Numer. Meth. Biomed. Eng. 2017, 33, e2826. [Google Scholar] [CrossRef] [PubMed]
- Asllanaj, F.; Fumeron, S. Applying a new computational method for biological tissue optics based on the time-dependent two-dimensional radiative transfer equation. J. Biomed. Opt. 2012, 17, 075007. [Google Scholar]
- Fujii, H.; Yamada, Y.; Chiba, G.; Hoshi, Y.; Kobayashi, K.; Watanabe, M. Accurate and efficient computation of the 3D radiative transfer equation in highly forward-peaked scattering media using a renormalization approach. J. Comput. Phys. 2018, 374, 591–604. [Google Scholar] [CrossRef]
- Paasschens, J.C.J. Solution of the time-dependent Boltzmann equation. Phys. Rev. E 1997, 56, 1135–1141. [Google Scholar] [CrossRef]
- Martelli, F.; Sassaroli, A.; Pifferi, A.; Torricelli, A.; Spinelli, L.; Zaccanti, G. Heuristic Green’s function of the time dependent radiative transfer equation for a semi-infinite medium. Opt Express 2007, 26, 18168–18175. [Google Scholar] [CrossRef]
- Liemert, A.; Kienle, A. Infinite space Green’s function of the time-dependent radiative transfer equation. Biomed. Opt. Express 2012, 3, 543–551. [Google Scholar] [CrossRef]
- Liemert, A.; Kienle, A. Green’s function of the time-dependent radiative transport equation in terms of rotated spherical harmonics. Phys. Rev. E 2012, 86, 036603. [Google Scholar] [CrossRef]
- Simon, E.; Foschum, F.; Kienle, A. Hybrid Green’s function of the time-dependent radiative transfer equation for anisotropically scattering semi-infinite media. J. Biomed. Opt. 2013, 18, 015001. [Google Scholar] [CrossRef] [PubMed]
- Ferwerda, H.A. The radiative transfer equation for scattering media with a spatially varying refractive index. J. Opt. A Pure Appl. Opt. 1999, 1, L1–L2. [Google Scholar] [CrossRef]
- Khan, T.; Jiang, H. A new diffusion approximation to the radiative transfer equation for scattering media with spatially varying refractive indices. J. Opt. A Pure Appl. Opt. 2003, 5, 137–141. [Google Scholar] [CrossRef]
- Tualle, J.-M.; Tinet, E. Derivation of the radiative transfer equation for scattering media with a spatially varying refractive index. Opt. Commun. 2003, 228, 33–38. [Google Scholar] [CrossRef]
- Kumar, S.; Mitra, K.; Yamada, Y. Hyperbolic damped-wave models for transient light-pulse propagation in scattering media. Appl. Opt. 1996, 36, 3372–3378. [Google Scholar] [CrossRef] [PubMed]
- Durian, D.J.; Rudnick, J. Photon migration at short times and distances and in cases of strong absorption. J. Opt. Soc. Am. A 1997, 14, 235–245. [Google Scholar] [CrossRef]
- Polonsky, I.N.; Box, M.A. General perturbation technique for the calculation of radiative effects in scattering and absorbing media. J. Opt. Soc. Am. A 2002, 19, 2281–2292. [Google Scholar] [CrossRef]
- Hebden, J.C.; Arridge, S.R. Imaging through scattering media by the use of an analytical model of perturbation amplitudes in the time domain. Appl. Opt. 1996, 35, 6788–6796. [Google Scholar] [CrossRef] [PubMed]
- Morin, M.; Verreault, S.; Mailloux, A.; Fre’chette, J.; Chatigny, S.; Painchaud, Y.; Beaudry, P. Inclusion characterization in a scattering slab with time-resolved transmittance measurements: Perturbation analysis. Appl. Opt. 2000, 39, 2840–2852. [Google Scholar] [CrossRef]
- Carraresi, S.; Mohamed Shatir, T.S.; Martelli, F.; Zaccanti, G. Accuracy of a perturbation model to predict the effect of scattering and absorbing inhomogeneities on photon migration. Appl. Opt. 2001, 40, 4622–4632. [Google Scholar] [CrossRef]
- Spinelli, L.; Torricelli, A.; Pifferi, A.; Taroni, P.; Cubeddu, R. Experimental test of a perturbation model for time-resolved imaging in diffusive media. Appl. Opt. 2003, 42, 3145–3153. [Google Scholar] [CrossRef] [PubMed]
- Martelli, F.; Del Bianco, S.; Zaccanti, G. Perturbation model for light propagation through diffusive layered media. Phys. Med. Biol. 2005, 50, 2159–2166. [Google Scholar] [CrossRef] [PubMed]
- Wassermann, B. Limits of high-order perturbation theory in time-domain optical mammography. Phys. Rev. E 2006, 74, 031908. [Google Scholar] [CrossRef]
- Grosenick, D.; Kummrow, A.; Macdonald, R.; Schlag, P.M.; Rinneberg, H. Evaluation of higher-order time-domain perturbation theory of photon diffusion on breast-equivalent phantoms and optical mammograms. Phys. Rev. E 2007, 76, 061908. [Google Scholar] [CrossRef] [PubMed]
- Sassaroli, A.; Martelli, F.; Fantini, S. Perturbation theory for the diffusion equation by use of the moments of the generalized temporal point-spread function. I. Theory. J. Opt. Soc. Am. A 2006, 23, 2105–2118. [Google Scholar] [CrossRef]
- Sassaroli, A.; Martelli, F.; Fantini, S. Perturbation theory for the diffusion equation by use of the moments of the generalized temporal point-spread function. III. Frequency-domain and time-domain results. J. Opt. Soc. Am. A 2010, 27, 1723–1742. [Google Scholar] [CrossRef]
- Martelli, F.; Sassaroli, A.; Del Bianco, S.; Yamada, Y.; Zaccanti, G. Solution of the time-dependent diffusion equation for layered diffusive media by the eigenfunction method. Phys. Rev. E 2003, 67, 056623. [Google Scholar] [CrossRef]
- Martelli, F.; Sassaroli, A.; Del Bianco, S.; Zaccanti, G. Effect of the refractive index mismatch on light propagation through diffusive layered media. Phys. Rev. E 2004, 70, 011907. [Google Scholar] [CrossRef]
- Kienle, A.; Glanzmann, T.; Wagnières, G.; van den Bergh, H. Investigation of two-layered turbid media with time-resolved reflectance. Appl. Opt. 1998, 37, 6852–6862. [Google Scholar] [CrossRef]
- Tualle, J.-M.; Prat, J.; Tinet, E.; Avrillier, S. Real-space Green’s function calculation for the solution of the diffusion equation in stratified turbid media. J. Opt. Soc. Am. A 2000, 17, 2046–2055. [Google Scholar] [CrossRef]
- Tualle, J.-M.; Nghiem, H.L.; Ettori, D.; Sablong, R.; Tinet, E.; Avrillier, S. Asymptotic behavior and inverse problem in layered scattering media. J. Opt. Soc. Am. A 2004, 21, 24–34. [Google Scholar] [CrossRef]
- Liemert, A.; Kienle, A. Light diffusion in N-layered turbid media: Frequency and time domains. J. Biomed. Opt. 2010, 15, 025002. [Google Scholar] [CrossRef] [PubMed]
- Martelli, F.; Sassaroli, A.; Yamada, Y.; Zaccanti, G. Analytical approximate solutions of the time-domain diffusion equation in layered slabs. J. Opt. Soc. Am. A 2002, 19, 71–80. [Google Scholar] [CrossRef]
- Martelli, F.; Sassaroli, A.; Del Bianco, S.; Zaccanti, G. Solution of the time-dependent diffusion equation for a three-layer medium: Application to study photon migration through a simplified adult head model. Phys. Med. Biol. 2007, 52, 2827–2843. [Google Scholar] [CrossRef]
- Barnett, A.H. A fast numerical method for time-resolved photon diffusion in general stratified turbid media. J. Comput. Phys. 2004, 201, 771–797. [Google Scholar] [CrossRef]
- Kienle, A.; Patterson, M.S. Determination of the optical properties of turbid media from a single Monte Carlo simulation. Phys. Med. Biol. 1996, 41, 2221–2227. [Google Scholar] [CrossRef] [PubMed]
- Alerstam, E.; Andersson-Engels, S.; Svensson, T. White Monte Carlo for time-resolved photon migration. J. Biomed. Opt. 2008, 13, 041304. [Google Scholar] [CrossRef]
- Sassaroli, A.; Blumetti, C.; Martelli, F.; Alianelli, L.; Contini, D.; Ismaelli, A.; Zaccanti, G. Monte Carlo procedure for investigating light propagation and imaging of highly scattering media. Appl. Opt. 1998, 37, 7392–7400. [Google Scholar] [CrossRef]
- Hayakawa, C.K.; Spanier, J.; Bevilacqua, F.; Dunn, A.K.; You, J.S.; Tromberg, B.J.; Venugopalan, V. Perturbation Monte Carlo methods to solve inverse photon migration problems in heterogeneous tissues. Opt. Lett. 2001, 26, 1335–1337. [Google Scholar] [CrossRef]
- Sassaroli, A. Fast perturbation Monte Carlo method for photon migration in heterogeneous turbid media. Opt. Lett. 2011, 36, 2095–2097. [Google Scholar] [CrossRef]
- Kumar, Y.P.; Vasu, R.M. Reconstruction of optical properties of low-scattering tissue using derivative estimated through perturbation Monte-Carlo method. J. Biomed. Opt. 2004, 9, 1002–1012. [Google Scholar] [CrossRef]
- Chen, J.; Intes, X. Time-gated perturbation Monte Carlo for whole body functional imaging in small animals. Opt. Express 2009, 17, 19566–19570. [Google Scholar] [CrossRef]
- Yao, R.; Intes, X.; Fang, Q.Q. Direct approach to compute Jacobians for diffuse optical tomography using perturbation Monte Carlo-based photon “replay”. Biomed. Opt. Express 2018, 9, 4588–4602. [Google Scholar] [CrossRef]
- Fang, Q.Q.; Boas, D.A. Monte Carlo simulation of photon migration in 3D turbid media accelerated by graphics processing units. Opt. Express 2009, 17, 20178–20190. [Google Scholar] [CrossRef]
- Zoller, C.J.; Hohmann, A.; Foschum, F.; Geiger, S.; Geiger, M.; Ertl, T.P.; Kienle, A. Parallelized Monte Carlo software to efficiently simulate the light propagation in arbitrarily shaped objects and aligned scattering media. J. Biomed. Opt. 2018, 23, 065004. [Google Scholar]
- Voit, F.; Hohmann, A.; Schäfer, J.; Kienle, A. Multiple scattering of polarized light: Comparison of Maxwell theory and radiative transfer theory. J. Biomed. Opt. 2012, 17, 045003. [Google Scholar] [CrossRef]
- Jia, M.; Zhao, H.; Li, J.; Liu, L.; Zhang, L.; Jiang, J.; Gao, F. Coupling between radiative transport and diffusion approximation for enhanced near-field photon-migration modeling based on transient photon kinetics. J. Biomed. Opt. 2016, 21, 050501. [Google Scholar] [CrossRef]
- Lehtikangas, O.; Tarvainen, T. Hybrid forward-peaked-scattering diffusion approximations for light propagation in turbid media with low-scattering regions. J. Quant. Spectrosc. Radiat. Transf. 2013, 116, 132–144. [Google Scholar] [CrossRef]
- Gorpas, D.; Andersson-Engels, S. Evaluation of a radiative transfer equation and diffusion approximation hybrid forward solver for fluorescence molecular imaging. J. Biomed. Opt. 2012, 17, 126010. [Google Scholar] [CrossRef]
- Fujii, H.; Okawa, S.; Yamada, Y.; Hoshi, Y. Hybrid model of light propagation in random media based on the time-dependent radiative transfer and diffusion equations. J. Quant. Spectrosc. Radiat. Transf. 2014, 147, 145–154. [Google Scholar] [CrossRef]
- Roger, M.; Caliot, C.; Crouseilles, N.; Coelho, P.J. A hybrid transport-diffusion model for radiative transfer in absorbing and scattering media. J. Comput. Phys. 2014, 275, 346–362. [Google Scholar] [CrossRef]
- Coelho, P.J.; Crouseilles, N.; Pereira, P.; Roger, M. Multi-scale methods for the solution of the radiative transfer equation. J. Quant. Spectrosc. Radiat. Transf. 2015, 172, 36–49. [Google Scholar] [CrossRef]
- Nickell, S.; Hermann, M.; Essenpreis, M.; Farrell, T.J.; Krämer, U.; Patterson, M.S. Anisotropy of light propagation in human skin. Phys. Med. Biol. 2000, 45, 2873–2886. [Google Scholar] [CrossRef] [PubMed]
- Heino, J.; Arridge, S.; Sikora, J.; Somersalo, E. Anisotropic effects in highly scattering media. Phys. Rev. E 2003, 68, 031908. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, Y.; Yamada, Y.; Tamura, M.; Nomura, Y. Monte Carlo simulation of light transmission through living tissues. Appl. Opt. 1991, 30, 4515–4520. [Google Scholar] [CrossRef] [PubMed]
- Nomura, Y.; Hazeki, O.; Tamura, M. Relationship between time-resolved and non-time-resolved Beer–Lambert law in turbid media. Phys. Med. Biol. 1997, 42, 1009–1022. [Google Scholar] [CrossRef]
- Okada, E.; Firbank, M.; Schweiger, M.; Arridge, S.R.; Cope, M.; Delpy, D.T. Theoretical and experimental investigation of near-infrared light propagation in a model of the adult head. Appl. Opt. 1997, 36, 21–31. [Google Scholar] [CrossRef]
- Fukui, Y.; Ajichi, Y.; Okada, E. Monte Carlo prediction of near-infrared light propagation in realistic adult and neonatal head models. Appl. Opt. 2003, 42, 2881–2887. [Google Scholar] [CrossRef]
- Firbank, M.; Okada, E.; Delpy, D.T. A Theoretical Study of the Signal Contribution of Regions of the Adult Head to Near-Infrared Spectroscopy Studies of Visual Evoked Responses. NeuroImage 1998, 8, 69–78. [Google Scholar] [CrossRef]
- Steinbrink, J.; Wabnitz, H.; Obrig, H.; Villringer, A.; Rinneberg, H. Determining changes in NIR absorption using a layered model of the human head. Phys. Med. Biol. 2001, 46, 879–896. [Google Scholar] [CrossRef]
- Del Bianco, S.; Martelli, F.; Zaccanti, G. Penetration depth of light re-emitted by a diffusive medium: Theoretical and experimental investigation. Phys. Med. Biol. 2002, 47, 4131–4144. [Google Scholar] [CrossRef] [PubMed]
- Torricelli, A.; Pifferi, A.; Spinelli, L.; Cubeddu, R. Time-Resolved Reflectance at Null Source-Detector Separation: Improving Contrast and Resolution in Diffuse Optical Imaging. Phys. Rev. Lett. 2005, 95, 078101. [Google Scholar] [CrossRef]
- Spinelli, L.; Martelli, F.; Del Bianco, S.; Pifferi, A.; Torricelli, A.; Cubeddu, R.; Zaccanti, G. Absorption and scattering perturbations in homogeneous and layered diffusive media probed by time-resolved reflectance at null source-detector separation. Phys. Rev. E 2006, 74, 021919. [Google Scholar] [CrossRef] [PubMed]
- Mazurenka, M.; Jelzow, A.; Wabnitz, H.; Contini, D.; Spinelli, L.; Pifferi, A.; Cubeddu, R.; Dalla Mora, A.; Tosi, A.; Zappa, F.; et al. Non-contact time-resolved diffuse reflectance imaging at null source-detector separation. Opt. Express 2012, 20, 283–290. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Tanikawa, Y.; Gao, F.; Onodera, Y.; Sassaroli, A.; Tanaka, K.; Yamada, Y. Maps of optical differential pathlength factor of human adult forehead, somatosensory motor, occipital regions at multi-wavelengths in NIR. Phys. Med. Biol. 2002, 47, 2075–2093. [Google Scholar] [CrossRef]
- Bonnéry, C.; Leclerc, P.-O.; Desjardins, M.; Hoge, R.; Bherer, L.; Pouliot, P.; Lesage, F. Changes in diffusion path length with old age in diffuse optical tomography. J. Biomed. Opt. 2012, 17, 056002. [Google Scholar] [CrossRef]
- Jacques, S.L. Time-Resolved Reflectance Spectroscopy in Turbid Tissues. IEEE Trans. Biomed. Eng. 1989, 36, 1155–1161. [Google Scholar] [CrossRef]
- Sassarol1, A.; Martelli, F.; Tanikawa, Y.; Tanaka, K.; Araki, R.; Onodera, Y.; Yamada, Y. Time-Resolved Measurements of in vivo Optical Properties of Piglet Brain. Opt. Rev. 2000, 7, 420–425. [Google Scholar] [CrossRef]
- Comelli, D.; Bassi, A.; Pifferi, A.; Taroni, P.; Torricelli, A.; Cubeddu, R.; Martelli, F.; Zaccanti, G. In vivo time-resolved reflectance spectroscopy of the human forehead. Appl. Opt. 2007, 46, 1717–1725. [Google Scholar] [CrossRef]
- Quarto, G.; Spinelli, L.; Pifferi, A.; Torricelli, A.; Cubeddu, R.; Abbate, F.; Balestreri, N.; Menna, S.; Cassano, E.; Taroni, P. Estimate of tissue composition in malignant and benign breast lesions by time-domain optical mammography. Biomed. Opt. Express 2014, 5, 3684–3698. [Google Scholar] [CrossRef]
- Guggenheim, J.A.; Bargigia, I.; Farina, A.; Pifferi, A.; Dehghani, H. Time resolved diffuse optical spectroscopy with geometrically accurate models for bulk parameter recovery. Biomed. Opt. Express 2016, 7, 3784–3794. [Google Scholar] [CrossRef] [PubMed]
- Kienle, A.; Glanzmann, T. In vivo determination of the optical properties of muscle with time-resolved reflectance using a layered model. Phys. Med. Biol. 1999, 44, 2689–2702. [Google Scholar] [CrossRef] [PubMed]
- Gagnon, L.; Gauthier, C.; Hoge, R.D.; Lesage, F.; Selb, J.; Boas, D.A. Double-layer estimation of intra- and extracerebral hemoglobin concentration with a time-resolved system. J. Biomed. Opt. 2008, 13, 054019. [Google Scholar] [CrossRef] [PubMed]
- Martelli, F.; Del Bianco, S.; Zaccanti, G. Procedure for retrieving the optical properties of a two-layered medium from time-resolved reflectance measurements. Opt. Lett. 2003, 28, 1236–1238. [Google Scholar] [CrossRef] [PubMed]
- Martelli, F.; Del Bianco, S.; Zaccanti, G.; Pifferi, A.; Torricelli, A.; Bassi, A.; Taroni, P.; Cubeddu, R. Phantom validation and in vivo application of an inversion procedure for retrieving the optical properties of diffusive layered media from time-resolved reflectance measurements. Opt. Lett. 2004, 29, 2037–2039. [Google Scholar] [CrossRef]
- Sato, C.; Shimada, M.; Yamada, Y.; Hoshi, Y. Extraction of depth-dependent signals from time-resolved reflectance in layered turbid media. J. Biomed. Opt. 2005, 10, 064008. [Google Scholar] [CrossRef]
- Shimada, M.; Hoshi, Y.; Yamada, Y. Simple algorithm for the measurement of absorption coefficients of a two-layered medium by spatially resolved and time-resolved reflectance. Appl. Opt. 2005, 44, 7554–7563. [Google Scholar] [CrossRef]
- Shimada, M.; Sato, C.; Hoshi, Y.; Yamada, Y. Estimation of the absorption coefficients of two-layered media by a simple method using spatially and time-resolved reflectances. Phys. Med. Biol. 2009, 54, 5057–5071. [Google Scholar] [CrossRef]
- Hoshi, Y.; Shimada, M.; Sato, C.; Iguchi, Y. Reevaluation of near-infrared light propagation in the adult human head: Implications for functional near-infrared spectroscopy. J. Biomed. Opt. 2005, 10, 064032. [Google Scholar] [CrossRef]
- Jäger, M.; Kienle, A. Non-invasive determination of the absorption coefficient of the brain from time-resolved reflectance using a neural network. Phys. Med. Biol. 2011, 56, N139–N144. [Google Scholar] [CrossRef]
- Martelli, F.; Del Bianco, S.; Zaccanti, G. Retrieval procedure for time-resolved near-infrared tissue spectroscopy based on the optimal estimation method. Phys. Med. Biol. 2012, 57, 2915–2929. [Google Scholar] [CrossRef]
- Martelli, F.; Del Bianco, S.; Spinelli, L.; Cavalieri, S.; Di Ninni, P.; Binzoni, T.; Jelzow, A.; Macdonald, R.; Wabnitz, H. Optimal estimation reconstruction of the optical properties of a two-layered tissue phantom from time-resolved single-distance measurements. J. Biomed. Opt. 2015, 20, 115001. [Google Scholar] [CrossRef] [PubMed]
- Zucchelli, L.; Contini, D.; Re, R.; Torricelli, A.; Spinelli, L. Method for the discrimination of superficial and deep absorption variations by time domain fNIRS. Biomed. Opt. Express 2013, 4, 2893–2910. [Google Scholar] [CrossRef]
- Re, R.; Contini, D.; Zucchelli, L.; Torricelli, A.; Spinelli, L. Effect of a thin superficial layer on the estimate of hemodynamic changes in a two-layer medium by time domain NIRS. Biomed. Opt. Express 2016, 7, 264–277. [Google Scholar] [CrossRef] [PubMed]
- Farina, A.; Torricelli, A.; Bargigia, I.; Spinelli, L.; Cubeddu, R.; Foschum, F.; Jäger, M.; Simon, E.; Fugger, O.; Kienle, A.; et al. In-vivo multilaboratory investigation of the optical properties of the human head. Biomed. Opt. Express 2015, 6, 2609–2623. [Google Scholar] [CrossRef] [PubMed]
- Liebert, A.; Wabnitz, H.; Steinbrink, J.; Obrig, H.; Möller, M.; Macdonald, R.; Villringer, A.; Rinneberg, H. Time-resolved multidistance near-infrared spectroscopy of the adult head: Intracerebral and extracerebral absorption changes from moments of distribution of times of flight of photons. Appl. Opt. 2004, 43, 3037–3047. [Google Scholar] [CrossRef] [PubMed]
- Benaron, D.A.; Stevenson, D.K. Optical Time-of-Flight and Absorbance Imaging of Biologic Media. Science 1993, 259, 1463–1466. [Google Scholar] [CrossRef] [PubMed]
- Ntziachristos, V.; Ma, X.H.; Yodh, A.G.; Chance, B. Multichannel photon counting instrument for spatially resolved near infrared spectroscopy. Rev. Sci. Instrum. 1999, 70, 193–201. [Google Scholar] [CrossRef]
- Yamada, Y.; Hasegawa, Y.; Yamashita, Y. Simulation of fan-beam-type optical computed-tomography imaging of strongly scattering and weakly absorbing media. Appl. Opt. 1993, 32, 4808–4814. [Google Scholar] [CrossRef] [PubMed]
- Oda, I.; Eda, H.; Tsunazawa, Y.; Takada, M.; Yamada, Y.; Nishimura, G.; Tamura, M. Optical tomography by the temporally extrapolated absorbance method. Appl. Opt. 1996, 35, 169–175. [Google Scholar] [CrossRef]
- Hebden, J.C.; Wong, K.S. Time-resolved optical tomography. Appl. Opt. 1993, 32, 372–380. [Google Scholar] [CrossRef]
- Zevallos, M.E.; Gayen, S.K.; Das, B.B.; Alrubaiee, M.; Alfano, R.R. Picosecond Electronic Time-Gated Imaging of Bones in Tissues. IEEE Select. Top. Quant. Electron. 1999, 5, 916–922. [Google Scholar] [CrossRef]
- Chen, K.; Perelman, L.T.; Zhang, Q.G.; Dasari, R.R.; Feld, M.S. Optical computed tomography in a turbid medium using early arriving photons. J. Biomed. Opt. 2000, 5, 144–154. [Google Scholar] [CrossRef] [PubMed]
- Turner, G.M.; Zacharakis, G.; Soubret, A.; Ripoll, J.; Ntziachristos, V. Complete-angle projection diffuse optical tomography by use of early photons. Opt. Lett. 2005, 30, 409–411. [Google Scholar] [CrossRef]
- Arridge, S.R.; van der Zee, P.; Cope, M.; Delpy, D.T. Reconstruction methods for infrared absorption imaging. Proc. Spie 1991, 1431, 204–215. [Google Scholar]
- Schweiger, M.; Arridge, S. The Toast++ software suite for forward and inverse modeling in optical tomography. J. Biomed. Opt. 2014, 19, 040801. [Google Scholar] [CrossRef] [PubMed]
- Yamada, Y.; Okawa, S. Diffuse Optical Tomography: Present Status and Its Future. Opt. Rev. 2014, 21, 185–205. [Google Scholar] [CrossRef]
- Arridge, S.R.; Schweiger, M. A gradient-based optimisation scheme for optical tomography. Opt. Express 1998, 2, 213–226. [Google Scholar] [CrossRef]
- Intes, X.; Ntziachristos, V.; Culver, J.P.; Yodh, A.; Chance, B. Projection access order in algebraic reconstruction technique for diffuse optical tomography. Phys. Med. Biol. 2002, 47, N1–N10. [Google Scholar] [CrossRef]
- Schweiger, M.; Arridge, S.R. Application of temporal filters to time resolved data in optical tomography. Phys. Med. Biol. 1999, 44, 1699–1717. [Google Scholar] [CrossRef]
- Gao, F.; Zhao, H.; Yamada, Y. Improvement of image quality in diffuse optical tomography by use of full time-resolved data. Appl. Opt. 2002, 41, 778–791. [Google Scholar] [CrossRef]
- Gao, F.; Zhao, H.; Tanikawa, Y.; Yamada, Y. Time-Resolved Diffuse Optical Tomography Using a Modified Pulse Spectrum Technique. IEICE Trans. Inf. Syst. 2002, E85-D, 133–142. [Google Scholar]
- Gao, F.; Tanikawa, Y.; Zhao, H.; Yamada, Y. Semi-three-dimensional algorithm for time-resolved diffuse optical tomography by use of the generalized pulse spectrum technique. Appl. Opt. 2002, 41, 7346–7358. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, F.; Tanikawa, Y.; Onodera, Y.; Ohmi, M.; Haruna, M.; Yamada, Y. Imaging of in vitro chicken leg using time-resolved near-infrared optical tomography. Phys. Med. Biol. 2002, 47, 1979–1993. [Google Scholar] [CrossRef]
- Gao, F.; Zhao, H.; Tanikawa, Y.; Yamada, Y. Optical tomographic mapping of cerebral haemodynamics by means of time-domain detection: Methodology and phantom validation. Phys. Med. Biol. 2004, 49, 1055–1078. [Google Scholar] [CrossRef]
- Gao, F.; Zhao, H.; Tanikawa, Y.; Homma, K.; Yamada, Y. Influences of target size and contrast on near infrared diffuse optical tomography—a comparison between featured-data and full time-resolved schemes. Opt. Quant. Electron. 2005, 37, 1287–1304. [Google Scholar] [CrossRef]
- Lyubimov, V.V.; Kalintsev, A.G.; Konovalov, A.B.; Lyamtsev, O.V.; Kravtsenyuk, O.V.; Murzin, A.G.; Golubkina, O.V.; Mordvinov, G.B.; Soms, L.N.; Yavorskaya, L.M. Application of the photon average trajectories method to real-time reconstruction of tissue inhomogeneities in diffuse optical tomography of strongly scattering media. Phys. Med. Biol. 2002, 47, 2109–2128. [Google Scholar] [CrossRef]
- Hervé, L.; Puszka, A.; Planat-Chrétien, A.; Dinten, J.-M. Time-domain diffuse optical tomography processing by using the Mellin–Laplace transform. Appl. Opt. 2012, 51, 5978–5988. [Google Scholar] [CrossRef]
- Puszka, A.; Hervé, L.; Planat-Chrétien, A.; Koenig, A.; Derouard, J.; Dinten, J.-M. Time-domain reflectance diffuse optical tomography with Mellin-Laplace transform for experimental detection and depth localization of a single absorbing inclusion. Biomed. Opt. Express 2013, 4, 569–583. [Google Scholar] [CrossRef] [PubMed]
- Puszka, A.; Di Sieno, L.; Mora, A.D.; Pifferi, A.; Contini, D.; Planat-Chrétien, A.; Koenig, A.; Boso, G.; Tosi, A.; Hervé, L.; et al. Spatial resolution in depth for time-resolved diffuse optical tomography using short source detector separations. Biomed. Opt. Express 2015, 6, 1–10. [Google Scholar] [CrossRef]
- Naser, M.A.; Deen, M.J. Time-domain diffuse optical tomography using recursive direct method of calculating Jacobian at selected temporal points. Biomed. Phys. Eng. Express 2015, 1, 045207. [Google Scholar] [CrossRef]
- Benaron, D.A.; Van Houten, J.P.; Cheong, W.-F.; Kermit, E.L.; King, R.A. Early clinical results of time-of-flight optical tomography in a neonatal intensive care unit. Proc. Spie 1995, 2389, 582–596. [Google Scholar]
- Benaron, D.A.; Hintz, S.R.; Villringer, A.; Boas, D.; Kleinschmidt, A.; Frahm, J.; Hirth, C.; Obrig, H.; van Houten, J.C.; Kermit, E.L.; et al. Noninvasive Functional Imaging of Human Brain Using Light. J. Cereb. Blood Flow Metab. 2000, 20, 469–477. [Google Scholar] [CrossRef] [PubMed]
- Hebden, J.C.; Gibson, A.; Yusof, R.M.; Everdell, N.; Hillman, E.M.C.; Delpy, D.T.; Arridge, S.R.; Austin, T.; Meek, J.H.; Wyatt, J.S. Three-dimensional optical tomography of the premature infant brain. Phys. Med. Biol. 2002, 47, 4155–4166. [Google Scholar] [CrossRef] [PubMed]
- Hebden, J.C.; Gibson, A.; Austin, T.; Yusof, R.M.; Everdell, N.; Delpy, D.T.; Arridge, S.R.; Meek, J.H.; Wyatt, J.S. Imaging changes in blood volume and oxygenation in the newborn infant brain using three-dimensional optical tomography. Phys. Med. Biol. 2004, 49, 1117–1130. [Google Scholar] [CrossRef] [PubMed]
- Gibson, A.P.; Austin, T.; Everdell, N.L.; Schweiger, M.; Arridge, S.R.; Meek, J.H.; Wyatt, J.S.; Delpy, D.T.; Hebden, J.C. Three-dimensional whole-head optical tomography of passive motor evoked responses in the neonate. NeuroImage 2006, 30, 521–528. [Google Scholar] [CrossRef] [PubMed]
- Boas, D.A.; Gaudette, T.; Arridge, S.R. Simultaneous imaging and optode calibration with diffuse optical tomography. Opt. Express 2001, 8, 263–270. [Google Scholar] [CrossRef]
- Zeff, B.W.; White, B.R.; Dehghani, H.; Schlaggar, B.L.; Culver, J.P. Retinotopic mapping of adult human visual cortex with high-density diffuse optical tomography. PNAS 2007, 104, 12169–12174. [Google Scholar] [CrossRef]
- Ntziachristos, V.; Ma, X.H.; Chance, B. Time-correlated single photon counting imager for simultaneous magnetic resonance and near-infrared mammography. Rev. Sci. Instrum. 1998, 69, 4221–4233. [Google Scholar] [CrossRef]
- Ntziachristos, V.; Yodh, A.G.; Schnall, M.; Chance, B. Concurrent MRI and diffuse optical tomography of breast after indocyanine green enhancement. Proc. Natl. Acad. Sci. USA 2000, 97, 2767–2772. [Google Scholar] [CrossRef]
- Intes, X.; Djeziri, S.; Ichalalene, Z.; Mincu, N.; Wang, Y.; St.-Jean, P.; Lesage, F.; Hall, D.; Boas, D.A.; Polyzos, M. Time-Domain Optical Mammography Softscan®: Initial Results on Detection and Characterization of Breast Tumors. Proc. Spie 2004, 5578, 188–197. [Google Scholar]
- Enfield, L.; Cantanhede, G.; Douek, M.; Ramalingam, V.; Purushotham, A.; Hebden, J.; Gibson, A. Monitoring the response to neoadjuvant hormone therapy for locally advanced breast cancer using three-dimensional time-resolved optical mammography. J. Biomed. Opt. 2013, 18, 056012. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, L.-H.; Li, J.; Yi, X.; Wang, X.; Lu, Y.-M.; Chen, W.-T.; Zhou, Z.-X.; Zhang, L.-M.; Zhao, H.-J.; et al. Combined hemoglobin and fluorescence diffuse optical tomography for breast tumor diagnosis: A pilot study on time-domain methodology. Biomed. Opt. Express 2013, 4, 331–348. [Google Scholar] [CrossRef]
- Hillman, E.M.C.; Hebden, J.C.; Schweiger, M.; Dehghani, H.; Schmidt, F.E.W.; Delpy, D.T.; Arridge, S.R. Time resolved optical tomography of the human forearm. Phys. Med. Biol. 2001, 46, 1117–1130. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, F.; Tanikawa, Y.; Homma, K.; Yamada, Y. Time-resolved diffuse optical tomographic imaging for the provision of both anatomical and functional information about biological tissue. Appl. Opt. 2005, 44, 1905–1916. [Google Scholar] [CrossRef]
- Massoud, T.F.; Gambhir, S.S. Molecular imaging in living subjects: Seeing fundamental biological processes in a new light. Genes Dev. 2003, 17, 545–580. [Google Scholar] [CrossRef]
- Cherry, S.R. In vivo molecular and genomic imaging: New challenges for imaging physics. Phys. Med. Biol. 2004, 49, R13–R48. [Google Scholar] [CrossRef]
- Patterson, M.S.; Pogue, B.W. Mathematical model for time-resolved and frequency-domain fluorescence spectroscopy in biological tissues. Appl. Opt. 1994, 33, 1963–1974. [Google Scholar] [CrossRef]
- Sadoqi, M.; Riseborough, P.; Kumar, S. Analytical models for time resolved fluorescence spectroscopy in tissues. Phys. Med. Biol. 2001, 46, 2725–2743. [Google Scholar] [CrossRef]
- Butte, P.V.; Pikul, B.K.; Hever, A.; Yong, W.H.; Black, K.L.; Marcu, L. Diagnosis of meningioma by time-resolved fluorescence spectroscopy. J. Biomed. Opt. 2005, 10, 064026. [Google Scholar] [CrossRef]
- Milej, D.; Gerega, A.; Żołek, N.; Weig, W.; Kacprzak, M.; Sawosz, P.; Mączewska, J.; Fronczewska, K.; Mayzner-Zawadzka, E.; Królicki, L.; et al. Time-resolved detection of fluorescent light during inflow of ICG to the brain—a methodological study. Phys. Med. Biol. 2012, 57, 6725–6742. [Google Scholar] [CrossRef] [PubMed]
- Milej, D.; Gerega, A.; Wabnitz, H.; Liebert, A. A Monte Carlo study of fluorescence generation probability in a two-layered tissue model. Phys. Med. Biol. 2014, 59, 1407–1424. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Zhao, H.; Zhang, L.; Tanikawa, Y.; Marjono, A.; Yamada, Y. A self-normalized, full time-resolved method for fluorescence diffuse optical tomography. Opt. Express 2008, 16, 13104–13121. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Yi, X.; Wang, X.; Lu, Y.M.; Zhang, L.M.; Zhao, H.; Gao, F. Overlap time-gating approach for improving time-domain diffuse fluorescence tomography based on the IRF-calibrated Born normalization. Opt. Lett. 2013, 38, 1841–1843. [Google Scholar] [CrossRef]
- Riley, J.; Hassan, M.; Chernomordik, V.; Gandjbakhche, A. Choice of data types in time resolved fluorescence enhanced diffuse optical tomography. Med. Phys. 2007, 34, 4890–4900. [Google Scholar] [CrossRef]
- Wu, J.; Perelman, L.; Dasari, R.R.; Feld, M.S. Fluorescence tomographic imaging in turbid media using early-arriving photons and Laplace transforms. Proc. Natl. Acad. Sci. USA 1997, 94, 8783–8788. [Google Scholar] [CrossRef]
- Niedre, M.J.; de Kleine, R.H.; Aikawa, E.; Kirsch, D.G.; Weissleder, R.; Ntziachristos, V. Early photon tomography allows fluorescence detection of lung carcinomas and disease progression in mice in vivo. Proc. Natl. Acad. Sci. USA 2008, 105, 19126–19131. [Google Scholar] [CrossRef] [PubMed]
- Patwardhan, S.V.; Culver, J.P. Quantitative diffuse optical tomography for small animals using an ultrafast gated image intensifier. J. Biomed. Opt. 2008, 13, 011009. [Google Scholar] [CrossRef] [PubMed]
- Leblond, F.; Dehghani, H.; Kepshire, D.; Pogue, B.W. Early-photon fluorescence tomography: Spatial resolution improvements and noise stability considerations. J. Opt. Soc. Am. A 2009, 26, 1444–1457. [Google Scholar] [CrossRef]
- Zhu, Q.; Dehghani, H.; Tichauer, K.M.; Holt, R.W.; Vishwanath, K.; Leblond, F.; Pogue, B.W. A three-dimensional finite element model and image reconstruction algorithm for time-domain fluorescence imaging in highly scattering media. Phys. Med. Biol. 2011, 56, 7419–7434. [Google Scholar] [CrossRef]
- Cheng, J.; Cai, C.; Luo, J. Reconstruction of high-resolution early-photon tomography based on the first derivative of temporal point spread function. J. Biomed. Opt. 2018, 23, 060503. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Zhao, H.; Tanikawa, Y.; Yamada, Y. A linear, featured-data scheme for image reconstruction in time-domain fluorescence molecular tomography. Opt. Express 2006, 14, 7109–7124. [Google Scholar] [CrossRef] [PubMed]
- Marjono, A.; Okawa, S.; Gao, F.; Yamada, Y. Light Propagation for Time-Domain Fluorescence Diffuse Optical Tomography by Convolution Using Lifetime Function. Opt. Rev. 2007, 14, 131–138. [Google Scholar]
- Marjono, A.; Yano, A.; Okawa, S.; Gao, F.; Yamada, Y. Total light approach of time-domain fluorescence diffuse optical tomography. Opt. Express 2008, 16, 15268–15285. [Google Scholar] [CrossRef] [PubMed]
- Nishimura, G.; Awasthi, K.; Furukawa, D. Fluorescence lifetime measurements in heterogeneous scattering medium. J. Biomed. Opt. 2016, 21, 075013. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.T.N.; Skoch, J.; Hammond, F.L., III; Dunn, A.K.; Boas, D.A.; Bacskai, B.J. Time resolved fluorescence imaging in diffuse media. Spie Proc. 2005, 6009, 60090Y. [Google Scholar]
- Soloviev, V.Y.; D’Andrea, C.; Valentini, G.; Cubeddu, R.; Arridge, S.R. Combined reconstruction of fluorescent and optical parameters using time-resolved data. Appl. Opt. 2009, 48, 28–36. [Google Scholar] [CrossRef]
- Yi, X.; Wang, B.-Y.; Wan, W.-B.; Wang, Y.-H.; Zhang, Y.-Q.; Zhao, H.; Gao, F. Full time-resolved diffuse fluorescence tomography accelerated with parallelized Fourier-series truncated diffusion approximation. J. Biomed. Opt. 2015, 20, 056003. [Google Scholar] [CrossRef]
- Chen, J.; Intes, X. Comparison of Monte Carlo methods for fluorescence molecular tomography—computational efficiency. Med. Phys. 2011, 38, 5788–5798. [Google Scholar] [CrossRef]
- Chen, J.; Venugopal, V.; Intes, X. Monte Carlo based method for fluorescence tomographic imaging with lifetime multiplexing using time gates. Biomed. Opt. Express 2011, 2, 871–886. [Google Scholar] [CrossRef]
- Kusaka, T.; Hisamatsu, Y.; Kawada, K.; Okubo, K.; Okada, H.; Namba, M.; Imai, T.; Isobe, K.; Itoh, S. Measurement of Cerebral Optical Pathlength as a Function of Oxygenation Using Near-Infrared Time-resolved Spectroscopy in a Piglet Model of Hypoxia. Opt. Rev. 2003, 10, 466–469. [Google Scholar] [CrossRef]
- Ijichi, S.; Kusaka, T.; Isobe, K.; Islam, F.; Okubo, K.; Okada, H.; Namba, M.; Kawada, K.; Imai, T.; Itoh, S. Quantification of cerebral hemoglobin as a function of oxygenation using near-infrared time-resolved spectroscopy in a piglet model of hypoxia. J. Biomed. Opt. 2005, 10, 024026. [Google Scholar] [CrossRef] [PubMed]
- Ijichi, S.; Kusaka, T.; Isobe, K.; Okubo, K.; Kawada, K.; Namba, M.; Okada, H.; Nishida, T.; Imai, T.; Itoh, S. Developmental Changes of Optical Properties in Neonates Determined by Near-Infrared Time-Resolved Spectroscopy. Pediatric Res. 2005, 58, 568–573. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, K.; Kusaka, T.; Tanimoto, K.; Nishida, T.; Isobe, K.; Itoh, S. Changes in Breast Hemodynamics in Breastfeeding Mothers. J. Hum. Lat. 2008, 24, 415–421. [Google Scholar] [CrossRef]
- Koyano, K.; Kusaka, T.; Nakamura, S.; Nakamura, M.; Konishi, Y.; Miki, T.; Ueno, M.; Yasuda, S.; Okada, H.; Nishida, T.; et al. The effect of blood transfusion on cerebral hemodynamics in preterm infants. Transfusion 2013, 53, 1459–1467. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, S.; Koyano, K.; Jinnai, W.; Hamano, S.; Yasuda, S.; Konishi, Y.; Kuboi, T.; Kanenishi, K.; Nishida, T.; Kusaka, T. Simultaneous measurement of cerebral hemoglobin oxygen saturation and blood volume in asphyxiated neonates by near-infrared time-resolved spectroscopy. Brain Dev. 2015, 37, 925–932. [Google Scholar] [CrossRef]
- Kusaka, T.; Isobe, K.; Yasuda, S.; Koyano, K.; Nakamura, S.; Nakamura, M.; Ueno, M.; Miki, T.; Itoh, S. Evaluation of cerebral circulation and oxygen metabolism in infants using near-infrared light. Brain Dev. 2014, 36, 277–283. [Google Scholar] [CrossRef] [PubMed]
- Ohmae, E.; Oda, M.; Suzuki, T.; Yamashita, Y.; Kakihana, Y.; Matsunaga, A.; Kanmura, Y.; Tamura, M. Clinical evaluation of time-resolved spectroscopy by measuring cerebral hemodynamics during cardiopulmonary bypass surgery. J. Biomed. Opt. 2007, 12, 062112. [Google Scholar] [CrossRef]
- Kakihana, Y.; Okayama, N.; Matsunaga, A.; Yasuda, T.; Imabayashi, M.; Nakahara, M.; Kiyonaga, N.; Ikoma, K.; Kikuchi, T.; Kanmura, Y.; et al. Cerebral Monitoring Using Near-Infrared Time-Resolved Spectroscopy and Postoperative Cognitive Dysfunction. Oxyg. Transp. Tissue Xxxiiiadv. Exp. Med. Biol. 2012, 737, 19–24. [Google Scholar]
- Yasuda, T.; Yamaguchi, K.; Futatsuki, T.; Furubeppu, H.; Nakahara, M.; Eguchi, T.; Miyamoto, S.; Madokoro, Y.; Terada, S.; Nakamura, K.; et al. Non-invasive Monitoring of Hepatic Oxygenation Using Time-Resolved Spectroscopy. Oxyg. Transp. Tissue Xxxviiadv. Exp. Med. Biol. 2016, 876, 407–412. [Google Scholar]
- Kakihana, Y.; Kamikokuryo, C.; Furubeppu, H.; Madokoro, Y.; Futatsuki, T.; Miyamoto, S.; Haraura, H.; Hatanaka, K.; Eguchi, T.; Saitoh, Y.; et al. Monitoring of Brain Oxygenation During and After Cardiopulmonary Resuscitation: A Prospective Porcine Study. Oxyg. Transp. Tissue Xladv. Exp. Med. Biol. 2018, 1072, 83–87. [Google Scholar]
- Sakatani, K.; Yamashita, D.; Yamanaka, T.; Oda, M.; Yamashita, Y.; Hoshino, T.; Fujiwara, N.; Murata, Y.; Katayama, Y. Changes of cerebral blood oxygenation and optical pathlength during activation and deactivation in the prefrontal cortex measured by time-resolved near infrared spectroscopy. Life Sci. 2006, 78, 2734–2741. [Google Scholar] [CrossRef] [PubMed]
- Yokose, N.; Sakatani, K.; Murata, Y.; Awano, T.; Igarashi, T.; Nakamura, S.; Hoshino, T.; Katayama, Y. Bedside Monitoring of Cerebral Blood Oxygenation and Hemodynamics after Aneurysmal Subarachnoid Hemorrhage by Quantitative Time-Resolved Near-Infrared Spectroscopy. World Neurosurg. 2010, 73, 508–513. [Google Scholar] [CrossRef]
- Tanida, M.; Sakatani, K.; Tsujii, T.; Katayama, Y. Relation between working memory performance and evoked cerebral blood oxygenation changes in the prefrontal cortex evaluated by quantitative time-resolved near-infrared spectroscopy. Neurolog. Res. 2012, 34, 114–119. [Google Scholar] [CrossRef] [PubMed]
- Sakatani, K.; Tanida, M.; Hirao, N.; Takemura, N. Ginkobiloba Extract Improves Working Memory Performance in Middle-Aged Women: Role of Asymmetry of Prefrontal Cortex Activity during a Working Memory Task. Oxyg. Transp. Tissue Xxxviadv. Exp. Med. Biol. 2014, 812, 295–301. [Google Scholar]
- Machida, A.; Shirato, M.; Tanida, M.; Kanemaru, C.; Nagai, S.; Sakatani, K. Effects of Cosmetic Therapy on Cognitive Function in Elderly Women Evaluated by Time-Resolved Spectroscopy Study. Oxyg. Transp. Tissue Xxxviiadv. Exp. Med. Biol. 2016, 876, 289–295. [Google Scholar]
- Tanida, M.; Okabe, M.; Tagai, K.; Sakatani, K. Evaluation of Pleasure-Displeasure Induced by Use of Lipsticks with Near-Infrared Spectroscopy (NIRS): Usefulness of 2-Channel NIRS in Neuromarketing. Oxyg. Transp. Tissue Xxxixadv. Exp. Med. Biol. 2017, 977, 215–220. [Google Scholar]
- Murayama, Y.; Sato, Y.; Hu, L.; Brugnera, A.; Compare, A.; Sakatani, K. Relation Between Cognitive Function and Baseline Concentrations of Hemoglobin in Prefrontal Cortex of Elderly People Measured by Time-Resolved Near-Infrared Spectroscopy. Oxyg. Transp. Tissue Xxxixadv. Exp. Med. Biol. 2017, 977, 269–276. [Google Scholar]
- Hamaoka, T.; Katsumura, T.; Murase, N.; Nishio, S.; Osada, T.; Sako, T.; Higuchi, H.; Kurosawa, Y.; Shimomitsu, T.; Miwa, M.; et al. Quantification of ischemic muscle deoxygenation by near infrared time-resolved spectroscopy. J. Biomed. Opt. 2000, 5, 102–105. [Google Scholar] [CrossRef] [PubMed]
- Nirengi, S.; Yoneshiro, T.; Sugie, H.; Saito, M.; Hamaoka, T. Human Brown Adipose Tissue Assessed by Simple, Noninvasive Near-Infrared Time-Resolved Spectroscopy. Obesity 2015, 23, 973–980. [Google Scholar] [CrossRef]
- Nirengi, S.; Homma, T.; Inoue, N.; Sato, H.; Yoneshiro, T.; Matsushita, M.; Kameya, T.; Sugie, H.; Tsuzaki, K.; Saito, M.; et al. Assessment of human brown adipose tissue density during daily ingestion of thermogenic capsinoids using near-infrared time-resolved spectroscopy. J. Biomed. Opt. 2016, 21, 091305. [Google Scholar] [CrossRef] [PubMed]
- Fuse, S.; Nirengi, S.; Amagasa, S.; Homma, T.; Kime, R.; Endo, T.; Sakane, N.; Matsushita, M.; Saito, M.; Yoneshiro, T.; et al. Brown adipose tissue density measured by near-infrared time-resolved spectroscopy in Japanese, across a wide age range. J. Biomed. Opt. 2018, 23, 065002. [Google Scholar] [CrossRef] [PubMed]
- Ohmae, E.; Ouchi, Y.; Oda, M.; Suzuki, T.; Nobesawa, S.; Kanno, T.; Yoshikawa, E.; Futatsubashi, M.; Ueda, Y.; Okada, H.; et al. Cerebral hemodynamics evaluation by near-infrared time-resolved spectroscopy: Correlation with simultaneous positron emission tomography measurements. Neuroimage 2006, 29, 697–705. [Google Scholar] [CrossRef]
- Sato, C.; Yamaguchi, T.; Seida, M.; Ota, Y.; Yu, I.; Iguchi, Y.; Nemoto, M.; Hoshi, Y. Intraoperative monitoring of depth-dependent hemoglobin concentration changes during carotid endarterectomy by time-resolved spectroscopy. Appl. Opt. 2007, 46, 2785–2792. [Google Scholar] [CrossRef] [PubMed]
- Yamazaki, K.; Suzuki, K.; Itoh, H.; Muramatsu, K.; Nagahashi, K.; Tamura, N.; Uchida, T.; Sugihara, K.; Maeda, H.; Kanayama, N. Cerebral oxygen saturation evaluated by near-infrared time-resolved spectroscopy (TRS) in pregnant women during caesarean section—a promising new method of maternal monitoring. Clin. Physiol. Funct. Imaging 2013, 33, 109–116. [Google Scholar] [CrossRef] [PubMed]
- Ueda, S.; Nakamiya, N.; Matsuura, K.; Shigekawa, T.; Sano, H.; Hirokawa, E.; Shimada, H.; Suzuki, H.; Oda, M.; Yamashita, Y.; et al. Optical imaging of tumor vascularity associated with proliferation and glucose metabolism in early breast cancer: Clinical application of total hemoglobin measurements in the breast. BMC Cancer 2013, 13, 514. [Google Scholar] [CrossRef] [PubMed]









| Year | Event | Ref. |
|---|---|---|
| 1988 | TD-NIRS system using a streak camera or TCSPC | [34,36] |
| 1999 | 2-wavelength multi-Ch TD-NIRS oximeter using pLDs and multi-anode PMTs | [39] |
| Commercial 1-Ch TD-NIRS system using TCSPC for research use: “TRS-10” | [40] | |
| 1-wavelength 1-Ch TD optical mammography using a pLD and PMT-TCSPC | [41] | |
| 64-channel TD-DOT system using pLDs and PMT-TCSPCs | [45] | |
| 2000 | 32-channel TD-DOT system (MONSTIR) | [49] |
| 2003 | TD-NIRS system using the spread spectrum technique and pseudo-random bit sequences | [63] |
| 2005 | TD-NIRS system using time-gated ICCD | [65] |
| 16-channel TD-DOT system using pLDs and PMT-TCSPCs | [50] | |
| 2009 | Commercial 2-Ch TD-NIRS system using TCSPC for research use: “TRS-20” | [43] |
| 2011 | 48-Ch 3-wavelength TD-NIRS optical mammography | [52] |
| 2013 | TD-DOT system incorporating SPADs into TCSPC | [58] |
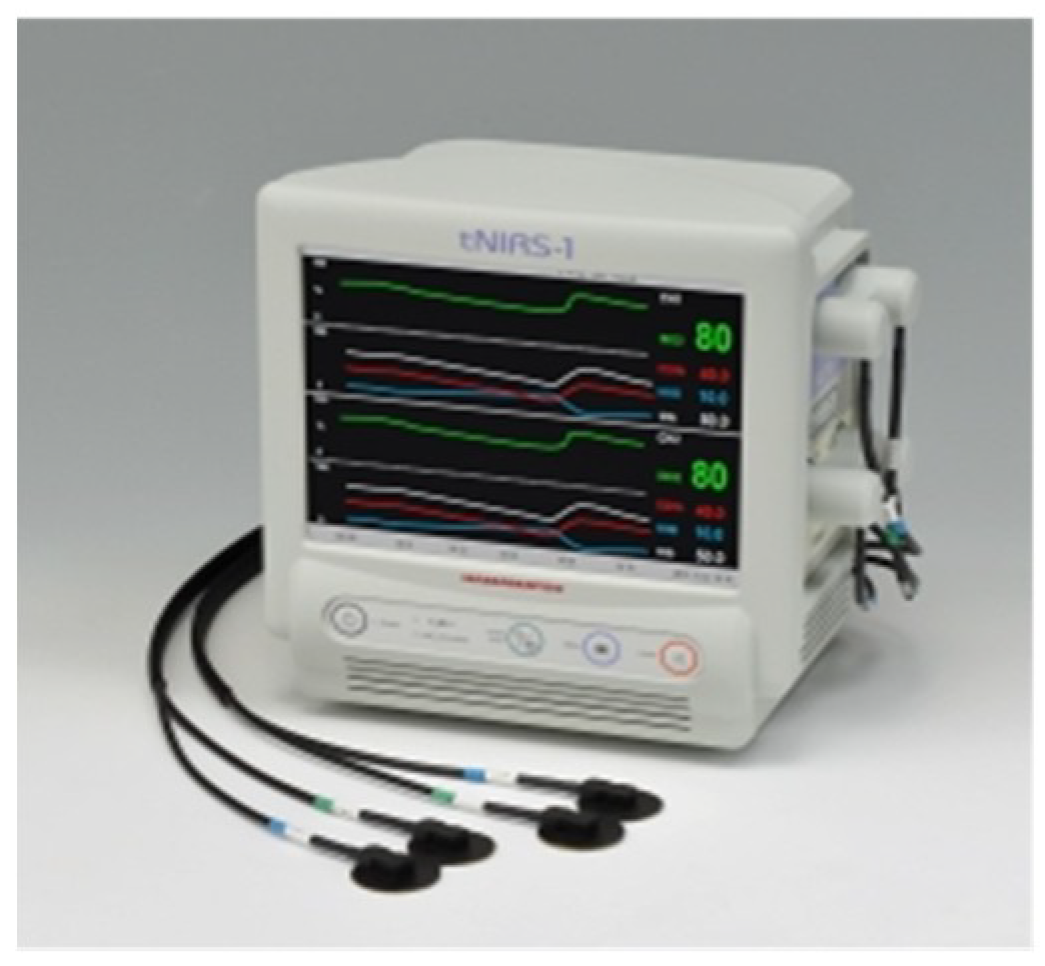
| 2014 | Commercial 2-Ch TD-NIRS system using MPPCs for medical use: “tNIRS-1” | [55] |
| MONSTIR II employing an SC laser with an AOTF for 4 wavelengths | [51] | |
| 2016 | TD-NIRS mammography for imaging the contents of water, lipid, collagen, oxy-Hb and deoxy-Hb using 7 wavelengths | [54] |
| Compact 2-wavelength TD-NIRS system and detector probe using SiPM | [56,57] | |
| TD-NIRS system using an SC laser and SPADs for non-contact measurements | [60] | |
| 2017 | 12-Ch TD-NIRS mammography with a hand-held probe | [53] |
| 2018 | TD-DOT system using an SC laser and SPAD camera | [62] |
| Compact TD-NIRS system for measuring the contents of water, lipid, oxy-Hb, and deoxy-Hb using 6 wavelengths | [68] | |
| Compact 1-Ch TD-NIRS system using telecommunication devices | [3] |
| Year | Event | Ref. |
|---|---|---|
| 1983 | Monte Carlo method applied to photon migration | [22] |
| 1988 | TD measurement of optical pathlength | [34] |
| TD-NIRS of hemoglobin and myoglobin in muscle | [36] | |
| 1989 | Analytical solutions of the TD-DE for semi-infinite and slab media | [18] |
| 1991~1995 | TD sensitivity functions | [26,27,28,29] |
| 1991, 1993 | Method of TD-DOT image reconstruction including forward and inverse models | [69,164] |
| 1992 | Analytical solutions of the TD-DE for various simple geometries | [19] |
| Monte Carlo code for multi-layered tissue, MCML | [23] | |
| 1993, 1995 | TOF and absorbance imaging of biological media and neonates | [156,181] |
| 1994 | Mathematical model for TD-FT | [197] |
| 1994, 2006 | Diffusion coefficient independent of the absorption coefficient | [8,17] |
| 1996 | TD imaging based on the perturbation model | [87] |
| 1996, 1998 | Perturbation Monte Carlo simulation | [105,107] |
| 1997 | Light propagation in a model of the adult head | [126] |
| TD-FT using early-arriving photons | [205] | |
| 1998 | TR reflectance from two-layered media | [98] |
| Simultaneous MR and TD-NIRS mammography | [191 | |
| 2000, 2014 | Open source software for TD-DOT: TOAST and TOAST++ | [49,165] |
| 2001 | TD-DOT of human forearm | [193] |
| Photon path distribution based on the microscopic Beer–Lambert law | [9] | |
| 2002 | GPST and full TR algorithms for TD-DOT | [170,171] |
| 3D TD-DOT of premature infant brain | [185] | |
| 2005 | Perturbation model for layered media | [91] |
| TR reflectance at null space SD distance | [131] | |
| Measurements of optical properties in neonates using a commercial TD-NIRS system: TRS-10 | [222] | |
| 2010 | (Monograph) Light propagation through biological tissue | [32] |
| 2014 | Hybrid TD-RTE and TD-DE | [119,120] |
| 2014, 2016 | Estimate of tissue composition in breasts using TR reflectance at 7 wavelengths | [54,139] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, Y.; Suzuki, H.; Yamashita, Y. Time-Domain Near-Infrared Spectroscopy and Imaging: A Review. Appl. Sci. 2019, 9, 1127. https://doi.org/10.3390/app9061127
Yamada Y, Suzuki H, Yamashita Y. Time-Domain Near-Infrared Spectroscopy and Imaging: A Review. Applied Sciences. 2019; 9(6):1127. https://doi.org/10.3390/app9061127
Chicago/Turabian StyleYamada, Yukio, Hiroaki Suzuki, and Yutaka Yamashita. 2019. "Time-Domain Near-Infrared Spectroscopy and Imaging: A Review" Applied Sciences 9, no. 6: 1127. https://doi.org/10.3390/app9061127
APA StyleYamada, Y., Suzuki, H., & Yamashita, Y. (2019). Time-Domain Near-Infrared Spectroscopy and Imaging: A Review. Applied Sciences, 9(6), 1127. https://doi.org/10.3390/app9061127





