Cluster Analysis of Pedestrian Mobile Channels in Measurements and Simulations
Abstract
:1. Introduction
- The KPM-Kalman filter (KPMKF) algorithm is used for massive MIMO urban macro (UMa) pedestrian mobile scenario measurement. With this method, evolution including the birth and death rate and lifetime of clusters can be clearly shown. The difference of clustering results with and without Kalman filter (KF) part is also shown.
- The spatial-consistency feature is introduced and implemented to complement the primary module of the IMT-2020 channel model. It makes the channel evolve smoothly without discontinuity when Transmitter (Tx)/Receiver (Rx) moves. With this feature, cluster characteristics are highly correlated among neighboring moving locations, which is closer to real conditions. In the meantime, comparisons among between measurements and simulations with and without this feature are shown.
- Inspired by Reference [11], a novel clustering method based on the gradient boosted decision-tree (GBDT) algorithm is explored to train and validate the results from the above measurements and simulations. It was proven to be an effective way to characterize cluster evolution in certain scenarios during linear movement.
2. Cluster Tracking in Mobile Measurements
2.1. Measurement Setup and Data Processing
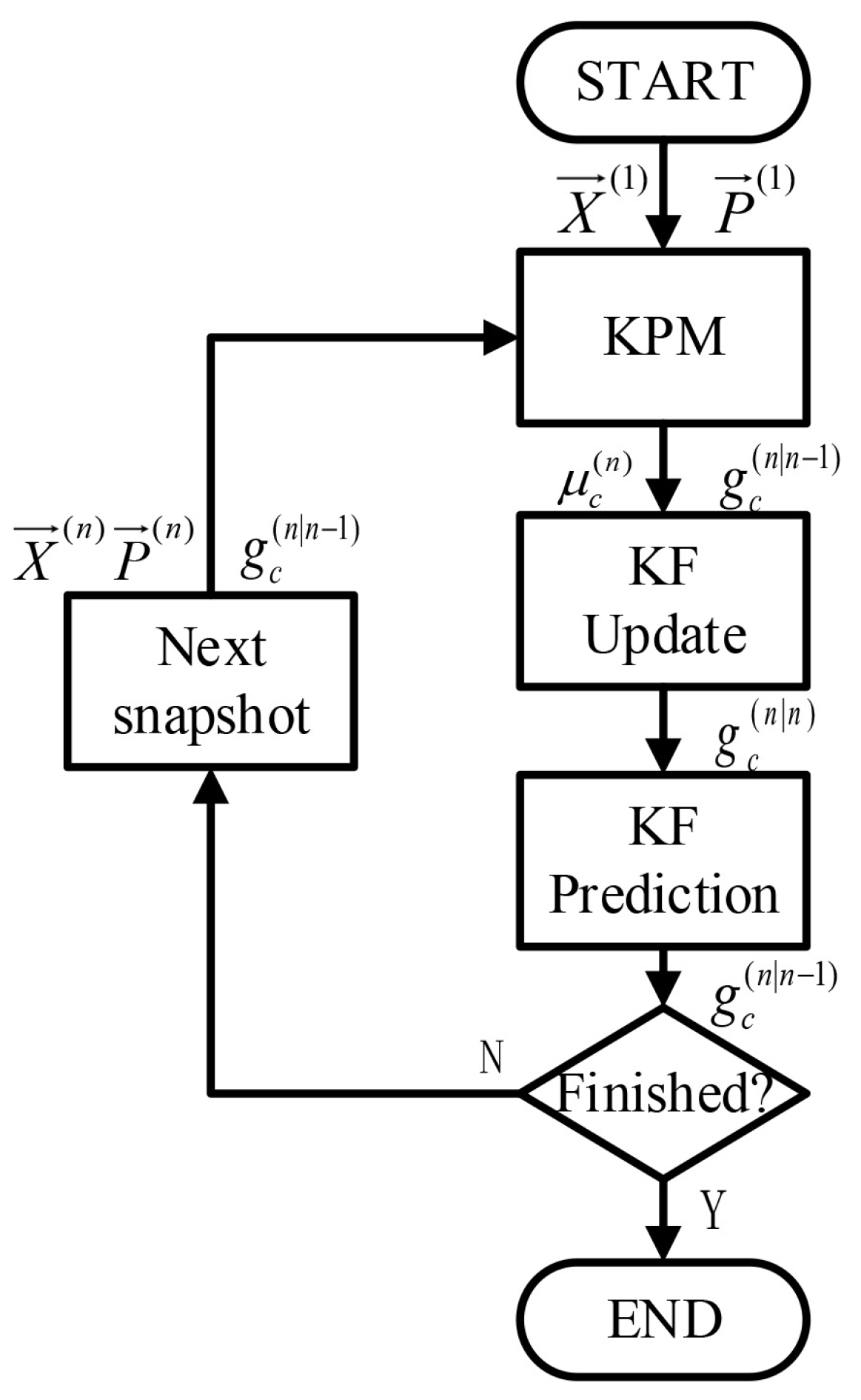
2.1.1. K-Power Means Part
- Assign MPCs to cluster centroids and store indices:where is the cluster index of the lth MPC in the ith iteration. is the set of MPCs indices belonging to the kth cluster in the ith iteration.
- Recalculate positions of cluster centroids from the allocated MPCs to coincide with the clusters’ centers of gravity:
- If for all , then we go out of the iterations. Otherwise, we keep performing iterations up to the setting maximum iteration times.
2.1.2. Kalman Filter Part
2.2. Clustering and Tracking Results
3. Mobile Channel Simulations by IMT-2020 Channel Model
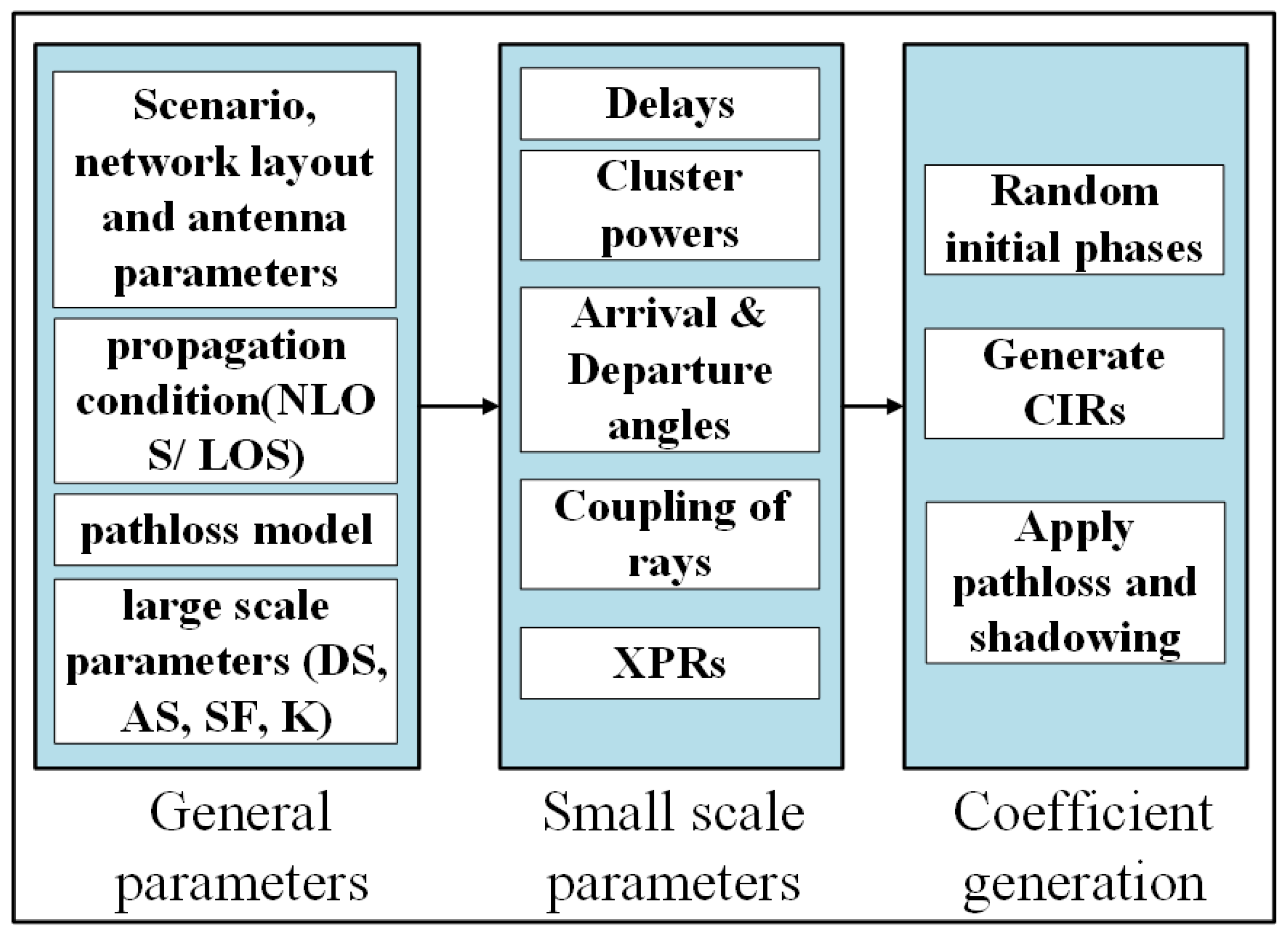
3.1. Simulation Generation Procedures
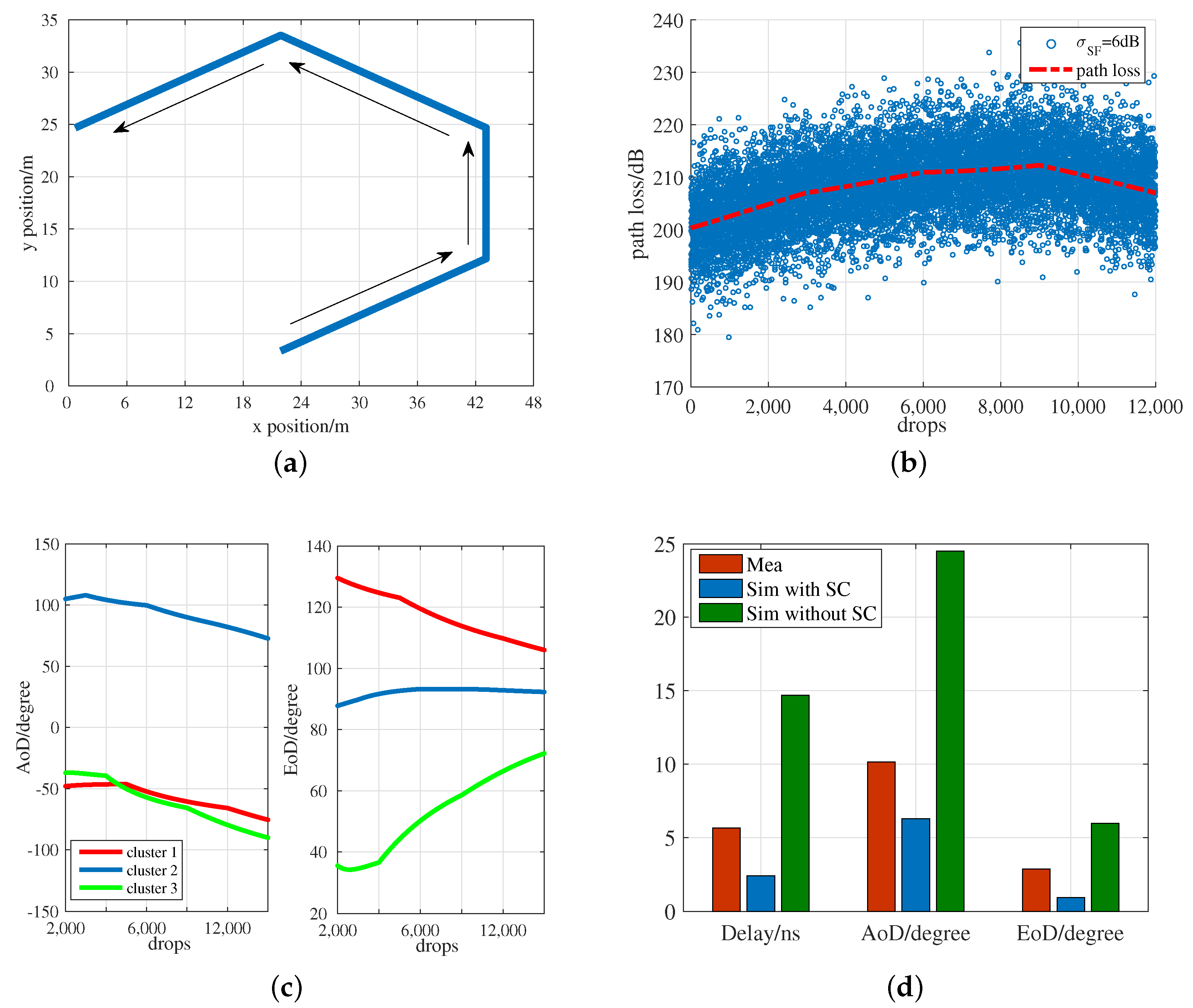
3.2. Simulation Results
4. Gradient Boosted Decision Tree-Based Model
4.1. Model Description
4.2. Numerical Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- ITU M. 1225: Guidelines for Evaluation of Radio Transmission Technologies For IMT-2000. Report ITU 1997.
- ITU M. 2135: Guidelines for Evaluation of Radio Interface Technologies for IMT-Advanced. Report ITU 2009.
- ITU M. 2412: Guidelines for Evaluation of Radio Interface Technologies for IMT-2020. Report ITU 2017.
- Czink, N.; Yin, X.; Ozcelik, H.; Herdin, M.; Bonek, E.; Fleury, B.H. Cluster Characteristics in a MIMO Indoor Propagation Environment. IEEE Trans. Wirel. Commun. 2007, 6, 1465–1475. [Google Scholar] [CrossRef]
- Hentila, L.; Alatossava, M.; Czink, N.; Kyosti, P. Cluster-level Parameters at 5.25 GHz Indoor-to-Outdoor and Outdoor-to-Indoor MIMO Radio Channels. In Proceedings of the 2007 16th IST Mobile and Wireless Communications Summit, Budapest, Hungary, 1–5 July 2007; pp. 1–5. [Google Scholar]
- Poutanen, J.; Haneda, K.; Salmi, J.; Kolmonen, V.M.; Tufvesson, F.; Vainikainen, P. Analysis of Radio Wave Scattering Processes for Indoor MIMO Channel Models. In Proceedings of the 2009 IEEE 20th International Symposium on Personal, Indoor and Mobile Radio Communications, Tokyo, Japan, 13–16 September 2009; pp. 102–106. [Google Scholar]
- Poutanen, J.; Haneda, K.; Salmi, J.; Kolmonen, V.M.; Vainikainen, P. Modeling the Evolution of Number of Clusters in Indoor Environments. In Proceedings of the 2010 Fourth European Conference on Antennas and Propagation (EuCAP), Barcelona, Spain, 12–16 April 2010; pp. 1–5. [Google Scholar]
- Huang, C.; He, R.; Zhong, Z.; Geng, Y.; Li, Q.; Zhong, Z. A Novel Tracking-Based Multipath Component Clustering Algorithm. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2679–2683. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.; Tian, L.; Liu, M.; Wu, Y. The Spatial Evolution of Clusters in Massive MIMO Mobile Measurement at 3.5 GHz. In Proceedings of the 2017 IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, Australia, 4–7 June 2017; pp. 1–6. [Google Scholar]
- Wang, C.; Zhang, J.; Tian, L.; Liu, M.; Wu, Y. The Variation of Clusters with Increasing Number of Antennas by Virtual Measurement. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017; pp. 648–652. [Google Scholar]
- Zhang, J. The Interdisciplinary Research of Big Data and Wireless Channel: A Cluster-nuclei Based Channel Model. China Commun. 2016, 13, 14–26. [Google Scholar] [CrossRef]
- Gao, J.; Zhang, J.; Xiong, Y.; Sun, Y.; Tao, X. Performance Evaluation of Closed-loop Spatial Multiplexing Codebook based on Indoor MIMO Channel Measurement. Int. J. Antennas Propag. 2012, 2012, 701985. [Google Scholar] [CrossRef]
- Zhang, J.; Pan, C. Validation of Antenna Modeling Methodology in IMT-Advanced Channel Model. Int. J. Antennas Propag. 2012, 2012. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, J.; Zhang, P. Outage Probability of Dual-hop Multiple Antenna Relay Systems with Interference at the Relay and Destination. Int. J. Antennas Propag. 2014, 13, 2308–2321. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, J.; Zheng, Q.; Zheng, Z.; Tian, L.; Wu, Y. The Rationality Analysis of Massive MIMO Virtual Measurement at 3.5 GHz. In Proceedings of the 2016 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Beijing, China, 16–18 August 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Fleury, B.H.; Tschudin, M.; Heddergott, R.; Dahlhaus, D.; Pedersen, K.I. Channel Parameter Estimation in Mobile Radio Environments using the SAGE Algorithm. IEEE J. Sel. Areas Commun. 1999, 17, 434–450. [Google Scholar] [CrossRef]
- Sengijpta, S.K. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Czink, N.; Tian, R.; Wyne, S.; Eriksson, G.; Tufvesson, F.; Zemen, T.; Nuutinen, J.; Ylitalo, J.; Bonek, E.; Molisch, A. Tracking Time-variant Cluster Parameters in MIMO Channel Measurements: Algorithm and Results. In Proceedings of the International Conference on Communications and Networking in China (ChinaCOM), Shanghai, China, 22–24 August 2007. [Google Scholar]
- Czink, N.; Cera, P.; Salo, J.; Bonek, E.; Nuutinen, J.; Ylitalo, J. A Framework for Automatic Clustering of Parametric MIMO Channel Data Including Path Powers. In Proceedings of the IEEE Vehicular Technology Conference, Melbourne, Australia, 7–10 May 2006; pp. 1–5. [Google Scholar]
- Liu, L.; Oestges, C.; Poutanen, J.; Haneda, K.; Vainikainen, P.; Quitin, F.; Tufvesson, F.; Doncker, P.D. The COST 2100 MIMO Channel Model. IEEE Wirel. Commun. 2012, 19, 92–99. [Google Scholar] [CrossRef]
- 3GPP TR 38.900 V14.2.0 Technical Report: Study on Channel Model for Frequency Spectrum above 6 GHz (Release 14) 2016. Available online: http://www.3gpp.org/ (accessed on 26 February 2019).
- 3GPP TR 36.873 V12.4.0 Technical Report: Study on 3D Channel Model for LTE (release 12) 2017. Available online: http://www.3gpp.org/ (accessed on 26 February 2019).
- Zhang, J.; Zheng, Z.; Zhang, Y.; Xi, J.; Zhao, X.; Gui, G. 3D MIMO for 5G NR: Several Observations from 32 to Massive 256 Antennas Based on Channel Measurement. IEEE Commun. Mag. 2018, 56, 62–70. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, S.; Shao, X.; Guo, Q.; Tang, W. Statistical Modeling of the High Altitude Platform Dual-polarized MIMO Propagation Channel. China Commun. 2017, 14, 43–54. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Breiman, L. Arcing the Edge; Technical Report, Technical Report 486; Statistics Department, University of California at Berkeley: Berkeley, CA, USA, 1997. [Google Scholar]
- Friedman, J.H. Stochastic Gradient Boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A Working Guide to Boosted Regression Trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef] [PubMed]
- Vezhnevets, A.; Barinova, O. Avoiding Boosting Overfitting by Removing Confusing Samples. In Proceedings of the European Conference on Machine Learning, Warsaw, Poland, 17–21 September 2007; Springer: Berlin, Germany, 2007; pp. 430–441. [Google Scholar]

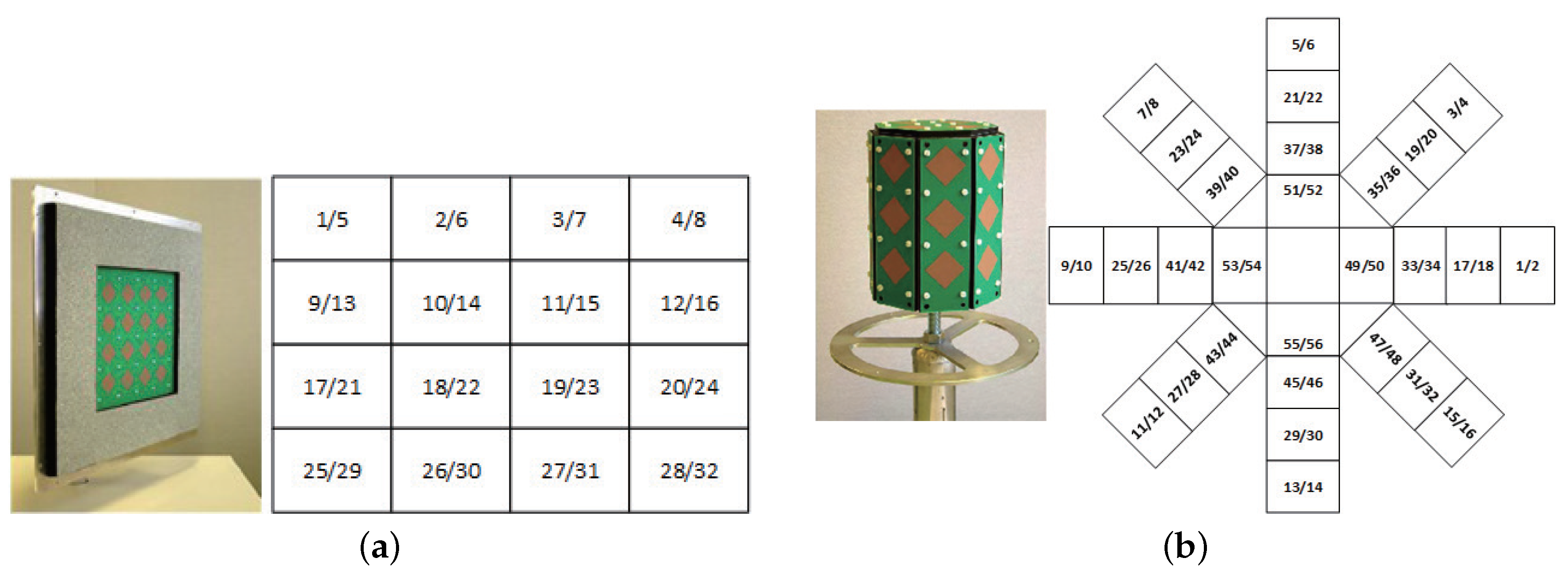
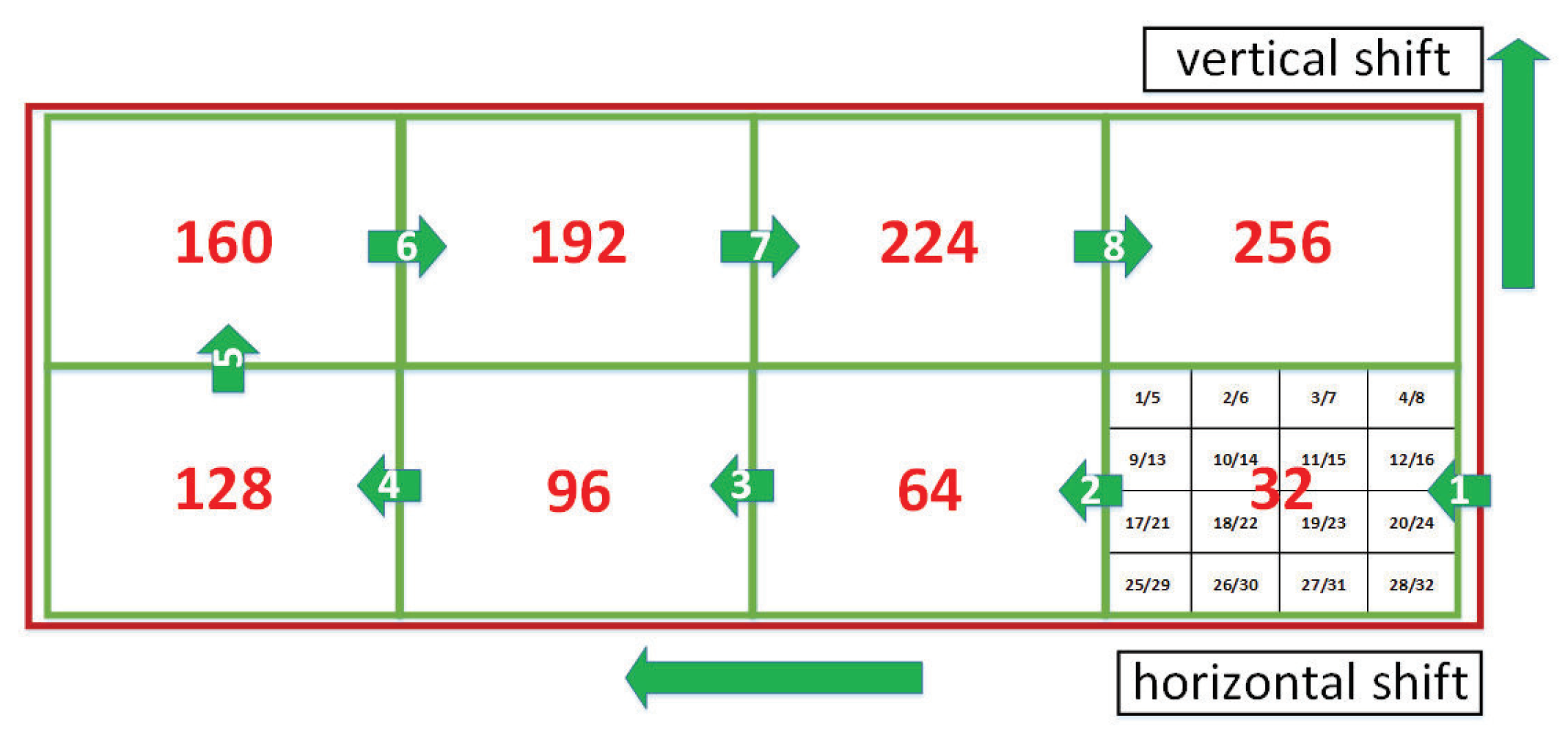


| Antenna Type | ODA(Rx) | UPA(Tx) | |
|---|---|---|---|
| Number of antenna ports | 56 (16 ports were used) | 32 | |
| Radiation pattern | Omnidirectional | Hemispherical | |
| Inter element spacing | 41 mm | 41 mm | |
| Number of elements | 28 | 16 | |
| Polarized | |||
| Angle range | Azimuth | ∼ | ∼ |
| Elevation | ∼ | ∼70 | |
| Center frequency | 3.5 GHz | ||
| Bandwidth | 200 MHz | ||
| PN sequence | 255 chips | ||
| Speed of Rx | 1.4 m/s (pedestrian) | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhang, J.; Yu, G. Cluster Analysis of Pedestrian Mobile Channels in Measurements and Simulations. Appl. Sci. 2019, 9, 886. https://doi.org/10.3390/app9050886
Wang C, Zhang J, Yu G. Cluster Analysis of Pedestrian Mobile Channels in Measurements and Simulations. Applied Sciences. 2019; 9(5):886. https://doi.org/10.3390/app9050886
Chicago/Turabian StyleWang, Chao, Jianhua Zhang, and Guangzhong Yu. 2019. "Cluster Analysis of Pedestrian Mobile Channels in Measurements and Simulations" Applied Sciences 9, no. 5: 886. https://doi.org/10.3390/app9050886
APA StyleWang, C., Zhang, J., & Yu, G. (2019). Cluster Analysis of Pedestrian Mobile Channels in Measurements and Simulations. Applied Sciences, 9(5), 886. https://doi.org/10.3390/app9050886







