A Low-Complexity Ordered Statistics Decoding Algorithm for Short Polar Codes
Abstract
1. Introduction
2. Preliminary
2.1. Polar Code Construction
2.2. Codeword Likelihood in BIAWGN Channels
2.3. The OSD Decoding Algorithm
3. The Threshold-Based OSD Decoding Algorithm
- Sort into the set based on their absolute values in descending order. The corresponding permutation is denoted by . We then reorder the columns of G using to obtain a new matrix .
- Use Gaussian elimination to obtain the reduced row echelon form of , denoted as matrix T. Perform a column swap to move the K columns with pivot elements to the front of the matrix, denoted as . ( denotes the permutations of the column swapping process.) Next, reorder using to obtain . There is a one-to-one mapping between the original and , which can be written as . Thus, decoding is equivalent to decoding .
- Use the first K bits of hard decision of as the initial message sequence, and use f of the codeword as the current minimal f value, denoted as . Then, perform the OSD-2 flipping process by the pseudo code described in Algorithm 1.
| Algorithm 1 Flipping process. |
|
4. A Threshold Determination Method
5. Performance and Complexity Analysis
5.1. WER Performance Analysis
5.2. Complexity Analysis
- Sorting the columns of G into descending order of absolute values of Y takes time and space.
- The Gaussian elimination process for takes time and space. Since we are dealing with short codes, the binary addition of two length-N sequences requires only one instruction instead of N instructions. Thus, the complexity of this step simplifies to .
- In the bit-flipping process, we restrict the maximum number of flipped bits to 2. Thus, the time complexity is as there are K 1-bit flipping operations and 2-bit flipping operations at most with each flipping operation needing time to compute the f value of the new codeword. The space complexity is since we only need to store the flipped positions of current most likely codeword and its f value.
6. Methods to Improve WER Performance
7. Extend to Long Polar Codes
8. Simulation Results
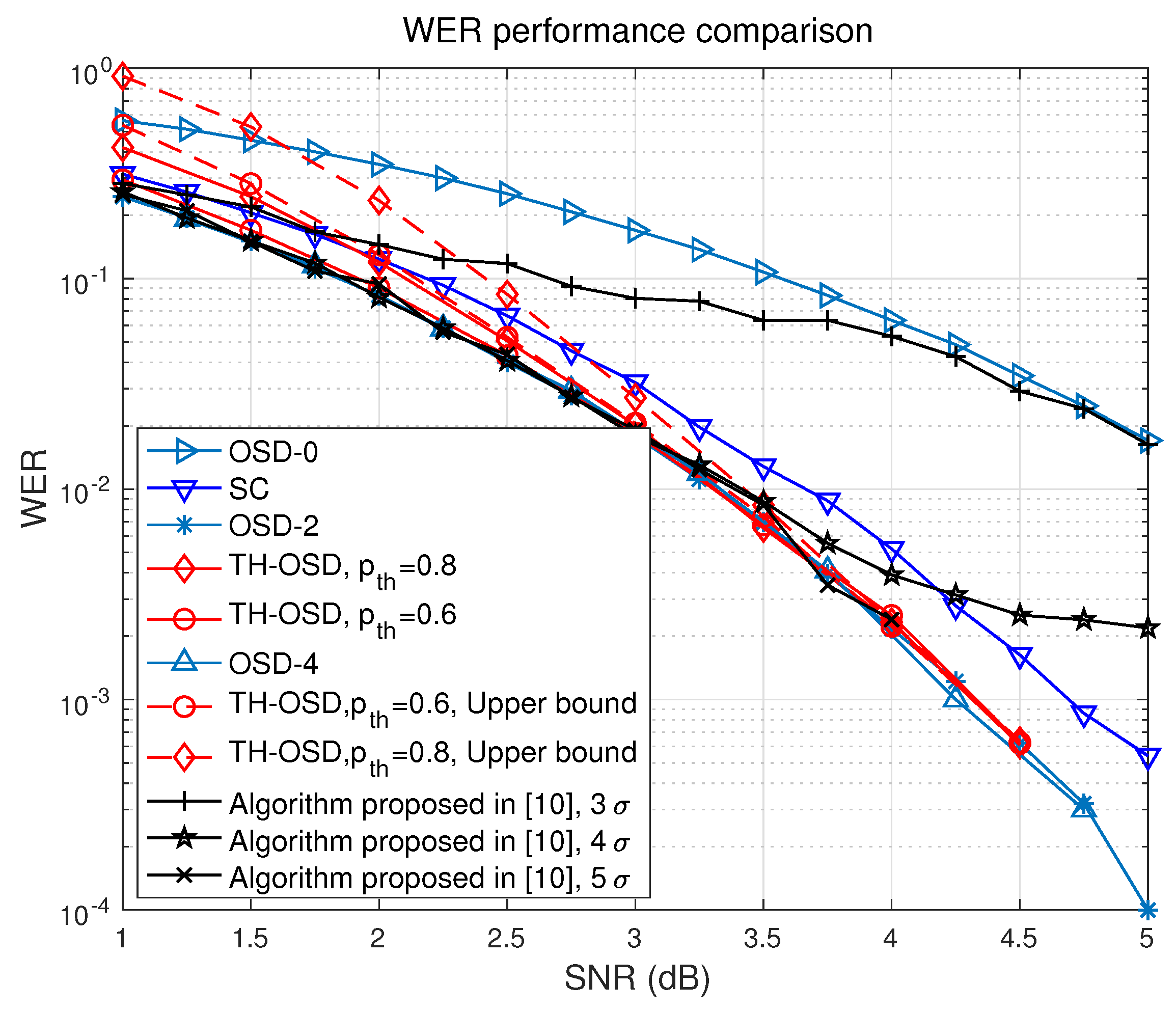
8.1. WER Performance
8.2. Complexity Performance
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. The Mean of the Random Variable r Defined in Equation (4)
Appendix A.2. The Variance of the Random Variable r Defined in Equation (4)
Appendix B. Upper-Bound on the Gap
Appendix C. Complexity Analysis of the SC Decoding Algorithm
References
- Arikan, E. A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef]
- Tal, I.; Vardy, A. List decoding of polar codes. ISIT 2011. [Google Scholar] [CrossRef]
- Niu, K.; Chen, K. Stack decoding of polar codes. Electron. Lett. 2012, 48, 695–697. [Google Scholar] [CrossRef]
- Balatsoukas-Stimming, A.; Parizi, M.B.; Burg, A. LLR-based successive cancellation list decoding of polar codes. ICASSP 2014. [Google Scholar] [CrossRef]
- Niu, K.; Chen, K. CRC-aided decoding of polar codes. IEEE Commun. Lett. 2012, 16, 1668–1671. [Google Scholar] [CrossRef]
- Kaneko, T.; Nishijima, T.; Inazumi, H.; Hirasawa, S. An efficient maximum-likelihood-decoding algorithm for linear block codes with algebraic decoder. IEEE Trans. Inf. Theory 1994, 40, 320–327. [Google Scholar] [CrossRef]
- Kaneko, T.; Nishijima, T.; Hirasawa, S. An improvement of soft-decision maximum-likelihood decoding algorithm using hard-decision bounded-distance decoding. IEEE Trans. Inf. Theory 1997, 43, 1314–1319. [Google Scholar] [CrossRef]
- Wu, X.; Sadjadpour, H.R.; Tian, Z. A new adaptive two-stage maximum-likelihood decoding algorithm for linear block codes. IEEE Trans. Commun. 2005, 53, 909–913. [Google Scholar] [CrossRef]
- Kahraman, S.; Çelebi, M.E. Code based efficient maximum-likelihood decoding of short polar codes. ISIT 2012, 1967–1971. [Google Scholar] [CrossRef]
- Wu, D.; Li, Y.; Guo, X.; Sun, Y. Ordered statistic decoding for short polar codes. IEEE Commun. Lett. 2016, 20, 1064–1067. [Google Scholar] [CrossRef]
- Fossorier, M.P.; Lin, S. Soft-decision decoding of linear block codes based on ordered statistics. IEEE Trans. Inf. Theory 1995, 41, 1379–1396. [Google Scholar] [CrossRef]
- Trifonov, P. Efficient design and decoding of polar codes. IEEE Trans. Commun. 2012, 60, 3221–3227. [Google Scholar] [CrossRef]
- Lin, S.; Costello, D.J. Error Control Coding, 2nd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Hussami, N.; Korada, S.B.; Urbanke, R. Performance of polar codes for channel and source coding. ISIT 2009, 1488–1492. [Google Scholar] [CrossRef]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables, and Stochastic Processes; McGraw-Hill Higher Education: New York, NY, USA, 2002. [Google Scholar]
- Li, B.; Shen, H.; Tse, D.; Tong, W. Low-latency polar codes via hybrid decoding. ISTC 2014, 223–227. [Google Scholar] [CrossRef]
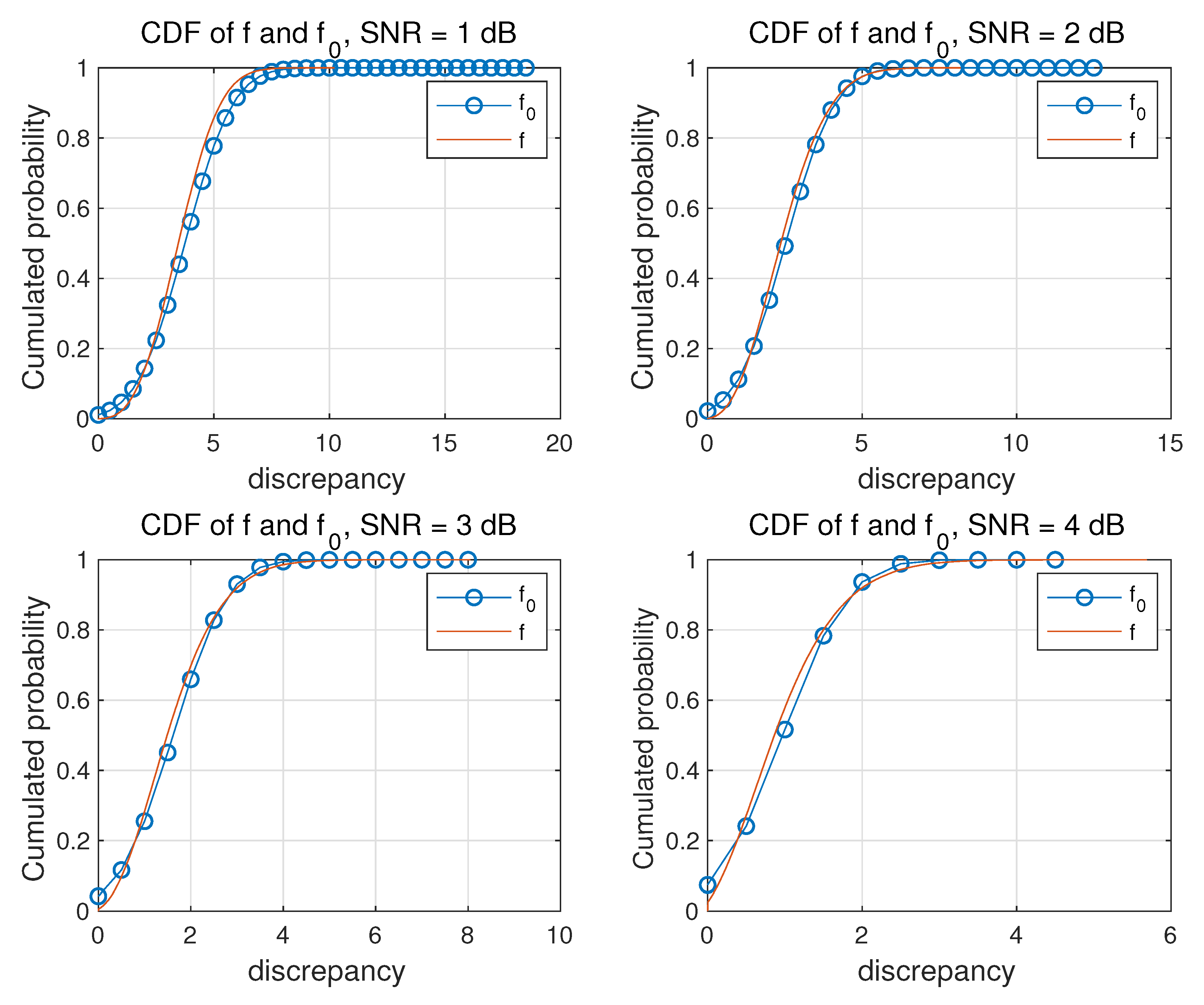




| SNR(dB) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 |
|---|---|---|---|---|---|---|---|---|
| 5.1573 | 4.1801 | 3.3512 | 2.6543 | 2.0743 | 1.5971 | 1.2096 | 0.8995 |
| SNR(dB) | |||
|---|---|---|---|
| 1 | 53.6% | 74.9% | 90.1% |
| 1.5 | 36.8% | 58.3% | 78.0% |
| 2 | 20.1% | 38.3% | 59.5% |
| 2.5 | 11.9% | 20.9% | 37.6% |
| 3 | 7.5% | 12.3% | 19.0% |
| 3.5 | 4.2% | 6.9% | 11.0% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Y.; Tu, G. A Low-Complexity Ordered Statistics Decoding Algorithm for Short Polar Codes. Appl. Sci. 2019, 9, 831. https://doi.org/10.3390/app9050831
Xing Y, Tu G. A Low-Complexity Ordered Statistics Decoding Algorithm for Short Polar Codes. Applied Sciences. 2019; 9(5):831. https://doi.org/10.3390/app9050831
Chicago/Turabian StyleXing, Yusheng, and Guofang Tu. 2019. "A Low-Complexity Ordered Statistics Decoding Algorithm for Short Polar Codes" Applied Sciences 9, no. 5: 831. https://doi.org/10.3390/app9050831
APA StyleXing, Y., & Tu, G. (2019). A Low-Complexity Ordered Statistics Decoding Algorithm for Short Polar Codes. Applied Sciences, 9(5), 831. https://doi.org/10.3390/app9050831




