Accurate Evaluation of the Average Probability of Error of Pulse Position Modulation in Amplified Optical Wireless Communications under Turbulence

Abstract

We present exact and approximate results on the average probability of error (PER) for pulse position modulation (PPM) in pre-amplified optical wireless communication systems with diversity. The approximate results are obtained by combining a new mathematical formula that we derive for binary PPM and an existing formula that associates higher-order PPM PERs with their binary PPM counterpart. The approximate results are compared with the exact in weak, moderate, and strong turbulence, and it is demonstrated that they are in good agreement under all fading conditions. Moreover, the accuracy of the approximation improves with the optical signal-to-noise ratio and the number of diversity branches that are used, which correspond to implementation scenarios that are typically anticipated in practice.

1. Introduction

Pulse position modulation (PPM) is particularly appealing in optical wireless communications (OWC) over lossy and turbulent channels [1,2], including space and underwater transmissions [3,4,5], since it provides a trade-off between bandwidth use and receiver sensitivity. Combined with optical amplification, PPM has the potential of providing a significant link gain but in OWCs it has been studied mainly for the binary modulation case [6,7,8,9,10]. The study of Q-ary PPM in pre-amplified OWC systems has received far less attention [11], even though binary PPM performs worse than on-off keying in terms of the receiver sensitivity that is required to target a specific probability of error (PER) [6].

The goal of this work is to assess the performance of Q-ary PPM in a pre-amplified OWC receiver, where the signal and noise statistics are governed by ${\chi }^2$ distributions. To this end, we first analyze the binary PPM case and derive analytical results for the PER using the non-central F-distribution. Similar to [6,10], we provide a closed-form analytical relation for the binary PPM PER, which requires a simple and finite summation of the hypergeometric function and can be computed efficiently using standard mathematical software. We then use a tight upper bound [12], which has been previously reported for Gaussian noise statistics, to approximate the Q-ary PPM PER with a combination of the modulation order Q and the binary PPM PER. By comparing the approximation with the exact results, which are obtained via numerical integration, we demonstrate that the upper bound is highly accurate in ${\chi }^2$ statistics. Moreover, the bound accuracy actually increases at lower PERs, which are of practical importance in any real-world OWC system.

Given the accuracy of the presented bound, we use it further to evaluate the average PER of the OWC system performance in weak, strong, and saturated turbulence. The evaluation is performed via numerical integration with and without the proposed approximation; the corresponding approximated and exact results are in good agreement with each other for $\gamma -\gamma$ and negative-exponential fading. In addition, the combination of Q-ary PPM, optical amplification, and spatial diversity is considered to be a means to further reduce the impact of turbulence. Spatial diversity is implemented by adding multiple identical pre-amplified receivers and adding the received signals in an equal-gain combiner (EGC) architecture that provides close to optimal PER performance. Despite the increased noise from the additional amplifiers and the split of the signal power over the diversity branches, the results show that very low average PERs can be achieved by combining the three proposed methods.

The rest of the paper is organized as follows: in Section 2 we detail the PER performance of Q-ary PPM in ${\chi }^2$ noise, and provide analytical relations and the approximation for calculating it. In Section 3 we present results for the average PER in weak, moderate, and strong fading and compare approximated and exact results. The approximation accuracy is discussed in all three fading regimes and it is shown that the accuracy improves with the diversity order and worsens with the modulation order. Finally, Section 4 summarizes the main results of this work and concludes the paper.

2. PPM Reception

2.1. Receiver Model

The considered setup is shown in Figure 1. L identical synchronized branches are used to detect and demodulate the optical signal and optical amplifiers are introduced prior to detection to improve the receiver sensitivity. Each amplifier provides a gain equal to G and adds a noise component of spectral density $N_0=n_{sp}hf(G-1)$, and optical filters at the amplifier outputs reject the out-of-band spontaneous emission noise. The optical signals are converted into electrical on photodiodes, and the electrical signals from all branches are added prior to demodulation. The demodulator estimates the optical signal energy at each respective PPM slot [6] and decides upon the transmitted symbol via soft-decision decoding.

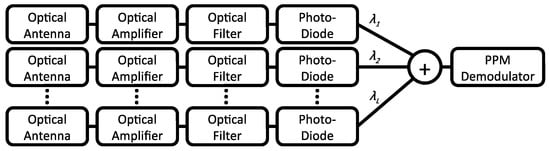
Figure 1. Amplification and diversity with equal-gain-combining. PPM: Pulse position modulation.

We now focus on acquiring the PER for one of the receiving branches, leaving the treatment of multiple branches for Section 3. Due to square-law detection on the photodiodes, the electrical signal at the photodiode output is a central ${\chi }_{k,0}^2$ random variable (RV) with a pdf equal to [6]

$$p_0\left(x;k\right)=\frac{x^{k-1}}{(k-1)!}{e}^{-x},$$

(1)

in slots where the optical signal is absent. Similarly, in the single slot that the optical signal is present, the electrical signal is a non-central ${\chi }_{k,\lambda }^2$ RV with a pdf equal to [6]

$$p_1\left(x;k,\lambda \right)=e^{-\left(x+\lambda \right)}{\left(\frac{x}{\lambda }\right)}^{\frac{k-1}{2}}{I}_{k-1}\left(2\sqrt{x\lambda }\right),$$

(2)

where $I_n(·)$ denotes the modified Bessel function of the first kind. In the previous equations, $\lambda =E/N_0=E_b/N_0{log}_{2}Q$ is the optical signal-to-noise-ratio (OSNR) at the output of the amplifier and $E=E_b{log}_{2}Q$ is the symbol energy after amplification. k corresponds to the degrees of freedom of the distribution and is determined by the optical filter and the signal bandwidths. For the purposes of this work k is considered to be an integer.

2.2. PPM PER

In soft-decision decoding, the demodulator selects the transmitted PPM symbol from the slot with the highest energy value. The PPM symbol error probability (SER) and PER are then given by

$$SER\left(k,\lambda \right)=1-\underset{0}{\overset{\infty }{\int }}{p}_1\left(x;k,\lambda \right)\times {\left[\underset{0}{\overset{x}{\int }}{p}_0\left(z;k\right)dz\right]}^{Q-1}dx,$$

(3)

and

$$P_e\left(k,\lambda \right)=\frac{Q/2}{Q-1}SER\left(k,\lambda \right),$$

(4)

respectively.

An analytical solution to the integral of (3) is not available to our knowledge for ${\chi }^2$ noise statistics, except for binary PPM. As it has already been discussed in [6], binary PPM performs worse than on-off keying and higher modulation orders must be considered in pre-amplified systems, which calls for numerical integration or approximation of (3). Numerical integration is feasible, but is also time consuming and therefore may find limited applicability the performance evaluation of OWC systems, where additional integrations are required to take into account the impact of turbulence in the received OSNR.

Within this context, an approximation of (3) is more appealing for calculating the average PER in OWC systems. Typically, a union bound approximation is used; however, it proves inaccurate in low OSNRs and we make use of a tighter approximation that has been proposed for Gaussian noise detection [12]. Following the results presented therein, the SER (and therefore PER) is bound by

$$SER\left(k,\lambda \right)\le 1-{\left(\underset{0}{\overset{\infty }{\int }}{p}_1\left(x;k,\lambda \right)\times \left[\underset{0}{\overset{x}{\int }}{p}_0\left(z;k\right)dz\right]dx\right)}^{Q-1}=1-{(1-P_{e,bppm}\left(k,\lambda \right))}^{Q-1}.$$

(5)

The expression inside the parenthesis equals the binary PPM PER and formulas for calculating it have been previously reported by [6,10]. An equivalent result can be obtained by noting than the soft-decision binary PPM demodulator compares two ${\chi }^2$ RVs, one non-central and one central, with equal degrees of freedom. An error occurs when the non-central RV is less than the central one, or whenever their ratio $f={\chi }_{k,\lambda }^2/{\chi }_{k,0}^2$ is less than unity. The ratio f follows the non-central F-distribution ([13], eq. (26.6.20)) with a cdf equal to

$$\begin{array}{cc}\hfill P(f\le F)=& P\left(F\right|v_1,v_2,\lambda )=e^{-\lambda }\sum _{i=0}^{\infty }\frac{{\lambda }^i}{i!}{I}_p(\frac{v_1}{2}+i,\frac{v_2}{2}),\hfill \\ \hfill p=& \frac{v_{1}F}{v_{1}F+v_2},\hfill \end{array}$$

(6)

where $I_p(·)$ denotes the regularized incomplete beta function. Thus, the binary PPM PER is calculated from the F-distribution for $F=1$, $v_1=v_2=2k$

$$P_{e,bppm}\left(k,\lambda \right)=e^{-\lambda }\sum _{i=0}^{\infty }\frac{{\lambda }^i}{i!}{I}_{1/2}(k+i,k).$$

(7)

For an integer k it holds that ([13], eq. (26.5.7))

$$I_{1/2}(k+i,k)={(1/2)}^{2k+i-1}\sum _{j=0}^{k-1}\left(\genfrac{}{}{0pt}{}{2k+i-1}{j}\right),$$

(8)

and it is straightforward to show that

$$\begin{array}{ccc}\hfill P_{e,bppm}\left(k,\lambda \right)& \hfill =& e^{-\lambda }\sum _{j=0}^{\infty }\frac{{\lambda }^i}{i!}{(1/2)}^{2k+i-1}\sum _{j=0}^{k-1}\left(\genfrac{}{}{0pt}{}{2k+i-1}{j}\right)\hfill \\ & \hfill =& {(1/2)}^{2k-1}{e}^{-\lambda }\sum _{j=0}^{k-1}\sum _{i=0}^{\infty }\left(\genfrac{}{}{0pt}{}{2k+i-1}{j}\right)\frac{{(\lambda /2)}^i}{i!}\hfill \\ & \hfill =& {(1/2)}^{2k-1}{e}^{-\lambda }\sum _{j=0}^{k-1}\left(\genfrac{}{}{0pt}{}{2k-1}{j}\right){}_1{F}_1\left(2k;2k-j;\lambda /2\right)\hfill \\ & \hfill =& {(1/2)}^{2k-1}{e}^{-\lambda /2}\sum _{j=0}^{k-1}\left(\genfrac{}{}{0pt}{}{2k-1}{j}\right){}_1{F}_1\left(-j;2k-j;-\lambda /2\right),\hfill \end{array}$$

(9)

where ${}_1{F}_1\left(·;·;·\right)$ denotes the hypergeometric function. The last relation only requires a finite summation, since the hypergeometric function reduces to a polynomial for the given representation, and it enables the efficient and fast calculation of the PPM PER in standard mathematical software that implements ${}_1{F}_1\left(·;·;·\right)$. Following (4), (5) and (9), an upper bound for the PPM PER is finally calculated as

$$P_e\left(k,\lambda \right)\le \frac{Q/2}{Q-1}\left[1-{\left(1-{(1/2)}^{2k-1}{e}^{-\lambda /2}\sum _{j=0}^{k-1}\left(\genfrac{}{}{0pt}{}{2k-1}{j}\right){}_1{F}_1\left(-j;2k-j;-\lambda /2\right)\right)}^{Q-1}\right].$$

(10)

2.3. PER Results

The PER is plotted in Figure 2 against $E_b/N_0$ for several degrees of freedom k and modulation orders Q. Exact PER results are obtained via the numerical integration of (3), while approximate results are obtained from (10). As it is expected, the binary PPM results coincide, which validates the soundness of the PER derivation. A deviation between exact and approximate results is also observed at increasing modulation orders. The deviation becomes less important as the OSNR gets better, and the approximation is highly accurate for PERs lower than ${10}^{-3}$. Given the accuracy of the approximation in ${\chi }^2$ statistics, we further explore its applicability in assessing the impact of turbulence on OWC systems in the following Section.

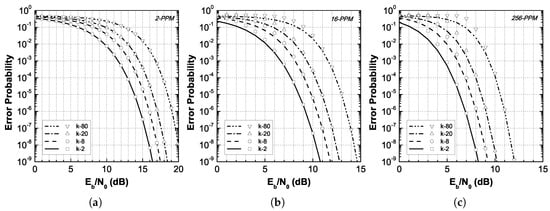
Figure 2. Probability of error (PER) vs. $E_b/N_0$ for $Q=2,16,256$. The plot lines and points correspond to the exact and approximated results, respectively.

3. Average PER in Turbulent Channels

3.1. Channel Model

Several applications of OWC systems, including terrestrial, ground-to-space, and underwater high-speed connections, require the transmission of the optical beams through long lengths of turbulent media (i.e., the atmosphere or water volumes). This transmission introduces fluctuations in the received OSNR $\lambda$, which negatively affect the OWC system performance. Since the media response is stochastic, $\lambda$ follows the channel fluctuations and becomes a RV that is distributed according to their intensity (weak, moderate, or strong). The system performance is then summarized by an average PER, which is calculated from the instantaneous PER, presented earlier, and the distribution function of the OSNR fluctuations $f_{\lambda }\left(y\right)$, following

$${\overline{P}}_e=\underset{y}{\int }{P}_e\left(k,y\right)f_{\lambda }\left(y\right)dy.$$

(11)

The impact of turbulence can be partially alleviated by introducing multiple receivers that are spatially separated by a few cm and operate in parallel, as shown in Figure 1. The electrical signals from all $\ell =1,\dots ,L$ receivers are added prior to detection in a simple EGC architecture, which achieves almost-optimal signal combining in ${\chi }^2$ statistics [14]. The sum of ${\chi }^2$ RVs (either central or non-central) also follows a ${\chi }^2$ distribution with parameters

$$\begin{array}{cc}\hfill k_{egc}=& \sum _{\ell =1}^L{k}_{\ell },\hfill \\ \hfill {\lambda }_{egc}=& \sum _{\ell =1}^L{\lambda }_{\ell },\hfill \end{array}$$

(12)

where $k_{\ell }$ and ${\lambda }_{\ell }$ denote the degrees of freedom and instantaneous OSNR, respectively, at receiver ℓ. For identical receivers $k_{\ell }=k$, we find that the EGC output is either a non-central or a central RV with $kL$ degrees of freedom, depending on whether the PPM slot contains the symbol energy or not. In the non-central case, the combiner OSNR equals the sum of the individual receiver OSNRs that are not equal, but depend on the instantaneous fading conditions of each transmission path. As a result, the instantaneous EGC PER can be readily derived from the single-receiver case by using

$$P_{e,egc}=P_e\left(kL,{\lambda }_{egc}\right)$$

(13)

and the average PER is obtained from

$${\overline{P}}_{e,egc}=\underset{y}{\int }{P}_e\left(kL,y\right)f_{{\lambda }_{egc}}\left(y\right)dy,$$

(14)

where $f_{{\lambda }_{egc}}\left(y\right)$ is the distribution function of the summed OSNR fluctuations.

3.2. Weak and Moderate Fading

In weak and moderate fading, the OSNR fluctuations at each branch can be accurately described by the $\gamma -\gamma$ distribution [15,16,17]

$$f_{\lambda }\left(y\right)=\frac{2{\left(m_y{m}_x\right)}^{\frac{m_y+m_x}{2}}}{\Gamma \left(m_x\right)\Gamma \left(m_y\right)y}{\left(\frac{Ly}{\overline{\lambda }}\right)}^{\frac{m_y+m_x}{2}}{K}_{m_y-m_x}\left(2\sqrt{m_y{m}_x\frac{Ly}{\overline{\lambda }}}\right),$$

(15)

where $m_x$ and $m_y$ are related to the effective numbers of large and small-scale scatterers in the OWC link and $\overline{\lambda }=\overline{E}/N_0=\overline{E_b}/N_0{log}_{2}Q$ is the average OSNR. $\Gamma \left(·\right)$ and $K_v\left(·\right)$ denote the Gamma and second-kind modified Bessel functions, respectively. For a plane wave transmission [15], $m_x$ and $m_y$ are calculated from

$$\begin{array}{cc}\hfill m_x=& \frac{1}{exp\left({\sigma }_{lnx}^2\right)-1},\hfill \\ \hfill m_y=& \frac{1}{exp\left({\sigma }_{lny}^2\right)-1},\hfill \end{array}$$

(16)

where the log-intensity variances are given by

$$\begin{array}{cc}\hfill {\sigma }_{lnx}^2=& \frac{0.49{\sigma }_R^2}{{\left(1+1.11{\sigma }_R^{12/5}\right)}^{7/6}},\hfill \\ \hfill {\sigma }_{lny}^2=& \frac{0.51{\sigma }_R^2}{{\left(1+0.69{\sigma }_R^{12/5}\right)}^{5/6}},\hfill \end{array}$$

(17)

and the Rytov variance is equal to

$${\sigma }_R^2=1.23C_n^2{k}^{7/6}{l}^{11/6}.$$

(18)

l is the link length, k is the wavenumber and $C_n^2$ is the refractive index structure parameter.

Table 1 summarizes the $m_x$ and $m_y$ values that have been obtained for a link that operates at 1550 nm and a structure constant of $C_n^2=4.58·{10}^{-13}$ m${}^{-2/3}$. The link length is either 100 m (weak turbulence) or 500 m (moderate turbulence). The EGC output fading distribution $f_{{\lambda }_{egc}}\left(y\right)$ is not known, but it can be efficiently approximated by the $\alpha -\mu$ distribution [18]

$$\begin{array}{c}\hfill f_{{\lambda }_{egc}}\left(y\right)=\frac{\alpha {\mu }^{\mu }{y}^{\alpha \mu -1}}{{\widehat{y}}^{\alpha \mu }\Gamma \left(\mu \right)}exp\left(-\mu \frac{y^{\alpha }}{{\widehat{y}}^{\alpha }}\right).\end{array}$$

(19)

Table 1. $\gamma -\gamma$ distribution parameters.

l (m)	${\mathbf{m}}_{\mathbf{x}}$	${\mathbf{m}}_{\mathbf{y}}$
100	16.53	14.91
500	4.04	1.53

The parameters $\alpha$, $\mu$ and $\widehat{y}$ are calculated from $m_x$, $m_y$ and L using the methodology that is presented in [19] and Table 2 summarizes their values for the link and diversity arrangements under consideration.

Table 2. $\alpha -\mu$ distribution parameters.

	l–100 m			l–500 m
	L-2	L-5	L-10	L-2	L-5	L-10
$\alpha$	0.49	0.48	0.47	0.51	0.46	0.43
$\mu$	64.76	167.71	339.61	7.72	23.09	50.45
$L\widehat{y}$	1.97	4.97	9.97	1.78	4.73	9.71

Figure 3 presents the average PER of the OWC system in weak $\gamma -\gamma$ fading ($l=100$ m) for both the exact and approximate instantaneous PER relations. The noise modes and the diversity order are equal to $k=2,8$ and $L=1,2,5,10$, respectively, resulting in 2–80 degrees of freedom in the ${\chi }^2$ distributions. The results demonstrate that the approximation is in good agreement with the exact relation in weak fading. In addition, it becomes more accurate at higher OSNRs where the average PER improves. On the other hand, the modulation order, diversity order, and number of noise modes do not seem to affect the approximation accuracy in weak fading. The results also show that the PPM modulation order plays the most important role than diversity in weak fading. 16-PPM provides a 5 dB OSNR gain, while 256-PPM introduces 2 dB on top of that. The diversity gain is approximately 3 dB at high OSNRs, but the use of amplified diversity may actually degrade the performance in low OSNRs due to the fact that excess optical noise is introduced in the system.

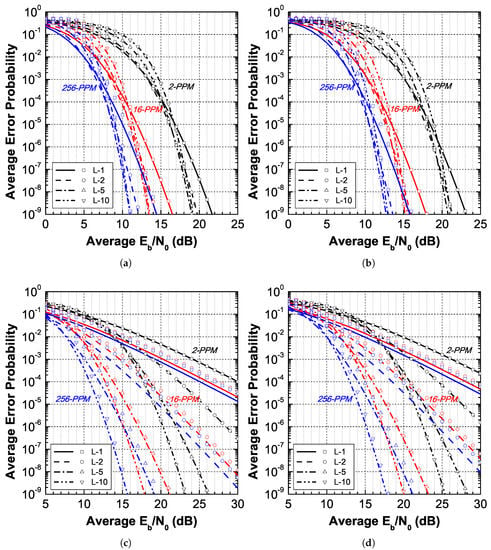
Figure 3. Average PER vs $\overline{E_b}/N_0$ for $Q=2,16,256$ in weak (top row) and moderate (bottom row) $\gamma -\gamma$ fading. The plot lines and points correspond to the exact and approximated results, respectively. The optical noise modes are equal to $k=2$ (left column) and $k=8$ (right column).

The conclusions are somewhat different in moderate $\gamma -\gamma$ fading, which is also presented in Figure 3. Again, good agreement between approximate and exact results is observed, and the accuracy improves with the OSNR and with the diversity order. This is expected since fading becomes less intense when more branches are introduced, and it was demonstrated earlier that the approximation is highly accurate in weak fading. One the other hand, the accuracy is negatively affected from increasing the modulation order.

One may also verify that the modulation and diversity orders now both strongly affect the system performance. The diversity, however, now plays the most important role: without any diversity it is possible to improve the average PER to some extent by increasing the modulation order, but it is evident that the introduction of a second branch is more critical and that a dual-branch binary PPM receiver outperforms its single-branch 256-PPM counterpart. Similar observations can be made for higher diversity orders and a 16-PPM receiver with $L=10$ branches outperforms a 256-PPM receiver with $L=5$ branches at high OSNRs, even though the former arrangement doubles the inband optical noise that enters the receiver. As such, one may exchange hardware complexity (diversity branches) with excess bandwidth (modulation order) to achieve the desired performance in moderate fading.

3.3. Strong Fading

In longer links, the fading saturates and the OSNR fluctuations at each branch are modelled by a negative-exponential distribution [15]

$$f_{\lambda }\left(y\right)=\frac{L}{\overline{\lambda }}exp\left(-\frac{Ly}{\overline{\lambda }}\right).$$

(20)

The corresponding EGC output follows and Erlang distribution

$$f_{{\lambda }_{egc}}\left(y\right)={\left(\frac{L}{\overline{\lambda }}\right)}^L\frac{y^{L-1}}{\left(L-1\right)!}exp\left(-\frac{Ly}{\overline{\lambda }}\right).$$

(21)

Using (14) and (21) we evaluate the average BER in strong fading, and the results are presented in Figure 4. Good agreement between the approximate and exact results is observed in this fading regime, as well, and the key observations remain same as in the $\gamma -\gamma$ case: the approximation accuracy worsens with the modulation order and improves with the diversity order and the OSNR.

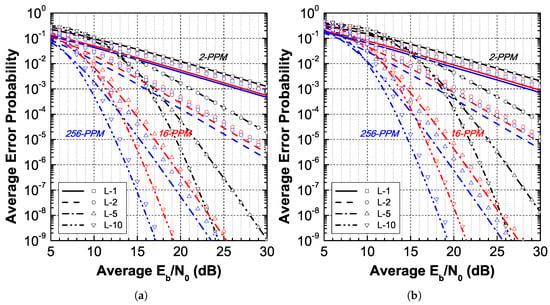
Figure 4. Average PER vs $\overline{E_b}/N_0$ for $Q=2,16,256$ in strong fading. The plot lines and points correspond to the exact and approximated results, respectively. $k=2$ (a) and $k=8$ (b).

4. Conclusions

We have presented results on the PER performance of PPM in pre-amplified OWC systems with diversity. To this end, we derived an exact expression for the binary PPM PER and combined it with an existing approximation to extend it to Q-ary PPM. We demonstrated that the combination of the new and existing formulas is accurate for ${\chi }^2$ noise statistics, which model the amplified optical receiver operation, and tested its accuracy in weak, moderate, and strong fading. The approximated results were in good agreement with the exact ones in all fading scenarios, and it was shown that the approximation becomes more accurate with the diversity order and the OSNR. These conditions are typically expected in any practical OWC system that operates in low PERs, and therefore this work may prove of use in designing high performance systems.