Comparison for the Effect of Different Attachment of Point Masses on Vibroacoustic Behavior of Parabolic Tapered Annular Circular Plate
Abstract
:1. Introduction
2. Materials and Methods
2.1. Free Vibration of Plate
2.2. Acoustic Radiation Formulation of Plate with Point Masses
2.3. Thickness Variation of the Plate
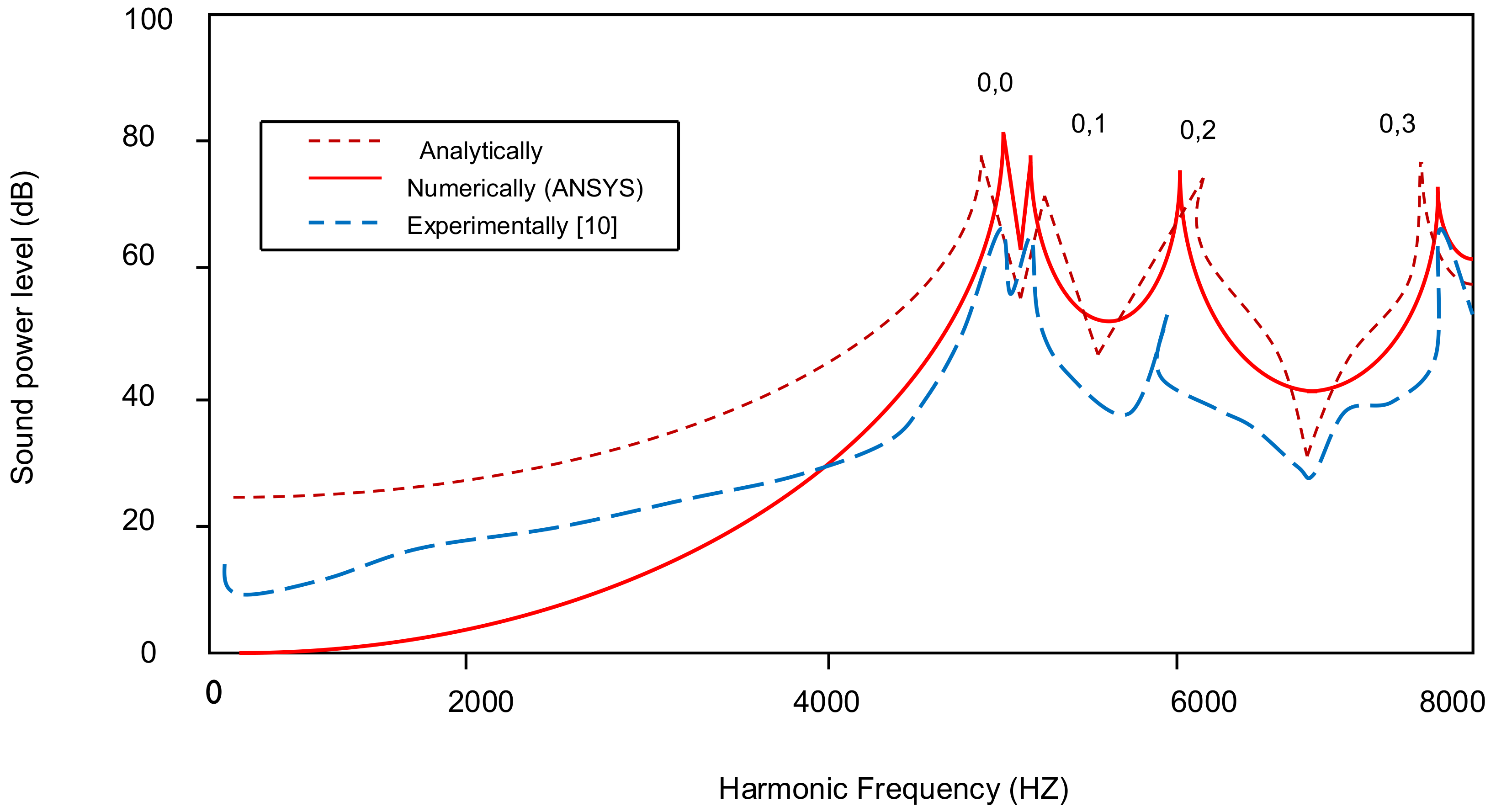
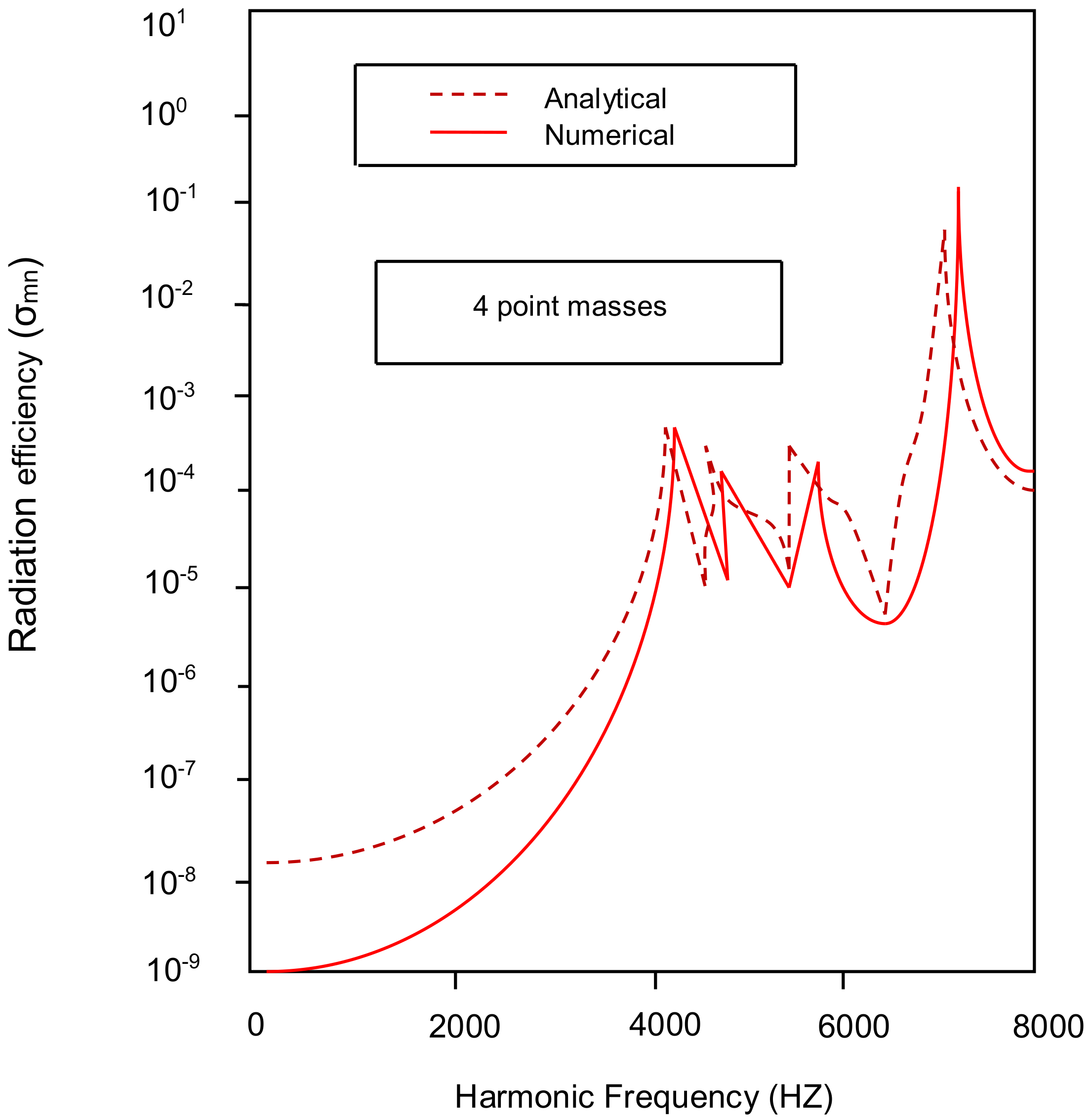
3. Validation of the Present Study
4. Result and Discussion
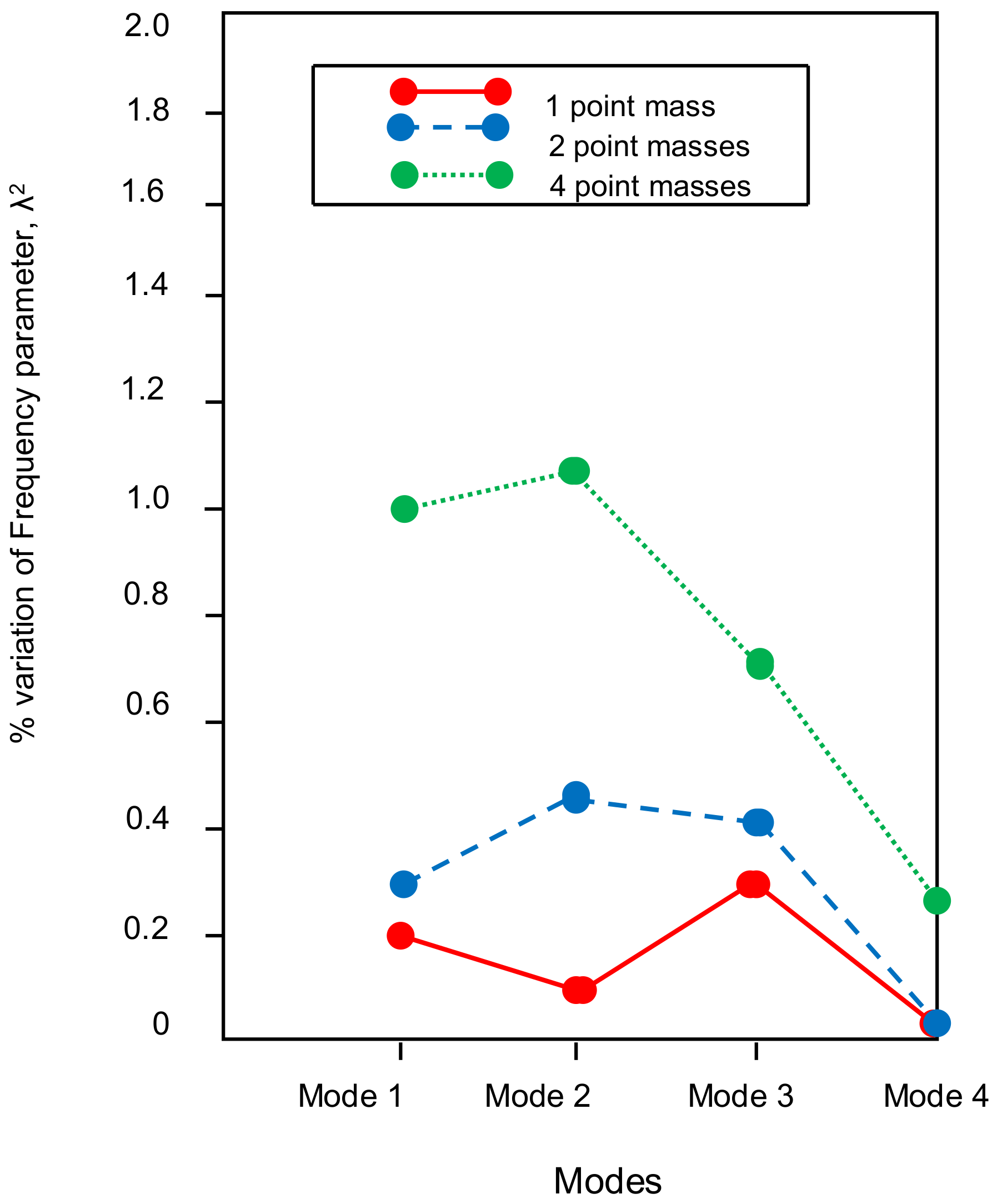
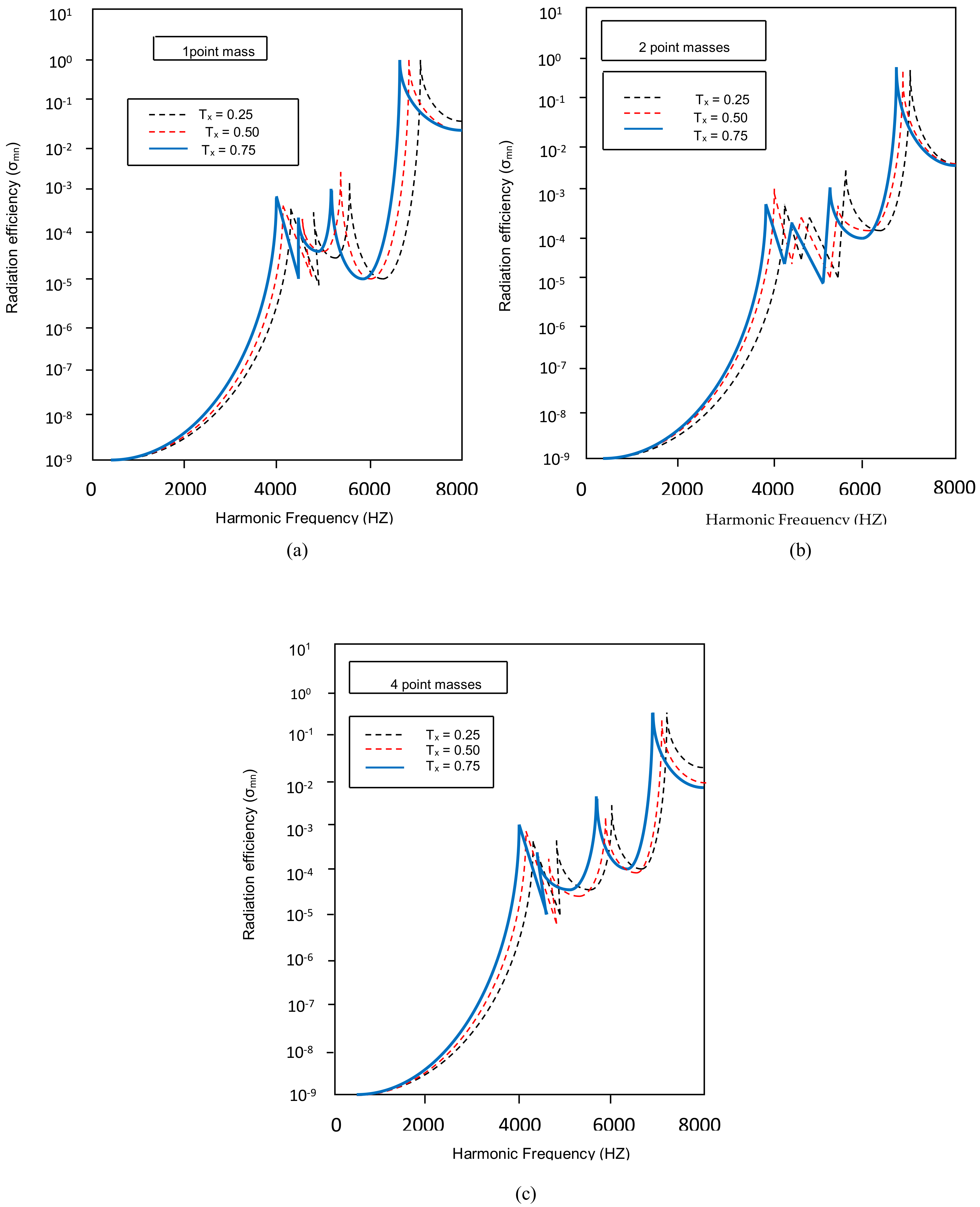
4.1. Effect of Natural Frequency Parameter (λ2) of Plate with Different Combinations of Point Masses with Different Taper Ratios
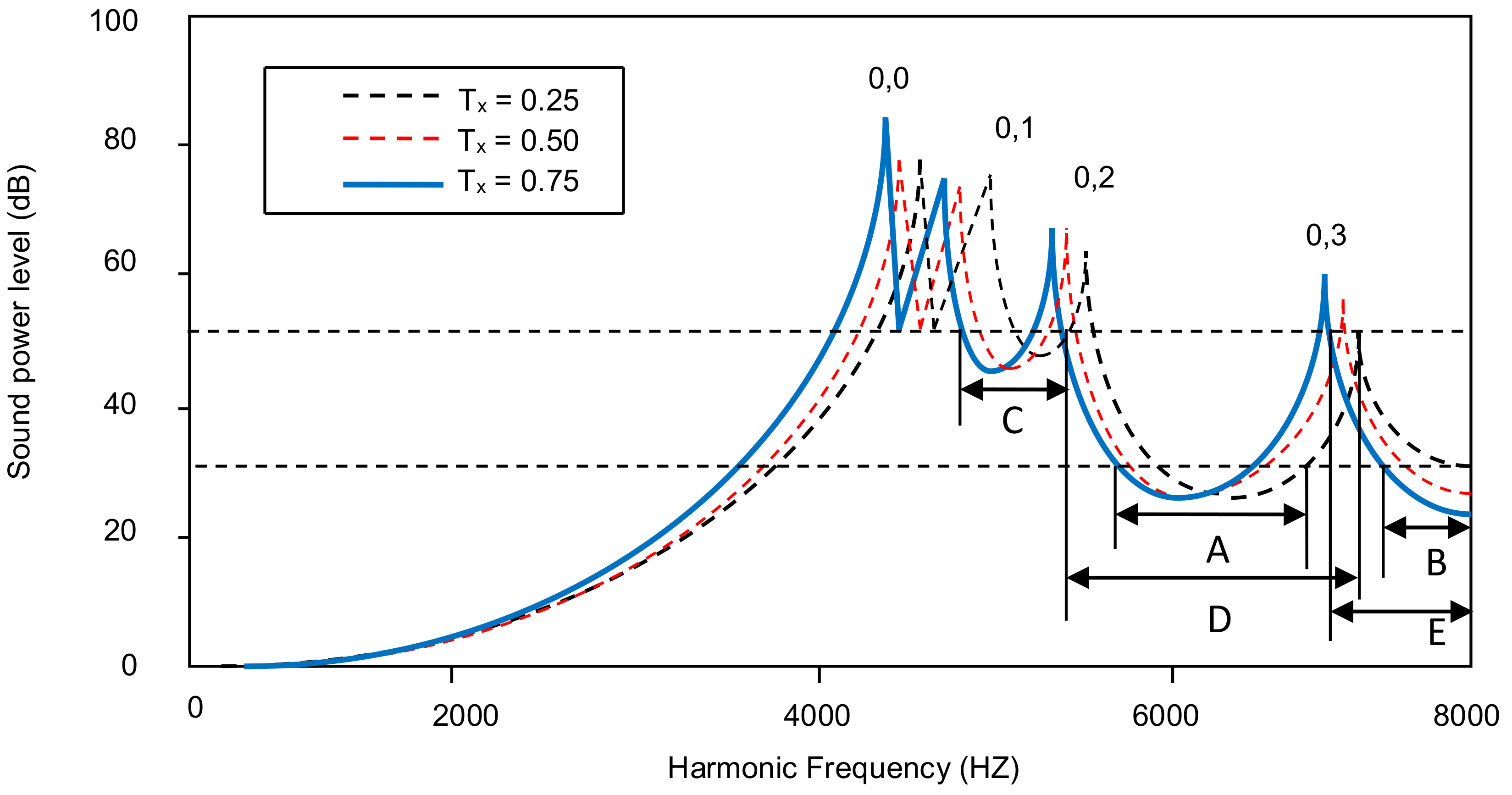
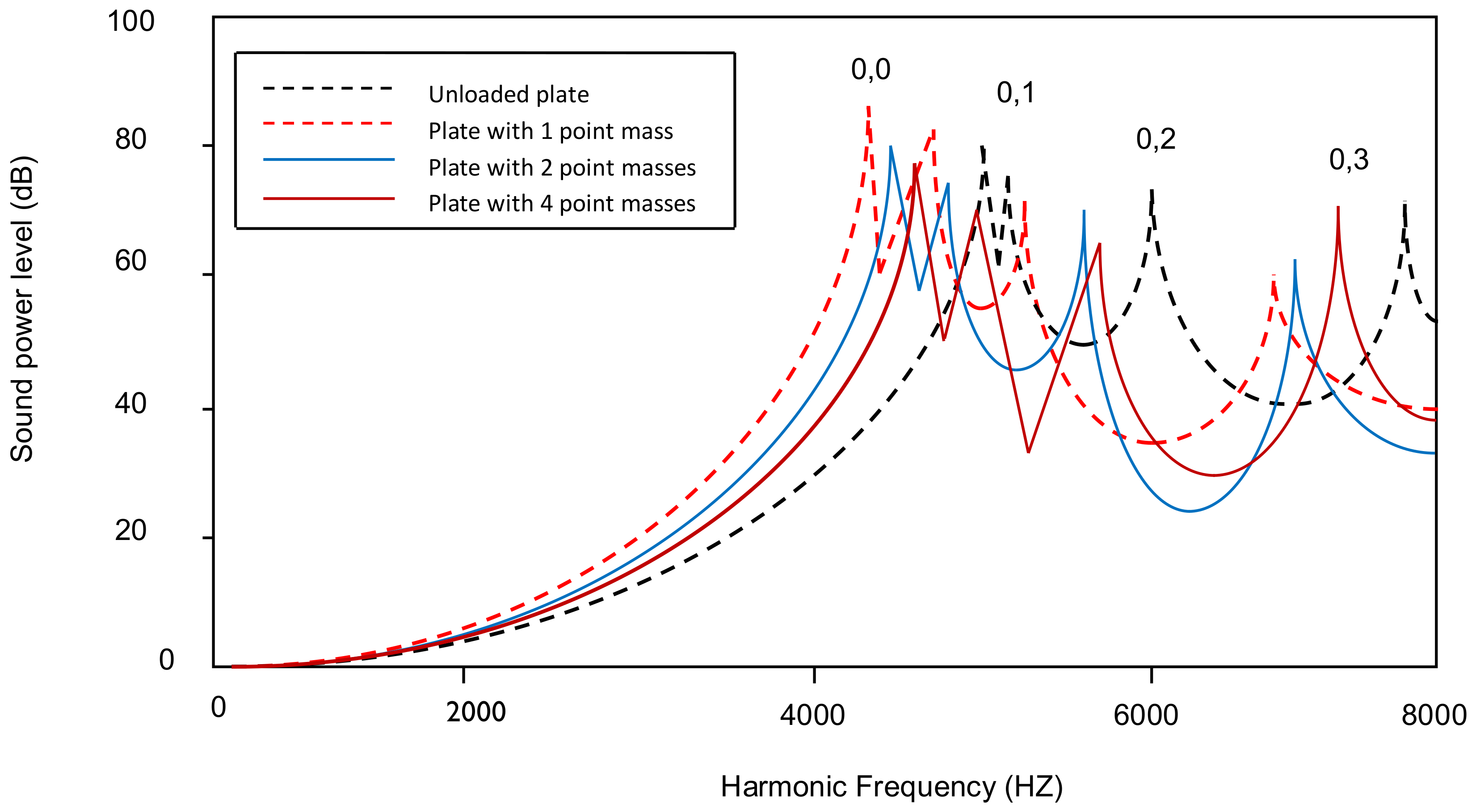
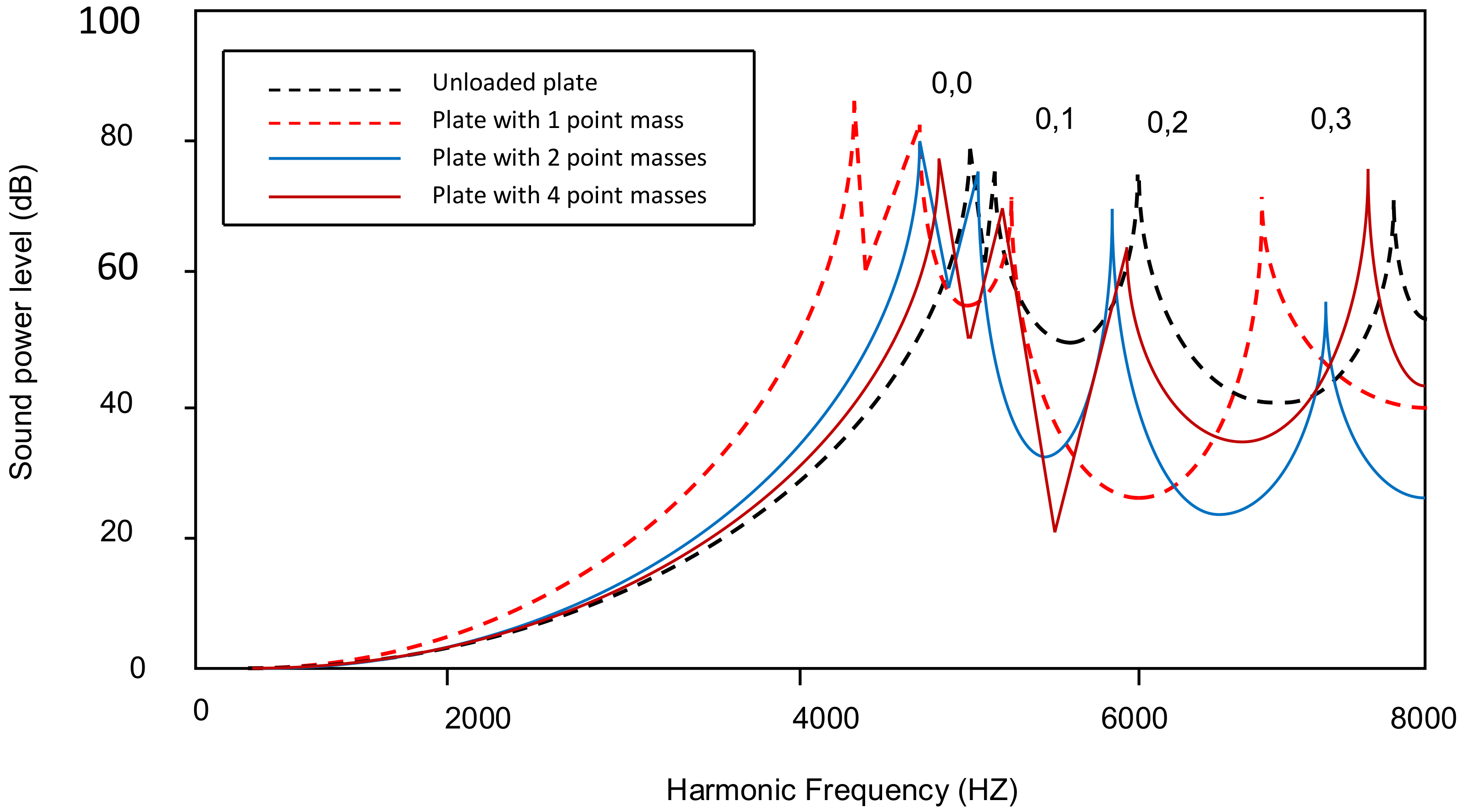
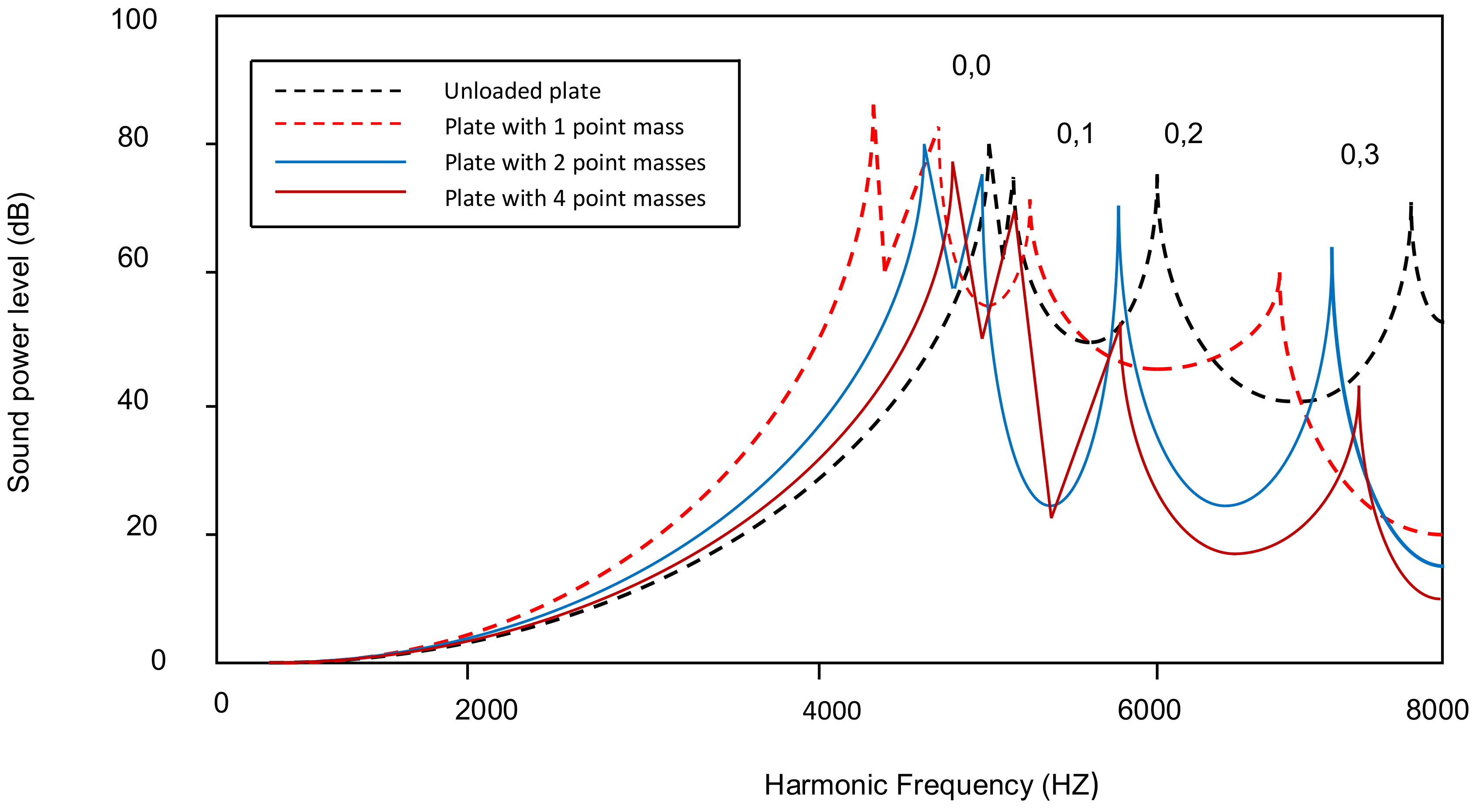
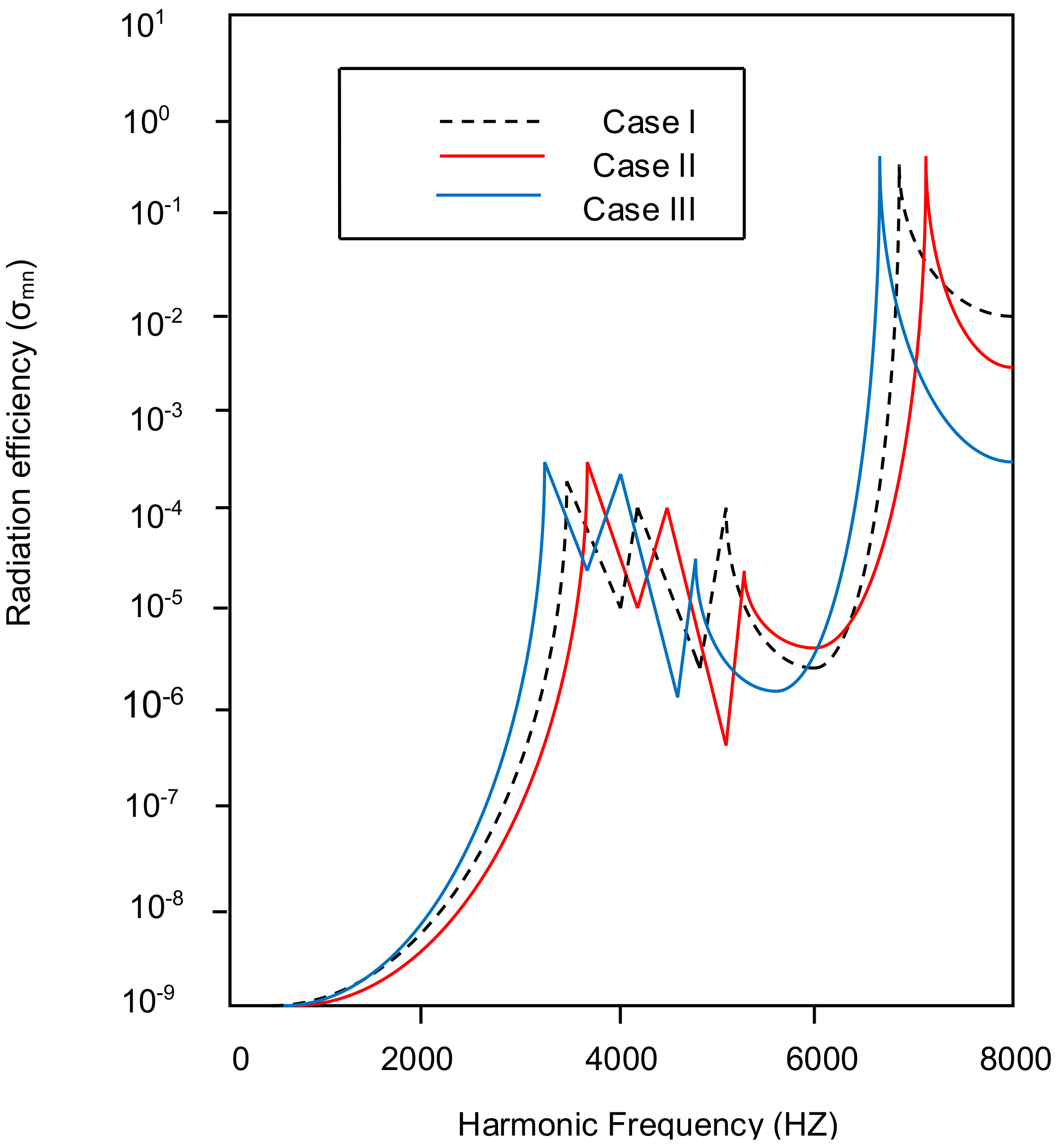
4.2. Acoustic Radiation of Tapered Annular Circular Plate with Different Attachment of Point Masses with Different Taper Ratios
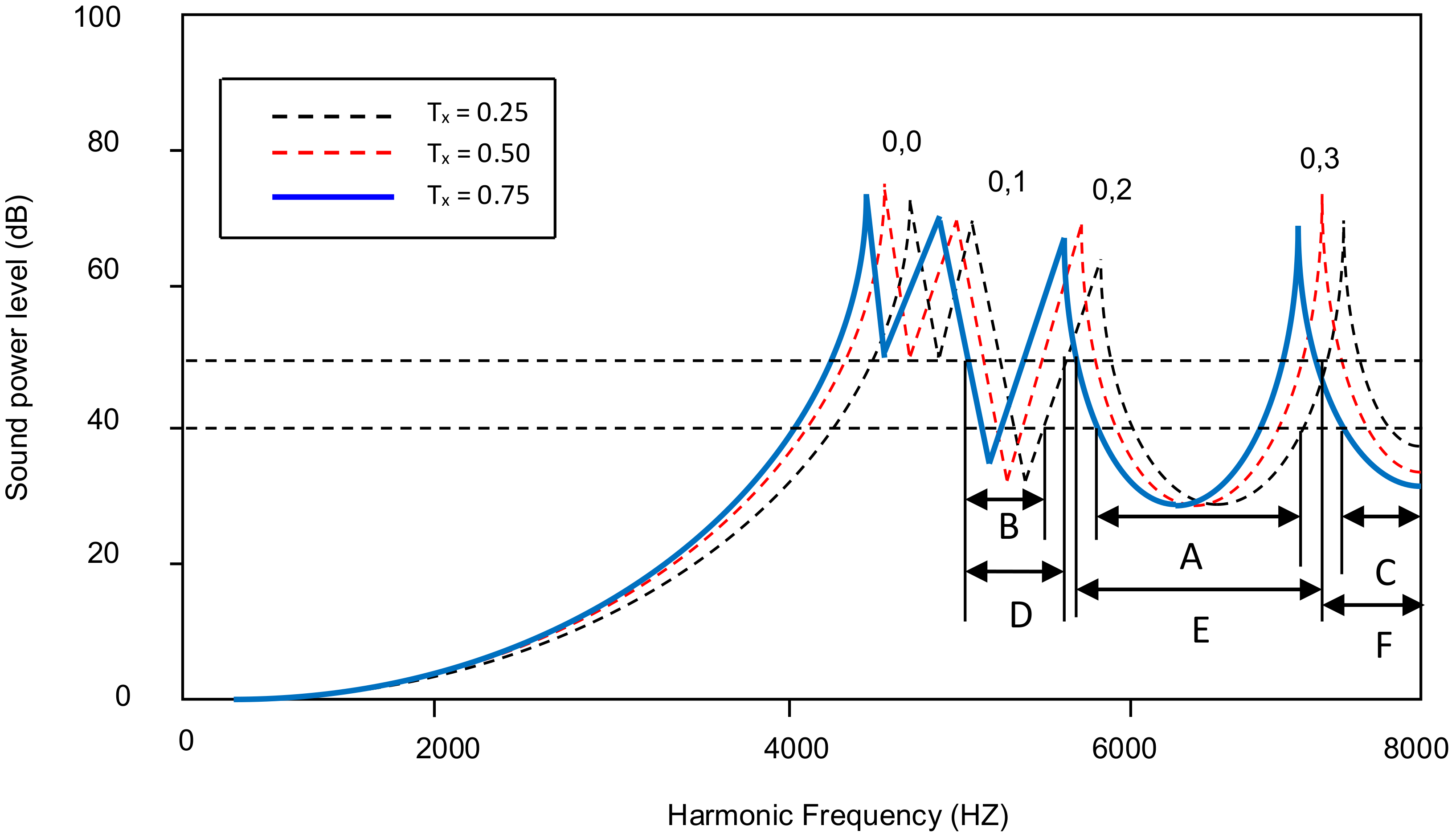
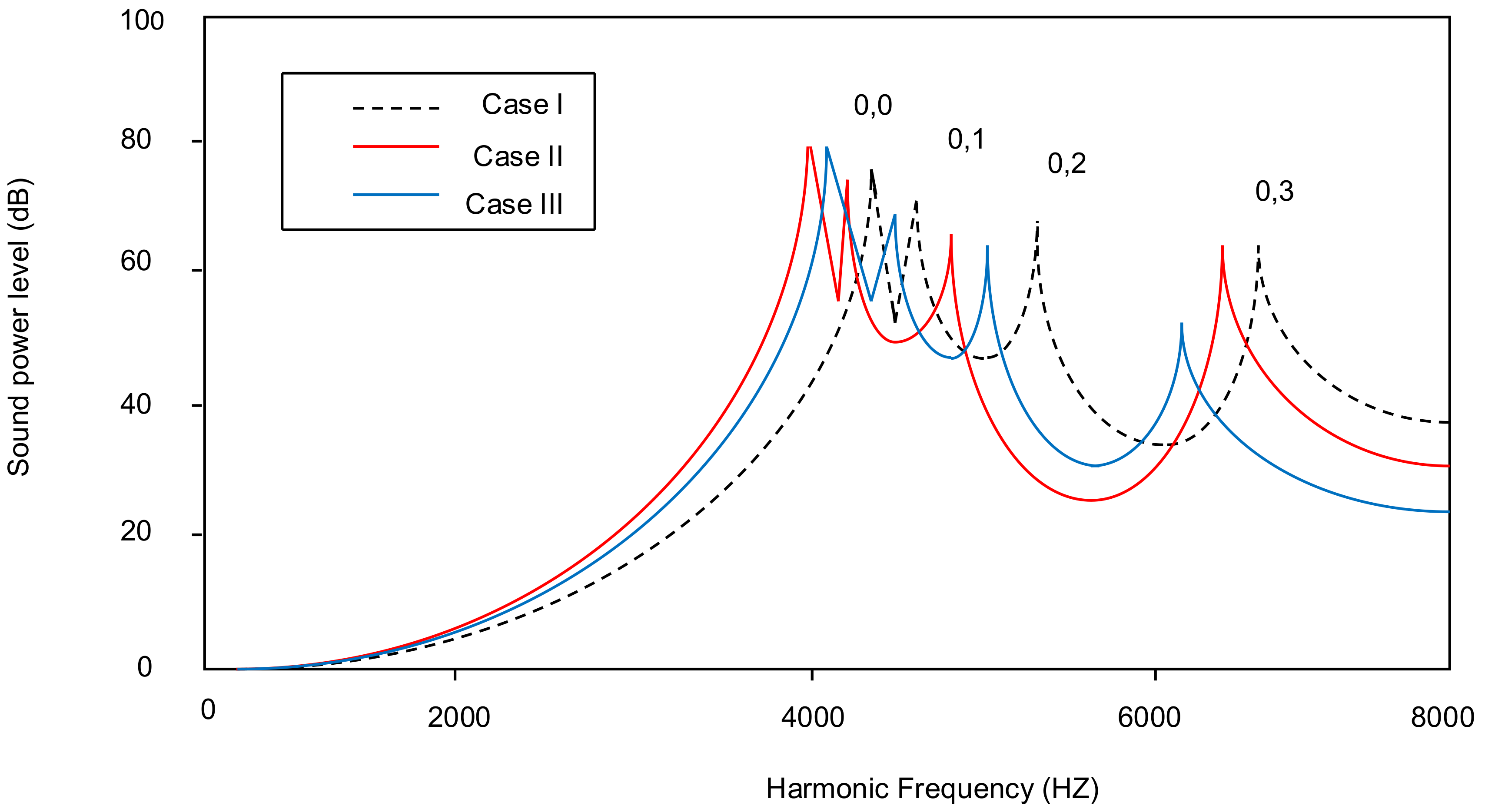
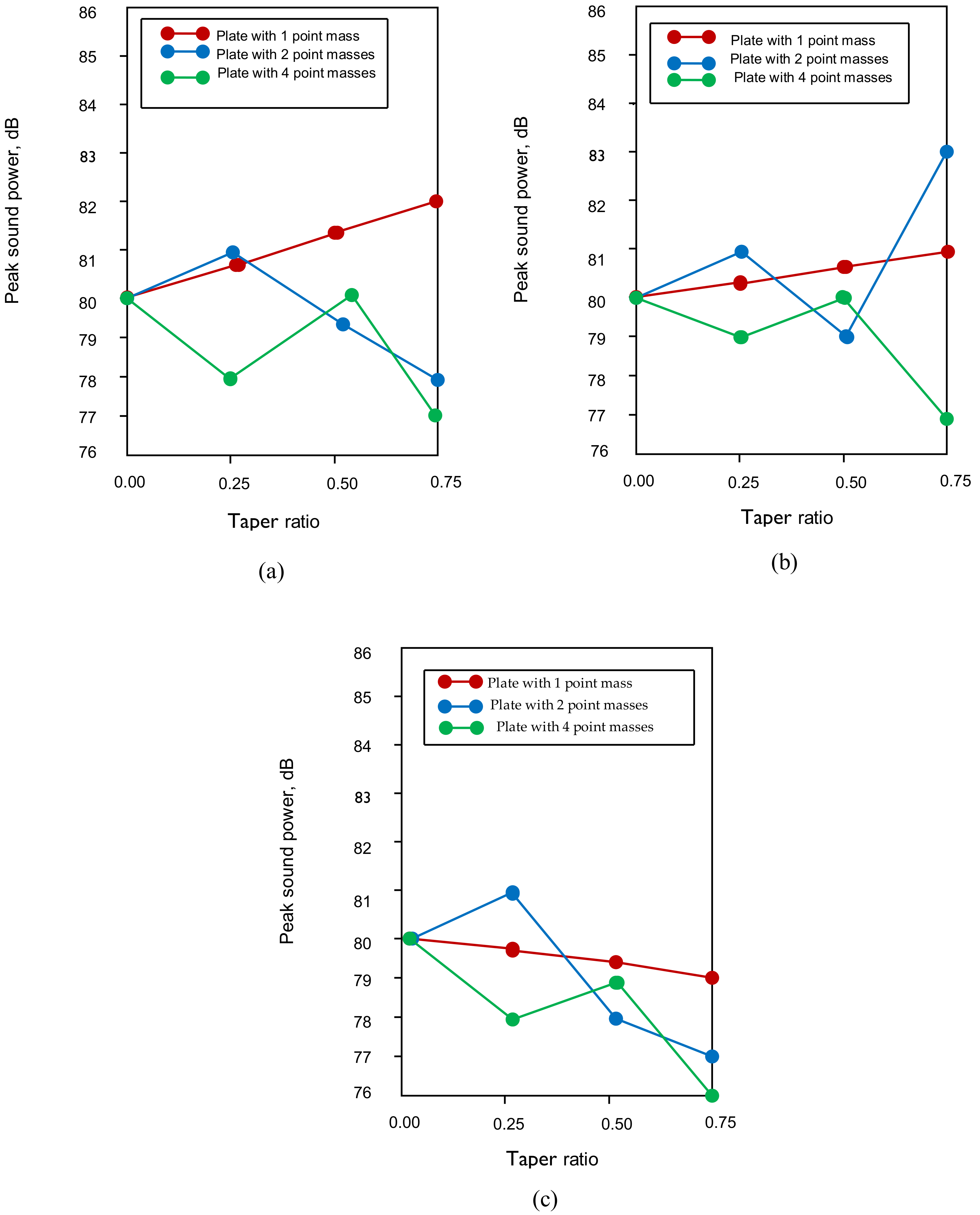
4.3. Peak Sound Power Level Variation with Different Taper Ratios for All Combinations of Point Masses Attached to a Plate
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, C.M.; Hong, G.M.; Tan, T.J. Elasting buckling of tapered circular plates. Comput. Struct. 1995, 55, 1055–1061. [Google Scholar] [CrossRef]
- Gupta, A.P.; Goyal, N. Forced asymmetric response of linearly tapered circular plates. J. Sound Vib. 1999, 220, 641–657. [Google Scholar] [CrossRef]
- Vivio, F.; Vullo, V. Closed form solutions of axisymmetric bending of circular plates having non-linear variable thickness. Int. J. Mech. Sci. 2010, 52, 1234–1252. [Google Scholar] [CrossRef]
- Sharma, S.; Lal, R.; Neelam, N. Free transverse vibrations of non-homogeneous circular plates of linearly varying thickness. J. Int. Acad. Phys. Sci. 2011, 15, 187–200. [Google Scholar]
- Wang, C.Y. The vibration modes of concentrically supported free circular plates. J. Sound Vib. 2014, 333, 835–847. [Google Scholar] [CrossRef]
- Liu, T.; Kitipornchai, S.; Wang, C.M. Bending of linearly tapered annular Mindlin plates. Int. J. Mech. Sci. 2001, 43, 265–278. [Google Scholar] [CrossRef]
- Duana, W.H.; Wang, C.M.; Wang, C.Y. Modification of fundamental vibration modes of circular plates with free edges. J. Sound Vib. 2008, 317, 709–715. [Google Scholar] [CrossRef]
- Gupta, U.S.; Lal, R.; Sharma, S. Vibration of non-homogeneous circular Mindlin plates with variable thickness. J. Sound Vib. 2007, 302, 1–17. [Google Scholar] [CrossRef]
- Kang, J.H. Three-dimensional vibration analysis of thick circular and annular plates with nonlinear thickness variation. Comput. Struct. 2003, 81, 1663–1675. [Google Scholar] [CrossRef]
- Lee, H.; Singh, R. Acoustic radiation from out-of-plane modes of an annular disk using thin and thick plate theories. J. Sound Vib. 2005, 282, 313–339. [Google Scholar] [CrossRef]
- Thompson, W., Jr. The computation of self- and mutual-radiation impedances for annular and elliptical pistons using Bouwkamp integral. J. Sound Vib. 1971, 17, 221–233. [Google Scholar] [CrossRef]
- Levine, H.; leppington, F.G. A note on the acoustic power output of a circular plate. J. Sound Vib. 1988, 21, 269–275. [Google Scholar]
- Rdzanek, W.P., Jr.; Engel, W. Asymptotic formula for the acoustic power output of a clamped annular plate. Appl. Acoust. 2000, 60, 29–43. [Google Scholar] [CrossRef]
- Wodtke, H.W.; Lamancusa, J.S. Sound power minimization of circular plates through damping layer placement. J. Sound Vib. 1998, 215, 1145–1163. [Google Scholar] [CrossRef]
- Wanyama, W. Analytical Investigation of the Acoustic Radiation from Linearly-Varying Circular Plates. Doctoral Dissertation, Texas Tech University, Lubbock, TX, USA, 2000. [Google Scholar]
- Lee, H.; Singh, R. Self and mutual radiation from flexural and radial modes of a thick annular disk. J. Sound Vib. 2005, 286, 1032–1040. [Google Scholar] [CrossRef]
- Cote, A.F.; Attala, N.; Guyader, J.L. Vibro acoustic analysis of an unbaffled rotating disk. J. Acoust. Soc. Am. 1998, 103, 1483–1492. [Google Scholar] [CrossRef]
- Jeyraj, P. Vibro-acoustic behavior of an isotropic plate with arbitrarily varying thickness. Eur. J. Mech. A/Solds 2010, 29, 1088–1094. [Google Scholar] [CrossRef]
- Ranjan, V.; Ghosh, M.K. Forced vibration response of thin plate with attached discrete dynamic absorbers. Thin Walled Struct. 2005, 43, 1513–1533. [Google Scholar] [CrossRef]
- Kumar, B.; Ranjan, V.; Azam, M.S.; Singh, P.P.; Mishra, P.; PriyaAjit, K.; Kumar, P. A comparison of vibro acoustic response of isotropic plate with attached discrete patches and point masses having different thickness variation with different taper ratios. Shock Vib. 2016, 2016, 8431431. [Google Scholar]
- Lee, M.R.; Singh, R. Analytical formulations for annular disk sound radiation using structural modes. J. Acoust. Soc. Am. 1994, 95, 3311–3323. [Google Scholar] [CrossRef]
- Rdzanek, W.J.; Rdzanek, W.P. The real acoustic power of a planar annular membrane radiation for axially-symmetric free vibrations. Arch. Acoust. 1997, 4, 455–462. [Google Scholar]
- Doganli, M. Sound Power Radiation from Clamped-Clamped Annular Plates. Master’s Thesis, Texas Tech University, Lubbock, TX, USA, 2000. [Google Scholar]
- Nakayama, I.; Nakamura, A.; Takeuchi, R. Sound Radiation of a circular plate for a single sound pulse. Acta Acust. United Acust. 1980, 46, 330–340. [Google Scholar]
- Hasegawa, T.; Yosioka, K. Acoustic radiation force on a solid elastic sphere. J. Acoust. Soc. Am. 1969, 46, 1139–1143. [Google Scholar] [CrossRef]
- Lee, H.; Singh, R. Determination of sound radiation from a simplified disk brake rotor using a semi-analytical method. Noise Control Eng. J. 2000, 52. [Google Scholar] [CrossRef]
- Squicciarini, G.; Thompson, D.J.; Corradi, R. The effect of different combinations of boundary conditions on the average radiation efficiency of rectangular plates. J. Sound Vib. 2014, 333, 3931–3948. [Google Scholar] [CrossRef]
- Xie, G.; Thompson, D.J.; Jones, C.J.C. The radiation efficiency of baffled plates and strips. J. Sound Vib. 2005, 280, 181–209. [Google Scholar] [CrossRef]
- Rayleigh, J.W. The Theory of Sound, 2nd ed.; Dover: New York, NY, USA, 1945. [Google Scholar]
- Maidanik, G. Response of ribbed panels to reverberant acoustic fields. J. Acoust. Soc. Am. 1962, 34, 809–826. [Google Scholar] [CrossRef]
- Heckl, M. Radiation from plane sound sources. Acustica 1977, 37, 155–166. [Google Scholar]
- Williams, E.G. A series expansion of the acoustic power radiated from planar sources. J. Acoust. Soc. Am. 1983, 73, 1520–1524. [Google Scholar] [CrossRef]
- Keltie, R.F.; Peng, H. The effects of modal coupling on the acoustic power radiation from panels. J. Vib. Acoust. Stress Reliab. Des. 1987, 109, 48–55. [Google Scholar] [CrossRef]
- Snyder, S.D.; Tanaka, N. Calculating total acoustic power output using modal radiation efficiencies. J. Acoust. Soc. Am. 1995, 97, 1702–1709. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Vincenzi, N. Structural and elastodynamic analysis of rotary transfer machines by Finite Element model. J. Serb. Soc. Comput. Mech. 2017, 11, 1–16. [Google Scholar] [CrossRef]
- Croccolo, D.; Cavalli, O.; De Agostinis, M.; Fini, S.; Olmi, G.; Robusto, F.; Vincenzi, N. A Methodology for the Lightweight Design of Modern Transfer Machine Tools. Machines 2018, 6, 2. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M. Upgrade of an automated line for plastic cap manufacture based on experimental vibration analysis. Case Stud. Mech. Syst. Signal Process. 2016, 3, 28–33. [Google Scholar] [CrossRef]
- Pavlovic, A.; Fragassa, C.; Ubertini, F.; Martini, A. Modal analysis and stiffness optimization: The case of a tool machine for ceramic tile surface finishing. J. Serb. Soc. Comput. Mech. 2016, 10, 30–44. [Google Scholar] [CrossRef]

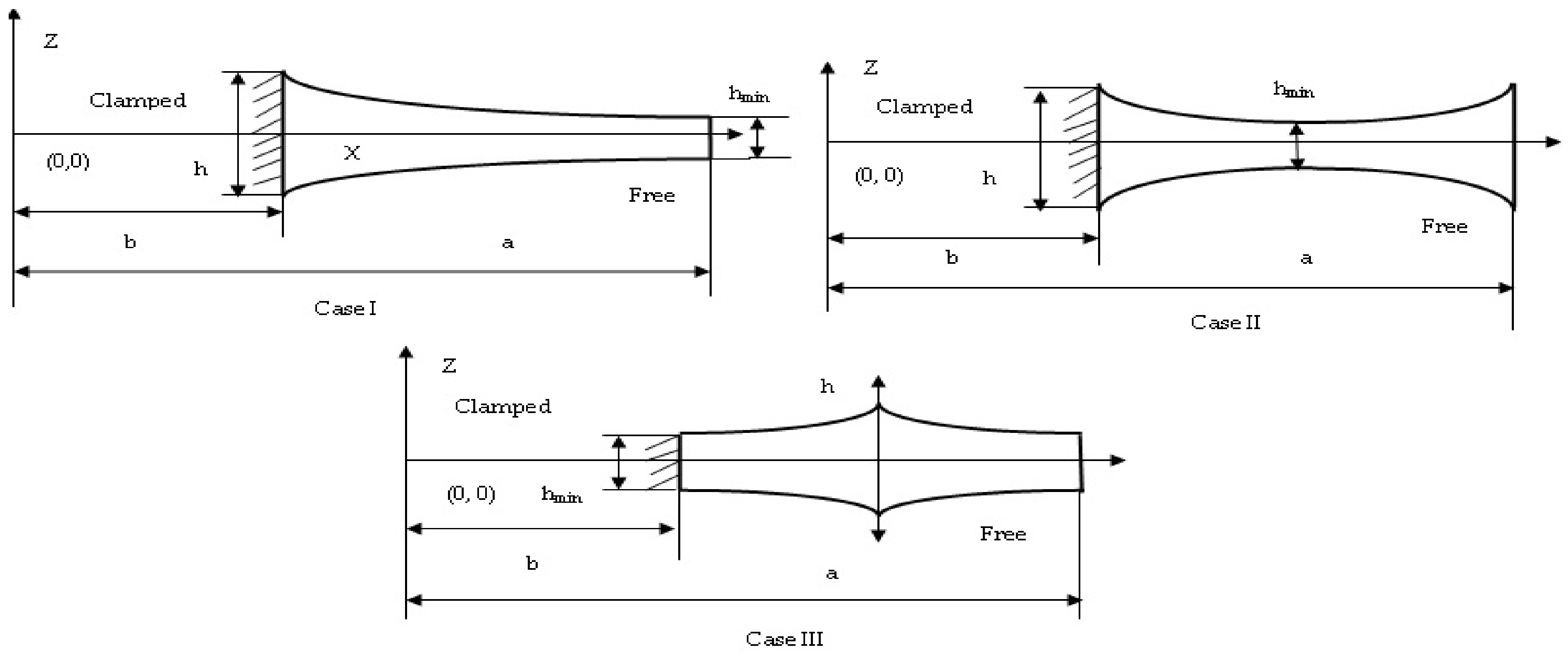




| Dimension of the Plate with Point Mass | Isotropic Annular Circular Plate |
|---|---|
| Outer radius (a) m | 0.1515 |
| Inner radius (b) m | 0.0825 |
| Radii ratio, (b/a) | 0.54 |
| Thickness (h) m | 0.0315 |
| Thickness ratio, (h/a) | 0.21 |
| Density, ρ (kg/m3) | 7905.9 |
| Young’s modulus, E (GPa) | 218 |
| Plate | Mode | Non Dimensional Frequency Parameter, λ2 | |
|---|---|---|---|
| H. Lee et al. [10] | Present Work | ||
| Uniform plate b/a = 0.54 h/a = 0.21 | (0, 0) | 13.61 | 13.49 |
| (0, 1) | 13.43 | 13.50 | |
| (0, 2) | 15.28 | 14.12 | |
| (0, 3) | 16.81 | 16.67 | |
| Mode | Un-Loaded Plate | Plate with One Point Mass | % λ2 | Plate with Two Point Masses | % λ2 | Plate with Four Point Masses | % λ2 |
|---|---|---|---|---|---|---|---|
| (0,0) | 13.49 | 13.46 | 0.223 | 13.45 | 0.296 | 13.35 | 1.033 |
| (0,1) | 13.50 | 13.48 | 0.148 | 13.44 | 0.444 | 13.32 | 1.333 |
| (0,2) | 14.12 | 14.08 | 0.283 | 14.06 | 0.424 | 14.02 | 0.708 |
| (0,3) | 16.67 | 16.64 | 0.017 | 16.64 | 0.017 | 16.62 | 0.299 |
| Case | Mode | Natural Frequency Parameter, λ2 | |||
|---|---|---|---|---|---|
| Tx = 0.00 | Tx = 0.25 | Tx = 0.50 | Tx = 0.75 | ||
| I | (0,0) | 13.4802 | 12.9904 | 12.4703 | 11.9305 |
| (0,1) | 13.4942 | 12.9745 | 12.4442 | 11.8918 | |
| (0,2) | 14.1132 | 13.6135 | 13.0936 | 12.5502 | |
| (0,3) | 16.6624 | 16.0733 | 15.4611 | 14.8254 | |
| II | (0,0) | 13.4811 | 12.8952 | 12.2718 | 11.6202 |
| (0,1) | 13.4932 | 12.8774 | 12.2414 | 11.5752 | |
| (0,2) | 14.1134 | 13.5187 | 12.8943 | 12.2384 | |
| (0,3) | 16.6624 | 15.9610 | 15.2277 | 14.4605 | |
| III | (0,0) | 13.4812 | 13.4891 | 13.4902 | 13.4904 |
| (0,1) | 13.4943 | 13.4784 | 13.4808 | 13.4804 | |
| (0,2) | 14.1136 | 14.1109 | 14.1134 | 14.1125 | |
| (0,3) | 16.6625 | 16.6600 | 16.6624 | 16.6618 | |
| Case | Mode | Natural Frequency Parameter, λ2 | |||
|---|---|---|---|---|---|
| Tx = 0.00 | Tx = 0.25 | Tx = 0.50 | Tx = 0.75 | ||
| I | (0,0) | 13.4753 | 12.9768 | 12.4592 | 11.9285 |
| (0,1) | 13.4825 | 12.9682 | 12.4392 | 11.8825 | |
| (0,2) | 14.0925 | 13.6092 | 13.0878 | 12.5325 | |
| (0,3) | 16.6532 | 16.0691 | 15.4592 | 14.8125 | |
| II | (0,0) | 13.4768 | 12.8825 | 12.2685 | 11.6125 |
| (0,1) | 13.4832 | 12.8785 | 12.2386 | 11.5624 | |
| (0,2) | 14.0965 | 13.5085 | 12.9186 | 12.2252 | |
| (0,3) | 16.6582 | 15.9528 | 15.2582 | 14.4518 | |
| III | (0,0) | 13.4793 | 13.4758 | 13.5076 | 13.4721 |
| (0,1) | 13.4825 | 13.4768 | 13.5195 | 13.4821 | |
| (0,2) | 14.0968 | 14.0952 | 14.1392 | 14.0926 | |
| (0,3) | 16.6582 | 16.6592 | 16.7002 | 16.6523 | |
| Case | Mode | Natural Frequency Parameter, λ2 | |||
|---|---|---|---|---|---|
| Tx = 0.00 | Tx = 0.25 | Tx = 0.50 | Tx = 0.75 | ||
| I | (0,0) | 13.4852 | 12.9877 | 12.4701 | 11.9301 |
| (0,1) | 13.4902 | 12.9765 | 12.4443 | 11.8937 | |
| (0,2) | 14.1025 | 13.6040 | 13.0838 | 12.5412 | |
| (0,3) | 16.6635 | 16.0712 | 15.4619 | 14.8258 | |
| II | (0,0) | 13.4842 | 12.8924 | 12.2715 | 11.6202 |
| (0,1) | 13.4902 | 12.8805 | 12.2418 | 11.5762 | |
| (0,2) | 14.1035 | 13.5102 | 12.8858 | 12.2304 | |
| (0,3) | 16.6638 | 15.9618 | 15.2302 | 14.4612 | |
| III | (0,0) | 13.4852 | 13.4820 | 13.4850 | 13.4852 |
| (0,1) | 13.4906 | 13.4853 | 13.4902 | 13.4902 | |
| (0,2) | 14.1037 | 14.1008 | 14.1022 | 14.1032 | |
| (0,3) | 16.6638 | 16.6612 | 16.6639 | 16.6635 | |
| Type | Plate Thickness Variation | Plate with One Point Mass | Plate with Two Point Masses | Plate with Four Point Masses | |||
|---|---|---|---|---|---|---|---|
| SPL (dB) | RE (σmn) | SPL (dB) | RE (σmn) | SPL (dB) | RE (σmn) | ||
| Point masses | Case I | 82 | 1.058 | 78 | 1.007 | 77 | 0.994 |
| Case II | 81 | 1.045 | 83 | 1.079 | 77 | 0.994 | |
| Case III | 79 | 1.020 | 77 | 0.994 | 76 | 0.935 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatterjee, A.; Ranjan, V.; Azam, M.S.; Rao, M. Comparison for the Effect of Different Attachment of Point Masses on Vibroacoustic Behavior of Parabolic Tapered Annular Circular Plate. Appl. Sci. 2019, 9, 745. https://doi.org/10.3390/app9040745
Chatterjee A, Ranjan V, Azam MS, Rao M. Comparison for the Effect of Different Attachment of Point Masses on Vibroacoustic Behavior of Parabolic Tapered Annular Circular Plate. Applied Sciences. 2019; 9(4):745. https://doi.org/10.3390/app9040745
Chicago/Turabian StyleChatterjee, Abhijeet, Vinayak Ranjan, Mohammad Sikandar Azam, and Mohan Rao. 2019. "Comparison for the Effect of Different Attachment of Point Masses on Vibroacoustic Behavior of Parabolic Tapered Annular Circular Plate" Applied Sciences 9, no. 4: 745. https://doi.org/10.3390/app9040745
APA StyleChatterjee, A., Ranjan, V., Azam, M. S., & Rao, M. (2019). Comparison for the Effect of Different Attachment of Point Masses on Vibroacoustic Behavior of Parabolic Tapered Annular Circular Plate. Applied Sciences, 9(4), 745. https://doi.org/10.3390/app9040745




