First-Principles Prediction of Skyrmionic Phase Behavior in GdFe2 Films Capped by 4d and 5d Transition Metals
Abstract
1. Introduction
2. Methods
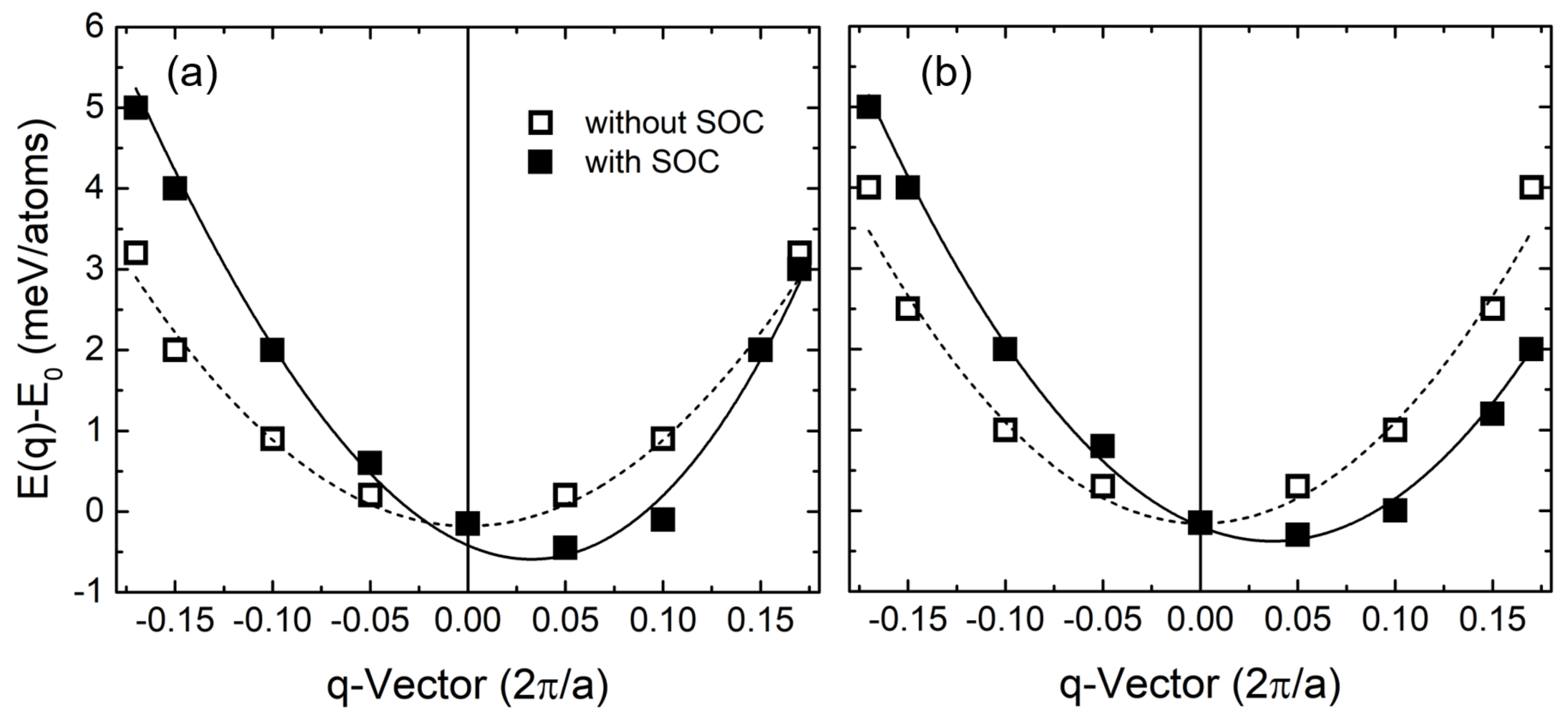
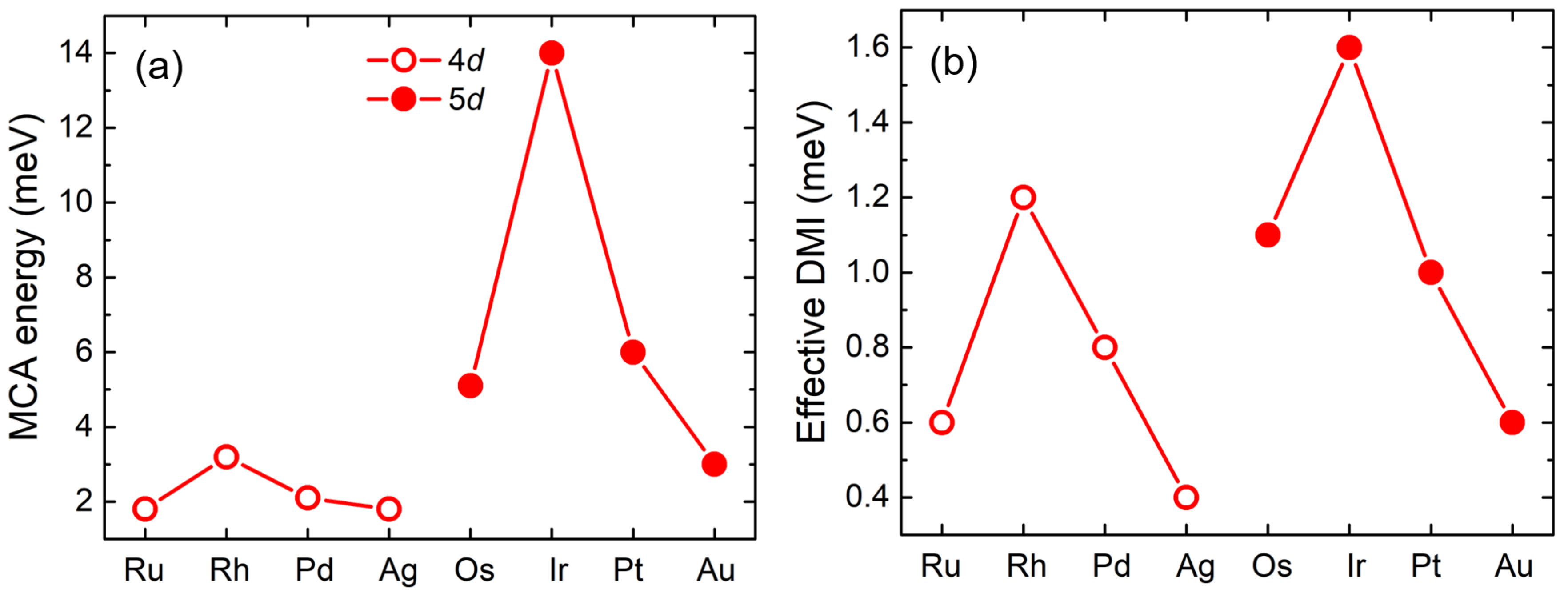
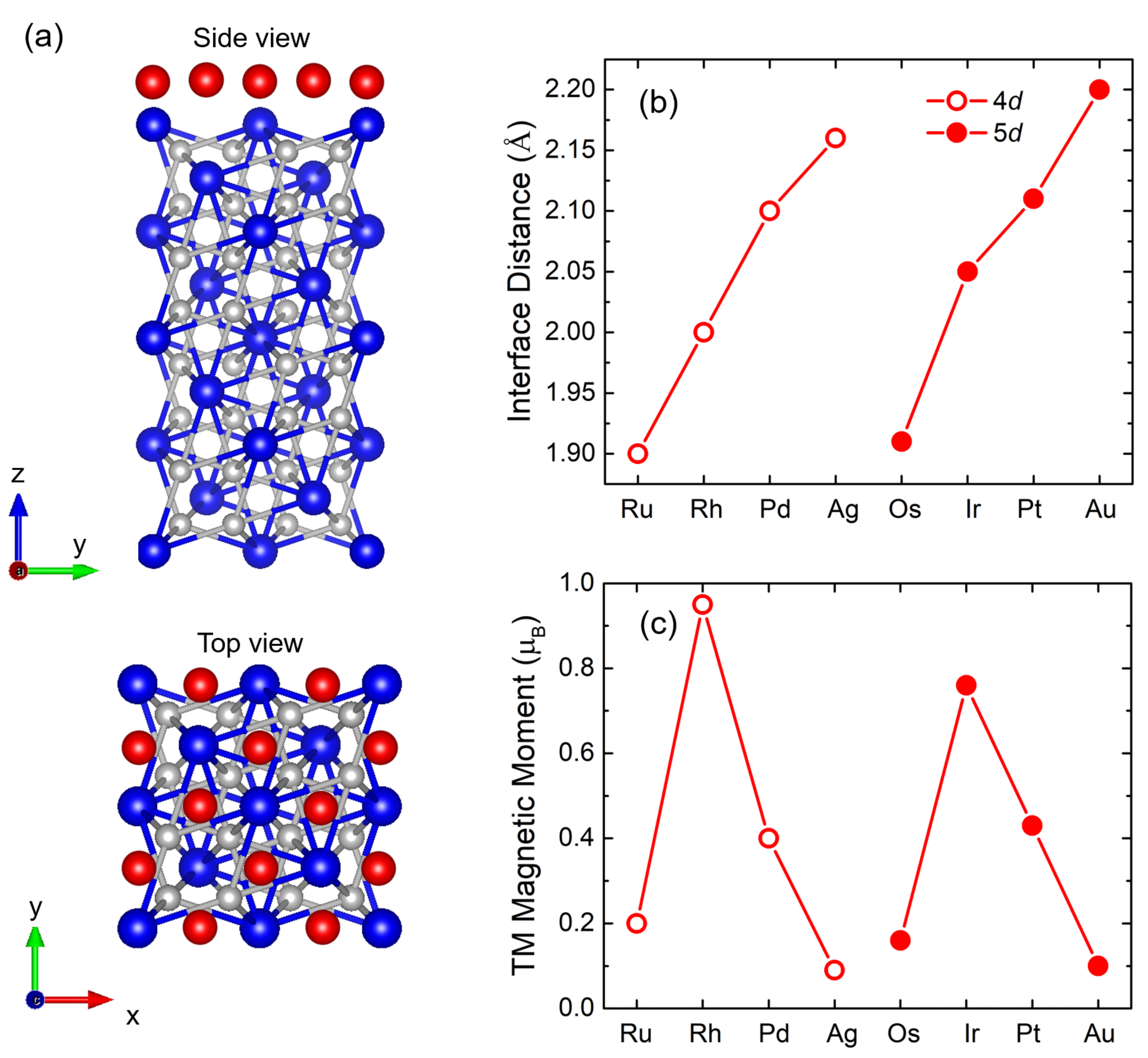
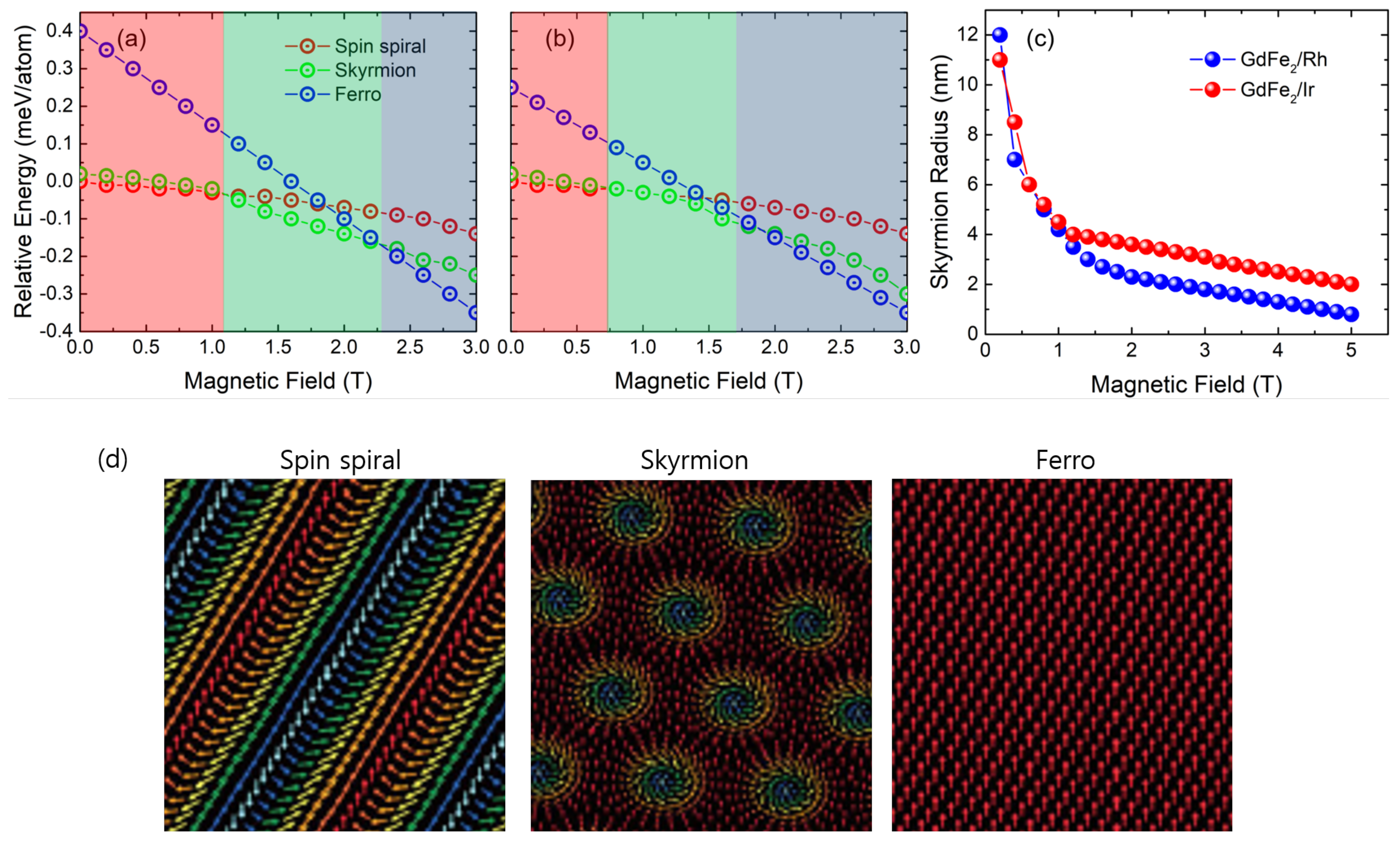
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152. [Google Scholar] [CrossRef]
- Wiesendanger, R. Nanoscale magnetic skyrmions in metallic films and multilayers: A new twist for spintronics. Nat. Rev. Mater. 2016, 1, 16044. [Google Scholar] [CrossRef]
- Kiselev, N.; Bogdanov, A.; Schäfer, R.; Rößler, U. Chiral skyrmions in thin magnetic films: New objects for magnetic storage technologies? J. Phys. D Appl. Phys. 2011, 44, 392001. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices” in magnetically ordered crystals. The mixed state of magnets. Sov. Phys. JETP 1989, 68, 101. [Google Scholar]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Bogdanov, A.; Rößler, U. Chiral symmetry breaking in magnetic thin films and multilayers. Phys. Rev. Lett. 2001, 87, 037203. [Google Scholar] [CrossRef]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915. [Google Scholar]
- Wilhelm, H.; Baenitz, M.; Schmidt, M.; Rößler, U.; Leonov, A.; Bogdanov, A. Precursor phenomena at the magnetic ordering of the cubic helimagnet FeGe. Phys. Rev. Lett. 2011, 107, 127203. [Google Scholar] [CrossRef]
- Münzer, W.; Neubauer, A.; Adams, T.; Mühlbauer, S.; Franz, C.; Jonietz, F.; Georgii, R.; Böni, P.; Pedersen, B.; Schmidt, M.; et al. Skyrmion lattice in the doped semiconductor Fe1−xCoxSi. Phys. Rev. B 2010, 81, 041203. [Google Scholar] [CrossRef]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.Z.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106. [Google Scholar]
- Tonomura, A.; Yu, X.; Yanagisawa, K.; Matsuda, T.; Onose, Y.; Kanazawa, N.; Park, H.S.; Tokura, Y. Real-space observation of skyrmion lattice in helimagnet MnSi thin samples. Nano Lett. 2012, 12, 1673–1677. [Google Scholar] [CrossRef] [PubMed]
- Heinze, S.; Von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R.; Bihlmayer, G.; Blügel, S. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713. [Google Scholar] [CrossRef]
- Romming, N.; Hanneken, C.; Menzel, M.; Bickel, J.E.; Wolter, B.; von Bergmann, K.; Kubetzka, A.; Wiesendanger, R. Writing and deleting single magnetic skyrmions. Science 2013, 341, 636–639. [Google Scholar] [CrossRef] [PubMed]
- Romming, N.; Kubetzka, A.; Hanneken, C.; von Bergmann, K.; Wiesendanger, R. Field-dependent size and shape of single magnetic skyrmions. Phys. Rev. Lett. 2015, 114, 177203. [Google Scholar] [CrossRef] [PubMed]
- Woo, S.; Litzius, K.; Krüger, B.; Im, M.Y.; Caretta, L.; Richter, K.; Mann, M.; Krone, A.; Reeve, R.M.; Weigand, M.; et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 2016, 15, 501. [Google Scholar] [CrossRef] [PubMed]
- Soumyanarayanan, A.; Raju, M.; Oyarce, A.G.; Tan, A.K.; Im, M.Y.; Petrović, A.P.; Ho, P.; Khoo, K.; Tran, M.; Gan, C.; et al. Tunable room-temperature magnetic skyrmions in Ir/Fe/Co/Pt multilayers. Nat. Mater. 2017, 16, 898. [Google Scholar] [CrossRef] [PubMed]
- Siemens, A.; Zhang, Y.; Hagemeister, J.; Vedmedenko, E.; Wiesendanger, R. Minimal radius of magnetic skyrmions: Statics and dynamics. New J. Phys. 2016, 18, 045021. [Google Scholar] [CrossRef]
- Büttner, F.; Lemesh, I.; Beach, G.S. Theory of isolated magnetic skyrmions: From fundamentals to room temperature applications. Sci. Rep. 2018, 8, 4464. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Zhang, X.; Yu, G.; Zhang, W.; Wang, X.; Jungfleisch, M.B.; Pearson, J.E.; Cheng, X.; Heinonen, O.; Wang, K.L.; et al. Direct observation of the skyrmion Hall effect. Nat. Phys. 2017, 13, 162. [Google Scholar] [CrossRef]
- Litzius, K.; Lemesh, I.; Krüger, B.; Bassirian, P.; Caretta, L.; Richter, K.; Büttner, F.; Sato, K.; Tretiakov, O.A.; Förster, J.; et al. Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy. Nat. Phys. 2017, 13, 170. [Google Scholar] [CrossRef]
- Tomasello, R.; Martinez, E.; Zivieri, R.; Torres, L.; Carpentieri, M.; Finocchio, G. A strategy for the design of skyrmion racetrack memories. Sci. Rep. 2014, 4, 6784. [Google Scholar] [CrossRef] [PubMed]
- Harris, V.G.; Pokhil, T. Selective-resputtering-induced perpendicular magnetic anisotropy in amorphous TbFe films. Phys. Rev. Lett. 2001, 87, 067207. [Google Scholar] [CrossRef] [PubMed]
- Hansen, P.; Clausen, C.; Much, G.; Rosenkranz, M.; Witter, K. Magnetic and magneto-optical properties of rare-earth transition-metal alloys containing Gd, Tb, Fe, Co. J. Appl. Phys. 1989, 66, 756–767. [Google Scholar] [CrossRef]
- Woo, S.; Song, K.M.; Zhang, X.; Zhou, Y.; Ezawa, M.; Liu, X.; Finizio, S.; Raabe, J.; Lee, N.J.; Kim, S.I.; et al. Current-driven dynamics and inhibition of the skyrmion Hall effect of ferrimagnetic skyrmions in GdFeCo films. Nat. Commun. 2018, 9, 959. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.T.; Chess, J.; Montoya, S.; Shi, X.; Tamura, N.; Mishra, S.; Fischer, P.; McMorran, B.; Sinha, S.; Fullerton, E.; et al. Synthesizing skyrmion bound pairs in Fe-Gd thin films. Appl. Phys. Lett. 2016, 109, 022402. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Cond. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Wimmer, E.; Krakauer, H.; Weinert, M.; Freeman, A.J. Full-potential self-consistent linearized-augmented-plane-wave method for calculating the electronic structure of molecules and surfaces: O2 molecule. Phys. Rev. B 1981, 24, 864. [Google Scholar] [CrossRef]
- Kurz, P.; Förster, F.; Nordström, L.; Bihlmayer, G.; Blügel, S. Ab initio treatment of noncollinear magnets with the full-potential linearized augmented plane wave method. Phys. Rev. B 2004, 69, 024415. [Google Scholar] [CrossRef]
- Eriksson, O.; Bergman, A.; Bergqvist, L.; Hellsvik, J. Atomistic Spin Dynamics: Foundations and Applications; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Antropov, V.P.; Katsnelson, M.I.; Harmon, B.N.; van Schilfgaarde, M.; Kusnezov, D. Spin dynamics in magnets: Equation of motion and finite temperature effects. Phys. Rev. B 1996, 54, 1019. [Google Scholar] [CrossRef]
- Katsnelson, M.I.; Irkhin, V.Y.; Chioncel, L.; Lichtenstein, A.I.; de Groot, R.A. Half-metallic ferromagnets: From band structure to many-body effects. Rev. Mod. Phys. 2008, 80, 315. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; van Waeyenberge, B. The design and verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I.E. IE Dzyaloshinskii. Sov. Phys. JETP 1957, 5, 1259. [Google Scholar]
- Moriya, T. New mechanism of anisotropic superexchange interaction. Phys. Rev. Lett. 1960, 4, 228. [Google Scholar] [CrossRef]
- Bode, M.; Heide, M.; Von Bergmann, K.; Ferriani, P.; Heinze, S.; Bihlmayer, G.; Kubetzka, A.; Pietzsch, O.; Blügel, S.; Wiesendanger, R. Chiral magnetic order at surfaces driven by inversion asymmetry. Nature 2007, 447, 190. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jekal, S.; Danilo, A.; Phuong, D.; Zheng, X. First-Principles Prediction of Skyrmionic Phase Behavior in GdFe2 Films Capped by 4d and 5d Transition Metals. Appl. Sci. 2019, 9, 630. https://doi.org/10.3390/app9040630
Jekal S, Danilo A, Phuong D, Zheng X. First-Principles Prediction of Skyrmionic Phase Behavior in GdFe2 Films Capped by 4d and 5d Transition Metals. Applied Sciences. 2019; 9(4):630. https://doi.org/10.3390/app9040630
Chicago/Turabian StyleJekal, Soyoung, Andreas Danilo, Dao Phuong, and Xiao Zheng. 2019. "First-Principles Prediction of Skyrmionic Phase Behavior in GdFe2 Films Capped by 4d and 5d Transition Metals" Applied Sciences 9, no. 4: 630. https://doi.org/10.3390/app9040630
APA StyleJekal, S., Danilo, A., Phuong, D., & Zheng, X. (2019). First-Principles Prediction of Skyrmionic Phase Behavior in GdFe2 Films Capped by 4d and 5d Transition Metals. Applied Sciences, 9(4), 630. https://doi.org/10.3390/app9040630



