Fast 3D Semantic Mapping in Road Scenes †
Abstract
:1. Introduction
2. Related Work
- a 3D semantic mapping system based on monocular vision,
- exploiting the correlation between semantic information and geometrical information to enforce spatial consistency,
- active sequence downsampling and sparse semantic segmentation so that to achieve a real-time performance and reduce the storage.
3. Problem Formulation
3.1. Notation
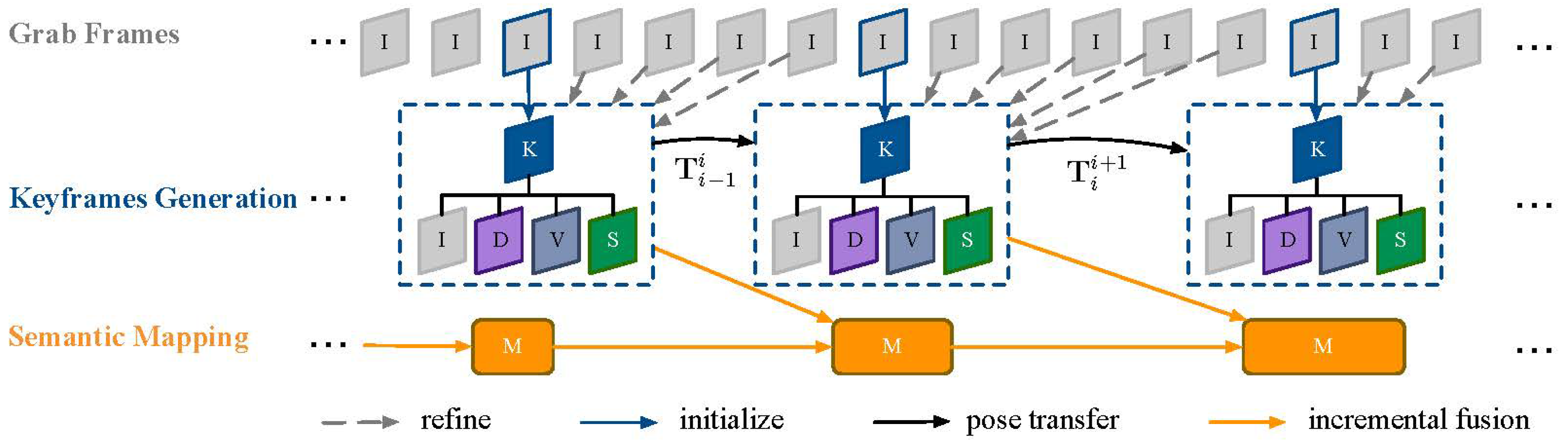
3.2. Framework
4. 3D Semantic Mapping
4.1. 2D Scene Parsing
4.2. Semi-Dense SLAM
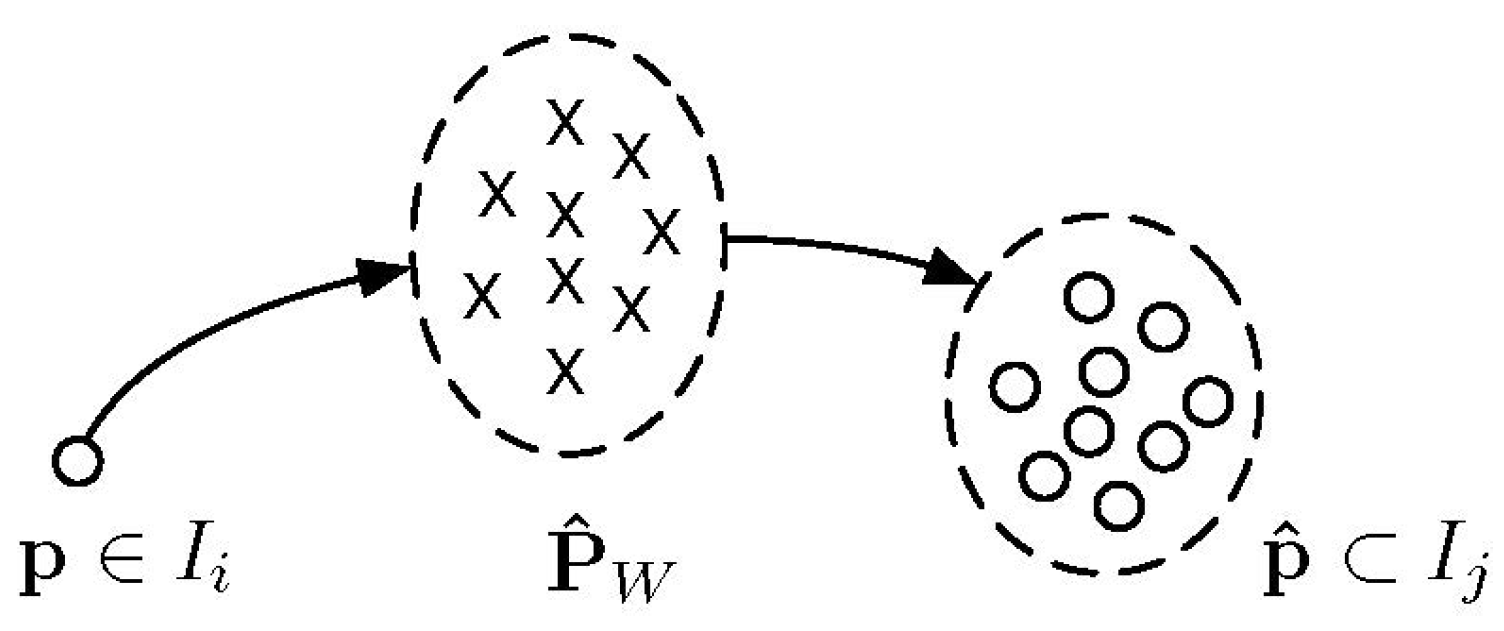
4.3. Incremental Fusion
4.4. Map Regularization
5. Experiments and Results
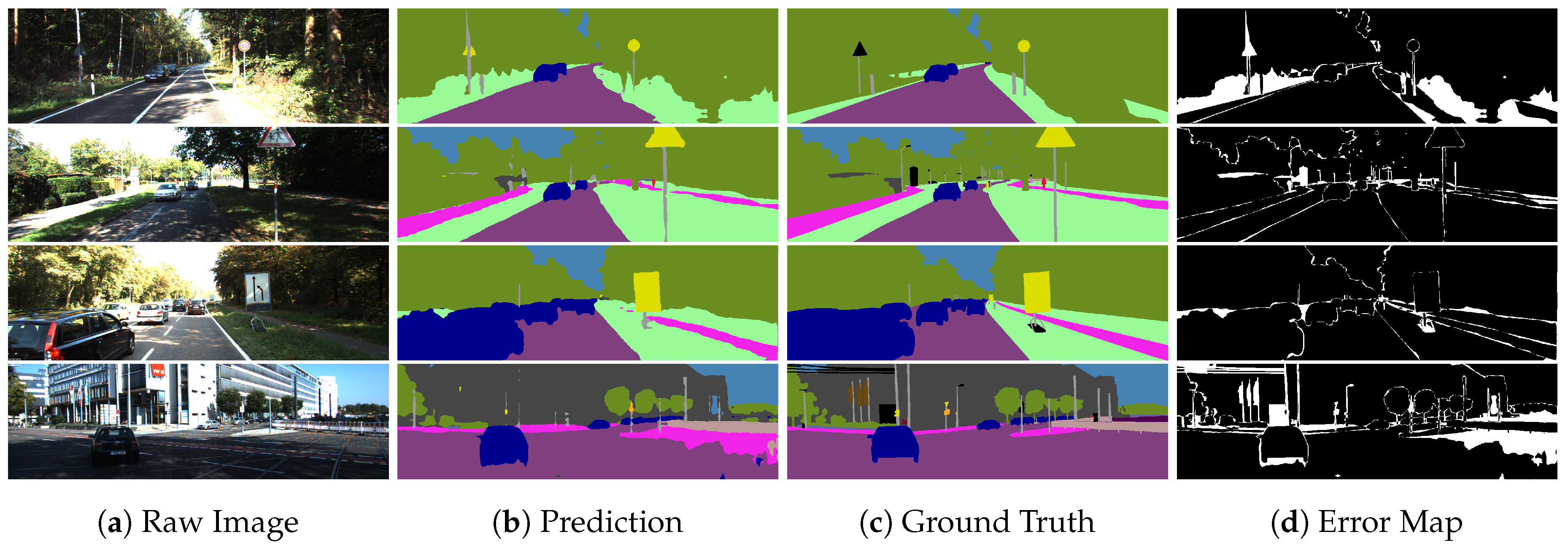
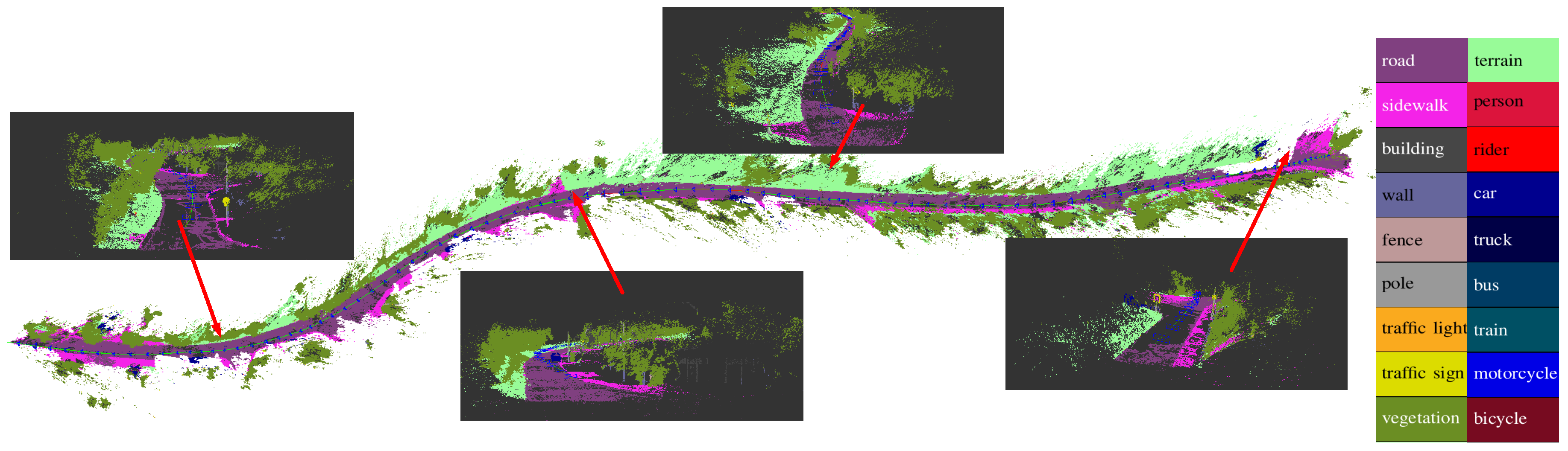
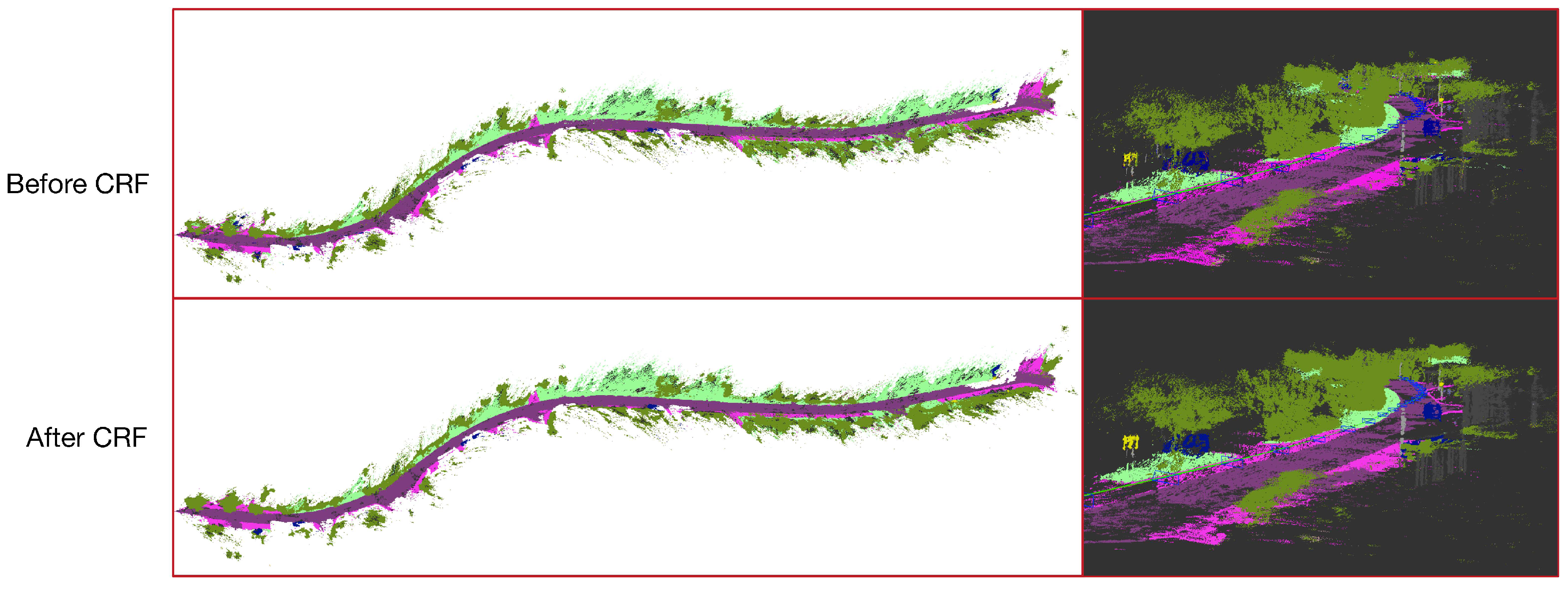
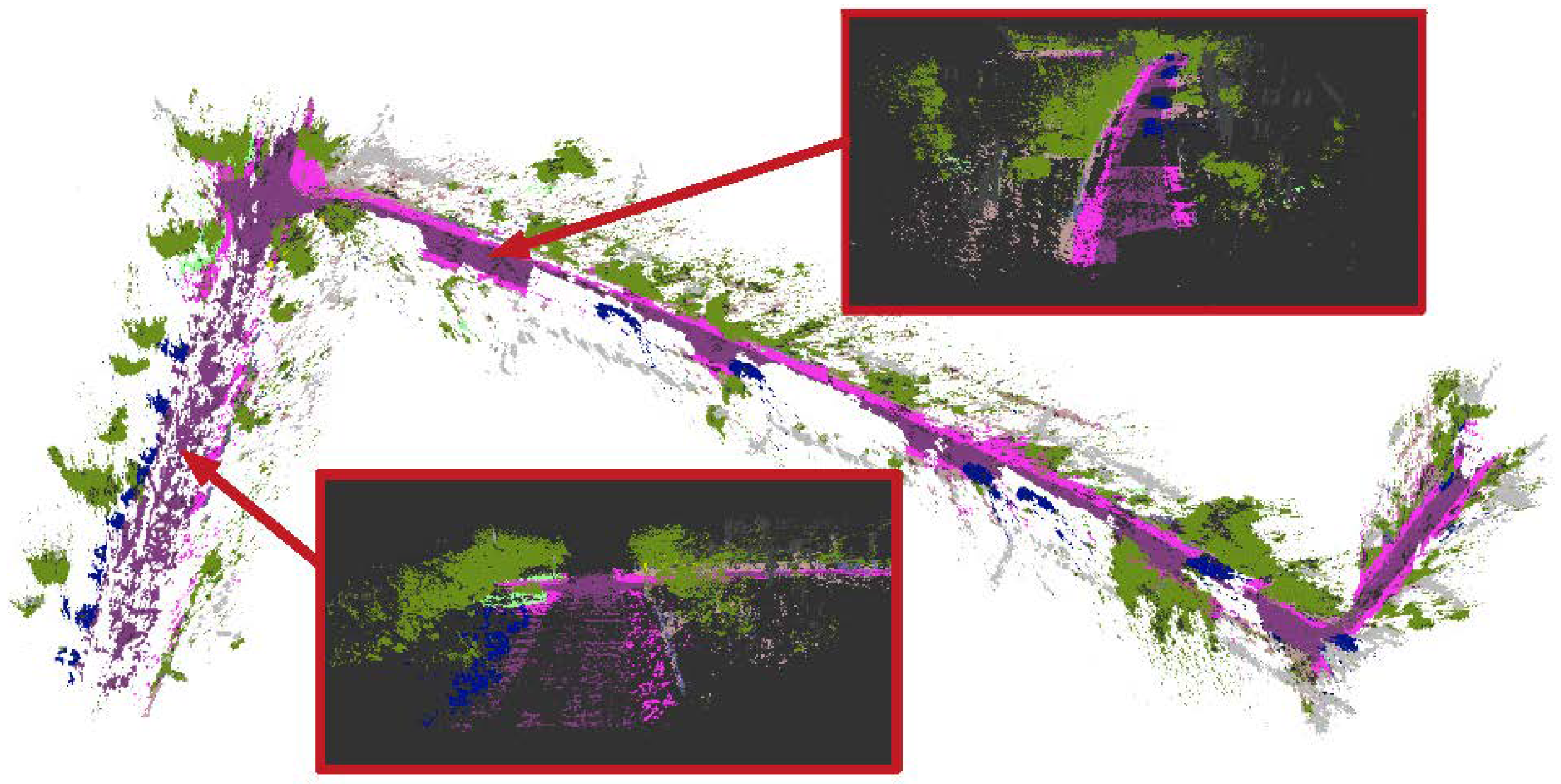
5.1. Qualitative Results
5.2. Quantitative Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chow, J.C.; Lichti, D.D.; Hol, J.D.; Bellusci, G.; Luinge, H. Imu and multiple RGB-D camera fusion for assisting indoor stop-and-go 3D terrestrial laser scanning. Robotics 2014, 3, 247–280. [Google Scholar] [CrossRef]
- Alzugaray, I.; Sanfeliu, A. Learning the hidden human knowledge of UAV pilots when navigating in a cluttered environment for improving path planning. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems, Deajeon, Korea, 9–14 October 2016; pp. 1589–1594. [Google Scholar]
- Alzugaray, I.; Teixeira, L.; Chli, M. Short-term UAV path-planning with monocular-inertial SLAM in the loop. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017; pp. 2739–2746. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Qi, X.; Shen, X.; Shi, J.; Jia, J. ICNet for Real-Time Semantic Segmentation on High-Resolution Images. In Proceedings of the 2018 European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 418–434. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the 15th European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 833–851. [Google Scholar]
- Wolf, D.; Prankl, J.; Vincze, M. Fast semantic segmentation of 3D point clouds using a dense CRF with learned parameters. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015; pp. 4867–4873. [Google Scholar]
- Hermans, A.; Floros, G.; Leibe, B. Dense 3d semantic mapping of indoor scenes from rgb-d images. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; pp. 2631–2638. [Google Scholar]
- McCormac, J.; Handa, A.; Davison, A.; Leutenegger, S. SemanticFusion: Dense 3D semantic mapping with convolutional neural networks. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017; pp. 4628–4635. [Google Scholar]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The cityscapes dataset for semantic urban scene understanding. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 3213–3223. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? the kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 18–20 June 2012; pp. 3354–3361. [Google Scholar]
- LI, X.; Ao, H.; Belaroussi, R.; Gruyer, D. Fast semi-dense 3D semantic mapping with monocular visual SLAM. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems, Yokohama, Japan, 16–19 October 2017; pp. 385–390. [Google Scholar]
- Whelan, T.; Salas-Moreno, R.F.; Glocker, B.; Davison, A.J.; Leutenegger, S. ElasticFusion: Real-time dense SLAM and light source estimation. Int. J. Rob. Res. 2016, 35, 1697–1716. [Google Scholar] [CrossRef]
- Noh, H.; Hong, S.; Han, B. Learning Deconvolution Network for Semantic Segmentation. In Proceedings of the 2015 IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 1520–1528. [Google Scholar]
- Salas-Moreno, R.F.; Newcombe, R.A.; Strasdat, H.; Kelly, P.H.; Davison, A.J. Slam++: Simultaneous localisation and mapping at the level of objects. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1352–1359. [Google Scholar]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-time single camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef] [PubMed]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Kerl, C.; Sturm, J.; Cremers, D. Dense visual SLAM for RGB-D cameras. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 2100–2106. [Google Scholar]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In Proceedings of the 2014 European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 834–849. [Google Scholar]
- Forster, C.; Zhang, Z.; Gassner, M.; Werlberger, M.; Scaramuzza, D. Svo: Semidirect visual odometry for monocular and multicamera systems. IEEE Trans. Robot. 2017, 33, 249–265. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv, 2017; arXiv:1704.04861. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- Valentin, J.P.; Sengupta, S.; Warrell, J.; Shahrokni, A.; Torr, P.H. Mesh based semantic modelling for indoor and outdoor scenes. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2067–2074. [Google Scholar]
- Kundu, A.; Li, Y.; Dellaert, F.; Li, F.; Rehg, J.M. Joint semantic segmentation and 3d reconstruction from monocular video. In Proceedings of the 2014 European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 703–718. [Google Scholar]
- Sengupta, S.; Sturgess, P. Semantic octree: Unifying recognition, reconstruction and representation via an octree constrained higher order MRF. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015; pp. 1874–1879. [Google Scholar]
- Vineet, V.; Miksik, O.; Lidegaard, M.; Nießner, M.; Golodetz, S.; Prisacariu, V.A.; Kähler, O.; Murray, D.W.; Izadi, S.; Pérez, P. Incremental dense semantic stereo fusion for large-scale semantic scene reconstruction. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015; pp. 75–82. [Google Scholar]
- Kochanov, D.; Ošep, A.; Stückler, J.; Leibe, B. Scene flow propagation for semantic mapping and object discovery in dynamic street scenes. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems, Deajeon, Korea, 9–14 October 2016; pp. 1785–1792. [Google Scholar]
- Landrieu, L.; Raguet, H.; Vallet, B.; Mallet, C.; Weinmann, M. A structured regularization framework for spatially smoothing semantic labelings of 3D point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 132, 102–118. [Google Scholar] [CrossRef]
- Jadidi, M.G.; Gan, L.; Parkison, S.A.; Li, J.; Eustice, R.M. Gaussian processes semantic map representation. arXiv, 2017; arXiv:1707.01532. [Google Scholar]
- Gan, L.; Jadidi, M.G.; Parkison, S.A.; Eustice, R.M. Sparse Bayesian Inference for Dense Semantic Mapping. arXiv, 2017; arXiv:1709.07973. [Google Scholar]
- Sengupta, S.; Greveson, E.; Shahrokni, A.; Torr, P.H. Urban 3d semantic modelling using stereo vision. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 580–585. [Google Scholar]
- Martinovic, A.; Knopp, J.; Riemenschneider, H.; Van Gool, L. 3d all the way: Semantic segmentation of urban scenes from start to end in 3d. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 4456–4465. [Google Scholar]
- Hu, H.; Munoz, D.; Bagnell, J.A.; Hebert, M. Efficient 3-d scene analysis from streaming data. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 2297–2304. [Google Scholar]
- Civera, J.; Davison, A.J.; Montiel, J.M.M. Inverse depth parametrization for monocular SLAM. IEEE Trans. Robot. 2008, 24, 932–945. [Google Scholar] [CrossRef]
- Krähenbühl, P.; Koltun, V. Efficient inference in fully connected crfs with gaussian edge potentials. In Proceedings of the 2011 Conference in Neural Information Processing Systems, Granada, Spain, 12–17 December 2011; pp. 109–117. [Google Scholar]
- Russell, C.; Kohli, P.; Torr, P.H. Associative hierarchical crfs for object class image segmentation. In Proceedings of the 2009 IEEE International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 739–746. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Chollet, F. Xception: Deep Learning With Depthwise Separable Convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the 2014 European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]



| Method | M | S/D | L | O | I | SDT | RT |
|---|---|---|---|---|---|---|---|
| Hu et al. [37] | √ | √ | √ | √ | √ | ||
| Sengupta et al. [35] | √ | √ | |||||
| Hermans et al. [9] | √ | √ | √ | ||||
| Kundu et al. [28] | √ | √ | √ | ||||
| Vineet et al. [30] | √ | √ | √ | √ | √ | ||
| Wolf et al. [8] | √ | √ | |||||
| McCormac et al. [10] | √ | √ | √ | √ | |||
| Ours | √ | √ | √ | √ | √ |
| Dataset | Encoder | Learning Rate | Learning Power | Momentum | Weight Decay | Batch | Steps |
|---|---|---|---|---|---|---|---|
| ResNet_50 | 0.003 | 0.9 | 0.9 | 0.0001 | 8 | 20,000 | |
| ResNet_101 | 0.003 | 0.9 | 0.9 | 0.0001 | 8 | 20,000 | |
| Xception_41 | 0.01 | 0.9 | 0.9 | 0.00004 | 8 | 10,000 | |
| Cityscapes | Xception_65 | 0.01 | 0.9 | 0.9 | 0.00004 | 8 | 10,000 |
| Xception_71 | 0.01 | 0.9 | 0.9 | 0.00004 | 8 | 10,000 | |
| MobileNet_v2 | 0.001 | 0.9 | 0.9 | 0.00004 | 64 | 10,000 | |
| ResNet_50 | 0.003 | 0.9 | 0.9 | 0.0001 | 8 | 20,000 | |
| ResNet_101 | 0.003 | 0.9 | 0.9 | 0.0001 | 8 | 20,000 | |
| Xception_41 | 0.01 | 0.9 | 0.9 | 0.00004 | 8 | 10,000 | |
| KITTI | Xception_65 | 0.01 | 0.9 | 0.9 | 0.00004 | 8 | 10,000 |
| Xception_71 | 0.01 | 0.9 | 0.9 | 0.00004 | 8 | 10,000 | |
| MobileNet_v2 | 0.001 | 0.9 | 0.9 | 0.00004 | 64 | 10,000 |
| Dataset | Encoder | Crop Size | mIOU[0.5:0.25:1.75] | Pb Size (MB) | Runtime (ms) | I | M | C |
|---|---|---|---|---|---|---|---|---|
| ResNet_50 | 769 | 63.9 | 107.8 | - | √ | |||
| ResNet_101 | 769 | 69.9 | 184.1 | - | √ | |||
| Xception_41 | 769 | 68.5 | 113.4 | - | √ | |||
| Cityscapes | Xception_65 | 769 | 78.7 | 165.7 | 1800 | √ | ||
| Xception_71 | 769 | 80.2 | 167.9 | 2000 | √ | √ | ||
| MobileNet_v2 | 513 | 70.7 | 8.8 | 400 | √ | |||
| MobileNet_v2 | 769 | 70.9 | 8.8 | 400 | √ | |||
| ResNet_50 | 769 | 51.4 | 107.8 | 120 | √ | √ | ||
| ResNet_101 | 769 | 57.1 | 184.1 | 140 | √ | √ | ||
| Xception_41 | 769 | 54.2 | 113.4 | 140 | √ | √ | ||
| KITTI | Xception_65 | 769 | 64.8 | 165.6 | 160 | √ | √ | |
| Xception_71 | 769 | 66.2 | 167.9 | 170 | √ | √ | √ | |
| MobileNet_v2 | 513 | 57.7 | 8.8 | 80 | √ | √ | ||
| MobileNet_v2 | 769 | 60.7 | 8.8 | 80 | √ | √ |
| Method | Road | Sidewalk | Building | Wall | Fence | Pole | Traffic Light | Traffic Sign | Vegetation | Terrain | Sky | Person | Rider | Car | Truck | Bus | Train | Motorcycle | Bicycle | IoU |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VAL | 95.7 | 73.9 | 87.1 | 38.1 | 44.2 | 42.7 | 48.6 | 60.3 | 89.1 | 52.3 | 90.1 | 70.1 | 36.5 | 89.1 | 44.6 | 62.2 | 37.4 | 36.1 | 67.7 | 60.3 |
| TEST | 96.1 | 73.7 | 86.2 | 37.9 | 41.4 | 40.1 | 50.3 | 58.3 | 90.2 | 66.8 | 91.3 | 72.4 | 40.3 | 91.8 | 33.7 | 46.4 | 37.1 | 46.0 | 62.4 | 60.9 |
| Encoder | mIOU[0.5:0.25:1.75] | WITH Cityscapes |
|---|---|---|
| ResNet_101 | 52.5 | |
| ResNet_101 | 57.1 | √ |
| Xception_65 | 56.0 | |
| Xception_65 | 64.8 | √ |
| MobileNet_v2 | 51.8 | |
| MobileNet_v2 | 60.7 | √ |
| Component | Average Consumed Time |
|---|---|
| Semantic segmentation | ≃100 ms |
| SLAM | ≃40 ms |
| Incremental fusion | ≃50 ms |
| 3D CRF 1 Iter. | 800–2000 ms |
| 3D CRF 2 Iter. | 1200–2400 ms |
| 3D CRF 3 Iter. | 1500–3000 ms |
| 3D CRF 4+ Iter. | >2000 ms |
| Kundu et al. [28] | ≃20 min/800 frames |
| Our ‘baseline’ | ≃200 s/800 frames |
| Our | ≃80 s/800 frames |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, D.; Ao, H.; Belaroussi, R.; Gruyer, D. Fast 3D Semantic Mapping in Road Scenes. Appl. Sci. 2019, 9, 631. https://doi.org/10.3390/app9040631
Li X, Wang D, Ao H, Belaroussi R, Gruyer D. Fast 3D Semantic Mapping in Road Scenes. Applied Sciences. 2019; 9(4):631. https://doi.org/10.3390/app9040631
Chicago/Turabian StyleLi, Xuanpeng, Dong Wang, Huanxuan Ao, Rachid Belaroussi, and Dominique Gruyer. 2019. "Fast 3D Semantic Mapping in Road Scenes" Applied Sciences 9, no. 4: 631. https://doi.org/10.3390/app9040631
APA StyleLi, X., Wang, D., Ao, H., Belaroussi, R., & Gruyer, D. (2019). Fast 3D Semantic Mapping in Road Scenes. Applied Sciences, 9(4), 631. https://doi.org/10.3390/app9040631






