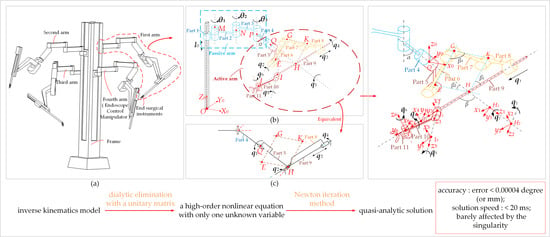
Solving the Time-Varying Inverse Kinematics Problem for the Da Vinci Surgical Robot
Abstract
:Featured Application
Abstract
1. Introduction
- (1)
- (2)
- do not satisfy the Pieper principle.
- (1)
- simplify the structure of RCM, using an equivalent mechanism to take the place of the RCM mechanism.
- (2)
- establish the coordinate system, this step can be realized by the D–H (Denavit–Hartenberg) method or combine the characteristics of the structure to make sure there are more origins of the coordinate system can be set up at the same point.
- (3)
- obtain the mathematical model of forward and inverse kinematics via the matrix transformation method. Then, transform the high-dimensional equations into a nonlinear equation containing only one unknown parameter using the dialytic elimination method, and solve it by the Newton iteration method.
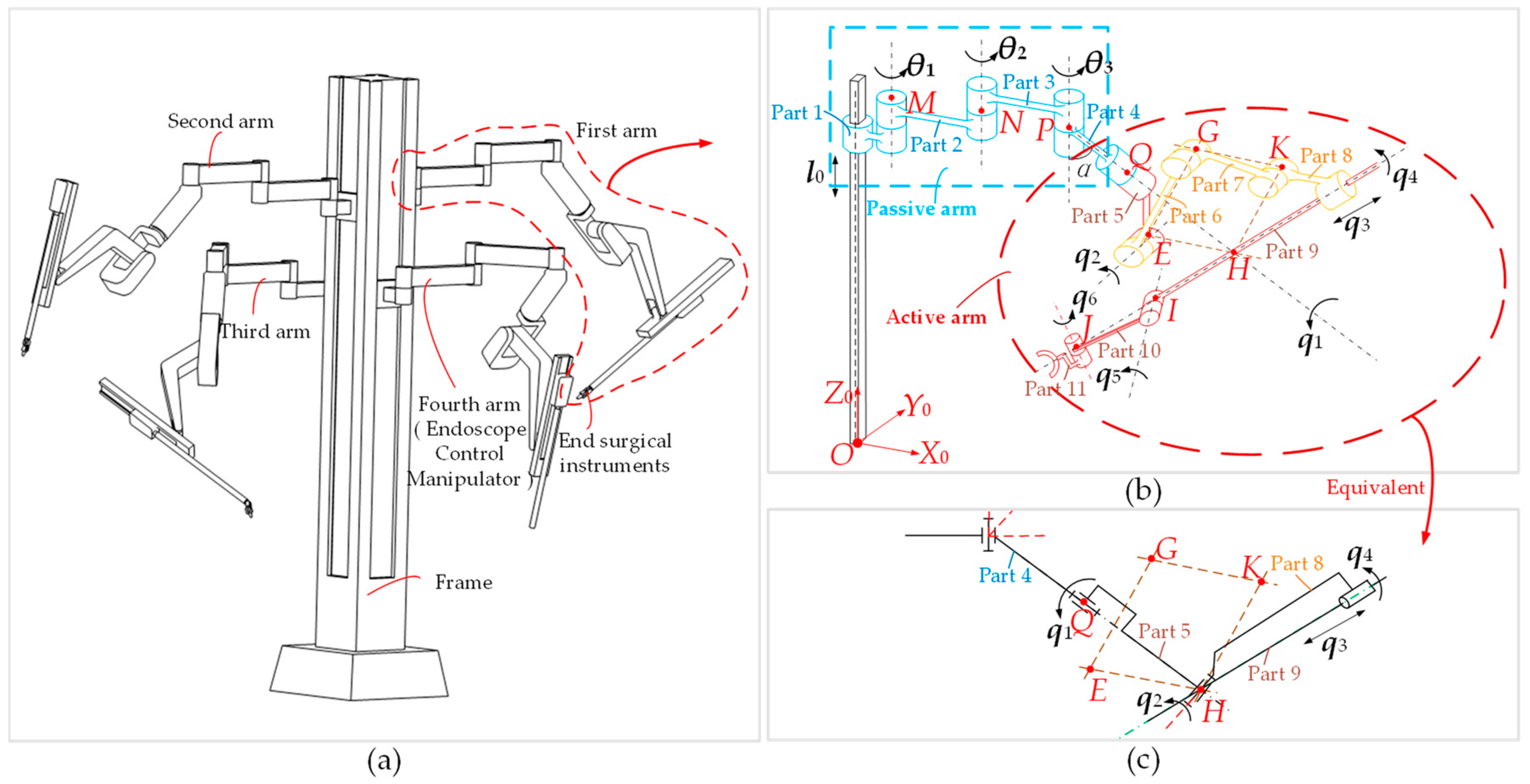
2. Kinematics Analysis
2.1. Forward Kinematics Analysis
2.2. Mathematical Model of Forward Kinematics
2.3. Mathematical Model of Inverse Kinematics
3. Inverse Kinematics Solution
3.1. Inverse Kinematics Solution Method
3.2. Initial Value of the Inverse Kinematics Solution
3.3. Inverse Kinematics Solution Process
4. Example Analysis and Discussion
4.1. Parameters of the Da Vinci Slave Manipulator
4.2. Solution of Proposed Method
4.3. Discussion of the Solution
4.4. Comparison with Other Methods
5. Conclusions
Supplementary Files
Supplementary File 1Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A.
References
- Taylor, R.H. A Perspective on Medical Robotics. Proc. IEEE 2006, 94, 1652–1664. [Google Scholar] [CrossRef]
- Turchetti, G.; Palla, I.; Pierotti, F.; Cuschieri, A. Economic evaluation of Da Vinci-assisted robotic surgery: A systematic review. Surg. Endosc. 2012, 26, 598. [Google Scholar] [CrossRef] [PubMed]
- Pugin, F.; Bucher, P.; Morel, P.; Bucher, P.; Morel, P. History of robotic surgery: From AESOP and ZEUS to Da Vinci. J. Visc. Surg. 2011, 148, e3–e8. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, N.; Watanabe, G. Robot-assisted cardiac surgery. Ann. Thorac. Cardiovasc. Surg. 2015, 21, 322. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.H.; Funda, J.; Grossman, D.D.; Karidis, J.P.; LaRose, D.A. Remote center-of-motion robot for surgery. U.S. Patent 5397323 A, 14 March 1995. [Google Scholar]
- Zhou, X.; Zhang, H.; Feng, M.; Zhao, J.; Fu, Y. New remote centre of motion mechanism for robot-assisted minimally invasive surgery. Biomed. Eng. Online 2018, 17, 170. [Google Scholar] [CrossRef] [PubMed]
- Ozgoren, M.K. Topological analysis of 6-joint serial manipulators and their inverse kinematic solutions. Mech. Mach. Theory 2002, 37, 511–547. [Google Scholar] [CrossRef]
- Balkan, T.; Ozgoren, M.K.; Arikan, M.A.S.; Baykurt, H.M. A kinematic structure-based classification and compact kinematic equations for six-dof industrial robotic manipulators. Mech. Mach. Theory 2001, 36, 817–832. [Google Scholar] [CrossRef]
- Balkan, T.; Ozgoren, M.K.; Arikan, M.A.S.; Baykurt, H.M. A method of inverse kinematics solution including singular and multiple configurations for a class of robotic manipulators. Mech. Mach. Theory 2000, 35, 1221–1237. [Google Scholar] [CrossRef]
- Vol, N. Structural kinematics of 6-revolute-axis robot manipulators. Mech. Mach. Theory 1996, 31, 647–658. [Google Scholar]
- Pieper, D.L. The Kinematics of Manipulators under Computer Control; Stanford University: Stanford, CA, USA, 1968. [Google Scholar]
- Ai, Y.; Pan, B.; Niu, G.; Fu, Y.; Wang, S. Master-slave control technology of isomeric surgical robot for minimally invasive surgery. In Proceedings of the IEEE International Conference on Robotics and Biomimetics, Qingdao, China, 3–7 December 2017; pp. 2134–2139. [Google Scholar]
- Podsędkowski, L. Forward and Inverse Kinematics of the Cardio-Surgical Robot with Non-Coincident Axis of the Wrist. IFAC Proc. Vol. 2003, 36, 437–442. [Google Scholar] [CrossRef]
- Zhang, X.; Nelson, C.A. Kinematic Analysis and Optimization of a Novel Robot for Surgical Tool Manipulation. J. Med. Devices 2008, 2, 737–745. [Google Scholar] [CrossRef]
- Mezouar, Y. Kinematic modeling and control of a robot arm using unit dual quaternions. Robot. Auton. Syst. 2016, 77, 66–73. [Google Scholar]
- Xie, Q.; Pan, B.; Fu, Y.; Wang, S. Master-slave control technology research based on abdominal minimally invasive surgery robot. Robot 2011, 33, 53–58. [Google Scholar] [CrossRef]
- Fu, Y.; Li, H.; Xie, Q. Master-slave control technology research for abdominal minimally invasive surgery robot. In ASME 2010 International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2010; pp. 53–58. [Google Scholar]
- Kajita, S. Humanoid Robots; Tsinghua University Press: Beijing, China, 2007. [Google Scholar]
- Bu, W.; Liu, Z.; Tan, J. Inverse displacement analysis of 6R robots with offset wrists based on decoupling degrees of freedom at the cutoff points. J. Mech. Eng. 2010, 46, 1–5. [Google Scholar] [CrossRef]
- Koker, R.; Oz, C.; Cakar, T.; Ekiz, H. A study of neural network based inverse kinematics solution for a three-joint robot. Robot. Auton. Syst. 2004, 49, 227–234. [Google Scholar] [CrossRef]
- Lin, Y.; Zhao, H.; Ding, H. Solution of inverse kinematics for general robot manipulators based on multiple population genetic algorithm. J. Mech. Eng. 2017, 53, 1. [Google Scholar] [CrossRef]
- Birbil, S.I.; Fang, S.C. An Electromagnetism-like Mechanism for Global Optimization. J. Glob. Optim. 2003, 25, 263–282. [Google Scholar] [CrossRef]
- Birbil, S.I.; Fang, S.C.; Sheu, R.L. On the Convergence of a Population-Based Global Optimization Algorithm. J. Glob. Optim. 2004, 30, 301–318. [Google Scholar] [CrossRef]
- Ren, Z.; Wang, Z.; Li, J.; Sun, L. Inverse Kinematics Solution for Robot Manipulator Based on Hybrid Electromagnetism-like Mechanism Algorithm. J. Mech. Eng. 2012, 48, 21–28. [Google Scholar] [CrossRef]
- Yin, B.; Yan, B.; Shuai, J.; Ren, W.-B. Solution for direct kinematics of 3-PRS parallel manipulator using sylvester dialytic elimination method. In Proceedings of the International Conference on Mechanics and Civil Engineering, Orlando, FL, USA, 23–25 June 2014. [Google Scholar]
- Roger, A.; Horn, R. Matrix Analysis: English; People Post Press: Beijing, China, 2015. [Google Scholar]
- Taylor, R.J. An Introduction to Error Analysis; University Science Books: New York, NY, USA, 1997. [Google Scholar]
- Hayashibe, M.; Suzuki, N.; Hashizume, M.; Konishi, K.; Hattori, A. Robotic surgery setup simulation with the integration of inverse-kinematics computation and medical imaging. Comput. Methods Programs Biomed. 2006, 83, 63–72. [Google Scholar] [CrossRef] [PubMed]






| β1 (°) | β2 (°) | lQH (mm) | β3 (°) | α (°) | lIJ (mm) |
|---|---|---|---|---|---|
| 30.45 | 7 | 784.29 | 0 | 20 | 10 |
| Step (°) | Output h = 20 | Error | Input | Step (°) | Output h = 20 | Error | Input | ||
| Joint | Joint | ||||||||
| θ1 (°) | 10.00000000000004 | 0.00000000000004 | 10 | θ1 (°) | 15.39999999999996 | 0.00000000000003 | 15.4 | ||
| θ2 (°) | −124.999999995 | 0.000000005 | −125 | θ2 (°) | −116.499999995 | 0.000000005 | −116.5 | ||
| lIH (mm) | 100.0000000000001 | 0.0000000000001 | 100 | lIH (mm) | 101.3000000000001 | 0.0000000000001 | 101.3 | ||
| θ3 (°) | 99.999999995 | 0.000000005 | 100 | θ3 (°) | 86.3999999999996 | 0.0000000000004 | 86.4 | ||
| θ4 (°) | −14.0000000000008 | 0.0000000000008 | −14 | θ4 (°) | 13.6999999999998 | 0.0000000000002 | 13.7 | ||
| θ5 (°) | 18.000000002 | 0.000000002 | 18 | θ5 (°) | −15.899999996 | 0.000000004 | −15.9 | ||
| t (s) | 0.421 | t (s) | 0.406 | ||||||
| Step (°) | Output h = 10 | Error | Input | Step (°) | Output h = 20 | Error | Input | ||
| Joint | Joint | ||||||||
| θ1 (°) | −50.240000000000009 | 0.000000000000009 | −50.24 | θ1 (°) | 48.3689999999998 | 0.0000000000002 | 48.369 | ||
| θ2 (°) | −60.759999999999998 | 0.000000000000002 | −60.76 | θ2 (°) | −80.59700000000002 | 0.00000000000002 | −80.597 | ||
| lIH (mm) | 126.94000000000001 | 0.00000000000001 | 126.94 | lIH (mm) | 125.4680000000002 | 0.0000000000002 | 125.468 | ||
| θ3 (°) | 101.379999995 | 0.000000005 | 101.38 | θ3 (°) | −80.593999999998 | 0.000000000002 | −80.594 | ||
| θ4 (°) | −15.9400000000002 | 0.0000000000002 | −15.94 | θ4 (°) | −68.5920000000003 | 0.0000000000003 | −68.592 | ||
| θ5 (°) | 24.78999999 | 0.00000001 | 24.79 | θ5 (°) | 15.237999998966513 | 15.238 | |||
| t (s) | 0.484 | t (s) | 0.390 | ||||||
| Step (°) | Output h = 20 | Error | Input | Step (°) | Output h = 20 | Error | Input | ||
| Joint | Joint | ||||||||
| θ1 (°) | −56.54835000000004 | 0.00000000000004 | −56.54835 | θ1 (°) | 43.36587495200008 | 0.00000000000008 | 43.365874952 | ||
| θ2 (°) | −53.89575999999999 | 0.00000000000001 | −53.89576 | θ2 (°) | −125.687459795 | 0.000000005 | −125.6874598 | ||
| lIH (mm) | 168.85324 | 0.00004 | 168.8532 | lIH (mm) | 136.8452159699998 | 0.0000000000002 | 136.84521597 | ||
| θ3 (°) | −96.358469995 | 0.000000005 | −96.35847 | θ3 (°) | 75.312548960004 | 0.000000000004 | 75.31254896 | ||
| θ4 (°) | −50.268430000001 | 0.000000000001 | −50.26843 | θ4 (°) | 25.984572680002 | 0.000000000002 | 25.98457268 | ||
| θ5 (°) | 50.468509999 | 0.000000001 | 50.46851 | θ5 (°) | −42.58794151 | 0.00000001 | −42.587941523 | ||
| t (s) | 0.437 | t (s) | 0.437 | ||||||
| Step (°) | Output h = 20 | Error | Input | Step (°) | Output h = 20 | Error | Input | ||
| Joint | Joint | ||||||||
| θ1 (°) | 9.999999999999998 | 0.000000000000002 | 10 | θ1 (°) | 15.39999999999995 | 0.00000000000005 | 15.4 | ||
| θ2 (°) | −124.999999995 | 0.000000005 | −125 | θ2 (°) | −116.499999995 | 0.000000005 | −116.5 | ||
| lIH (mm) | 99.9999999999999 | 0.0000000000001 | 100 | lIH (mm) | 101.3000000000002 | 0.0000000000002 | 101.3 | ||
| θ3 (°) | 99.999999995 | 0.000000005 | 100 | θ3 (°) | 86.3999999999998 | 0.0000000000002 | 86.4 | ||
| θ4 (°) | −13.9999999999995 | 0.0000000000005 | −14 | θ4 (°) | 13.69999999999991 | 0.00000000000009 | 13.7 | ||
| θ5 (°) | 18.000000002 | 0.000000002 | 18 | θ5 (°) | −15.899999996 | 0.000000004 | −15.9 | ||
| t (s) | 0.016 | t (s) | 0.016 | ||||||
| Step (°) | Output h = 10 | Error | Input | Step (°) | Output h = 20 | Error | Input | ||
| Joint | Joint | ||||||||
| θ1 (°) | −50.240000000000002 | 0.000000000000002 | −50.24 | θ1 (°) | 48.3689999999998 | 0.0000000000002 | 48.369 | ||
| θ2 (°) | −60.759999999999998 | 0.000000000000002 | −60.76 | θ2 (°) | −80.59699999999998 | 0.00000000000002 | −80.597 | ||
| lIH (mm) | 126.9400000000001 | 0.0000000000001 | 126.94 | lIH (mm) | 125.4680000000002 | 0.0000000000002 | 125.468 | ||
| θ3 (°) | 101.379999995 | 0.000000005 | 101.38 | θ3 (°) | −80.593999999998 | 0.0000000000002 | −80.594 | ||
| θ4 (°) | −15.9400000000008 | 0.0000000000008 | −15.94 | θ4 (°) | −68.5920000000003 | 0.0000000000003 | −68.592 | ||
| θ5 (°) | 24.78999999 | 0.00000001 | 24.79 | θ5 (°) | 15.237999999 | 0.000000001 | 15.238 | ||
| t (s) | 0.016 | t (s) | 0.016 | ||||||
| Step (°) | Output h = 20 | Error | Input | Step (°) | Output h = 20 | Error | Input | ||
| Joint | Joint | ||||||||
| θ1 (°) | −56.54835000000004 | 0.00000000000004 | −56.54835 | θ1 (°) | 43.36587495200008 | 0.00000000000008 | 43.365874952 | ||
| θ2 (°) | −53.89575999999999 | 0.00000000000001 | −53.89576 | θ2 (°) | −125.687459795 | 0.000000005 | −125.6874598 | ||
| lIH (mm) | 168.85320000000007 | 0.00000000000007 | 168.8532 | lIH (mm) | 136.8452159699999 | 0.0000000000001 | 136.84521597 | ||
| θ3 (°) | −96.358469995 | 0.000000005 | −96.35847 | θ3 (°) | 75.3125489599998 | 0.0000000000002 | 75.31254896 | ||
| θ4 (°) | −50.268430000001 | 0.000000000001 | −50.26843 | θ4 (°) | 25.9845726799996 | 0.0000000000004 | 25.98457268 | ||
| θ5 (°) | 50.468509999 | 0.000000001 | 50.46851 | θ5 (°) | −42.58794151 | 0.00000001 | −42.587941523 | ||
| t (s) | 0.016 | t (s) | 0.016 | ||||||
| Method | Applicability | Complexity of Calculation | Solution Precision | Solution Speed | Singularity Influences |
|---|---|---|---|---|---|
| separates the position and orientation [10,11] | especially for the structure satisfied Pieper principle | low | high | quick | need to consider about |
| method based on the Jacobian matrix [16,28] | all | high | middle | not quick | need to consider about |
| The proposed method | especially for the structure not satisfied Pieper principle | middle | high | quick | barely considering about |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, L.; Yang, J.; Chen, X.; Jiang, P.; Liu, F.; Zheng, F.; Sun, Y. Solving the Time-Varying Inverse Kinematics Problem for the Da Vinci Surgical Robot. Appl. Sci. 2019, 9, 546. https://doi.org/10.3390/app9030546
Bai L, Yang J, Chen X, Jiang P, Liu F, Zheng F, Sun Y. Solving the Time-Varying Inverse Kinematics Problem for the Da Vinci Surgical Robot. Applied Sciences. 2019; 9(3):546. https://doi.org/10.3390/app9030546
Chicago/Turabian StyleBai, Long, Jianxing Yang, Xiaohong Chen, Pei Jiang, Fuqiang Liu, Fan Zheng, and Yuanxi Sun. 2019. "Solving the Time-Varying Inverse Kinematics Problem for the Da Vinci Surgical Robot" Applied Sciences 9, no. 3: 546. https://doi.org/10.3390/app9030546
APA StyleBai, L., Yang, J., Chen, X., Jiang, P., Liu, F., Zheng, F., & Sun, Y. (2019). Solving the Time-Varying Inverse Kinematics Problem for the Da Vinci Surgical Robot. Applied Sciences, 9(3), 546. https://doi.org/10.3390/app9030546