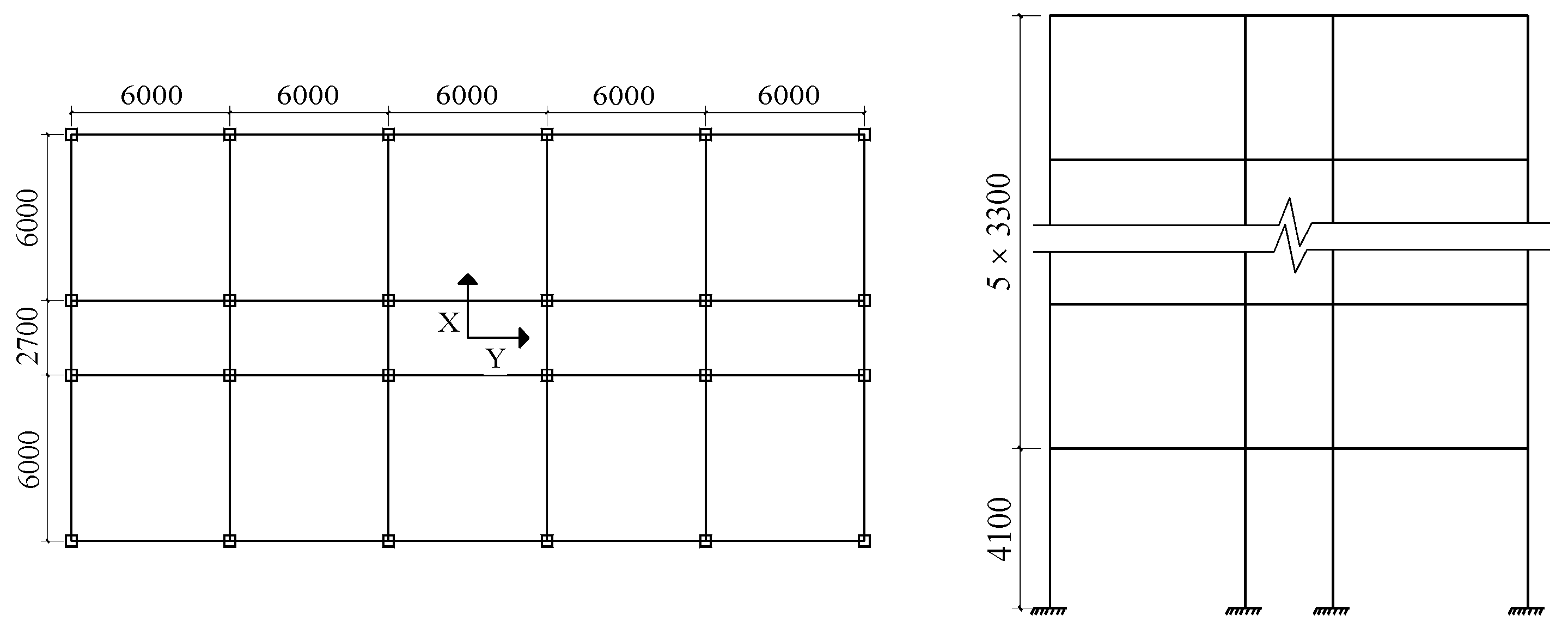
Figure 1.
Layout of frame structure (unit: mm).
Figure 1.
Layout of frame structure (unit: mm).
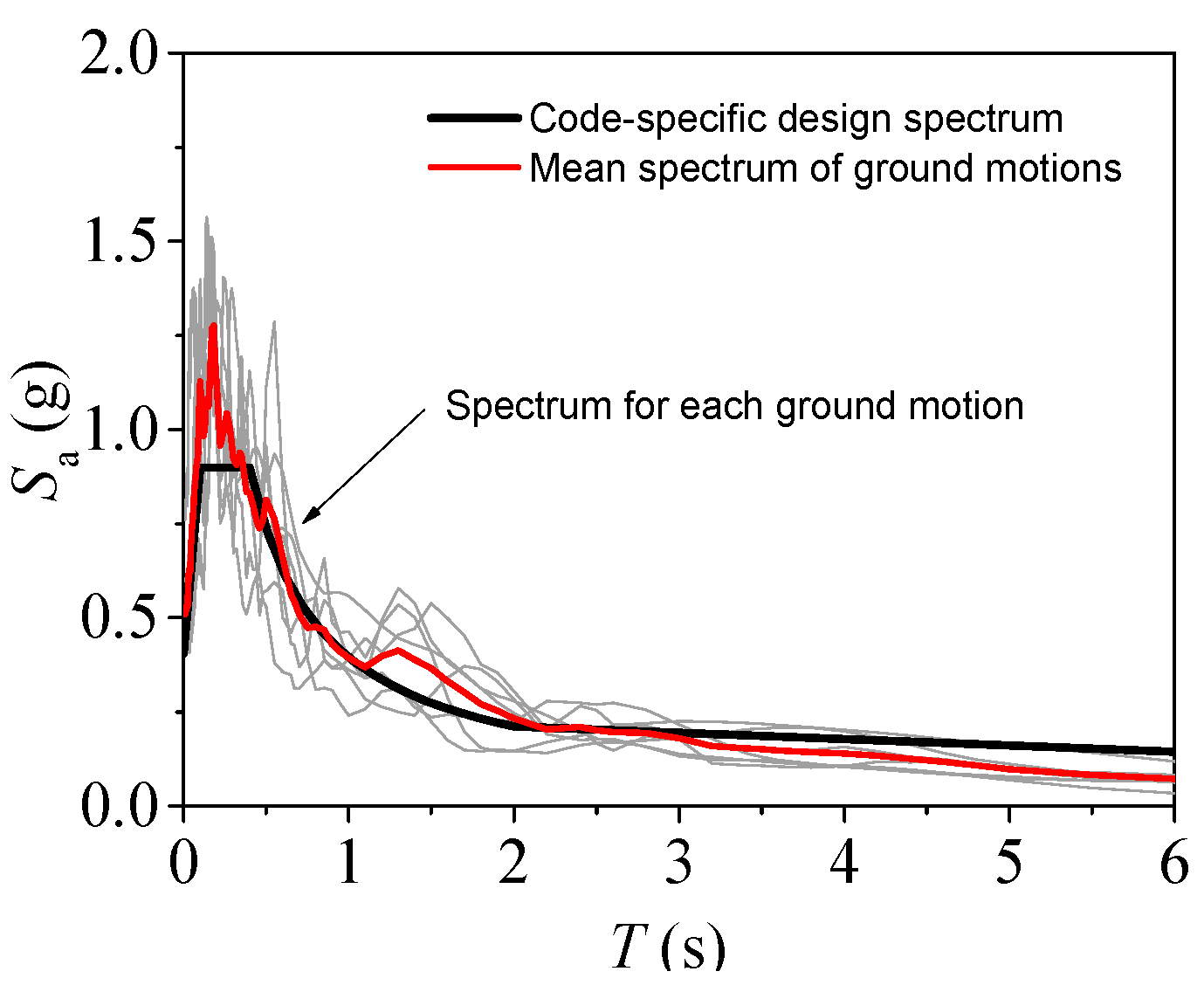
Figure 2.
Selected GMs compatible with the design spectrum.
Figure 2.
Selected GMs compatible with the design spectrum.
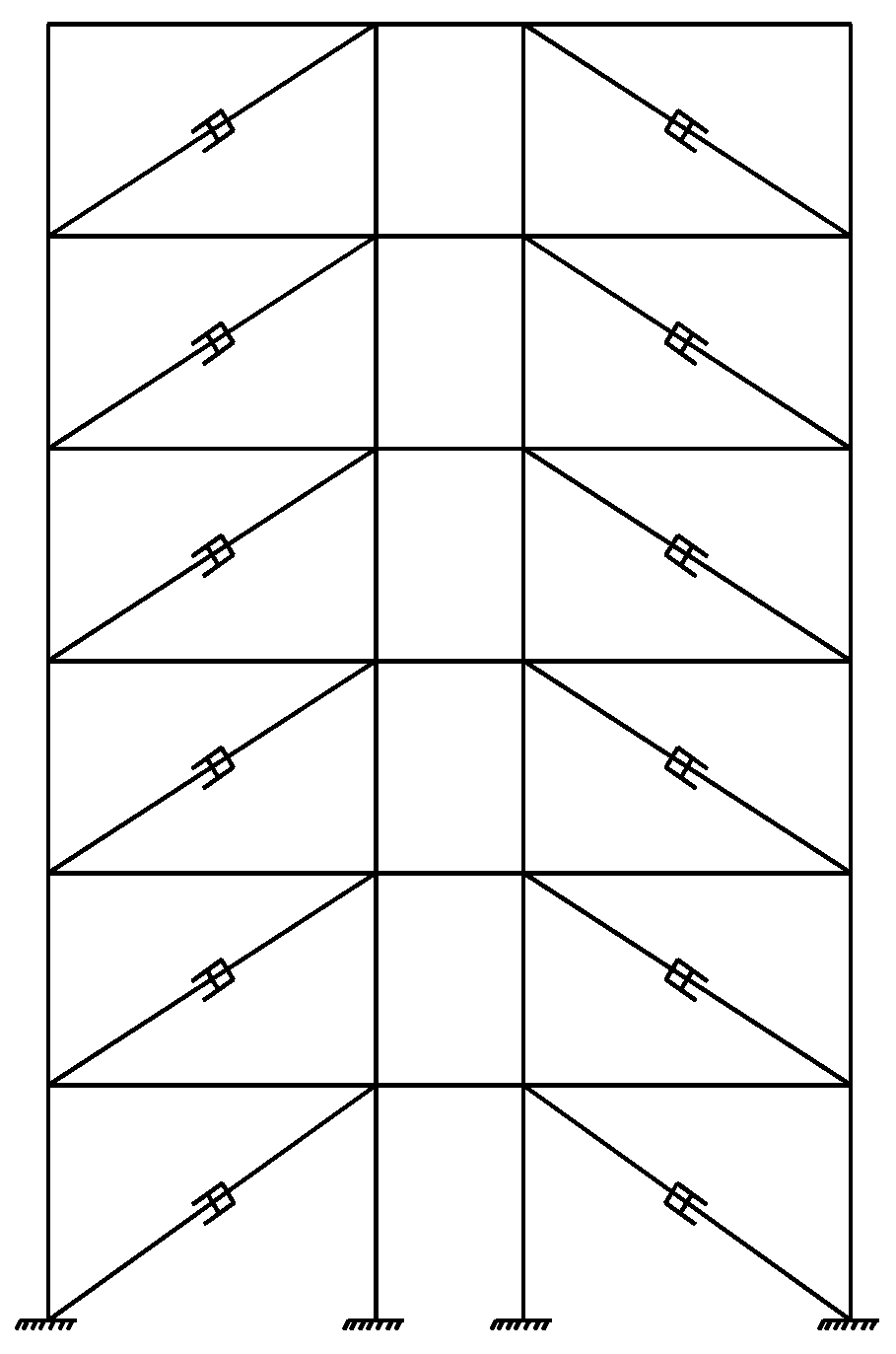
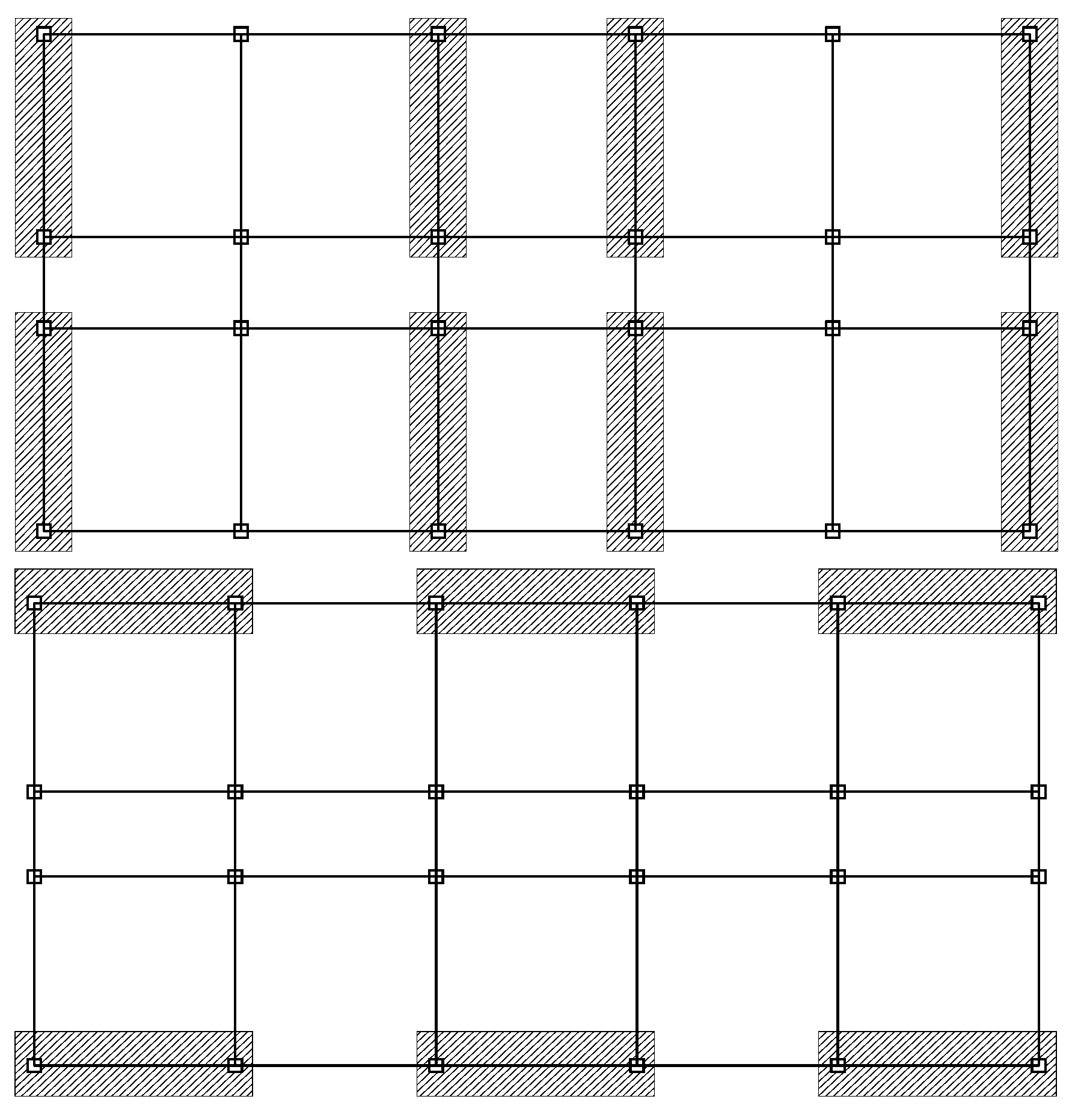
Figure 3.
Placement layout of viscous dampers in the structure (planar frame for illustration).
Figure 3.
Placement layout of viscous dampers in the structure (planar frame for illustration).
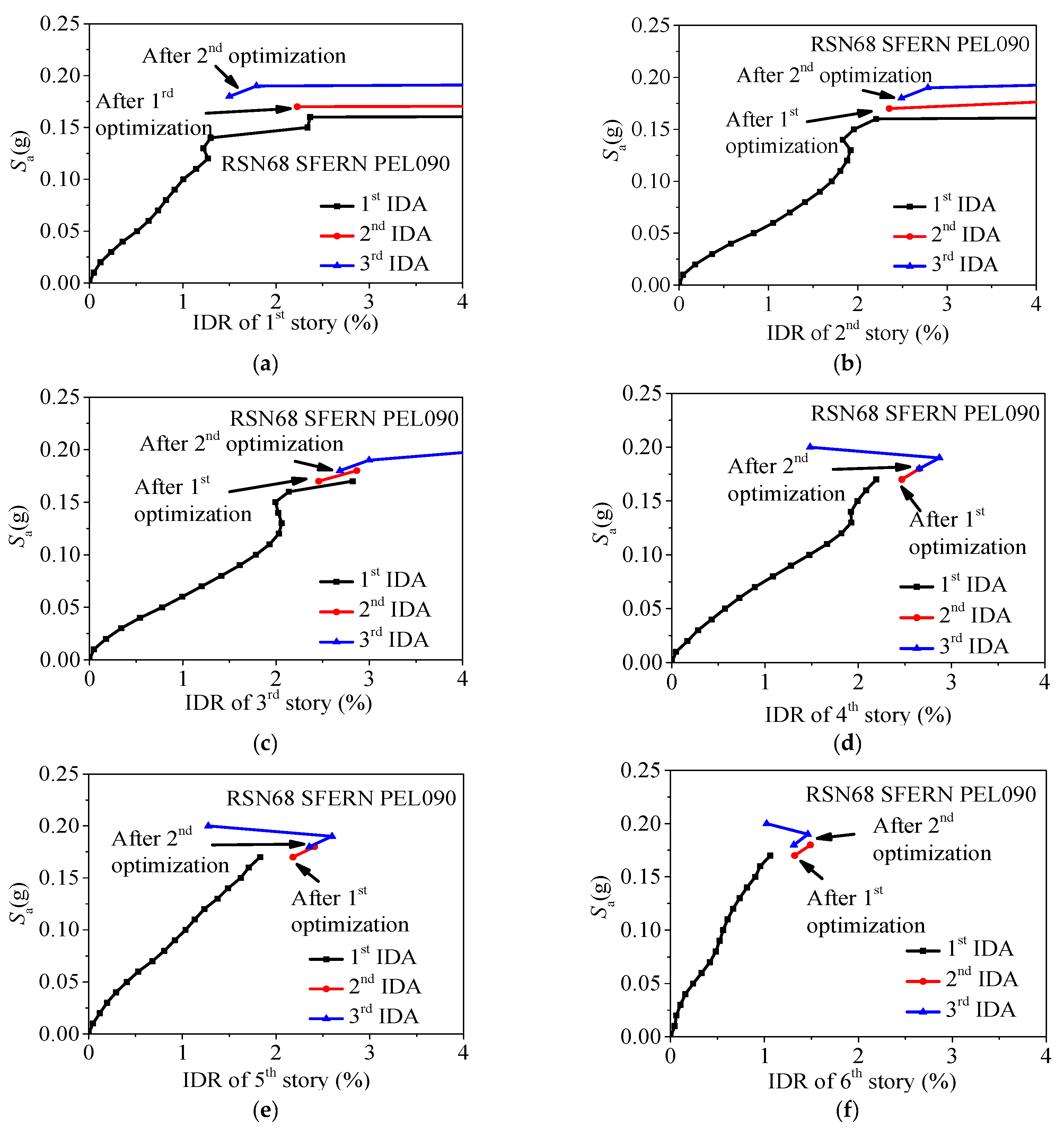
Figure 4.
Variation of the collapse resistance in the optimum procedure (using Initial scheme 1 as an example; IDR: Inter-story drift ratio): (a) 1st story, IDA (incremental dynamic analysis) curves; (b) 2nd story, IDA curves; (c) 3rd story, IDA curves; (d) 4th story, IDA curves; (e) 5th story, IDA curves; (f) 6th story, IDA curves.
Figure 4.
Variation of the collapse resistance in the optimum procedure (using Initial scheme 1 as an example; IDR: Inter-story drift ratio): (a) 1st story, IDA (incremental dynamic analysis) curves; (b) 2nd story, IDA curves; (c) 3rd story, IDA curves; (d) 4th story, IDA curves; (e) 5th story, IDA curves; (f) 6th story, IDA curves.
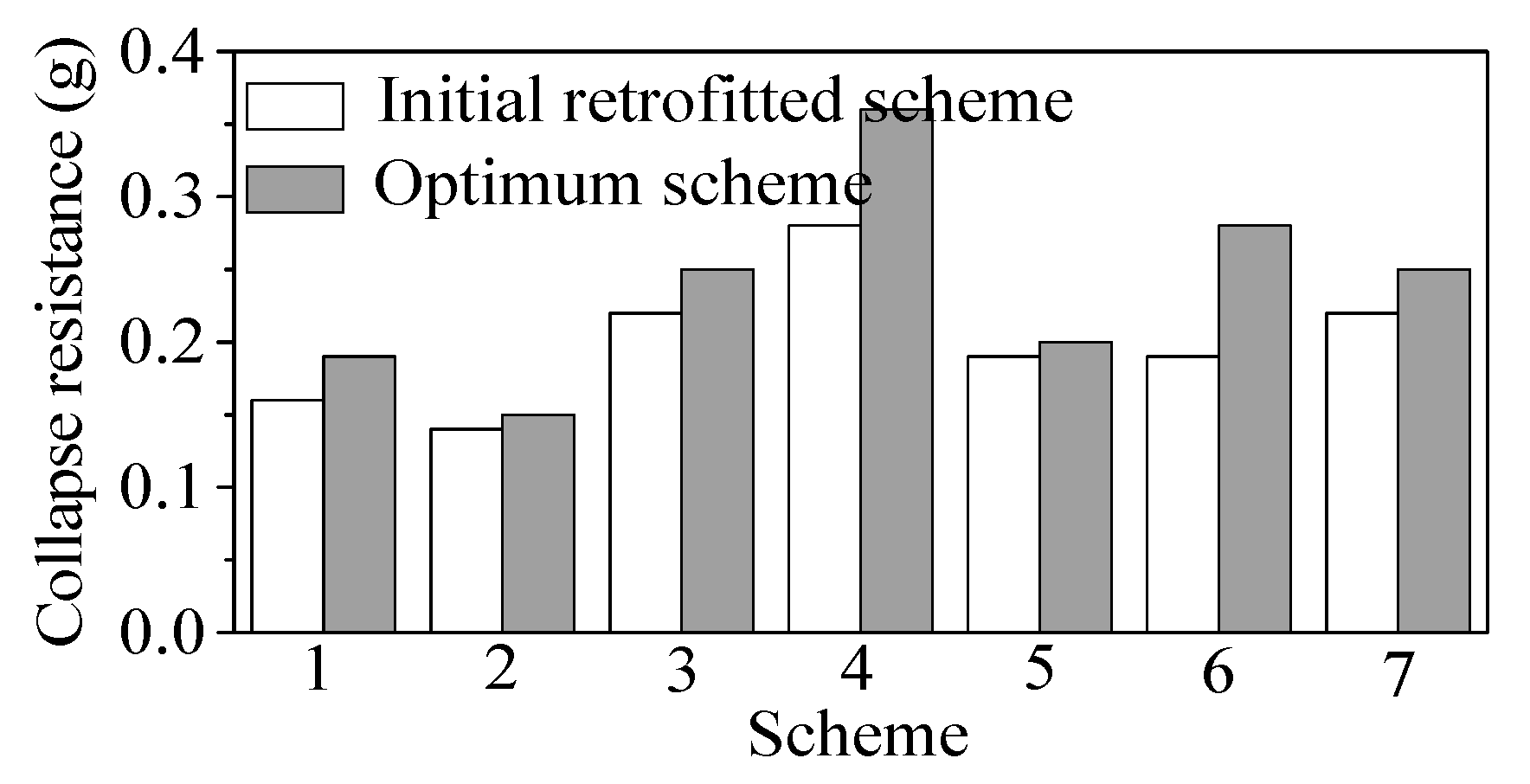
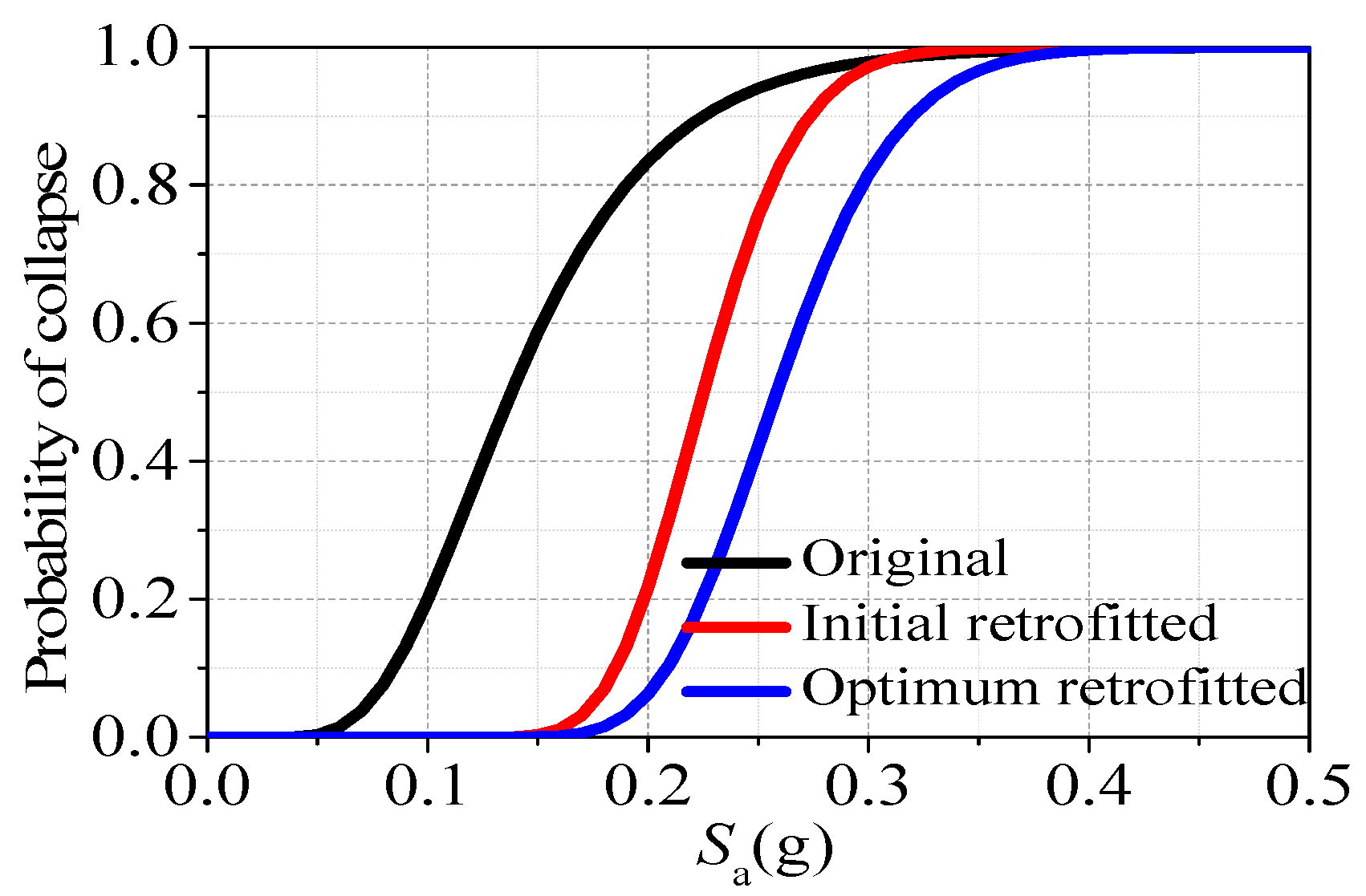
Figure 5.
Comparison between the structural collapse resistance of the initial retrofitted scheme and the optimum retrofitted scheme.
Figure 5.
Comparison between the structural collapse resistance of the initial retrofitted scheme and the optimum retrofitted scheme.
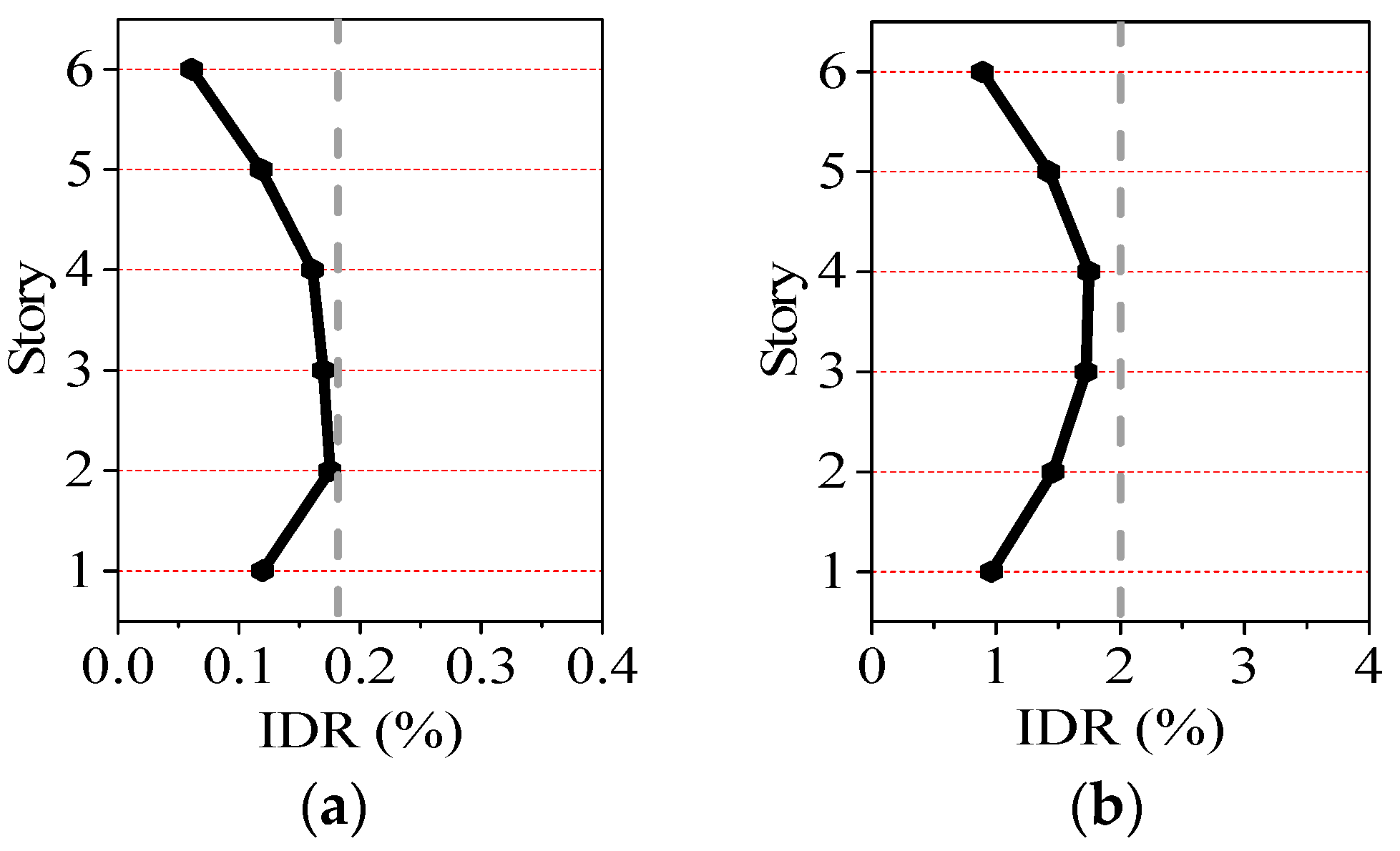
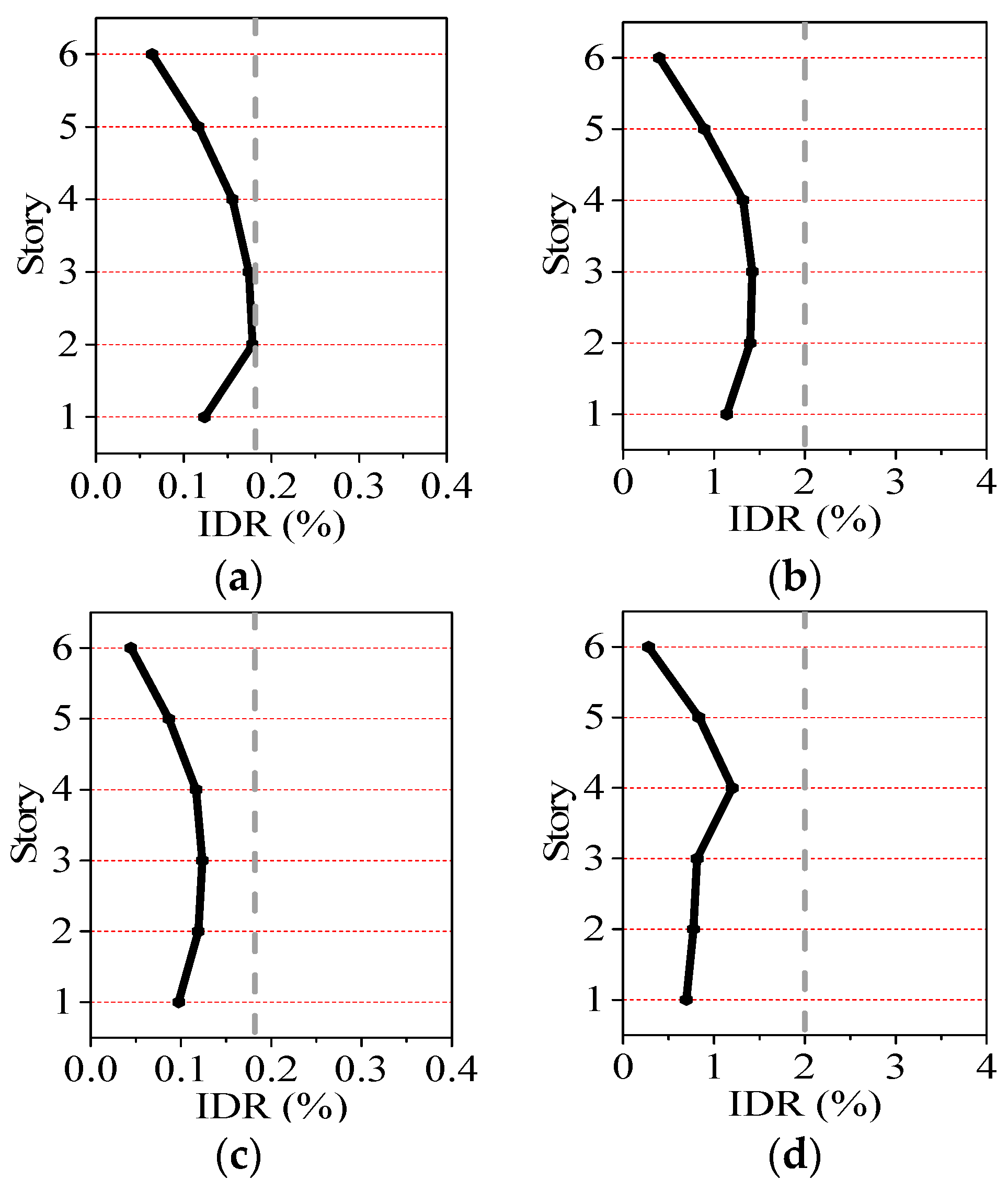
Figure 6.
Average inter-story drift ratio (IDR) under frequent and rare earthquakes: (a) Frequent earthquake; (b) Rare earthquake.
Figure 6.
Average inter-story drift ratio (IDR) under frequent and rare earthquakes: (a) Frequent earthquake; (b) Rare earthquake.
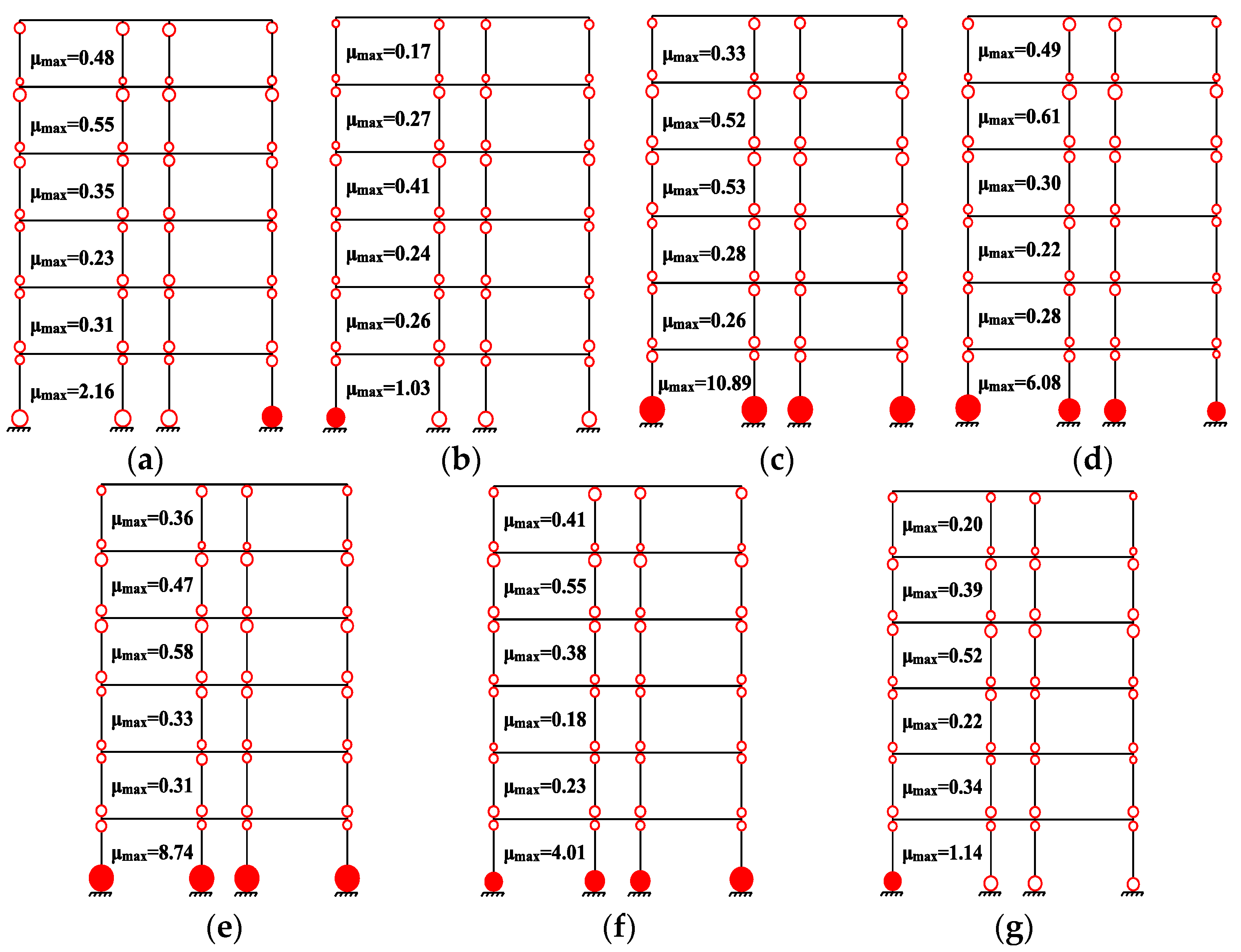
Figure 7.
Locations of yielding in columns of initial retrofitted frame (Initial scheme 5): (a) GM 1; (b) GM 2; (c) GM 3; (d) GM 4; (e) GM 5; (f) GM 6; (g) GM 7.
Figure 7.
Locations of yielding in columns of initial retrofitted frame (Initial scheme 5): (a) GM 1; (b) GM 2; (c) GM 3; (d) GM 4; (e) GM 5; (f) GM 6; (g) GM 7.
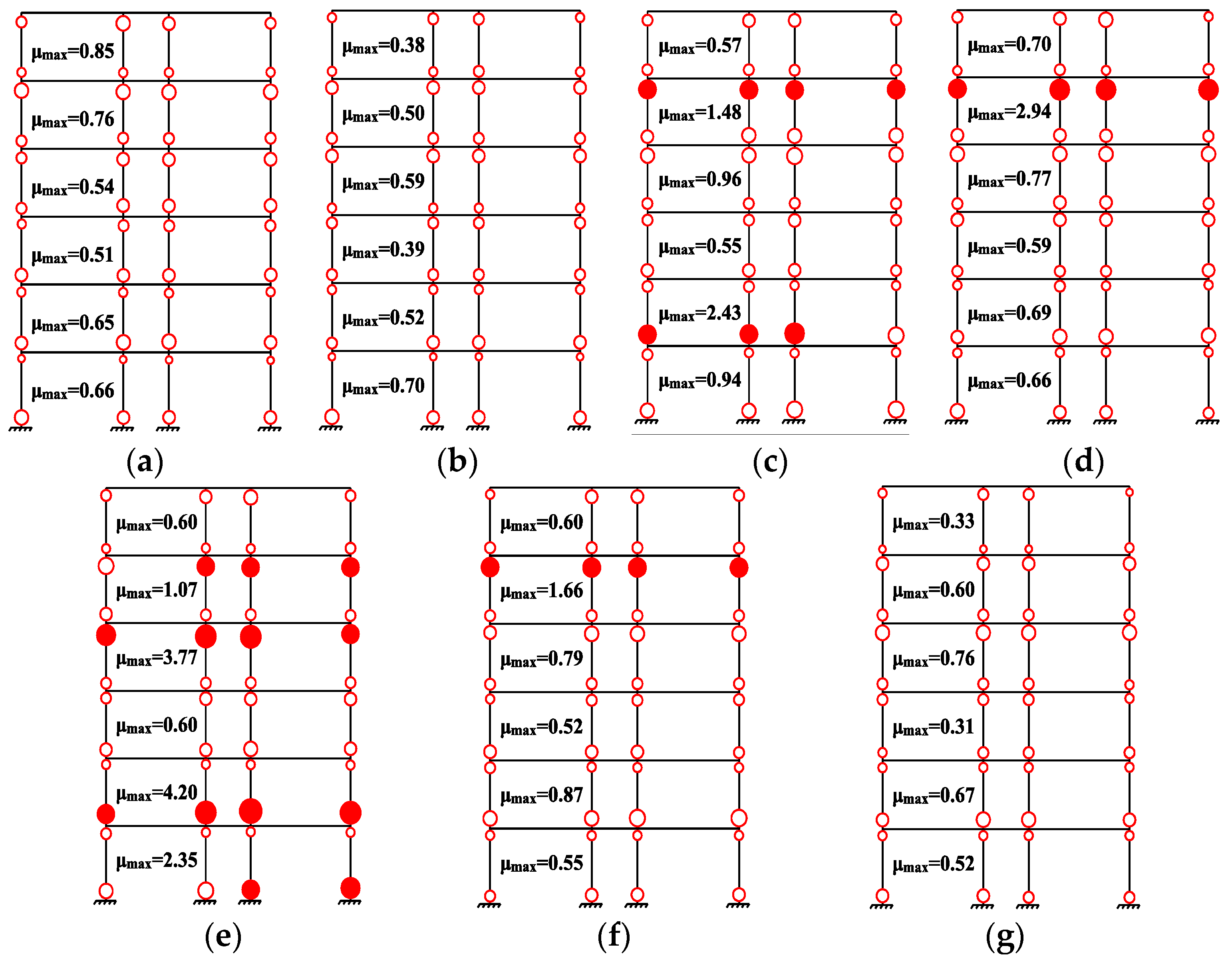
Figure 8.
Locations of yielding in columns of optimum retrofitted frame: (a) GM 1; (b) GM 2; (c) GM 3; (d) GM 4; (e) GM 5; (f) GM 6; (g) GM 7.
Figure 8.
Locations of yielding in columns of optimum retrofitted frame: (a) GM 1; (b) GM 2; (c) GM 3; (d) GM 4; (e) GM 5; (f) GM 6; (g) GM 7.
Figure 9.
Collapse fragility curves of the 2D frame.
Figure 9.
Collapse fragility curves of the 2D frame.
Figure 10.
Placement of viscous dampers in X and Y directions (placed at shadow bays).
Figure 10.
Placement of viscous dampers in X and Y directions (placed at shadow bays).
Figure 11.
Average inter-story drift ratio (IDR) under frequent and rare earthquakes: (a) X direction, frequent earthquake; (b) X direction, rare earthquake; (c) Y direction, frequent earthquake; (d) Y direction, rare earthquake.
Figure 11.
Average inter-story drift ratio (IDR) under frequent and rare earthquakes: (a) X direction, frequent earthquake; (b) X direction, rare earthquake; (c) Y direction, frequent earthquake; (d) Y direction, rare earthquake.
Figure 12.
Exceedance probabilities of economic loss under different earthquake intensities: (a) 3D original frame, frequent earthquake; (b) 3D retrofitted frame, frequent earthquake; (c) 3D original frame, occasional earthquake; (d) 3D retrofitted frame, occasional earthquake; (e) 3D original frame, rare earthquake (frame is collapse in this case); (f) 3D retrofitted frame, rare earthquake.
Figure 12.
Exceedance probabilities of economic loss under different earthquake intensities: (a) 3D original frame, frequent earthquake; (b) 3D retrofitted frame, frequent earthquake; (c) 3D original frame, occasional earthquake; (d) 3D retrofitted frame, occasional earthquake; (e) 3D original frame, rare earthquake (frame is collapse in this case); (f) 3D retrofitted frame, rare earthquake.
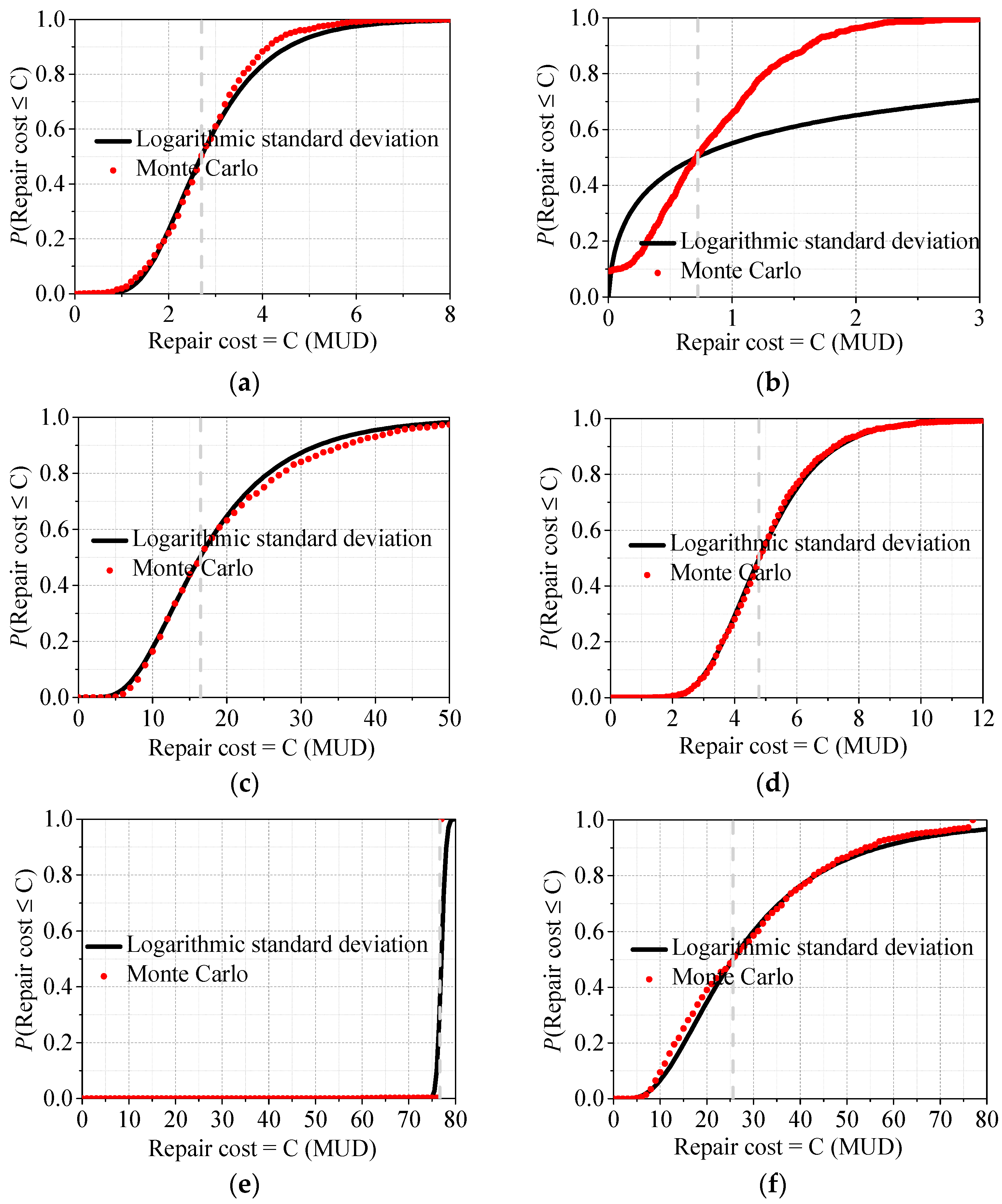
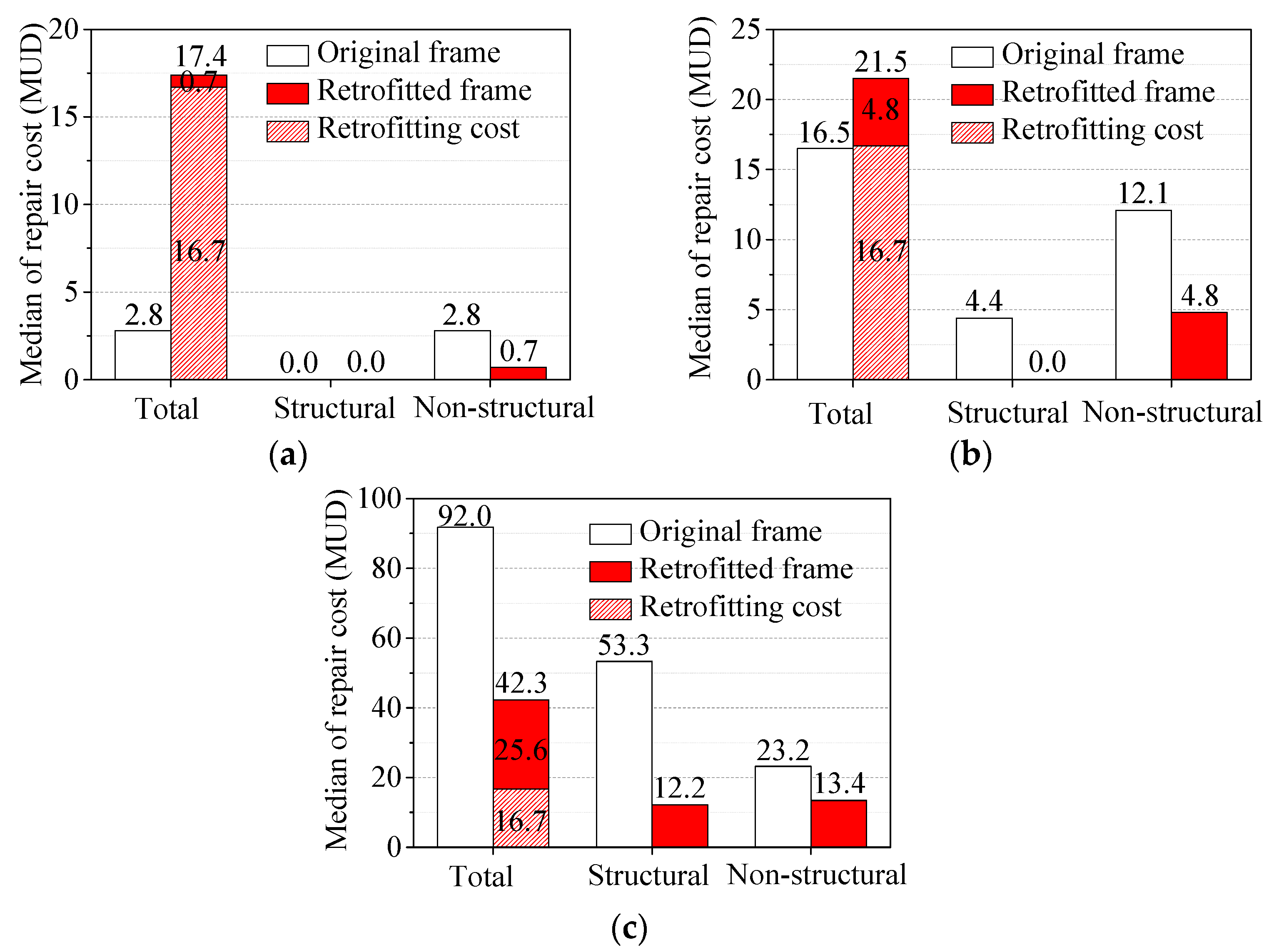
Figure 13.
Median values of repair costs under different earthquake intensities: (a) Frequent earthquake; (b) Occasional earthquake; (c) Rare earthquake.
Figure 13.
Median values of repair costs under different earthquake intensities: (a) Frequent earthquake; (b) Occasional earthquake; (c) Rare earthquake.
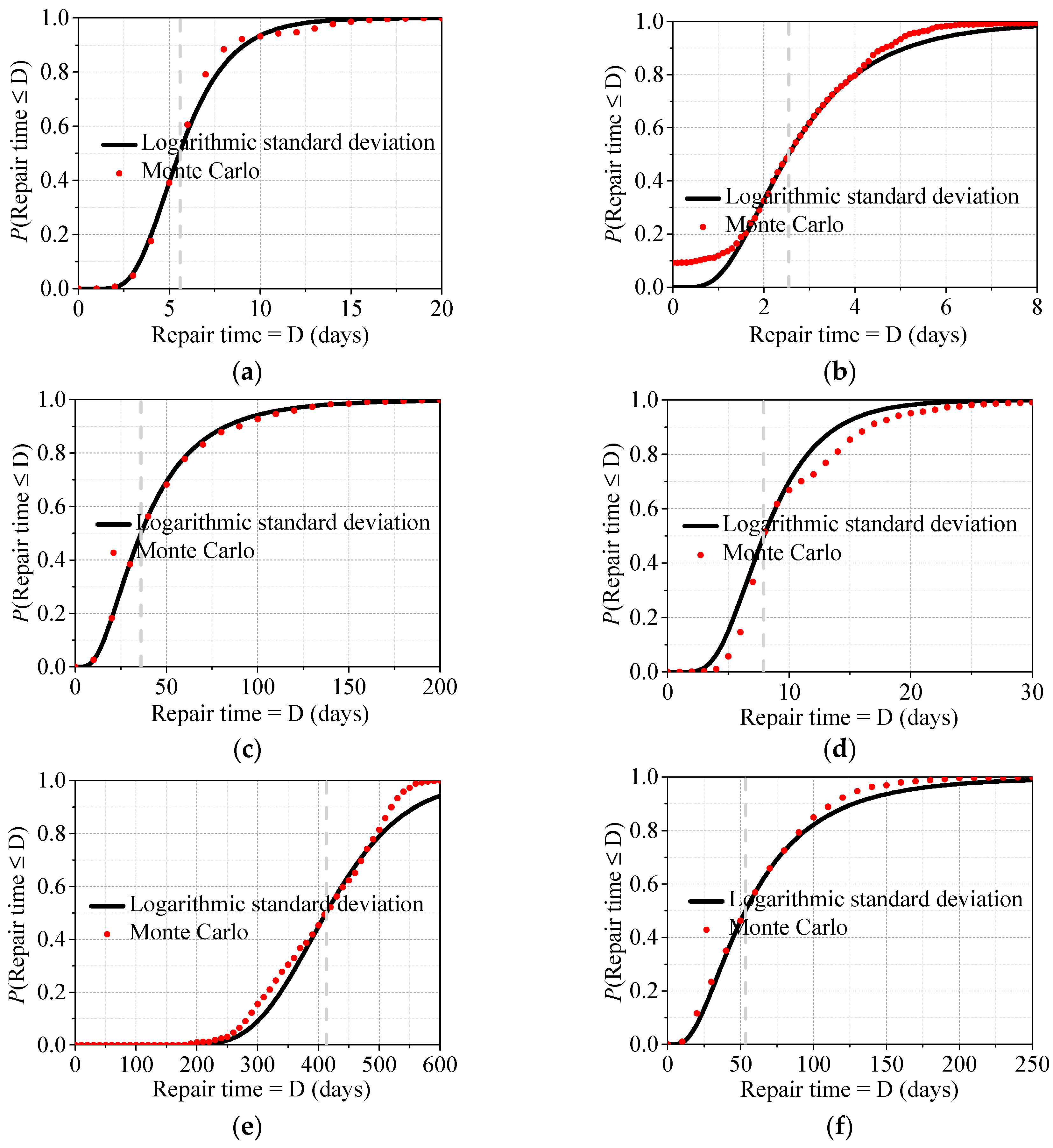
Figure 14.
Exceedance probabilities of repair time under different earthquake intensities (Parallel construction): (a) 3D original frame, frequent earthquake; (b) 3D retrofitted frame, frequent earthquake; (c) 3D original frame, occasional earthquake; (d) 3D retrofitted frame, occasional earthquake; (e) 3D original frame, rare earthquake; (f) 3D retrofitted frame, rare earthquake.
Figure 14.
Exceedance probabilities of repair time under different earthquake intensities (Parallel construction): (a) 3D original frame, frequent earthquake; (b) 3D retrofitted frame, frequent earthquake; (c) 3D original frame, occasional earthquake; (d) 3D retrofitted frame, occasional earthquake; (e) 3D original frame, rare earthquake; (f) 3D retrofitted frame, rare earthquake.
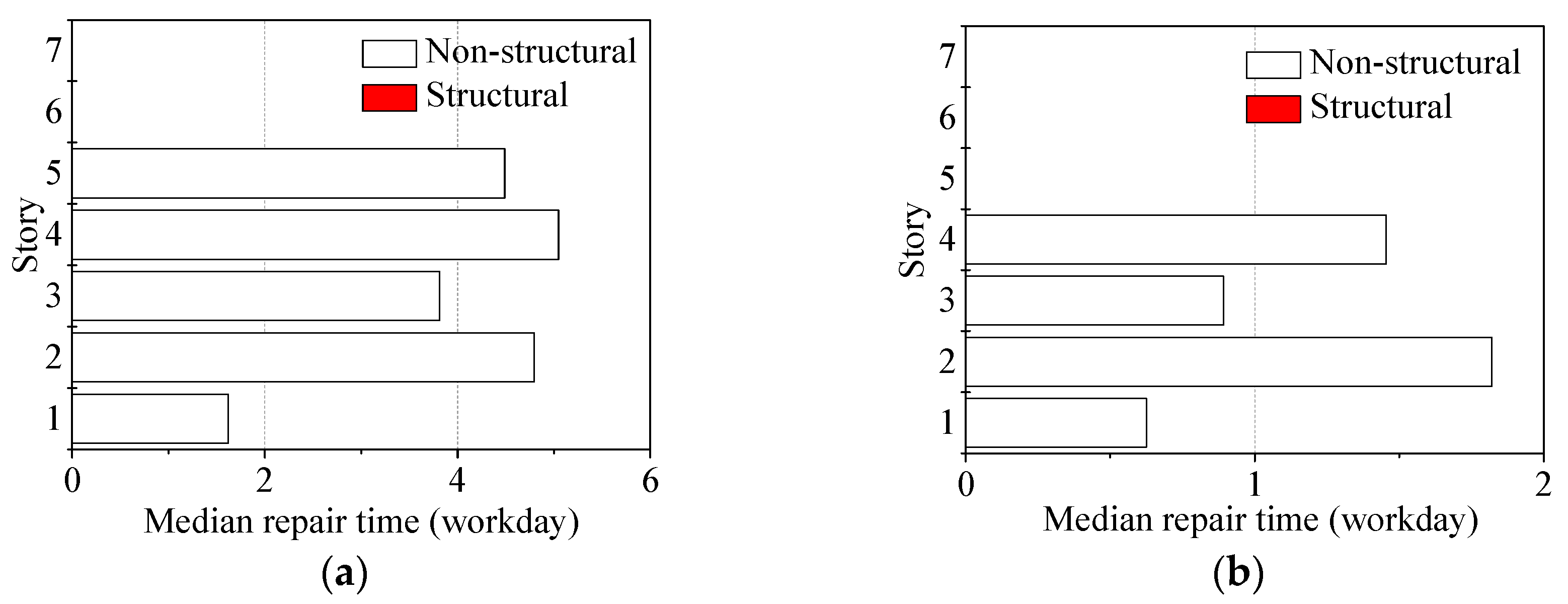
Figure 15.
Median values of repair times under different earthquake intensities (parallel construction): (a) 3D original frame, frequent earthquake; (b) 3D retrofitted frame, frequent earthquake; (c) 3D original frame, occasional earthquake; (d) 3D retrofitted frame, occasional earthquake; (e) 3D original frame, rare earthquake; (f) 3D retrofitted frame, rare earthquake.
Figure 15.
Median values of repair times under different earthquake intensities (parallel construction): (a) 3D original frame, frequent earthquake; (b) 3D retrofitted frame, frequent earthquake; (c) 3D original frame, occasional earthquake; (d) 3D retrofitted frame, occasional earthquake; (e) 3D original frame, rare earthquake; (f) 3D retrofitted frame, rare earthquake.
Table 1.
Dimensions of beams and rebars (X direction).
Table 1.
Dimensions of beams and rebars (X direction).
| Story | Size (mm × mm) Width × Height | Area of Longitudinal Rebars (mm2)/Stirrup |
|---|
| Side Bay | Middle Bay | Side Bay | Middle Bay |
|---|
| Beam Ends | Midspan | Beam Ends | Midspan |
|---|
| 1 | 200 × 50 | 200 × 300 | 2250/ϕ8@100 | 1600/ϕ8@200 | 2250/ϕ8@100 | 1350/ϕ8@200 |
| 2 | 200 × 50 | 200 × 300 | 2200/ϕ8@100 | 1600/ϕ8@200 | 2200/ϕ8@100 | 1250/ϕ8@200 |
| 3 | 200 × 50 | 200 × 300 | 2050/ϕ8@100 | 1600/ϕ8@200 | 2050/ϕ8@100 | 1100/ϕ8@200 |
| 4 | 200 × 50 | 200 × 300 | 1800/ϕ8@100 | 1650/ϕ8@200 | 1800/ϕ8@100 | 850/ϕ8@200 |
| 5 | 200 × 50 | 200 × 300 | 1450/ϕ8@100 | 1650/ϕ8@200 | 1450/ϕ8@100 | 750/ϕ8@200 |
| 6 | 200 × 50 | 200 × 300 | 850/ϕ8@100 | 1400/ϕ8@200 | 850/ϕ8@100 | 600/ϕ8@200 |
Table 2.
Dimensions of columns and rebars.
Table 2.
Dimensions of columns and rebars.
| Story | Size (mm × mm) | Area of Longitudinal Rebars (mm2)/Stirrup |
|---|
| Side Column | Middle Column | Side Column | Middle Column |
|---|
| 1 | 400 × 400 | 400 × 400 | 2000/ϕ8@100 | 1400/ϕ8@100 |
| 2 | 400 × 400 | 400 × 400 | 800/ϕ8@100 | 1000/ϕ8@100 |
| 3 | 400 × 400 | 400 × 400 | 800/ϕ8@100 | 1000/ϕ8@100 |
| 4 | 400 × 400 | 400 × 400 | 700/ϕ8@100 | 700/ϕ8@100 |
| 5 | 400 × 400 | 400 × 400 | 700/ϕ8@100 | 700/ϕ8@100 |
| 6 | 400 × 400 | 400 × 400 | 1300/ϕ8@100 | 1000/ϕ8@100 |
Table 3.
Selected ground motions (GMs).
Table 3.
Selected ground motions (GMs).
| Tag | Earthquake | NGA ID and Component | Year | Magnitude |
|---|
| 1 | San Fernando, USA | RSN68 SFERN PEL090 | 1971 | 6.61 |
| 2 | San Fernando, USA | RSN93 SFERN WND143 | 1971 | 6.61 |
| 3 | Tabas, Iran, USA | RSN143 TABAS TAB-T1 | 1978 | 7.35 |
| 4 | Imperial valley—06, USA | RSN161 IMPVALL.H H-BRA315 | 1979 | 6.53 |
| 5 | Imperial valley—06, USA | RSN178 IMPVALL.H H-E03230 | 1979 | 6.53 |
| 6 | Imperial valley—06, USA | RSN180 IMPVALL.H H-E05140 | 1979 | 6.53 |
| 7 | Imperial valley—06, USA | RSN183 IMPVALL.H H-E08140 | 1979 | 6.53 |
Table 4.
Initial placements of dampers to satisfy code-specific requirements (unit: N·(s/m)).
Table 4.
Initial placements of dampers to satisfy code-specific requirements (unit: N·(s/m)).
| Retrofitting Scheme | | | | | | | |
|---|
| Initial scheme 1 | 300,000 | 20,000 | 250,000 | 250,000 | 20,000 | 20,000 | 860,000 |
| Initial scheme 2 | 150,000 | 150,000 | 50,000 | 50,000 | 20,000 | 20,000 | 440,000 |
| Initial scheme 3 | 1,300,000 | 1,300,000 | 1,000,000 | 500,000 | 50,000 | 20,000 | 4,170,000 |
| Initial scheme 4 | 1,000,000 | 1,000,000 | 800,000 | 250,000 | 20,000 | 20,000 | 3,090,000 |
| Initial scheme 5 | 1,200,000 | 1,300,000 | 750,000 | 200,000 | 50,000 | 50,000 | 3,550,000 |
| Initial scheme 6 | 800,000 | 750,000 | 600,000 | 100,000 | 20,000 | 20,000 | 2,290,000 |
| Initial scheme 7 | 20,000 | 20,000 | 500,000 | 50,000 | 20,000 | 20,000 | 630,000 |
Table 5.
Variation of damping coefficients in the optimum procedure (using Initial scheme 1 as an example) (unit: N·(s/m)).
Table 5.
Variation of damping coefficients in the optimum procedure (using Initial scheme 1 as an example) (unit: N·(s/m)).
| Optimum Times | Collapse Resistance | | | | | | | |
|---|
| Initial scheme 1 | 0.16 g | 300,000 | 20,000 | 250,000 | 250,000 | 20,000 | 20,000 | 860,000 |
| 1st time | 0.18 g | 499,230 | 32,883 | 185,666 | 127,186 | 7857 | 7178 | 860,000 |
| 2nd time | 0.19 g | 849,740 | 1476 | 5545 | 3329 | 0 | 0 | 860,000 |
| Optimum scheme 1 | 0.19 g | 849,740 | 1476 | 5455 | 3329 | 0 | 0 | 860,000 |
Table 6.
Damping coefficients in the optimum retrofitted scheme (unit: N·(s/m)).
Table 6.
Damping coefficients in the optimum retrofitted scheme (unit: N·(s/m)).
| Strengthen Scheme | | | | | | | |
|---|
| Optimum scheme 1 | 849,740 | 1476 | 5455 | 3329 | 0 | 0 | 860,000 |
| Optimum scheme 2 | 262,542 | 115,899 | 31,765 | 20,796 | 5172 | 3826 | 440,000 |
| Optimum scheme 3 | 3,335,742 | 543,619 | 164,958 | 125,681 | 0 | 0 | 4,170,000 |
| Optimum scheme 4 | 2,741,236 | 186,395 | 101,966 | 60,403 | 0 | 0 | 3,090,000 |
| Optimum scheme 5 | 1,610,247 | 1,339,753 | 553,541 | 46,459 | 0 | 0 | 3,550,000 |
| Optimum scheme 6 | 1,604,274 | 412,497 | 139,411 | 133,818 | 0 | 0 | 2,290,000 |
| Optimum scheme 7 | 602,094 | 3659 | 22,695 | 1551 | 0 | 0 | 630,000 |
Table 7.
Optimum damping coefficients of 3D frame (unit: N·(s/m)).
Table 7.
Optimum damping coefficients of 3D frame (unit: N·(s/m)).
| 3D Frame | | | | | | | |
|---|
| X direction | 2,415,000 | 2,010,000 | 825,000 | 75,000 | 0 | 0 | 5,325,000 |
| Y direction | 4,025,000 | 3,350,000 | 1,375,000 | 125,000 | 0 | 0 | 8,875,000 |
Table 8.
Performance groups considered in the loss estimation of 6-story RC (reinforced concrete) frame.
Table 8.
Performance groups considered in the loss estimation of 6-story RC (reinforced concrete) frame.
| Group | Fragility ID [49] | EDP | Cost/Each (Unit: US Dollar) | Number in Each Story | Total Number |
|---|
| Teaching platform | E2202.020 | PFA | 194.3 | 10 | 60 |
| Projector | C3033.002 | PFA | 448.4 | 10 | 60 |
| Table and chair | E2022.020 | PFA | 14.9 | 300 | 1800 |
| Blackboard | E2022.021 | PFA | 29.9 | 10 | 60 |
| Computer | E2022.022 | PFA | 448.4 | 10 | 60 |
Table 9.
Construction periods of key items of the 6-story RC frame.
Table 9.
Construction periods of key items of the 6-story RC frame.
| Construction Items | Construction Period (Unit: Workday) |
|---|
| Foundation project | 30 |
| Upper structure project | 305 |
| Decorate project | 60 |
| Elevator system installation | 50 |
| Heat-supply system installation | 50 |
| Air conditioning system installation | 65 |
| Electric power substation project | 40 |
| Total required workdays | 600 |
Table 10.
Statistical data on the performance groups of the 6-story frame.
Table 10.
Statistical data on the performance groups of the 6-story frame.
| | Performance Group | Fragility ID [49] | EDP | Costing Based Upon in PACT [49] | Number in Each Story | Total Number |
|---|
| Structural member | Beam joints | B1041.101b | IDR | 1 EA | 24 | 144 |
| Non-structural member | Curtain walls | B2022.001 | IDR | 30 SF | 34.82 | 208.92 |
| Partitions | C1011.001a | IDR | 100 LF | 5.32 | 31.92 |
| Wall finishes | C3011.001a | IDR | 100 LF | 1.34 | 8.04 |
| Cold water piping | D2021.011a | PFA | 1000 LF | 0.07 | 0.42 |
| Hot water piping | D2022.011a | PFA | 1000 LF | 0.40 | 2.40 |
| D2022.021a | PFA | 1000 LF | 0.16 | 0.96 |
| Sanitary waste piping | D2031.011b | PFA | 1000 LF | 0.21 | 1.26 |
| HVAC equipment | D3041.011a | PFA | 1000 LF | 0.24 | 1.44 |
| D3041.031a | PFA | 10 EA | 2.37 | 14.22 |
| Variable Air Volume (VAV) box | D3041.041a | PFA | 10 EA | 1.90 | 11.4 |
| Concrete tile roof | B3011.011 | PFA | 100 SF | 32.28 | 32.28 |
| Recessed ceiling lighting | C3033.001 | PFA | 1 EA | 71.21 | 427.26 |
| Independent pendant lighting | C3034.001 | PFA | 1 EA | 71.21 | 427.26 |
| Sprinkler water supply | D4011.021a | PFA | 1000 LF | 0.85 | 5.1 |
| D4011.031a | PFA | 100 EA | 0.38 | 2.28 |
| Stairs | C2011.001a | IDR | 1 EA | 2.00 | 12 |
| Low voltage switchgear | D5012.021a | PFA | 225 AMP | 1.00 | 6 |
| Elevator | D1014.011 | PFA | 1 EA | 1.00 | 1.00 |
| Motor control center | D5012.013a | PFA | 1 EA | 2.00 | 2.00 |
Table 11.
Median repair times of the original frame and retrofitted frame (unit: workday).
Table 11.
Median repair times of the original frame and retrofitted frame (unit: workday).
| Frame | Frequent Earthquake PGA = 0.07 g | Occasional Earthquake PGA = 0.2 g | Rare Earthquake PGA = 0.4 g |
|---|
| 3D original frame | 5 | 34 | 482 |
| 3D retrofitted frame | 2 | 7 | 53 |