Equivalent Frame Model with a Decaying Nonlinear Moment-Curvature of Steel-Reinforced Concrete Joints
Abstract
1. Introduction
2. Description
2.1. Description of the Model
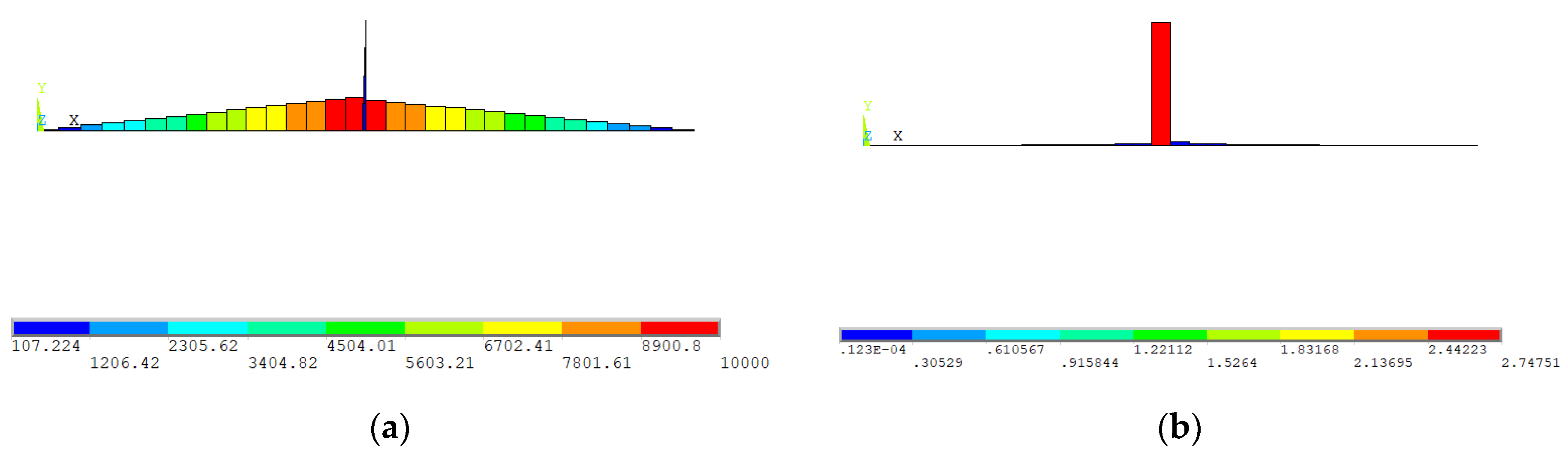
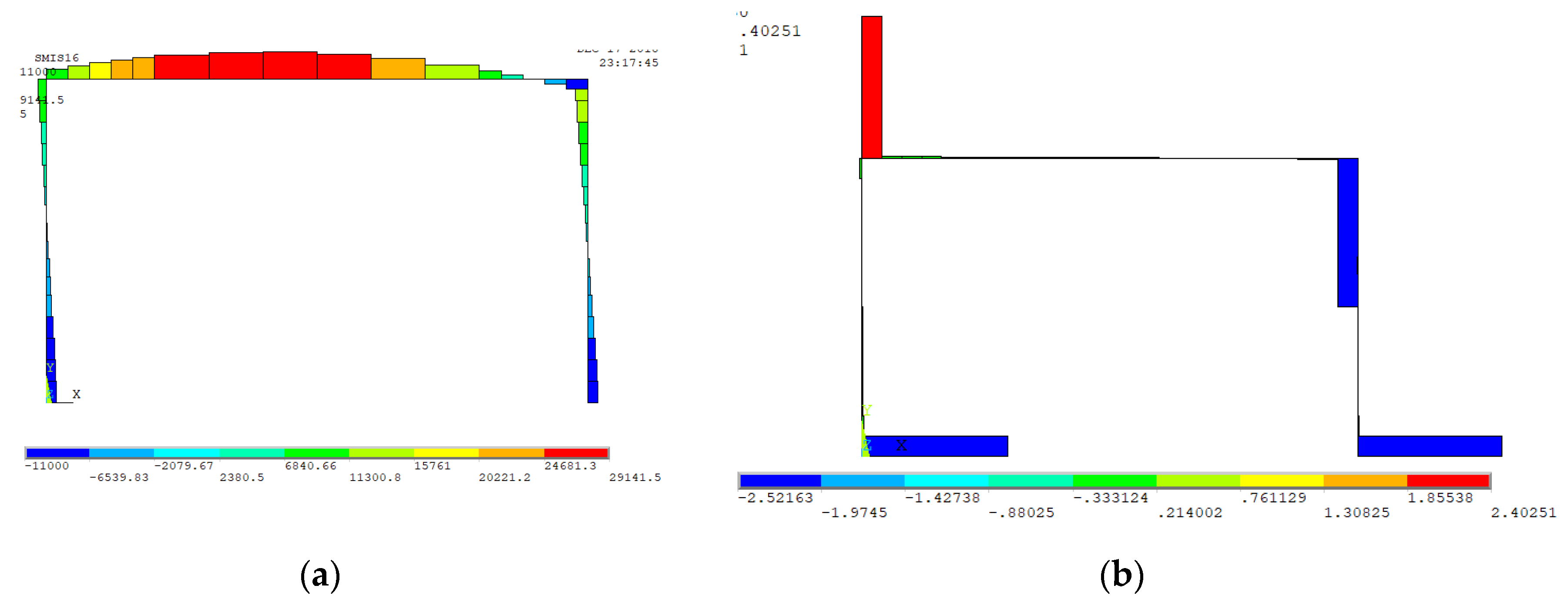
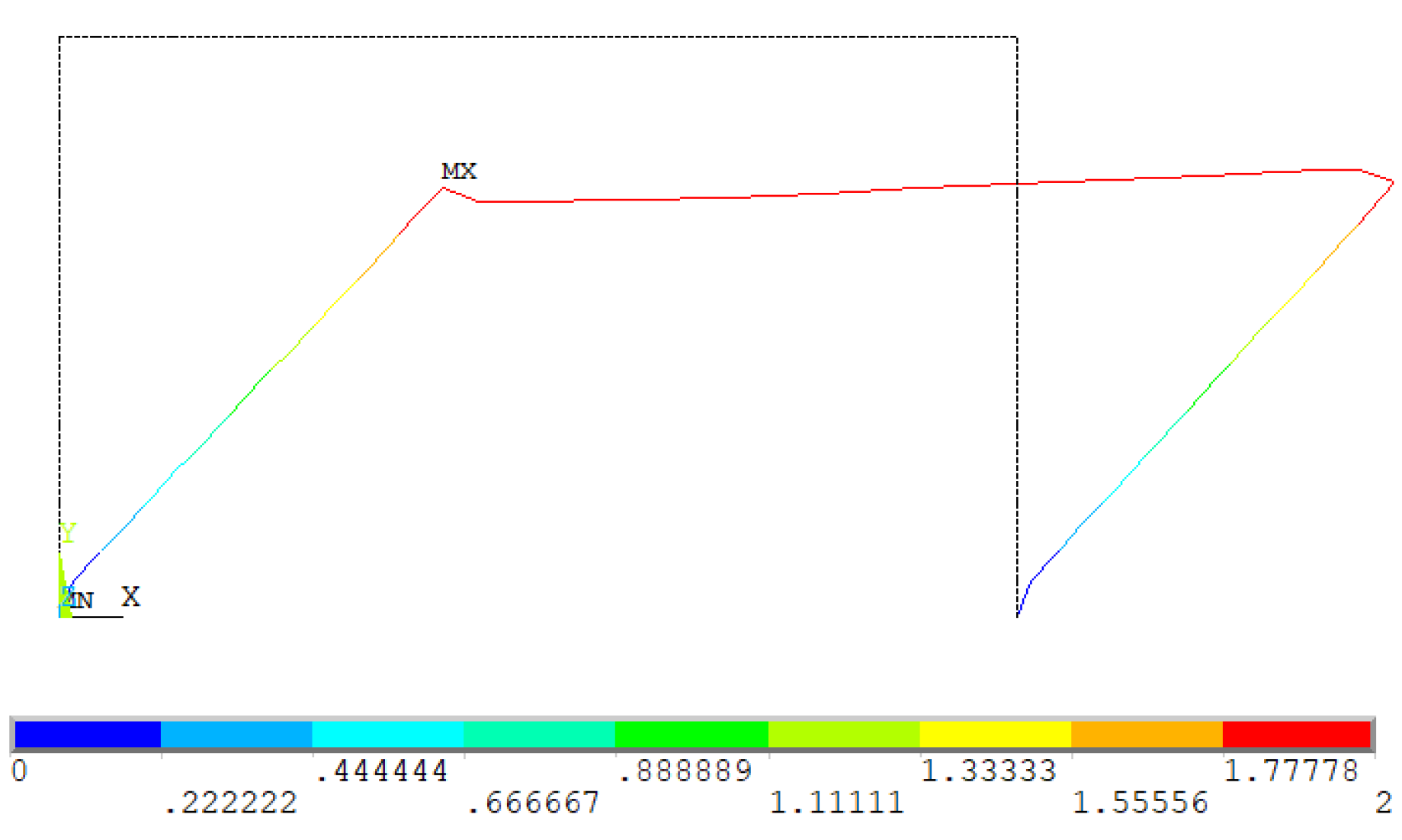
2.2. Equivalent Frame Model with Ansys APDL M–χ Nonlinear Relationship
3. Simulated Models
3.1. Prototypes P03, P04 and P05
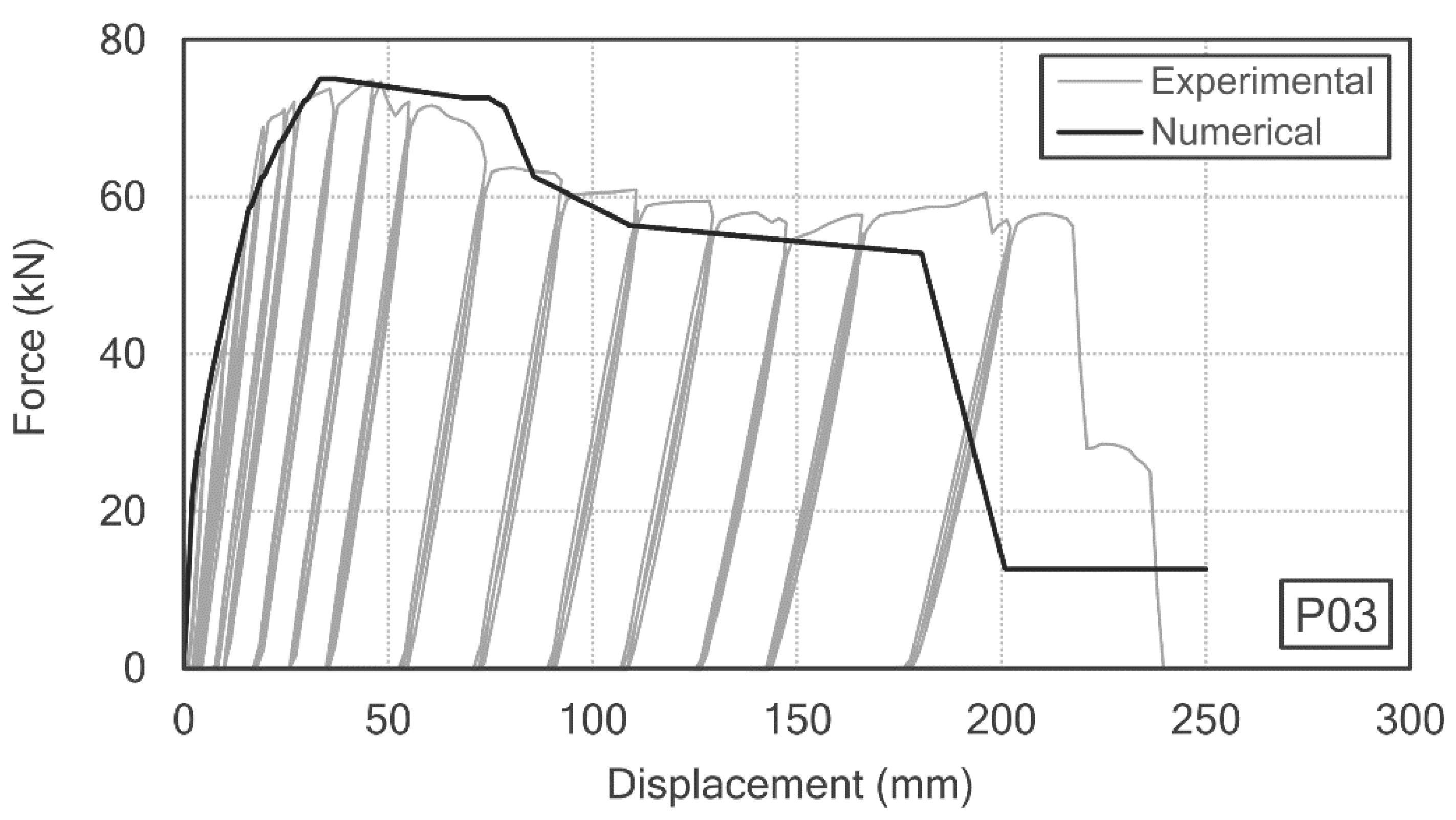
3.1.1. Reinforced Concrete P03 Prototype
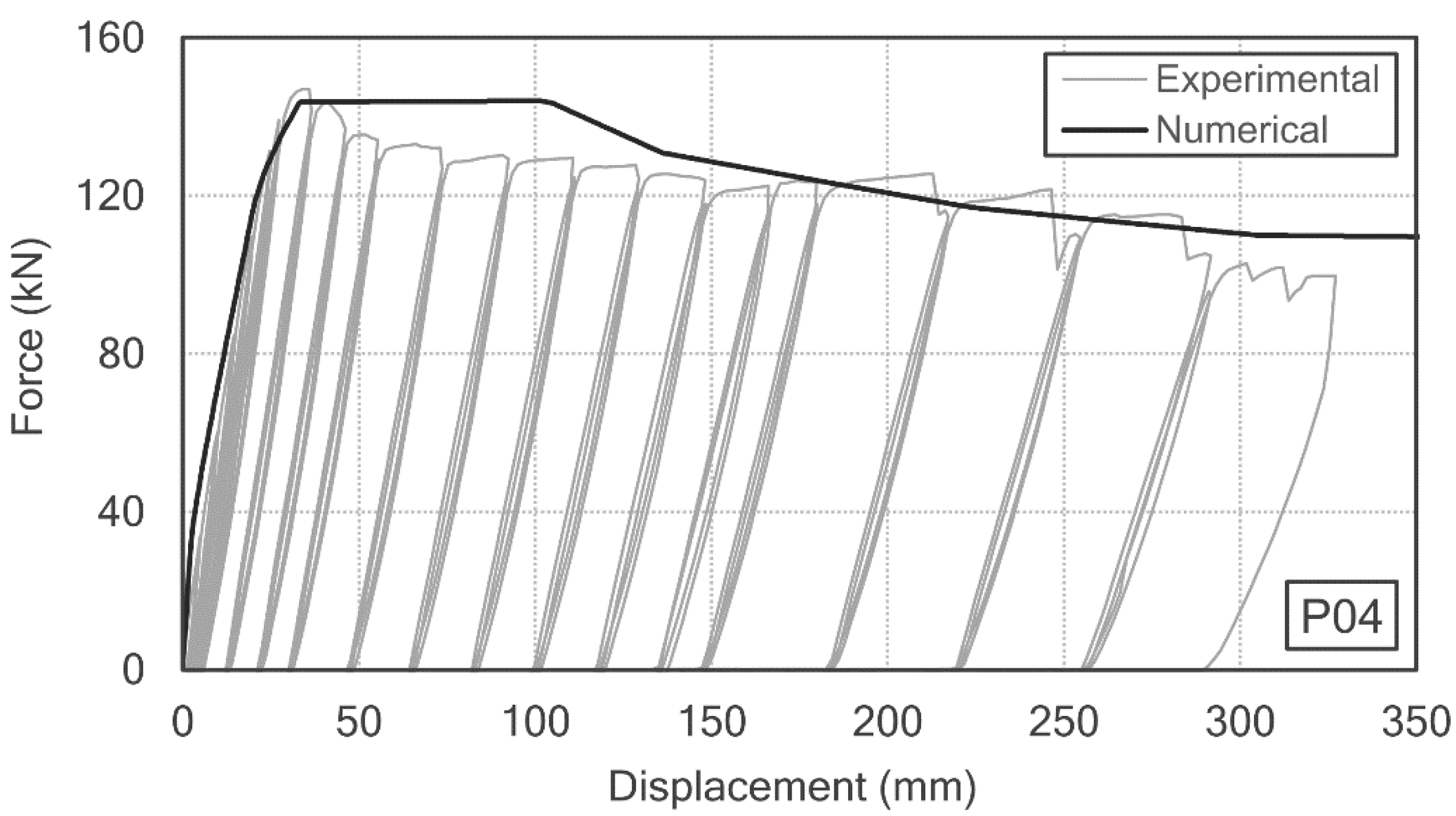
3.1.2. Steel Reinforced Concrete P04 Prototype
3.1.3. Reinforced Concrete P05 Prototype
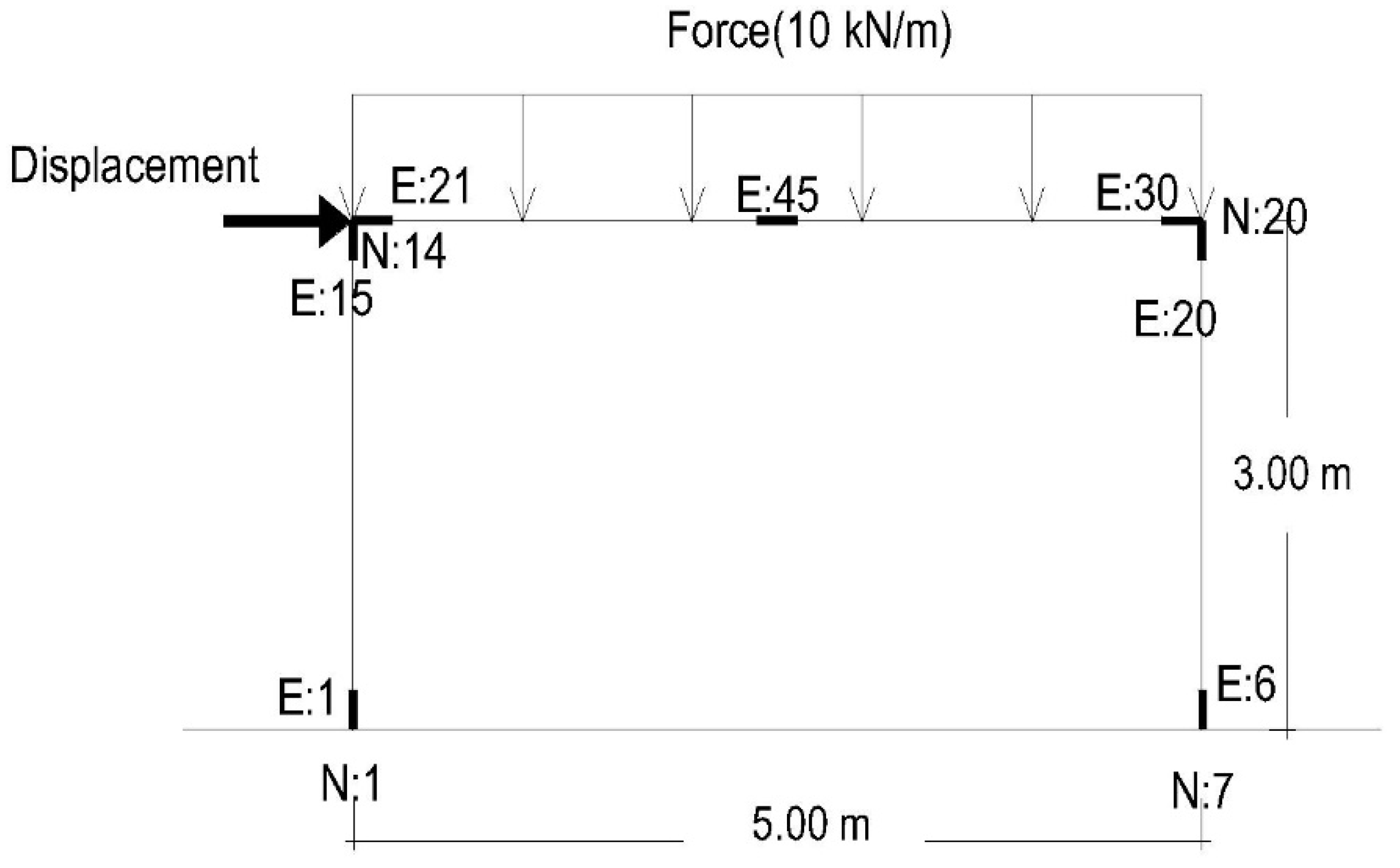
3.2. Frame Structure in 2D
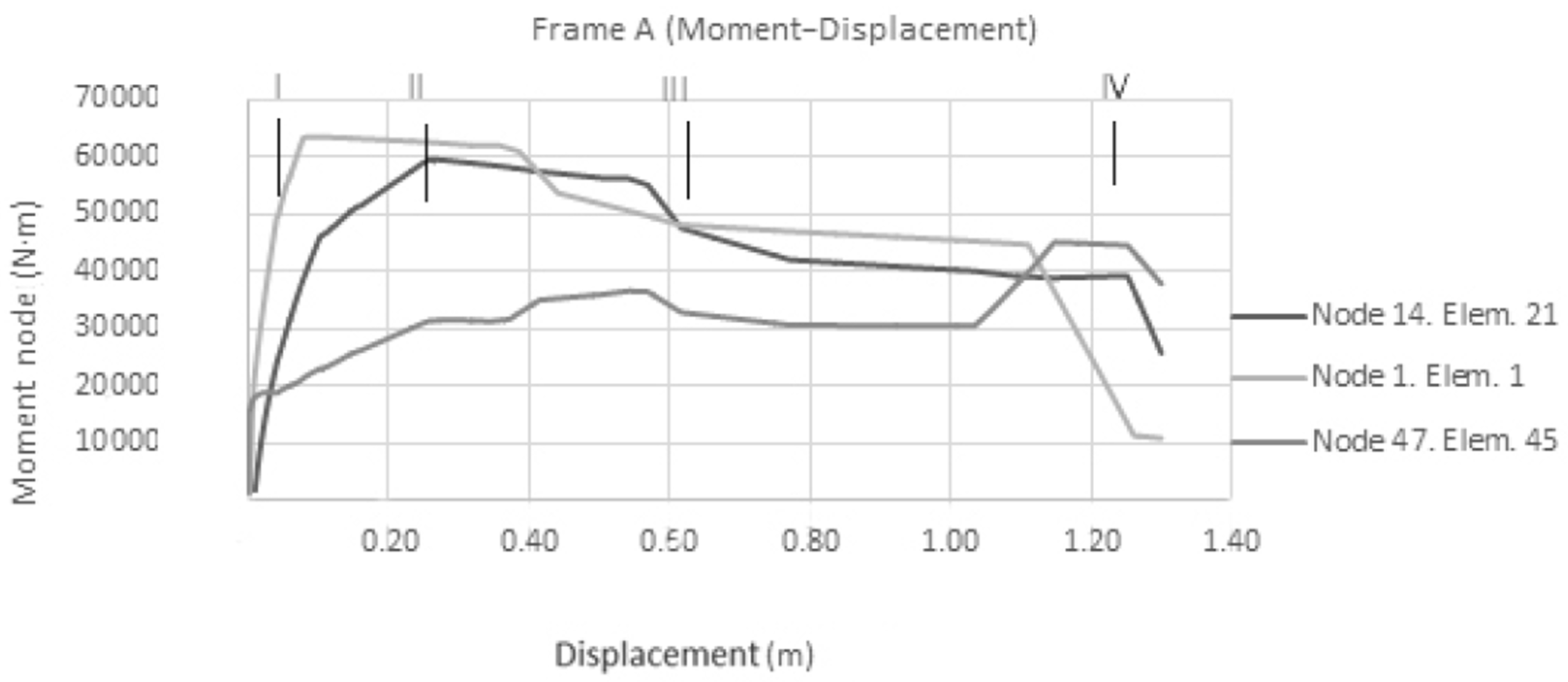
3.2.1. Frame A (RC P03 Section)
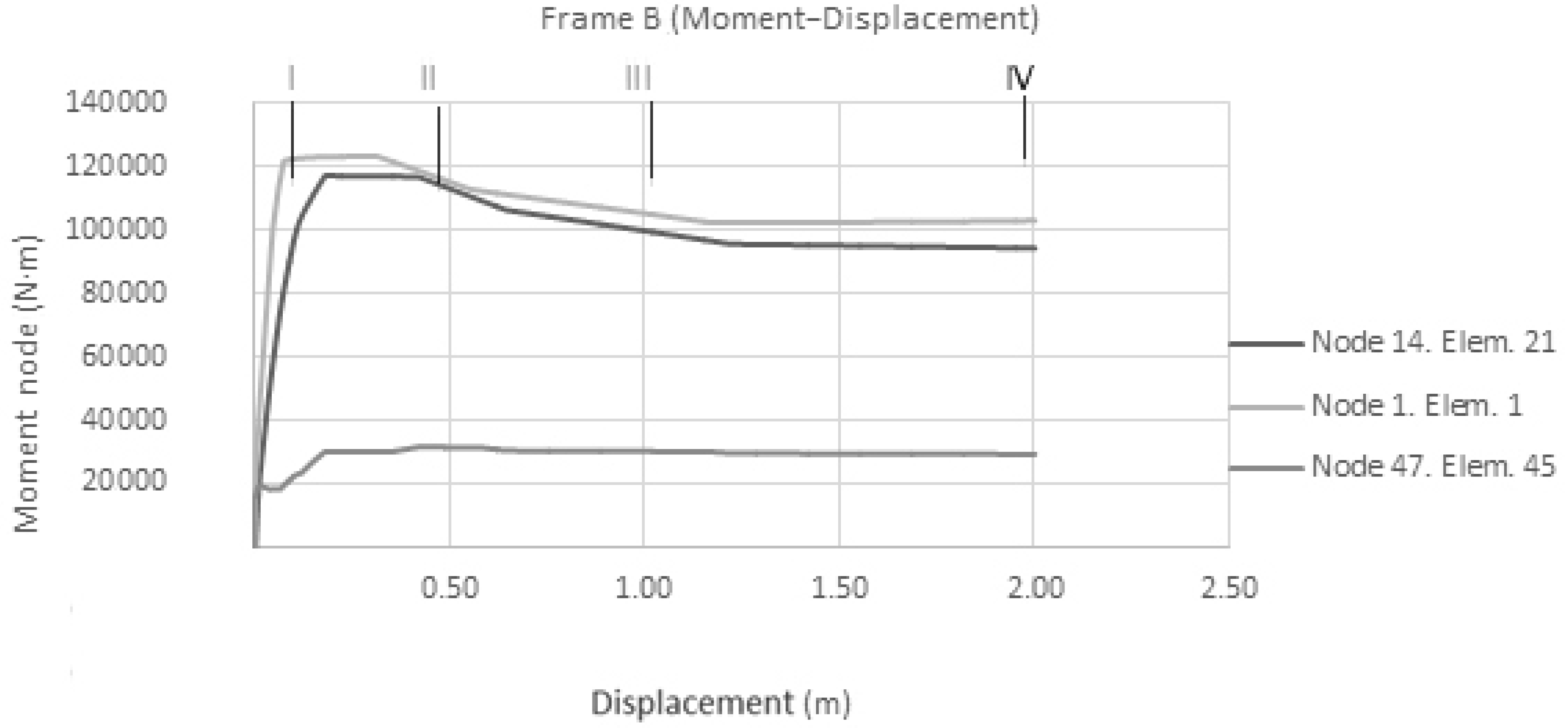
3.2.2. Frame B (SRC P04 Section)
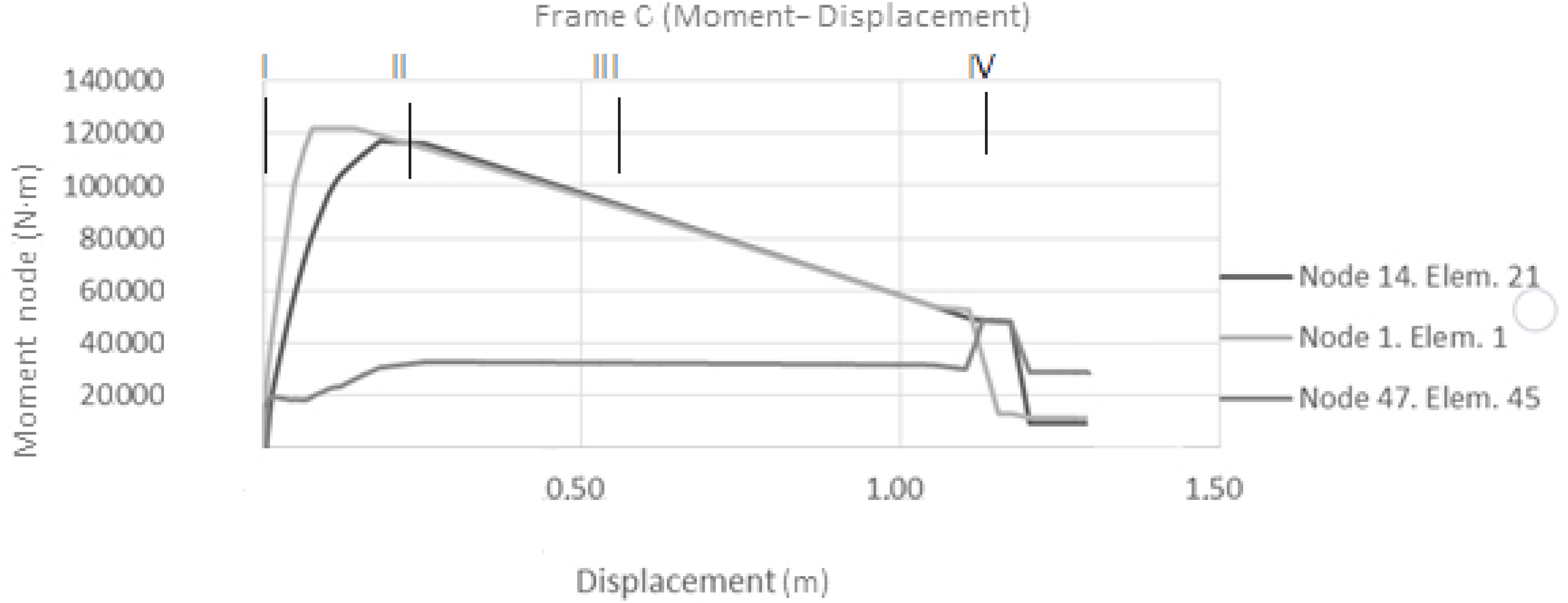
3.2.3. Frame C (RC P05 Section)
3.2.4. Frame D (RC P05 Section + SRC P03 Section Joint Only)
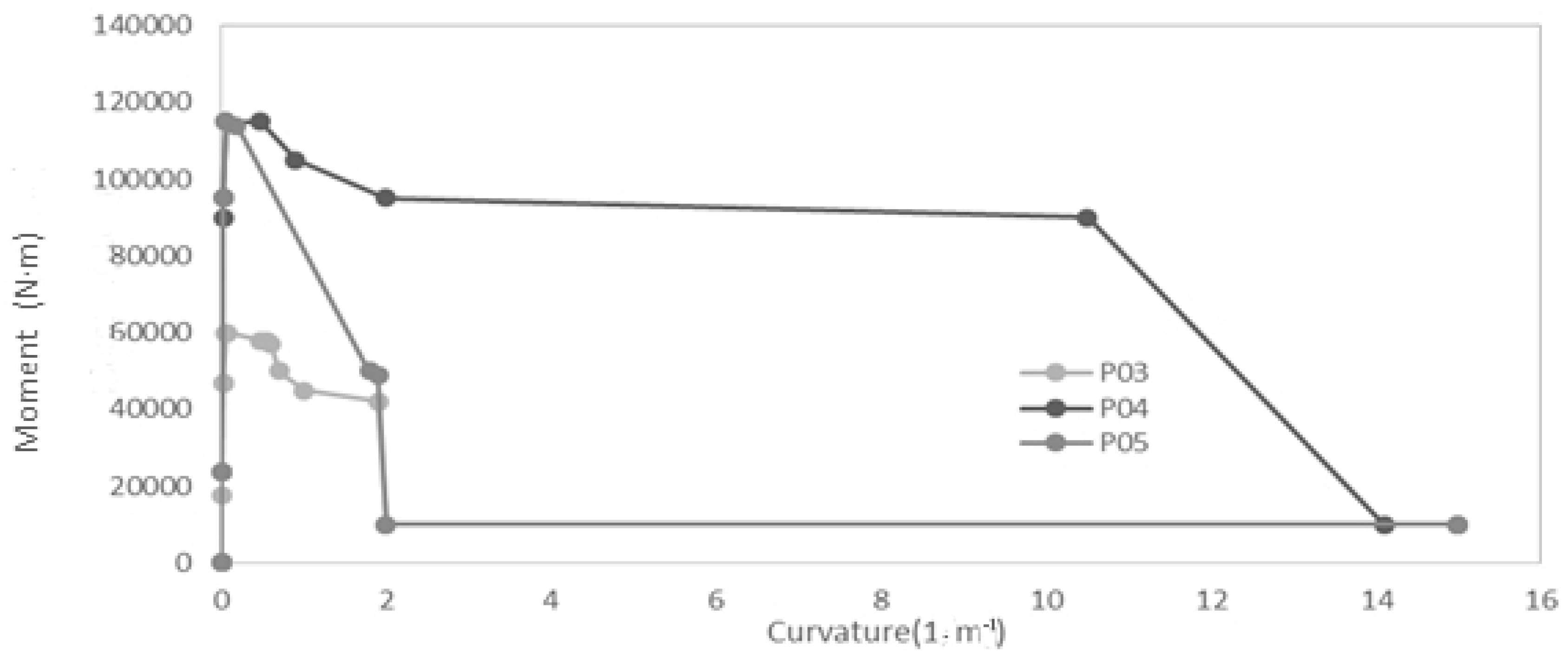
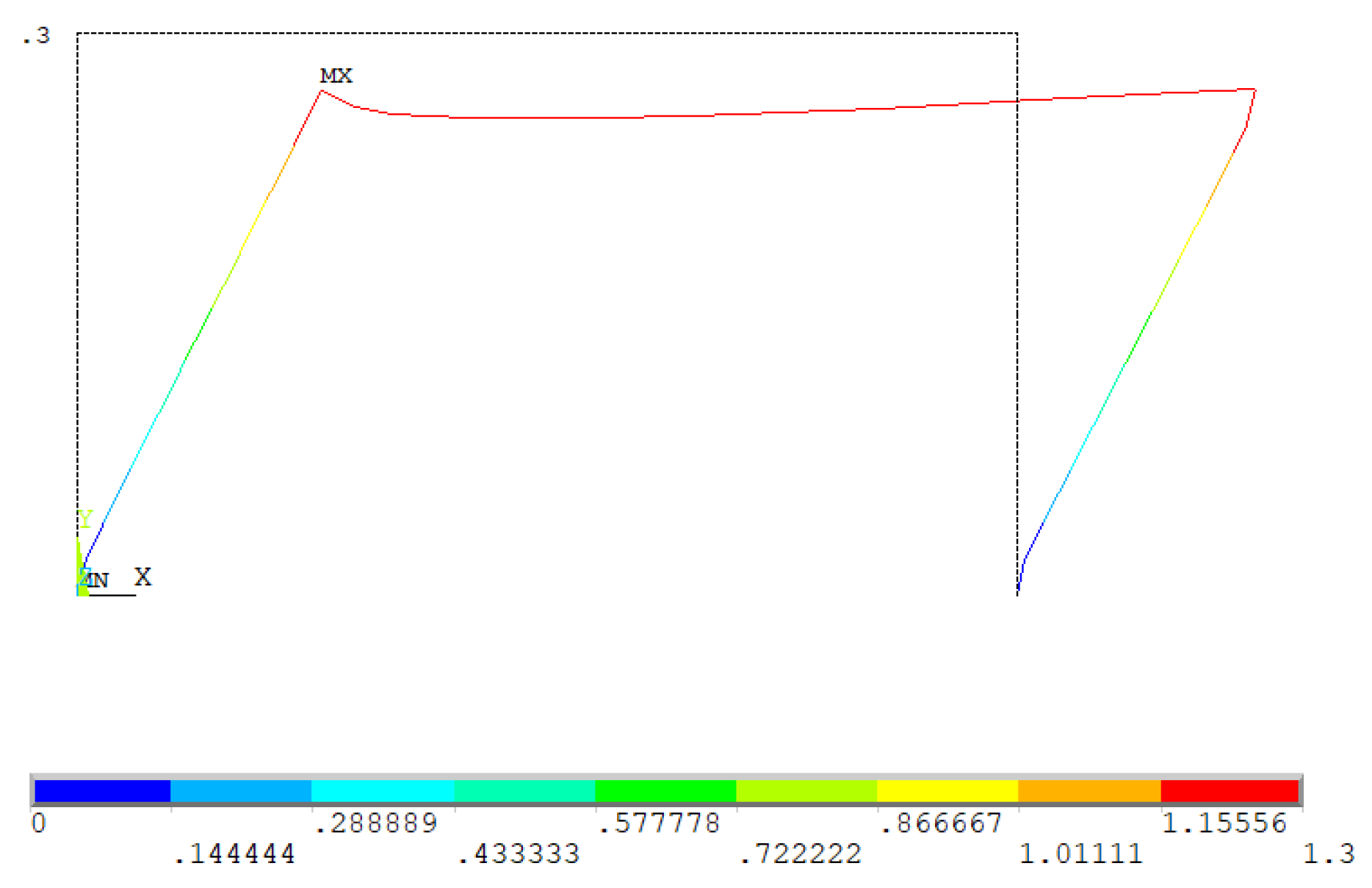
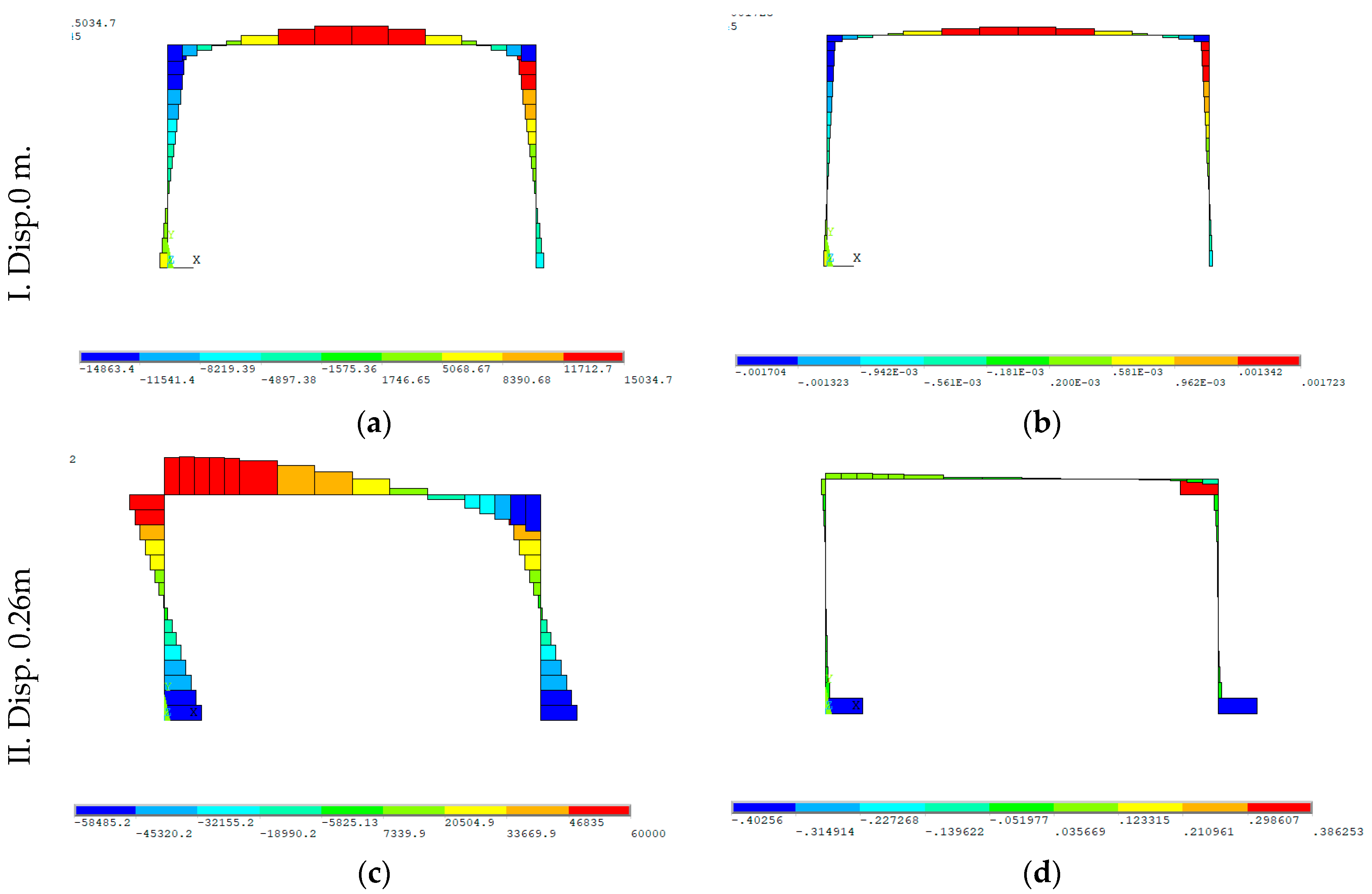
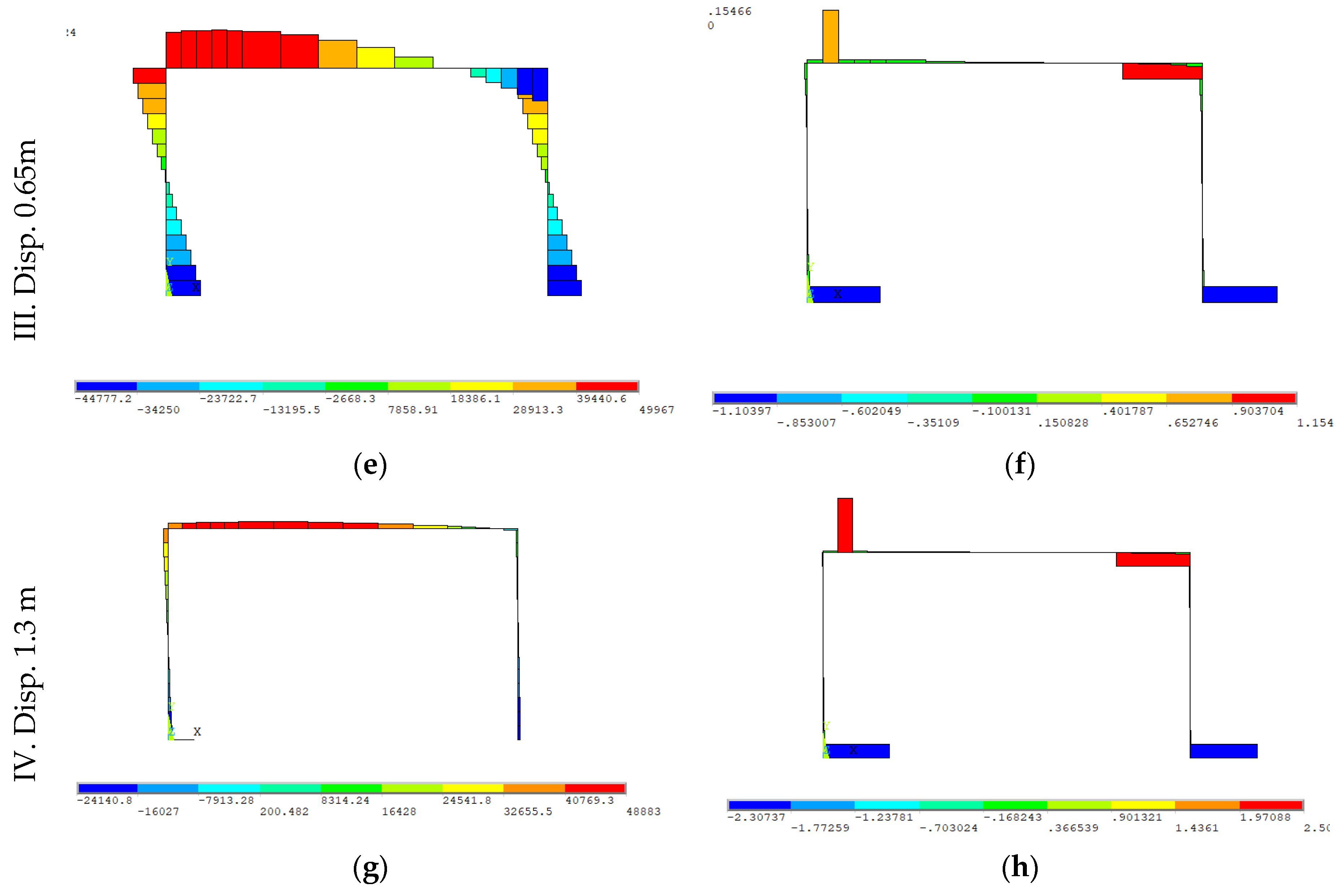
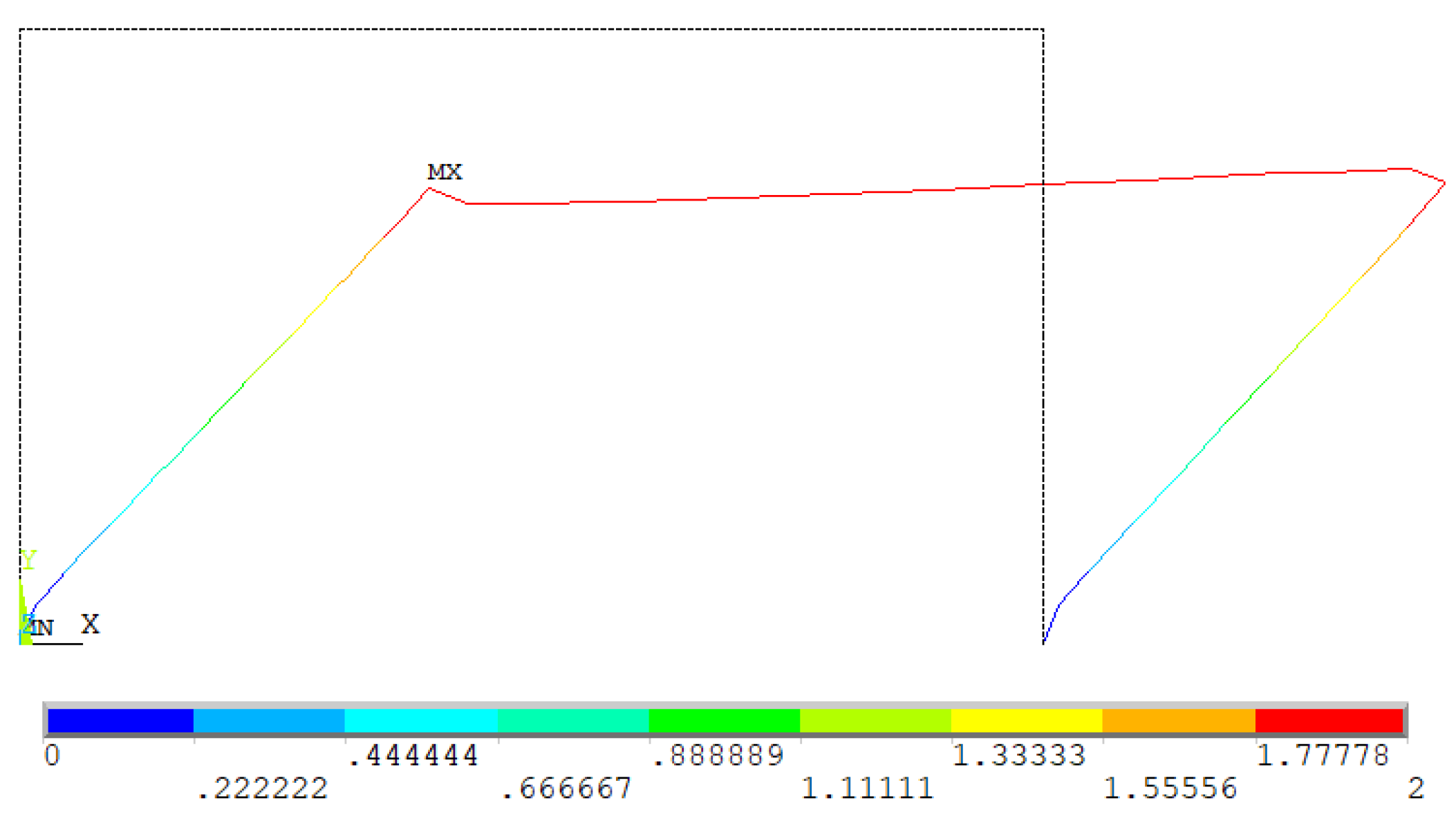
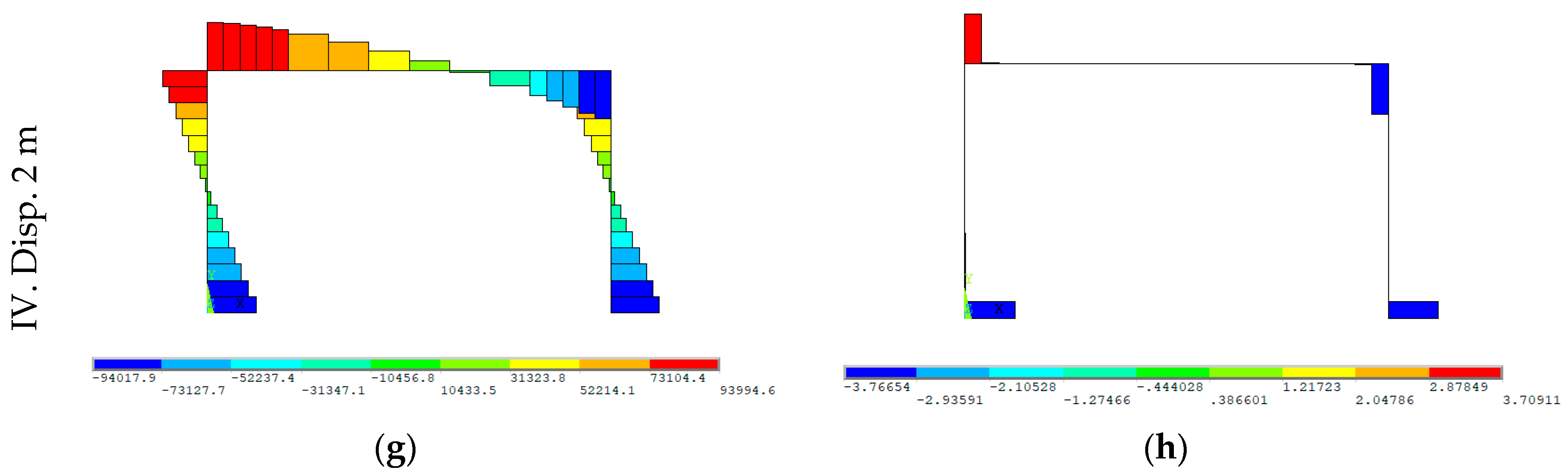
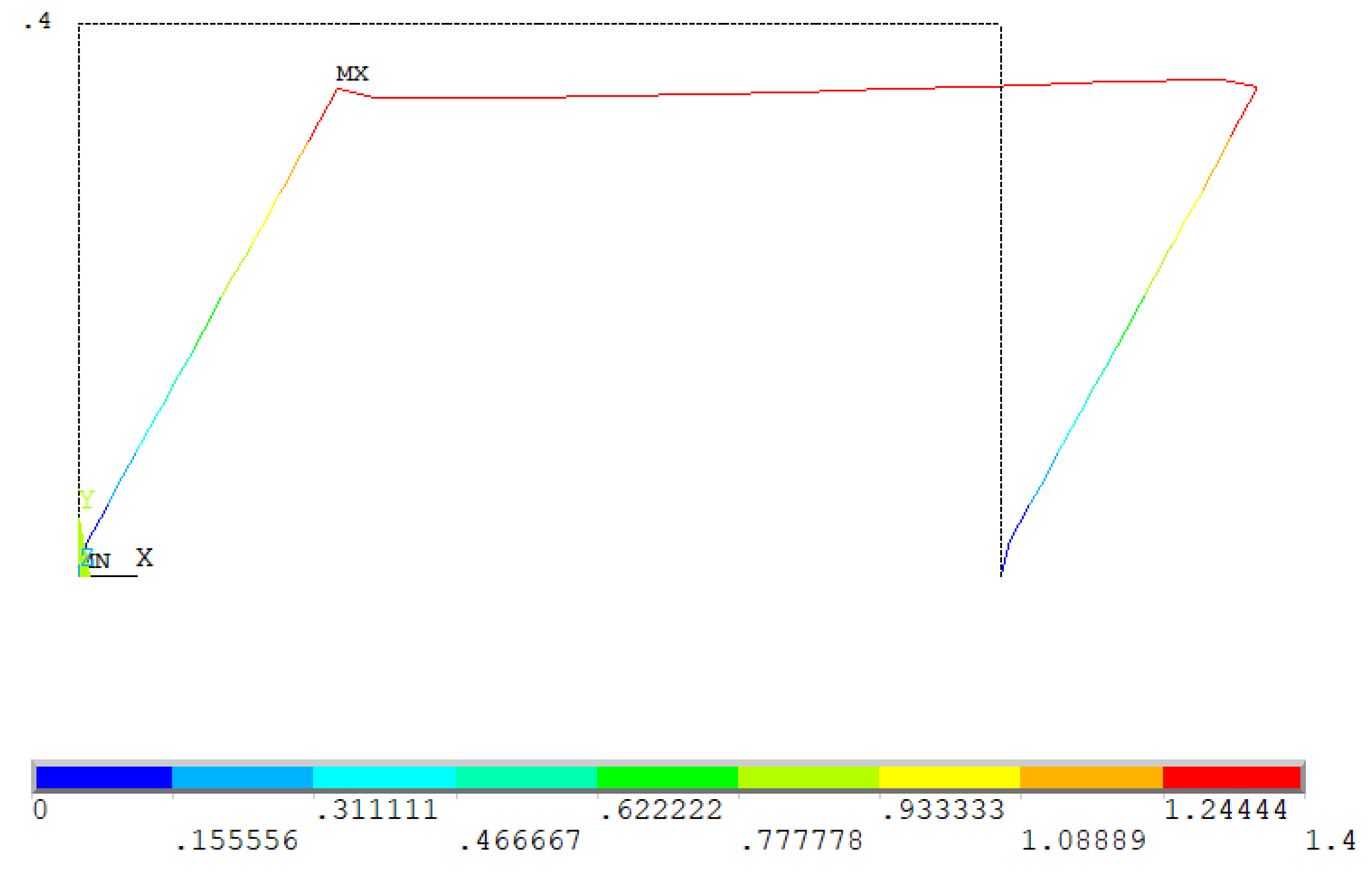
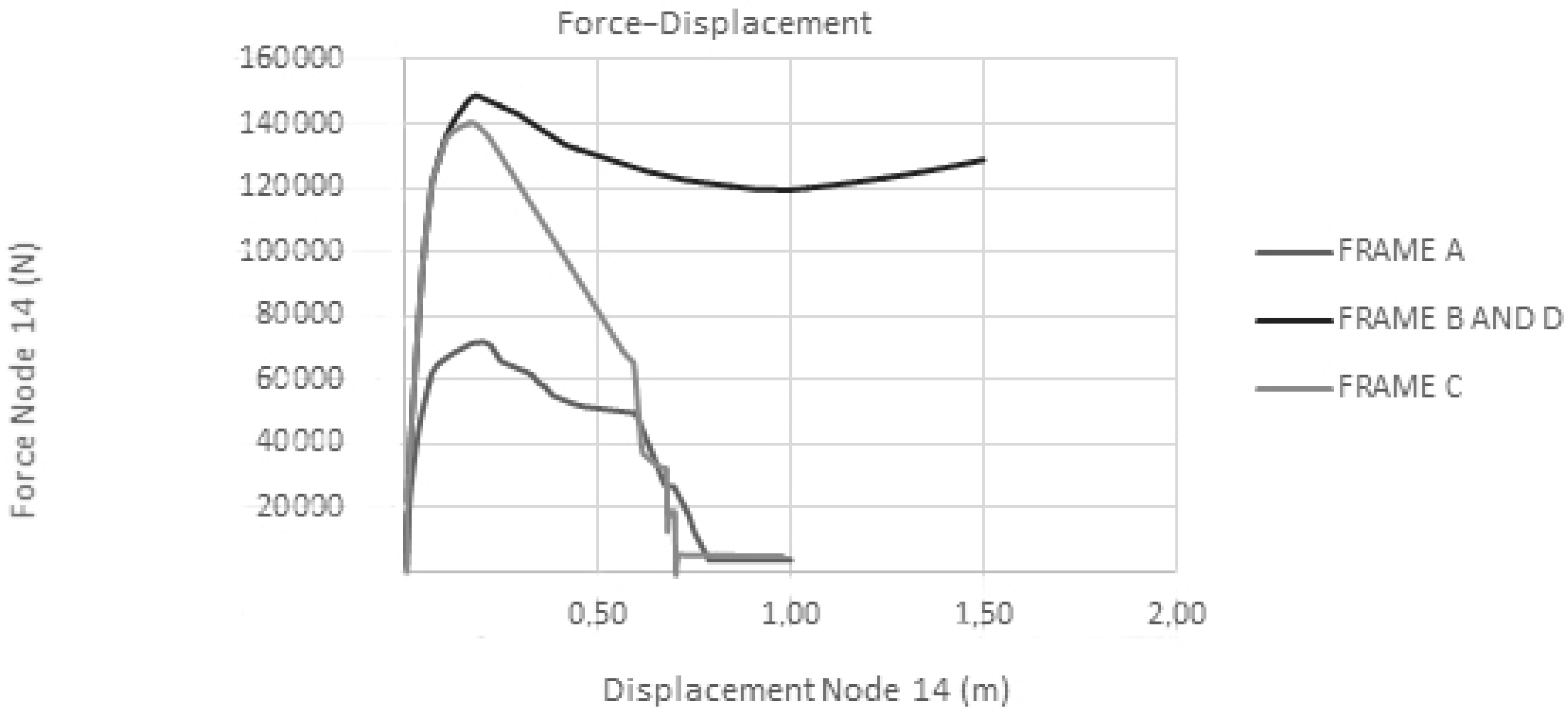
3.2.5. Analysis of the Results
4. Conclusions
- -
- Steel-reinforced concrete (SRC) structures double the ductility compared to the reinforced concrete (RC) structures, where a break prevented greater strains being reached.
- -
- It was possible to simulate the elastoplastic or post-critical behavior until a section broke. A drastic reduction in the moment that simulated the deterioration of concrete, breakage of reinforcements, and loss resistance of steel cross-sections has been included in the moment-curvature graph.
- -
- Hinges appeared simultaneously by redistributing forces along sections until collapse took place.
- -
- SRC structures reinforced only at joints reduced the steel cross-section used in the structure compared to reinforcing all the bars with equal strength, ductility, and safety against a structure collapsing during earthquakes.
- -
- Frame models with nonlinear moment-curvatures until the point of collapse were able to satisfactorily reproduce the behavior of three-dimensional models and the experimental test of the prototypes. The frame model was used to elucidate the hyperstatic behavior. It described the redistribution of strength and the structure’s general behavior until a break occurred. It provides designers with a much simpler tool than the complete three-dimensional modeling of the contributed structure.
- -
- It would be interesting to consider the generalization of the reinforcement with steel cross-sections embedded in the joint of reinforced concrete structures to achieve more earthquake-resistant structures, especially in public buildings and for emergencies where excellent seismic safety must be guaranteed.
- -
- In the reinforced concrete structures, it would be convenient to explicitly consider the possibility of including reinforcements of reinforced concrete joints with embedded steel cross-sections as a solution for creating structures with very high ductility using Eurocode 4 as the current regulation for designing structures with mixed steel and concrete.
- -
- The extension of Eurocode 4 would be interesting for designing reinforced concrete structures with joints having fully embedded steel cross-sections, and not only in columns, as contemplated by Japanese JIA(The Japan Institute of Architects) regulations. The design can be achieved by using moment-curvature graphs.
- -
- Simulation with numerical models allowed for the analysis of complex situations. In particular, the model of simplified frames with the relationship of moment-curvature allowed for nonlinear calculations until large displacements were reached, taking into account the reduction of rigidity because of the cracking of the concrete.
- -
- A new procedure was developed to obtain the moment-curvature graphs of the sections from the numerical models. The moment-curvature graph can be used in the simplified frame analysis by contemplating post-critical behavior in future research.
- -
- The principal scientific contribution is that, using the Ansys program, it was possible to numerically validate a procedure to simulate until the breaking of a bar structure from some bar elements with a behavior introduced by means of the moment-curvature graph. The behavior was the same independent of whether all the bars were reinforced or only the joints were reinforced.
Author Contributions
Funding
Conflicts of Interest
Data Availability
References
- Wakabayashi, M. Design of Earthquake—Resistant Buildings; McGraw: New York, NY, USA, 1986. [Google Scholar]
- Chen, C.C.; Lin, K.T. Behavior and strength of steel reinforced concrete beam–Column joints with two-side force inputs. J. Constr. Steel Res. 2009, 65, 641–649. [Google Scholar] [CrossRef]
- Yan, C.; Yang, D.; Ma, Z.J.; Jia, J. Hysteretic model of SRUHSC column and SRC beam joints considering damage effects. Mater. Struct. 2017, 50, 88. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, J.; Xue, J. Hysteretic behavior of special shaped columns composed of steel and reinforced concrete (SRC). Earthquake Eng. Eng. Vibr. 2015, 14, 329–345. [Google Scholar] [CrossRef]
- Wilkinson, T.; Hancock, G.J. Compact or Class 1 Limits for Rectangular Hollow Sections in Bending. In Proceedings of the 8th International Symposium on Tubular Structures, Singapore, 26–28 August 1998. [Google Scholar]
- Gioncu, V.; Mosoarca, M.; Anastasiadis, A. Prediction of available rotation capacity and ductility of wide-flange beams. Part 1: DUCTROT-M computer program. J. Constr. Steel Res. 2012, 69, 8–19. [Google Scholar] [CrossRef]
- European Committee for Standardization. EN 1993-1-8, Eurocode 3: Design of Steel Structures—Part 1–8: Design of Joints; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Li, J.; Wang, Y.; Lu, Z.; Li, J. Experimental Study and Numerical Simulation of a Laminated Reinforced Concrete Shear Wall with a Vertical Seam. Appl. Sci. 2017, 7, 6299. [Google Scholar] [CrossRef]
- European Committee for Standardization. EN 1992-1-1, Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2014; p. 730. [Google Scholar]
- Lu, Z.; He, X.D.; Zhou, Y. Studies on damping behavior of vertically mixed structures with upper steel and lower concrete substructures. Struct. Des. Tall Spec. Build. 2017, 26. [Google Scholar] [CrossRef]
- Gioncu, V.; Petcu, D. Available Rotation Capacity of Wide-Flange Beams and Beam-Columns. Part 1. Theoretical Approaches. J. Constr. Steel Res. 1997, 43, 161–217. [Google Scholar] [CrossRef]
- Bossio, A.; Fabbrocino, F.; Lignola, G.P.; Prota, A.; Manfredi, G. Design Oriented Model for the Assessment of T-Shaped Beam-Column Joints in Reinforced Concrete Frames. Buildings 2017, 7, 118. [Google Scholar] [CrossRef]
- Bossio, A.; Fabbrocino, F.; Lignola, G.P.; Prota, A.; Manfredi, G. Simplified Model for Strengthening Design of Beam–Column Internal Joints in Reinforced Concrete Frames. Polymers 2015, 7, 1732–1754. [Google Scholar] [CrossRef]
- Santarsiero, G. FE Modelling of the Seismic Behavior of Wide Beam-Column Joints Strengthened with CFRP Systems. Buildings 2018, 8, 31. [Google Scholar] [CrossRef]
- Kabir, M.R.; Alam, M.S.; Said, A.M.; Ayad, A. Performance of Hybrid Reinforced Concrete Beam Column Joint: A Critical Review. Fibers 2016, 4, 13. [Google Scholar] [CrossRef]
- Bağcı, M. Neural Network Model for Moment-Curvature Relationship of Reinforced Concrete Sections. Math. Comput. Appl. 2010, 15, 66–78. [Google Scholar] [CrossRef]
- Montava, I.; Irles, R.; Pomares, J.C.; Gonzales, A. Experimental Study of Steel Reinforced Concrete (SRC) Joints. Appl. Sci. 2019, 9, 1528. [Google Scholar] [CrossRef]
- Montava, I.; Irles, R.; Segura, J.; Gadea, J.M.; Juliá, E. Numerical Simulation of Steel Reinforced Concrete (SRC) Joints. Metals 2019, 9, 131. [Google Scholar] [CrossRef]
- Lu, Z.; Yang, Y.L.; Lu, X.; Liu, C. Preliminary study on the damping effect of a lateral damping buffer under a debris flow load. Appl. Sci. 2017, 7, 201. [Google Scholar] [CrossRef]
- Lu, Z.; Chen, X.Y.; Zhang, D.C.; Dai, K.S. Experimental and analytical study on the performance of particle tuned mass dampers under seismic excitation. Earthq. Eng. Struct. Dyn. 2016, 46, 697–714. [Google Scholar] [CrossRef]
- Sun, Z.; Yang, Y.; Yan, W.; Wu, G.; He, X. Moment-Curvature Behaviors of Concrete Beams Singly Reinforced by Steel-FRP Composite Bars. Adv. Civ. Eng. 2017, 2017. [Google Scholar] [CrossRef]
- European Committee for Standardization. EN 1994 1-1, Eurocode 4: Design of Composite Steel and Concrete Structures; European Committee for Standardization: Brussels, Belgium, 1993. [Google Scholar]
- European Committee for Standardization. EN 1998, Eurocode 8: Design of Structures for Earthquake Resistance; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]

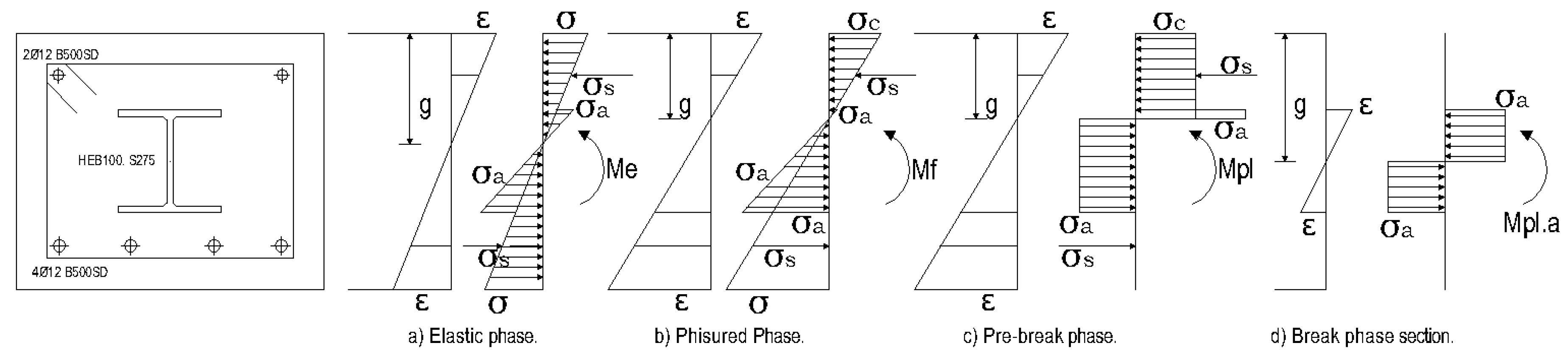
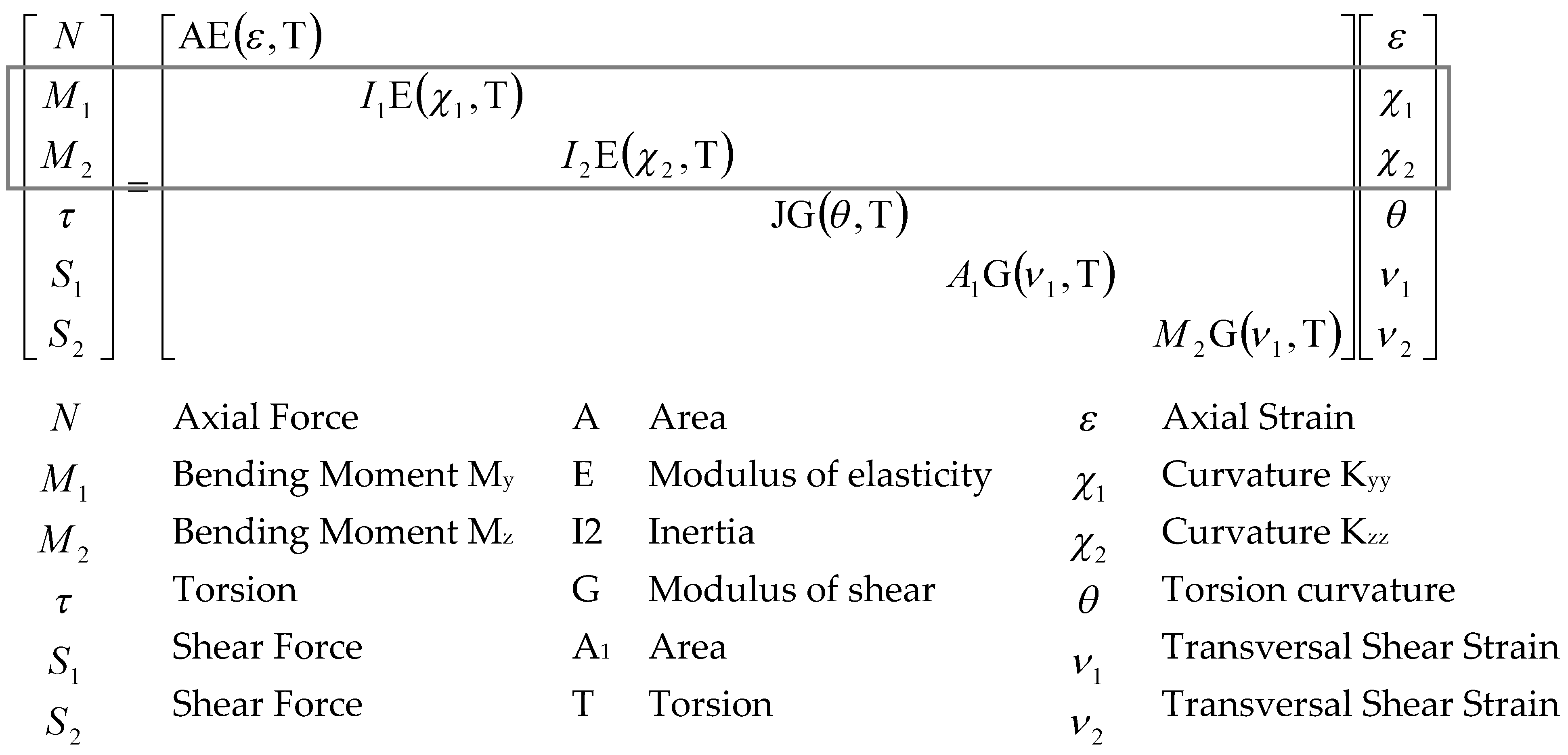
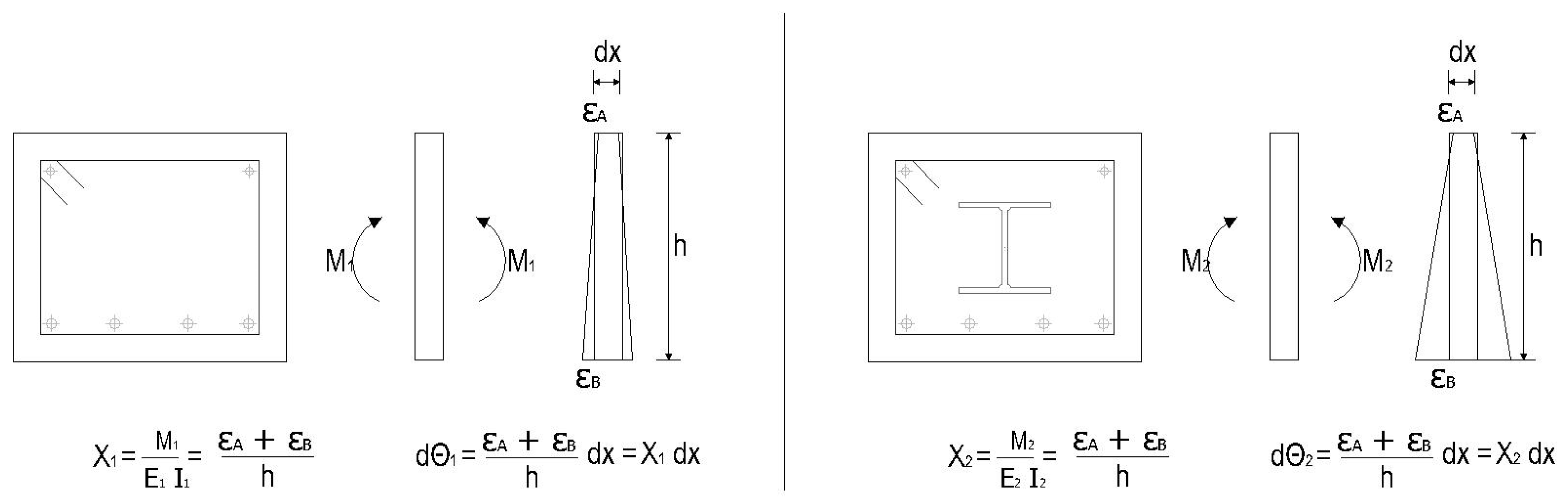
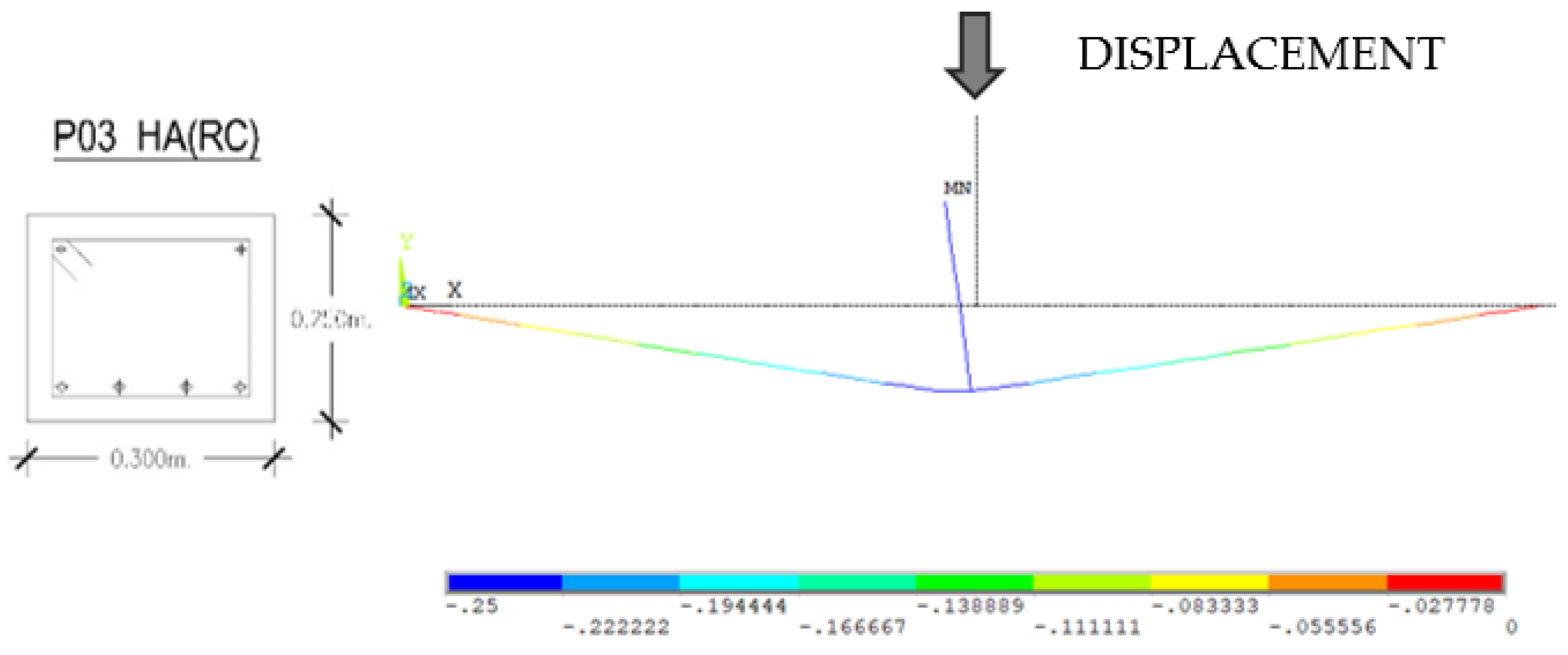


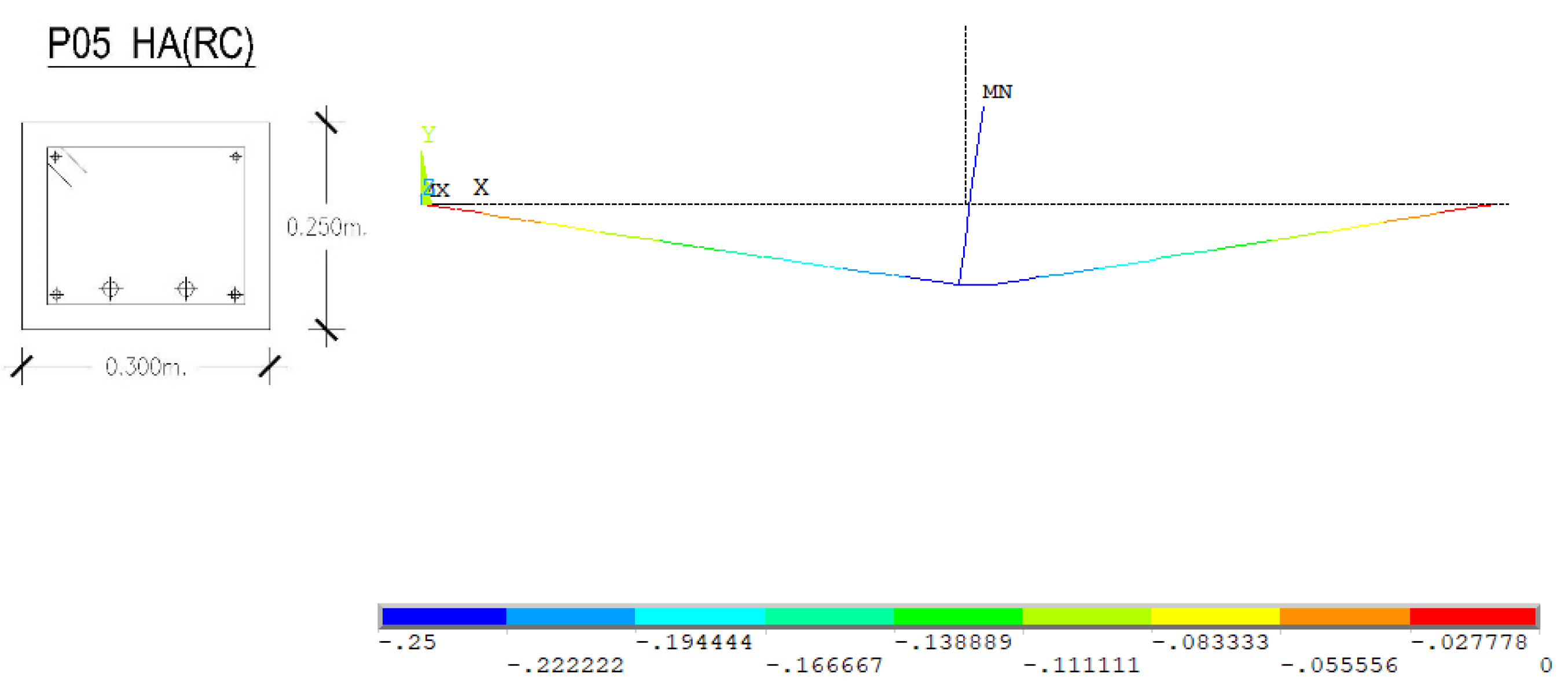
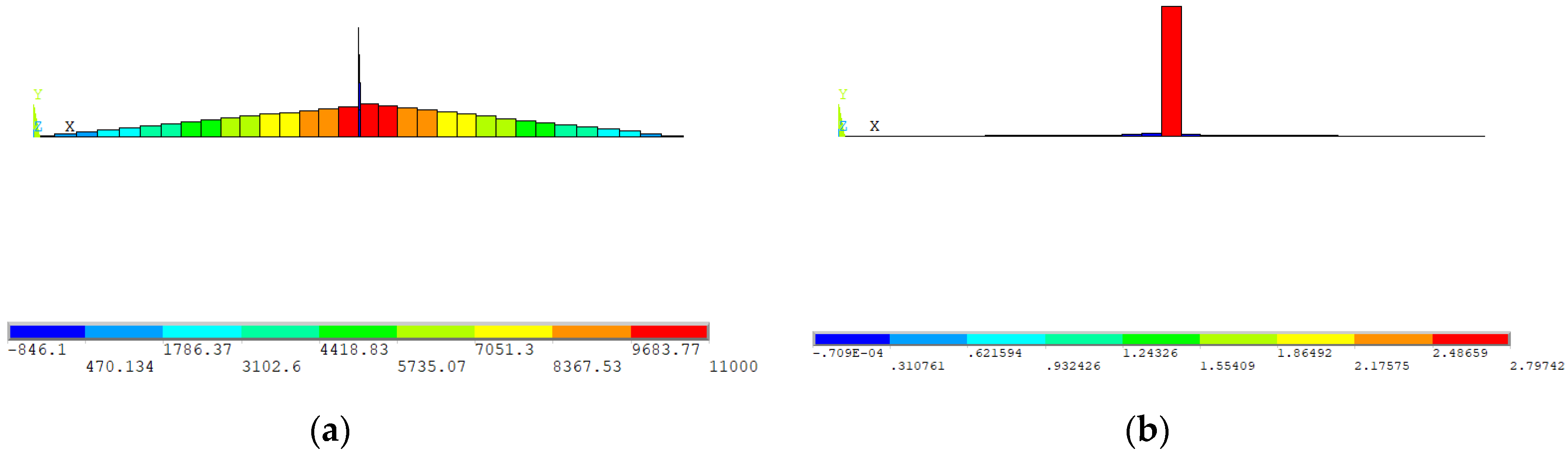
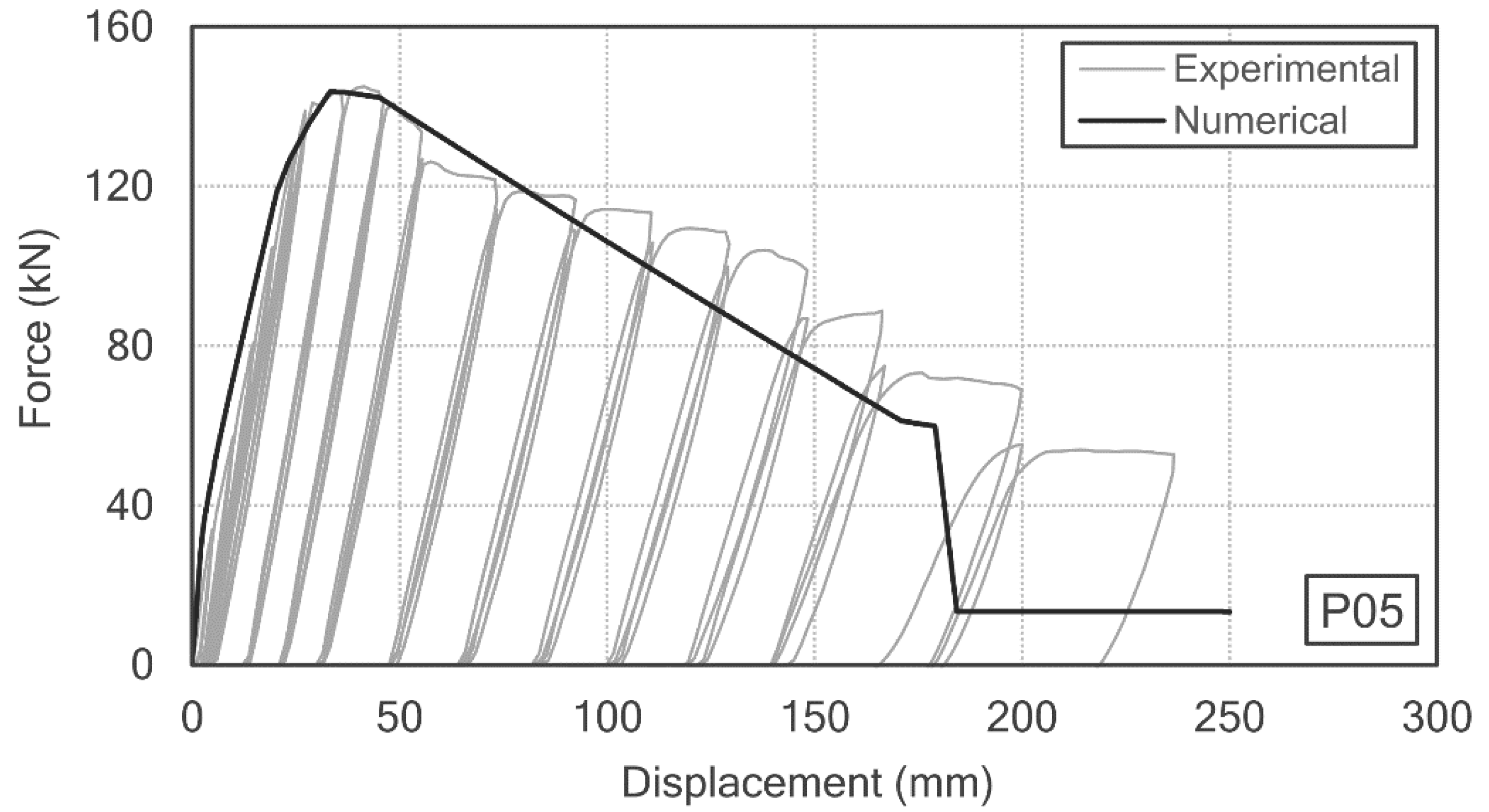

| Prototype | Typology | Concrete Sections (mm × mm) | Rebar Reinforcement | Cross-Sections | Distance between Supports (mm) |
|---|---|---|---|---|---|
| P03 | RC | 300 × 250 | 4 ø 12 | - | 3300 |
| P04 | SRC | 300 × 250 | 4 ø 12 | HEB-100 | 3300 |
| P05 | RC | 300 × 250 | 2 ø 16 + 2 ø 20 | - | 3300 |
| Frame | Typology | Concrete Sections | Rebar Reinforcement | Cross-Sections |
|---|---|---|---|---|
| A | RC | 300 × 250 | 4 ø 12 | NONE |
| B | SRC | 300 × 250 | 4 ø 12 | HEB-100 (FULL FRAME) |
| C | RC | 300 × 250 | 2 ø 16 + 2 ø 20 | NONE |
| D | SRC + RC | 300 × 250 | 4 ø 12 | HEB-100 (JOINT ONLY) |
| Frame A | Frame B | Frame C | Frame D | |
|---|---|---|---|---|
| Displacement node 14 (m) | 1.3 | 2 | 1.3 | 2 |
| Force node 14 (kN) | 75 | 160 | 160 | 160 |
| Absorbed energy from the horizontal load (kN·m) | 60 | 280 | 90 | 280 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montava, I.; Irles, R.; Estevan, L.; Vives, I. Equivalent Frame Model with a Decaying Nonlinear Moment-Curvature of Steel-Reinforced Concrete Joints. Appl. Sci. 2019, 9, 5533. https://doi.org/10.3390/app9245533
Montava I, Irles R, Estevan L, Vives I. Equivalent Frame Model with a Decaying Nonlinear Moment-Curvature of Steel-Reinforced Concrete Joints. Applied Sciences. 2019; 9(24):5533. https://doi.org/10.3390/app9245533
Chicago/Turabian StyleMontava, Isaac, Ramón Irles, Luis Estevan, and Ismael Vives. 2019. "Equivalent Frame Model with a Decaying Nonlinear Moment-Curvature of Steel-Reinforced Concrete Joints" Applied Sciences 9, no. 24: 5533. https://doi.org/10.3390/app9245533
APA StyleMontava, I., Irles, R., Estevan, L., & Vives, I. (2019). Equivalent Frame Model with a Decaying Nonlinear Moment-Curvature of Steel-Reinforced Concrete Joints. Applied Sciences, 9(24), 5533. https://doi.org/10.3390/app9245533





