Frequency Response Analysis of Perforated Shells with Uncertain Materials and Damage
Abstract
1. Introduction
2. Preliminaries
2.1. Shell Eigenproblems
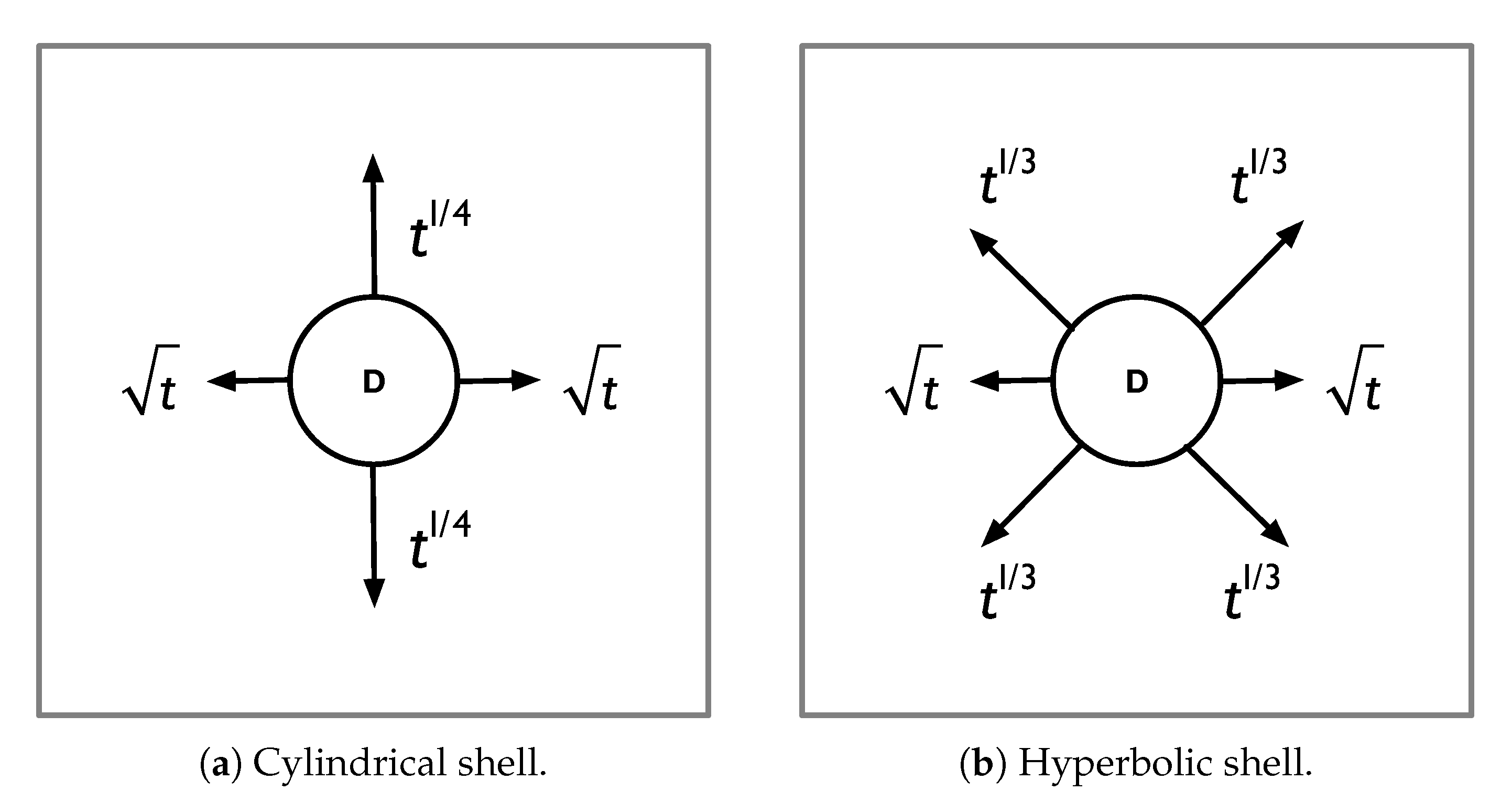
2.1.1. Shell Geometry
2.1.2. Reduction in Thickness
2.1.3. Two-Dimensional Model
2.2. Perforated Domains
2.2.1. Penetration Patterns
2.2.2. Damage Model
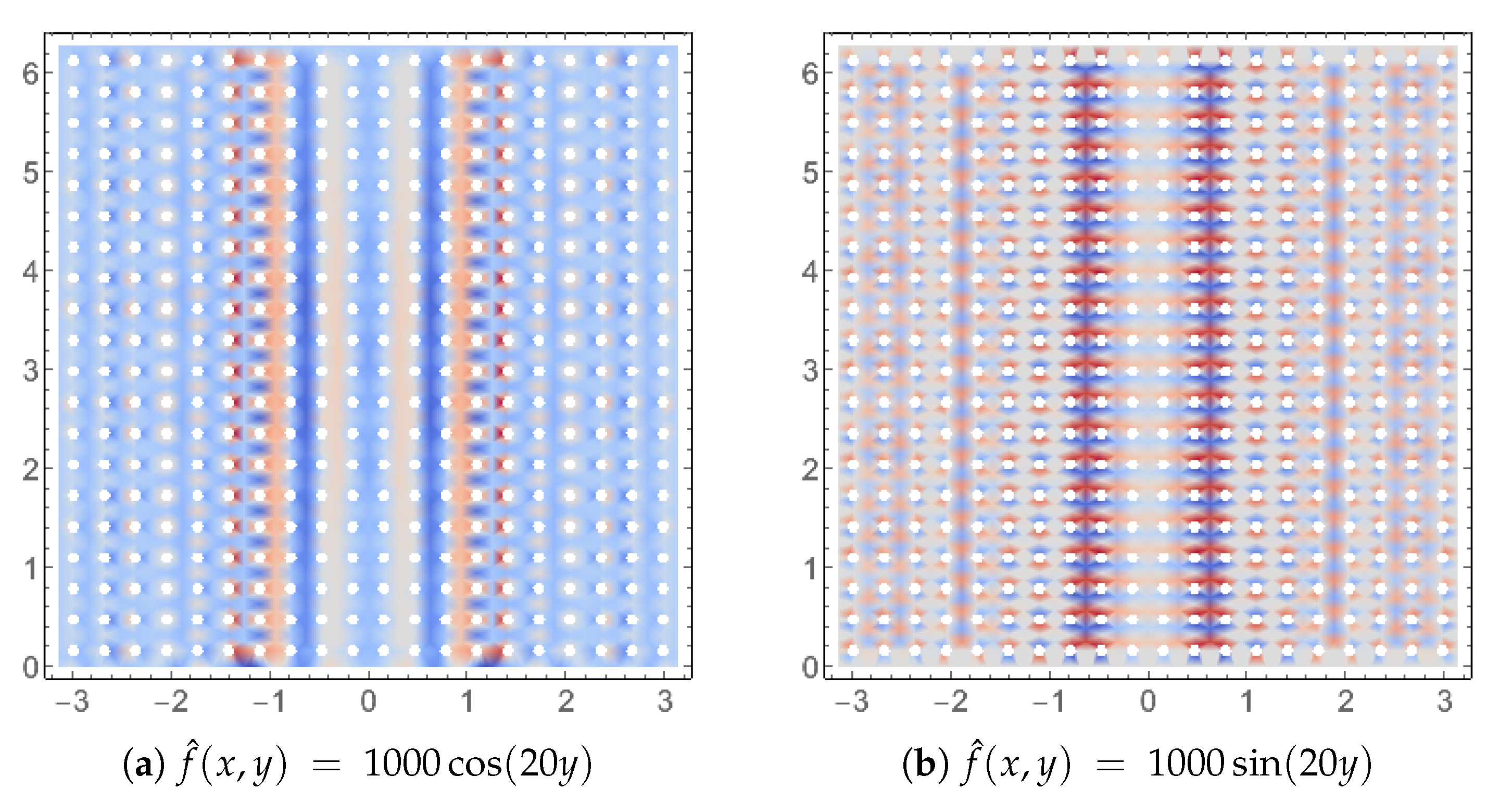
2.2.3. Layer Chart over Representative Cells
3. Free Vibration of Reference Configurations
4. Frequency Response Analysis under Uncertainty
4.1. The Stochastic Eigenproblem
4.2. Frequency Response Analysis
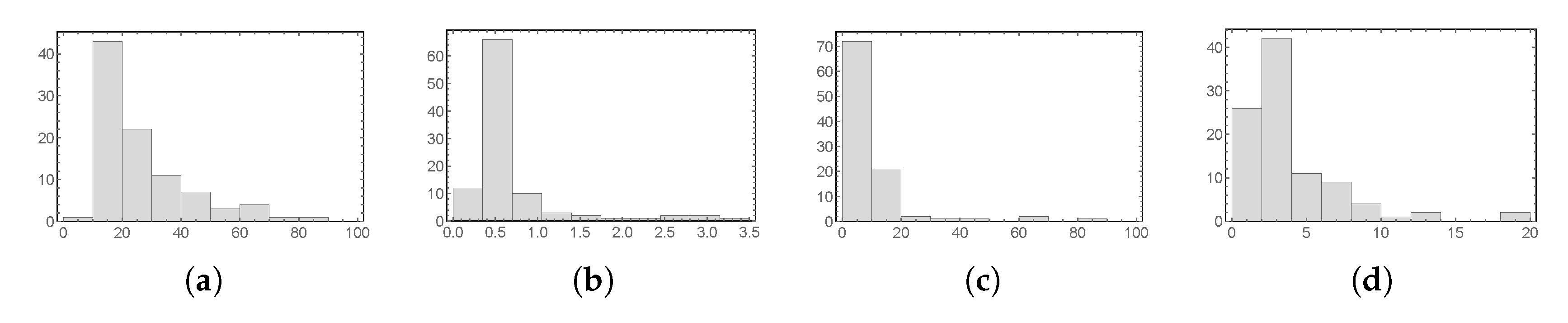
4.3. Stochastic Collocation
4.4. Computing Statistics under Hybrid Uncertainty
| Algorithm 1 |
Let and . For do
|
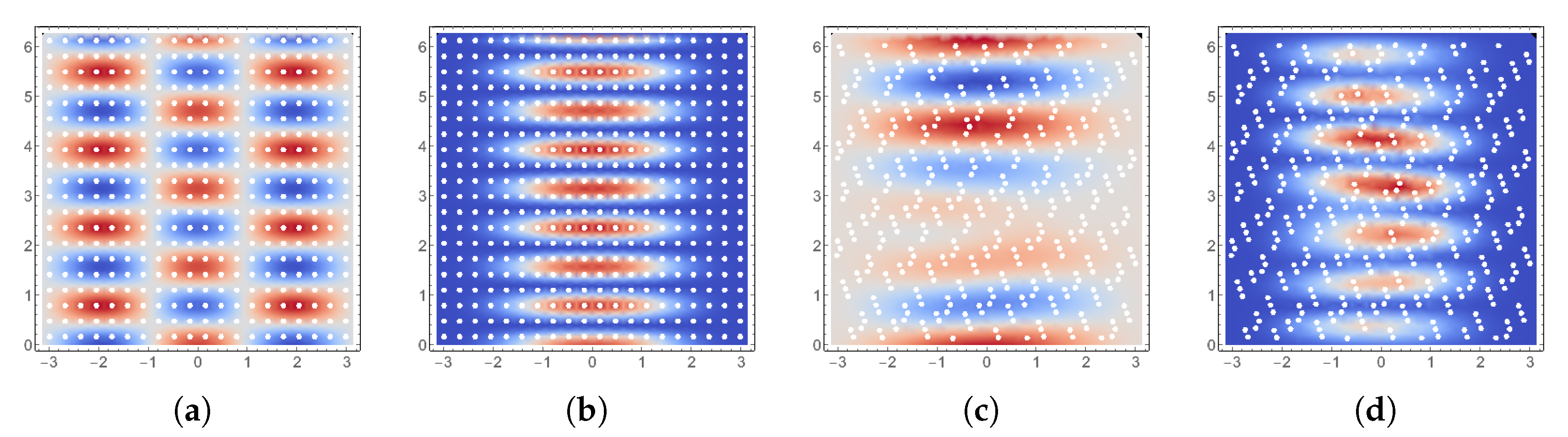
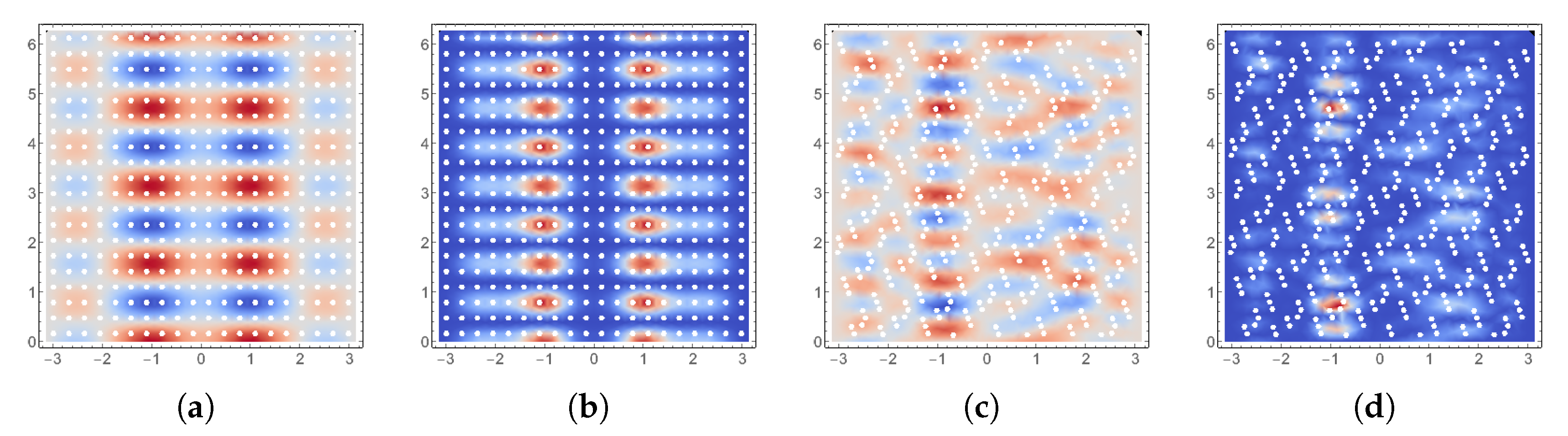
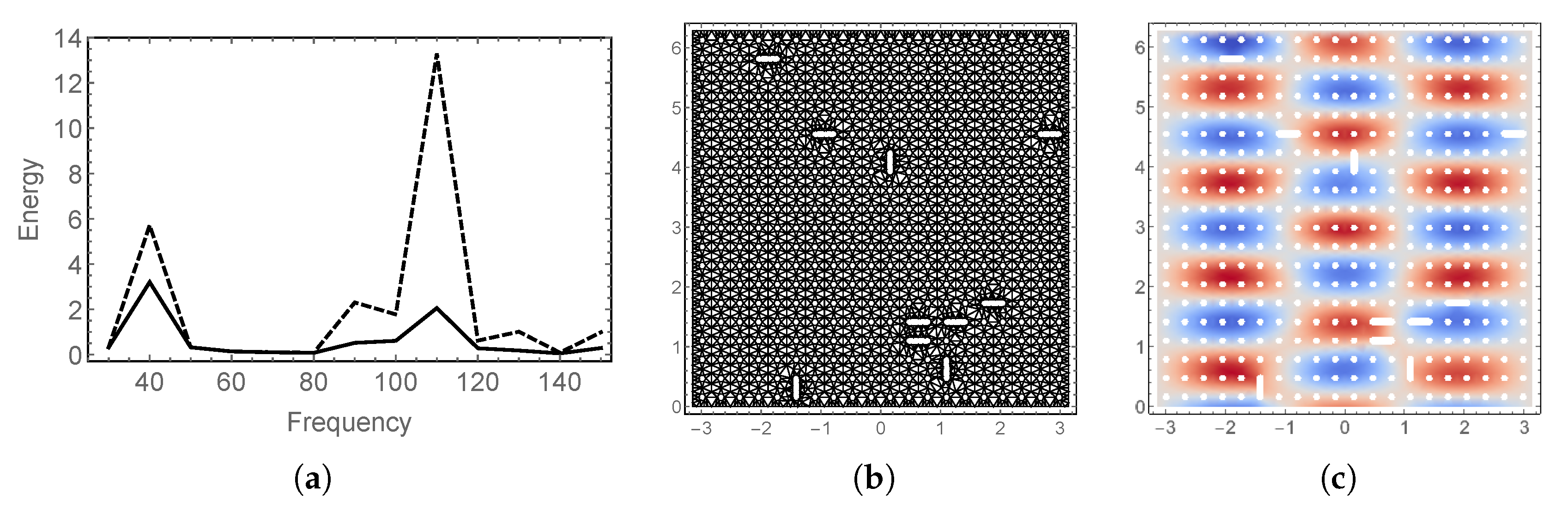
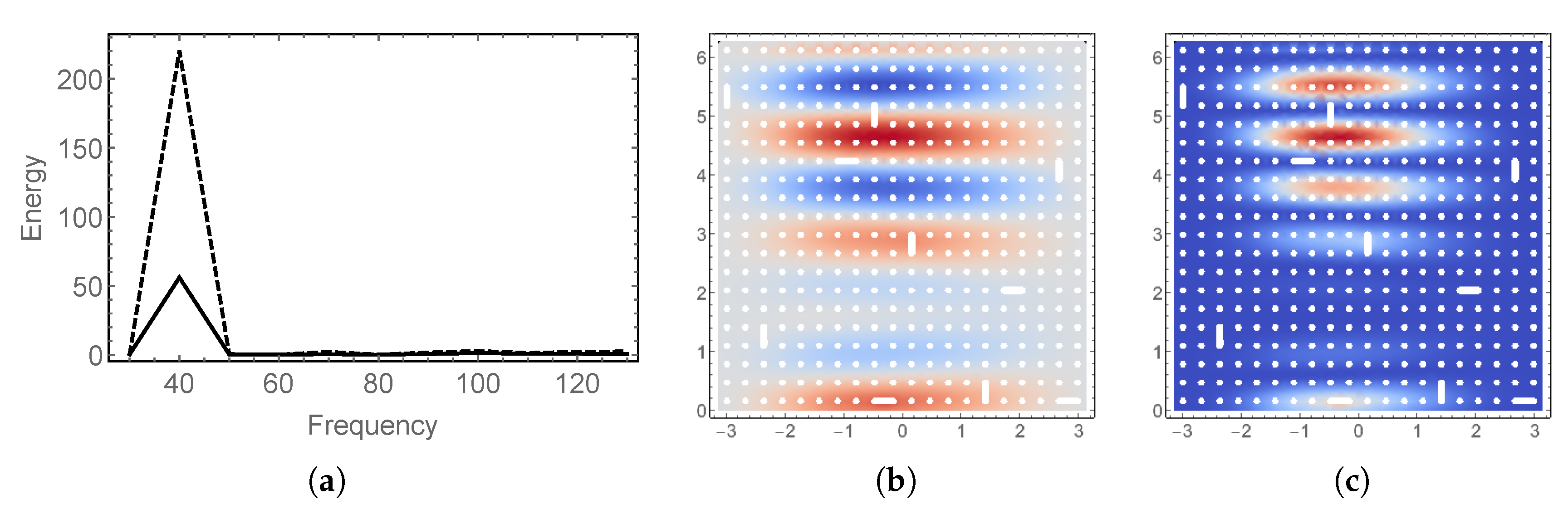
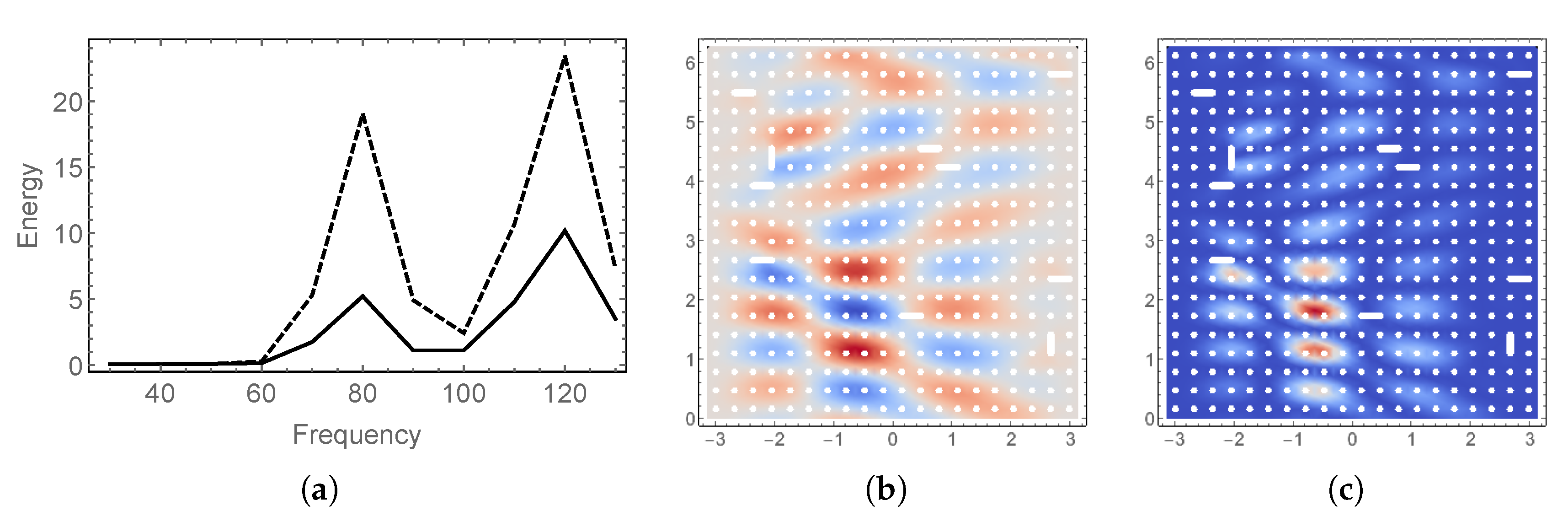
5. Numerical Experiments: Frequency Response
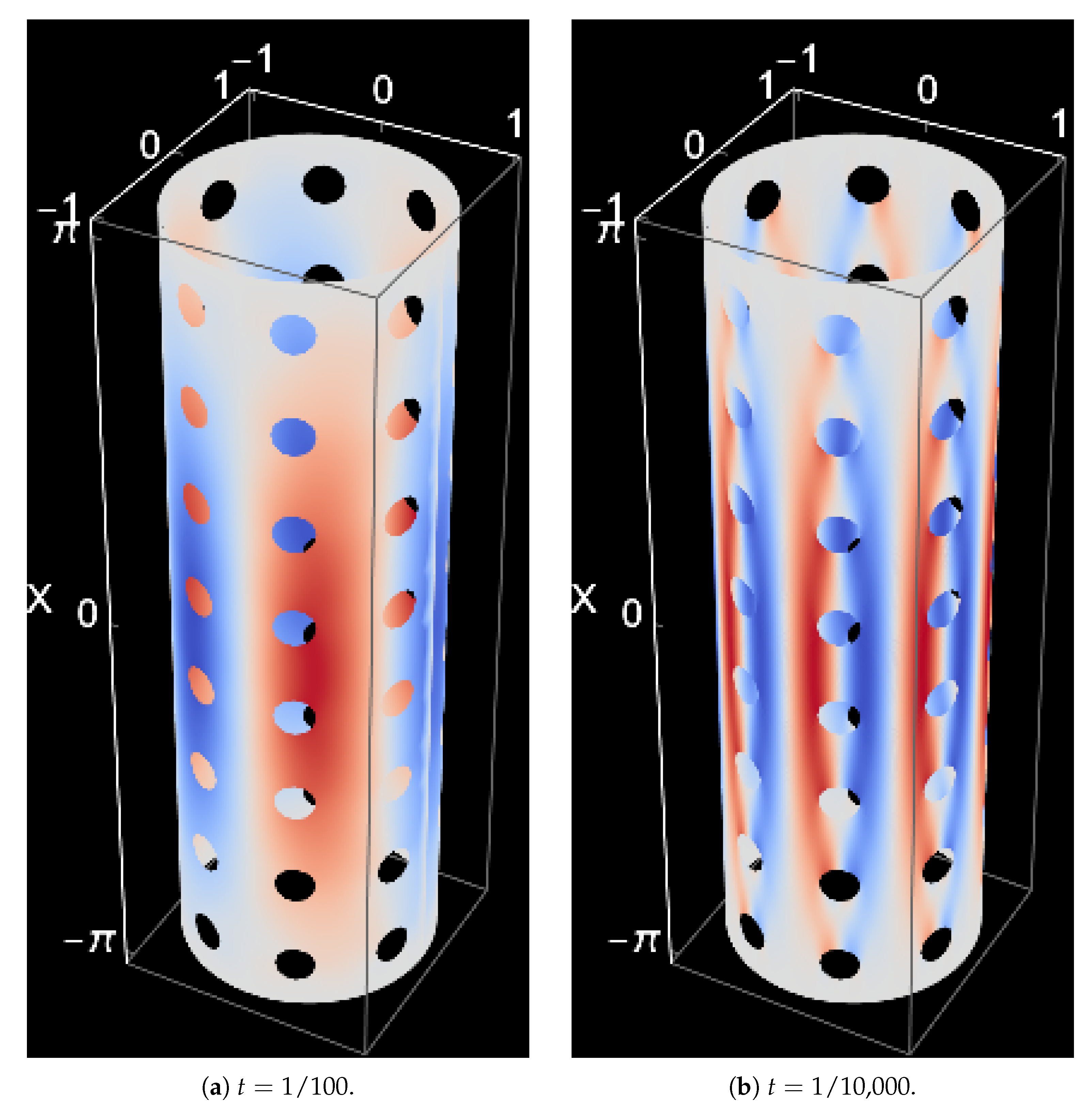
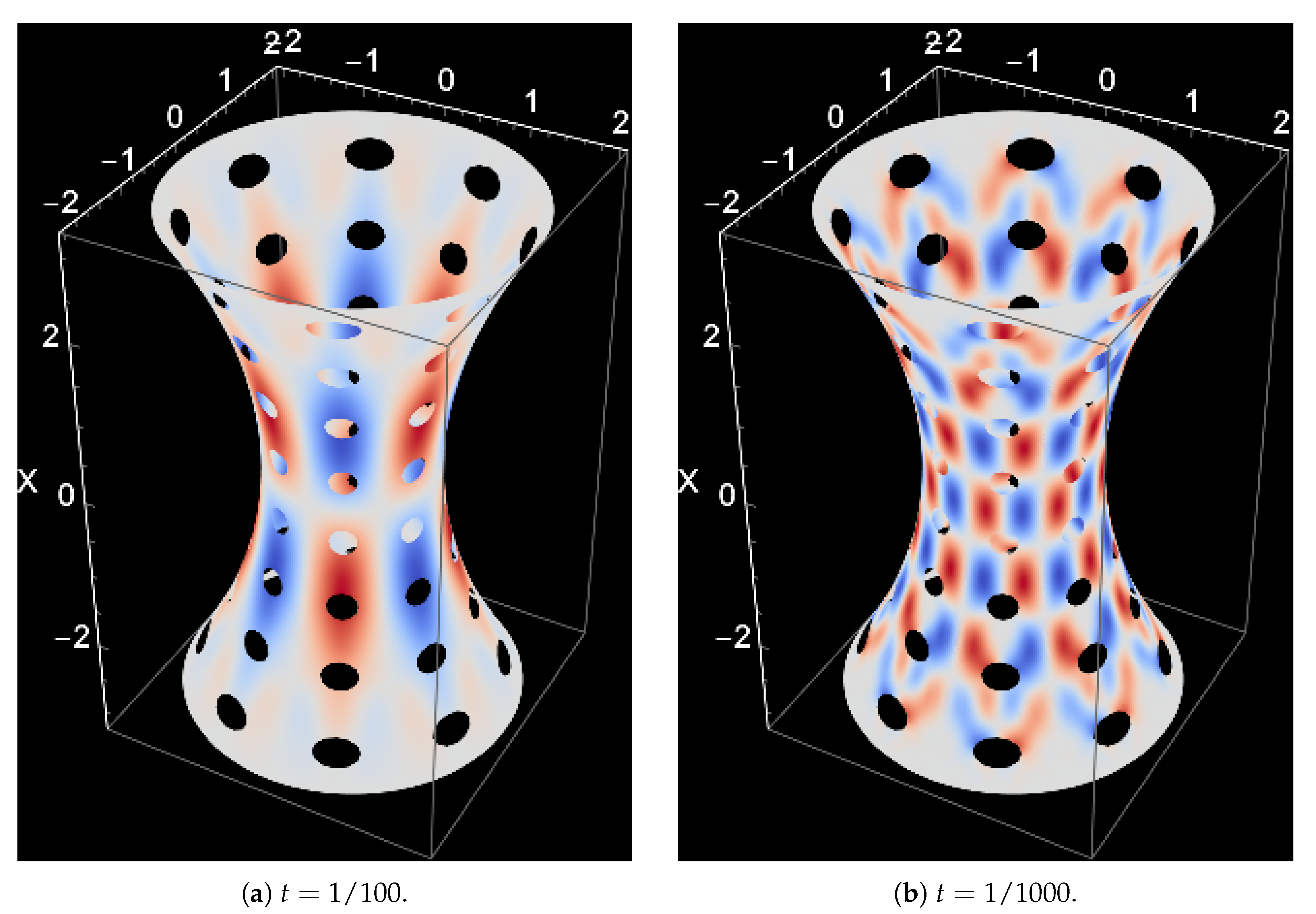
5.1. Effect of Loading
5.2. Effect of the Random Material Parameter
5.3. Effect of Local Low Intensity Damage
5.4. Hybrid Uncertainty
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Carden, E.P.; Fanning, P.; Carden, E.P.; Fanning, P. Vibration based condition monitoring: A review. J. Struct. Health Monit. 2004, 3, 355–377. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. Vibration-based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. Int. J. 2011. [Google Scholar] [CrossRef]
- Martikka, H.; Taitokari, E. Design of perforated shell dryings drums. Mech. Eng. Res. 2012, 2. [Google Scholar] [CrossRef]
- Jhung, M.J.; Jo, J.C. Equivalent material properties of perforated plate with triangular or square penetration pattern for dynamic analysis. Nucl. Eng. Technol. 2006, 38, 689–696. [Google Scholar]
- Jhung, M.J.; Yu, S.O. Study on modal characteristics of perforated shell using effective Young’s modulus. Nucl. Eng. Des. 2011, 241, 2026–2033. [Google Scholar] [CrossRef]
- Jhung, M.J.; Jeong, K.H. Free vibration analysis of perforated plate with square penetration pattern using equivalent material properties. Nucl. Eng. Technol. 2015, 47, 500–511. [Google Scholar] [CrossRef]
- Korea Institute of Nuclear Safety. Free Vibration Analysis of Perforated Cylindrical Shell Submerged in Fluid; Technical Report, KINS/RR-493; Korea Institute of Nuclear Safety: Daejeon, Korea, 2007. [Google Scholar]
- Hakula, H.; Laaksonen, M. Multiparametric shell eigenvalue problems. Comput. Methods Appl. Mech. Eng. 2019, 343, 721–745. [Google Scholar] [CrossRef]
- Hakula, H.; Kaarnioja, V.; Laaksonen, M. Cylindrical Shell with Junctions: Uncertainty Quantification of Free Vibration and Frequency Response Analysis. Shock Vib. 2018, 2018, 5817940. [Google Scholar] [CrossRef]
- Szabo, B.; Babuska, I. Finite Element Analysis; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Schwab, C. p- and hp-Finite Element Methods; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Chapelle, D.; Bathe, K.J. The Finite Element Analysis of Shells; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Malinen, M. On the classical shell model underlying bilinear degenerated shell finite elements: General shell geometry. Int. J. Numer. Methods Eng. 2002, 55, 629–652. [Google Scholar] [CrossRef]
- Forskitt, M.; Moon, J.R.; Brook, P.A. Elastic properties of plates perforated by elliptical holes. Appl. Math. Model. 1991, 15, 182–190. [Google Scholar] [CrossRef]
- Burgemeister, K.A.; Hansen, C.H. Calculating resonance frequencies of perforated panels. J. Sound Vib. 1996, 196, 387–399. [Google Scholar] [CrossRef]
- Halton, J.H. Algorithm 247: Radical-inverse Quasi-random Point Sequence. Commun. ACM 1964, 7, 701–702. [Google Scholar] [CrossRef]
- Pitkäranta, J.; Matache, A.M.; Schwab, C. Fourier mode analysis of layers in shallow shell deformations. Comput. Methods Appl. Mech. Eng. 2001, 190, 2943–2975. [Google Scholar] [CrossRef]
- Ghanem, R.; Spanos, P. Stochastic Finite Elements: A Spectral Approach; Dover Publications, Inc.: Mineola, NY, USA, 2003. [Google Scholar]
- Inman, D.J. Engineering Vibration; Pearson: London, UK, 2008. [Google Scholar]
- Babuška, I.; Nobile, F.; Tempone, R. A stochastic collocation method for elliptic partial differential equations with random input data. SIAM J. Numer. Anal. 2007, 45, 1005–1034. [Google Scholar] [CrossRef]
- Nobile, F.; Tempone, R.; Webster, C.G. An Anisotropic Sparse Grid Stochastic Collocation Method for Partial Differential Equations with Random Input Data. SIAM J. Numer. Anal. 2008, 46, 2411–2442. [Google Scholar] [CrossRef]
- Bieri, M. A Sparse Composite Collocation Finite Element Method for Elliptic SPDEs. SIAM J. Numer. Anal. 2011, 49, 2277–2301. [Google Scholar] [CrossRef]
- Andreev, R.; Schwab, C. Sparse Tensor Approximation of Parametric Eigenvalue Problems. In Lecture Notes in Computational Science and Engineering; Springer: Berlin, Germany, 2012; Volume 83, pp. 203–241. [Google Scholar]


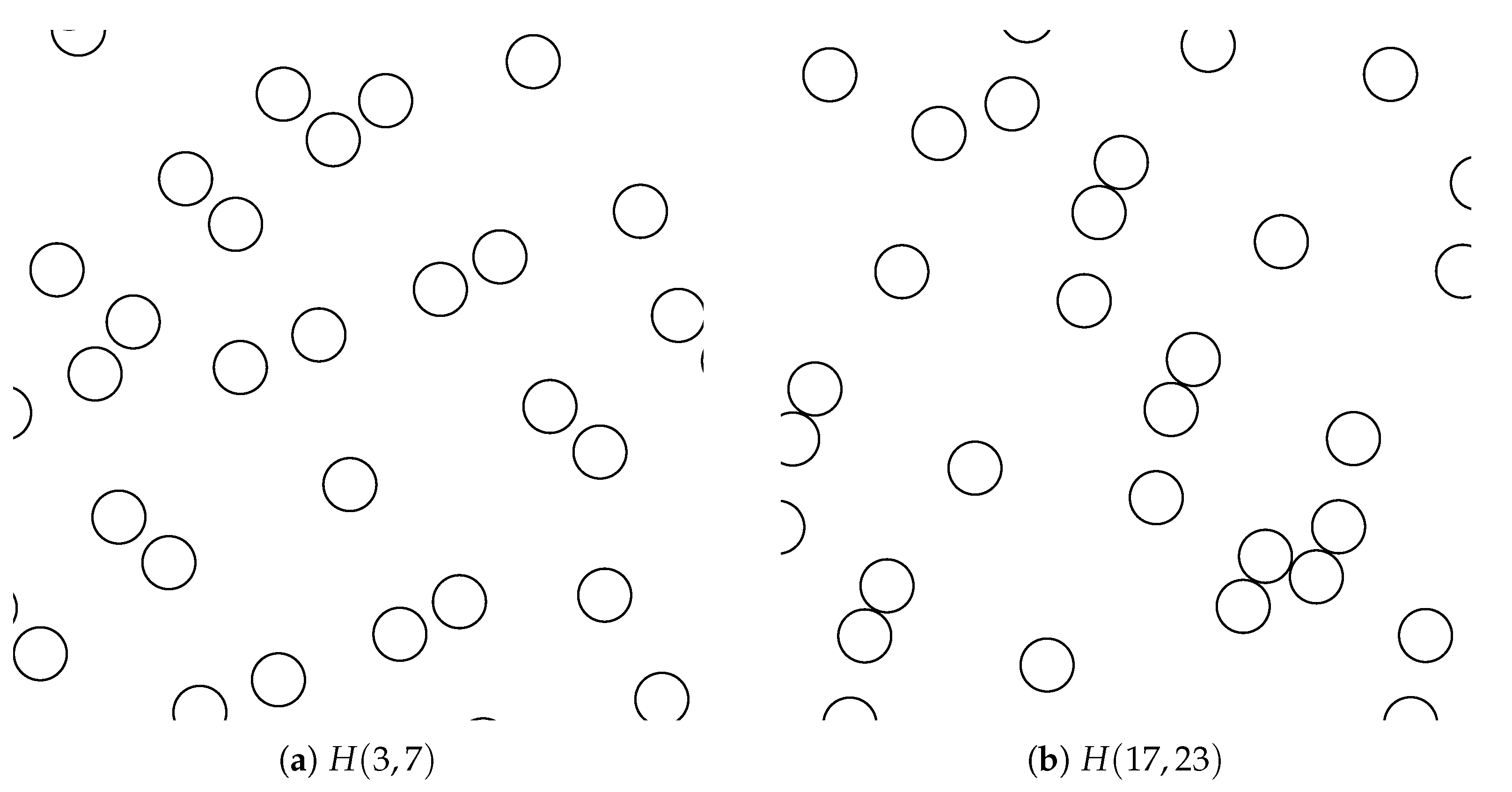






| a Parabolic | b Hyperbolic | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 0.0325658 | 1/2 | 4 | 1 | 0.129749 | 3/2 | 5 |
| 2 | 0.0325658 | 1/2 | 4 | 2 | 0.129749 | 3/2 | 5 |
| 3 | 0.0344515 | 1/2 | 3 | 3 | 0.136477 | 2 | 5 |
| 4 | 0.0344515 | 1/2 | 3 | 4 | 0.136477 | 2 | 5 |
| 5 | 0.0613855 | 1/2 | 5 | 5 | 0.138588 | 2 | 4 |
| 6 | 0.0613855 | 1/2 | 5 | 6 | 0.138588 | 2 | 4 |
| 7 | 0.0920303 | 1 | 4 | 7 | 0.142168 | 3/2 | 4 |
| 8 | 0.0920303 | 1 | 4 | 8 | 0.142168 | 3/2 | 4 |
| 9 | 0.0922696 | 1 | 5 | 9 | 0.156955 | 2 | 6 |
| 10 | 0.0922696 | 1 | 5 | 10 | 0.156955 | 2 | 6 |
| a Regular | b Halton: | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 0.028346 | 1/2 | 4 | 1 | 0.0275997 | 1/2 | 3 |
| 2 | 0.0283483 | 1/2 | 4 | 2 | 0.0280266 | 1/2 | 3 |
| 3 | 0.0288704 | 1/2 | 3 | 3 | 0.0282583 | 1/2 | 4 |
| 4 | 0.028872 | 1/2 | 3 | 4 | 0.0286645 | 1/2 | 4 |
| 5 | 0.0543918 | 1/2 | 5 | 5 | 0.0551038 | 1/2 | 5 |
| 6 | 0.0543927 | 1/2 | 5 | 6 | 0.0553621 | 1/2 | 5 |
| 7 | 0.0773403 | 1 | 4 | 7 | 0.0743065 | 1/2 | 2 |
| 8 | 0.0773436 | 1 | 4 | 8 | 0.0744545 | 1/2 | 2 |
| 9 | 0.0779846 | 1/2 | 2 | 9 | 0.075735 | 1 | 4 |
| 10 | 0.0779899 | 1/2 | 2 | 10 | 0.0759866 | 1 | 4 |
| a Regular | b Halton: | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 0.108012 | 3/2 | 5 | 1 | 0.106164 | 3/2 | 5 |
| 2 | 0.108026 | 3/2 | 5 | 2 | 0.106785 | 3/2 | 5 |
| 3 | 0.112789 | 2 | 5 | 3 | 0.110631 | 1 | 4 |
| 4 | 0.112798 | 2 | 5 | 4 | 0.110981 | 1 | 4 |
| 5 | 0.112905 | 1 | 4 | 5 | 0.113495 | 2 | 5 |
| 6 | 0.112909 | 1 | 4 | 6 | 0.113902 | 2 | 5 |
| 7 | 0.114934 | 3/2 | 4 | 7 | 0.114367 | 3/2 | 4 |
| 8 | 0.114939 | 3/2 | 4 | 8 | 0.114711 | 3/2 | 4 |
| 9 | 0.132725 | 2 | 6 | 9 | 0.131692 | 2 | 6 |
| 10 | 0.132736 | 2 | 6 | 10 | 0.132256 | 2 | 6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hakula, H.; Laaksonen, M. Frequency Response Analysis of Perforated Shells with Uncertain Materials and Damage. Appl. Sci. 2019, 9, 5299. https://doi.org/10.3390/app9245299
Hakula H, Laaksonen M. Frequency Response Analysis of Perforated Shells with Uncertain Materials and Damage. Applied Sciences. 2019; 9(24):5299. https://doi.org/10.3390/app9245299
Chicago/Turabian StyleHakula, Harri, and Mikael Laaksonen. 2019. "Frequency Response Analysis of Perforated Shells with Uncertain Materials and Damage" Applied Sciences 9, no. 24: 5299. https://doi.org/10.3390/app9245299
APA StyleHakula, H., & Laaksonen, M. (2019). Frequency Response Analysis of Perforated Shells with Uncertain Materials and Damage. Applied Sciences, 9(24), 5299. https://doi.org/10.3390/app9245299





