Mixed Convective Flow of Micropolar Nanofluid across a Horizontal Cylinder in Saturated Porous Medium
Abstract
:1. Introduction
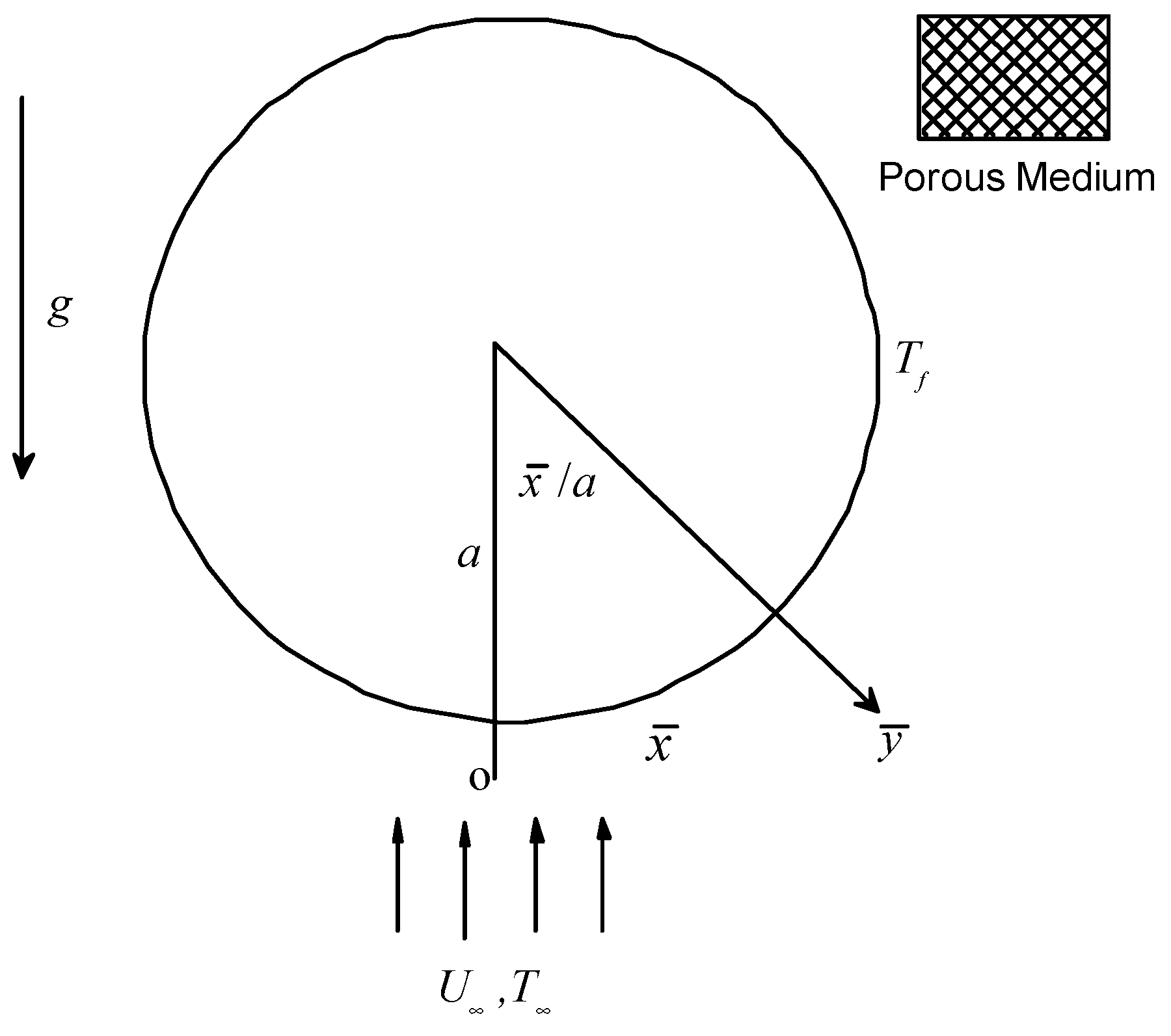
2. Basic Equations
3. Numerical Method
3.1. First Level of Truncation (Local Similarity Solution)
3.2. Second Level of Truncation (Local Non-Similarity)
4. Results and Discussions
5. Conclusions
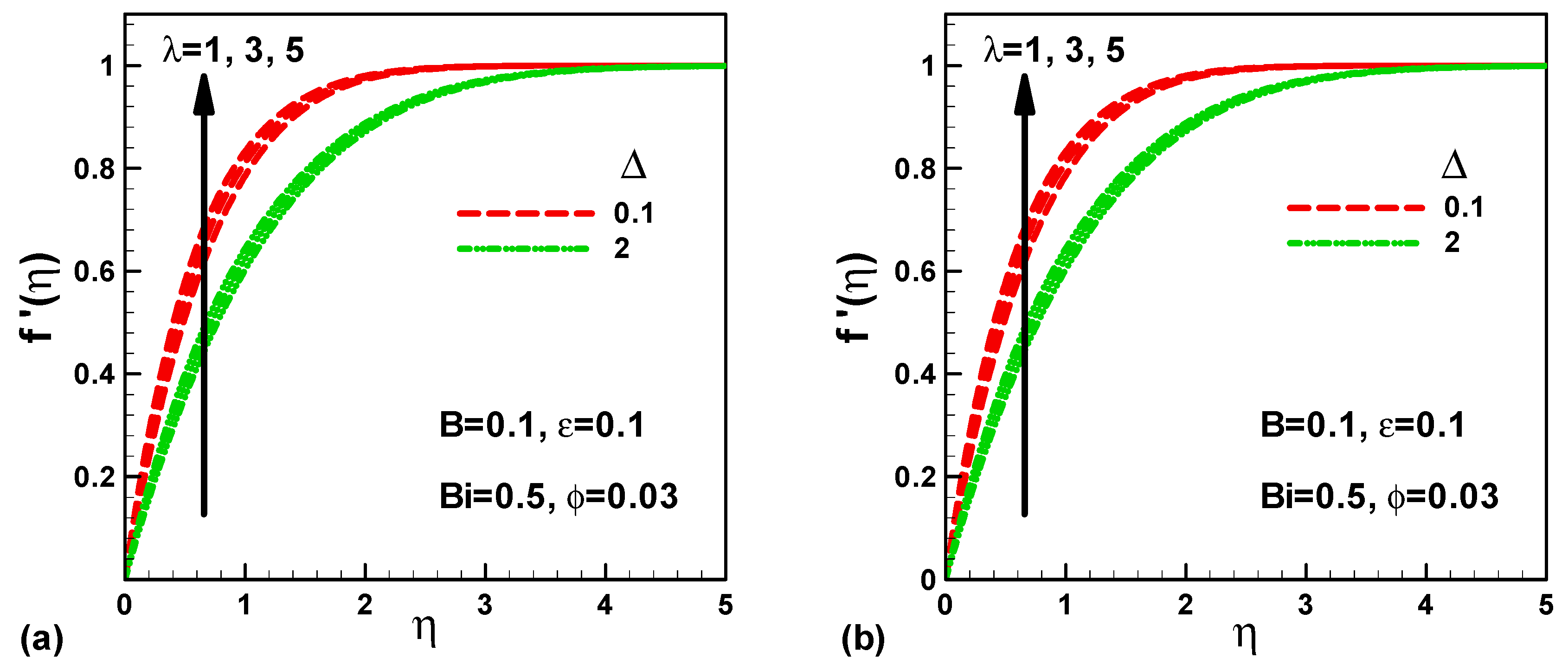
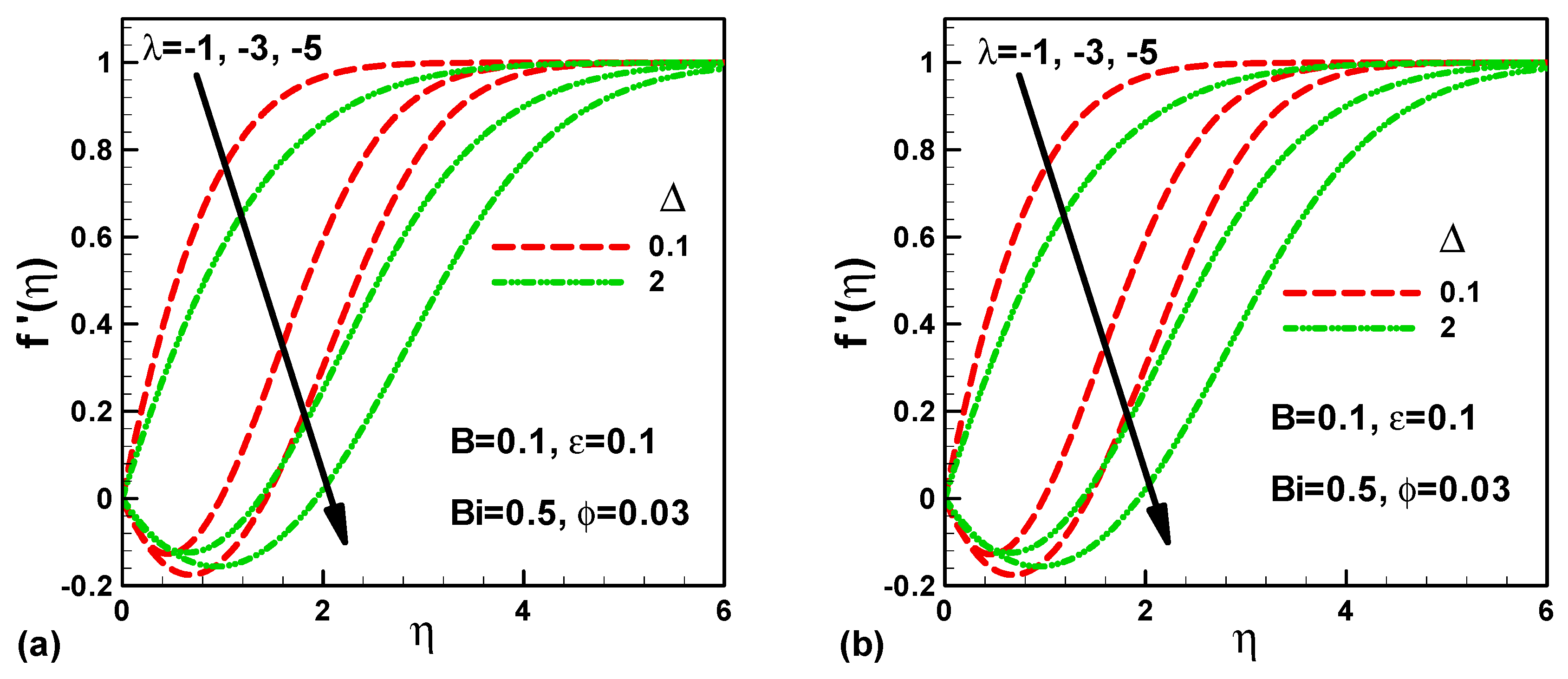
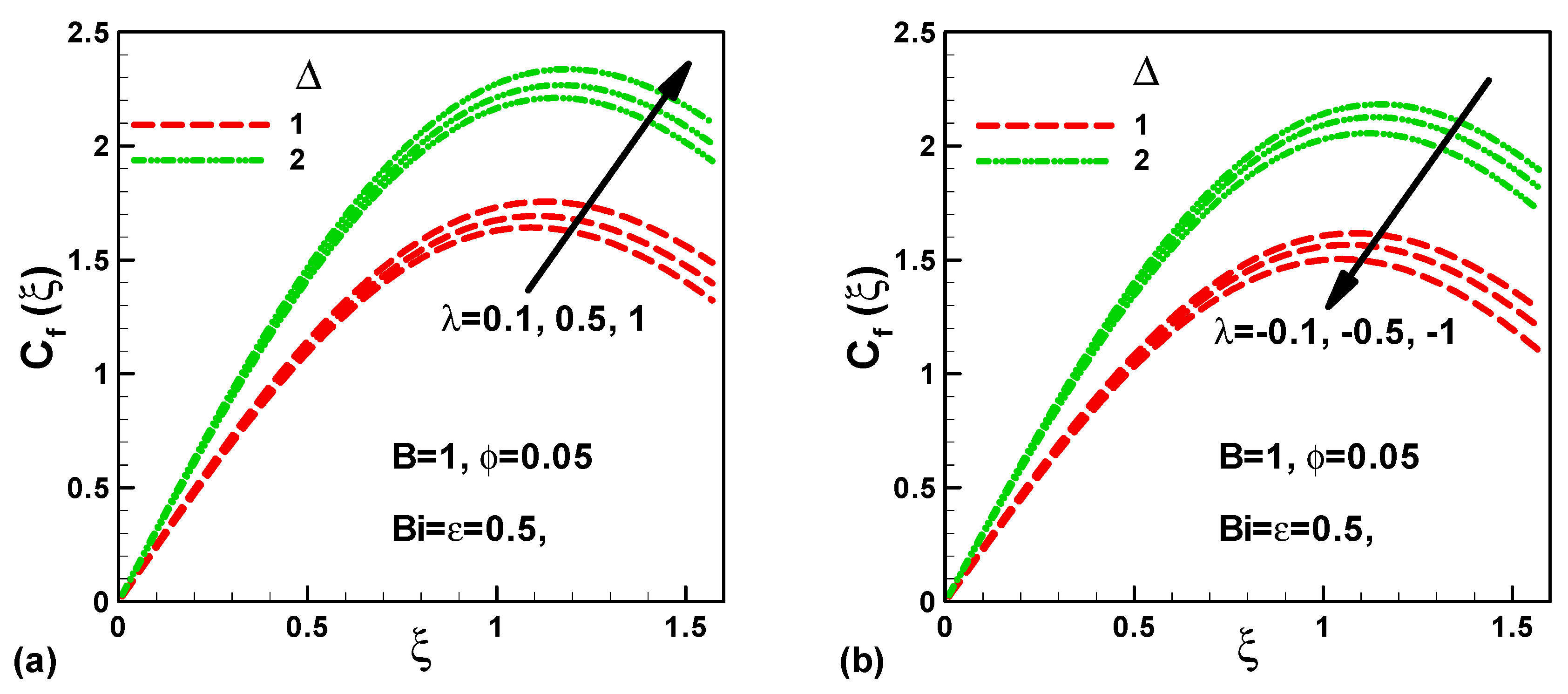
- For opposing flows, the dimensionless velocity decreases with the mixed convection and material parameters inside the boundary layer;
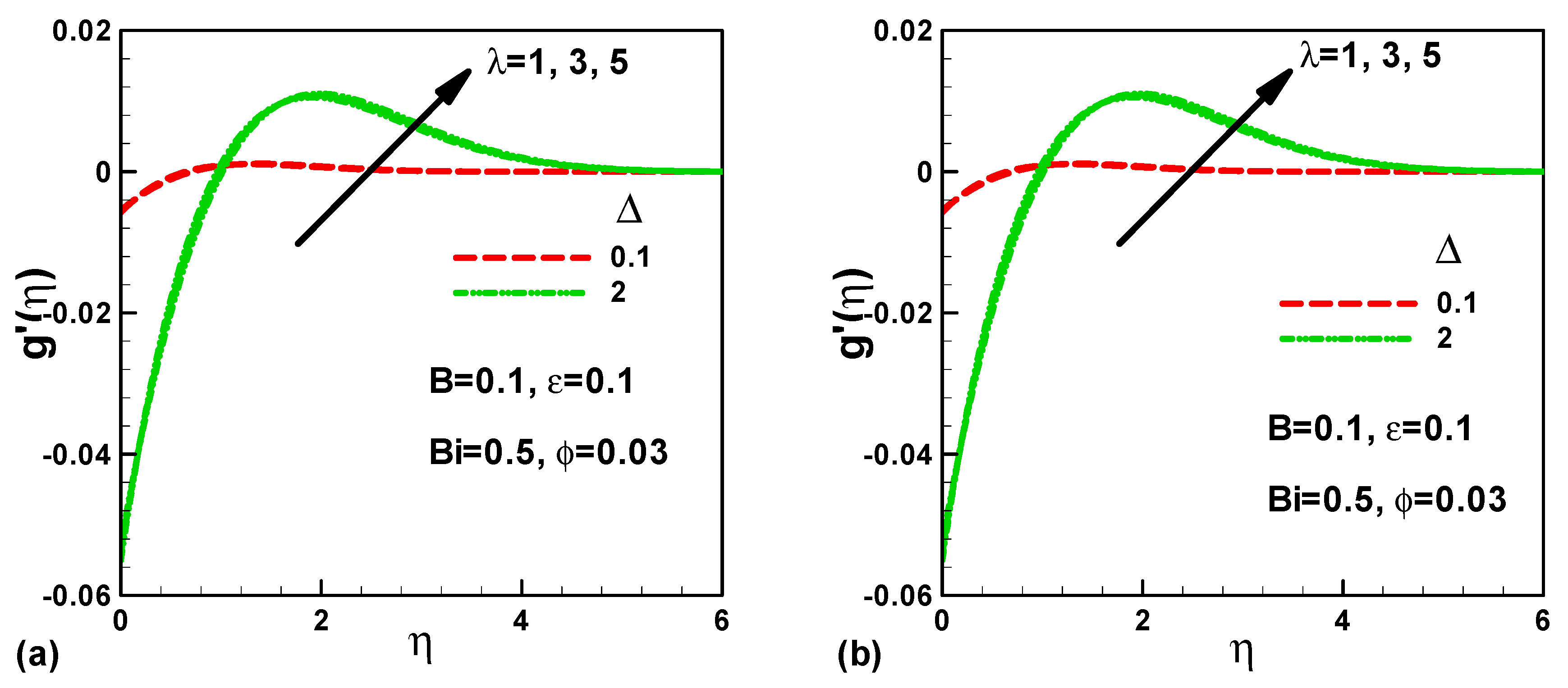
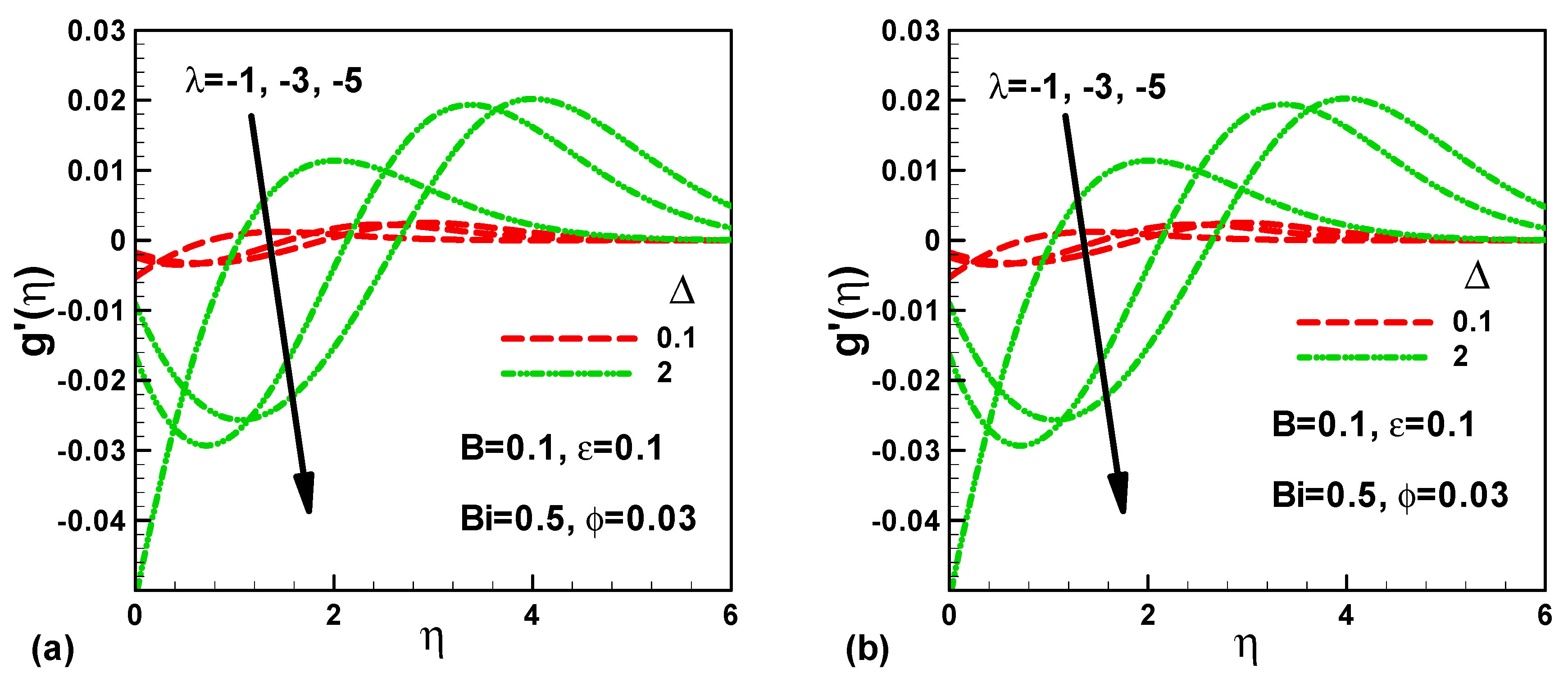
- The smaller values of ∆ show no effect on the microrotation velocity. However, for large values of ∆, the microrotation velocity shows oscillatory behavior;
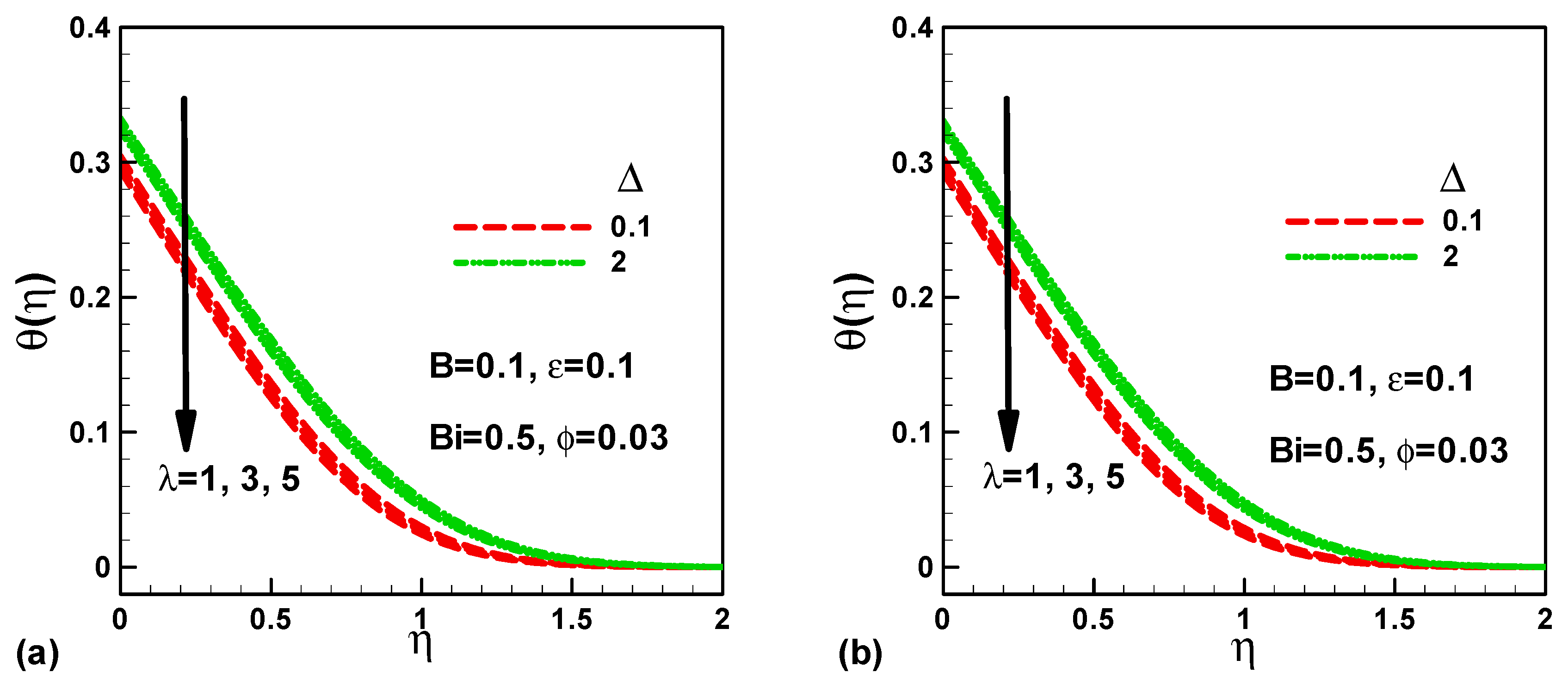
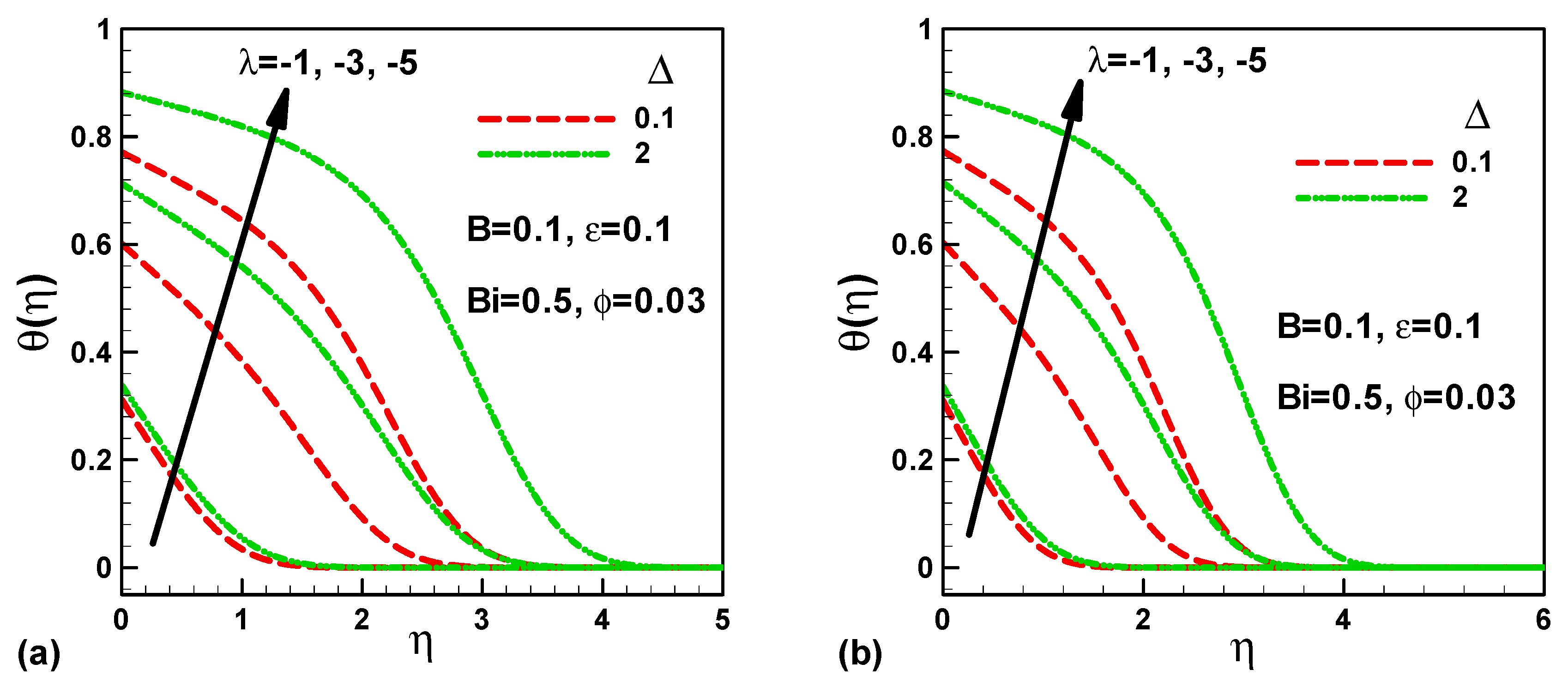
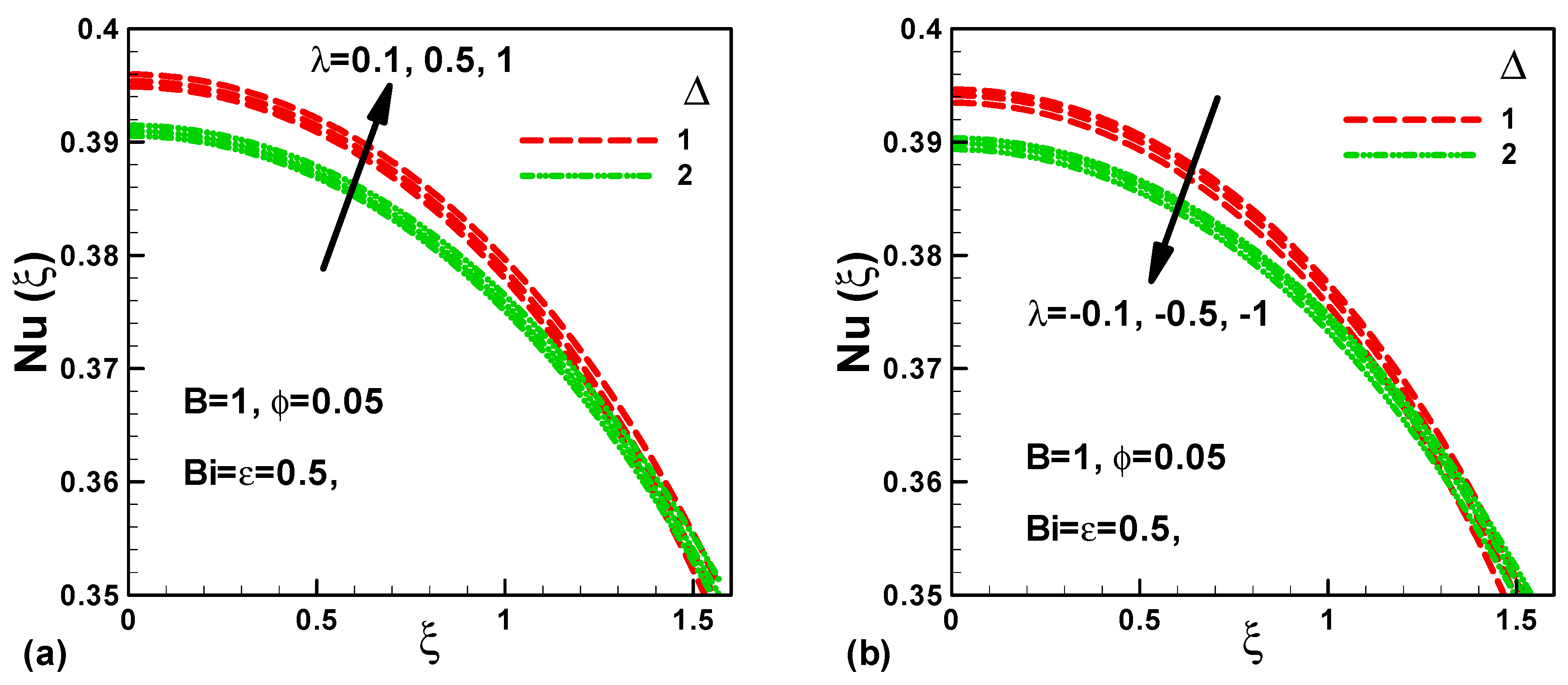
- For opposing flows of micropolar nanofluids, the dimensionless temperature increases with λ and decreases with ∆;
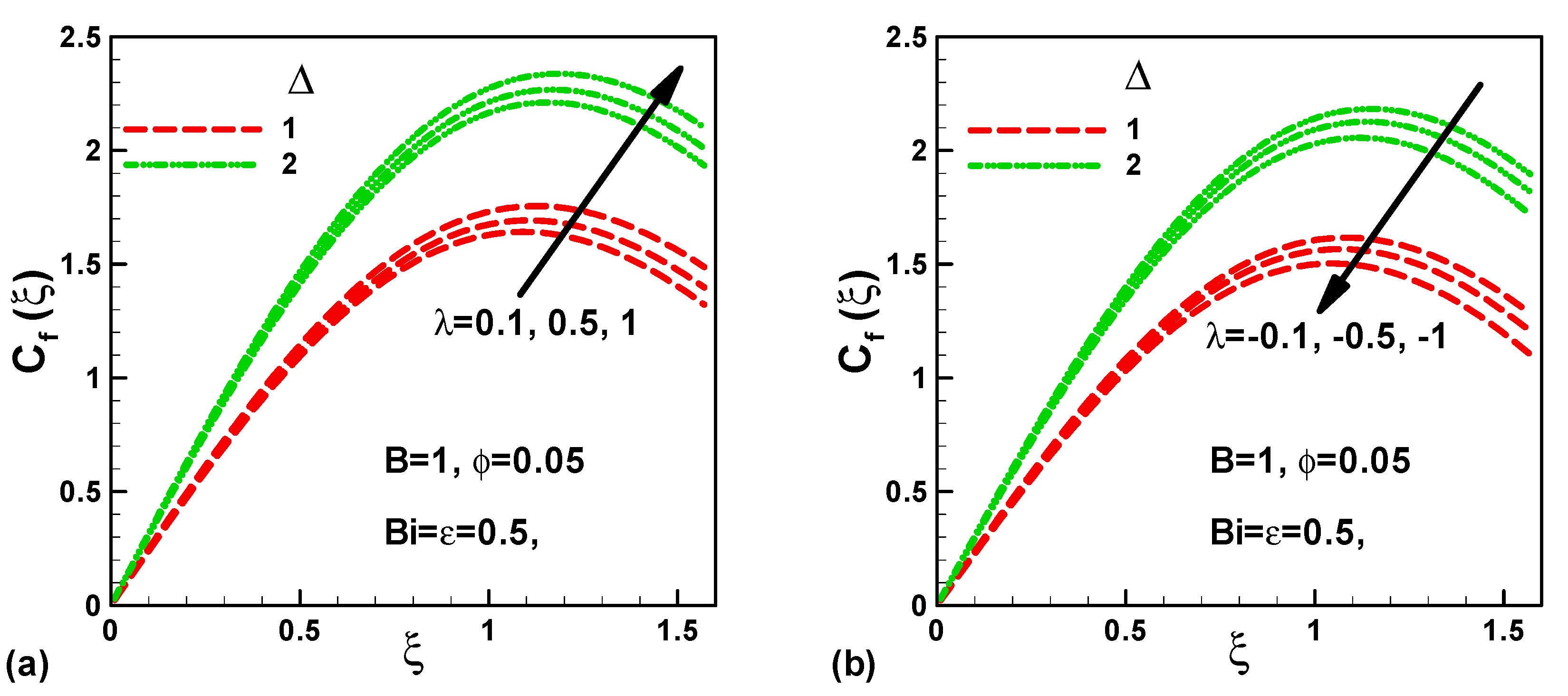
- In assisting flows, the maximum friction increases with both mixed convection and material parameters;
- The skin friction at the front stagnation point is zero and increases up to the maximum along the cylinder surface;
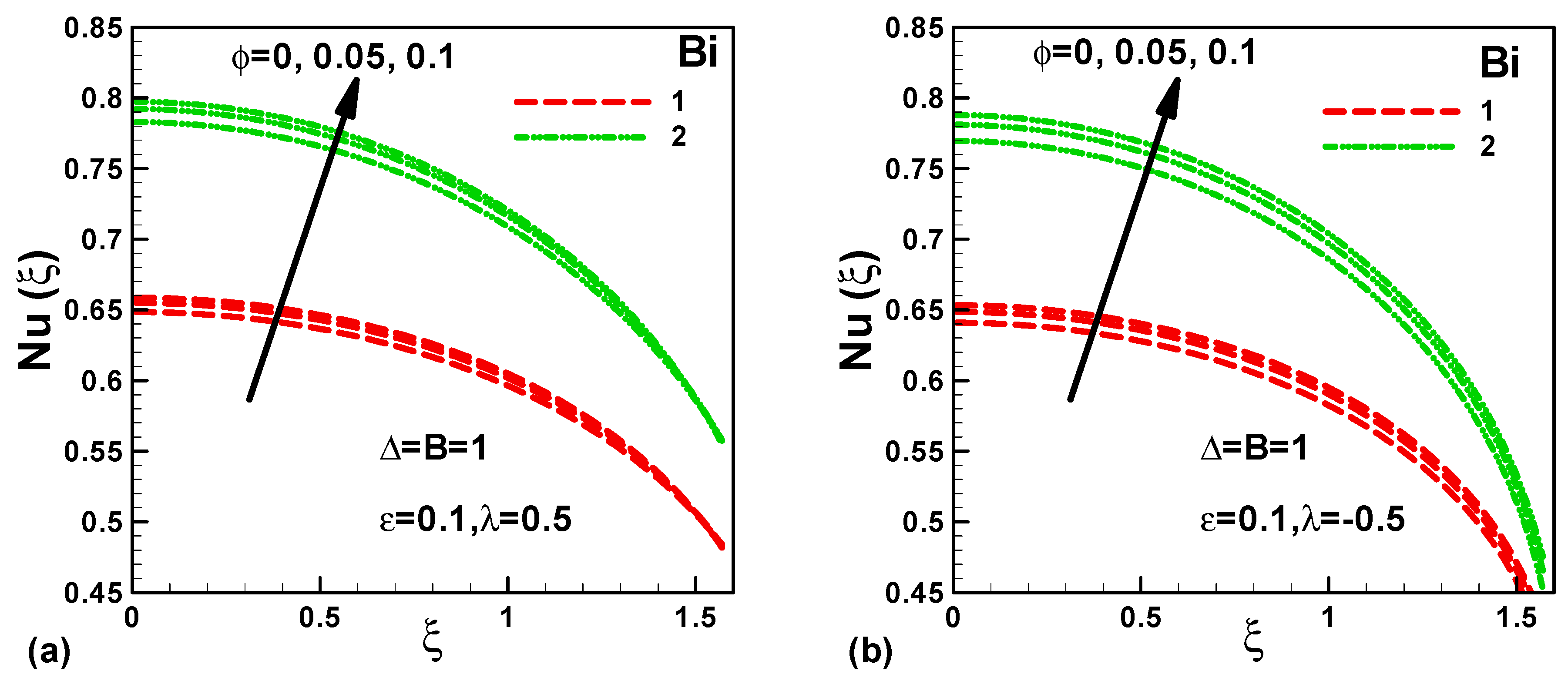
- In the case of assisting flow, the local Nusselt numbers are found to be higher than the opposing flow;
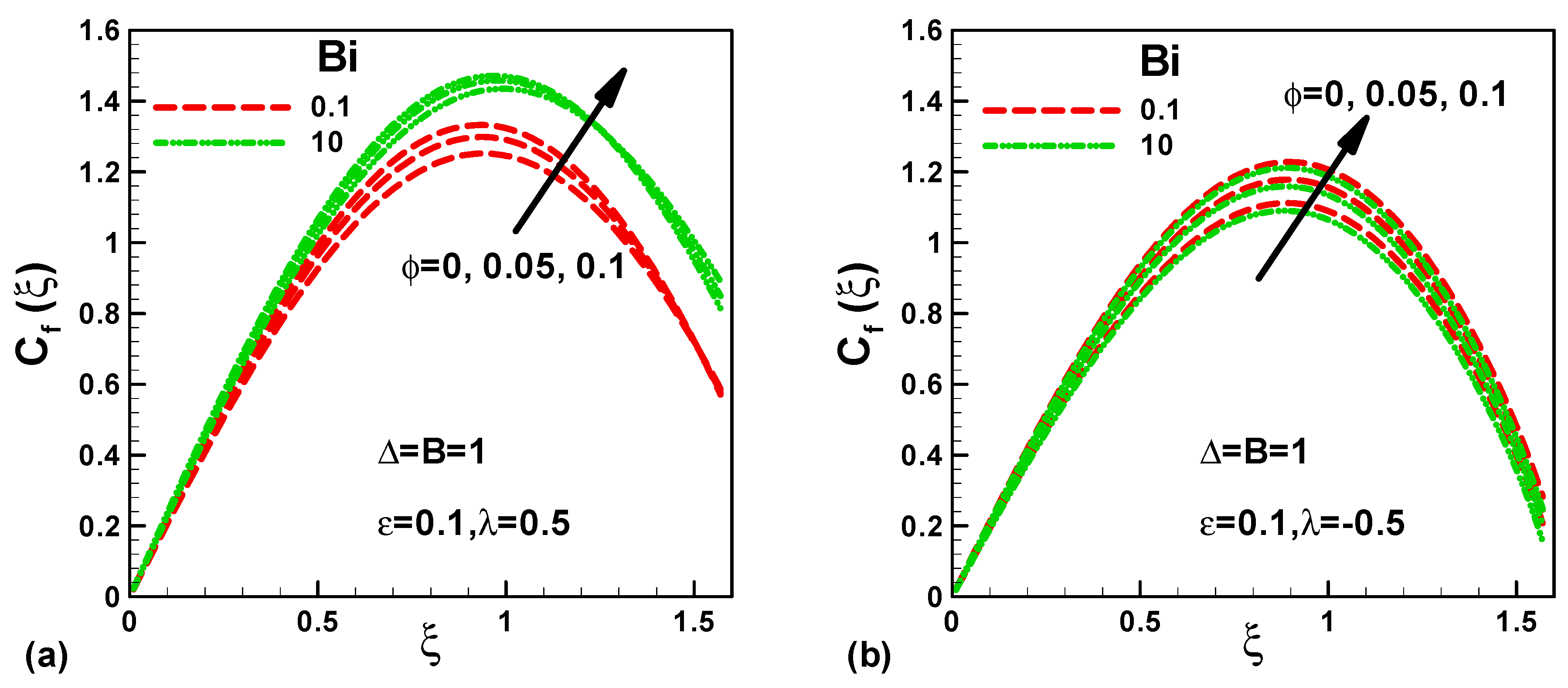
- The local Nusselt number increases with an increase in the solid volume fraction of TiO2 nanoparticles and Biot number.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| B | Material parameter |
| Bi | Biot number |
| Specific heat at constant pressure | |
| Skin-friction coefficient | |
| Dimensionless stream function | |
| f’ | Dimensionless velocity |
| Acceleration due to gravity | |
| Local Grash of number | |
| hf | Convective heat transfer coefficient |
| Thermal conductivity | |
| K | Permeability of porous medium |
| Local Nusselt number | |
| Prandtl number | |
| Temperature of the fluid in the boundary layer | |
| Temperature of the ambient fluid | |
| Uniform temperature of the cylinder surface | |
| Velocity of the external flow | |
| U∞ | Free stream velocity |
| u, v | Dimensionless fluid velocities in the directions |
| Dimensional fluid velocities in the directions | |
| Dimensional axes in the direction along and normal to the surface | |
| Volumetric coefficient of thermal expansion | |
| Stream function | |
| ε | Permeability parameter |
| λ | Mixed convection parameter |
| Fluid density | |
| Dynamic viscosity of the fluid | |
| Kinematic viscosity of the fluid | |
| Dimensionless temperature function | |
| ϕ | Nanoparticles volume fraction |
| ξ | Dimensionless coordinate |
| pseudo-similarity variable | |
| Δ | Dimensionless material parameter |
| Subscripts | |
| Pure fluid | |
| nanofluid | |
| s | Solid nanoparticle |
References
- Erigen, A.C. Theory of micropolar fluid. J. Math. Mech. 1966, 16, 1–18. [Google Scholar]
- Modather, M.; Rashad, A.M.; Chamkha, A.J. An analytical study of MHD heat and mass transfer oscillatory flow of a micropolar fluid over a vertical permeable plate in a porous medium. Turkish J. Eng. Environ. Sci. 2009, 33, 245–257. [Google Scholar]
- Li, W. Derivation of modified Reynolds equation—A porous media model. J. Tribol. 1999, 121, 823–829. [Google Scholar] [CrossRef]
- El-Kabeir, S.M.M.; Rashad, A.M.; Gorla, R. Heat transfer in a micropolar fluid flow past a permeable continuous moving surface. ZAMM J. Appl. Math. Mech. 2011, 91, 360–370. [Google Scholar] [CrossRef]
- Shukla, J.B.; Isa, M. Generalized Reynolds equation for micropolar lubricants and its application to optimum one-dimensional slider bearings: Effects of solid-particle additives in solution. J. Mech. Eng. Sci. 1975, 17, 280–284. [Google Scholar] [CrossRef]
- Verma, P.D.S.; Agrawal, V.K.; Bhatt, S.B. Porous inclined slider bearing lubricated with micropolar fluid. Wear 1979, 53, 101–106. [Google Scholar] [CrossRef]
- Modather, M.; Rashad, A.M.; El-Kabeir, S.M.M. Influences of temperature-dependent viscosity and thermal conductivity on the unsteady flow and heat transfer of a micropolar fluid over a stretching sheet. Latin Am. Appl. Res. 2012, 42, 121–126. [Google Scholar]
- Chamkha, A.J.; L-Kabeir, S.M.M.E.; Rashad, A.M. Unsteady coupled heat and mass transfer by mixed convection flow of a micropolar fluid near the stagnation point on a vertical surface in the presence of radiation and chemical reaction. Prog. Comput. Fluid Dyn. 2015, 15, 186–196. [Google Scholar] [CrossRef]
- Prakash, J.; Sinha, P. Lubrication theory for micropolar fluids and its application to a journal bearing. Int. J. Eng. Sci. 1975, 13, 217–232. [Google Scholar] [CrossRef]
- Modather, M.; El-Kabeir, S.M.M.; Rashad, A.M. Heat and mass transfer flow of a micropolar fluid under convective boundary condition from a horizontal cylinder with temperature-dependent viscosity and chemical reaction. J. Comput. Theor. Nanosci. 2015, 12, 4506–4514. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticle. ASME FED 1995, 231, 99–105. [Google Scholar]
- Chamkha, A.J.; Abbasbandy, S.; Rashad, A.M.; Vajravelu, K. Radiation Effects on Mixed Convection about a Cone Embedded in a Porous Medium Filled with a Nanofluid. Meccanica 2013, 48, 275–285. [Google Scholar] [CrossRef]
- Nazar, R.; Tham, L.; Pop, I.; Ingham, D.B. Mixed convection boundary layer flow from a horizontal circular cylinder embedded in a porous medium filled with a nanofluid. Transp. Porous Media. 2011, 86, 517–536. [Google Scholar] [CrossRef]
- Tham, L.; Nazar, R. Mixed convection flows about a solid sphere embedded in a porous medium filled with a nanofluid. Sains Malays. 2012, 41, 1643–1649. [Google Scholar]
- Tham, L.; Nazar, R.; Pop, I. Mixed convection boundary layer flow past a horizontal circular cylinder embedded in a porous medium saturated by a nanofluid. Brinkman Model. J. Porous Media 2013, 16, 445–457. [Google Scholar] [CrossRef]
- Rashad, A.M.; Chamkha, A.J.; Abdou, M.M.M. Mixed Convection Flow Of Non-Newtonian Fluid From Vertical Surface Saturated In A Porous Medium Filled with A Nanofluid. J. Appl. Fluid Mech. 2013, 6, 301–309. [Google Scholar]
- Tlili, I.; Khan, W.A.; Khan, I. Multiple Slip Effects on MHD SA-Al2O3 and SA-Cu non-Newtonian Nanofluids Flow over a Stretching Cylinder in Porous Medium with Radiation and Chemical Reaction. Results Phys. 2018, 8, 213–222. [Google Scholar] [CrossRef]
- Mabood, F.; Khan, W.A.; Yovanovich, M.M. Forced Convection of Nanofluid Flow across Horizontal Circular Cylinder with Convective Boundary Condition. J. Mol. Liq. 2016, 222, 172–180. [Google Scholar] [CrossRef]
- Rashad, A.M.; Chamkha, A.J.; Modather, M. Mixed Convection Boundary-Layer Flow of a Nanofluid From a Horizontal Circular Cylinder Embedded in a Porous Medium Under Convective Boundary Condition. Comput. Fluids 2013, 86, 380–386. [Google Scholar] [CrossRef]
- L-Kabeir, S.M.M.E.; Chamkha, A.J.; Rashad, A.M. The Effect Of Thermal Radiation On Non-Darcy Free Convection from a Vertical Cylinder Embedded in a Nanofluid Porous Media. J. Porous Media 2014, 17, 269–278. [Google Scholar] [CrossRef]
- L-Kabeir, S.M.M.E.; Modather, M.; Rashad, A.M. Effect Of Thermal Radiation On Mixed Convection Flow of A Nanofluid About A Solid Sphere In A Saturated Porous Medium Under Convective Boundary Condition. J. Porous Media 2015, 18, 569–584. [Google Scholar] [CrossRef]
- Tlili, I.; Khan, W.A.; Ramadan, K. MHD Flow of Nanofluid Flow Across Horizontal Circular Cylinder: Steady Forced Convection. J. Nanofluids 2019, 8, 179–186. [Google Scholar] [CrossRef]
- Gorla, R.S.R.; Khan, W. Natural Convective Boundary-Layer Flow Over a Vertical Cylinder Embedded in a Porous Medium Saturated With a Nanofluid. J. Nanotechnol. Eng. Med. 2012, 3, 034501–034505. [Google Scholar] [CrossRef]
- Merkin, J.H. Mixed convection from a horizontal circular cylinder. Int. J. Heat Mass Transf. 1977, 20, 73–77. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Pop, I. Mixed convection boundary-layer flow from a horizontal circular cylinder in micropolar fluids: A case of constant wall temperature. Int. J. Numer. Methods Heat Fluid Flow 2003, 13, 86–109. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. The boundary layer assumptions and the mathematical nanofluid model. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Quack, H.; Boerner, C.J. Local nonsimilarity boundary-layer solutions. AIAA Journal 1970, 8, 1936–1942. [Google Scholar] [CrossRef]
- Minkowycz, W.J.; Sparrow, E.M. Numerical solution scheme for local non- similarity boundary-layer analysis. Num. Heat Transf. Part B Fundam. An Int. J. Compu. Meth. 1978, 1, 69–85. [Google Scholar] [CrossRef]
| λ | Merkin [24] | Nazar et al. [25] | Present Results |
|---|---|---|---|
| −1.75 | 0.4199 | 0.4205 | 0.4159 |
| −1.5 | 0.4576 | 0.4601 | 0.4589 |
| −1.0 | 0.5067 | 0.5080 | 0.5060 |
| −0.5 | 0.5420 | 0.5430 | 0.5406 |
| 0.0 | 0.5705 | 0.5710 | 0.5700 |
| 0.5 | 0.5943 | 0.5949 | 0.5923 |
| 0.88 | 0.6096 | 0.6112 | 0.6054 |
| 0.89 | 0.6110 | 0.6116 | 0.6103 |
| 1.0 | 0.6158 | 0.6160 | 0.6154 |
| 2.0 | 0.6497 | 0.6518 | 0.6468 |
| 5.0 | 0.7315 | 0.7320 | 0.7304 |
| Property | Pure Water | Alumina Al2O3 | Titanium Oxide (TiO2) |
|---|---|---|---|
| ρ (kg m−3) | 997.1 | 3970 | 4250 |
| Cp (J kg−1 K−1) | 4179 | 765 | 686.2 |
| k (W m−1 K−1) | 0.613 | 40 | 8.9538 |
| β (K−1) | 21 × 10−5 | 0.85 × 10−5 | 0.9 × 10−5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashad, A.M.; Khan, W.A.; EL-Kabeir, S.M.M.; EL-Hakiem, A.M.A. Mixed Convective Flow of Micropolar Nanofluid across a Horizontal Cylinder in Saturated Porous Medium. Appl. Sci. 2019, 9, 5241. https://doi.org/10.3390/app9235241
Rashad AM, Khan WA, EL-Kabeir SMM, EL-Hakiem AMA. Mixed Convective Flow of Micropolar Nanofluid across a Horizontal Cylinder in Saturated Porous Medium. Applied Sciences. 2019; 9(23):5241. https://doi.org/10.3390/app9235241
Chicago/Turabian StyleRashad, Ahmed M., Waqar A. Khan, Saber M. M. EL-Kabeir, and Amal M. A. EL-Hakiem. 2019. "Mixed Convective Flow of Micropolar Nanofluid across a Horizontal Cylinder in Saturated Porous Medium" Applied Sciences 9, no. 23: 5241. https://doi.org/10.3390/app9235241
APA StyleRashad, A. M., Khan, W. A., EL-Kabeir, S. M. M., & EL-Hakiem, A. M. A. (2019). Mixed Convective Flow of Micropolar Nanofluid across a Horizontal Cylinder in Saturated Porous Medium. Applied Sciences, 9(23), 5241. https://doi.org/10.3390/app9235241






