Forecasting Landslides via Three-Dimensional Discrete Element Modeling: Helong Landslide Case Study
Abstract
1. Introduction
2. Background
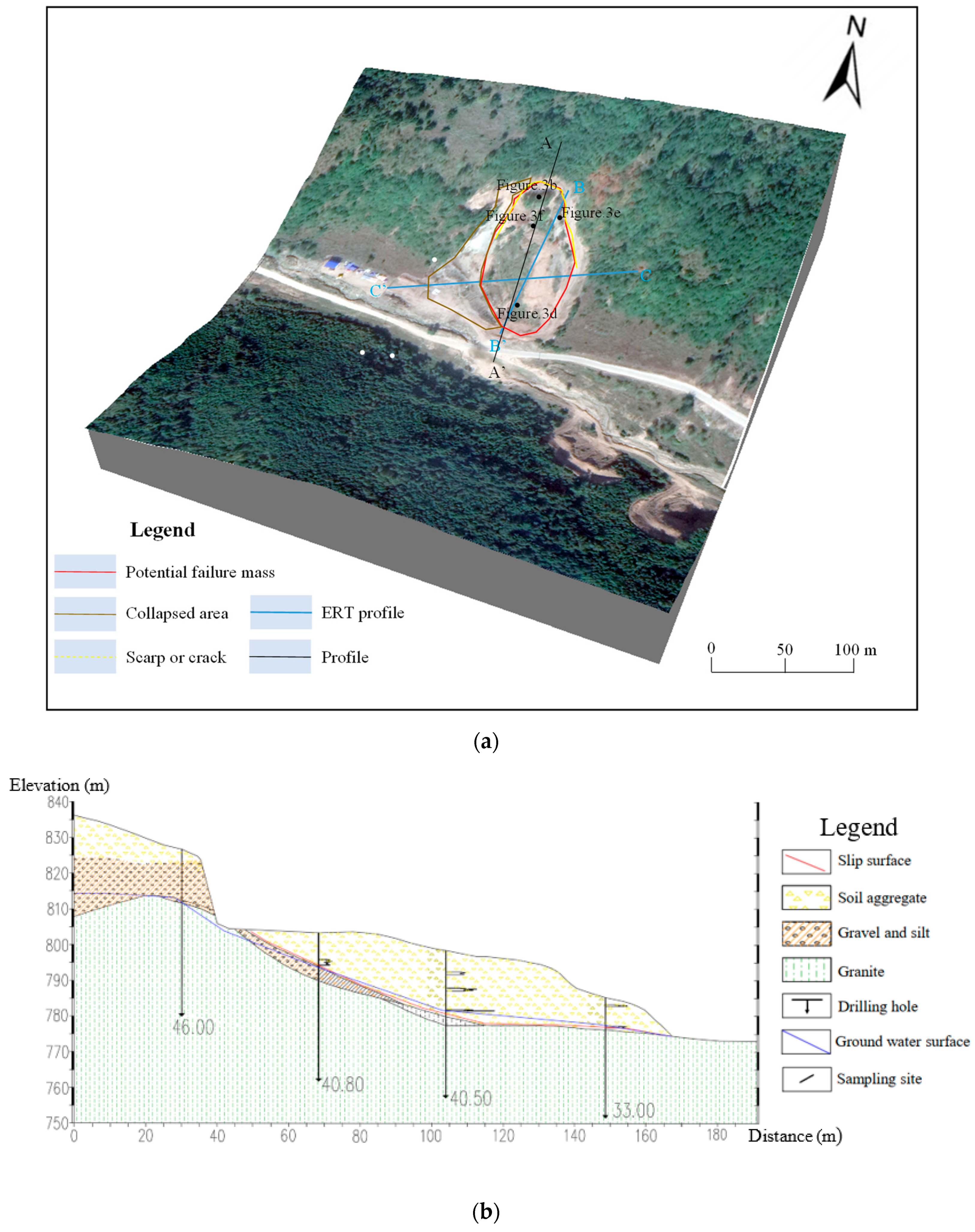
2.1. Study Area
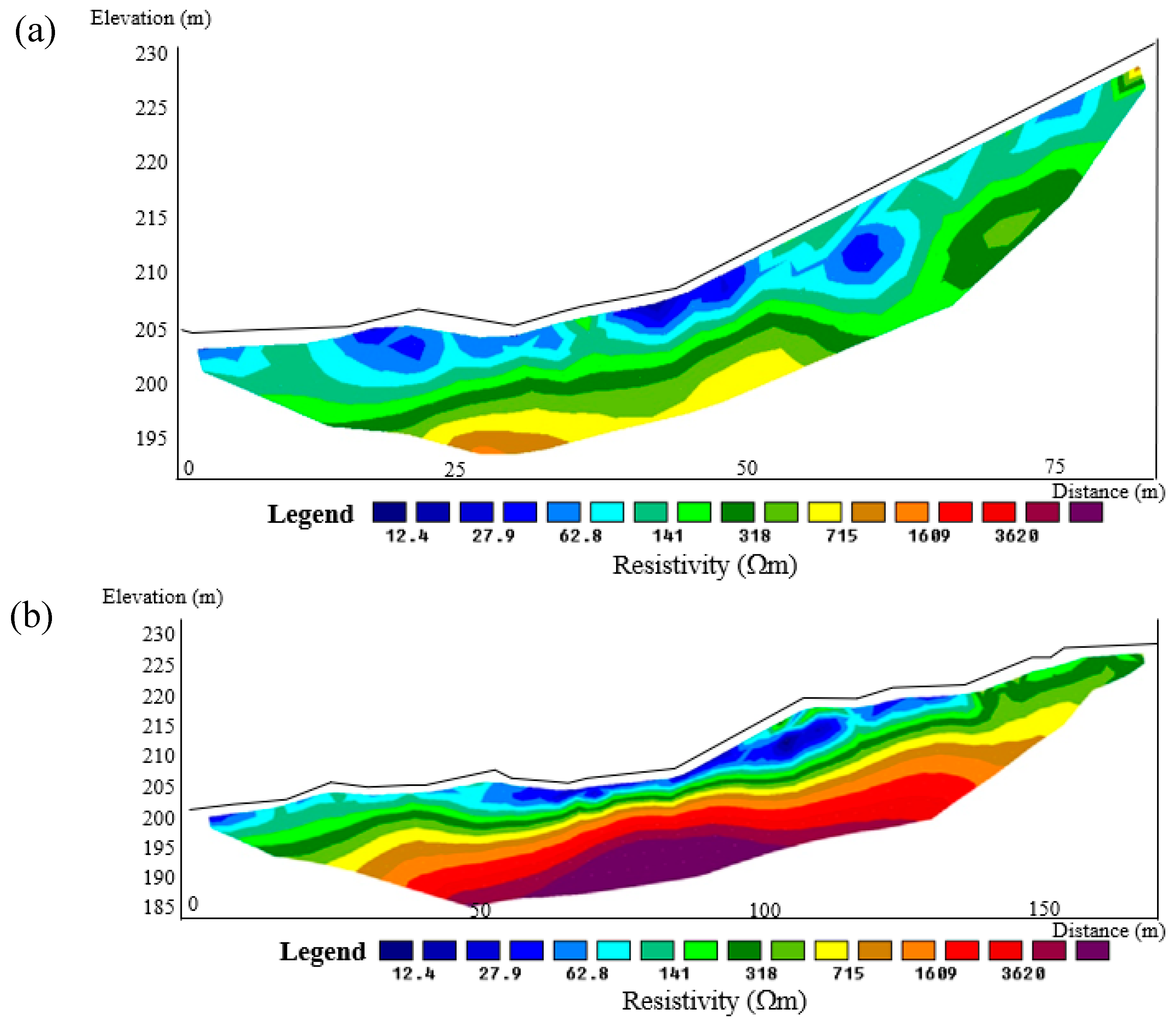
2.2. Helong Landslide
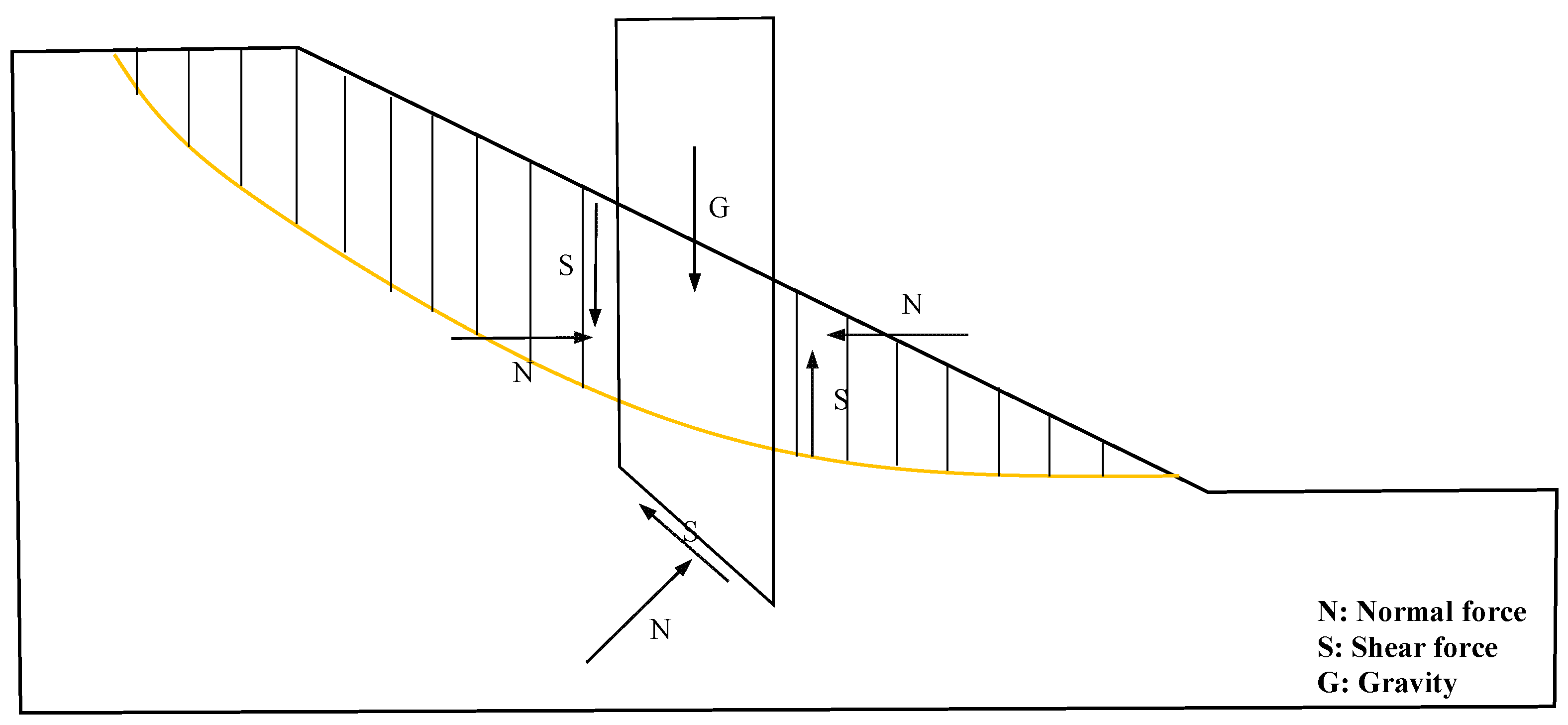
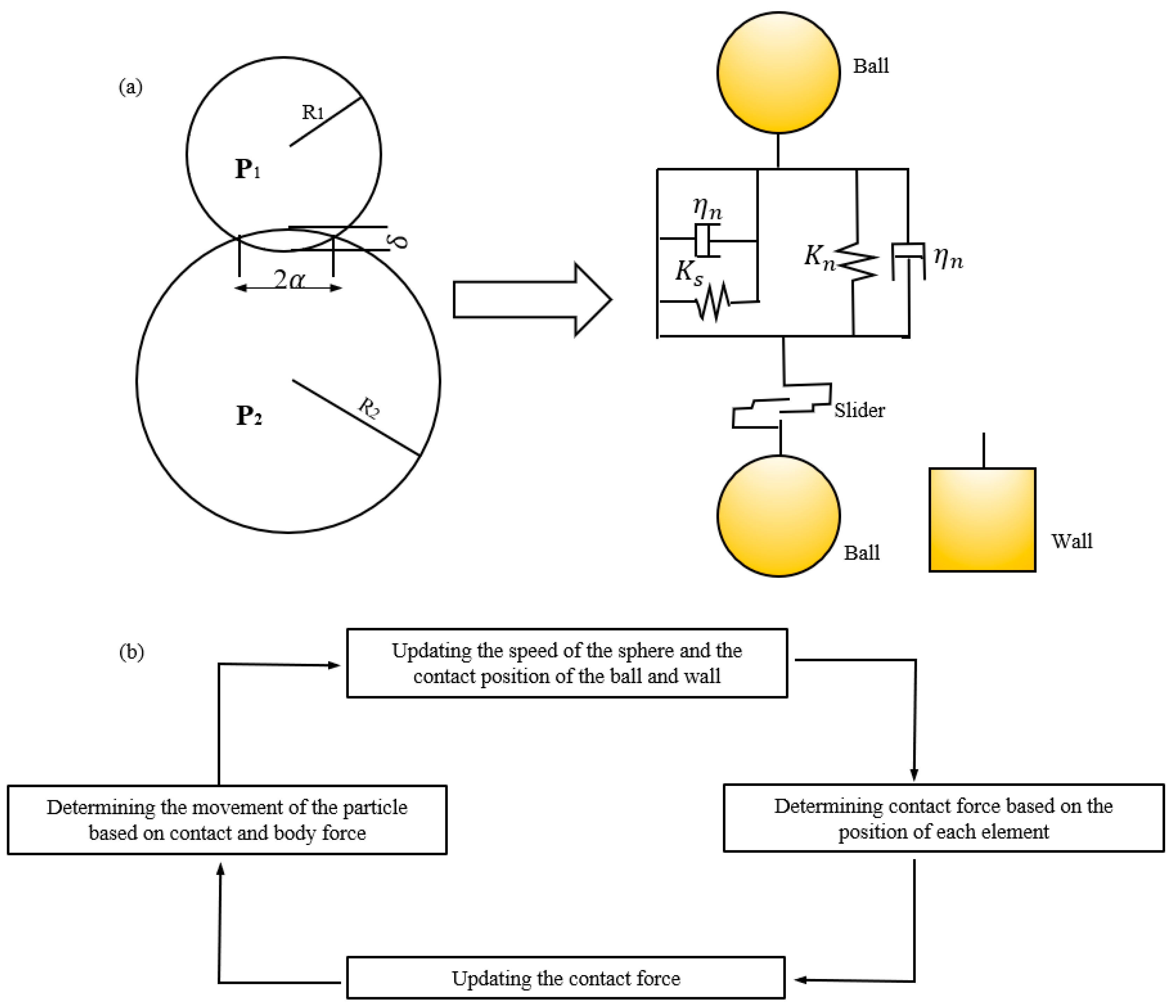
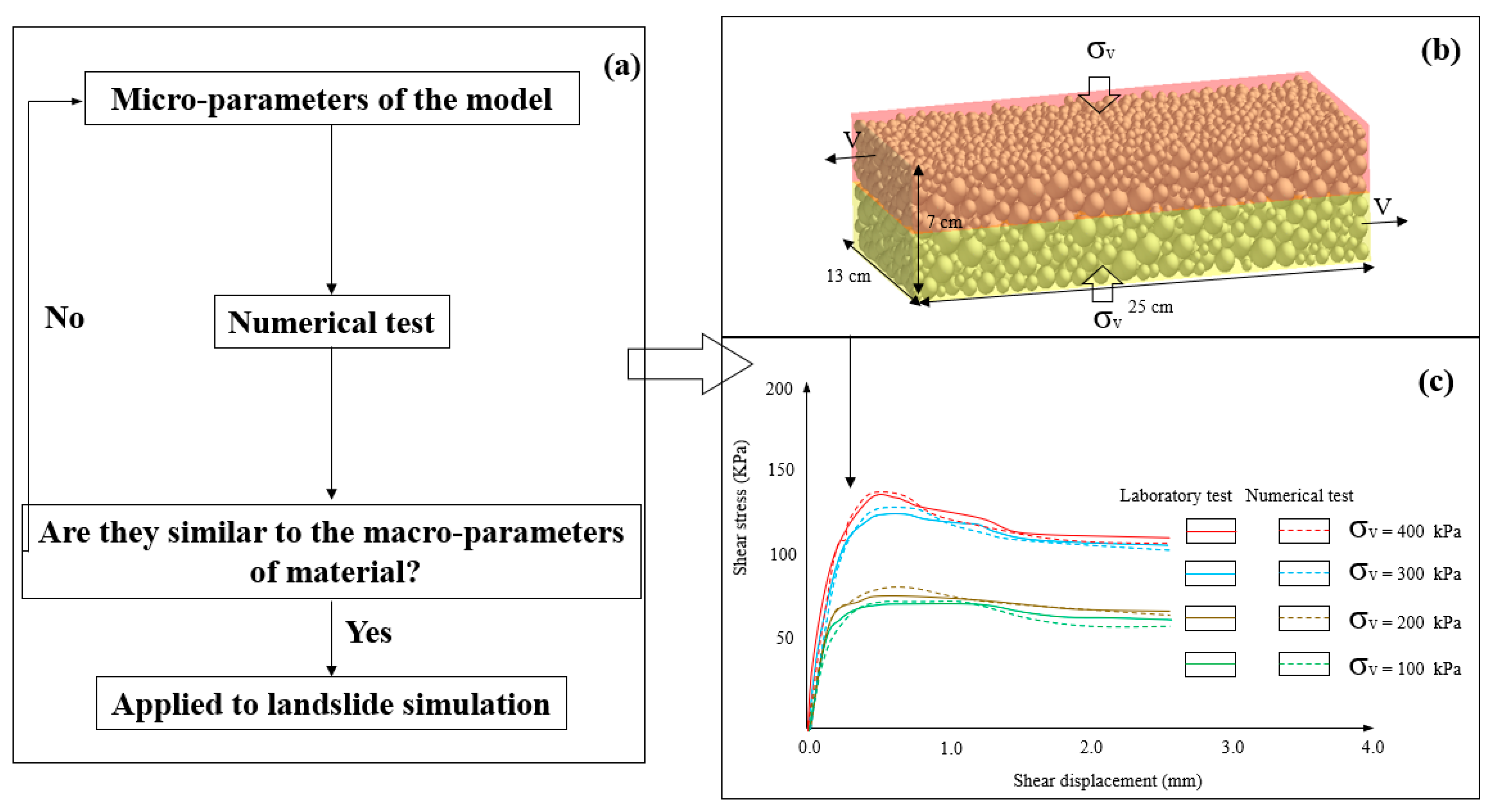
3. Methodology
4. Results and Discussions
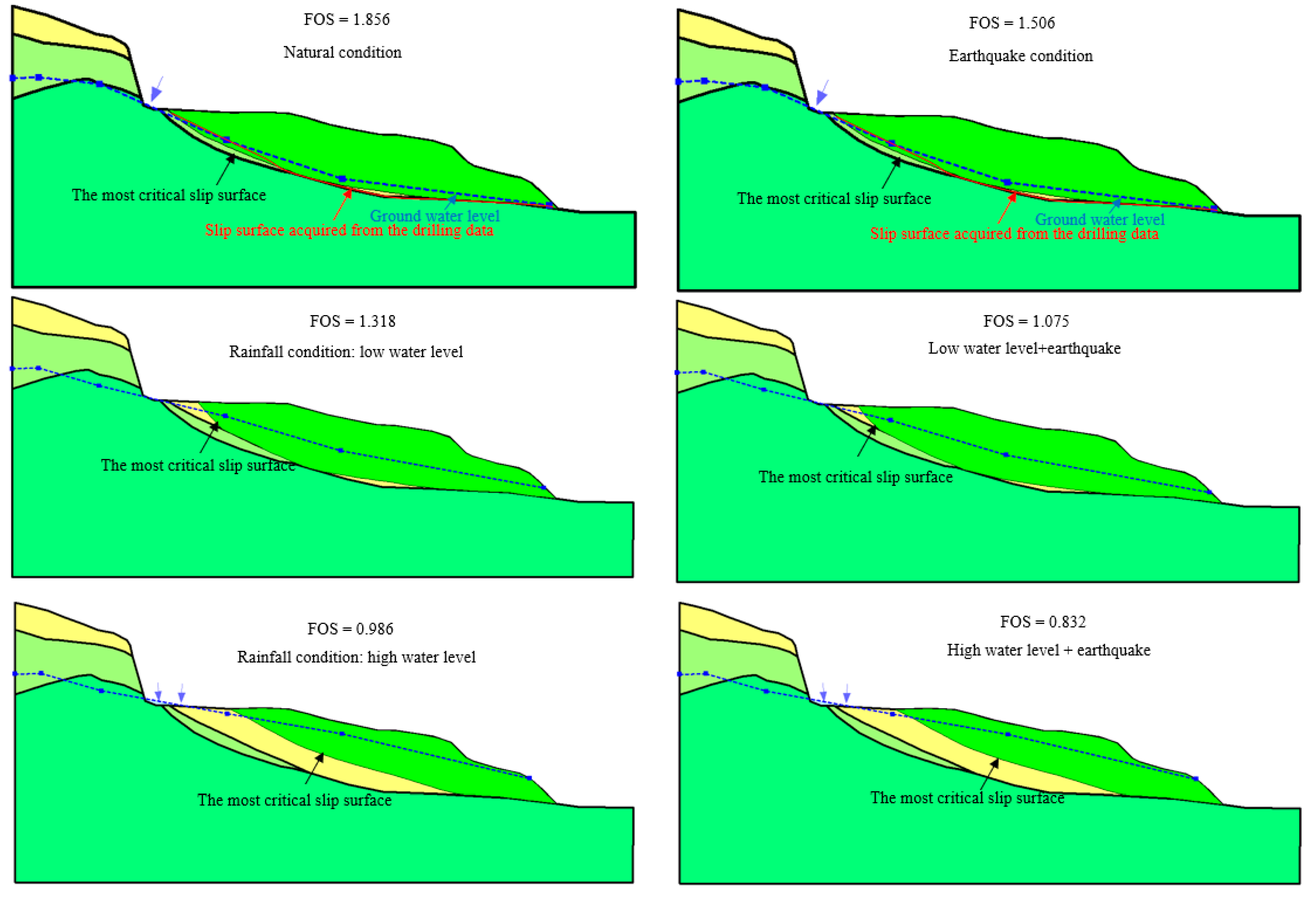
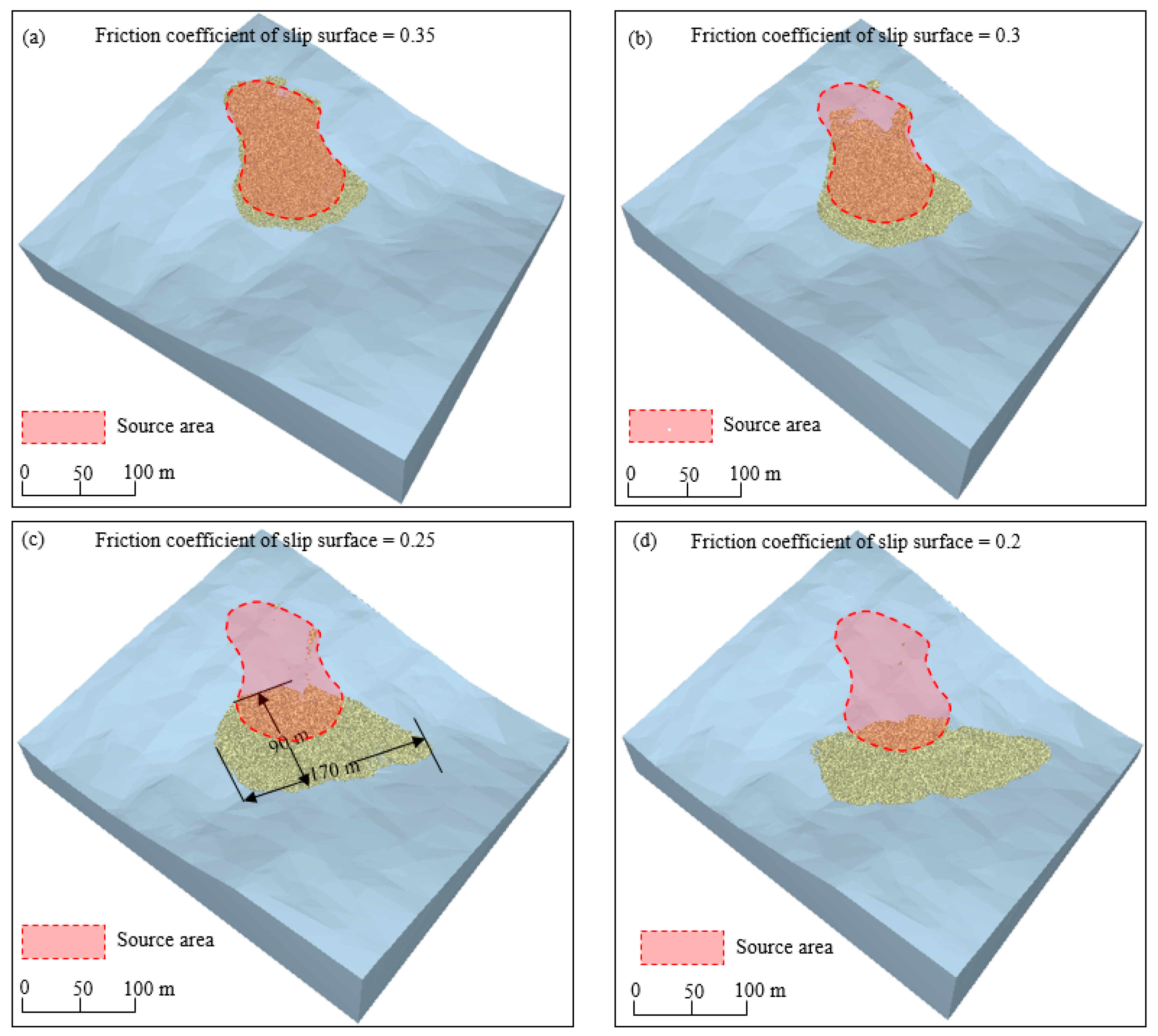
4.1. Stability Analysis
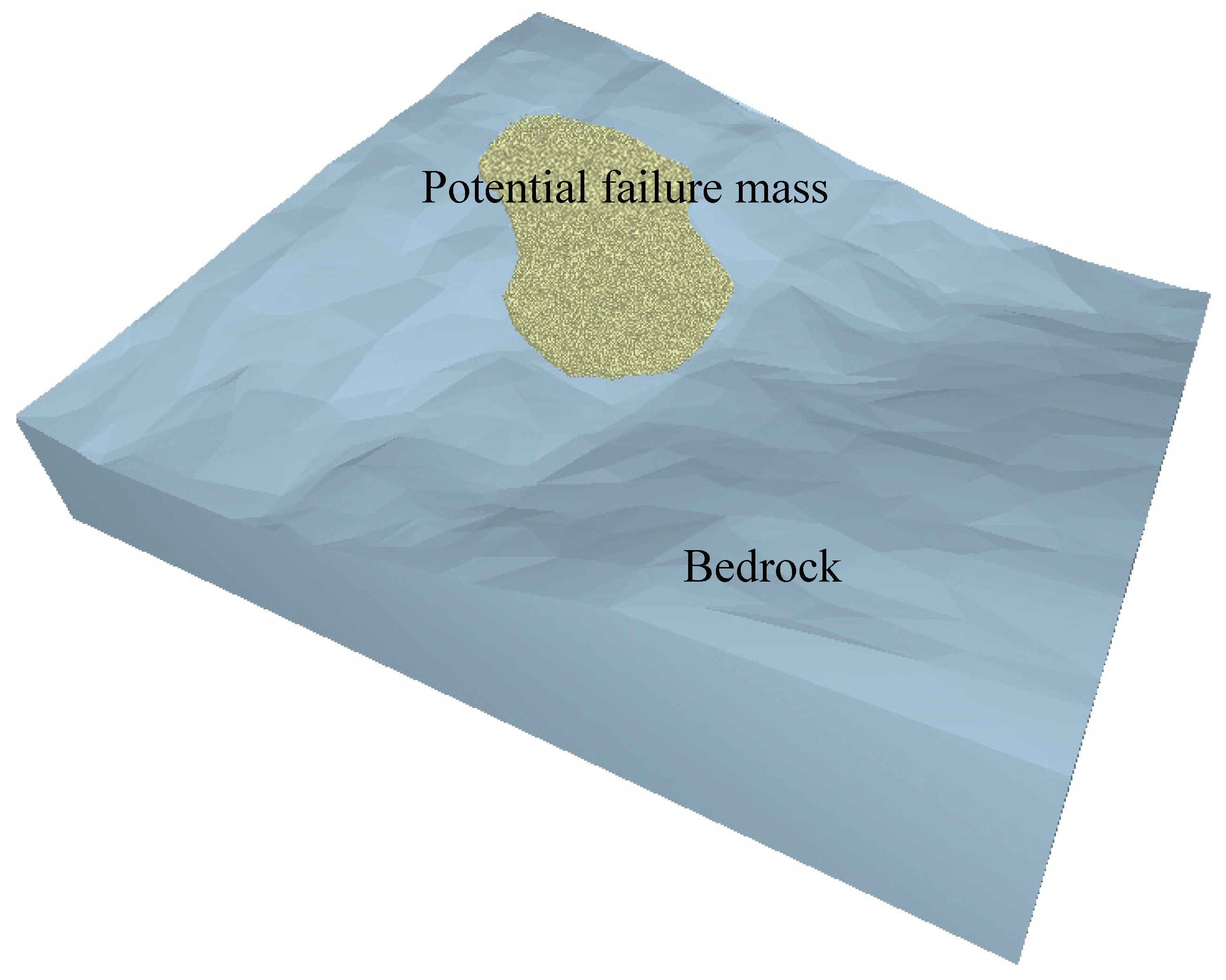
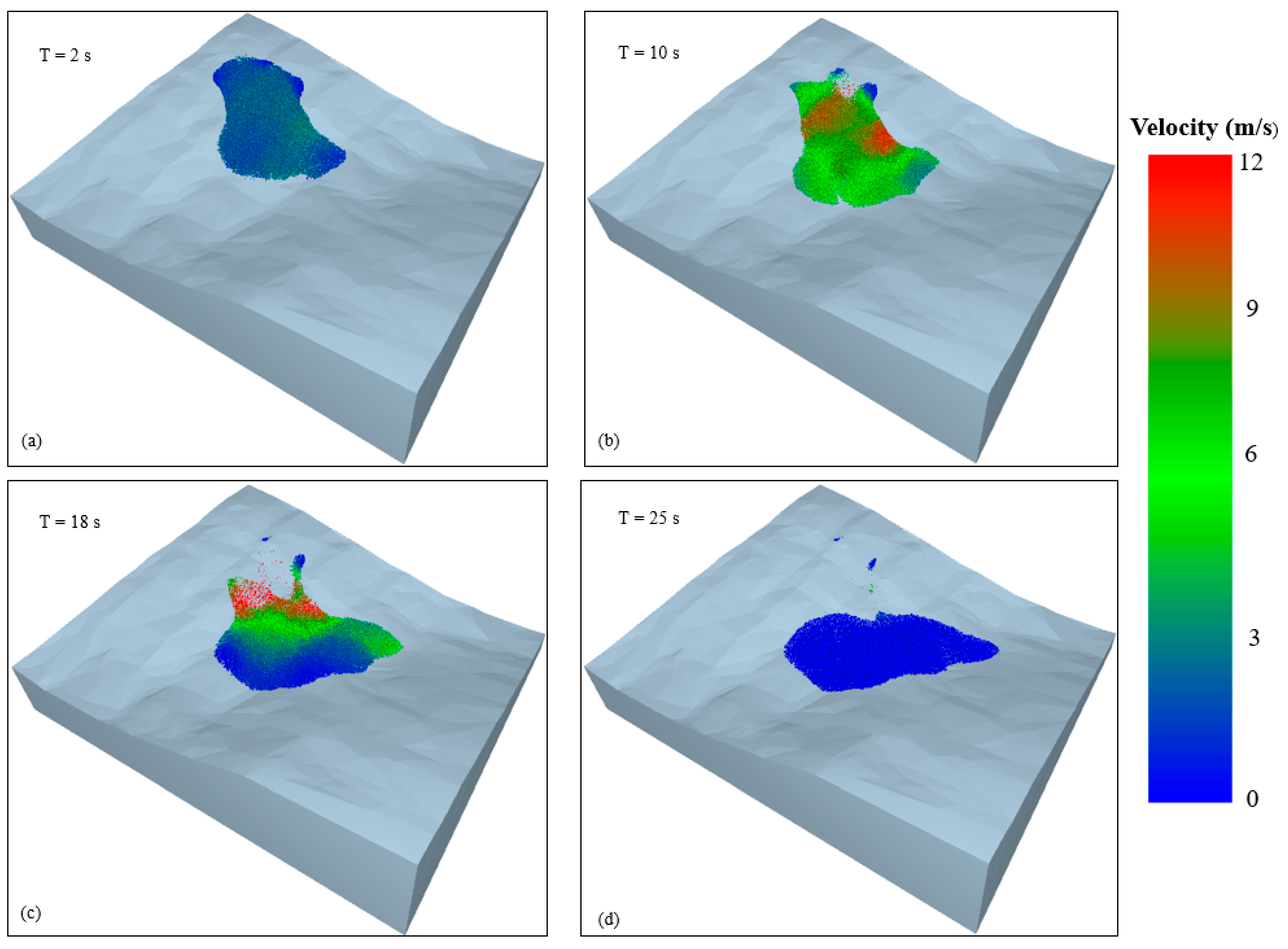
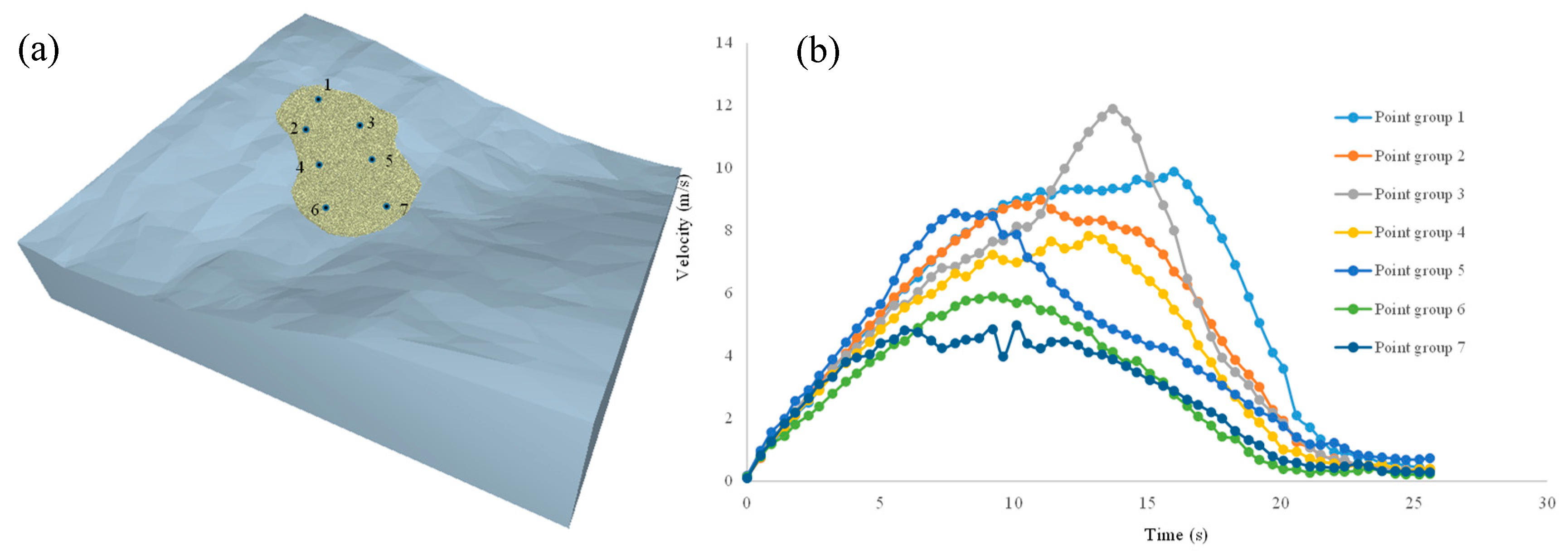
4.2. Post-Failure Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, F.; Cheng, Q.; Highland, L.; Miyajima, M.; Wang, H.; Yan, C. Preliminary investigation of some large landslides triggered by the 2008 Wenchuan earthquake, Sichuan Province, China. Landslides 2009, 6, 47–54. [Google Scholar] [CrossRef]
- Ibañez, J.; Hatzor, Y. Rapid sliding and friction degradation: Lessons from the catastrophic Vajont landslide. Eng. Geol. 2018, 244, 96–106. [Google Scholar] [CrossRef]
- García-Delgado, H.; Machuca, S.; Medina, E. Dynamic and geomorphic characterizations of the Mocoa debris flow (March 31, 2017, Putumayo Department, southern Colombia). Landslides 2019, 16, 597–609. [Google Scholar] [CrossRef]
- Tsuguti, H.; Seino, N.; Kawase, H.; Imada, Y.; Nakaegawa, T.; Takayabu, I. Meteorological overview and mesoscale characteristics of the Heavy Rain Event of July 2018 in Japan. Landslides 2019, 16, 363–371. [Google Scholar] [CrossRef]
- Hirota, K.; Konagai, K.; Sassa, K.; Dang, K.; Yoshinaga, Y.; Wakita, E.K. Landslides triggered by the West Japan Heavy Rain of July 2018, and geological and geomorphological features of soaked mountain slopes. Landslides 2019, 16, 189–194. [Google Scholar] [CrossRef]
- Bishop, A.W. The stability of tips and spoil heaps. Q. J. Eng. Geol. Hydrogeol. 1973, 6, 335–376. [Google Scholar] [CrossRef]
- Seed, R.B.; Mitchell, J.K.; Seed, H.B. Kettleman Hills Waste Landfill Slope Failure. II: Stability Analyses. J. Geotech. Geoenviron. Eng. 1990, 116, 669–690. [Google Scholar] [CrossRef]
- Koerner, R.M.; Soong, T.Y. Stability Assessment of Ten Large Landfill Failures. Geo-Denver 2000, 1–38. [Google Scholar] [CrossRef]
- Omraci, K.; Tisot, J.P.; Piguet, J.P. Stability analysis of lateritic waste deposits. Eng. Geol. 2003, 68, 189–199. [Google Scholar] [CrossRef]
- Qu, G.; Hinchberger, S.D.; Lo, K.Y. Case studies of three-dimensional effects on the behaviour of test embankments. Can. Geotech. J. 2009, 46, 1356–1370. [Google Scholar] [CrossRef]
- Rai, R.; Khandelwal, M.; Jaiswal, A. Application of geogrids in waste dump stability: A numerical modeling approach. Environ. Earth Sci. 2012, 66, 1459–1465. [Google Scholar] [CrossRef]
- Bao, Y.; Han, X.; Chen, J.; Zhang, W.; Zhan, J.; Sun, X.; Chen, M. Numerical assessment of failure potential of a large mine waste dump in Panzhihua City, China. Eng. Geol. 2019, 253, 171–183. [Google Scholar] [CrossRef]
- Bao, Y.; Chen, J.; Sun, X.; Han, X.; Song, S. Stability analysis of large waste dumps considering cracks and earthquake via a three-dimension numerical modeling: A case study of Zhujiabaobao waste dump. Q. J. Eng. Geol. Hydrogeol. 2019. [Google Scholar] [CrossRef]
- Li, Y.; Qian, C.; Fu, Z.; Li, Z. On Two Approaches to Slope Stability Reliability Assessments Using the Random Finite Element Method. Appl. Sci. 2019, 9, 4421. [Google Scholar] [CrossRef]
- Dong, L.; Yang, Y.; Qian, B.; Tan, Y.; Sun, H.; Xu, N. Deformation Analysis of Large-Scale Rock Slopes Considering the Effect of Microseismic Events. Appl. Sci. 2019, 9, 3409. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y.; Zhang, L.; Choi, C.; Ng, C.W.W. Evaluation of Critical Slip Surface in Limit Equilibrium Analysis of Slope Stability by Smoothed Particle Hydrodynamics. Int. J. Geomech. 2019, 19, 5. [Google Scholar] [CrossRef]
- Ray, R.; Deb, K.; Shaw, A. Pseudo-Spring smoothed particle hydrodynamics (SPH) based computational model for slope failure. Eng. Anal. Bound. Elem. 2019, 101, 139–148. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Li, D. Investigation of slope failure mode evolution during large deformation in spatially variable soils by random limit equilibrium and material point methods. Comput. Geotech. 2019, 111, 301–312. [Google Scholar] [CrossRef]
- Conte, E.; Pugliese, L.; Troncone, A. Post-failure stage simulation of a landslide using the material point method. Eng. Geol. 2019, 253, 149–159. [Google Scholar] [CrossRef]
- Han, X.; Chen, J.; Xu, P.; Niu, C.; Zhan, J. Runout analysis of a potential debris flow in the dongwopu gully based on a well-balanced numerical model over complex topography. Bull. Eng. Geol. Environ. 2018, 77, 679–689. [Google Scholar] [CrossRef]
- Han, X.; Chen, J.; Xu, P.; Zhan, J. A well-balanced numerical scheme for debris flow run-out prediction in Xiaojia Gully considering different hydrological designs. Landslides 2017, 14, 2105–2114. [Google Scholar] [CrossRef]
- Bao, Y.; Sun, X.; Chen, J.; Zhang, W.; Han, X.; Zhan, J. Stability assessment and dynamic analysis of a large iron mine waste dump in Panzhihua, Sichuan, China. Environ. Earth Sci. 2019, 78, 48. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, K.; Shi, C.; Hao, M. Discrete element modeling of the mass movement and loose material supplying the gully process of a debris avalanche in the Bayi Gully, Southwest China. J. Asian Earth Sci. 2015, 99, 95–111. [Google Scholar] [CrossRef]
- Lin, C.; Lin, M. Evolution of the large landslide induced by Typhoon Morakot: A case study in the Butangbunasi River, southern Taiwan using the discrete element method. Eng. Geol. 2015, 197, 172–187. [Google Scholar] [CrossRef]
- Lo, C.; Huang, W.; Lin, M. Earthquake-induced deep-seated landslide and landscape evolution process at Hungtsaiping, Nantou County, Taiwan. Environ. Earth Sci. 2016, 75, 645. [Google Scholar] [CrossRef]
- Bao, Y.; Zhai, S.; Chen, J.; Xu, P.; Sun, X.; Zhan, J.; Zhang, W.; Zhou, X. The evolution of the Samaoding paleolandslide river blocking event at the upstream reaches of the Jinsha River, Tibetan Plateau. Geomorphology 2019, 351, 106970. [Google Scholar] [CrossRef]
- Chen, X.; Wang, H. Slope Failure of Noncohesive Media Modelled with the Combined Finite–Discrete Element Method. Appl. Sci. 2019, 9, 579. [Google Scholar] [CrossRef]
- Koyama, T.; Nishiyama, S.; Yang, M.; Ohnishi, Y. Modeling the interaction between fluid flow and particle movement with discontinuous deformation analysis (DDA) method. Int. J. Numer. Anal. Methods Geomech. 2014, 35, 1–20. [Google Scholar] [CrossRef]
- Chen, K.T.; Wu, J.H. Simulating the failure process of the xinmo landslide using discontinuous deformation analysis. Eng. Geol. 2018, 239, 261–281. [Google Scholar] [CrossRef]
- Zhan, J.; Wang, Q.; Zhang, W.; Shangguan, Y.; Song, S.; Chen, J. Soil-engineering properties and failure mechanisms of shallow landslides in soft-rock materials. Catena 2019, 181, 104093. [Google Scholar] [CrossRef]
- Yin, Y.P.; Li, B.; Wang, W.P.; Zhan, L.T.; Xue, Q.; Gao, Y.; Zhang, N.; Chen, H.Q.; Liu, T.K.; Li, A.G. Mechanism of the december catastrophic landslide at the shenzhen landfill and controlling geotechnical risks of urbanization. Engineering 2016, 2, 230–249. [Google Scholar] [CrossRef]
- Aaron, J.; Hungr, O. Dynamic analysis of an extraordinarily mobile rock avalanche in the Northwest Territories, Canada. Can. Geotech. J. 2016, 53, 899–908. [Google Scholar] [CrossRef]
- Aaron, J.; McDougall, S. Rock avalanche mobility: The role of path material. Eng. Geol. 2019, 257, 105126. [Google Scholar] [CrossRef]
- Acharya, K.P.; Bhandary, N.P.; Dahal, R.K.; Yatabe, R. Seepage and slope stability modelling of rainfall-induced slope failures in topographic hollows. Geomat. Nat. Hazards Risk 2016, 7, 721–746. [Google Scholar] [CrossRef]
- Lee, D.; Lai, M.; Wu, J.; Chi, Y.; Ko, W.; Lee, B. Slope management criteria for Alishan Highway based on database of heavy rainfall-induced slope failures. Eng. Geol. 2013, 162, 97–107. [Google Scholar] [CrossRef]
- Qin, Z.; Fu, H.; Chen, X. A study on altered granite meso-damage mechanisms due to water invasion-water loss cycles. Environ. Earth Sci. 2019, 78, 428. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Li, L.; Lin, P.; Xu, Z.; Gao, C. Attribute recognition model for risk assessment of water inrush. Bull. Eng. Geol. Environ. 2019, 78, 1067–1071. [Google Scholar] [CrossRef]
- Lu, C.; Tang, C.; Chan, Y.; Hu, J.; Chi, C. Forecasting landslide hazard by the 3D discrete element method: A case study of the unstable slope in the Lushan hot spring district, central Taiwan. Eng. Geol. 2014, 183, 14–30. [Google Scholar] [CrossRef]
- Matsui, T.; San, K.C. Finite element slope stability analysis by shear strength reduction technique. Soils Found. 1992, 32, 59–70. [Google Scholar] [CrossRef]


| Soil Type | Natural State | Saturated State | ||||
|---|---|---|---|---|---|---|
| Weight (kN/m3) | Cohesion C (kPa) | Friction φ (°) | Weight (kN/m3) | Cohesion C (kPa) | Friction φ (°) | |
| Soil aggregate | 18.2 | 16.5 | 21 | 19.1 | 9.5 | 18 |
| Gravel and silt | 18.5 | 18.5 | 19 | 19.0 | 11.0 | 15 |
| Granite | 27.2 | \ | \ | 29.7 | \ | \ |
| Parameters | Values from the Shear Test | Values from the Landslide Modeling |
|---|---|---|
| Number of particles | 3788 | 30872 |
| Radius (m) | 0.0025–0.01 | 0.5–2 |
| Particle density (kg/m3) | 2500 | 2500 |
| Friction between balls | 0.5 | 0.25 |
| Friction between balls and slip surface | 0.5 | 0.2–0.35 |
| E (MPa) | 20 | 20 |
| ν | 0.4 | 0.4 |
| (Pa) | 2 × 106 | 2 × 106 |
| (Pa) | 1 × 106 | 1 × 106 |
| (N/m3) | 8 × 1010 | 2 × 108 |
| (N/m3) | 4 × 1010 | 1 × 108 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, W.; Song, S.; Yu, C.; Bao, Y.; Sui, J.; Hu, Y. Forecasting Landslides via Three-Dimensional Discrete Element Modeling: Helong Landslide Case Study. Appl. Sci. 2019, 9, 5242. https://doi.org/10.3390/app9235242
Peng W, Song S, Yu C, Bao Y, Sui J, Hu Y. Forecasting Landslides via Three-Dimensional Discrete Element Modeling: Helong Landslide Case Study. Applied Sciences. 2019; 9(23):5242. https://doi.org/10.3390/app9235242
Chicago/Turabian StylePeng, Wei, Shengyuan Song, Chongjia Yu, Yiding Bao, Jiaxuan Sui, and Ying Hu. 2019. "Forecasting Landslides via Three-Dimensional Discrete Element Modeling: Helong Landslide Case Study" Applied Sciences 9, no. 23: 5242. https://doi.org/10.3390/app9235242
APA StylePeng, W., Song, S., Yu, C., Bao, Y., Sui, J., & Hu, Y. (2019). Forecasting Landslides via Three-Dimensional Discrete Element Modeling: Helong Landslide Case Study. Applied Sciences, 9(23), 5242. https://doi.org/10.3390/app9235242






