Abstract
We explore the optical bistability in aperiodic parity–time-symmetric (PT-symmetric) photonic lattices that are composed of Fibonacci sequence dielectrics and graphene at terahertz frequencies. Two Fibonacci sequence dielectrics, viz. aperiodic photonic lattices, are utilized for enhancing band-edge resonances and achieving the electric field localization that can enhance the nonlinearity of graphene. Modulating the gain-loss factor of dielectrics in the PT symmetry lattices further strengthens the nonlinearity effect and, consequently, low threshold bistability is realized. The interval between the upper and lower bistability thresholds enlarges as the momentum relaxation time of graphene changes. Moreover, we show that the bistability threshold can also be flexibly tuned by modulating the graphene chemical potential. The study might be applied in photomemories and optical switches.
1. Introduction
Nonlinear optics induced by strong field has become a study hotspot, such as second or high harmonic [1,2,3,4,5], four-wave mixing [6], optical solitons [7,8,9,10], and optical bistability (OB) [11,12,13,14]. OB is one of the significant nonlinear phenomena, in which the transmission characteristics of an optical system depend on the input light intensity [11]. Of which, an input intensity corresponds to two stable resonant outputs. OB has many great application values in optical transistors [12], optical switches [13], and photomemories [14]. How to design and find appropriate structures or materials to reduce the thresholds of OB and the interval of bistability thresholds are the key problems that are to be considered at present [15,16,17]. With reference to the lattice structure of solid, people put forward the concept of photonic crystals (PCs), which provides a new approach for solving the above two problems. At the bandgap edge of PCs, the optical field localization at the defect in PCs can effectively reduce the bistability threshold [18,19]. Otherwise, graphene, which is viewed as a developing two-dimensional material, has many unique optical, mechanical, and electrical properties [20,21,22,23]. In the terahertz band, graphene not only possesses fast speed optical response and tunable conductivity, but it also owns significant nonlinear effects [24,25], which also affords a golden opportunity for the exploration of OB.
In recent studies, synthetic PCs have been widely utilized in manipulating photons to realize the miniaturization and integration of photonic devices [26,27,28,29,30]. By modulating the refractive indices of materials to form periodic distribution, it can achieve specific optical properties, such as the localization of light field [30,31,32], unidirectional transmission [33,34], directional cloaking [35], and solitons [36,37]. In the past, it mainly focused on the control of the real part for the index of refraction in periodic PCs, while, in recent years, the regulation of the imaginary part and aperiodic PCs have triggered the exploring enthusiasm of researchers [38,39,40]. A system that has loss or gain is non-Hermitian based on quantum mechanics. The eigenvalues of Hamiltonian for the Schrödinger equation generally have complex spectra. However, as the Hamiltonian satisfies parity-time (PT) symmetry, its eigenvalues are real [41]. The concept of non-Hermite can be extended to the regime of optics [42,43], and then the refractive index of PT-symmetric system obeys n(r) = n × (−r) [44,45,46,47,48]. PT-symmetric systems could induce many unique optical properties, including unidirectional invisibility [49], optical transparency [43,50], power oscillations [51], and the lateral shift of reflected light beam [52]. Otherwise, anti-PT-symmetric systems that satisfy n(r) = −n × (−r) can induce coherent perfect absorption laser points and unidirectional invisibility [53,54].
In particular, the aperiodic photonic lattices with PT symmetry support defect cavity with a high Q-factor and the energy of light field can be greatly localized at the defect [8,29]. The nonlinear refractive index of graphene is proportional to the local optical field intensity. The composite system of aperiodic PT-symmetric lattice dielectrics and graphene could therefore be used to realize low-threshold OB.
In this study, we simulate the OB of graphene that is embedded in the PT-symmetric system composed of aperiodic photonic lattice dielectrics at terahertz frequencies. Two aperiodic Fibonacci sequence dielectrics constitute a resonant cavity to form a strong local electric field. Subsequently, we show the transverse distribution of the optical field in the resonant cavity. Next, the influences of the gain-loss factor on the Q-factor of resonant cavity and OB are explored. We furthermore demonstrate that the momentum relaxation time of electrons in graphene can regulate the bistability threshold. Finally, we investigate the modulating of graphene chemical potential in the threshold of OB.
2. Aperiodic PT Symmetry Lattices
We explore the nonlinear optical properties in the aperiodic PT-symmetric lattices that were constructed by the Fibonacci sequence dielectrics. Aperiodic quasicrystals of Fibonacci multilayer dielectrics have many fascinating optical properties, such as mode beating, strong pulse stretching, and band-edge resonances [55]. The band-edge resonances can localize the electric field [56]. Moreover, the localization of field can be further enhanced by increasing the gain and loss in our PT-symmetric structure [19]. The strong resonance of cavity can greatly localized to the electric field. Therefore, the aperiodic PT-symmetric multilayers can be used to enhance the nonlinearity of graphene and achieve low-threshold optical bistability. The primitive aperiodic unit-cell dielectrics A and B are considered. The thicknesses of dielectrics A and B are da,b = λ0/4Re(na,b), where λ0 represents the midgap wavelength of aperiodic lattices with a defect and Re(na,b) are the real parties of refractive indices. Fibonacci sequences are constructed in Figure 1a based on the production rule: Fj = {Fj−1Fj−2} for j ≥ 3, with F1 = {B}, F2 = {BA} [55,57]. Integrating two Fibonacci (F6) sequence dielectrics together with graphene, in which the PT symmetry is satisfied for the whole structure, further incorporates the aperiodic PT symmetry lattices in Figure 1b. The thicknesses of dielectrics C and D are dc = db and dd = da, respectively. The indices of the refraction of dielectrics are regulated with respect to PT symmetry n(z) = n*(−z). We define the parameter q as gain-loss factor. Dielectrics A and B are MgF2 and ZnS, respectively. The gain in Fibonacci sequence dielectrics might be realized by doping Ge/Cr or nonlinear two-wave mixing [43,47,58,59], and the loss of material could result from acoustic modulators [60].

Figure 1.
(a) Fibonacci sequence created by the law B→BA, A→B with F1 = B, F2 = BA and Fj = Fj–1|Fj–2 for j ≥ 3. (b) Schematic of PT-symmetric lattices with Fibonacci sequence dielectrics and graphene, where the indices of refraction are respected for n(z) = n*(−z) about z = 0. For the primitive unit-cell layers A, B, C, and B, the complex refractive indices are na = 1.38 + qi, nb = 2.35 − qi, nc = 2.35 + qi, and nd = 1.38 − qi, respectively.
Graphene, as an ultrathin two-dimensional material, is embedded in the middle of the lattices z = 0; therefore, the addition of graphene has no effect on the PT symmetry. However, here, we view graphene as an equivalent dielectric with a thickness of dg = 0.34 nm [61,62]. The permittivity of the equivalent dielectric for graphene is expressed as εg = 1 + iσgη0/(kdg) [44], where σg is defined as the total surface conductivity of graphene. The parameter σg is composed by two parts, i.e., linear surface conductivity σ(1) and nonlinear surface conductivity σ(3)|Ez|2, where σ(3) is the nonlinear coefficient of surface conductivity. The surface conductivity can be denoted by σg = σ(1) + σ(3)|Ez|2. The Kubo formula could estimate the linear surface conductivity [63]. In this study, the incident wavelength is defined in the range of terahertz waves, and we set the temperature as T = 300 K. The incident wave is a transverse magnetic (TM) polarization wave. We can derive the transmittance T and transmission coefficient t through the transfer matrix method (TMM), as a TM wave is normally incident upon the PT-symmetric lattices [18,64].
3. Transmittance and Optical Bistability
Figure 2a gives the transmission spectrum, as a TM wave normally impinges upon the lattices that are incorporated without graphene. The transmittance is defined as T = tt*, where t is the transmission coefficient. We define the photonic bandgap of multilayers as ωgap = 4ω0arcsin|(nb − na)/(nb + na)|2/π [65], where ω0 = 2πc/λ0 (λ0 = 150 μm) is the center frequency of the bandgap. For three given gain-loss factors, such as q = 0, 0.05, and 0.1, there are seven peaks in each curve in the display range of abscissa. The abscissa represents the normalized frequency. The maxima of transmittance are denoted by P1–P7 (being labeled by blue stats) in sequence. The transmittance at P1 and P7 will be grater than 1, that is, T > 1, since the gain existing in dielectrics for the gain-loss factor q > 0. The corresponding transmittance for P7 is the largest, followed by P1. The gain in dielectrics and the PT symmetry of structure induce the transmittance to exceed 1. The maxima P1–P7 correspond to different defect modes, and the resonance of defect modes at P1 and P7 is stronger than that at other points. The transmittance of peak P7 is as high as T = 15 for q = 0.1, while the maximum transmittance of other points is T = 2. We cut the transmittance near P7 in order to make the transmittance of most other points more clear. Meanwhile, the transmittance near P7 is shown as a whole in the inset. The dotted box is used to mark the area near the P7 shown in the inset. The momentum relaxation time of graphene is τ = 0.8 ps. This order of magnitude ps for τ is often found in references. Further, it is found that the bistable threshold and threshold interval are moderate through simulation with τ = 0.8 ps, which is convenient for us to conduct image display as a typical parameter.
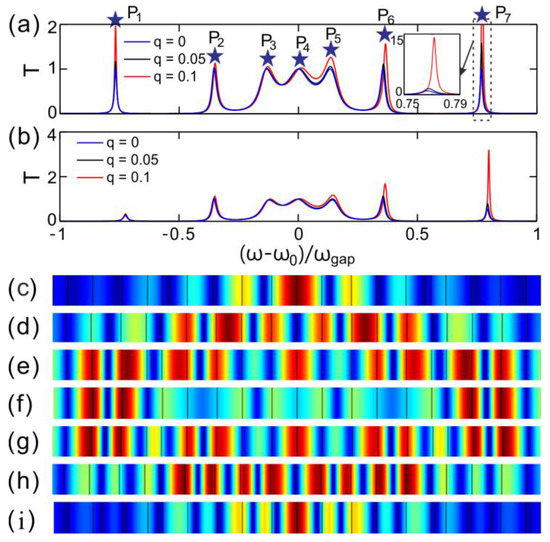
Figure 2.
(a,b) Transmission spectra for PT-symmetric lattices. For (a) the lattices incorporated without graphene and for (b) the lattices with graphene. The chemical potential of graphene is μ = 0.05 eV and the momentum relaxation time is τ = 0.8 ps. (c–i) The electric field intensity (|Ez|2) distributions of the resonant states at the peaks P1–P7 of T [labeled successively by blue stars in (a)].
Figure 2b gives the corresponding transmittance for the lattices with graphene embedded in the middle. When compared with the structure without graphene, P7 is also at the maximum peak, but overall, the transmittance has gone down. Figure 2a,b show the transmittance of light in the lattices without and with graphene, respectively. The transmission curves are similar, because the aperiodic PT-symmetric lattices that cause the resonance have not changed. The addition of graphene, due to the loss of graphene, will only cause the decrease of transmittance, but it will not affect the resonance of the lattices and the distribution of mode field. Similarly, in both structures, we can enhance the transmittance by increasing the gain-loss factor. Light is reflected back and forth in the resonator. The loss in optical field energy results in a decrease of transmittance because of the loss that existed in graphene.
Figure 2c–i orderly give the corresponding transverse distributions of electric field intensity (|Ez|2) for the defect states at peaks p1–p7, such as Figure 2c corresponding to P1, Figure 2d corresponding to P2, etc. The peaks P1–P7 are all resonant states and P1 and P7 correspond to band-edge resonances. The aperiodic quasicrystals of Fibonacci multilayer dielectrics can enhance the band-edge resonances [55], which can be further enhanced by increasing the gain in our PT-symmetric structure. The mode distribution is designed to show the localization of electric field for different resonance states, that is, the electric fields are restricted in different defect layers. It can be seen from the mode distribution diagram that the resonant states of P1 and P7 originates from the central defect layer, as shown in Figure 2c,i, and the electric field distribution of these two states is more concentrated than that of other resonant states. However, when compared with P1, the resonant state of P7 is more localized to the electric field. Therefore, the nonlinear of graphene is the strongest around P7, and the threshold for realizing optical bistability is relatively low. The bistable state will be simulated near P7 in the following study. This can not only enhance the third-order equivalent nonlinear refractive index of graphene, thereby reducing the bistable thresholds, but also obtain a large transmitted light intensity.
We first give the nonlinear surface conductivity coefficient of graphene when it comes to calculating the bistable effect. We will continuously modify the nonlinear transmittance and transmission intensity through inverse TMM, and finally obtain the stable transmittance and output light intensity [9]. In this case, the dielectric constant of graphene is ε1 = 1 + iσ(1)η0/(kdg) is the linear dielectric constant and χg(3) = iσ3η0/(kdg) is the cubic volume susceptibility. The coefficient is governed by σ(3) = −3ie4V2/8πħω3μ [66,67], where V is the Fermi velocity and, here, we set it as V ≈ c/300 [28]. The equivalent dielectric constant for graphene can be denoted by two parts, viz. εg = ε1 + χg(3)|Ez|2. The calculation of nonlinear transmission is based on a nonlinear correction for the linear permittivity of dielectrics. The output electric field and magnetic field are Eo and Ho = Eo/η0, respectively. The total transfer matrix of dielectrics from the l + 1th layer to the last layer is denoted by M′ = [m′11, m′12; m′21, m′22]. The input electric field intensity of the l + 1th layer |Ez,l+1|2 = |Eo|2/T′, where T′ is the transmittance of light that impinges upon the dielectrics from the l + 1th layer.
Figure 3a plots the transmittance surface of light in the parameter space of the incident intensity of light and gain-loss factor q. The slope of transmittance curve can be negative and positive, as q and incident intensity change under considering the third-order nonlinear correction for the equivalent index of graphene. We can see that the curve of transmittance is positive for a small q ≤ 0.0275 and the slope of transmittance curve can be negative for a great q > 0.0275. Meanwhile, around the maximum transmittance in each curve with a fixed value of q, the transmittance abruptly changes with the incident light intensity. Otherwise, it shows there is a corresponding transmission curve on the transmittance surface for each gain-loss factor. The ridge of the curves family is composed by the maximum in each transmission curve. The peak value in the transmission curve is the transmittance of the defect (resonant) state. Figure 3b shows the influence of q on the maximum transmittance. It demonstrates that the maximum increases with q and the incident light intensity that calls for achieving the resonant state can be decreased as q increases.
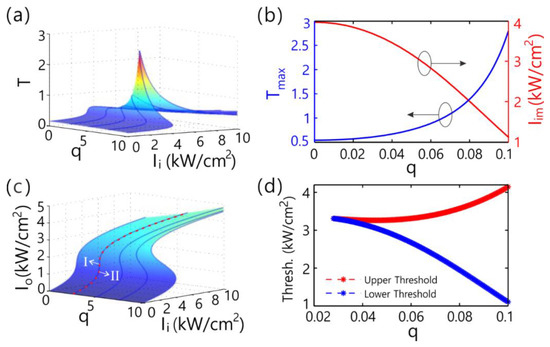
Figure 3.
(a,c) Transmittance and transmitted intensity of light, respectively. The parameter space is composed of the gain-loss factor q and the incident intensity. (b) The peak transmittance and relevant incident intensity versus q. (d) Threshold of bistability for different gain-loss factors. The chemical potential of graphene is μ = 0.05 eV and the momentum relaxation time of graphene is τ = 0.8 ps. The incident wavelength is λ = 119.25 μm.
Figure 3c is the profile of input-output intensity relation that changes with q. The bistability can occur as the gain-loss factor q > 0.0275. We call the lowest q to realize OB for the critical factor. The slope of the transmittance curve can be negative when the local electric field is strong enough and the nonlinear correction of dielectric refractive index reaches the same magnitude of the linear refractive index. At this time, the input-output curve shows bistable profiles. The white dotted line divides the focusing area in the parameter space is divided into two parts. Part I represents the non-bistable region and part II represents the bistable region. Figure 3d demonstrates the lower threshold and upper threshold for OB as the bistability occurs. It shows that OB can be obtained as q > 0.0275. It is worth noting that, as the gain-loss factor increases, the interval between the upper and lower thresholds increases. At the same time, the upper threshold bistability increases with the increase of q, while the lower threshold always decreases with the increase of q. One can see that, when compared with the case for q = 0.028, the lower threshold of bistability could be lowered by 30% for q = 0.1 with a fixed incident wavelength. Modulating the gain-loss factor q = 0.1, the lowest incident light intensity in our structure is far below the threshold in projects by means of Fano-like resonance and Fano resonance [68,69]. The lower threshold could be further decreased by enlarging q.
Figure 4a provides the peak value of transmittance at P7 in the transmission spectra for different gain-loss factor q. The curve observably demonstrates that the maximum transmittance increases with the increase of q. The blue circles denote the transmittance of light for the lattices incorporated with graphene, and the red circles presents the transmittance, as the lattices are without graphene. For the same gain-loss q, the transmittance of light that is injected in the structure with graphene is lower than that without graphene. The conductivity of graphene, the embedding graphene can lead to an increase in the reflectivity as a light impinges on the lattices, and graphene is a lossy material to light. In contrast to the absence of graphene, these two factors cause the decrease in transmittance, as the lattices contain graphene.
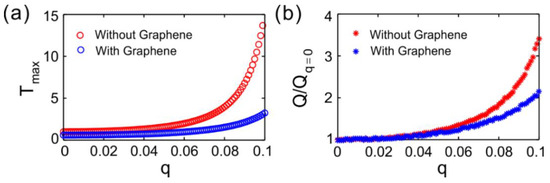
Figure 4.
(a) Transmittance at P7 in the transmission spectra varying with the gain-loss factor q. (b) Q-factor of PT-symmetric photonic lattices.
Figure 4b gives the Q-factor of the microcavity in the PT-symmetric photonic lattices. We define the Q-factor as the center frequency over the FWHM of the transmission peak [39]. It shows that, as the gain-loss factor increases, the Q-factor also increases. When compared with the structure without graphene, the Q-factor is larger for the lattices that were incorporated with graphene. For q = 0, the values of Q-factor for the lattices without or with graphene are Qq=0 = 519.2 and 361.9, respectively. The Q-factor increases by 35% by modulating q = 0.1 in contrast to passive systems (q = 0), as the graphene is embedded in the structure. For a resonant microcavity, the higher its quality factor, the stronger the confinement of the resonator to the light field. The Q-factors of the lattices without or with graphene are Qq=1 = 1769.1 and 783, respectively. Therefore, the restraint of light field at the defect can be tremendously enhanced by modulating the gain-loss factor. The mainly aim in bistability is to enhance the nonlinearity and sequentially to lower the threshold of bistability. Subsequently, we place a single-layer graphene at the middle of the lattices. Low-threshold OB could be achieved by increasing q.
4. Modulation of Optical Bistability
The graphene conductivity is a function of the momentum relaxation time τ, so τ affects not only the transmittance, but also the bistable properties. Figure 5a provides the transmittance of light for different momentum relaxation time. We can see that there is a peak in each spectrum. As the momentum relaxation time is longer, the maximum of transmittance is larger. That is because the loss of light in graphene is inversely proportional to the momentum relaxation time. As the input light intensity is powerful enough, the nonlinear effect on the refractive index needs to be considered. Figure 5b gives the dependence of transmittance on the incident light intensity. For some larger τ, the slope of the transmittance curve can be negative with the increase of input intensity, which indicates that the bistable phenomena will be induced. At the same time, we can see that the maximum value of nonlinear transmittance is larger than that of linear transmittance, this could be attributed to the loss of graphene is reduced when the third-order nonlinear correction for the index of graphene is counted.
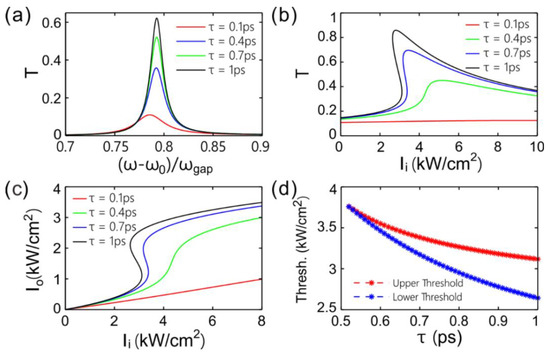
Figure 5.
(a) Transmittance versus angular frequency for different momentum relaxation time τ around P7 in the transmission spectrum. (b,c) Transmittance and transmitted intensity varying with the incident intensity of light for different τ, respectively. (d) Upper and lower bistability threshold versus τ.
Figure 5c shows the relationship between the output strength and the input strength, as the third-order nonlinear correction for the equivalent index of graphene is included, for different momentum relaxation times. For a smaller τ, the input-output relationship is linear within the given interval of input intensity. For a larger τ, the input-output curve is bistable. The most striking feature of bistability is that, as the input intensity of light enlarges, the slope of the curve changes from positive to negative and then to positive. Figure 5d demonstrates that the lower threshold and upper threshold change as the momentum relaxation time varies. It shows that the bistability occurs as the momentum relaxation time τ > 0.52 ps. Afterwards, the lower threshold and upper threshold decrease with the increase of τ, but the width between the lower and upper thresholds increases. This shows that it can improve the three-order nonlinearity of graphene and switching discrimination through increasing the time constant.
The input-output relationship of light intensity is dependent on the chemical potential in graphene. Figure 6a gives three input-output profiles of intensity for the chemical potential μ = 0.03, 0.06, and 0.09 eV. The chemical potential of graphene can be modulated by chemical doping and gate voltages. One can see that the curve is non-bistable, as μ = 0.03, while the curves are bistable as μ = 0.06 and 0.09 eV. The bistable thresholds and the interval of thresholds are larger in bistabilities, as the chemical potential is higher. For different given chemical potentials, Figure 6b shows the lower and upper thresholds of OB. One can see that, as the chemical potential μ > 0.043 eV, the bistable profile could be exported. The thresholds and the interval of thresholds increases with the chemical potential. These phenomenon can be attributed to the fact that the nonlinear surface conductivity coefficient of graphene σ(3) is inversely proportional to the chemical potential. The switch threshold can be adjusted flexibly though the chemical potential in graphene, as the optical bistability is applied to all-optical switches.
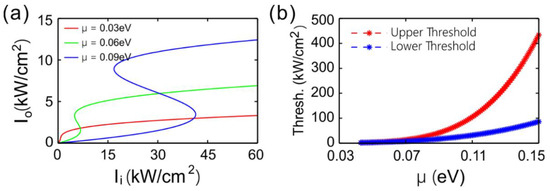
Figure 6.
(a) Transmitted intensity varying with the incident intensity for three different chemical potentials. (b) Lower and upper bistability threshold versus the chemical potential.
5. Conclusions
To summarize, we have theoretically investigated bistability in aperiodic PT symmetry lattices incorporated with Fibonacci sequence dielectrics and graphene at terahertz frequencies. Two aperiodic Fibonacci sequence dielectrics are utilized to enhance the band-edge resonance in which the light field is restricted at the defect layer. The localization of light field and the Q-factor for the resonant cavity can be further enhanced through improving the gain-loss factor q of the PT symmetry system. The electric field localization can greatly strengthen the third-order nonlinearity of graphene and low-threshold OB is achieved. The threshold of OB could been decreased as low as the magnitude kW/cm2. Meanwhile, the interval between the upper and lower thresholds of OB expands. The bistability thresholds and the interval of thresholds decrease with the increase of the momentum relaxation time of graphene. Furthermore, the chemical potential in graphene can also flexibly tune bistability. This research provides an option for development in photomemories and optical switches.
Author Contributions
Formal analysis, B.X., W.X. and S.K.; funding acquisition, D.Z. (Dong Zhao), H.G., W.X. and D.Z. (Dong Zhong); investigation, D.Z. (Dong Zhao), B.X., H.G. and W.X.; software, D.Z. (Dong Zhao) and S.K.; supervision, D.Z. (Dong Zhong); writing—original draft, D.Z. (Dong Zhao); writing—review & editing, D.Z. (Dong Zhao), B.X., H.G., W.X., D.Z. (Dong Zhong) and S.K.
Funding
This research was funded by National Natural Science Foundation of China (51479155); the Colleges and Universities of National Innovation and Entrepreneurship the Training Plan (S201910927024); the Scientific Research Project of Hubei University of Science and Technology (2018-20XB010); the Science and Technology Plan Research Project of Hubei Education Department (B2019162).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, B.; He, L.; He, Y.; Zhang, Y.; Shao, R.; Lan, P.; Lu, P. All-optical measurement of high-order fractional molecular echoes by high-order harmonic generation. Opt. Express 2019, 27, 30172–30181. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Liu, W.; Song, Y.; Zhang, C.; Long, H.; Wang, K.; Wang, B.; Lu, P. Enhancement of the second harmonic generation from WS2 monolayers by cooperating with dielectric microspheres. Adv. Opt. Mater. 2019, 7, 1801270. [Google Scholar] [CrossRef]
- Wei, W.J.; Jiang, X.; Dong, L.Y.; Liu, W.W.; Han, X.B.; Qin, Y.; Li, K.; Lin, Z.S.; Bu, X.H.; Lu, P.X. Regulating second-harmonic generation by van der Waals interactions in 2D lead halide perovskite nanosheets. J. Am. Chem. Soc. 2019, 141, 9134–9139. [Google Scholar] [CrossRef] [PubMed]
- Tong, A.; Li, Q.; Ma, X.; Zhou, Y.; Lu, P. Internal collision induced strong-field nonsequential double ionization in molecules. Opt. Express 2019, 27, 6415–6425. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Li, M.; Xie, W.; Liu, K.; Feng, Y.; Du, B.; Zhou, Y.; Lu, P. Exit momentum and instantaneous ionization rate of nonadiabatic tunneling ionization in elliptically polarized laser fields. Phys. Rev. A 2019, 99, 053422. [Google Scholar] [CrossRef]
- Li, W.; Qin, C.; Han, T.; Chen, H.; Wang, B.; Lu, P. Bloch oscillations in photonic spectral lattices through phase-mismatched four-wave mixing. Opt. Lett. 2019, 44, 5430–5433. [Google Scholar] [CrossRef]
- Xu, S.L.; Zhao, G.P.; Belić, M.R.; He, J.R.; Xue, L. Light bullets in coupled nonlinear Schrödinger equations with variable coefficients and a trapping potential. Opt. Express 2017, 25, 9094–9104. [Google Scholar] [CrossRef]
- Chen, S.F.; Guo, Y.W.; Guo, Q.; Zhao, D.; Belić, M.R.; Zhao, Y.; Xu, S.L. Vortex soliton in a cold atomic gas via electromagnetically induced transparency. arXiv 2019, arXiv:1903.03433. [Google Scholar]
- Li, H.; Xu, S.L.; Belić, M.R.; Cheng, J.X. Three-dimensional solitons in Bose-Einstein condensates with spin-orbit coupling and Bessel optical lattices. Phys. Rev. A 2018, 98, 033827. [Google Scholar] [CrossRef]
- Xu, S.L.; Cheng, J.X.; Belić, M.R.; Hu, Z.L.; Zhao, Y. Dynamics of nonlinear waves in two-dimensional cubic-quintic nonlinear Schrödinger equation with spatially modulated nonlinearities and potentials. Opt. Express 2016, 24, 10066–10077. [Google Scholar] [CrossRef]
- Lugiato, L.A. II Theory of Optical Bistability; Progress in Optics; Elsevier: Amsterdam, The Netherlands, 1984; Volume 21, pp. 69–216. [Google Scholar]
- Ballarini, D.; De Giorgi, M.; Cancellieri, E.; Houdré, R.; Giacobino, R.; Cingolani, R.; Bramati, A.; Gigli, G.; Sanvitto, D. All-optical polariton transistor. Nat. Commun. 2013, 4, 1778. [Google Scholar] [CrossRef] [PubMed]
- Yanik, M.F.; Fan, S.; Soljačić, M. High-contrast all-optical bistable switching in photonic crystal microcavities. Appl. Phys. Lett. 2003, 83, 2739–2741. [Google Scholar] [CrossRef]
- Nihei, H.; Okamoto, A. Photonic crystal systems for high-speed optical memory device on an atomic scale. Proc. SPIE 2001, 4416, 470–473. [Google Scholar]
- Zang, Z.G.; Zhang, Y.J. Low-switching power (<45 mW) optical bistability based on optical nonlinearity of ytterbium-doped fiber with a fiber Bragg grating pair. J. Mod. Opt. 2012, 59, 161–165. [Google Scholar]
- Dai, X.; Jiang, L.; Xiang, Y. Low threshold optical bistability at terahertz frequencies with graphene surface plasmons. Sci. Rep. 2015, 5, 12271. [Google Scholar] [CrossRef]
- Huang, Y.; Miroshnichenko, A.E.; Gao, L. Low-threshold optical bistability of graphene-wrapped dielectric composite. Sci. Rep. 2016, 6, 23354. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, Z.Q.; Long, H.; Wang, K.; Wang, B.; Lu, P.X. Optical bistability in defective photonic multilayers doped by graphene. Opt. Quantum Electron. 2017, 49, 163. [Google Scholar] [CrossRef]
- Zhao, D.; Ke, S.; Hu, Y.; Wang, B.; Lu, P. Optical bistability in parity-time-symmetric dielectric multilayers incorporated with graphene. J. Opt. Soc. Am. B 2019, 36, 1731–1737. [Google Scholar] [CrossRef]
- Novoselov, S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mat. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Grigorenko, A.N.; Polini, M.; Novoselov, K.S. Graphene plasmonics. Nat. Photon. 2012, 6, 749–758. [Google Scholar] [CrossRef]
- Avouris, P.; Freitag, M. Graphene photonics, plasmonics, and optoelectronics. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 72–83. [Google Scholar] [CrossRef]
- Mikhailov, S.A. Theory of the giant plasmon enhanced second harmonic generation in graphene and semiconductor two-dimensional electron systems. Phys. Rev. B 2011, 84, 2109–2119. [Google Scholar] [CrossRef]
- Dean, J.J.; Driel, H.M.V. Graphene and few-layer graphite probed by second-harmonic generation: Theory and experiment. Phys. Rev. B 2010, 82, 3893–3898. [Google Scholar] [CrossRef]
- Xu, S.L.; Petrović, N.; Belić, M.R. Exact solutions of the (2 + 1)-dimensional quintic nonlinear Schrödinger equation with variable coefficients. Nonlinear Dyn. 2015, 80, 583–589. [Google Scholar] [CrossRef]
- Meng, P.; Zhao, D.; Zhong, D.; Liu, W. Topological plasmonic modes in graphene-coated nanowire arrays. Opt. Quantum Electron. 2019, 51, 156. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, P.; Zhao, D.; Guo, H.; Huang, M.; Ke, S. Plasmonic Jackiw-Rebbi Modes in Graphene Waveguide Arrays. Appl. Sci. 2019, 9, 4152. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Z.; Qu, X.; Wang, S.; Peng, J. Pattern transfer of hexagonal packed structure via ultrathin metal nanomesh masks for formation of Si nanopore arrays. J. Alloys Compd. 2017, 695, 458–461. [Google Scholar] [CrossRef]
- Chen, H.; Qin, C.; Wang, B.; Lu, P. Discrete refraction and reflection in temporal lattice heterostructures. Opt. Lett. 2019, 44, 363–366. [Google Scholar] [CrossRef]
- Soukoulis, C.M. Photonic Crystals and Light Localization in the 21st Century; Springer Science and Business Media: Dordrecht, The Netherlands, 2012; Volume 563. [Google Scholar]
- Mingaleev, S.F.; Kivshar, Y.S. Nonlinear transmission and light localization in photonic-crystal waveguides. J. Opt. Soc. Am. B 2002, 19, 2241–2249. [Google Scholar] [CrossRef]
- Zhao, D.; Zhong, D.; Hu, Y.; Ke, S.; Liu, W. Imaginary modulation inducing giant spatial Goos-Hänchen shifts in one-dimensional defective photonic lattices. Opt. Quantum Electron. 2019, 51, 113. [Google Scholar] [CrossRef]
- Cakmak, A.O.; Colak, E.; Serebryannikov, A.E.; Ozbay, E. Unidirectional transmission in photonic-crystal gratings at beam-type illumination. Opt. Express 2010, 18, 22283–22298. [Google Scholar] [CrossRef] [PubMed]
- Khanikaev, A.B.; Steel, M.J. Low-symmetry magnetic photonic crystals for nonreciprocal and unidirectional devices. Opt. Express 2009, 17, 5265–5272. [Google Scholar] [CrossRef] [PubMed]
- Vasić, B.; Gajić, R. Self-focusing media using graded photonic crystals: Focusing, Fourier transforming and imaging, directive emission, and directional cloaking. J. Appl. Phys. 2011, 110, 053103. [Google Scholar] [CrossRef]
- Xu, S.L.; Xue, L.; Belić, M.R.; He, J.R. Spatiotemporal soliton clusters in strongly nonlocal media with variable potential coefficients. Nonlinear Dyn. 2017, 87, 827–834. [Google Scholar] [CrossRef]
- Xu, S.L.; Petrovi, N.; Belić, M.R.; Deng, W. Exact solutions for the quintic nonlinear Schrödinger equation with time and space. Nonlinear Dyn. 2017, 84, 251–259. [Google Scholar] [CrossRef]
- Ke, S.; Zhao, D.; Liu, Q.; Wu, S.; Wang, B.; Lu, P. Optical imaginary directional couplers. J. Lightwave Technol. 2018, 36, 2510–2515. [Google Scholar] [CrossRef]
- Zhu, X.F. Defect states and exceptional point splitting in the band gaps of one-dimensional parity-time lattices. Opt. Express 2015, 23, 22274–22284. [Google Scholar] [CrossRef]
- Kottos, T. Broken symmetry makes light work. Nat. Phys. 2010, 6, 166–167. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of parity–time symmetry in optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef]
- Longhi, S. Parity-time symmetry meets photonics: A new twist in non-Hermitian optics. EPL 2018, 120, 64001. [Google Scholar] [CrossRef]
- Ruschhaupt, A.; Delgado, F.; Muga, J.G. Physical realization of PT-symmetric potential scattering in a planar slab waveguide. J. Phys. A 2005, 38, L171. [Google Scholar] [CrossRef]
- Ke, S.; Zhao, D.; Liu, J.; Liu, Q.; Liao, Q.; Wang, B.; Lu, P. Topological bound modes in anti-PT-symmetric optical waveguide arrays. Opt. Express 2019, 27, 13858–13870. [Google Scholar] [CrossRef]
- Feng, L.; Xu, Y.L.; Fegadolli, W.S.; Lu, M.H.; Oliveira, J. E .B.; Almeida, V. .R.; Chen, Y.F.; Scherer, A. Experimental demonstration of a unidirectional reflectionless parity-time metamaterial at optical frequencies. Nat. Mater. 2013, 12, 108–113. [Google Scholar] [CrossRef]
- Wen, Z.; Yan, Z. Dynamical behaviors of optical solitons in parity-time (PT) symmetric sextic anharmonic double-well potentials. Phys. Lett. A 2015, 379, 2025–2029. [Google Scholar] [CrossRef]
- Lin, Z.; Ramezani, H.; Eichelkraut, T.; Kottos, T.; Cao, H.; Christodoulides, D.N. Unidirectional invisibility induced by PT-symmetric periodic structures. Phys. Rev. Lett. 2011, 106, 213901. [Google Scholar] [CrossRef]
- Li, W.; Jiang, Y.; Li, C.; Song, H. Parity-time-symmetry enhanced optomechanically-induced-transparency. Sci. Rep. 2016, 6, 31095. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.L.; Fegadolli, W.S.; Gan, L.; Lu, M.H.; Liu, X.P.; Li, Z.Y.; Scherer, A.; Chen, Y.F. Experimental realization of Bloch oscillations in a parity-time synthetic silicon photonic lattice. Nat. Commun. 2016, 7, 11319. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, W.W.; Ke, S.L.; Liu, Q.J. Large lateral shift in complex dielectric multilayers with nearly parity–time symmetry. Opt. Quantum Electron. 2018, 50, 323. [Google Scholar] [CrossRef]
- Wang, H.; Kong, W.; Zhang, P.; Li, Z.; Zhong, D. Coherent perfect absorption laser points in one-dimensional anti-parity–time-symmetric photonic Crystals. Appl. Sci. 2019, 9, 2738. [Google Scholar] [CrossRef]
- Cao, H.; Zhao, D.; Fang, M.; Guo, H.; Hu, Y.; Liu, F.; Zhong, D.; Xiong, H. Unidirectional invisibility induced by complex anti-parity–time symmetric periodic lattices. Appl. Sci. 2019, 9, 3808. [Google Scholar] [CrossRef]
- Dal Negro, L.; Oton, C.J.; Gaburro, Z.; Pavesi, L.; Johnson, P.; Lagendijk, A.; Righini, R.; Colocci, M.; Wiersma, D.S. Light transport through the band-edge states of Fibonacci quasicrystals. Phys. Rev. Lett. 2003, 90, 055501. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Li, M.; Luo, S.; Liu, K.; Du, B.; Zhou, Y.; Lu, P. Semiclassical analysis of photoelectron interference in a synthesized two-color laser pulse. arXiv 2019, arXiv:1911.04035. [Google Scholar]
- Zhu, X.F.; Xu, T.; Liu, S.C.; Cheng, J.C. Study of acoustic wave behavior in silicon-based one-dimensional phononic-crystal plates using harmony response analysis. J. Appl. Phys. 2009, 106, 104901. [Google Scholar]
- Ke, S.; Liu, J.; Liu, Q.; Zhao, D.; Liu, W. Strong absorption near exceptional points in plasmonic wave guide arrays. Opt. Quantum Electron. 2018, 50, 318. [Google Scholar] [CrossRef]
- Ke, S.; Zhao, D.; Liu, Q.; Liu, W. Adiabatic transfer of surface plasmons in non-Hermitian graphene waveguides. Opt. Quantum Electron. 2018, 50, 393. [Google Scholar] [CrossRef]
- Regensburger, A.; Bersch, C.; Miri, M.A.; Onishchukov, G.; Christodoulides, D.N.; Peschel, U. Parity-time synthetic photonic lattices. Nature 2012, 488, 167–171. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, B.; Long, H.; Wang, K.; Lu, P. Surface plasmonic lattice solitons in semi-infinite graphene sheet arrays. J. Lightwave Technol. 2017, 35, 2960–2965. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, F.; Meng, P.; Wen, J.; Xu, S.; Li, Z.; Zhong, D. Reflection enhancement and giant lateral shift in defective photonic crystals with graphene. Appl. Sci. 2019, 9, 2141. [Google Scholar] [CrossRef]
- Chen, P.Y.; Alù, A. Atomically thin surface cloak using graphene monolayers. ACS Nano 2011, 5, 5855–5863. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Ke, S.; Liu, Q.; Wang, B.; Lu, P. Giant Goos-Hänchen shifts in non-Hermitian dielectric multilayers incorporated with graphene. Opt. Express 2018, 26, 2817–2828. [Google Scholar] [CrossRef] [PubMed]
- Yariv, A.; Yeh, P. Photonics: Optical Electronics in Modern Communications, 6th ed.; Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Smirnova, D.A.; Shadrivov, I.V.; Smirnov, A.I.; Kivshar, Y.S. Dissipative plasmon-solitons in multilayer graphene. Laser Photonics Rev. 2014, 8, 291–296. [Google Scholar] [CrossRef]
- Mikhailow, S.A. Non-linear electromagnetic response of graphene. EPL 2007, 79, 27002. [Google Scholar] [CrossRef]
- Argyropoulos, C.; Chen, P.Y.; Monticone, F.; D’Aguanno, G.; Alù, A. Nonlinear plasmonic cloaks to realize giant all-optical scattering switching. Phys. Rev. Lett. 2012, 108, 263905. [Google Scholar] [CrossRef]
- Mattiucci, N.; D’Aguanno, G.; Bloemer, M.J. Long range plasmon assisted all-optical switching at telecommunication wavelengths. Opt. Lett. 2012, 37, 121–123. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).