Virtual Synchronous Generator Based on Hybrid Energy Storage System for PV Power Fluctuation Mitigation
Abstract
:1. Introduction
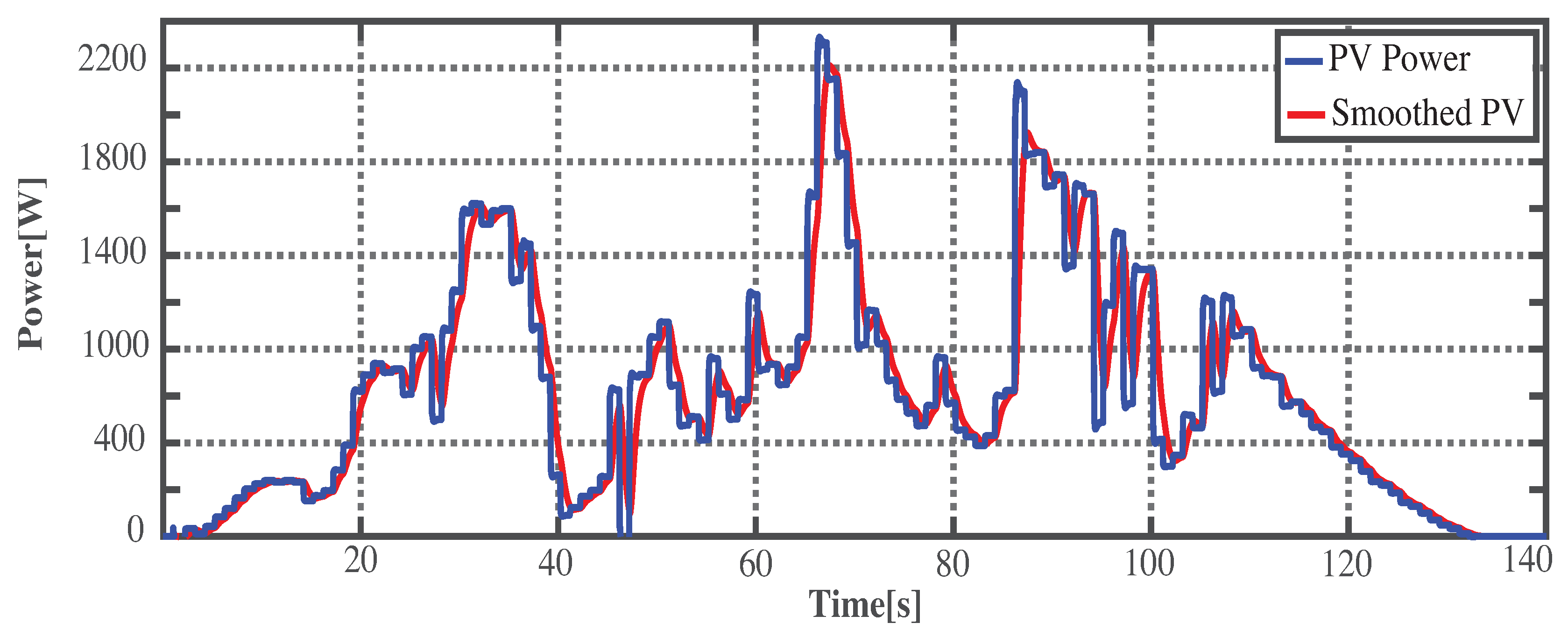
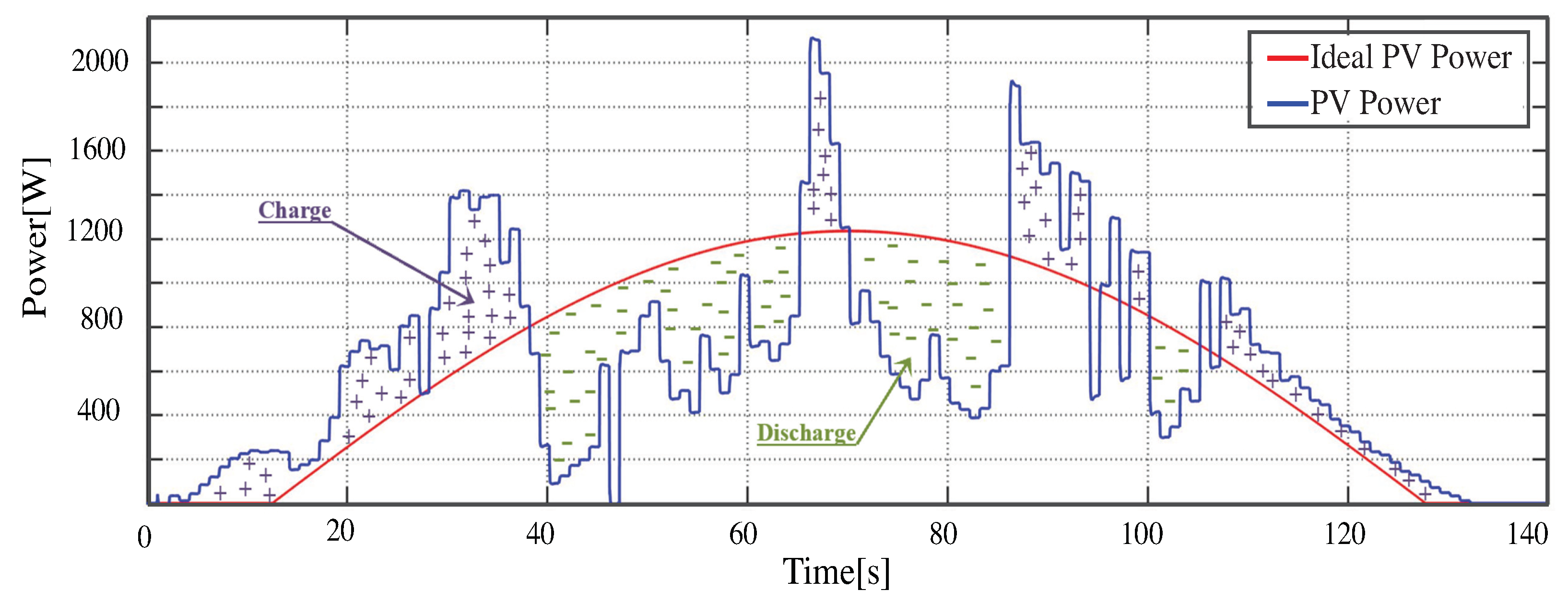
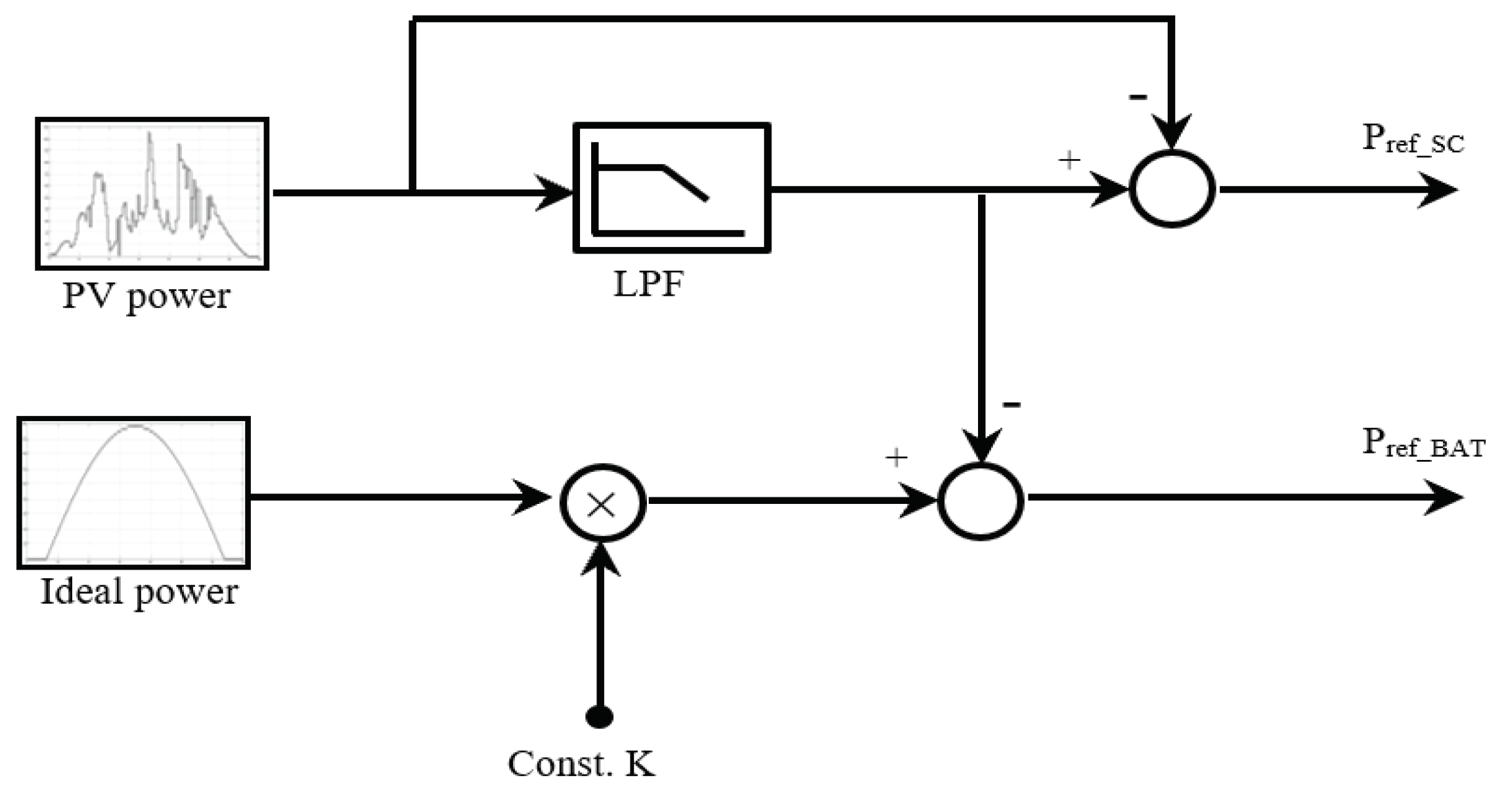
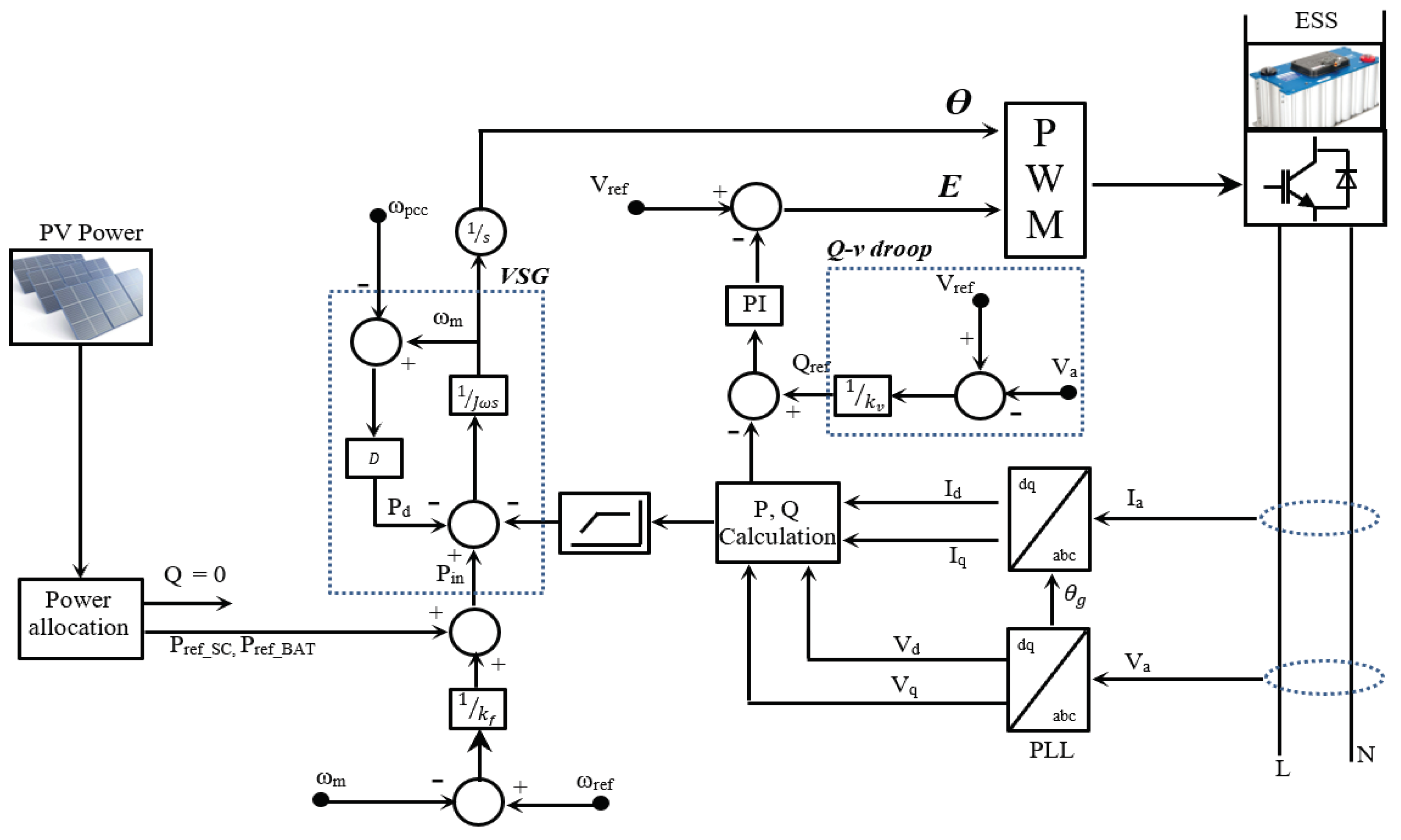
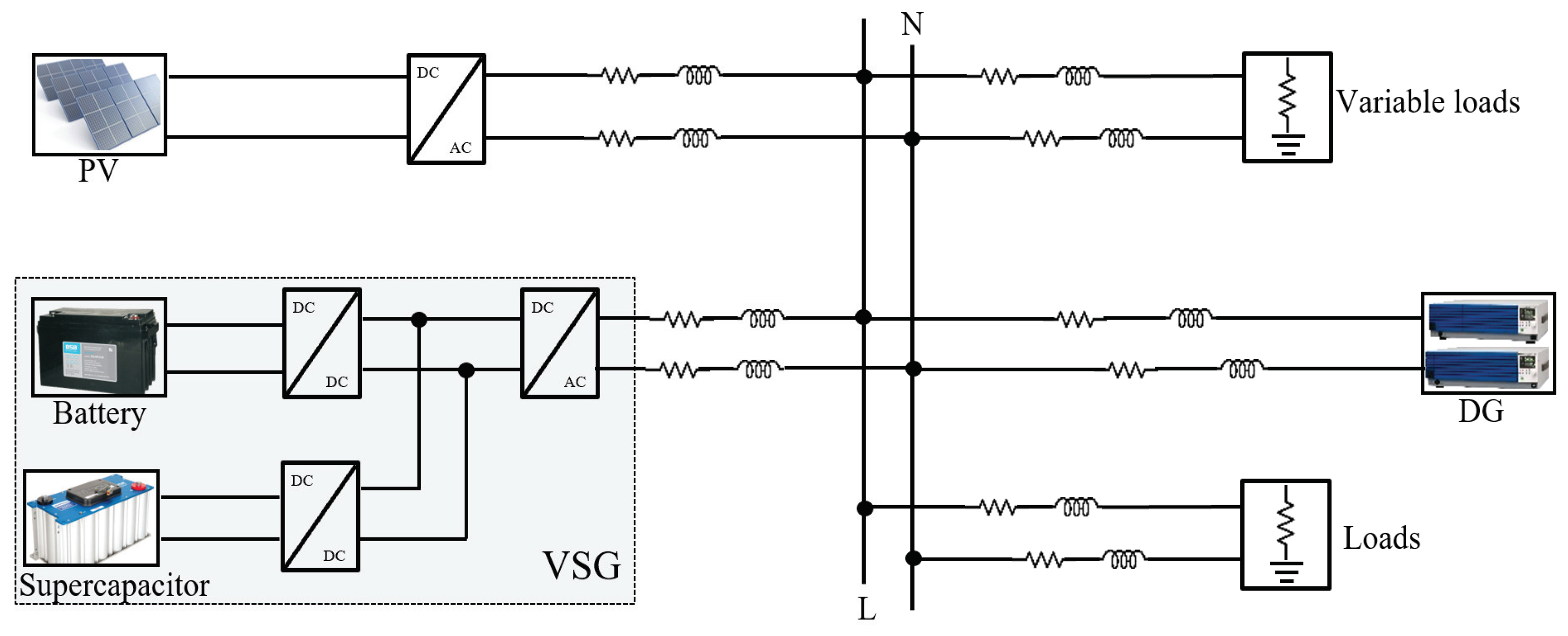
2. Power Allocation and Control for HESS
Methods Comparison
3. Frequency Deviation Suppression Based on VSG
3.1. VSG Model and Control
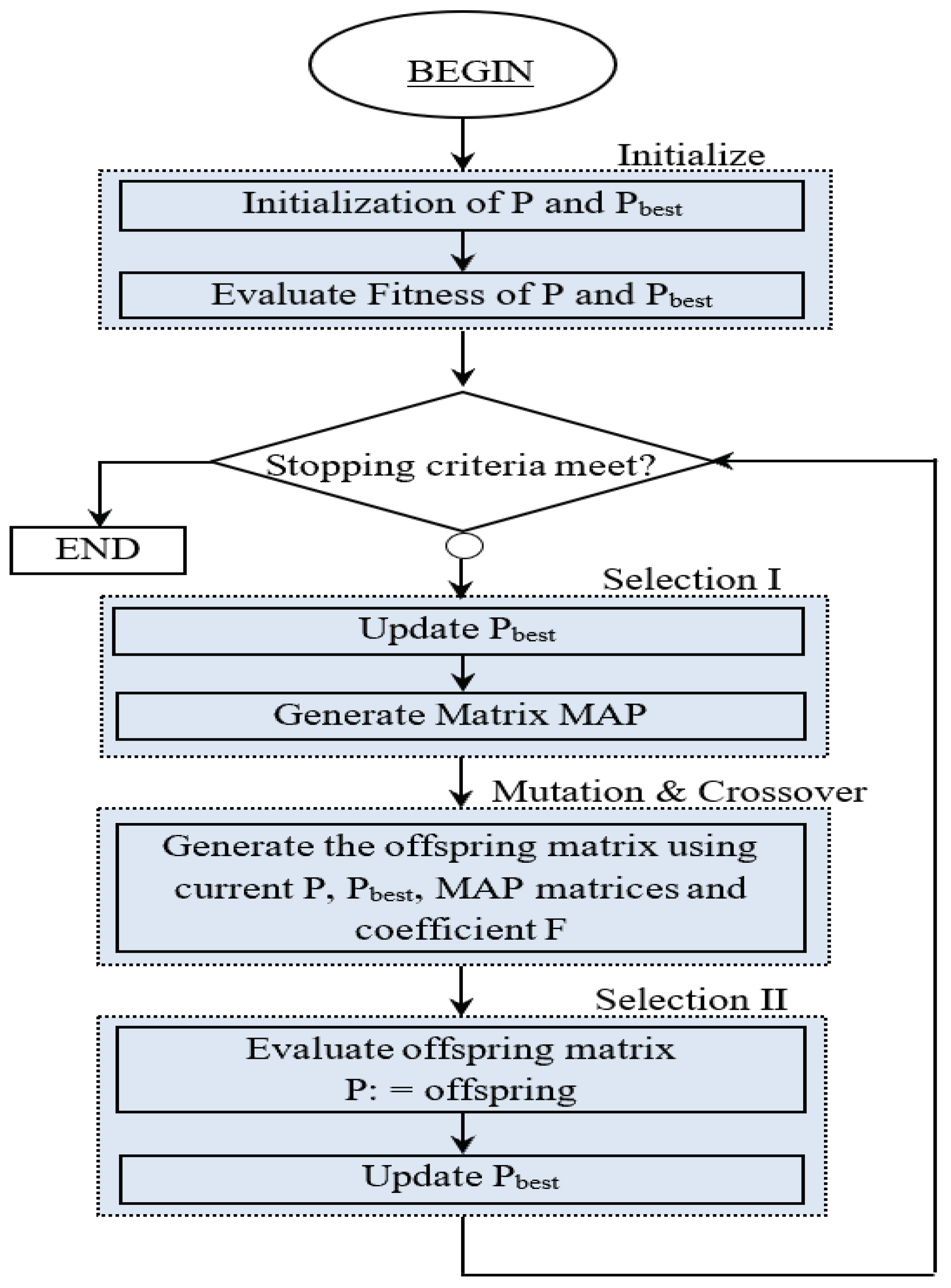
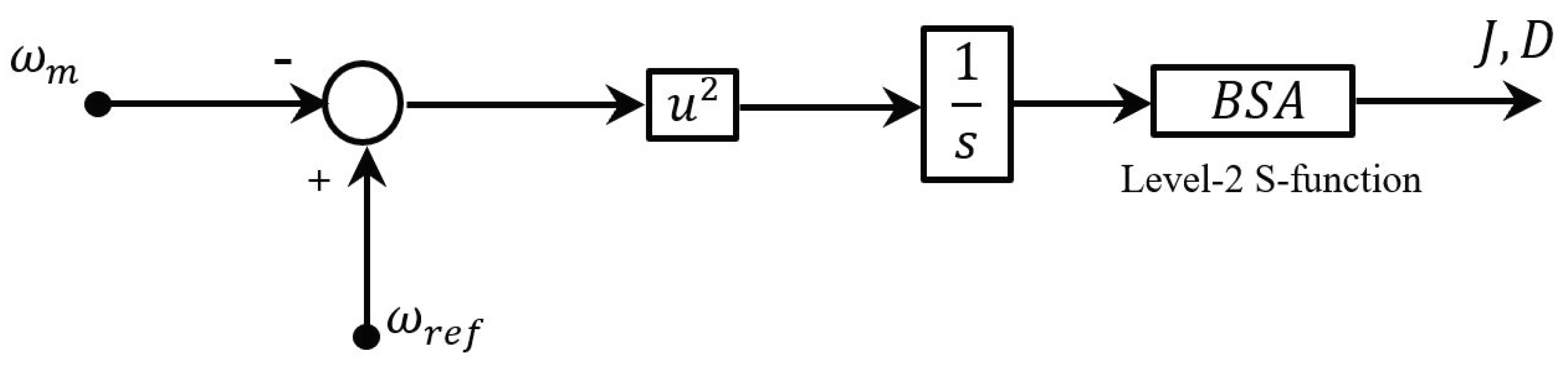
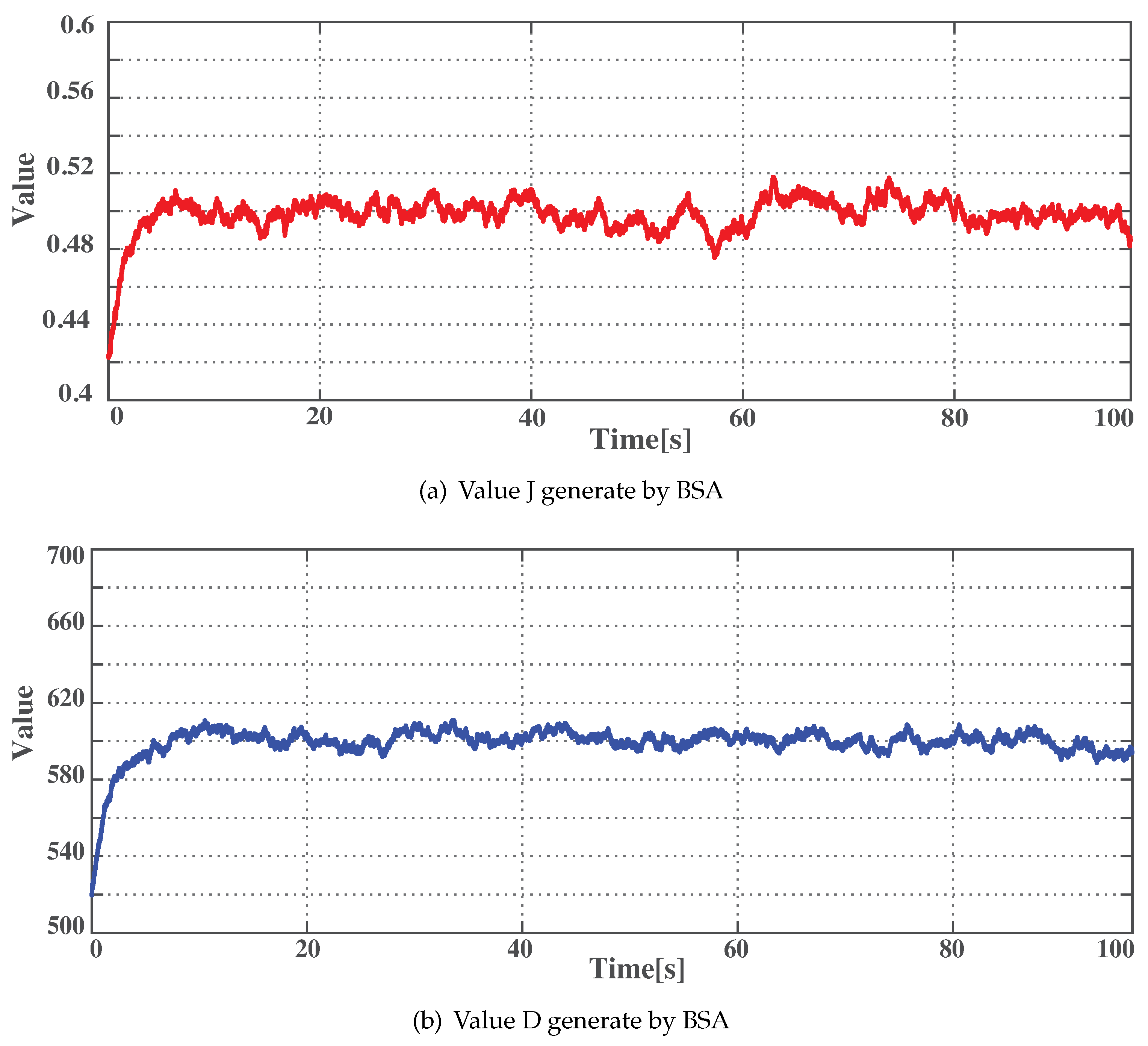
3.2. Tuning VSG Parameter Based on BSA
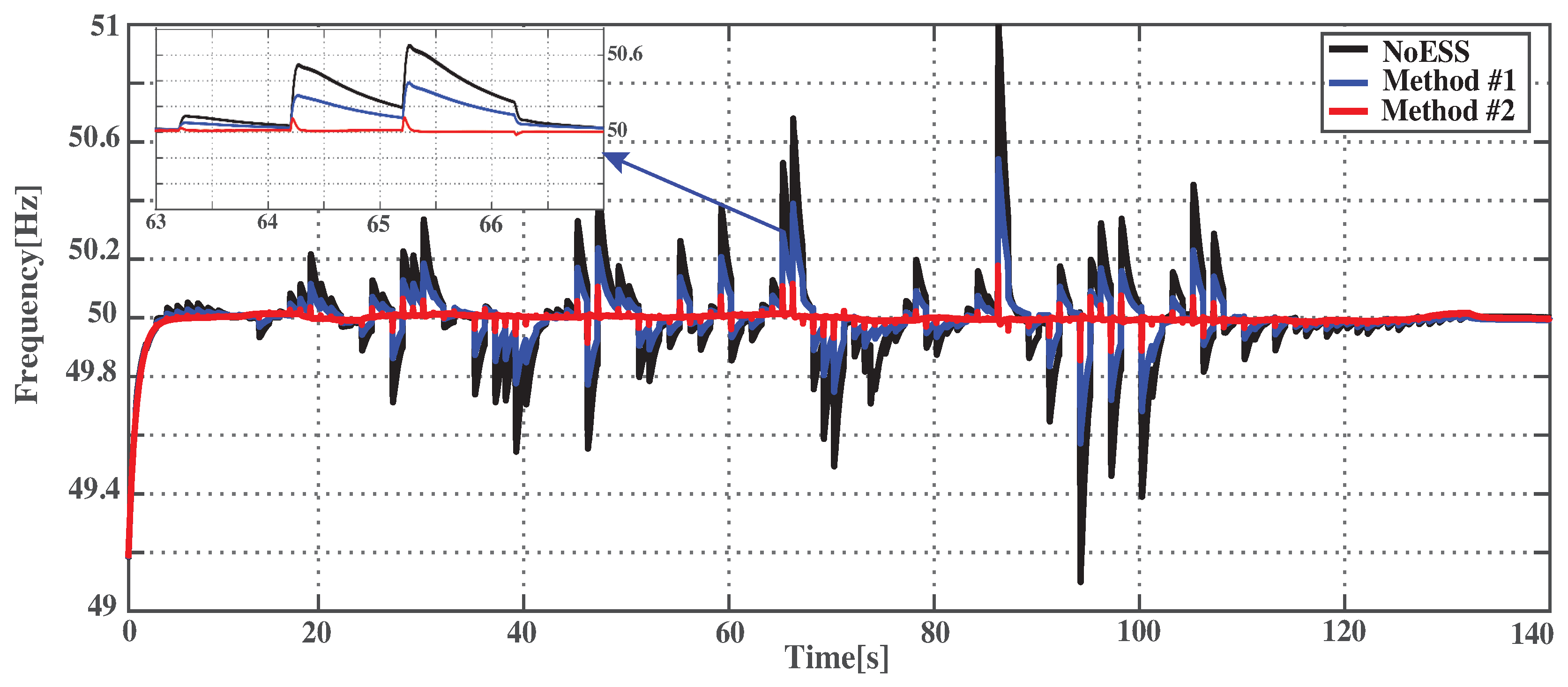
4. Simulation Results and Discussion
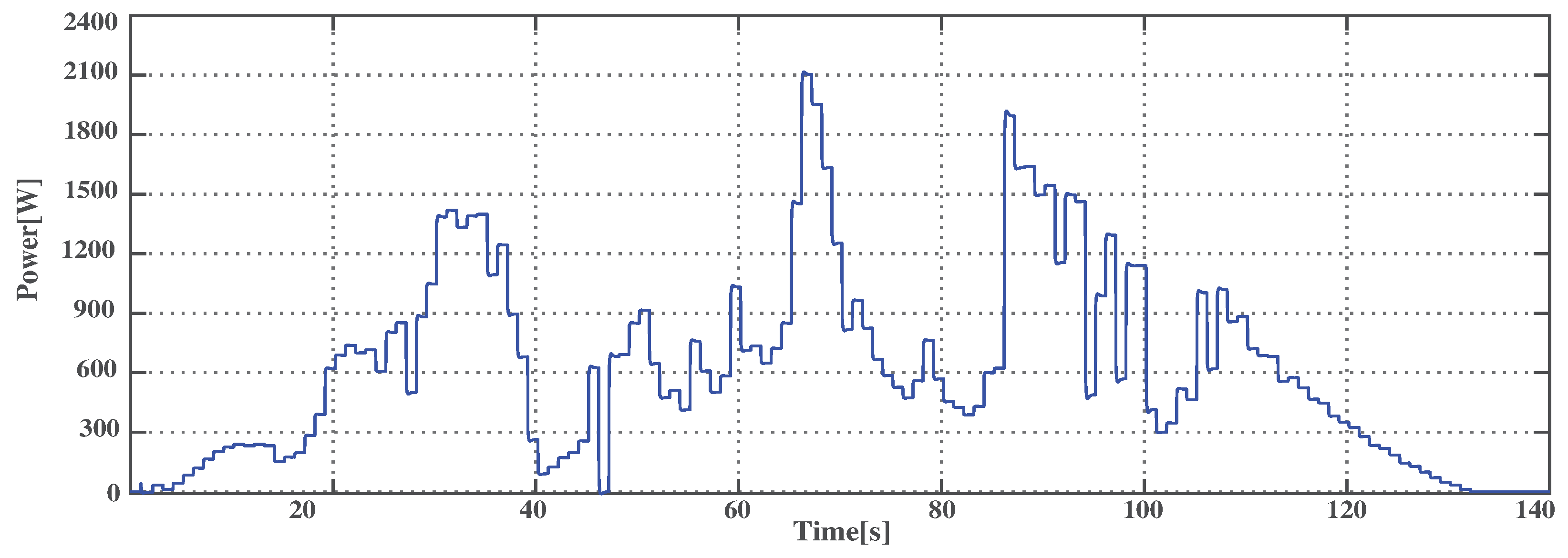
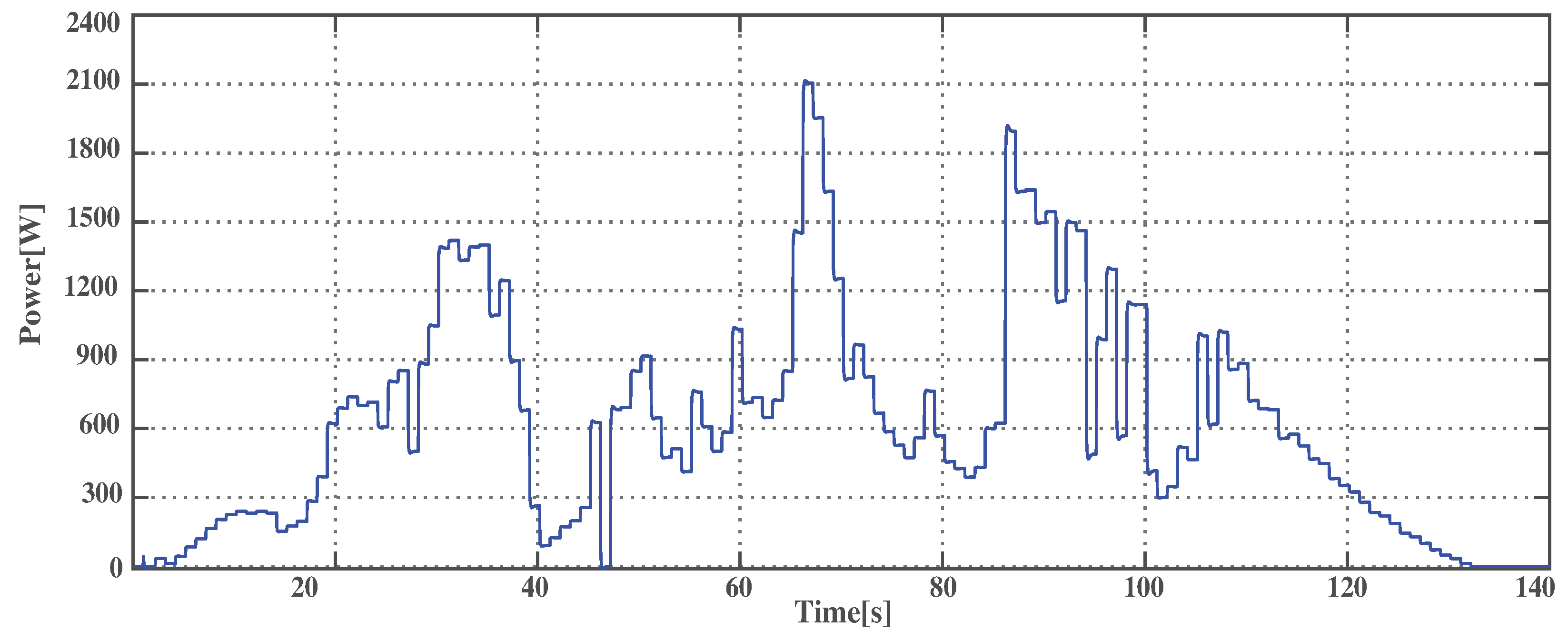
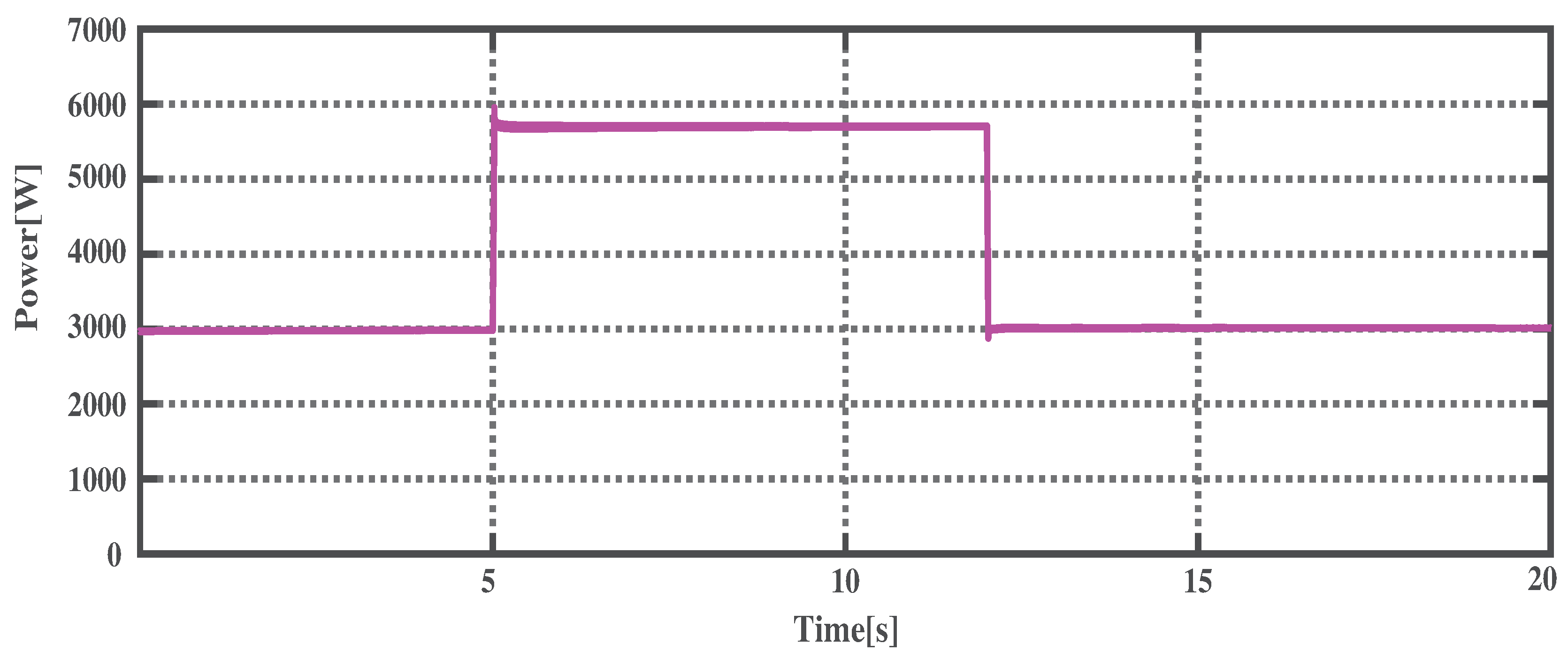
4.1. PV Power Variation
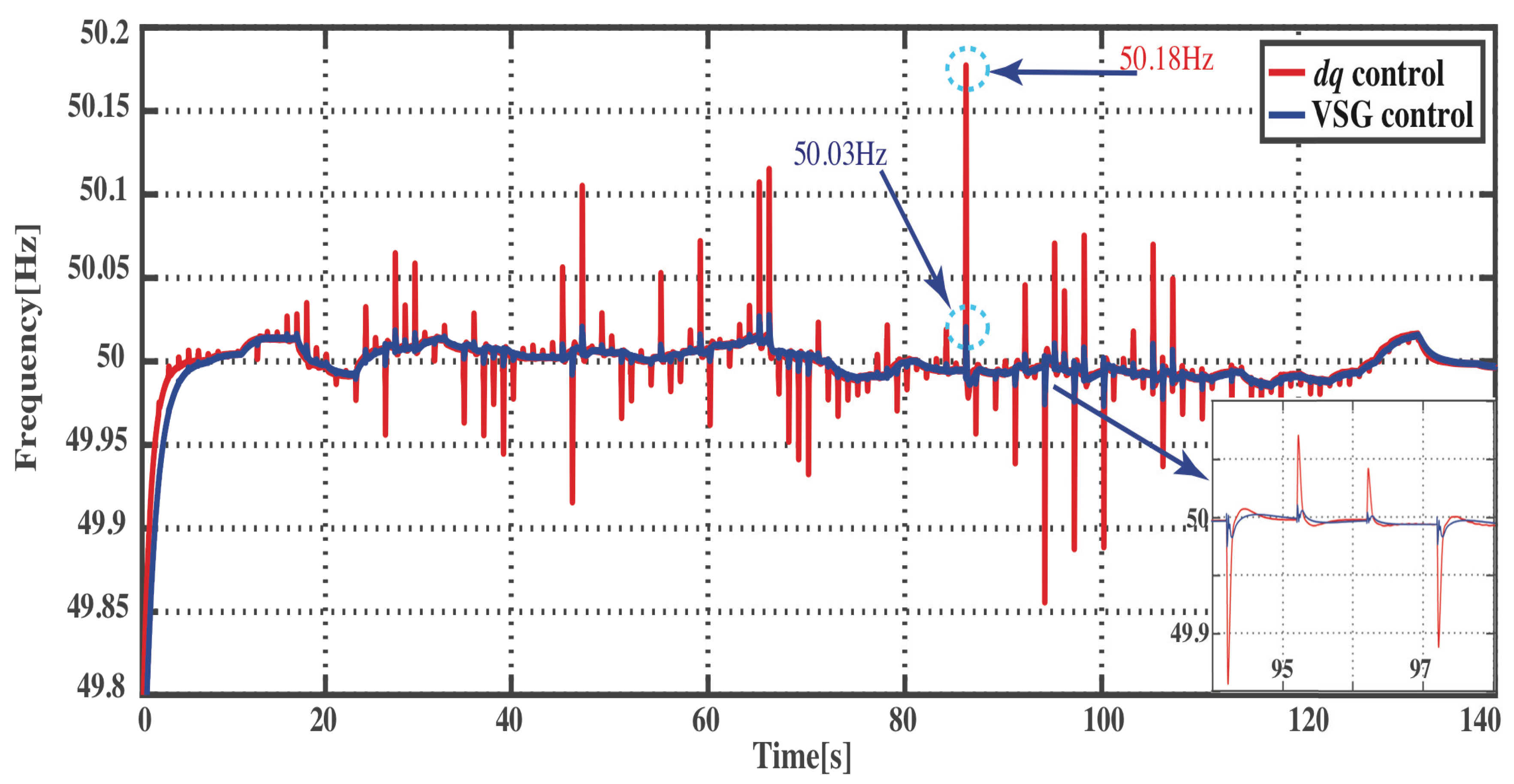
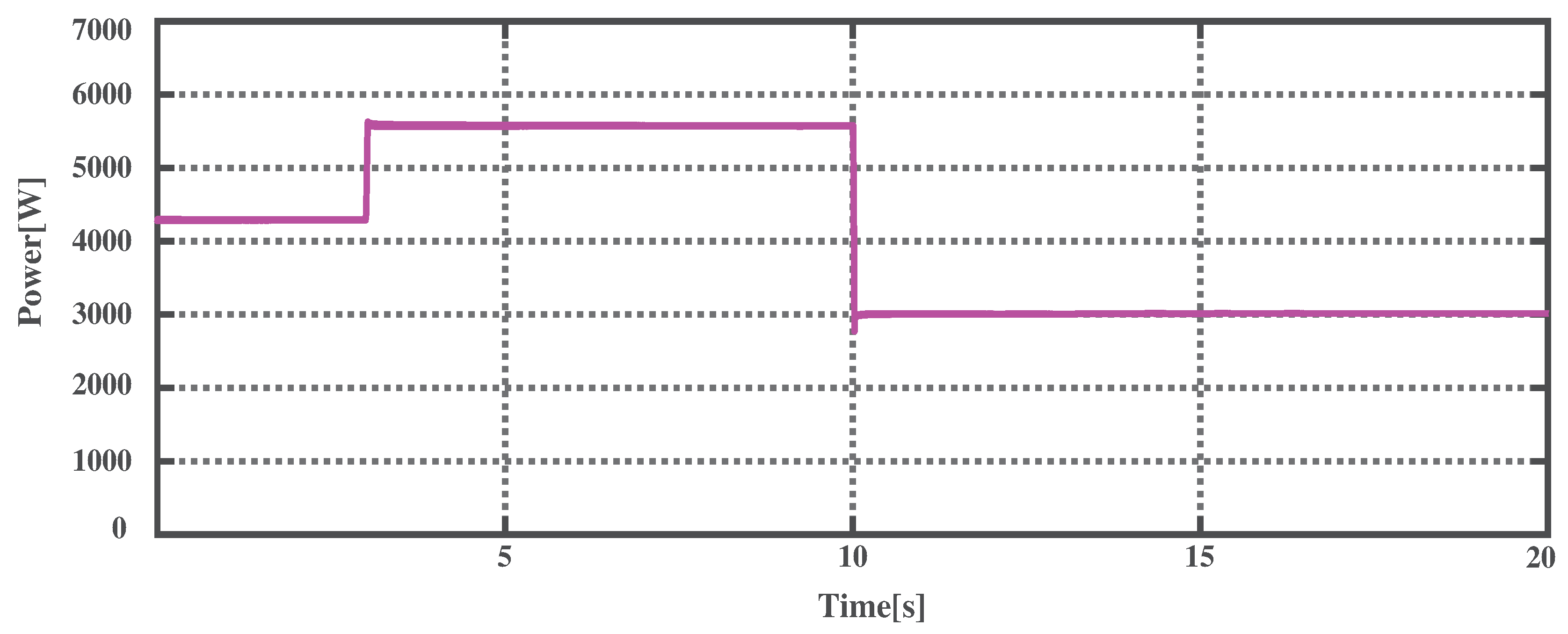
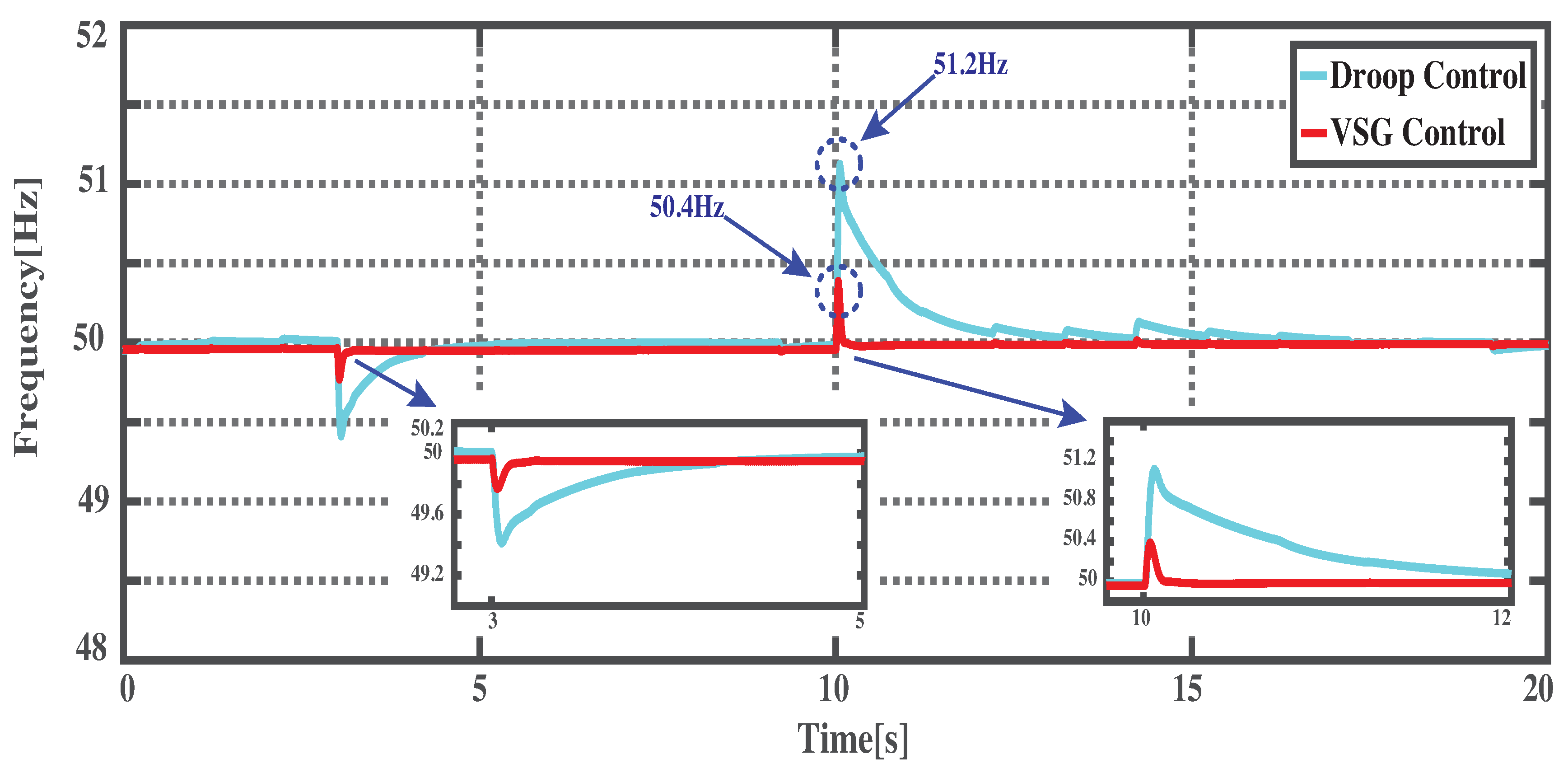
4.2. Load Transient
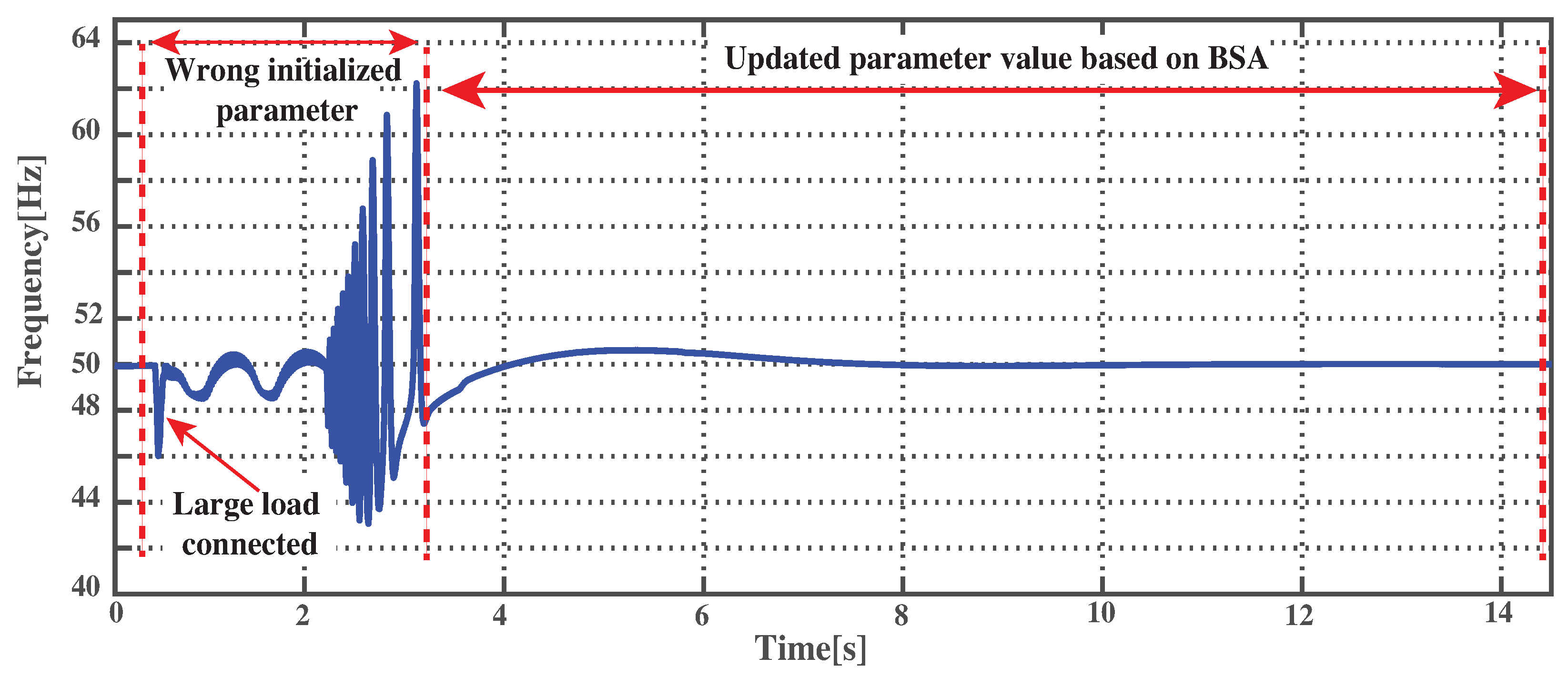
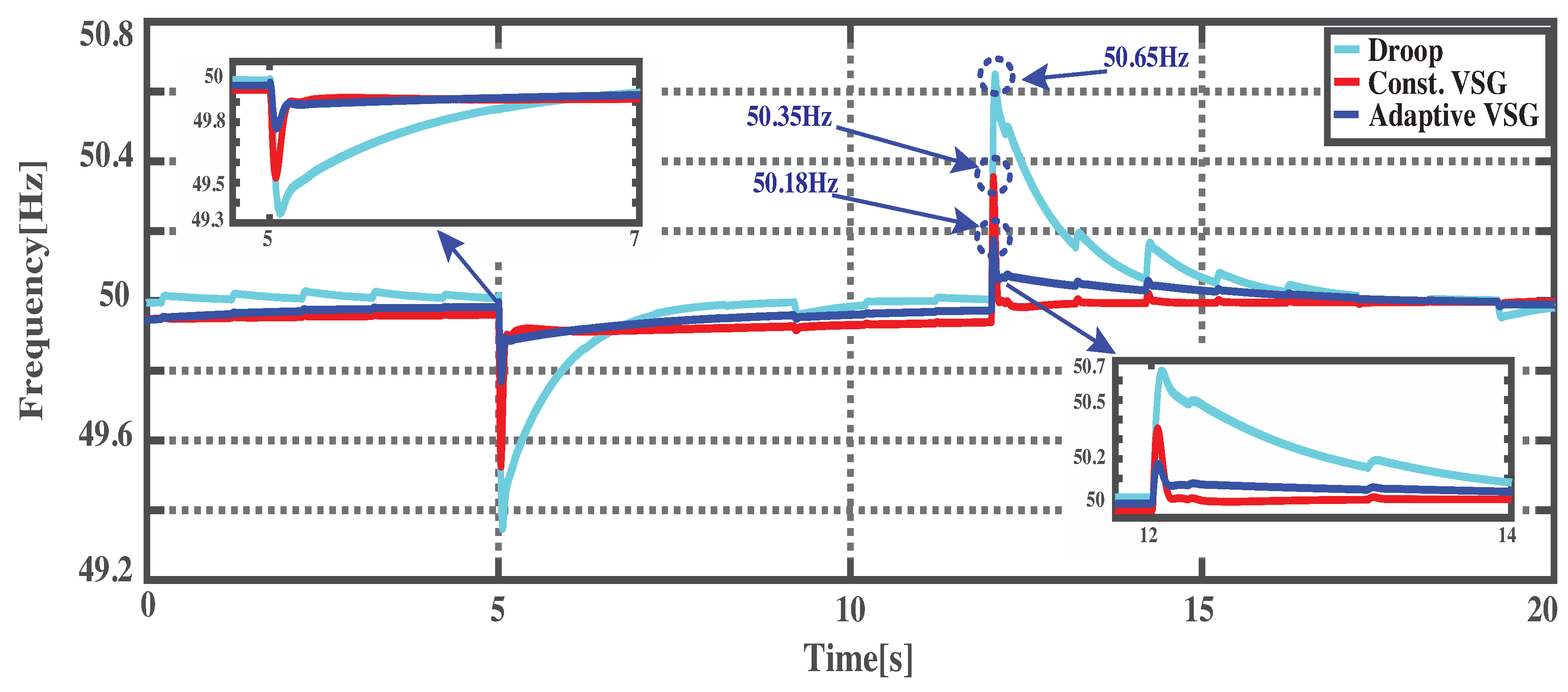
4.3. Comparison between Constant and Tuning Parameters of VSG
4.3.1. PV Power Variation
4.3.2. Load Transient
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BESS | Battery Energy Storage System |
| BSA | Backtracking Search Optimize Algorithm |
| DC | Direct Current |
| dq | Direct-quadrature |
| ESS | Energy Storage Systems |
| HESS | Hybrid Energy Storage Systems |
| IGBT | insulated-Gate Bipolar Transistor |
| LPF | Low-Pass Filter |
| PI | Proportional Integral |
| PLL | Phase Locked Loop |
| PV | PhotoVoltaic |
| PWM | Pulse Width Modulation |
| SOC | State of Charge |
| SG | Synchronous Generator |
| VSG | Virtual Synchronous Generator |
References
- Tan, X.; Li, Q.; Wang, H. Advances and trends of energy storage technology in Microgrid. Int. J. Electr. Power Energy Syst. 2013, 44, 179–191. [Google Scholar] [CrossRef]
- Li, X.; Hui, D.; Lai, X. Battery Energy Storage Station (BESS)-Based Smoothing Control of Photovoltaic (PV) and Wind Power Generation Fluctuations. IEEE Trans. Sustain. Energy 2013, 4, 451–458. [Google Scholar] [CrossRef]
- Kim, C.; Muljadi, E.; Chung, C.C. Coordinated Control of Wind Turbine and Energy Storage System for Reducing Wind Power Fluctuation. Energies 2018, 11, 52. [Google Scholar] [CrossRef]
- Lazzeronia, P.; Repetto, M. Optimal planning of battery systems for power losses reduction in distribution grids. Electr. Power Syst. Res. 2018, 167, 94–112. [Google Scholar] [CrossRef]
- Rodrigo, M.; Holger, C.; Johanna, J.; Thomas, V.; Peter, M. Optimal Component Sizing for Peak Shaving in Battery Energy Storage System for Industrial Applications. Energies 2018, 11, 2048. [Google Scholar] [CrossRef]
- Liu, H.; Peng, J.; Zang, Q.; Yang, K. Control Strategy of Energy Storage for Smoothing Photovoltaic Power Fluctuations. IFAC-Pap. OnLine 2015, 48, 162–165. [Google Scholar] [CrossRef]
- Hund, T.D.; Gonzalez, S.; Barrett, K. Grid-tied PV system energy smoothing. In Proceedings of the 2010 35th IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010; pp. 2762–2766. [Google Scholar]
- Wang, Y.; Wang, W.; Zhao, Y.; Yang, L.; Chen, W. A fuzzy-logic power management strategy based on markov random prediction for hybrid energy storage system. Energies 2016, 9, 25. [Google Scholar] [CrossRef]
- Lai, C.H.; Dennis Wong, M.L.; Wong, W.S. Smart hybrid energy storage for stand-alone PV microgrid: Optimization of battery lifespan through dynamicpower allocation. In Proceedings of the IEEE PES Asia-Pacific Power and Energy Engineering Conference, Brisbane, QLD, Australia, 15–18 November 2015. [Google Scholar]
- Spataru, C.; Chung, K.Y.; Barrett, M. Physical Energy Storage Employed Worldwide. Energy Procedia 2014, 62, 452–461. [Google Scholar] [CrossRef]
- Ma, Y.; Cao, X.; Liu, Y.; Wang, F.; Tolbert, L.M. Virtual Synchronous Generator Control of Full Converter Wind Turbines With Short-Term Energy Storage. IEEE Trans. Ind. Electron. 2017, 64, 8821–8831. [Google Scholar] [CrossRef]
- Mao, M.; Qian, C.; Ding, Y. Decentralized coordination power control for islanding microgrid based on PV/BES-VSG. CPSS Trans. Power Electron. Appl. 2018, 3, 14–24. [Google Scholar] [CrossRef]
- Fang, J.; Tang, Y.; Li, H.; Li, X. A Battery/Ultracapacitor Hybrid Energy Storage System for Implementing the Power Management of Virtual Synchronous Generators. IEEE Trans. Power Electron. 2018, 33, 2820–2824. [Google Scholar] [CrossRef]
- Ma, Y.; Lin, Z.; Yu, R.; Zhao, S. Research on Improved VSG Control Algorithm Based on Capacity-Limited Energy Storage System. Energies 2018, 11, 677. [Google Scholar] [CrossRef]
- Hirase, Y.; Abe, K.; Sugimoto, K.; Sakimoto, K.; Bevrani, H.; Ise, T. A novel control approach for virtual synchronous generators to suppress frequency and voltage fluctuations in microgrids. Appl. Energy 2018, 210, 699–710. [Google Scholar] [CrossRef]
- Shi, R.; Zhang, X. VSG-Based Dynamic Frequency Support Control for Autonomous PV–Diesel Microgrids. Energies 2018, 11, 1814. [Google Scholar] [CrossRef]
- Liu, J.; Yang, D.; Yao, W.; Fang, R.; Zhao, H.; Wang, B. PV-based virtual synchronous generator with variable inertia to enhance power system transient stability utilizing the energy storage system. Prot. Control Mod. Power Syst. 2017, 2. [Google Scholar] [CrossRef]
- Shi, R.; Zhang, X.; Hu, C.; Xu, H.; Gu, J.; Cao, W. Self-tuning virtual synchronous generator control for improving frequency stability in autonomous photovoltaic-diesel microgrids. J. Mod. Power Syst. Clean Energy 2018, 6, 482–494. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Bevrani, H.; Ise, T. Enhanced Virtual Synchronous Generator Control for Parallel Inverters in Microgrids. IEEE Trans. Smart Grid 2017, 8, 2268–2277. [Google Scholar] [CrossRef]
- Guan, M.; Pan, W.; Zhang, J.; Hao, Q.; Cheng, J.; Zheng, Z. Synchronous generator emulation control strategy for voltage source converter (VSC) stations. IEEE Trans. Power Syst. 2015, 30, 3093–3101. [Google Scholar] [CrossRef]
- Fang, J.; Li, X.; Tang, Y.; Li, H. Power management of virtual synchronous generators through using hybrid energy storage systems. In Proceedings of the Applied Power Electronics Conference and Exposition, San Antonio, TX, USA, 4–8 March 2018. [Google Scholar]
- Hazra, S.; Subhashish, B. Hybrid Energy Storage System Comprising of Battery and Ultra-capacitor For Smoothing of Oscillating Wave Energy. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Milwaukee, WI, USA, 18–22 September 2016. [Google Scholar]
- Krieger, E.M.; Arnold, C.B. Effects of Variability and Rate on Battery Charge Storage and Lifespan. Ph.D. Thesis, Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ, USA, 2013. [Google Scholar]
- Lee, H.-J.; Choi, J.-Y.; Park, G.-S.; Oh, K.-S.; Won, D.-J. Renewable Integration Algorithm to Compensate PV Power Using Battery Energy Storage System. In Proceedings of the International Youth Conference on Energy, Budapest, Hungary, 21–24 June 2017. [Google Scholar]
- Hasabelrasul, H.; Yan, X.; Gadalla, A.S. MW-Scale Medium Voltage Cascaded H-bridge Battery Storage System Based on Virtual Synchronous Generators. In Proceedings of the IEEE Region 10 Conference, Penang, Malaysia, 5–8 November 2017. [Google Scholar]
- Civicioglu, P. Backtracking search optimization algorithm for numerical optimization problems. Appl. Math. Comput. 2013, 219, 8121–8144. [Google Scholar] [CrossRef]
- Darith, L.; Sompob, S.; Kittichot, S. Experiment on Hierarchical Control Based Power Quality Enhancement for Standalone Microgrid. In Proceedings of the International Power Electronics Conference, Niigata, Japan, 20–24 May 2018. [Google Scholar]




| Energy Storage Systems | Energy Density | Power Density | Cycle Life | Response Time | Cost |
|---|---|---|---|---|---|
| Chemical battery | high | low | short | medium | low |
| Sodium-Sulphur(Nas) Battery | medium | low | short | slow | medium |
| flywheel | low | high | long | fast | high |
| suppercapacitor | low | high | long | fast | medium |
| SMES | medium | high | long | fast | high |
| DGs | |
|---|---|
| Model | Kikusui PCR2000M |
| Power Rating | 220 V, 50 Hz, 2 kVA |
| P-Angle Droop Coefficient (m) | 2 (0.000185) |
| Q-V Droop Coefficient (n) | 1/0.002592725 |
| Loads | |
| Variable Load | Load profile from MEA |
| ( = 1.5 kW) | |
| PV Simulator | |
| Model | Kikusui PCR2000M |
| Simulate | Based PV profile (= 2.1 kW) |
| Battery storage system | |
| SOLAR 12-65 | 8 * (12 V 65 Ah) |
| Supercapacitor storage system | |
| Maxwell BMOD0165 | 3 * (165 F, 48 V, 53 Wh) |
| VSG-Constant | |
| J | 0.4863 |
| D | 382 |
| VSG-BSA | |
| Population | 25 |
| Epoch | 5 |
| J | 0.51 |
| D | 597 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leng, D.; Polmai, S. Virtual Synchronous Generator Based on Hybrid Energy Storage System for PV Power Fluctuation Mitigation. Appl. Sci. 2019, 9, 5099. https://doi.org/10.3390/app9235099
Leng D, Polmai S. Virtual Synchronous Generator Based on Hybrid Energy Storage System for PV Power Fluctuation Mitigation. Applied Sciences. 2019; 9(23):5099. https://doi.org/10.3390/app9235099
Chicago/Turabian StyleLeng, Darith, and Sompob Polmai. 2019. "Virtual Synchronous Generator Based on Hybrid Energy Storage System for PV Power Fluctuation Mitigation" Applied Sciences 9, no. 23: 5099. https://doi.org/10.3390/app9235099
APA StyleLeng, D., & Polmai, S. (2019). Virtual Synchronous Generator Based on Hybrid Energy Storage System for PV Power Fluctuation Mitigation. Applied Sciences, 9(23), 5099. https://doi.org/10.3390/app9235099




