A Novel Adaptive Gain of Optimal Sliding Mode Controller for Linear Time-Varying Systems
Abstract
:1. Introduction
2. Design of Optimal Control Law
3. Illustrative Examples
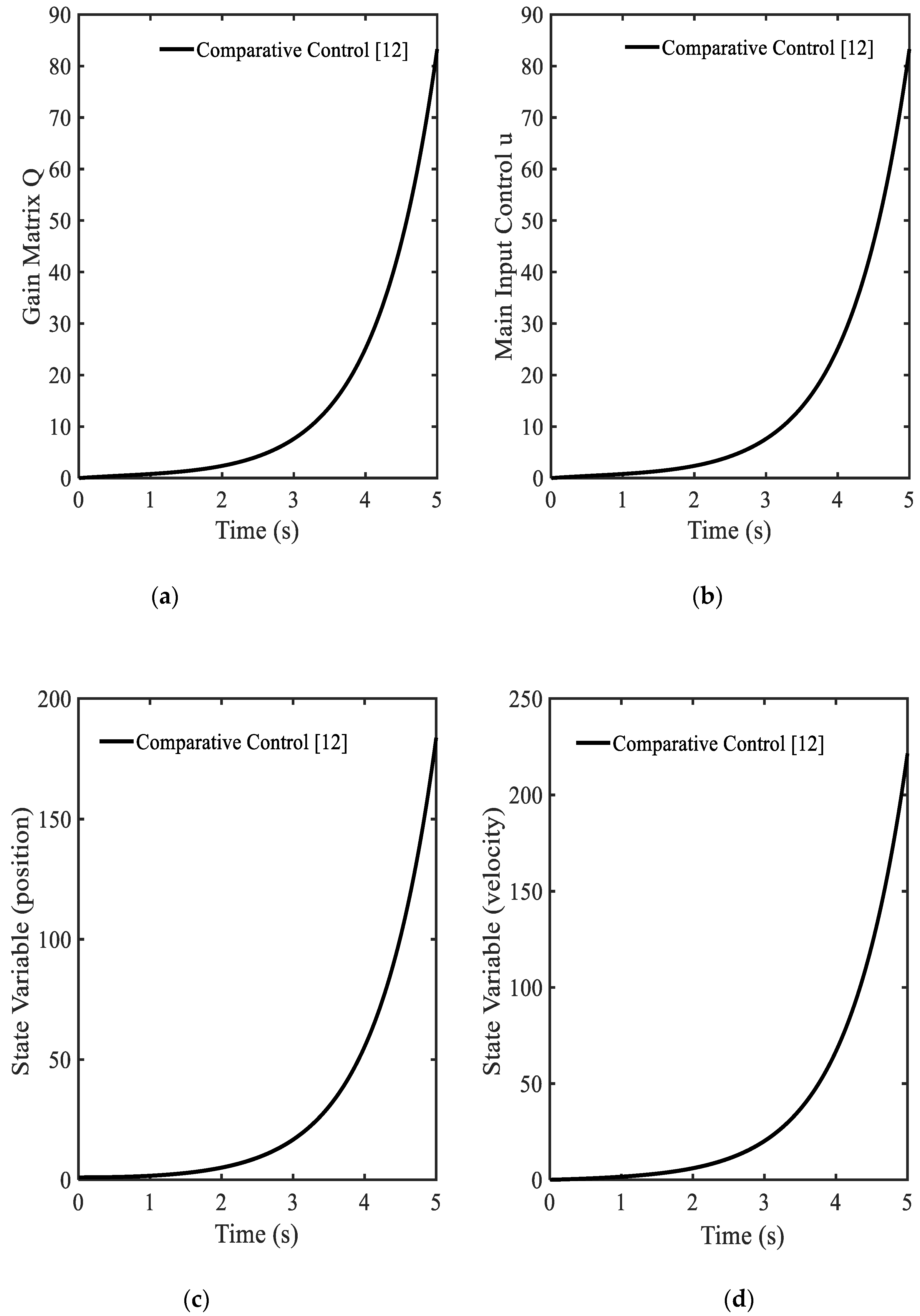
3.1. Example 1—Comparative Controller
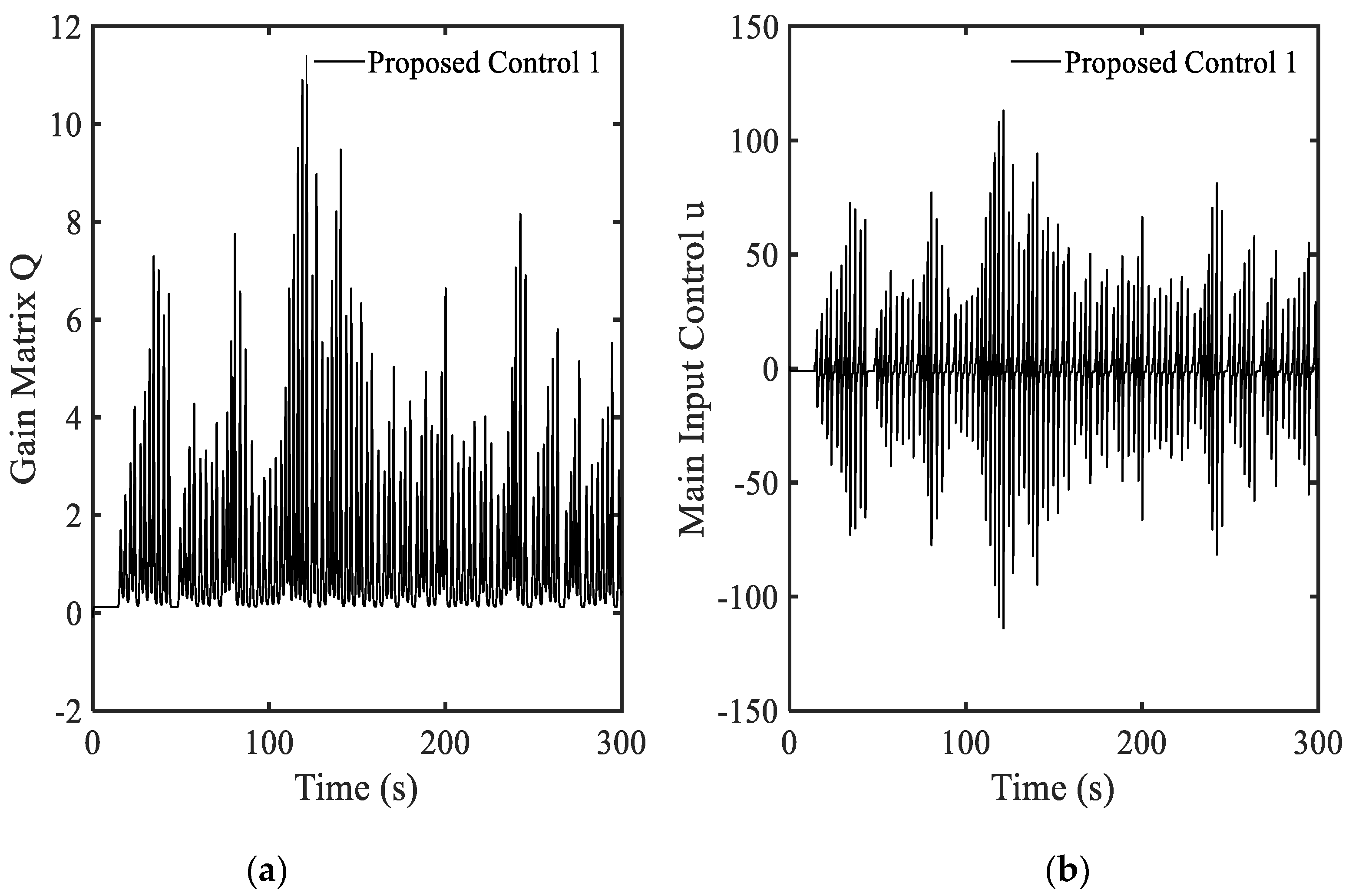
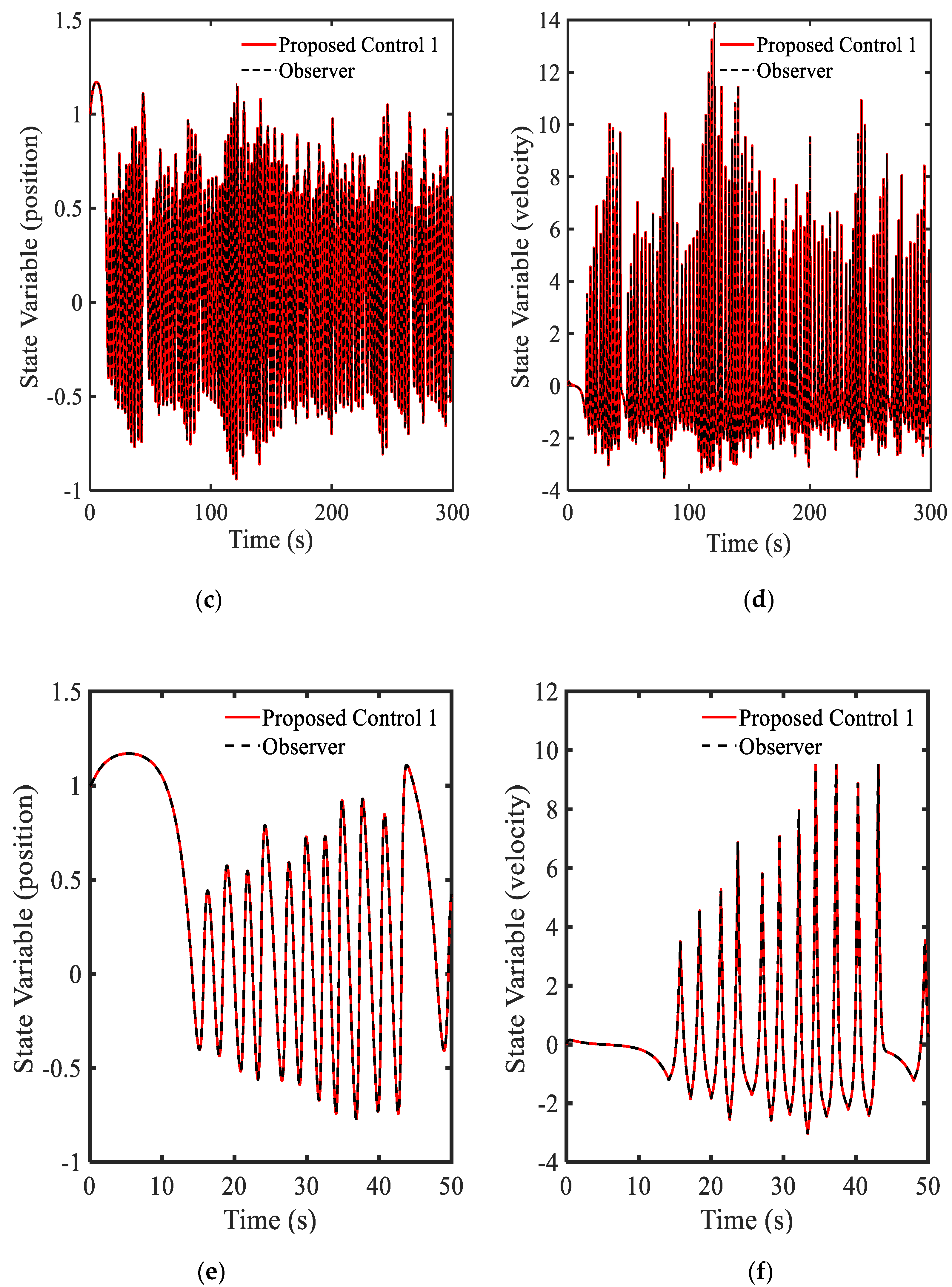
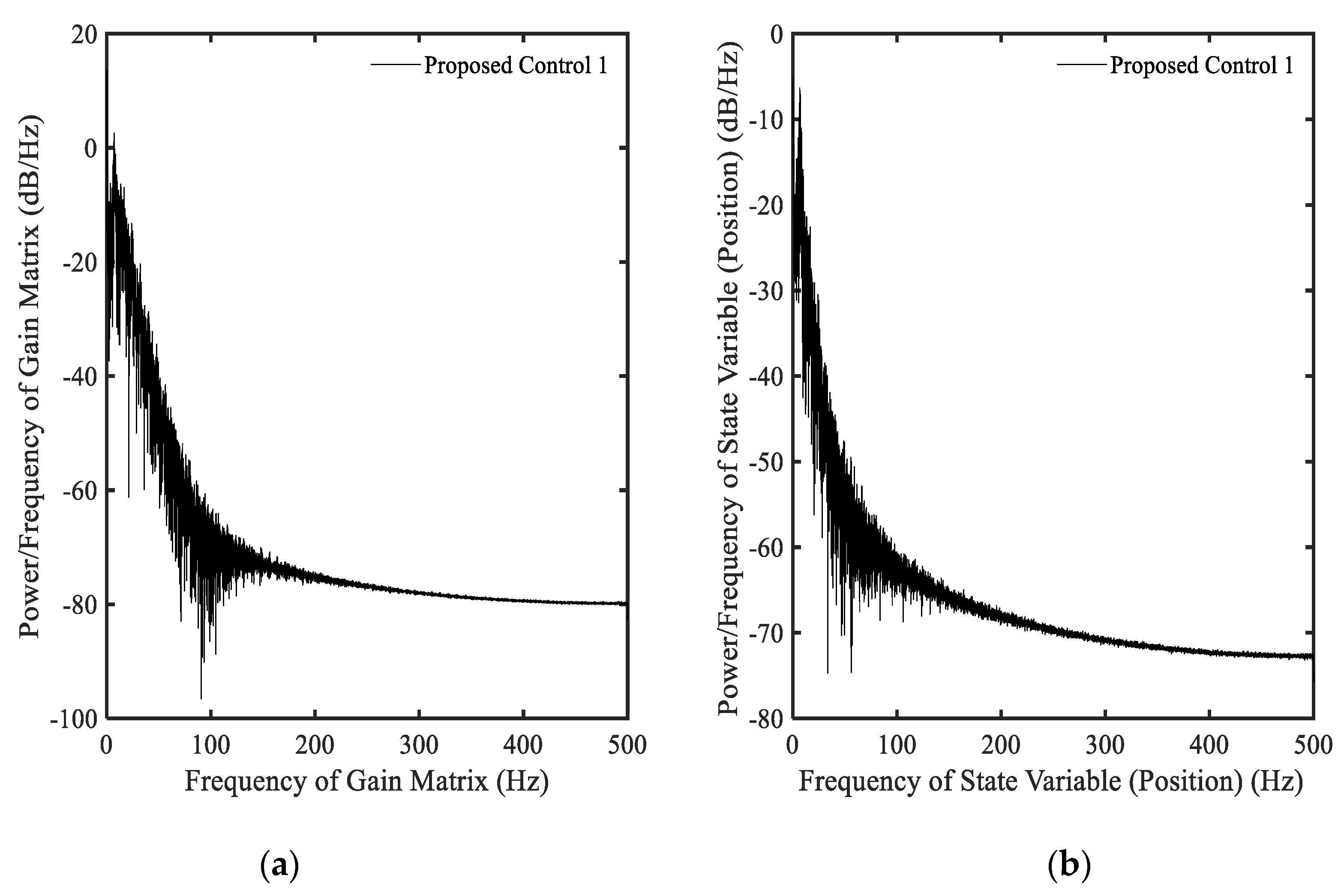
3.2. Example 2—Proposed Controller with Equation (12)
3.3. Example 3—Proposed Controller with Equation (7)
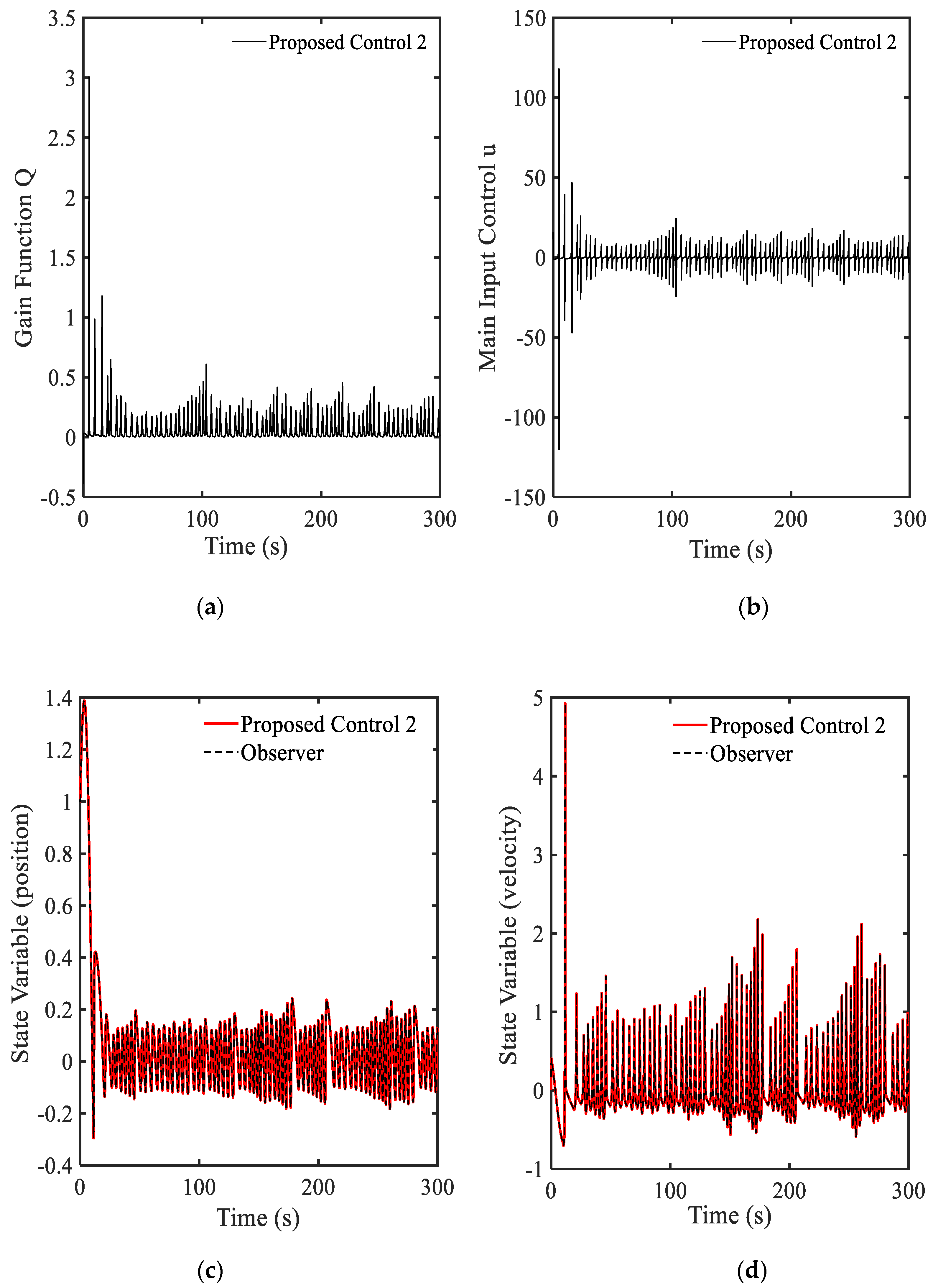
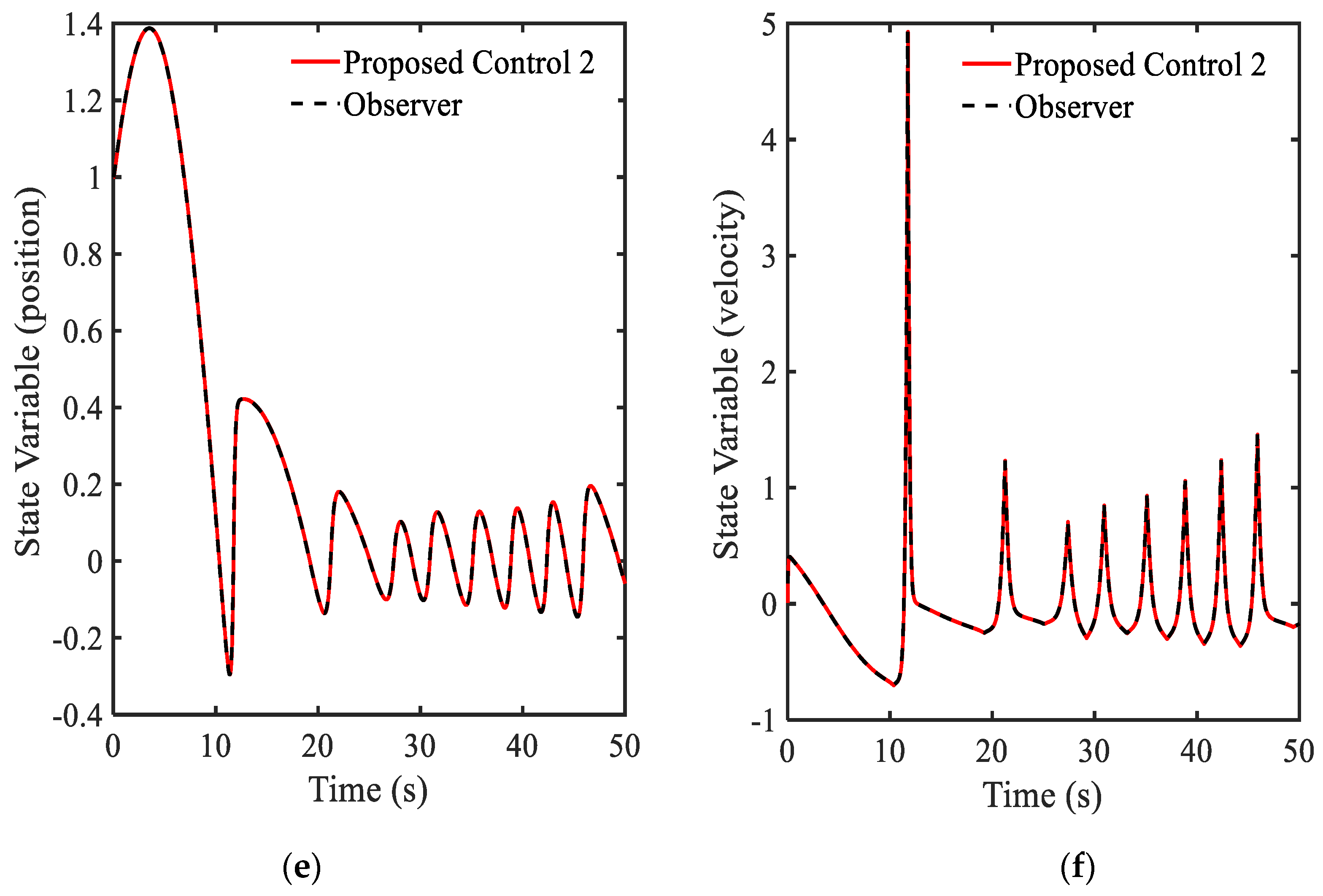
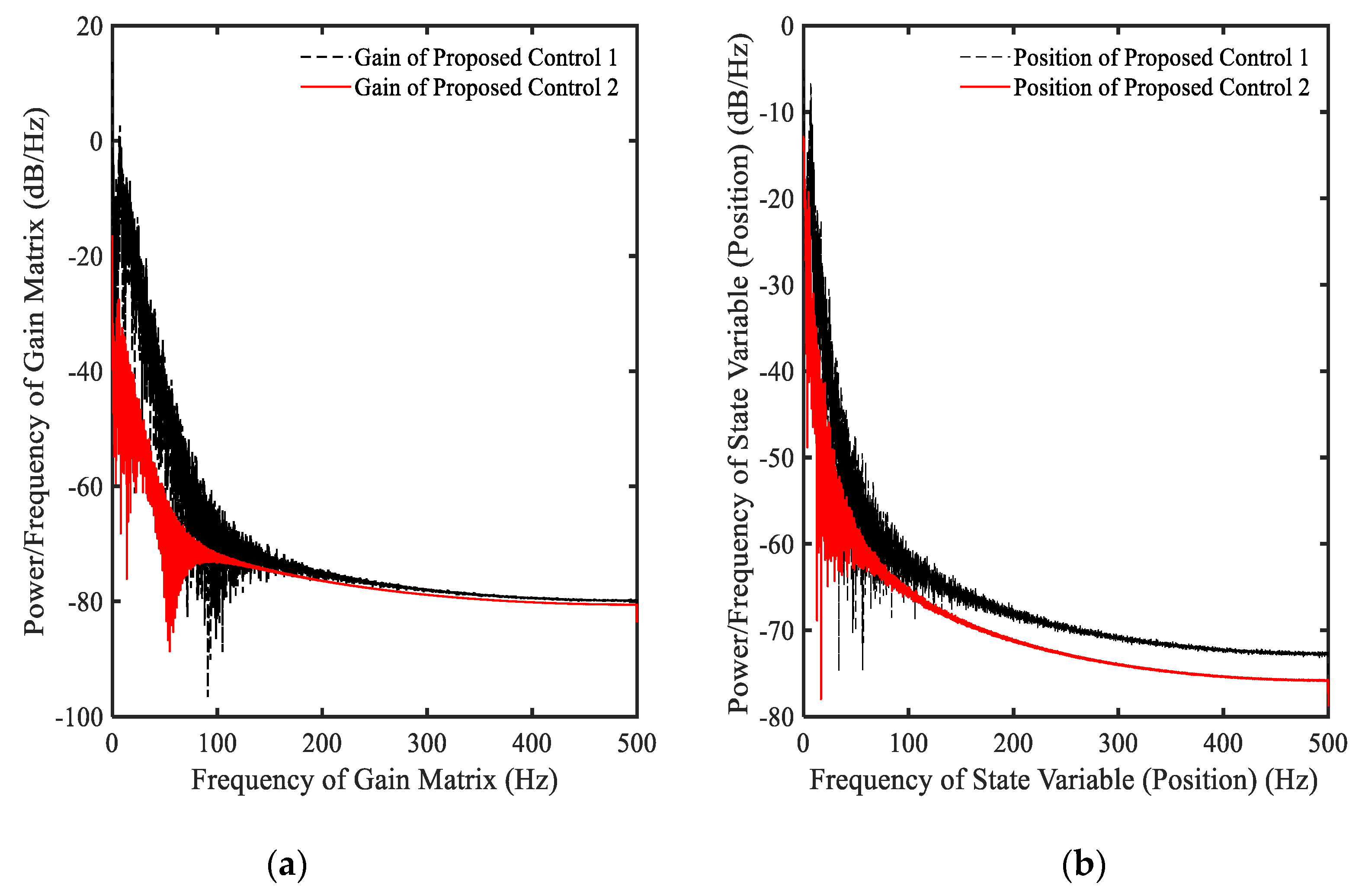
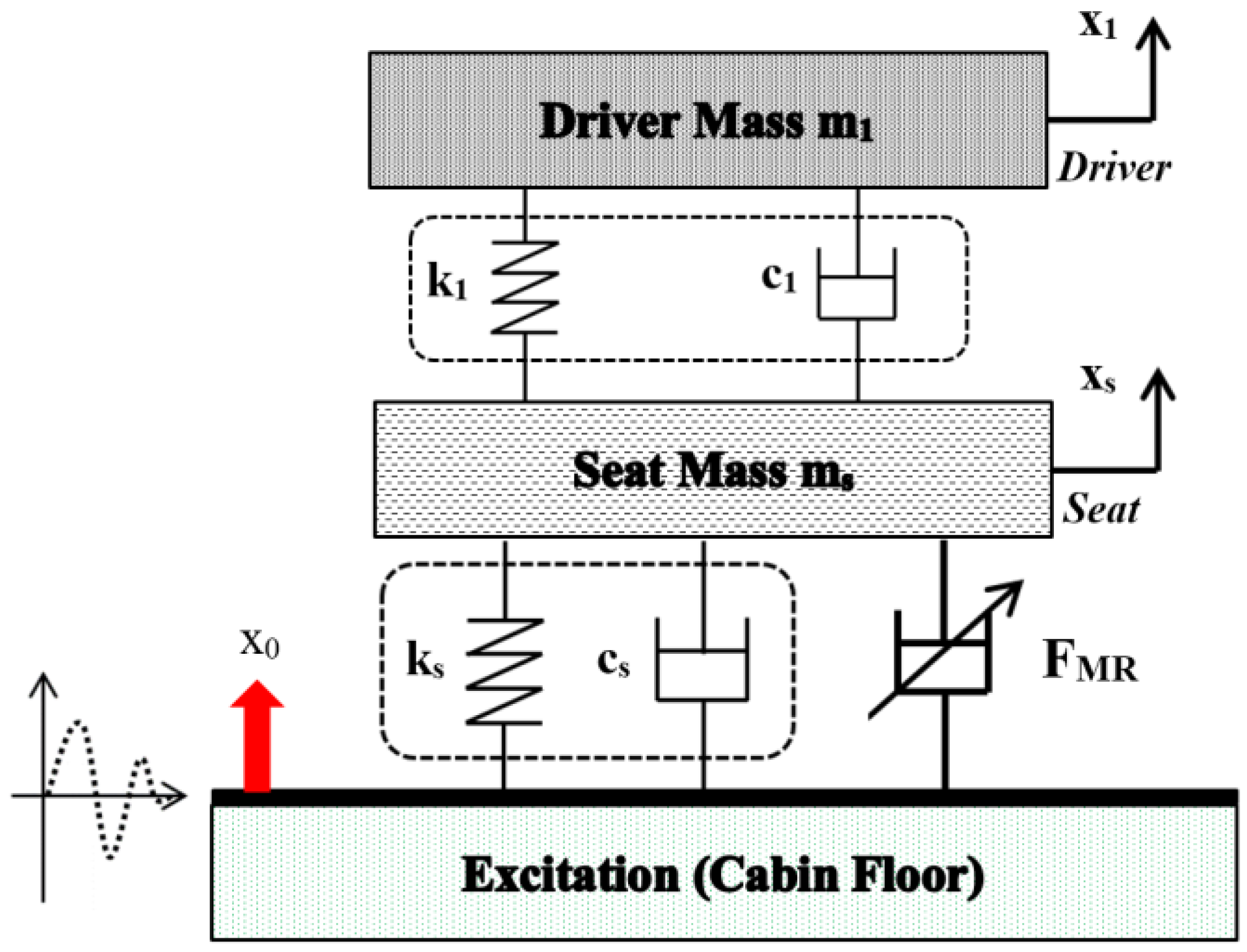
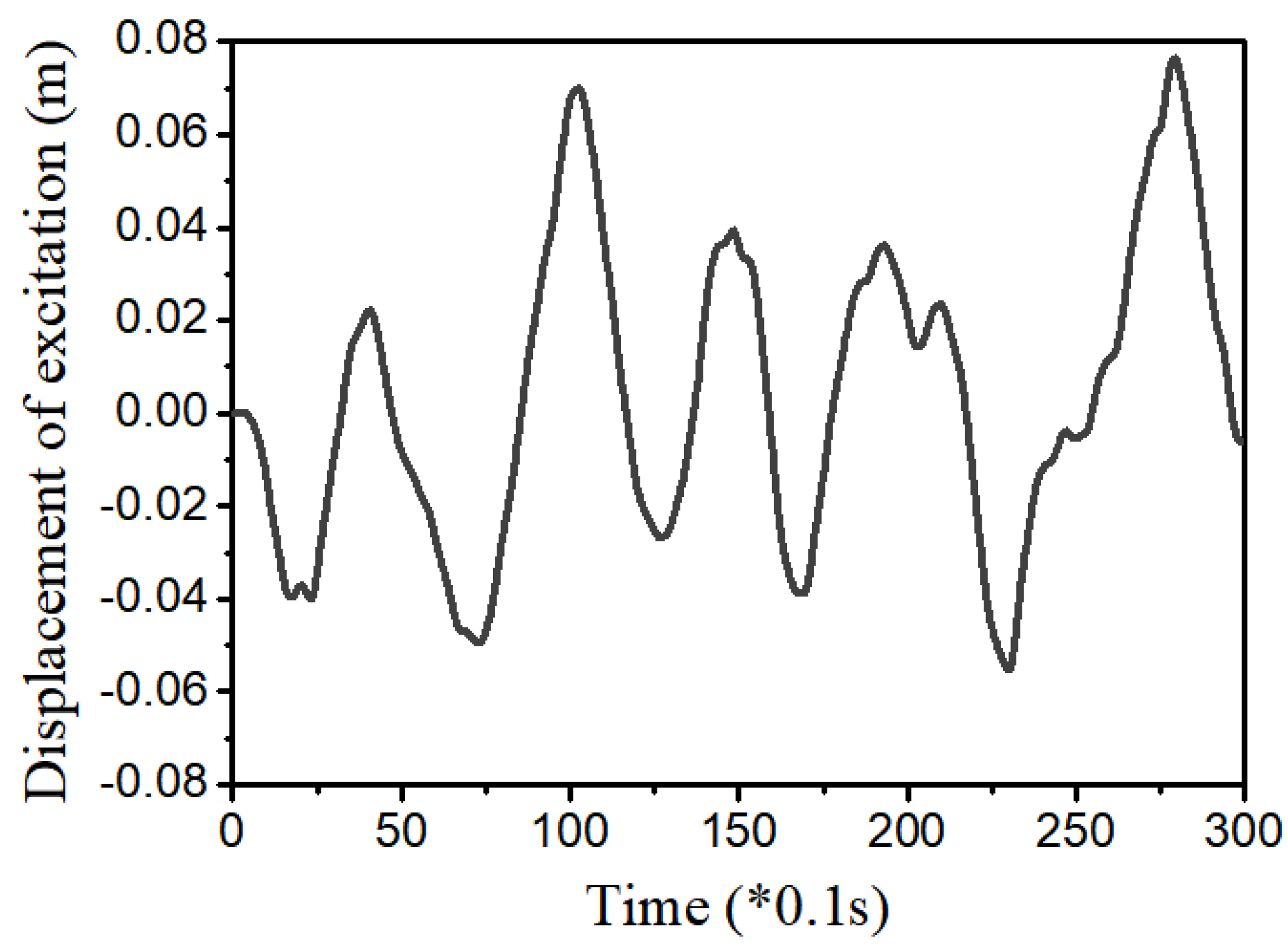
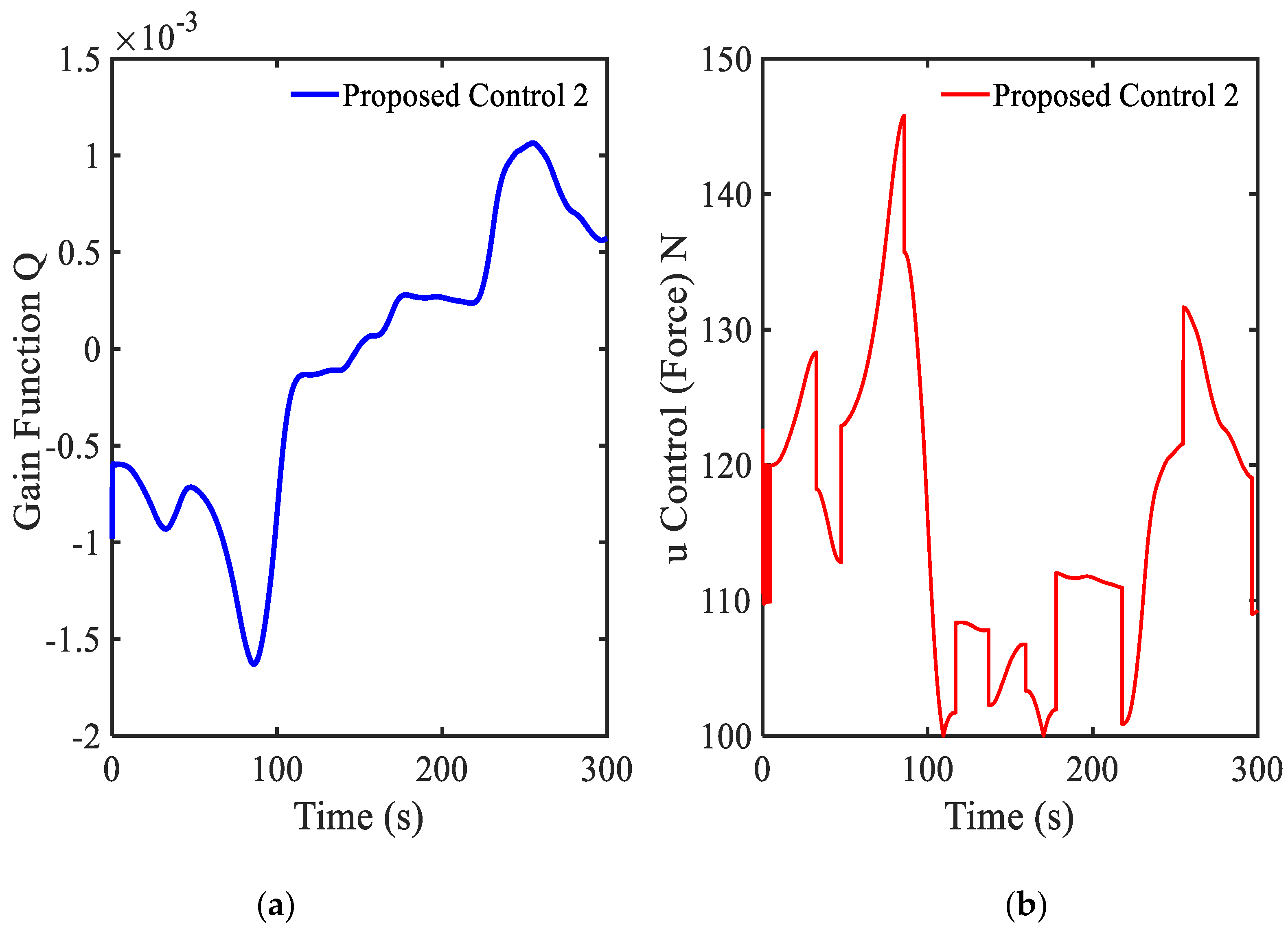
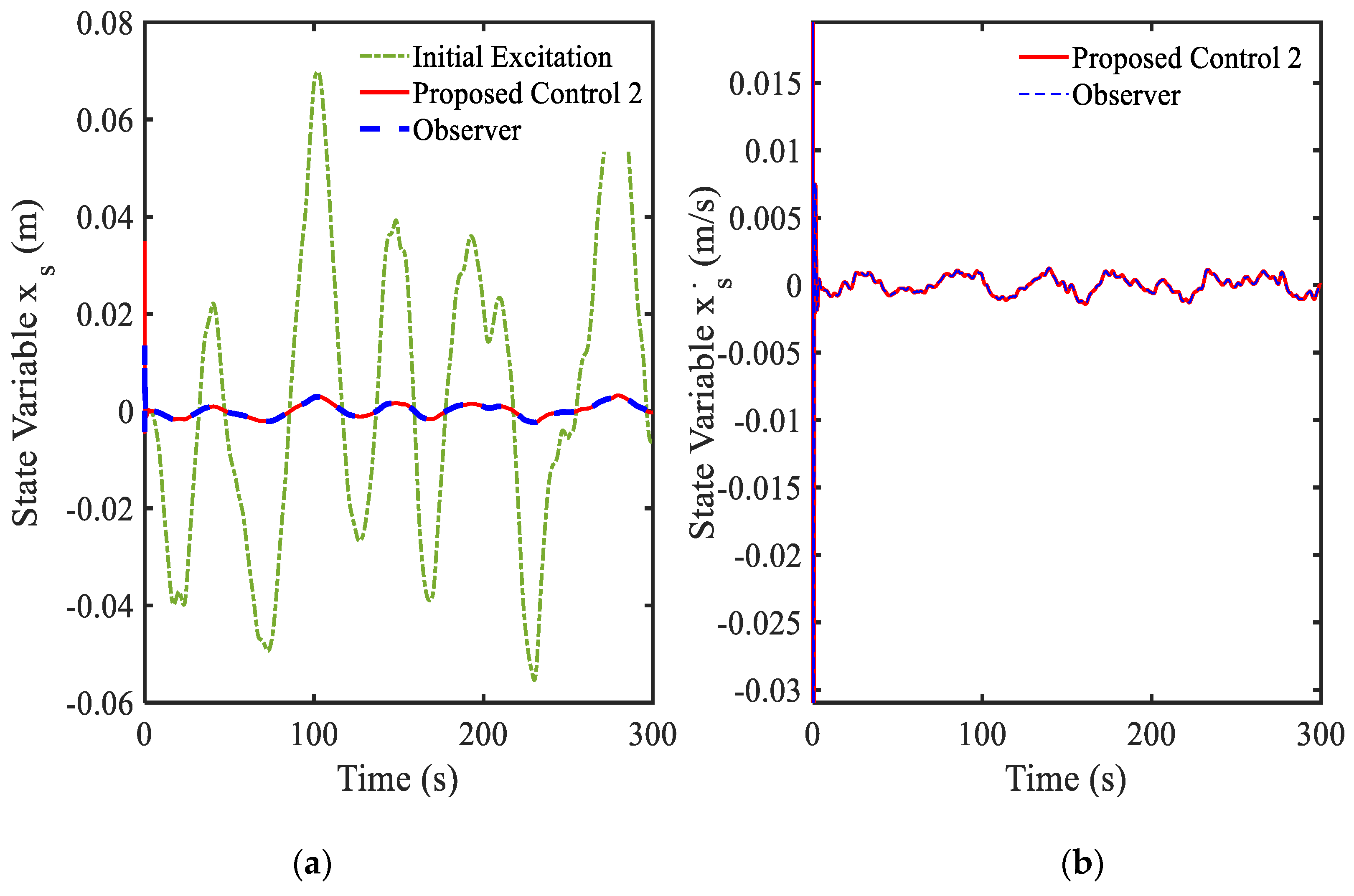
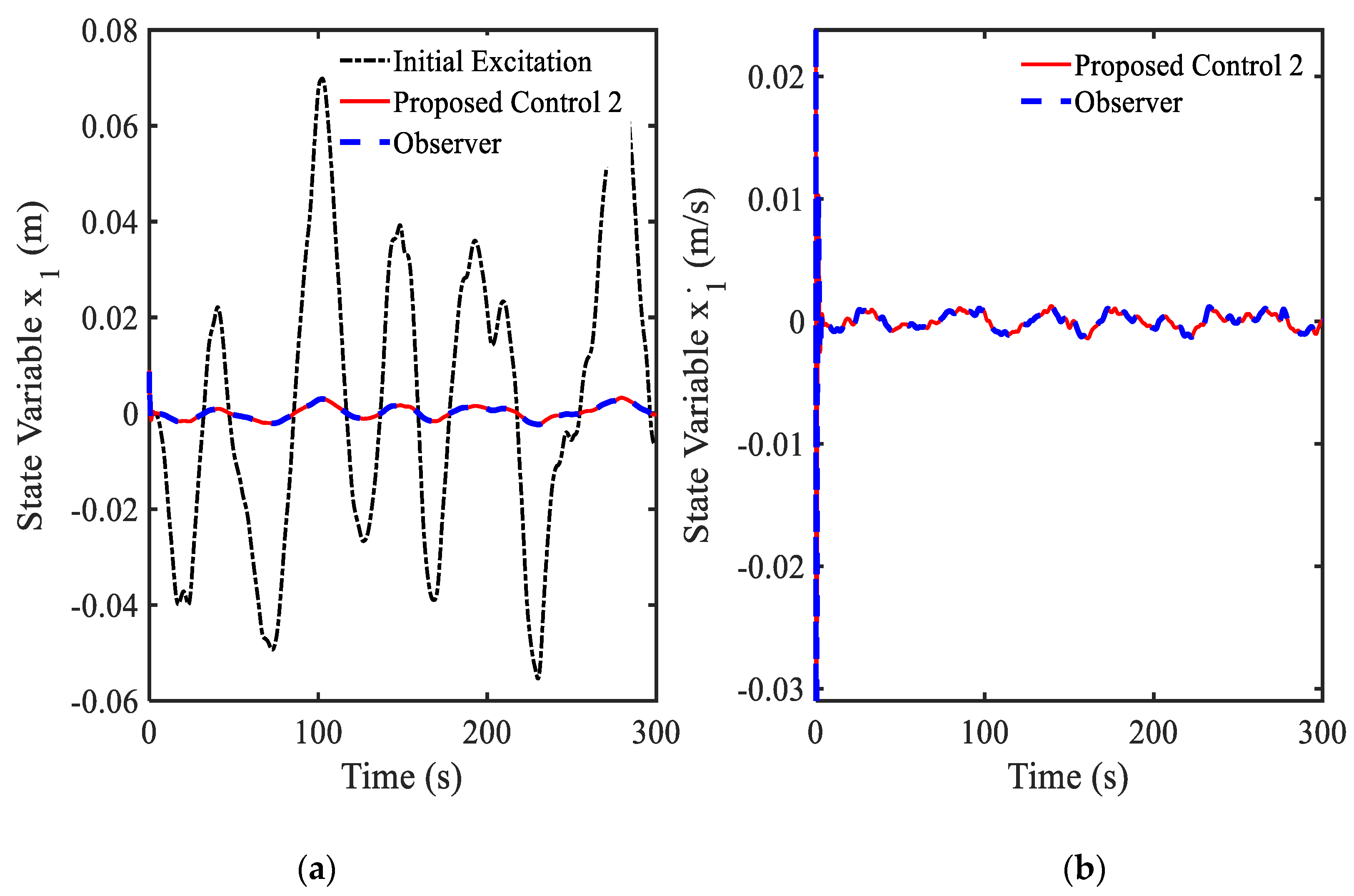
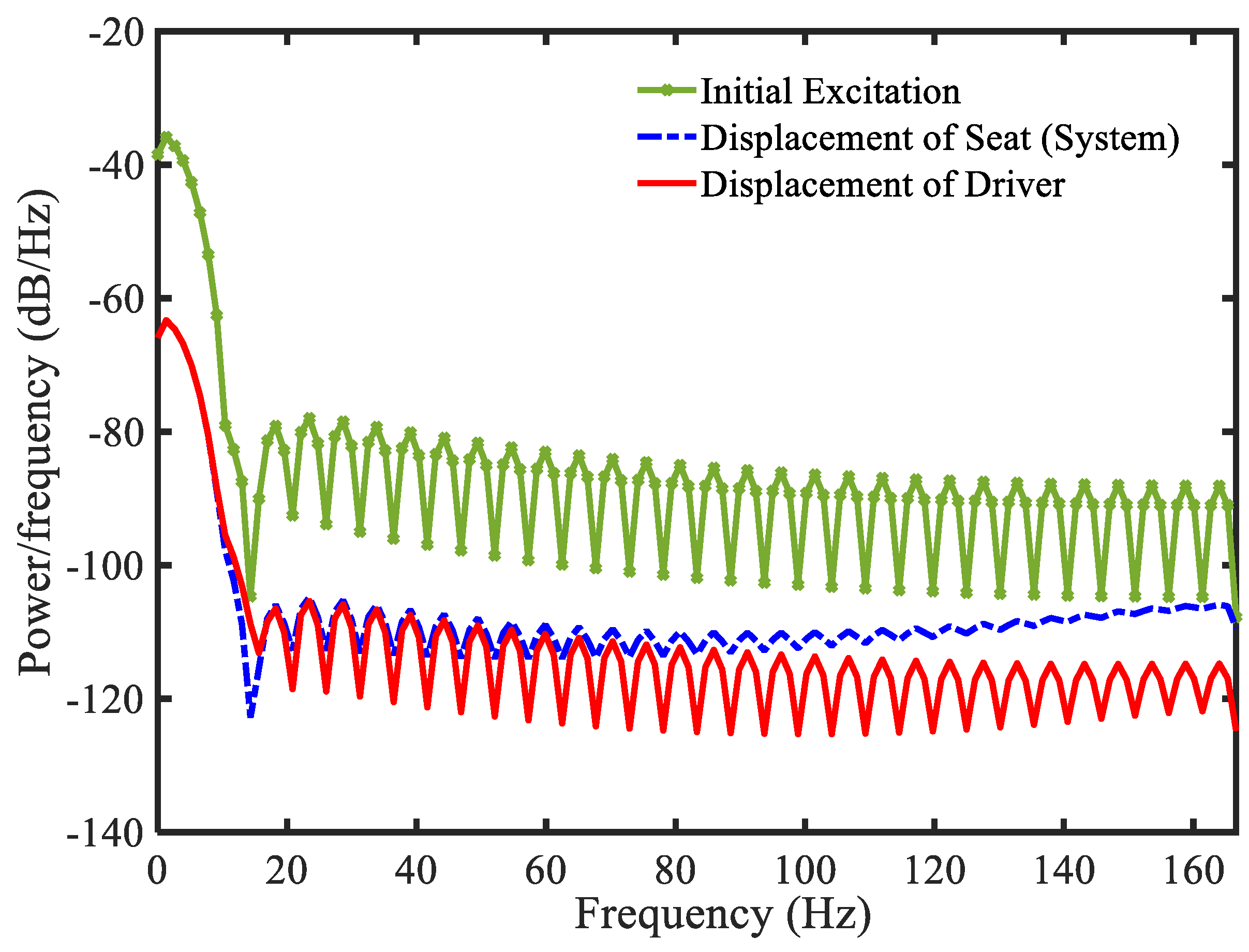
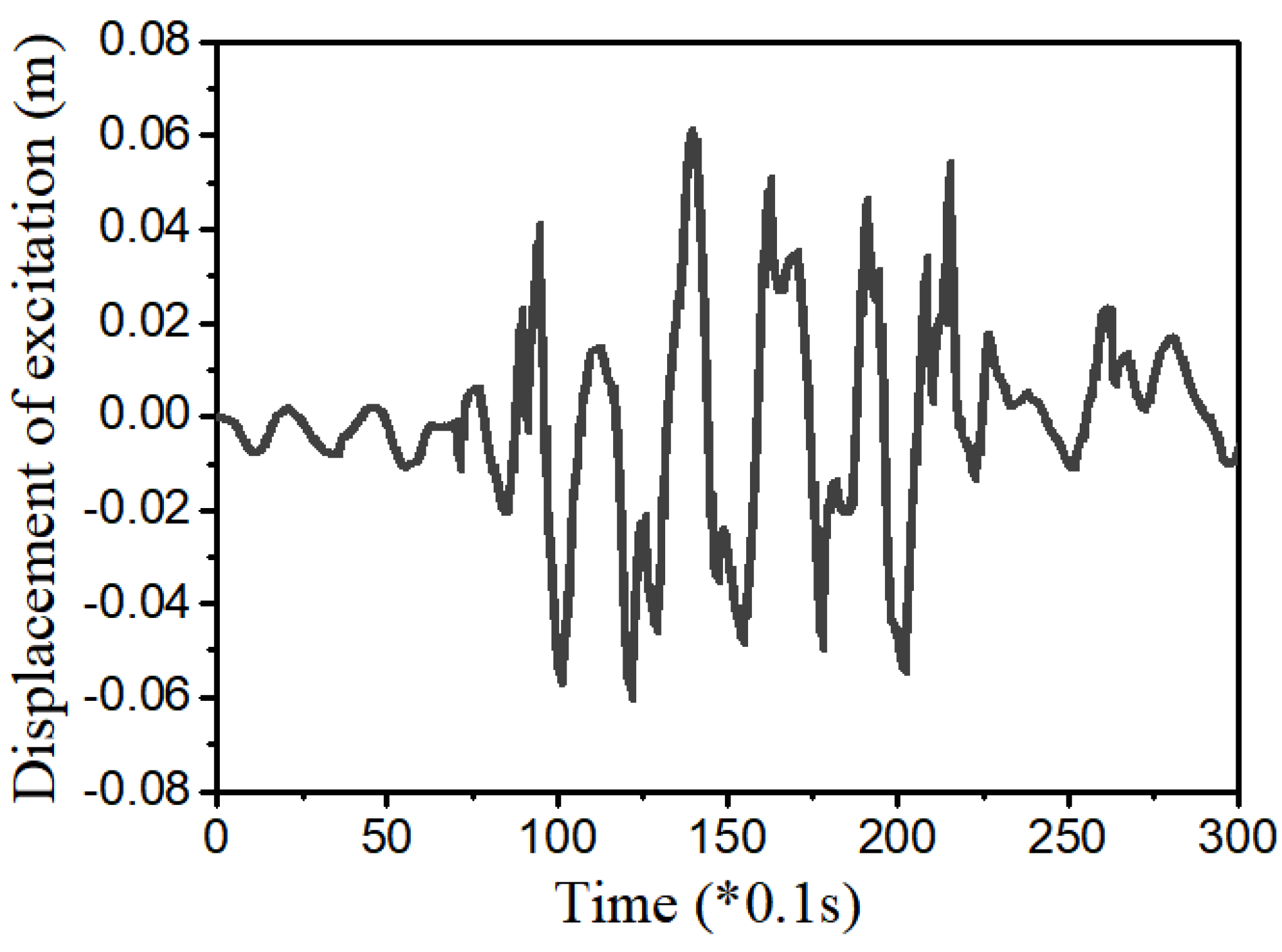
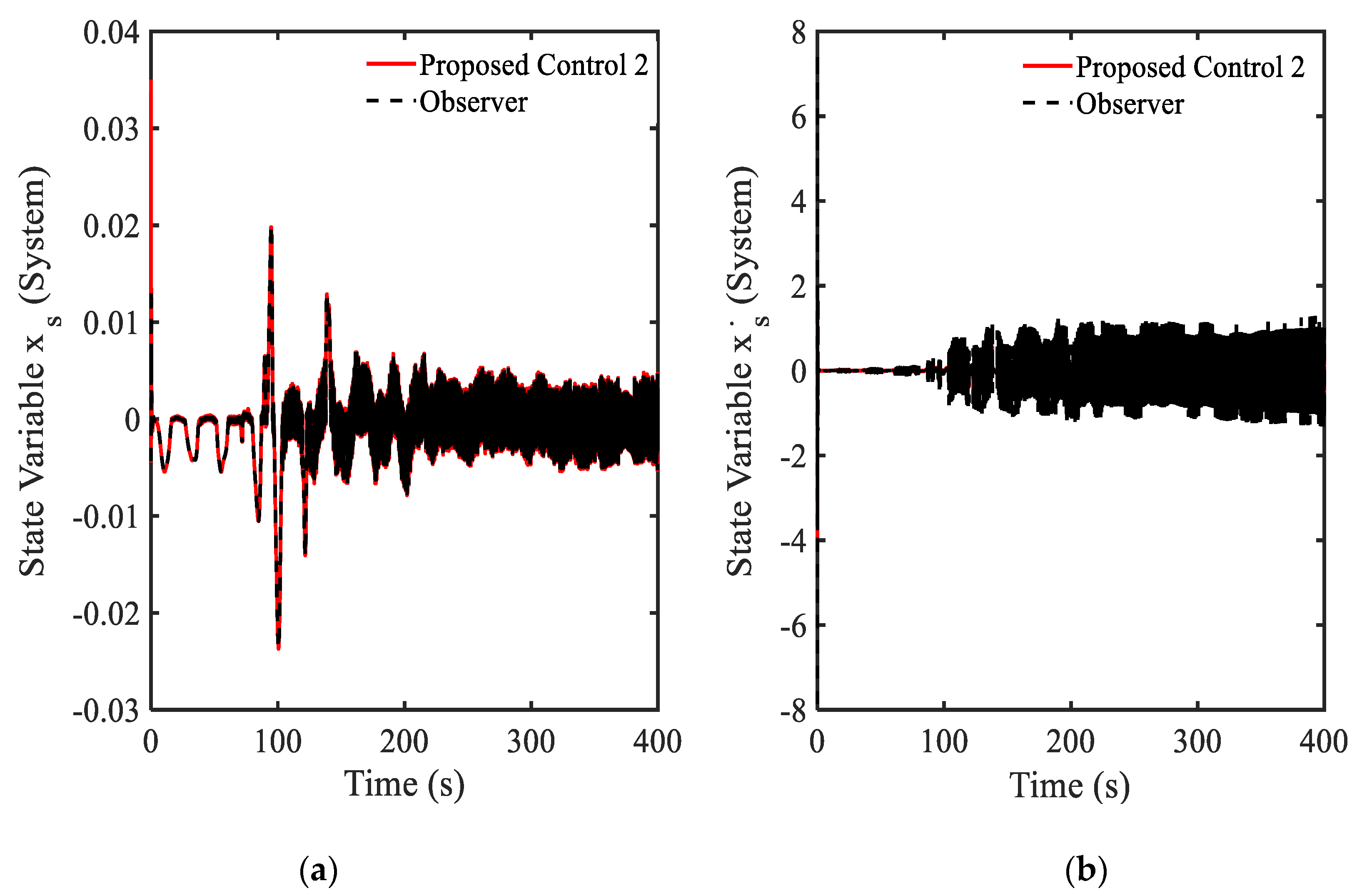
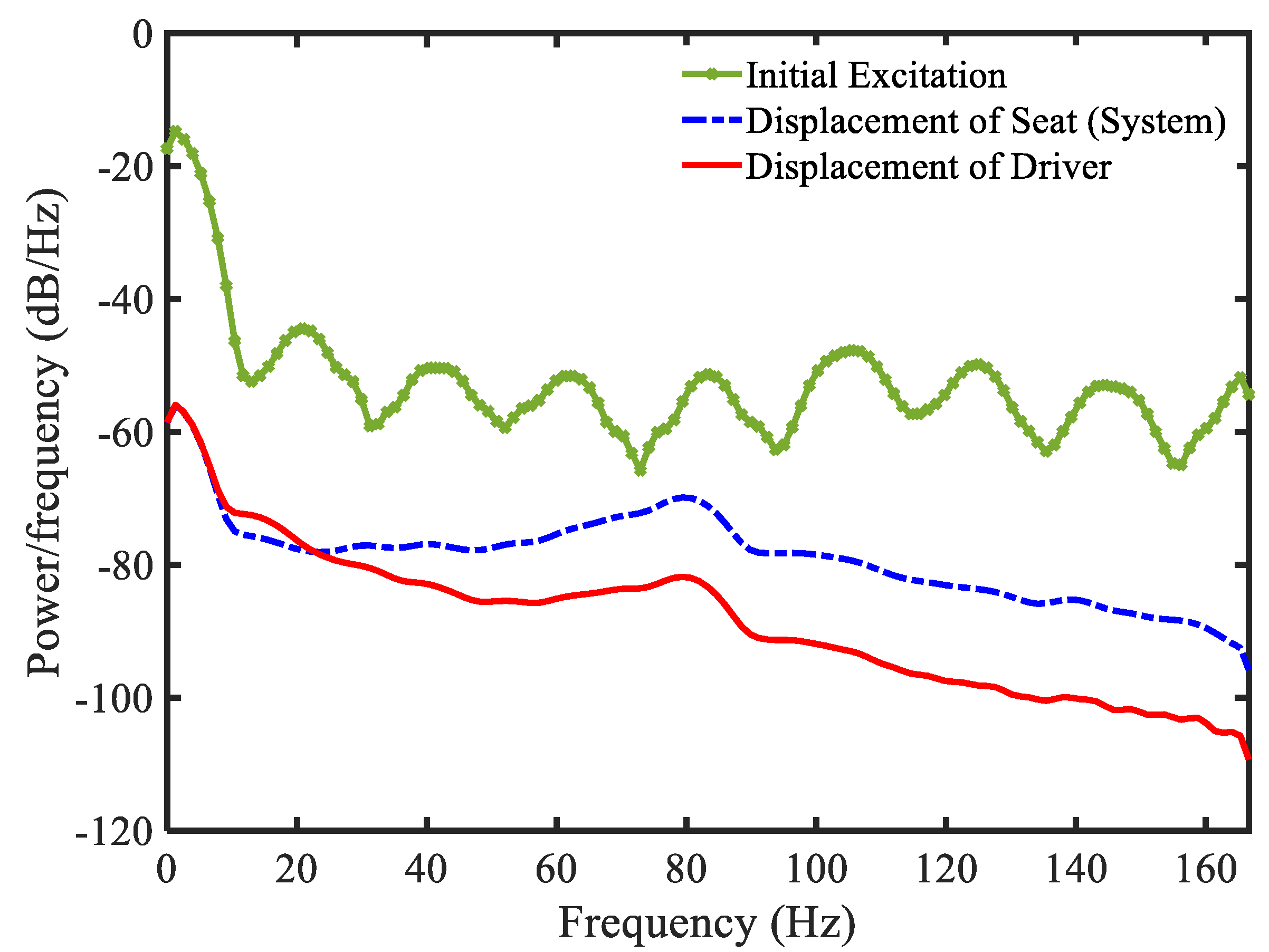
3.4. Example 4—Proposed Controller for Vibration Control with Random Bump Road Excitation (1)
3.5. Example 5—Proposed Controller for Vibration Control with Random Step Wave Excitation (2)
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Modares, H.; Lewis, F.L.; Naghibi-Sistani, M.B. Adaptive optimal control constrained input systems using policy iteration and neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1513–1525. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.; Chu, Y.C.; Ling, K.V. Inverse optimal adaptive control for attitude tracking of spacecraft. IEEE Trans. Autom. Control 2005, 50, 1639–1654. [Google Scholar]
- Bian, T.; Jiang, Y.; Jiang, Z.P. Decentralized adaptive optimal control of large scale systems with application to power systems. IEEE Trans. Ind. Electron. 2015, 62, 2439–2447. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Yang, G.H. Adaptive nearly optimal control for a class of continuous-time nonaffine nonlinear systems with inequality constraints. ISA Trans. 2017, 66, 122–133. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Kwon, S. Nonlinear optimal control design for underactuated two-wheeled inverted pendulum mobile platform. IEEE/ASME Trans. Mechatron. 2017; 22, 2803–2808. [Google Scholar]
- Xia, Y.; Yin, M.; Zou, Y. Implications of the degree of controllability of controlled plants in the sense of LQR optimal control. Int. J. Syst. Sci. 2018, 49, 358–370. [Google Scholar] [CrossRef]
- Yin, H.; Chen, Y.H.; Yu, D. Rendering optimal design in controlling fuzzy dynamical systems: A cooperative game approach. IEEE Trans. Ind. Inform. 2019, 15, 4430–4441. [Google Scholar] [CrossRef]
- Jin, W.; Kulić, D.; Lin, J.F.S.; Mou, S.; Hirche, S. Inverse optimal control for multiphase cost functions. IEEE Trans. Robot. (Early Access) 2019. [Google Scholar] [CrossRef]
- Basin, M.; Calderon-Alvarez, D.; Ferrara, A. Sliding mode regulator as solution to optimal control problem. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 2184–2189. [Google Scholar]
- Basin, M.; Calderon-Alvarez, D. Optimal controller for uncertain stochastic polynomial systems. J. Frankl. Inst. 2009, 346, 206–222. [Google Scholar] [CrossRef]
- Basin, M.V.; Rodríguez-Ramírez, P.C. Sliding mode regulator as solution to optimal control problem for non-linear polynomial systems. J. Frankl. Inst. 2010, 347, 910–922. [Google Scholar] [CrossRef]
- Basin, M.; Rodriguez-Ramirez, P.; Ferrara, A.; Calderon-Alvarez, D. Sliding mode optimal control for linear systems. J. Frankl. Inst. 2012, 349, 1350–1363. [Google Scholar] [CrossRef]
- Li, Y.M.; Min, X.; Tong, S. Adaptive fuzzy inverse optimal control for uncertain strict-feedback nonlinear systems. IEEE Trans. Fuzzy Syst. (Early Access) 2019. [Google Scholar] [CrossRef]
- Zeng, T.; Ren, X.; Zhang, Y.; Li, G.; Na, J. An Integrated optimal design for guaranteed cost control of motor driving system with uncertainty. IEEE/ASME Trans. Mech. (Early Access) 2019. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Liu, X. Adaptive near-optimal control of uncertain systems with application to underactuated surface vessels. IEEE Trans. Control Syst. Technol. 2017, 26, 1204–1218. [Google Scholar] [CrossRef]
- Choi, S.B. Vibration control of a ship engine system using high-load magnetorheological mounts associated with a new indirect fuzzy sliding mode controller. Smart Mater. Struct. 2015, 24, 025009. [Google Scholar]
- Do Xuan Phu, D.K.S.; Choi, S.B. Design of a new adaptive fuzzy controller and its application to vibration control of a vehicle seat installed with an MR damper. Smart Mater. Struct. 2015, 24, 085012. [Google Scholar]
- Huy, T.D.; Mien, V.; Choi, S.B. A new composite adaptive controller featuring the neural network and prescribed sliding surface with application to vibration control. Mech. Syst. Signal Process. 2018, 107, 409–428. [Google Scholar]
- Ciccarella, G.; Dalla Mora, M.; Germani, A. A Luenberger-like observer for nonlinear systems. Int. J. Control 1993, 57, 537–556. [Google Scholar] [CrossRef]



| Gain Matrix Function | Chosen Matrices | |||
|---|---|---|---|---|
| Property | Value | Property | Value | |
| Example 2 | Positive | Not fixed and change following the system | Not fixed with unit matrix | |
| Example 3 | Positive | Not fixed and change following the system | Not fixed with unit matrix | |
| Example 4 | Positive | Not fixed and change following the system | Not fixed with unit matrix | |
| Example 5 | Positive | Not fixed and change following the system | Not fixed with unit matrix | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phu, D.X.; Mien, V.; Choi, S.-B. A Novel Adaptive Gain of Optimal Sliding Mode Controller for Linear Time-Varying Systems. Appl. Sci. 2019, 9, 5050. https://doi.org/10.3390/app9235050
Phu DX, Mien V, Choi S-B. A Novel Adaptive Gain of Optimal Sliding Mode Controller for Linear Time-Varying Systems. Applied Sciences. 2019; 9(23):5050. https://doi.org/10.3390/app9235050
Chicago/Turabian StylePhu, Do Xuan, Van Mien, and Seung-Bok Choi. 2019. "A Novel Adaptive Gain of Optimal Sliding Mode Controller for Linear Time-Varying Systems" Applied Sciences 9, no. 23: 5050. https://doi.org/10.3390/app9235050
APA StylePhu, D. X., Mien, V., & Choi, S.-B. (2019). A Novel Adaptive Gain of Optimal Sliding Mode Controller for Linear Time-Varying Systems. Applied Sciences, 9(23), 5050. https://doi.org/10.3390/app9235050






