Damage Detection Using Modal Rotational Mode Shapes Obtained with a Uniform Rate CSLDV Measurement
Abstract
Featured Application
Abstract
1. Introduction
2. Methodology of Damage Detection Using Continuously Scanning Laser Doppler Vibrometer (CSLDV) Measurement Data
2.1. Methodology of Operational Deflection Shape (ODS) and Mode Shape
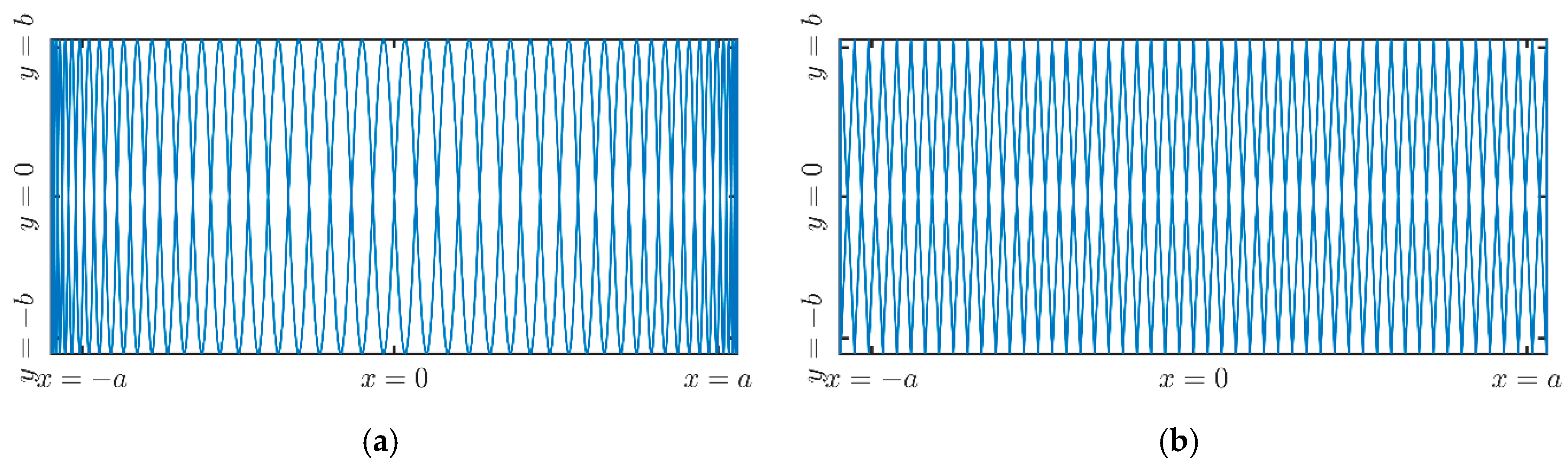
2.2. Continously Scanning Strategy for Damage Detection
2.3. Mode Shapes by Demodulation of Uniform—Rate Scanning CSLDV Output Signals
2.3.1. Measured Mode Shapes of the Damaged State
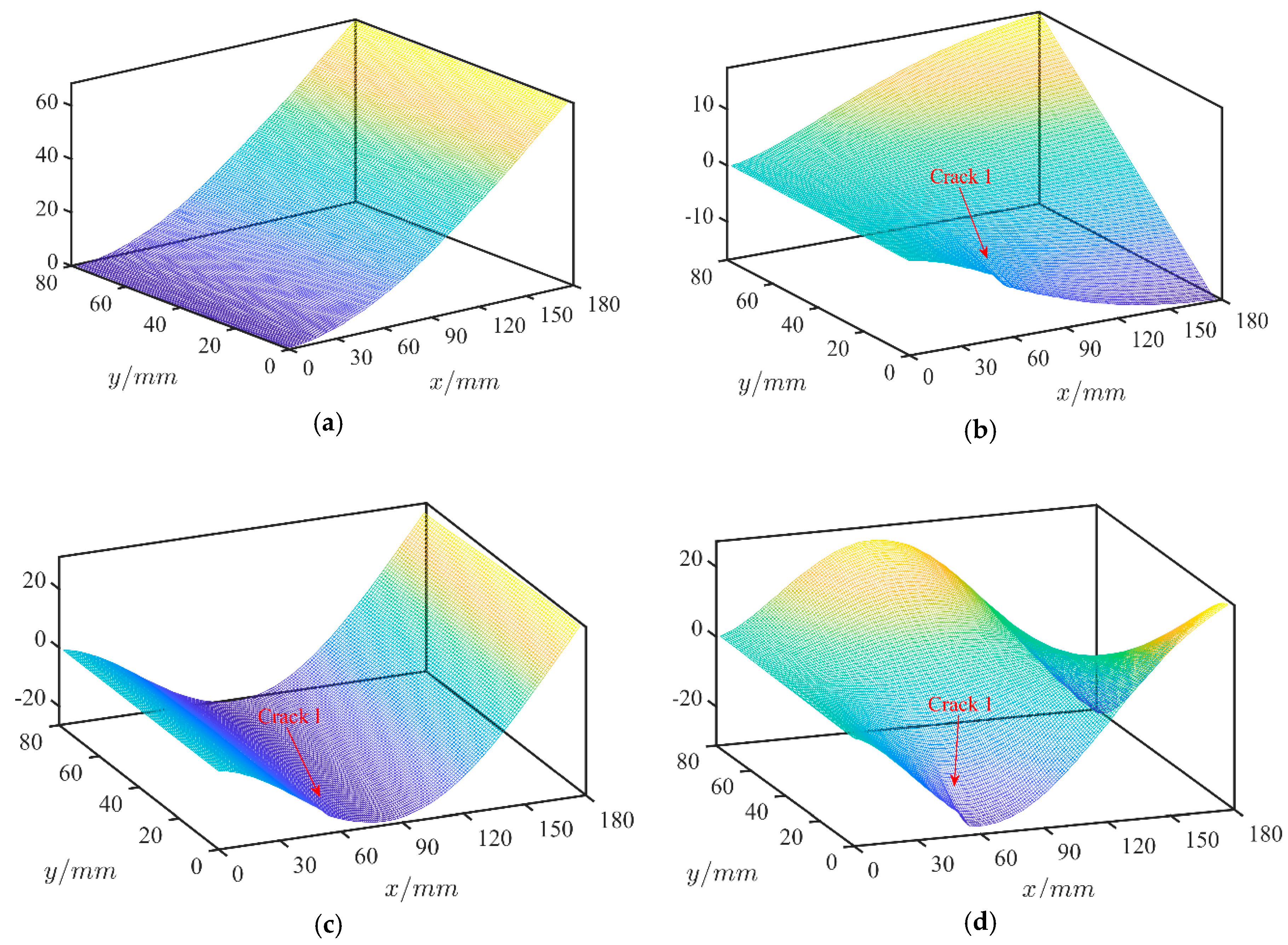
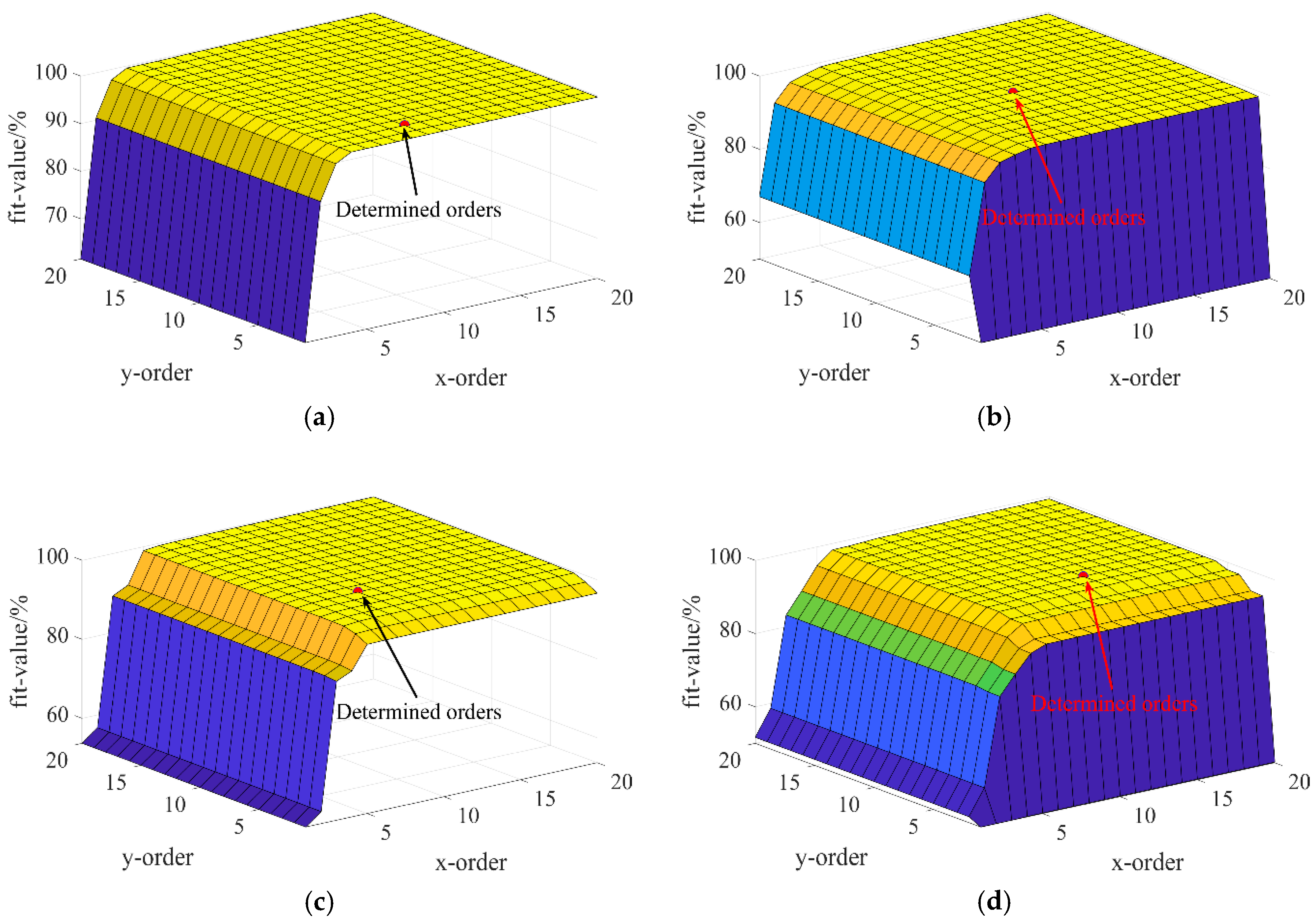
2.3.2. Surface Fitting of the Undamaged Mode Shapes
2.4. Modal Rotational Damage Indicators
3. Numerical Investigation
3.1. Finite Element Analysis
3.2. Damage Detection with Modal Rotational Damage Indicators
4. Experimental Validation
4.1. Experimental Configuration
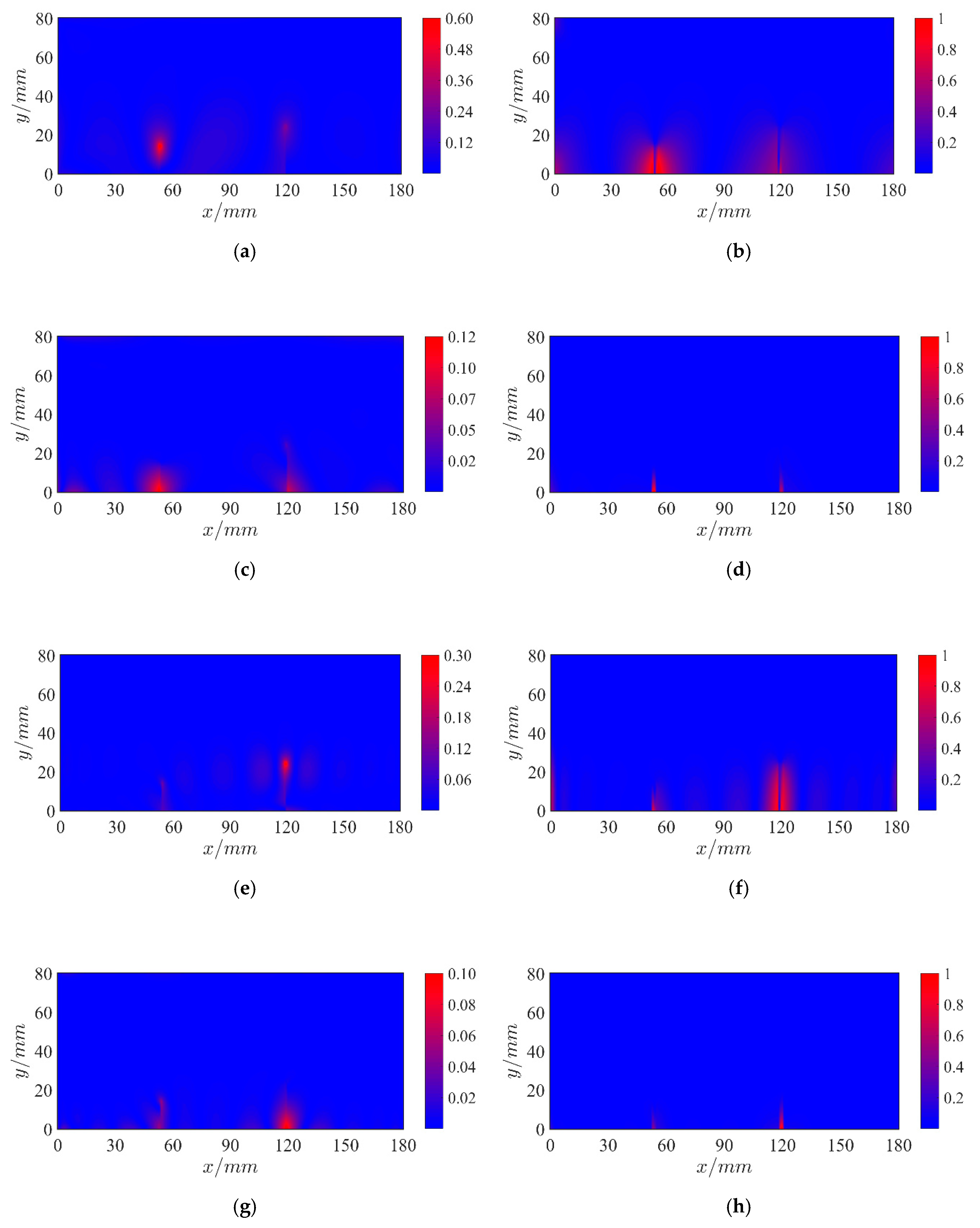
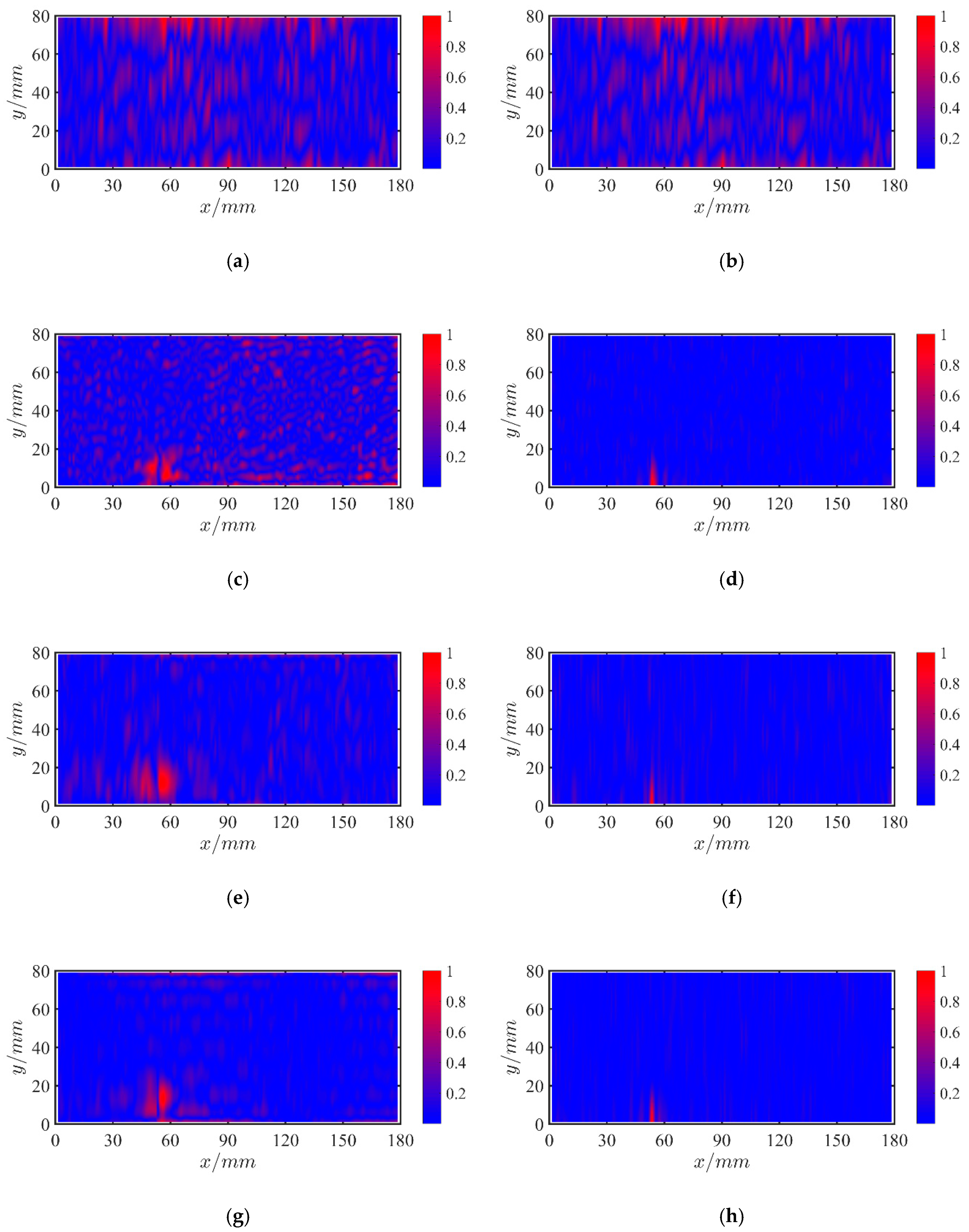
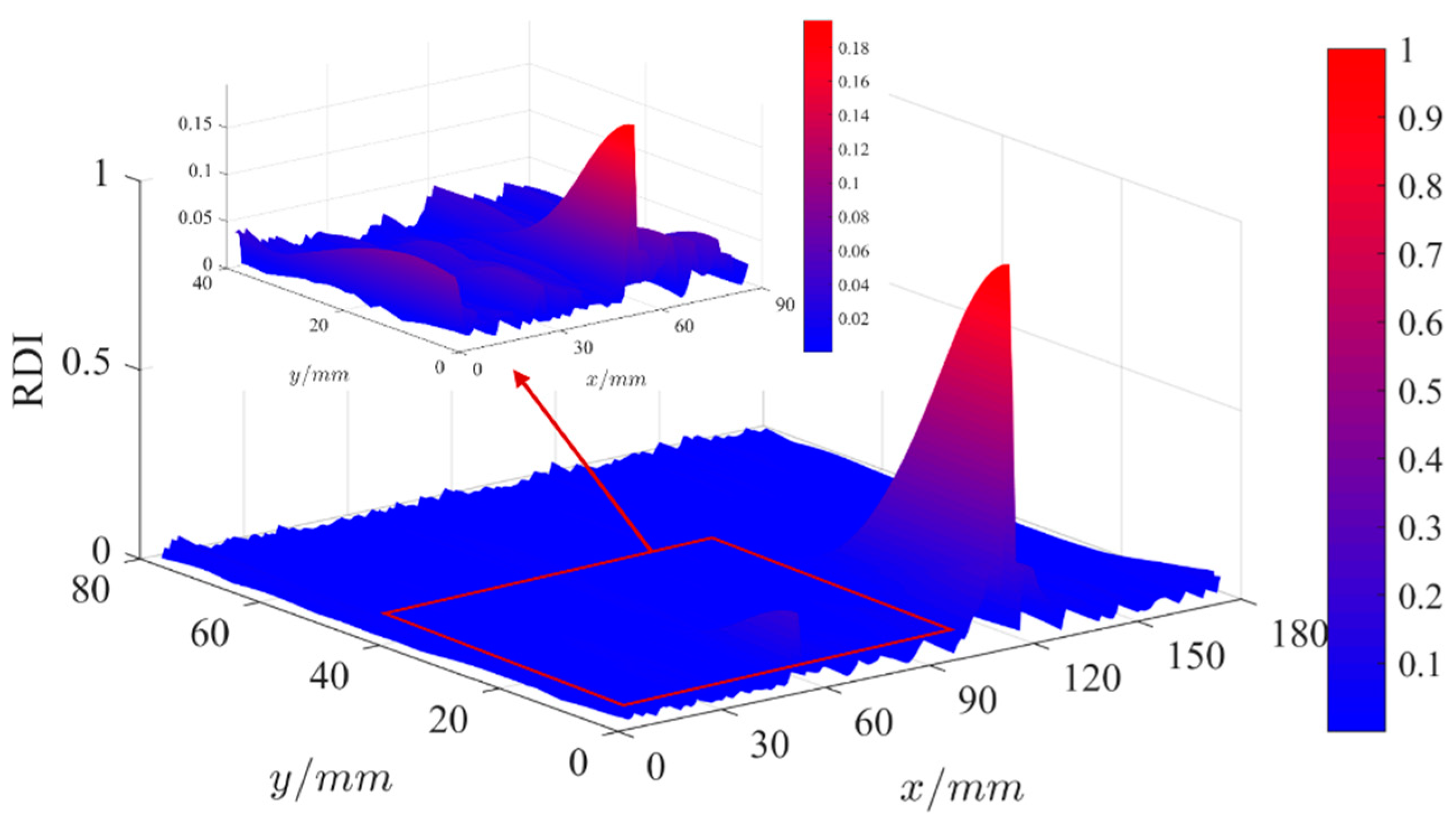
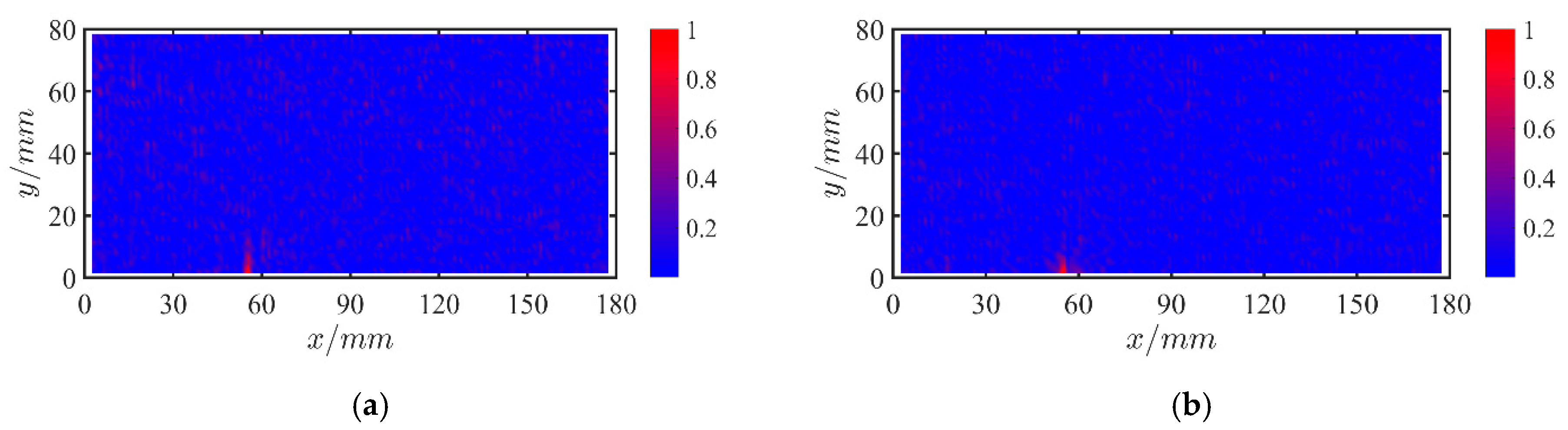
4.2. Results and Discussions of Three Damaged Cases
4.2.1. Case 1: A Single Crack
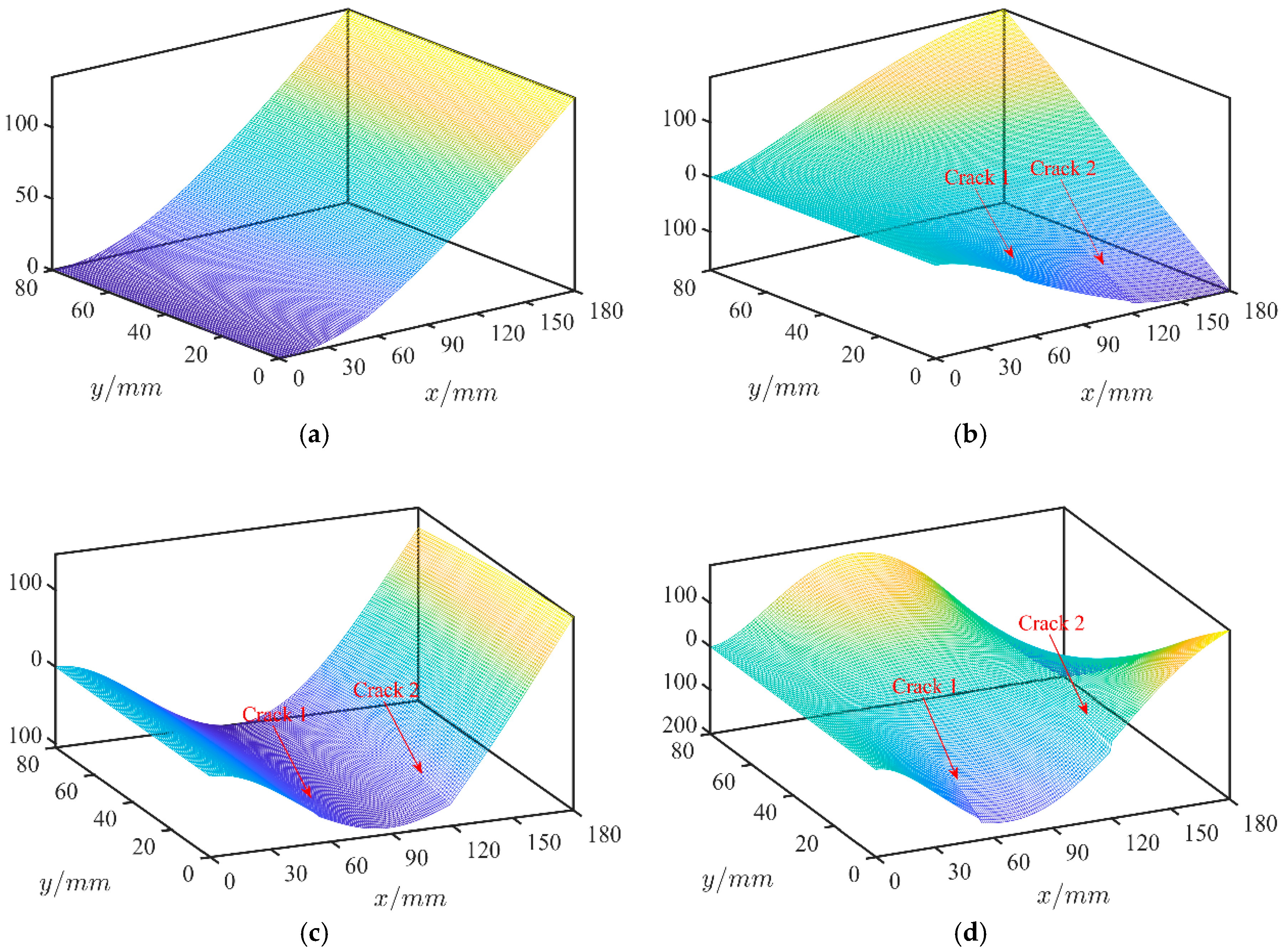
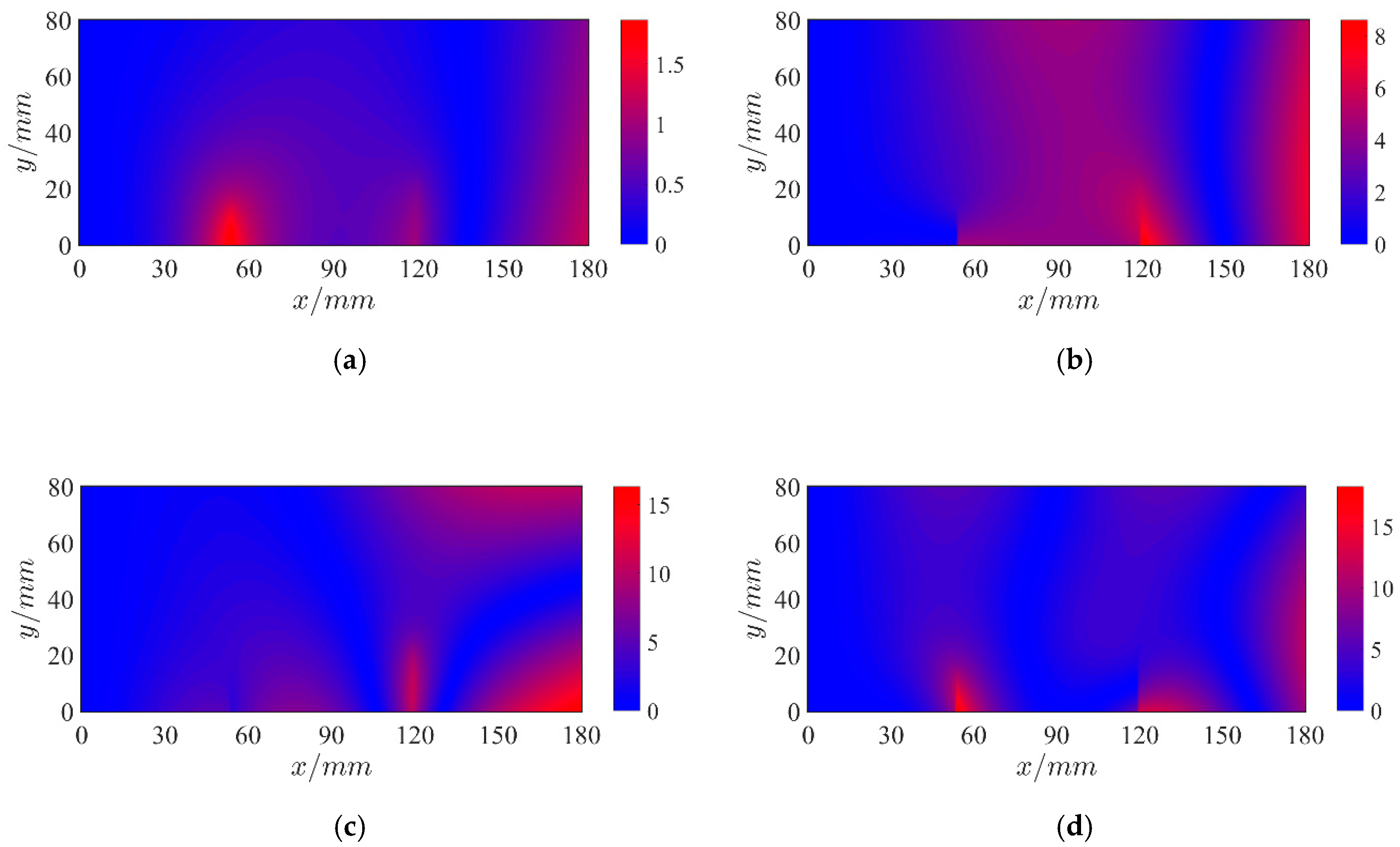
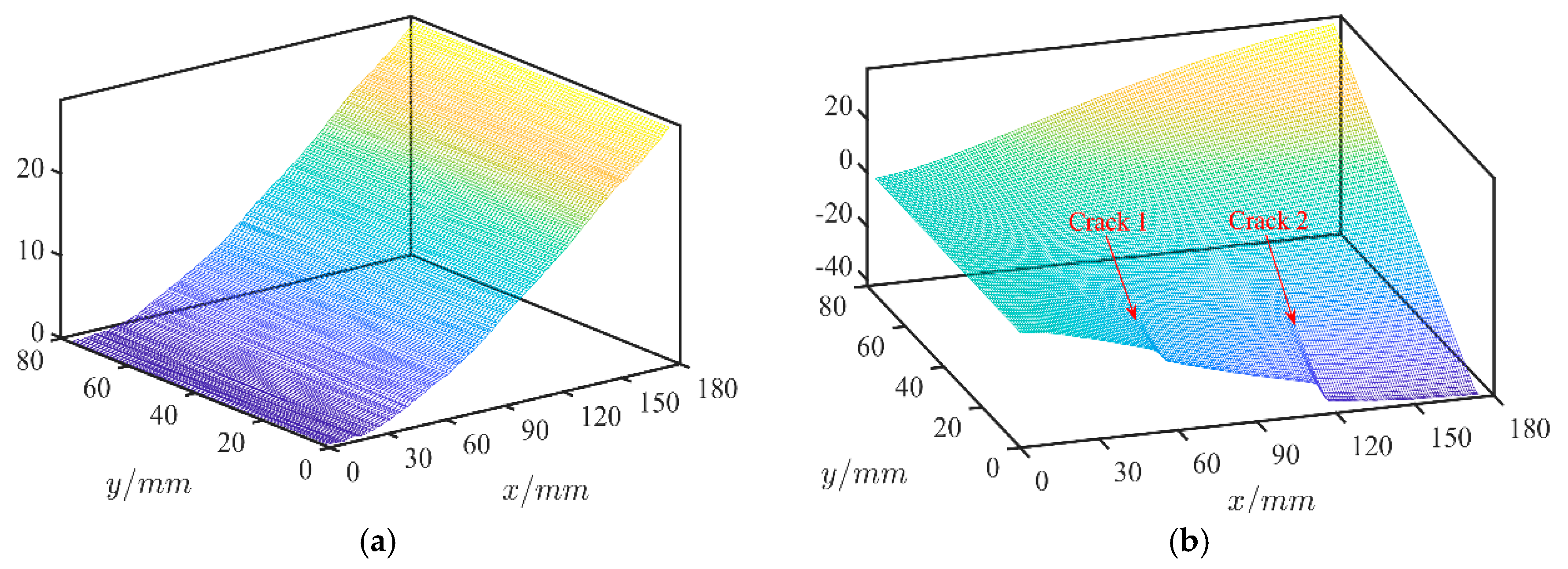
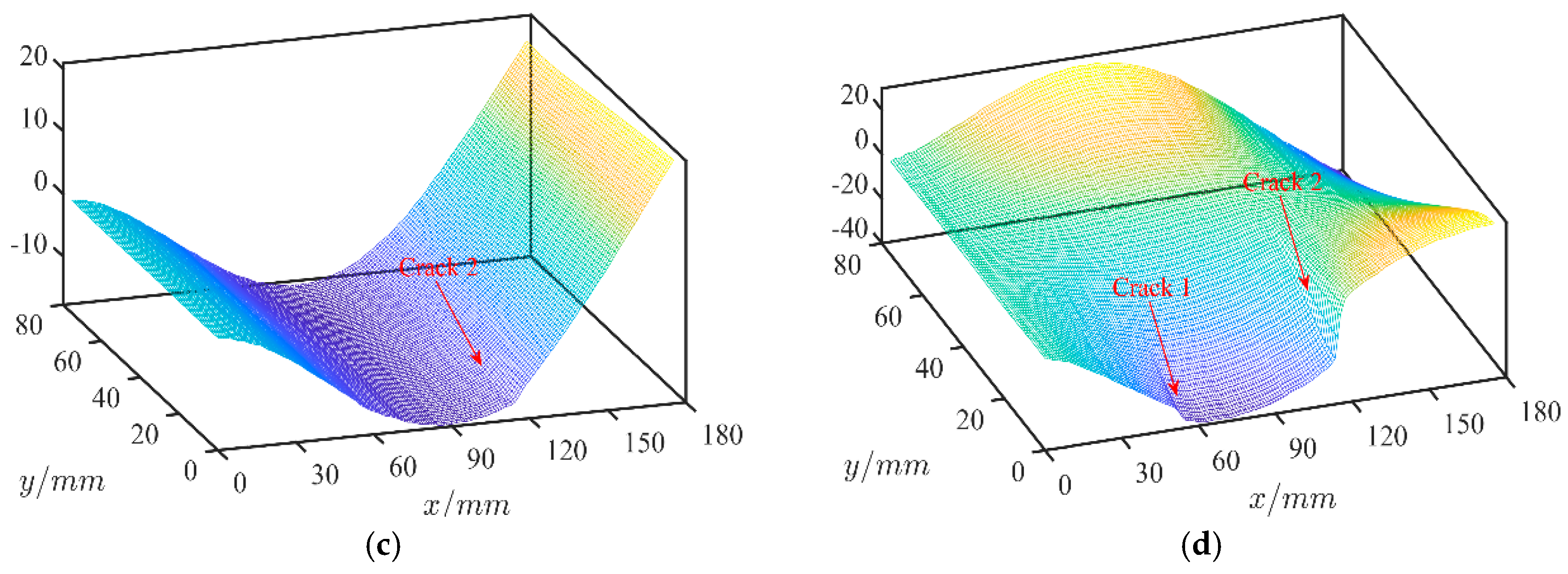
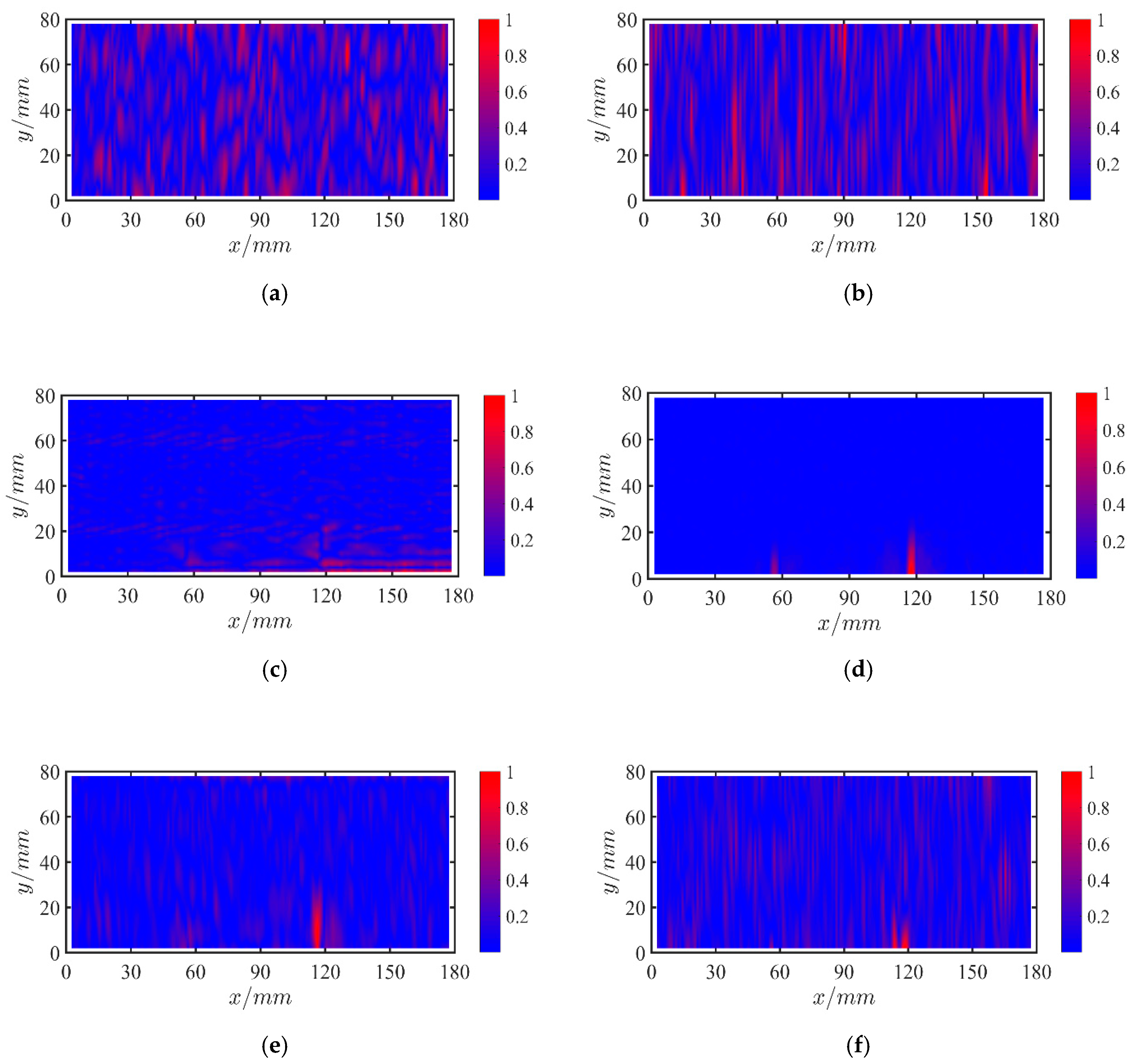
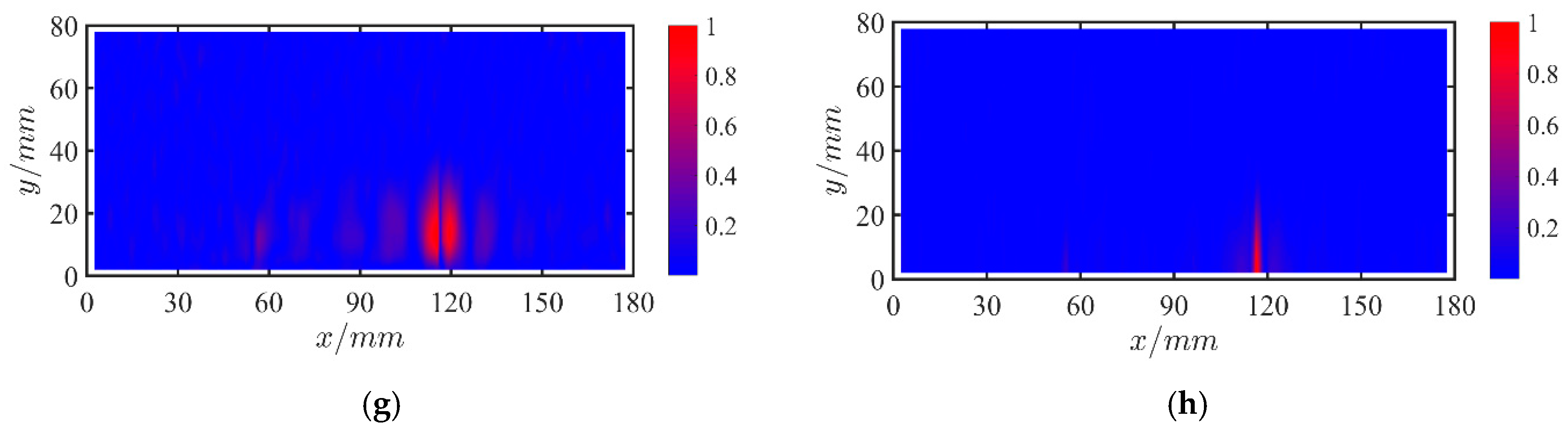
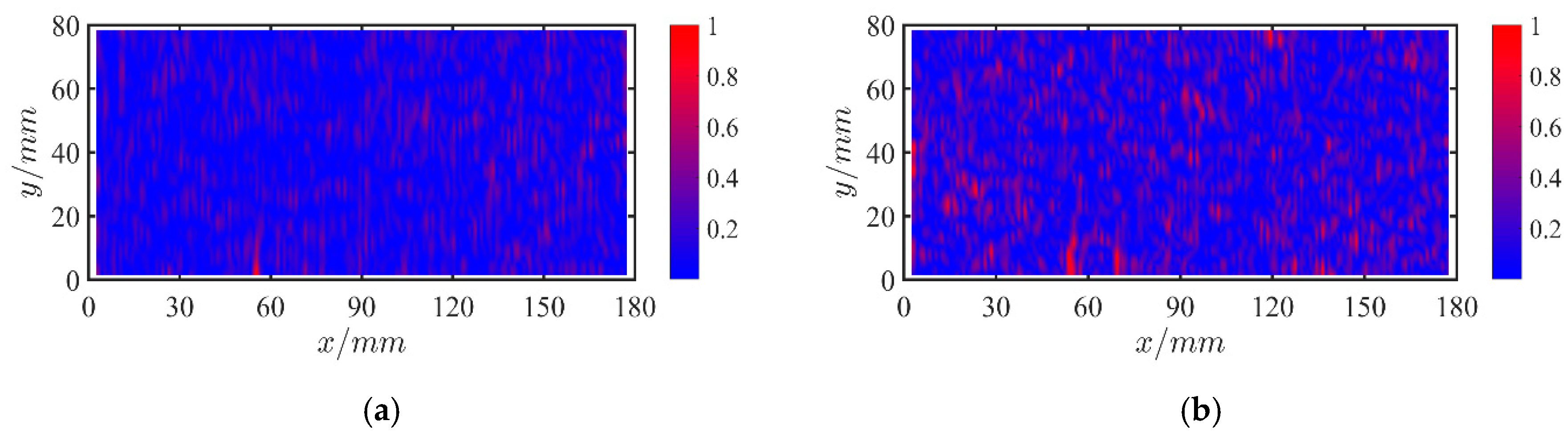
4.2.2. Case 2: Multi Cracks
4.2.3. Case 3: Slight Crack
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Doebling, S.W.; Farrar, C.R.; Prime, M.B.; Shevitz, D.W. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in the Vibration Characteristics. Shock Vib. 1996, 30, 1–127. [Google Scholar]
- Kim, J.-T.; Ryu, Y.-S.; Cho, H.-M.; Stubbs, N. Damage Identification in Beam-Type Structures Frequency-Based Method Vs Mode-Shape-Based Method. Eng. Struct. 2003, 25, 57–67. [Google Scholar] [CrossRef]
- Yan, Y.J.; Cheng, L.; Wu, Z.Y.; Yam, L.H. Development in Vibration-Based Structural Damage Detection Technique. Mech. Syst. Signal Process. 2007, 21, 2198–2211. [Google Scholar] [CrossRef]
- Jaishi, B.; Ren, W.-X. Damage Detection by Finite Element Model Updating Using Modal Flexibility Residual. J. Sound Vib. 2006, 290, 369–387. [Google Scholar] [CrossRef]
- Yang, Q.W.; Liu, J.K. A Coupled Method for Structural Damage Identification. J. Sound Vib. 2006, 296, 401–405. [Google Scholar] [CrossRef]
- Soman, R.; Kyriakides, M.; Onoufriou, T.; Ostachowicz, W. Numerical Evaluation of Multi-Metric Data Fusion Based Structural Health Monitoring of Long Span Bridge Structures. Struct. Infrastruct. Eng. 2017, 14, 673–684. [Google Scholar] [CrossRef]
- Pandey, A.K.; Biswas, M.; Samman, M.M. Damage Detection from Changes in Curvature Mode Shapes. J. Sound Vib. 1991, 145, 321–332. [Google Scholar] [CrossRef]
- Li, Y.Y. Hypersensitivity of Strain-Based Indicators for Structural Damage Identification: A Review. Mech. Syst. Signal Process. 2010, 24, 653–664. [Google Scholar] [CrossRef]
- Wei, F.; Pizhong, Q. Vibration-Based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. 2010, 10, 83–111. [Google Scholar]
- Cornwell, P.; Deobling, S.W.; Farrar, C.F. Application of the Strain Energy Damage Detection Method to Plate Like Structures. J. Sound Vib. 1999, 224, 359–374. [Google Scholar] [CrossRef]
- Dessi, D.; Camerlengo, G. Damage Identification Techniques Via Modal Curvature Analysis: Overview and Comparison. Mech. Syst. Signal Process. 2015, 52, 181–205. [Google Scholar] [CrossRef]
- Wang, S.; Xu, M. Modal Strain Energy-Based Structural Damage Identification: A Review and Comparative Study. Struct. Eng. Int. 2018, 29, 234–248. [Google Scholar] [CrossRef]
- Hu, H.; Wang, B.-T.; Lee, C.-H.; Su, J.-S. Damage Detection of Surface Cracks in Composite Laminates Using Modal Analysis and Strain Energy Method. Compos. Struct. 2006, 74, 399–405. [Google Scholar] [CrossRef]
- Hu, H.; Wu, C. Development of Scanning Damage Index for the Damage Detection of Plate Structures Using Modal Strain Energy Method. Mech. Syst. Signal Process. 2009, 23, 274–287. [Google Scholar] [CrossRef]
- Hu, H.; Wu, C.; Lu, W.-J. Damage Detection of Circular Hollow Cylinder Using Modal Strain Energy and Scanning Damage Index Methods. Comput. Struct. 2011, 89, 149–160. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P. A Strain Energy-Based Damage Severity Correction Factor Method for Damage Identification in Plate-Type Structures. Mech. Syst. Signal Process. 2012, 28, 660–678. [Google Scholar] [CrossRef]
- Sazonov, E.; Klinkhachorn, P. Optimal Spatial Sampling Interval for Damage Detection by Curvature or Strain Energy Mode Shapes. J. Sound Vib. 2005, 285, 783–801. [Google Scholar] [CrossRef]
- Cao, M.; Qiao, P. Novel Laplacian Scheme and Multiresolution Modal Curvatures for Structural Damage Identification. Mech. Syst. Signal Process. 2009, 23, 1223–1242. [Google Scholar] [CrossRef]
- Cao, M.-S.; Xu, W.; Ren, W.-X.; Ostachowicz, W.; Sha, G.-G.; Pan, L.-X. A Concept of Complex-Wavelet Modal Curvature for Detecting Multiple Cracks in Beams under Noisy Conditions. Mech. Syst. Signal Process. 2016, 76, 555–575. [Google Scholar] [CrossRef]
- Guan, H.; Karbhari, V.M. Improved Damage Detection Method Based on Element Modal Strain Damage Index Using Sparse Measurement. J. Sound Vib. 2008, 309, 465–494. [Google Scholar] [CrossRef]
- Castellini, P.; Martarelli, M.; Tomasini, E.P. Laser Doppler Vibrometry: Development of Advanced Solutions Answering to Technology’s Needs. Mech. Syst. Signal Process. 2006, 20, 1265–1285. [Google Scholar] [CrossRef]
- Di Maio, D.; Ewins, D.J. Continuous Scan, a Method for Performing Modal Testing Using Meaningful Measurement Parameters; Part I. Mech. Syst. Signal Process. 2011, 25, 3027–3042. [Google Scholar] [CrossRef]
- Shaw, A.D.; Neild, S.A.; Wagg, D.J.; Weaver, P.M. Single Source Three Dimensional Capture of Full Field Plate Vibrations. Exp. Mech. 2011, 52, 965–974. [Google Scholar] [CrossRef][Green Version]
- Wang, W.; Mottershead, J.E.; Ihle, A.; Siebert, T.; Reinhard Schubach, H. Finite Element Model Updating from Full-Field Vibration Measurement Using Digital Image Correlation. J. Sound Vib. 2011, 330, 1599–1620. [Google Scholar] [CrossRef]
- Ehrhardt, D.A.; Allen, M.S.; Yang, S.; Beberniss, T.J. Full-Field Linear and Nonlinear Measurements Using Continuous-Scan Laser Doppler Vibrometry and High Speed Three-Dimensional Digital Image Correlation. Mech. Syst. Signal Process. 2017, 86, 82–97. [Google Scholar] [CrossRef]
- Stanbridge, A.B.; Ewins, D.J. Modal Testing Using a Scanning Laser Doppler Vibrometer. Mech. Syst. Signal Process. 1999, 3, 255–270. [Google Scholar] [CrossRef]
- Chen, Q.; Zang, C. On the Laser Doppler Vibrometry Technique Based on the Continuous Scanning Ldv with Sinusoidal Rate. J. Exp. Mech. 2015, 30, 613–620. [Google Scholar]
- Chen, D.-M.; Xu, Y.F.; Zhu, W.D. Non-Model-Based Identification of Delamination in Laminated Composite Plates Using a Continuously Scanning Laser Doppler Vibrometer System. J. Vib. Acoust. 2018, 140, 4–11. [Google Scholar] [CrossRef]
- Chen, D.-M.; Xu, Y.F.; Zhu, W.D. A Comprehensive Study on Detection of Hidden Delamination Damage in a Composite Plate Using Curvatures of Operating Deflection Shapes. J. Nondestruct. Eval. 2019, 38, 38–54. [Google Scholar] [CrossRef]
- Xu, Y.F.; Chen, D.-M.; Zhu, W.D. Operational Modal Analysis Using Lifted Continuously Scanning Laser Doppler Vibrometer Measurements and Its Application to Baseline-Free Structural Damage Identification. J. Vib. Control 2019, 25, 1341–1364. [Google Scholar] [CrossRef]
- Seguel, F.; Meruane, V. Damage Assessment in a Sandwich Panel Based on Full-Field Vibration Measurements. J. Sound Vib. 2018, 417, 1–18. [Google Scholar] [CrossRef]
- Hu, Y.; Guo, W.; Zhu, W.; Xu, Y. Local Damage Detection of Membranes Based on Bayesian Operational Modal Analysis and Three-Dimensional Digital Image Correlation. Mech. Syst. Signal Process. 2019, 131, 633–648. [Google Scholar] [CrossRef]
- Katunin, A.; Lopes, H.; dos Santos, J.V.A. Identification of Multiple Damage Using Modal Rotation Obtained with Shearography and Undecimated Wavelet Transform. Mech. Syst. Signal Process. 2019, 116, 725–740. [Google Scholar] [CrossRef]
- Xu, W.; Zhu, W.D.; Smith, S.A.; Cao, M.S. Structural Damage Detection Using Slopes of Longitudinal Vibration Shapes. J. Vib. Acoust. 2016, 138, 034501. [Google Scholar] [CrossRef]
- Kim, Y.Y.; Kang, J.H. Strain Based Rotational Mode Measurement in a Beam. J. Sound Vib. 1999, 222, 225–237. [Google Scholar] [CrossRef]
- Li, S.; Wu, Z. Development of Distributed Long-Gage Fiber Optic Sensing System for Structural Health Monitoring. Struct. Health Monit. 2007, 6, 133–143. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, S.L.; Wu, Z.S.; Zhang, Q.Q. Structural Identification and Damage Detection through Long-Gauge Strain Measurements. Eng. Struct. 2015, 99, 173–183. [Google Scholar] [CrossRef]
- Hoerst, B.C.; Ratcliffe, C.P. Damage Detection in Beams Using Laplacian Operators on Experimental Modal Data. In Proceedings of the 15th International Modal Analysis Conference, Orlando, FL, USA, 3–6 February 1997. [Google Scholar]
- Ratcliffe, C.P. Damage Detection Using a Modified Laplacian Operator on Mode Shape Data. J. Sound Vib. 1997, 204, 505–517. [Google Scholar] [CrossRef]
- Yoon, M.K.; Heider, D.; Gillespie, J.W.; Ratcliffe, C.P.; Crane, R.M. Local Damage Detection Using the Two-Dimensional Gapped Smoothing Method. J. Sound Vib. 2005, 279, 119–139. [Google Scholar] [CrossRef]
- Limongelli, M.P. The Surface Interpolation Method for Damage Localization in Plates. Mech. Syst. Signal Process. 2019, 118, 171–194. [Google Scholar] [CrossRef]
- Xu, Y.F.; Chen, D.-M.; Zhu, W.D. Output-Only Modal Parameter Estimation Using a Continuously Scanning Laser Doppler Vibrometer System with Application to Structural Damage Detection. In Rotating Machinery, Optical Methods & Scanning Ldv Methods; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Zang, C. Structural Damage Detection Method Based on Decomposition of the Operating Deflection Shapes. Chin. J. Mech. Eng. 2011, 24, 480–486. [Google Scholar] [CrossRef]
- Cao, S.; Ouyang, H.; Cheng, L. Baseline-Free Adaptive Damage Localization of Plate-Type Structures by Using Robust Pca and Gaussian Smoothing. Mech. Syst. Signal Process. 2019, 122, 232–246. [Google Scholar] [CrossRef]
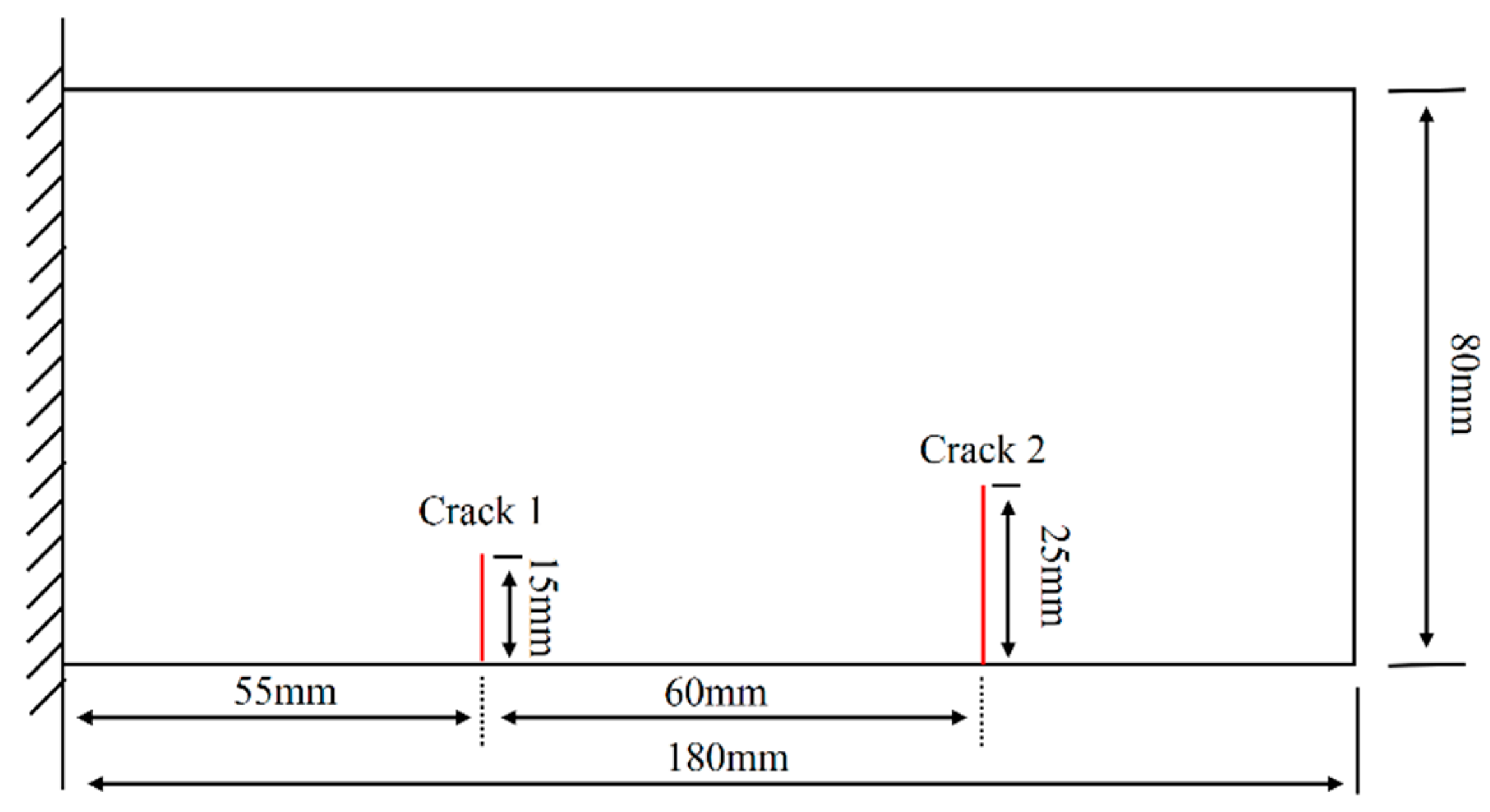

| Damage Case | Location | Size | Percent Length |
|---|---|---|---|
| Case 1 | Crack 1 | 13 mm × 1 mm | 16.25% |
| Case 2 | Crack 1 & Crack 2 | 13 mm × 1 mm & 22 mm × 1 mm | 16.25% & 27.5% |
| Case 3 | Crack 1 | 6 mm × 1 mm | 7.5% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Zang, C. Damage Detection Using Modal Rotational Mode Shapes Obtained with a Uniform Rate CSLDV Measurement. Appl. Sci. 2019, 9, 4982. https://doi.org/10.3390/app9234982
Huang Z, Zang C. Damage Detection Using Modal Rotational Mode Shapes Obtained with a Uniform Rate CSLDV Measurement. Applied Sciences. 2019; 9(23):4982. https://doi.org/10.3390/app9234982
Chicago/Turabian StyleHuang, Zi, and Chaoping Zang. 2019. "Damage Detection Using Modal Rotational Mode Shapes Obtained with a Uniform Rate CSLDV Measurement" Applied Sciences 9, no. 23: 4982. https://doi.org/10.3390/app9234982
APA StyleHuang, Z., & Zang, C. (2019). Damage Detection Using Modal Rotational Mode Shapes Obtained with a Uniform Rate CSLDV Measurement. Applied Sciences, 9(23), 4982. https://doi.org/10.3390/app9234982





