Abstract
This paper presents a new model based on the Monte Carlo simulation method for considering the uncertainty of electric vehicles’ charging station’s load in a day-ahead operation optimization of a smart micro-grid. In the proposed model, some uncertain effective factors on the electric vehicles’ charging station’s load including battery capacity, type of electric vehicles, state of charge, charging power level and response to energy price changes are considered. In addition, other uncertainties of operating parameters such as market price, photovoltaic generation and loads are also considered. Therefore, various stochastic scenarios are generated and involved in a cost minimization problem, which is formulated in the form of mixed-integer linear programming. Finally, the proposed model is simulated on a typical micro-grid with two 60 kW micro-turbines, a 60 kW photovoltaic unit and some loads. The results showed that by applying the proposed model for estimation of charging station load, the total operation cost decreased.
1. Introduction
Smart micro-grids (MGs) enable intelligent devices to adjust usage based on dynamic pricing or incentive signals. They also facilitate the integration of intermittent renewable resource and allow storage devices like electric batteries to discharge the stored energy back to the grid when it is economical [1,2,3]. There are some management strategies in order to operate the smart MGs, such as central management method in which the grid manager is responsible for the operation of the system [4], or the decentralized management method in which each group entity can be a decision maker [5].
Electric vehicles (EVs) and plug-in hybrid electric vehicles (PHEVs) are more appropriate both in terms of environmental pollution and energy costs compared to internal combustion engine vehicles [6]. One of the important advantages of the smart MG is the easier management of EVs and PHEVs due to the availability of the appropriate telecommunication infrastructure to link with them. An EV’s charging station as a load aggregator can be a good solution to manage EVs and PHEVs more easily in the smart MG and to increase consumer welfare. In this case, consumers can charge their vehicles and sell energy stored in their battery to the smart MG [7]. Therefore, unlike the typical loads, PHEVs can be discharged as the storage devices. Due to the random connection and various specifications of EVs and PHEVs, there will be severe uncertainty in their load quantities [8]. In the next section, we look for the papers in which the uncertainty of EVs loads is modeled.
1.1. Related Works
There are many papers in the field of optimal scheduling of energy systems by considering EVs uncertain behaviors. In [9], chi-square and normal distributions are used to obtain the arrival and detention time of 30 EVs in the MG, respectively. However, the type of all EVs is considered homogenous. A linear robust optimization framework is proposed in [10] to take into account the worst-case load quantities of EVs charging stations for minimizing the MG operating cost. Each EV in the aggregation has the same battery type. The problem of distributed generation of optimal placement in the presence of EVs is solved in [11], and the triangular fuzzy numbers are used to model the uncertainty of plug-in electric vehicles’ (PEVs) charging demand and another type of EVs, such as PHEVs, is not considered. In [12], the optimal operation of a virtual power plant, including EVs, wind turbines, photovoltaic (PV) system and conventional power plants, is presented. Uncertainty in the behavior of EVs is modeled by predicting their aggregated output power and calculating its deviation with the normal distribution without mentioning details about EVs. In [13], a new formulation for charging stations by considering their charging/discharging scheduling is presented for optimal planning. The scenario approach in the initial state of charge (SoC) of PHEVs batteries is used to consider their uncertainty. In this study the type of EVs and also the battery capacity of EVs are unknown. In [14], the bidding problem for a plug-in electric vehicle (PEV) aggregator in the day-ahead (DA) electricity market is investigated. The fleet is modeled as a virtual battery, clustering the batteries of PEVs connected to the grid, and there is no discussion about their different capacities and types. In [15], forecasting and modeling of load demand due to a large number of EVs fast chargers is investigated using a fitted fractional autoregressive integrated moving average model. This model is a high-quality forecasting model and includes the battery capacity and market sharing of them. However, the type of EVs and the level 2 EVs are not considered. In [16], the target for demand side management in a distribution grid including batteries and EVs is minimization of nodal, operational and power loss costs. The uncertainties lie in arrival time, departure time and energy demand of EVs, and are modeled with stochastic programming. The kernel density function is applied to model the distribution of these stochastic variables. In [17], a bi-level optimization is proposed for a fast charging station in order to maximize the profit of the station and EVs, simultaneously. Indeed, the station’s operator aggregates its EVs to participate in joint energy and reserve market, but the uncertain behaviors of EVs are not considered. In [18], the uncertainty of EVs arrival times is considered in a supply cost minimization problem by the Lyapunov optimization technique, and the battery capacities of them are unknown. In [19], the uncertainties in arrival times, dwell times, SoC, walking ranges of drivers and demand of EVs are handled by stochastic programming. Although this model includes various uncertain parameters of EVs, further parameters such as battery capacity and type of EVs can be considered. In [20], an EVs charging station is designed aiming at increasing the profitability of fast charging stations. The uncertainties of arrival time and the SoC are modeled using the Monte Carlo simulation (MCS) method. The scenario-based approach is used in [21] to consider the several types of uncertainties in the planning of charging stations including charging station type, EVs growth rate and traffic flow. A DA optimization model is proposed in [22] to determine the charging/discharging power of EVs, as well as the capacity of up and down regulation that the EV fleet can provide. The start time of EVs connection, the trip duration and the energy use are modeled by normal distributions. In [23], an algorithm based on fuzzy logic programming is proposed to consider the uncertainties of EVs parameters such as energy used by EVs and reserve prices. The proposed algorithm is capable of considering a large number of uncertainties without complexing the problem. The MCS is used in [24] to determine the expected value of PEVs load by normal distribution, and costs of underestimating or overestimating are also considered, however the technical specification of PEVs is unknown. The distribution grid in [25] is installed with multiple charging stations for EVs and deals with solar energy uncertainty. Stochastic programming is used to deal with uncertainty. Furthermore, the electrical characteristics of EVs, including charging rate and battery capacity, are used in [26] to generate different scenarios for stochastic behaviors of EVs in a parking lot. Although the type of EVs and their charger levels are considered, their price responsibility is not modeled.
1.2. Novelty and Contribution
According to a review of past references, a complete model that considers the uncertainty of EV behaviors in the charging stations is not addressed. Most of the existing models have investigated the stochastic behavior of EVs in terms of arrival times, departure times, the amount of charging energy demand, the type of EVs and battery capacity, but there is no model to see all of these factors together. There is also no model for considering the uncertainty of type of EVs chargers. Actually, the EVs in a charging station do not use a specific charger type. Some use a fast charger level 3, and some use a charger level 2. This factor is considered in the proposed model as a probabilistic parameter. Therefore, this paper tries to propose a complete model for considering this uncertainty in the optimal energy management of a smart MG. In this proposed model, some uncertain effective factors on the EVs charging station load such as battery capacity, type of EVs, SoC, charging power level and response to energy price changes (price sensitivity) are considered and simulated by the MCS method. Therefore, the contribution of this paper is as follows:
- A model for considering the uncertainty of the EVs charging station load is presented using MCS.
The remainder of this paper is organized as follows. The system model is presented in Section 2. Then in Section 3, the proposed model for charging station load is presented. The scenarios generation and the model implementation are described in Section 4 and Section 5 respectively. The optimization problem and the numerical results are provided in Section 6 and Section 7, respectively. Finally, Section 8 states the concluding remarks.
2. System Model
Figure 1 shows an overview of the intended model. The considered smart MG includes the EVs charging station, PV system as a renewable generation unit, micro-turbine (MTs) as a dispatchable generation unit and some loads. The main goal of the manager is to obtain minimum operating cost. It is assumed that all the system’s components, other than EVs, belong to the manager. To this end, the necessary information, such as PV historical data, upstream energy price forecast and the possible feathers of EVs in the charging station, is firstly collected. Then, based on the modeling of existing components and equipment, optimal decisions are taken by the manager. These decisions include optimal values of purchasing/selling power from the upstream grid, and the optimal dispatch of the micro-turbines. The uncertainties in price, load and PV generation are also modeled by stochastic scenarios. In this section, the EVs charging station load is firstly modeled by the MCS. In the next step, the stochastic scenarios generation and reduction are expressed and finally, the implementation of proposed optimization model is explained.
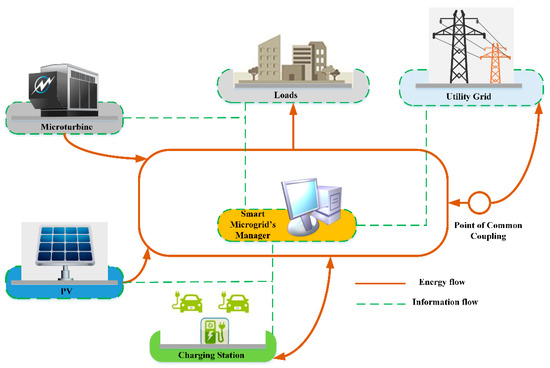
Figure 1.
Configuration of the proposed model.
3. EVs Charging Station Load Modeling
The power consumption or generation of an EVs charging station depends on several factors such as capacity of batteries; type of vehicle’s connection to the smart MG; SoC, which depends entirely on the vehicle’s driving patterns; and charging power level. There are two type of connection for EVs. Some vehicles only have charging capability and are unsuitable for vehicle-to-grid (V2G). Some vehicles have both charging and discharging capabilities and are suitable for V2G [10]. In addition, there are two rates of chargers named level 2 chargers with a low charge rate and level 3 chargers, which are known as fast chargers [27]. Furthermore, the shape of the charging station load profile can be affected by the changes in the charge and discharge programs of EVs in response to the electricity price and business hours of the charging station. In this section, all the mentioned factors are described below.
Figure 2 shows the possible states of the type and the mode of EVs in charging station. According to this figure, the EVs (which can include all types such as PEVs and PHEV, etc.) are divided into two types—suitable for V2G and unsuitable for V2G. Each EV’s owner can choose to charge or discharge their vehicle based on the electricity price at the time of use. Moreover, each EV’s owner uses a suitable charger according to its power level and the vehicle charging technology. Some EVs are not able to use a level 3 charger due to their lack of direct current charging ports. In this paper, it is assumed that the smart charger in the charging station, by connecting the vehicles, has the ability to receive the information divided in Figure 2 and also some other information like SoC and battery capacity [28]. This information is sent to the manager via the telecommunication network, as shown in Figure 3. By registering this information, a database is created in which the specifications of the vehicles used from the charging station are available on each day of the week. Therefore, by having this information for a long time (e.g., one year), the probability distributions can be fitted.
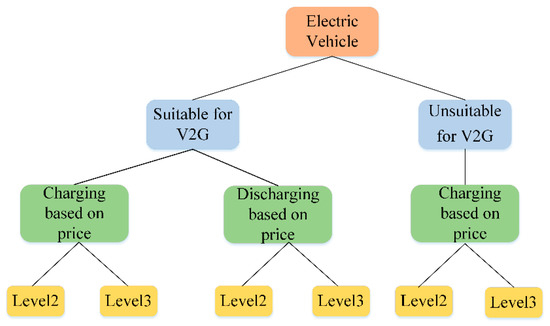
Figure 2.
Classification of possible electric vehicles’ (EVs) state in the charging station.
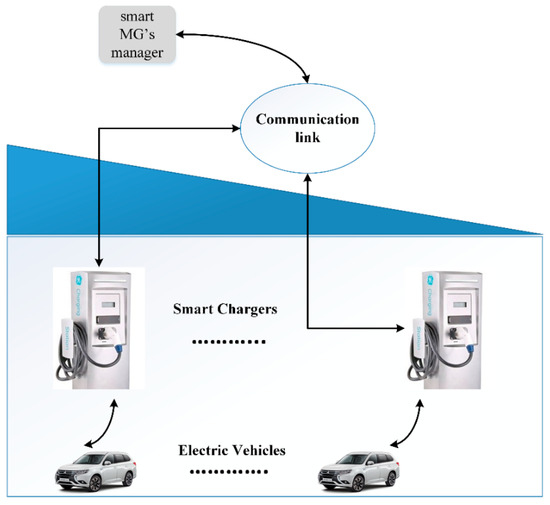
Figure 3.
Communication link between EVs and manager.
Therefore, the manager of smart MGs can use these probability distributions and estimate the amount of EVs charging station load before day of operation. This estimation for EVs helps the decision maker to operate the system in optimal points in presences of severe uncertainty of EVs behaviors. The considered distributions are described in Section 3.1 and the proposed algorithm based on MCS for modeling the EVs load is described in Section 3.2.
3.1. Probability Distributions for Stochastic Parameters of EVs
3.1.1. Type of EV j ()
It is assumed that the type of EVs is likely to have a binomial distribution. Here for simplicity, the probability of being V2G or not for each EV is considered to be 0.5 [29]. The maximum number of EVs is assumed to be 70 vehicles per day [30]. Thus, 70 random numbers based on the mentioned distribution are generated to determine the type of EVs in every repeat loop of the MCS. The value 1 for this random binary variable means that the type of EV j is suitable for V2G and 0 value for it means the type of EV j is unsuitable for V2G.
3.1.2. Price Sensitivity of EV j ()
The EVs respond to the electricity market price and set their charging or discharging program based on it. Here, the charging or discharging programs of EVs are assumed to have a binomial distribution with the probability of failure and success shown in Table 1 [31]. It shows the probability of responses to the price at different hours of the operating day. According to this table, the probabilities of charging an EV at off-peak and peak times are 0.95 and 0.15, respectively. Furthermore, the probabilities of discharging at these times are 0.5 and 0.85, respectively. Thus, the success probabilities of this random binary variable at off-peak and peak times are equal to 0.95 and 0.15, respectively. Furthermore, the failure probabilities at off-peak and peak times are equal to 0.05 and 0.15, respectively. Therefore, we are faced with a binomial distribution with an unequal chance of success and failure. So we use the roulette wheel selection method [32] to generate the binary random numbers. The value 1 for this random binary variable means that the EV j is charging and 0 value for it means the EV j is discharging.

Table 1.
Possible charging and discharging states of EVs at different times.
3.1.3. Type of Charger Used by EV j ()
The type of chargers used by EVs is modeled by a binomial distribution. In this case, the binary variable has a binomial distribution with the probability of failure and success shown in Table 2. According to this table, the probability of using level 2 and the level 3 chargers are equal to 0.6 and 0.4, respectively. Therefore, we are faced with a binomial distribution with an unequal chance of success and failure. So, we use the roulette wheel selection method [32] to generate the binary random numbers. The rates of level 2 and level 3 chargers are considered 5 kW and 20 kW, respectively [15]. The value 1 for this random binary variable means that the EV j uses charger level 2 and 0 value for it means the EV j uses charger level 3.

Table 2.
The probability of using the EVs from chargers.
3.1.4. The SoC of EV j ()
The initial SoCs of EVs batteries, with regard to [19], is determined in the form of possible scenarios. In this method, the SoCs follow a normal distribution with the mean and standard deviation shown in Table 3. According to Figure 4, the normal probability density function (PDF) for the SoC is divided into five scenarios, in which the probability of each scenario is shown in Table 4. Therefore, the roulette wheel selection method is used to obtain the initial SoC of EV j.

Table 3.
The parameters of normal probability density function (PDF).
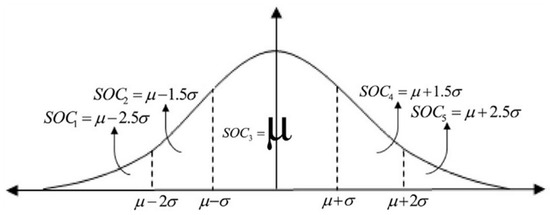
Figure 4.
The PDF for states of charge (SOCs) of EVs batteries.

Table 4.
Probability of scenarios in the considered normal PDF.
3.1.5. The Battery Capacity of EV j ()
According to [33], the batteries capacity of EVs follows a normal distribution with mean () and standard deviation () given in (1) and (2), respectively.
where and are the minimum and the maximum capacity of available batteries. According to Table 5, the random values for the battery capacity are generated based on normal PDF with the above random parameters [31]. Furthermore, due to the heterogeneity of the various types of EVs in the case of the market share, we are faced with a non-uniform distribution for generating the random numbers according to Table 5. So, the roulette wheel selection method is used to generate the random numbers.

Table 5.
Specifications of different EVs.
3.2. Probabilistic Estimation of EVs Charging Station Load
One of the most commonly used numerical methods for handling the uncertainties is MCS. This method is used when the system is highly non-linear or it has a lot of uncertain variables [34]. Although batteries have memory and it is better to use the sequential MCS, which generates sequential samples of SoCs for numerous time intervals [35], but we have used non-sequential MCS to avoid complicating the simulation and time-consuming convergence. Therefore, this method has been used in the proposed model because of its many uncertain parameters. The proposed algorithm for the estimation of EVs charging station load is as follows:
- g = 1.
- Set MCS counter M = 1.
- j = 1.
- Randomly generate samples for type of charger used by EV j, type of EV j, charging or discharging of EV j, SoC of EV j and battery capacity of EV j all based on their distribution functions assigned in Section 3.1.
- With and equal to 1, if is equal to 1, then the charging time of EV j can be calculated via (3) with the rate of a level 2 charger (i.e., cl = 2). Otherwise the discharging time of EV j can be calculated via (4) with cl = 2. If is equal to 0, thus the EV j can only be charged with the charging time as (3).where and are the charging and discharging time of EV j with charger level cl which uses charger g. and are the charging and discharging rates of charger level cl and charger g. Furthermore, and are the maximum and minimum SoC for EV j. The similar process occurs when equal to 0 with the difference that the rate of charger level 3 would be considered in (3) and (4) (i.e., with cl = 3).
- The charging or discharging energy of EV j or is calculated using (5).
- If j < , j = j + 1 and go back to 4; otherwise calculate the charger load using (6).where is the average consuming power of charger g in repetition M.
- Evaluation of . is the average consuming power of charger g in all repetitions.
- Check if is converged then go to 10, else M = M + 1 and go to 3.
- If g < , g = g + 1 and go back to 2; otherwise calculate the EVs charging station load through the sum of the calculated chargers loads using (7).
- Finish.
The proposed MCS-based algorithm is presented in Figure 5. The convergence condition of the loop is considered as follows. First the relative error RE is calculated every 10,000 simulations using , where represents the standard error and is the confidence level. Its equal to 1.96 for 95% confidence interval. Furthermore, is the mean of the simulation. The simulation stops if the RE is less than 1% [36].
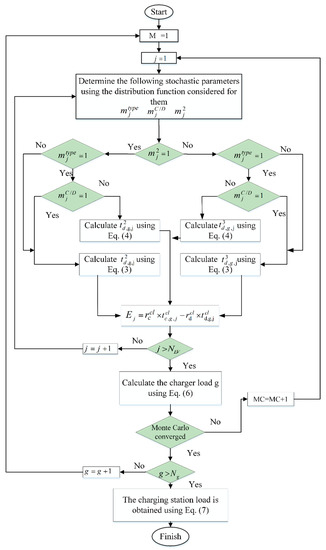
Figure 5.
The flowchart of the proposed Monte Carlo simulation (MCS)-based algorithm for the estimation of charging station load.
4. Uncertainties of Price, Load and PV Generation
In order to consider the forecasting uncertainties in the operating parameters such as load, price and PV generation, stochastic scenarios are generated. To this end, a large number of possible scenarios of the above parameters are generated based on their PDFs. In fact, we assume the manager can fit the appropriate distributions on the forecasting error data. Therefore, the forecasting error of the system’s load and price are modeled with a normal distribution with an average of zero and a standard deviation of 10% of their hourly forecasted values [37]. Furthermore, the historical solar irradiance data is modeled with the beta distribution [38]. Using the MCS method, 2000 stochastic scenarios are generated for each of the above parameters based on their PDFs. So, the probability of each scenario is 1/2000. Then, the set of system scenarios is formed. Each stochastic scenario represents a possible operating mode of the system and consists of a vector as which includes the PV generation, prices and loads scenarios. In this study, the correlation analysis between the scenarios of different parameters is ignored. Although the high number of stochastic scenarios increases the accuracy of the answers, it slows down the problem-solving time. In stochastic optimization problems, one of the most commonly used scenarios reduction methods is the Kantorovich distance. In this paper, this method is used to reduce the number of random scenarios. Further details of this method are given in [39]. So, the system scenarios are reduced to 200 numbers. In fact, it is assumed that these 200 stochastic scenarios can cover the most possible modes of the system.
5. Model Implementation
The operation optimization problem is simulated based on the following steps:
- Receiving the forecasted values of upstream market prices, demand power of loads and PV historical data.
- Organizing the normal and Beta PDFs of the uncertain parameters at all 24 operation time slots.
- Generating stochastic scenarios based on the mentioned PDFs and then reducing them by the Kantorovich distance algorithm. Each scenario consists of three parts as described before.
- Computing the EVs charging station load by the proposed method.
- Applying the scenarios and EVs charging station load to the optimal operation problem of smart MGs.
- Solving the optimal operation problem for all scenarios and saving the results for each decision variable, for each scenario and at each time slot.
Figure 6 illustrates the model implementation process.
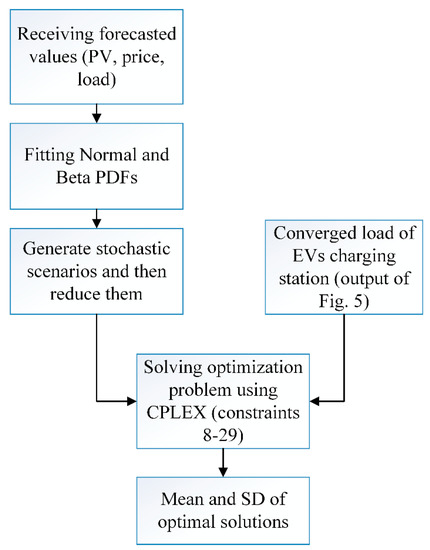
Figure 6.
Model implementation process.
6. Problem Formulation
6.1. Objective Function
The objective function is minimizing the operating cost as follows:
The objective function (8) is costs for day ahead operation. The costs consist of purchasing energy from the upstream grid and EVs, as well as the cost of the PV unit () and micro-turbines () operation. in (8) is the DA market price in scenario s at time t. is the selling/purchasing power from the upstream grid in scenario s at time t. The smart MG may sell energy in some intervals, so would be negative if the smart MG is selling energy to the upstream grid. There are interesting optimization methods in [40,41,42,43,44,45,46]. We formulate the optimization problem as mixed-integer linear problem (MILP).
6.2. Constraints
The system constraints are given in the following.
6.2.1. Operating Constraints for Micro-Turbines
For , the following constraints are considered:
where is the operation cost of micro-turbine i in scenario s at time t and consists of generation, startup and emission costs as (9). is the generation cost of micro-turbines i in scenario s at time t and is modeled in (10)–(14) by piecewise linear function [47]. is the generation cost of micro-turbine i at its minimum generation. is the segments index in the cost function of micro-turbine i. and are the number of segments in the cost function of micro-turbine and the marginal cost of segment in the cost function of micro-turbine i ($/kWh), respectively. is the maximum limit of power generation in the -th segment of micro-turbine i cost function (kW). is the power generation of micro-turbine i from the -th segment in scenario s at time t. Furthermore, Start-up cost and emission cost are given in (15) and (16), respectively. is startup constant cost. is carbon dioxide pollutant of micro-turbine i at time t and is externality cost of generation carbon dioxide ($/kg).
In (17), is the generating power of micro-turbine i in scenario s at time t and is limited to their bounded maximum and minimum capacity, i.e., and . and are the ramping up and down rates of micro-turbine i and are limited in (18) and (19), respectively. The (20) and (21) impose the minimum up/down time constraints for micro-turbines. and are the minimum up and down times of micro-turbine i. Finally, the binary variables relationships are formulated as (22) and (23). , and are the startup, shutdown and commitment indicators of micro-turbine i [48,49,50].
6.2.2. PV Operation Cost
The generation of PV unit is strongly dependent on environmental parameters such as temperature and amount of sunlight. The total output power of the PV system at a maximum power point is calculated in (24) [51].
where in (24), , , and are the output power of PV unit p at time t, the cell’s rated power in the standard measurement (i.e., at 25 °C, radiation levels 1000 W/m2 and wind speed 1 m/s), the radiation level at time , the temperature coefficient, respectively. and are the number of series and parallel cells. Furthermore, and NOCT are the ambient temperature and normal operating cell temperature. The generation cost of PV system (i.e., ) is calculated in (26), which includes the investment, operation and maintenance costs.
6.2.3. Technical Constraints
The amount of power exchanged with the upstream grid at any time is limited as (28).
where is the maximum exchangeable power with the upstream grid.
6.2.4. Power Balance
At any time, the total power of the micro-turbines and the actual power exchanged with the upstream grid should be equal to the net load of the system.
where is the MG load in scenario s at time t. is the calculated charging station load. It should be noted that network constraints of the smart MG are neglected. Based on [52], there are two justifications for this simplification. First, a MG practical size may be limited to a few MVA [53]. IEEE draft standard P1547.4 specifies an upper limit of 10 MVA [54]. Due to the limited capacity and the proximity of load and generation in an MG, the network is typically not the limiting constraint. Second, the network model greatly complicates operation model without much likely benefit.
7. Numerical Results
7.1. System Data
The proposed optimization problem is applied to a typical smart MG including two 60 kW similar micro-turbines, one 60 kW PV system, one EVs charging station and some loads. The micro-turbines’ parameters are shown in Table 6 [52]. The carbon dioxide (CO2) produced by a micro-turbine is considered to be 0.7 kg/kWh and its emission cost is 0.001 $/kg [55]. The micro-turbines’ quadratic production cost is approximated by a three-piecewise linear function.

Table 6.
Parameters of micro-turbines.
The PV system consists of 6 × 25 solar modules parallel to 25 rows, each with 6 series modules. The rated power of each module is 400 W in the standard condition. The price of each module including the power electronics (inverter) and installing costs, is considered $1 per watt. The operation and maintenance cost of the PV system is assumed to be 1.5% of its initial investment. The interest rate and the period for the loan repayment of the PV system are considered to be 7% and 20 years, respectively. According to the PV system’s specifications, its capacity factor is considered to be 26%. Historical data of direct solar irradiance power is extracted from [56]. The scheduling horizon is 24 h and each time interval is considered to be 1 h. The forecasted loads and upstream market prices are taken from [52]. As can be seen, hour 8 is the beginning of the peak periods. The PDFs of uncertain parameters are calculated and shown in Table 7. In this table, the mean values of parameters are hourly forecasted parameters. Based on this table and Section 2, the number of 200 scenarios are considered.

Table 7.
Statistic feathers of uncertain parameters.
The proposed EVs charging station load model and scenario generation and reduction process are simulated using MATLAB software while the proposed optimization model is solved using CPLEX under GAMS [57]. The computing time for calculating the MCS-based model is 75 s. Furthermore, the scenarios generation process takes 45 s and finally the optimization problem is successfully solved in 105 s.
7.2. Simulation Results
Figure 7 shows the simulation result of the proposed model for calculating the load profile of the EVs charging station. This figure is the result of using maximum numbers of charging station’s capacity (i.e., 70 EVs) during the operating day because we have considered 70 EVs for type of EVs random values. The batteries’ capacities for these EVs are based on their market share that have been mentioned in Table 5. As can be seen, given the changing behavior of the EVs charging program, the charging station will be considered as a power generator from the beginning of the peak period (i.e., hour 8) in response to the price changes at this time. In other words, due to Table 1, the probability of discharging at peak times is 85%. So, most of the EVs discharge at this period and hence we can consider charging stations as a power generator. On the other side, the probability of charging at off-peak times is 95%. Therefore, most of the EVs charge at hours 1–8 and hence we can consider a charging station as a load during this period.
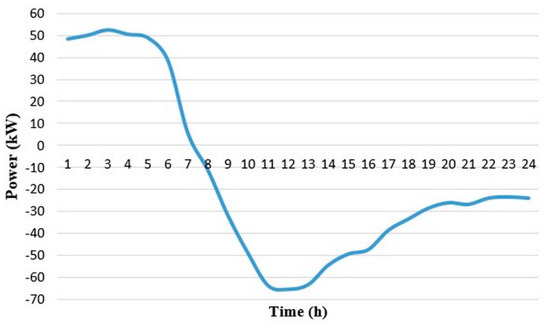
Figure 7.
Load curve of the EVs charging station according to the proposed method.
Table 8 shows the output values of the proposed DA operation. It contains mean and SD values of 200 scenarios and includes generation of micro-turbines and PV unit and buying from upstream grid. As can be seen, the amount of power purchases from the upstream grid is reduced between hours 11–17. However, the MG demand, as well as the market price will peak at these times. The reasons for this can be stated as follows. The PV unit generation in these period reaches the maximum, i.e., 50 kW and more. Furthermore, according to Figure 6, during these hours, the EVs charging station produces most of its energy between 40 kW and 65 kW because the high market price at these periods encourages the EVs to sell the stored energy to the MG. On the other hand, the high market price forces the MG to dispatch more of micro-turbines. In this regard, the production of micro-turbines is increased in these hours. Therefore, the MG can use its internal power resources instead of purchasing costly power from the upstream grid.

Table 8.
Output values for the day-ahead (DA) operation.
The maximum amount of purchased power from the upstream grid is 265 kW at hour 21 and at a price of 8.4 $/kWh. At this time, the micro-turbine generation is reduced to 44 kW. The output of PV unit is zero and the station’s generation is reduced to 21 kW because the market price is low and most of EVs will be discharged to the MG. So, the MG’s manager increases its DA power procurement from the main grid in this situation. The minimum amount of purchased power from the upstream grid is 98 kW at hour 14 and at a price of 21.31 $/kWh. However, the MG’s demand is high at this time (329.28 kW). The PV output is 57 kW and also the station sells 54 kW to the MG. Therefore, with increasing consumption and market prices, the MG manager will reduce its cost by operating more than internal power sources such as micro-turbines and PV units. The EVs charging station will be operated as an internal power source by engaging the EVs in the demand response program. The total cost of the operation in this simulation case study is $717.
In order to realize the effectiveness of the proposed MCS based algorithm for estimating of charging station load, a sensitivity analysis is performed. Table 9 shows the results of this sensitivity analysis on the uncertain parameters of EVs. i.e., each time the simulation of the proposed algorithm is performed, one of the uncertainty parameters is not considered. As it appears, the uncertainty of EVs type has not had much impact on the curve. In contrast, other parameters have changed the curve. If the uncertainty of the charger type is not taken into account (that means all EVs are charged or discharged by a level 2 charger), then the amount of energy level exchanged with the MG will be decreased because charging or discharging duration will be increased, so the fewer of EVs will be used in a 24 h operation period. On the other hand, if the uncertainties of SoC and battery capacity are not considered, the load curve will change more. In this case, the energy interaction of the station with the MG will change completely because according to (3) and (4), these parameters have direct effect on the station load curve. The station’s load curve in the case of ignoring the EVs price sensitivity has a different shape. In this case, the EVs do not discharge their stored energy despite the price increase. Table 8 is presented in order to understand how these curves effect on the optimal DA solutions.

Table 9.
The effects of the uncertain parameters on the amount of charging station load.
As previously mentioned, the total cost of the operation is $717. The total energy produced by the micro-turbines and the upstream grid is 1040 kWh and 5131.8 kWh in a period of 24 h, respectively. These values are calculated by applying the proposed method for the charging station load. This state is considered as the base case and the results of sensitivity analysis are compared with this case. Table 10 shows the results of sensitivity analysis on the EVs uncertainty parameters. According to this table, ignoring any of these parameters in the calculation of the EVs charging station load leads to higher operating costs. For example, if the uncertainty of the type of chargers is not taken into account, the total amount of micro-turbine generation will decrease by 2.7% (1012 kWh) and the purchasing power will increase by 0.1% (5182 kWh). Furthermore, the total operating cost will increase by 0.55% ($721).

Table 10.
The impact of ignoring the EVs uncertain parameters in the charging station load.
The type of EVs uncertainty has the least impact on the operation cost. It increases cost only 0.08%. In contrast, ignoring the uncertainty of the EVs price sensitivity has the largest impact on the optimal solutions. It increases the operating cost by 21.2%. This result shows the importance of uncertainty in EVs price sensitivity. Uncertainties in SoC and uncertainty in battery capacity have also increased the cost by 4.8% and 7.5%, respectively, which uncertainty of EVs battery capacity has a fairly large impact on cost and optimal solutions. Overall, uncertainties in SoC, battery capacity and price sensitivity have a higher impact on the load profile and operating cost compared to uncertainties in the type of EVs and type of chargers.
8. Conclusions
In this paper, a model based on the MCS was presented to estimate the load of the EVs charging station and was used in an optimal operation problem of a smart MG. This model covered the uncertainty parameters of EVs including type of EVs, type of chargers, SoC, battery capacity and price sensitivity. Ignoring any of these parameters changed the optimal solutions. The results of the sensitivity analysis on these parameters indicated that the uncertainty in price sensitivity, battery capacity and SoC of EVs have a higher influence on the operating cost. Therefore, ignoring them can lead to higher costs. The uncertainty of the types of chargers and types of EVs had not a significant impact on the cost because it did not increase the station’s demand and the MG’s manager prevents cost increases with a slight change in the dispatch of micro-turbine and buying from the upstream grid. The proposed MCS-based model takes into account the decisive factor on the EV’s load profile concurrently. It has also an easy implementation process through the proposed MCS method and efficient simulation time. Therefore, the manager of MGs can estimate the load profile of EVs one day before of operation. Although the proposed model covers the uncertainty of EVs behaviors but there is a possibility of deviation of considered parameters for PDFs and therefore for estimated load profile.
Author Contributions
All the authors conceived the idea, developed the method, and conducted the experiment. M.J.S. contributed to the formulation of methodology and experiments. B.R. contributed to the data analysis and performance analysis. J.W. and G.-J.K. contributed to the algorithm design and data sources. All authors read and approved the final manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (61772454, 61811530332, 61811540410). It was also supported by the open research fund of Key Lab of Broadband Wireless Communication and Sensor Net-work Technology (Nanjing University of Posts and Telecommunications), Ministry of Education (No. JZNY201905).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Indices | |
| In scenario s at time t | |
| cl | Charger level index |
| g | Charger index |
| i | Micro-turbine unit index |
| j | EVs index |
| p | PV unit index |
| t | Time index |
| Parameters and Constants | |
| Generation cost coefficients of micro-turbine i. | |
| Externality cost of generation CO2 ($/kg) | |
| Carbon dioxide pollutant of micro-turbines i (kg/kW) | |
| Operation and maintenance cost of PV unit p($) | |
| Capacity factor of PV unit p | |
| Capital cost of PV unit p ($) | |
| int | Interest rate |
| Startup constant cost of microturbines ($) | |
| Minimum up time of microturbine i (h). | |
| Minimum down time of micro-turbine i (h). | |
| Number of time slots | |
| Number of micro-turbines | |
| Number of PV unit | |
| Number of chargers | |
| Number of EVs | |
| Loan repayment term (yr) | |
| Loads (kW) | |
| Maximum power limits of micro-turbine i (kW). | |
| Minimum power limits of micro-turbine i (kW). | |
| Maximum exchangeable power (kW) | |
| EVs charging station load | |
| Available output power of PV unit p (kW) | |
| Rated power of PV unit p (kW) | |
| Ramp up rate of micro-turbine i (kW/h) | |
| Ramp down rate of micro-turbine i (kW/h). | |
| Charging rates of charger level cl (kW) and charger g | |
| Discharging rates of charger level cl (kW) and charger g | |
| Maximum SoC of EVs | |
| Minimum SoC of EVs | |
| State of charge EV j | |
| Charging time of EV j with charger level cl (h) using charger g | |
| Discharging time of EV j with charger level cl (h) using charger g | |
| Duration of time slot (h) | |
| Day-ahead market prices ($/kWh) | |
| Variables | |
| Operation cost of micro-turbine i ($) | |
| Generation cost of PV unit p ($/h) | |
| Generation cost of micro-turbine i ($) | |
| Startup cost of micro-turbine i ($) | |
| Emission cost of micro-turbine i ($) | |
| Startup indicators of micro-turbine i | |
| Shutdown indicators of micro-turbine i | |
| DA electricity market transactions (bids) (kW) | |
| Output power of micro-turbine i (kW) | |
| Commitment status of micro-turbine i | |
| Abbreviations | |
| DA | Day-ahead |
| EVs | Electric vehicles |
| MG | Micro-grid |
| PEVs | Plug-in electric vehicles |
| PHEVs | Plug-in hybrid electric vehicles |
| PV | Photovoltaic |
| Probability density function | |
| SoC | State of charge |
| V2G | Vehicle-to-grid |
References
- Sioshansi, F.P. Smart Grid: Integrating Renewable, Distributed and Efficient Energy; Academic Press: Canmbridge, MA, USA, 2011. [Google Scholar]
- Monfared, H.J.; Ghasemi, A.; Loni, A.; Marzband, M. A hybrid price-based demand response program for the residential micro-grid. Energy 2019, 185, 274–285. [Google Scholar] [CrossRef]
- Mirzaei, M.A.; Yazdankhah, A.S.; Mohammadi-Ivatloo, B.; Marzband, M.; Shafie-khah, M.; Catalão, J.P.S. Stochastic network-constrained co-optimization of energy and reserve products in renewable energy integrated power and gas networks with energy storage system. J. Clean. Prod. 2019, 223, 747–758. [Google Scholar] [CrossRef]
- Nejad, R.R.; Tafreshi, S.M.M. Operation Planning of a Smart Microgrid Including Controllable Loads and Intermittent Energy Resources by Considering Uncertainties. Arab. J. Sci. Eng. 2014, 39, 6297–6315. [Google Scholar] [CrossRef]
- Marzband, M.; Azarinejadian, F.; Savaghebi, M.; Pouresmaeil, E.; Guerrero, J.M.; Lightbody, G. Smart transactive energy framework in grid-connected multiple home microgrids under independent and coalition operations. Renew. Energy 2018, 126, 95–106. [Google Scholar] [CrossRef]
- Ehsani, Y.G.M.; Gay, S.E.; Emadi, A. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles: Fundamentals, Theory, and Design; CRC Press: Boca raton, FL, USA, 2004. [Google Scholar]
- Su, H.E.W.; Zeng, W.; Chow, M.Y. A Survey on the Electrification of Transportation in a Smart Grid Environment. IEEE Trans. Ind. Inform. 2012, 8, 1–10. [Google Scholar] [CrossRef]
- Peng, M.; Liu, L.; Jiang, C. A review on the economic dispatch and risk management of the large-scale plug-in electric vehicles (PHEVs)-penetrated power systems. Renew. Sustain. Energy Rev. 2012, 16, 1508–1515. [Google Scholar] [CrossRef]
- Thomas, D.; Deblecker, O.; Ioakimidis, C.S. Optimal operation of an energy management system for a grid-connected smart building considering photovoltaics’ uncertainty and stochastic electric vehicles’ driving schedule. Appl. Energy 2018, 210, 1188–1206. [Google Scholar] [CrossRef]
- Battistelli, C.; Baringo, L.; Conejo, A.J. Optimal energy management of small electric energy systems including V2G facilities and renewable energy sources. Electr. Power Syst. Res. 2012, 92, 50–59. [Google Scholar] [CrossRef]
- Ahmadian, A.; Sedghi, M.; Aliakbar-Golkar, M. Fuzzy Load Modeling of Plug-in Electric Vehicles for Optimal Storage and DG Planning in Active Distribution Network. IEEE Trans. Veh. Technol. 2017, 66, 3622–3631. [Google Scholar] [CrossRef]
- Ju, L.; Li, H.; Zhao, J.; Chen, K.; Tan, Q.; Tan, Z. Multi-objective stochastic scheduling optimization model for connecting a virtual power plant to wind-photovoltaic-electric vehicles considering uncertainties and demand response. Energy Convers. Manag. 2016, 128, 160–177. [Google Scholar] [CrossRef]
- Shojaabadi, S.; Abapour, S.; Abapour, M.; Nahavandi, A. Simultaneous planning of plug-in hybrid electric vehicle charging stations and wind power generation in distribution networks considering uncertainties. Renew. Energy 2016, 99, 237–252. [Google Scholar] [CrossRef]
- Andersson, M.G.V.a.G. Optimal Bidding Strategy of a Plug-In Electric Vehicle Aggregator in Day-Ahead Electricity Markets Under Uncertainty. IEEE Trans. Power Syst. 2015, 30, 2375–2385. [Google Scholar]
- Korolko, N.; Sahinoglu, Z.; Nikovski, D. Modeling and Forecasting Self-Similar Power Load Due to EV Fast Chargers. IEEE Trans. Smart Grid 2016, 7, 1620–1629. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, W.; Wang, B.; Chu, C.-C.; Gadh, R. Optimal operation of stationary and mobile batteries in distribution grids. Appl. Energy 2017, 190, 1289–1301. [Google Scholar] [CrossRef]
- Zhao, T.; Li, Y.; Pan, X.; Wang, P.; Zhang, J. Real-Time Optimal Energy and Reserve Management of Electric Vehicle Fast Charging Station: Hierarchical Game Approach. IEEE Trans. Smart Grid 2018, 9, 5357–5370. [Google Scholar] [CrossRef]
- Zhou, Y.; Yau, D.K.Y.; You, P.; Cheng, P. Optimal-Cost Scheduling of Electrical Vehicle Charging Under Uncertainty. IEEE Trans. Smart Grid 2018, 9, 4547–4554. [Google Scholar] [CrossRef]
- Faridimehr, S.V.S.; Chinnam, R.B. A Stochastic Programming Approach for Electric Vehicle Charging Network Design. IEEE Trans. Intell. Transp. 2017, 20, 1870–1882. [Google Scholar] [CrossRef]
- Domínguez-Navarro, J.A.; Dufo-López, R.; Yusta-Loyo, J.M.; Artal-Sevil, J.S.; Bernal-Agustín, J.L. Design of an electric vehicle fast-charging station with integration of renewable energy and storage systems. Int. J. Electr. Power Energy Syst. 2019, 105, 46–58. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, X.; Wang, H.; Peng, J.-C.; Jiang, H.; Liu, Y.; Wu, C.; Xu, Z.; Liu, W. Robust Planning of Electric Vehicle Charging Facilities With an Advanced Evaluation Method. IEEE Trans. Ind. Inform. 2018, 14, 866–876. [Google Scholar] [CrossRef]
- DeForest, N.; MacDonald, J.S.; Black, D.R. Day ahead optimization of an electric vehicle fleet providing ancillary services in the Los Angeles Air Force Base vehicle-to-grid demonstration. Appl. Energy 2018, 210, 987–1001. [Google Scholar] [CrossRef]
- Faddel, S.; Aldeek, A.; Al-Awami, A.T.; Sortomme, E.; Al-Hamouz, Z. Ancillary Services Bidding for Uncertain Bidirectional V2G Using Fuzzy Linear Programming. Energy 2018, 160, 986–995. [Google Scholar] [CrossRef]
- Arévalo, J.C.; Santos, F.; Rivera, S. Uncertainty cost functions for solar photovoltaic generation, wind energy generation, and plug-in electric vehicles: Mathematical expected value and verification by Monte Carlo simulation. Int. J. Power Energy Convers. 2019, 10, 171–207. [Google Scholar] [CrossRef]
- Mehrjerdi, H.; Rakhshani, E. Vehicle-to-grid technology for cost reduction and uncertainty management integrated with solar power. J. Clean. Prod. 2019, 229, 463–469. [Google Scholar] [CrossRef]
- Şengör, O.E.İ.; Yener, B.; Taşcıkaraoğlu, A.; Catalão, J.P.S. Optimal Energy Management of EV Parking Lots Under Peak Load Reduction Based DR Programs Considering Uncertainty. IEEE Trans. Sustain. Energy 2019, 10, 1034–1043. [Google Scholar] [CrossRef]
- Z.E.C.C.101. Types of Charging, Charging Networks, Apps, & More. 2015. Available online: www.evobsession.com (accessed on 21 May 2019).
- Muñiz, R.; Díaz, J.; Nuño, F.; Prieto, M.J.; Pernía, A.M. A Smart Power Meter to Recharge Electric Vehicles in Communal Parking Areas. IEEE Inter. Things J. 2019, 6, 3448–3454. [Google Scholar] [CrossRef]
- Billinton, R.; Allan, R.N. Reliability Evaluation of Engineering Systems; Springer: New York, NY, USA, 1983. [Google Scholar]
- Landi, M.M.; Mohammadi, M.; Rastegar, M. Simultaneous determination of optimal capacity and charging profile of plug-in electric vehicle parking lots in distribution systems. Energy 2018, 158, 504–511. [Google Scholar] [CrossRef]
- Kamankesh, H.; Agelidis, V.G.; Kavousi-Fard, A. Optimal scheduling of renewable micro-grids considering plug-in hybrid electric vehicle charging demand. Energy 2016, 100, 285–297. [Google Scholar] [CrossRef]
- Mohammadi, S.; Soleymani, S.; Mozafari, B. Scenario-based stochastic operation management of MicroGrid including Wind, Photovoltaic, Micro-Turbine, Fuel Cell and Energy Storage Devices. Int. J. Electr. Power Energy Syst. 2014, 54, 525–535. [Google Scholar] [CrossRef]
- Li, G.; Zhang, X. Modeling of Plug-in Hybrid Electric Vehicle Charging Demand in Probabilistic Power Flow Calculations. IEEE Trans. Smart Grid 2012, 3, 492–499. [Google Scholar] [CrossRef]
- Aien, M.; Hajebrahimi, A.; Fotuhi-Firuzabad, M. A comprehensive review on uncertainty modeling techniques in power system studies. Renew. Sustain. Energy Rev. 2016, 57, 1077–1089. [Google Scholar] [CrossRef]
- Arabali, A.; Ghofrani, M.; Etezadi-Amoli, M.; Fadali, M.S. Stochastic Performance Assessment and Sizing for a Hybrid Power System of Solar/Wind/Energy Storage. IEEE Trans. Sustain. Energy 2014, 5, 363–371. [Google Scholar] [CrossRef]
- Moghaddas-Tafreshi, S.M.; Salehpour, M.J. A two-stage stochastic optimization based-on monte carlo simulation for maximizing the profitability of a smart microgrid. J. Hyperstructures 2018, 7, 1–15. [Google Scholar]
- Al-Awami, A.T.; El-Sharkawi, M.A. Coordinated Trading of Wind and Thermal Energy. IEEE Trans. Sustain. Energy 2011, 2, 277–287. [Google Scholar] [CrossRef]
- Atwa, Y.M.; El-Saadany, E.F.; Salama, M.M.A.; Seethapathy, R. Optimal Renewable Resources Mix for Distribution System Energy Loss Minimization. IEEE Trans. Power Syst. 2010, 25, 360–370. [Google Scholar] [CrossRef]
- Growe-kuska, H.H.N.; Romisch, W. Scenario reduction and scenario tree construction for power management problems. Power Manag. Probl. IEEE Bologna Power Tech Proc. 2003, 3. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Liu, W.; Wu, W.; Lim, S.-J. An asynchronous clustering and mobile data gathering schema based on timer mechanism in wireless sensor networks. Comput. Mater. Contin. 2019, 58, 711–725. [Google Scholar] [CrossRef]
- Wang, J.; Ju, C.; Gao, Y.; Sangaiah, A.K.; Kim, G.J. A PSO based Energy Efficient Coverage Control Algorithm for Wireless Sensor Networks. Comput. Mater. Contin. 2018, 56, 433–446. [Google Scholar]
- Wang, J.; Gao, Y.; Yin, X.; Li, F.; Kim, H.J. An Enhanced PEGASIS Algorithm with Mobile Sink Support for Wireless Sensor Networks. Wirel. Commun. Mobile Comput. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Liu, W.; Sangaiah, A.K.; Kim, H.-J. An intelligent data gathering schema with data fusion supported for mobile sink in WSNs. Int. J. Distrib. Sens. Netw. 2019, 15, 1–10. [Google Scholar] [CrossRef]
- Wang, J.; Gao, Y.; Liu, W.; Sangaiah, A.K.; Kim, H.J. Energy Efficient Routing Algorithm with Mobile Sink Support for Wireless Sensor Networks. Sensors 2019, 19, 1494. [Google Scholar] [CrossRef]
- Wang, J.; Gu, X.; Liu, W.; Sangaiah, A.K.; Kim, H.J. An empower hamilton loop based data collection algorithm with mobile agent for WSNs. Hum.-Cent. Comput. Inf. Sci. 2019, 9, 18. [Google Scholar] [CrossRef]
- JSalehpour, M.; Radmanesh, H.; Rostami, M.S.H.; Wang, J.; Kim, H.-J. Effect of Load Priority Modeling on the Size of Fuel Cell as an Emergency Power Unit in a More-Electric Aircraft. Appl. Sci. 2019, 9, 3241. [Google Scholar] [CrossRef]
- Carrion, M.; Arroyo, J.M. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Le, L.B. Risk-Constrained Profit Maximization for Microgrid Aggregators With Demand Response. IEEE Trans. Smart Grid 2015, 6, 135–146. [Google Scholar] [CrossRef]
- Pourakbari-Kasmaei, M.; Lehtonen, M.; Fotuhi-Firuzabad, M.; Marzband, M.; Mantovani, J.R.S. Optimal power flow problem considering multiple-fuel options and disjoint operating zones: A solver-friendly MINLP model. Int. J. Electr. Power Energy Syst. 2019, 113, 45–55. [Google Scholar] [CrossRef]
- Valinejad, J.; Barforoshi, T.; Marzband, M.; Pouresmaeil, E.; Godina, R.; Catalão, J.P.S. Investment Incentives in Competitive Electricity Markets. Appl. Sci. 2018, 8, 1978. [Google Scholar] [CrossRef]
- Alavi, S.A.; Ahmadian, A.; Aliakbar-Golkar, M. Optimal probabilistic energy management in a typical micro-grid based-on robust optimization and point estimate method. Energy Convers. Manag. 2015, 95, 314–325. [Google Scholar] [CrossRef]
- Liu, G.; Xu, Y.; Tomsovic, K. Bidding Strategy for Microgrid in Day-Ahead Market Based on Hybrid Stochastic/Robust Optimization. IEEE Trans. Smart Grid 2016, 7, 227–237. [Google Scholar] [CrossRef]
- CERTS Microgrid Concept. 2003. Available online: http://certs.lbl.gov/certs-der-micro.html (accessed on 15 May 2019).
- IEEE Draft Guide for Design, Operation, and Integration of Distributed Resource Island Systems With Electric Power Systems; IEEE: Piscataway, NJ, USA, 2011.
- Salehpour, M.J.; Tafreshi, S.M.M. The effect of price responsive loads uncertainty on the risk-constrained optimal operation of a smart micro-grid. Int. J. Electr. Power Energy Syst. 2019, 106, 546–560. [Google Scholar] [CrossRef]
- Jamshidi, M.; Askarzadeh, A. Techno-economic analysis and size optimization of an off-grid hybrid photovoltaic, fuel cell and diesel generator system. Sustain. Cities Soc. 2019, 44, 310–320. [Google Scholar] [CrossRef]
- Brooke, A.; Kendrick, D.; Meeraus, A.; Raman, R. GAMS User’s Guide; GAMS development corporation: Washington, DC, USA, 1998. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).