X-ray Spectroscopies of High Energy Density Matter Created with X-ray Free Electron Lasers
Abstract
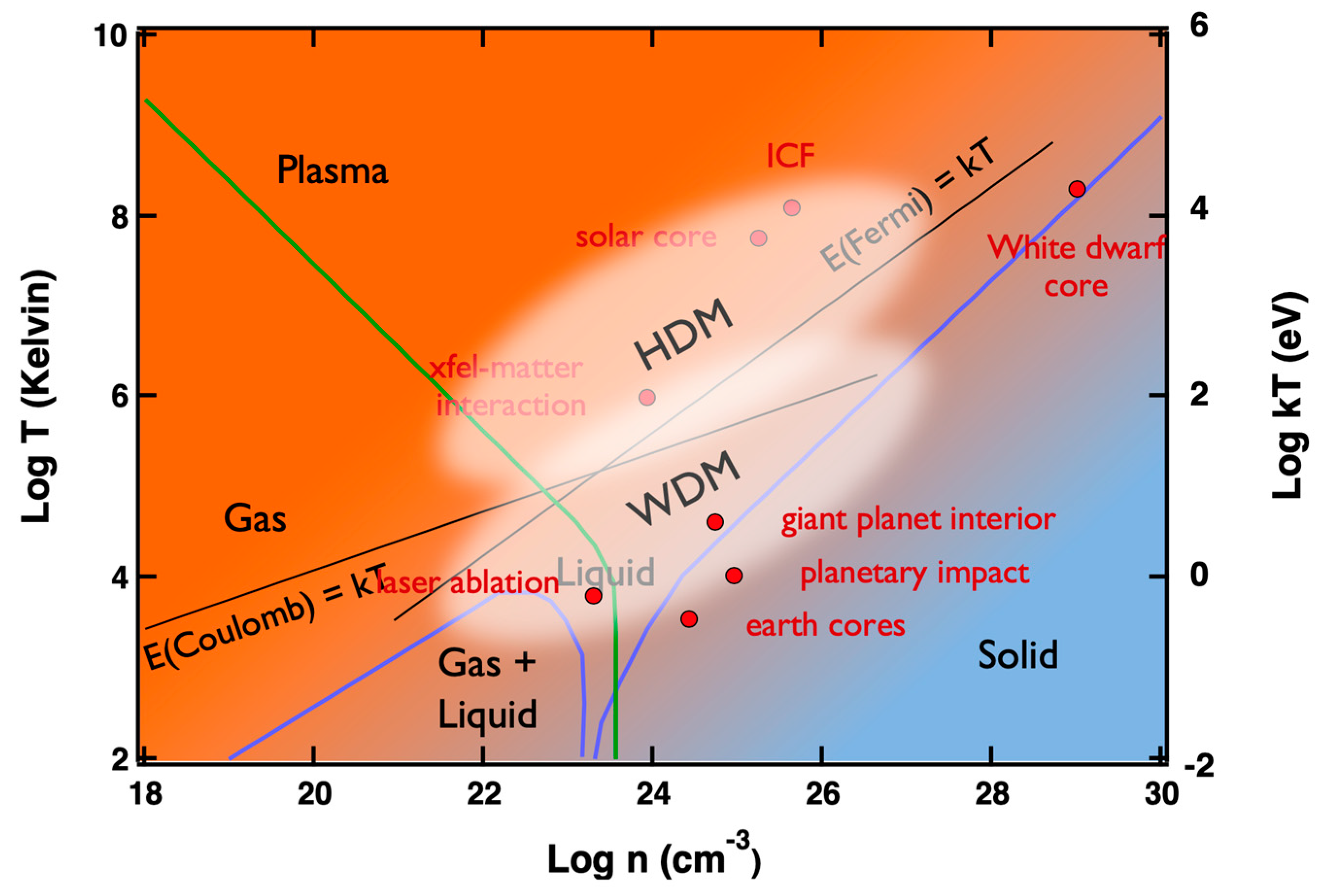
1. Introduction
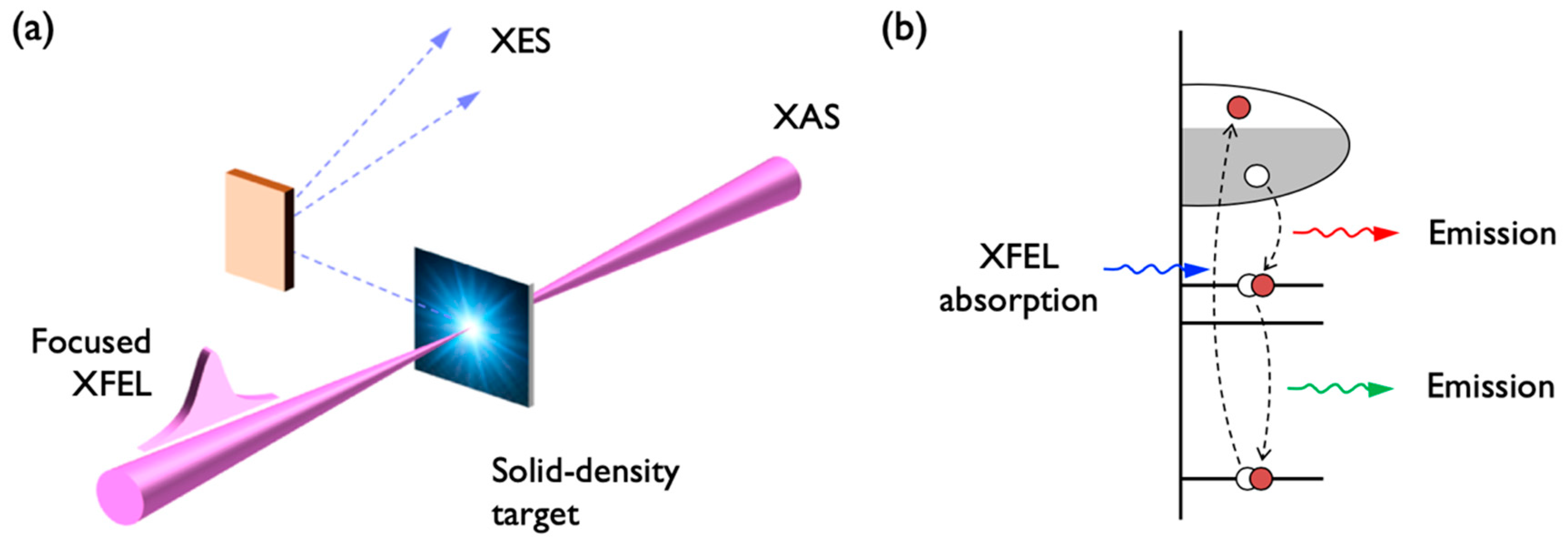
2. General Concept of Investigation
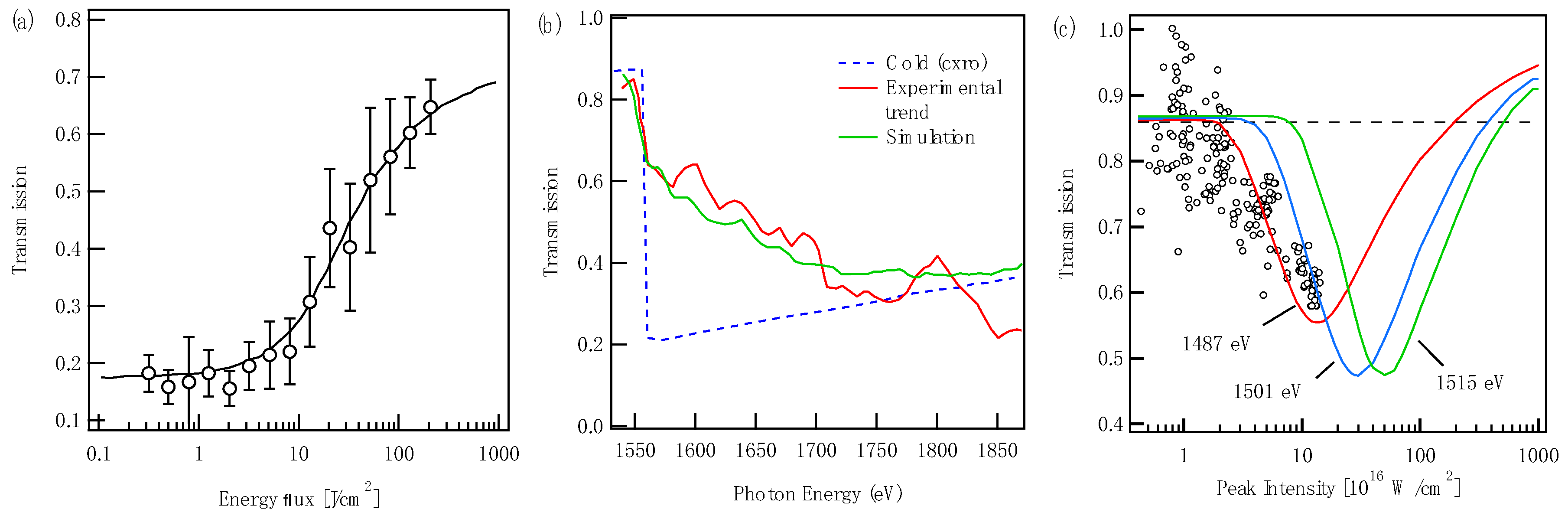
3. Intensity-Dependent EUV and X-ray Transmission
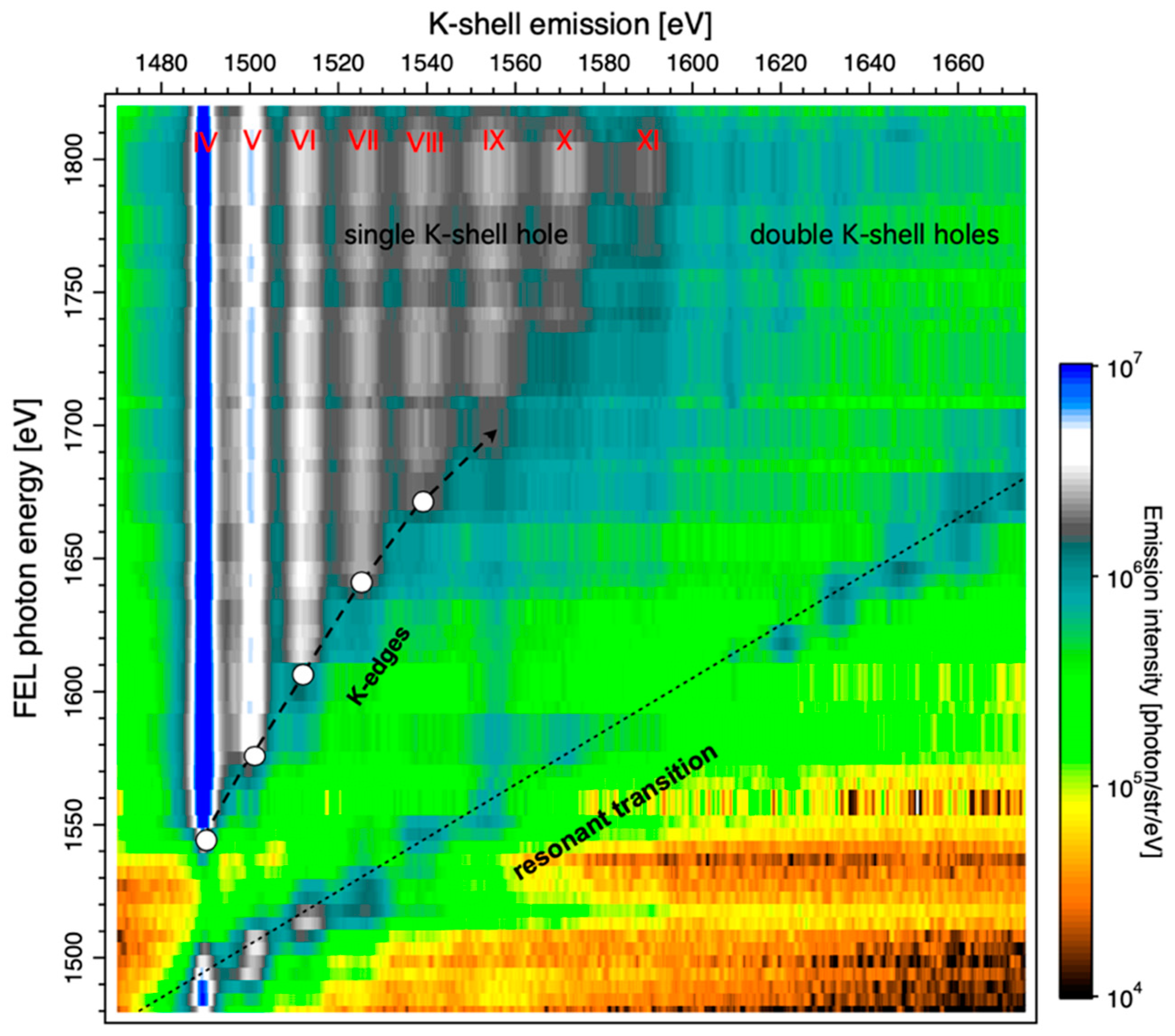
4. Isochoric Heating of Solid with X-ray
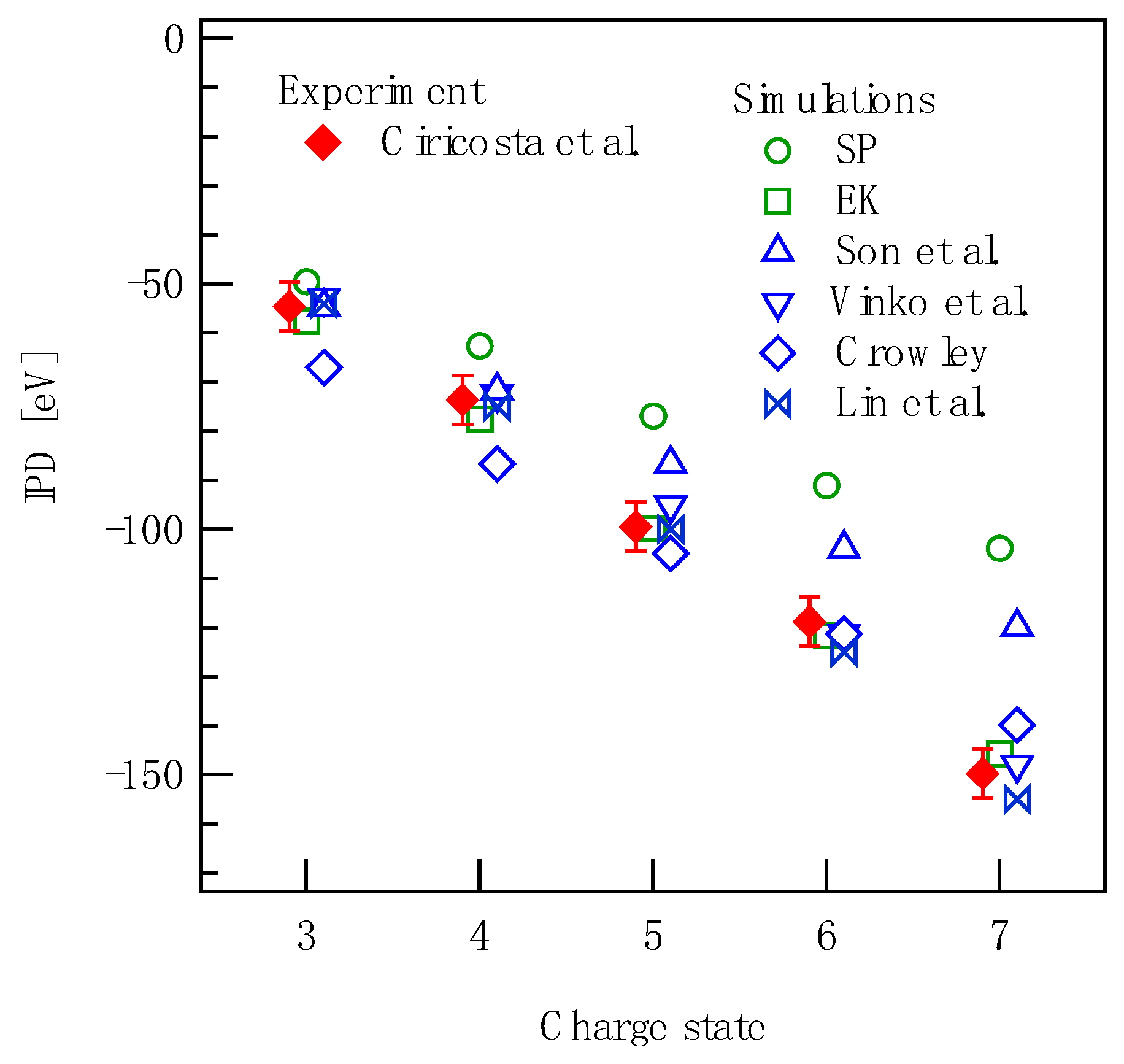
5. Continuum Lowering in HED Plasmas
6. Conclusions
Funding
Conflicts of Interest
References
- Ackermann, W.; Asova, G.; Ayvazyan, V.; Azima, A.; Baboi, N.; Bähr, J.; Balandin, V.; Beutner, B.; Brandt, A.; Bolzmann, A.; et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nat. Photonics 2007, 1, 336. [Google Scholar] [CrossRef]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.J.; et al. First lasing and operation of an angstrom-wavelength free-electron laser. Nat. Photonics 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Ishikawa, T.; Aoyagi, H.; Asaka, T.; Asano, Y.; Azumi, N.; Bizen, T.; Ego, H.; Fukami, K.; Fukui, T.; Furukawa, Y.; et al. A compact X-ray free-electron laser emitting in the sub-angstrom region. Nat. Photonics 2012, 6, 540–544. [Google Scholar] [CrossRef]
- Kang, H.-S.; Min, C.-K.; Heo, H.; Kim, C.; Yang, H.; Kim, G.; Nam, I.; Baek, S.Y.; Choi, H.-J.; Mun, G.; et al. Hard X-ray free-electron laser with femtosecond-scale timing jitter. Nat. Photonics 2017, 11, 708–713. [Google Scholar] [CrossRef]
- Daligault, J.; Gupta, S. Electron-Ion Scattering in Dense Multi-Component Plasmas: Application to the Outer Crust of an Accreting Neutron Star. Astrophys. J. 2009, 703, 994–1011. [Google Scholar] [CrossRef]
- Glenzer, S.H.; MacGowan, B.J.; Michel, P.; Meezan, N.B.; Suter, L.J.; Dixit, S.N.; Kline, J.L.; Kyrala, G.A.; Bradley, D.K.; Callahan, D.A.; et al. Symmetric inertial confinement fusion implosions at ultra-high laser energies. Science 2010, 327, 1228–1231. [Google Scholar] [CrossRef] [PubMed]
- Chan, J.W.; Huser, T.; Risbud, S.; Krol, D.M. Structural changes in fused silica after exposure to focused femtosecond laser pulses. Opt. Lett. 2001, 26, 1726–1728. [Google Scholar] [CrossRef] [PubMed]
- National Research Council. Frontiers in High Energy Density Physics: The X-Games of Contemporary Science; The National Academies Press: Washington, DC, USA, 2003; pp. 1–176. [Google Scholar]
- U.S. Department of Energy, Office of Science and National Nuclear Security Administration. Basic Research Needs for High Energy Density Laboratory Physics; U.S. Department of Energy: Washington, DC, USA, 2010.
- Lee, R.W.; Moon, S.J.; Chung, H.-K.; Rozmus, W.; Baldis, H.A.; Gregori, G.; Cauble, R.C.; Landen, O.L.; Wark, J.S.; Ng, A.; et al. Finite temperature dense matter studies on next-generation light sources. J. Opt. Soc. Am. B 2003, 20, 770–778. [Google Scholar] [CrossRef]
- Lee, R.W.; Baldis, H.A.; Cauble, R.C.; Landen, O.L.; Wark, J.S.; Ng, A.; Rose, S.J.; Lewis, C.; Riley, D.; Gauthier, J.C.; et al. Plasma-based studies with intense X-ray and particle beam sources. Laser Part. Beams 2002, 20, 527–536. [Google Scholar] [CrossRef]
- Beckwith, M.A.; Jiang, S.; Schropp, A.; Fernandez-Pañella, A.; Rinderknecht, H.G.; Wilks, S.C.; Fournier, K.B.; Galtier, E.C.; Xing, Z.; Granados, E.; et al. Imaging at an x-ray absorption edge using free electron laser pulses for interface dynamics in high energy density systems. Rev. Sci. Instrum. 2017, 88, 053501. [Google Scholar] [CrossRef]
- Medvedev, N.; Ziaja, B. Multistep transition of diamond to warm dense matter state revealed by femtosecond X-ray diffraction. Sci. Rep. 2018, 8, 5284. [Google Scholar] [CrossRef] [PubMed]
- Brown, C.R.D.; Gericke, D.O.; Cammarata, M.; Cho, B.I.; Döppner, T.; Engelhorn, K.; Förster, E.; Fortmann, C.; Fritz, D.; Galtier, E.; et al. Evidence for a glassy state in strongly driven carbon. Sci. Rep. 2014, 4, 5214. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, L.B.; Lee, H.J.; Doppner, T.; Galtier, E.; Nagler, B.; Heimann, P.; Fortmann, C.; LePape, S.; Ma, T.; Millot, M.; et al. Ultrabright X-ray laser scattering for dynamic warm dense matter physics. Nat. Photonics 2015, 9, 274–279. [Google Scholar] [CrossRef]
- Vinko, S.M.; Ciricosta, O.; Cho, B.I.; Engelhorn, K.; Chung, H.K.; Brown, C.R.; Burian, T.; Chalupsky, J.; Falcone, R.W.; Graves, C.; et al. Creation and diagnosis of a solid-density plasma with an X-ray free-electron laser. Nature 2012, 482, 59–62. [Google Scholar] [CrossRef]
- Yoneda, H.; Inubushi, Y.; Yabashi, M.; Katayama, T.; Ishikawa, T.; Ohashi, H.; Yumoto, H.; Yamauchi, K.; Mimura, H.; Kitamura, H. Saturable absorption of intense hard X-rays in iron. Nat. Commun. 2014, 5, 5080. [Google Scholar] [CrossRef]
- Mukamel, S.; Healion, D.; Zhang, Y.; Biggs, J.D. Multidimensional Attosecond Resonant X-Ray Spectroscopy of Molecules: Lessons from the Optical Regime. Ann. Rev. Phys. Chem. 2013, 64, 101–127. [Google Scholar] [CrossRef]
- Bennett, K.; Zhang, Y.; Kowalewski, M.; Hua, W.; Mukamel, S. Multidimensional resonant nonlinear spectroscopy with coherent broadband x-ray pulses. Phys. Scr. 2016, T169, 014002. [Google Scholar] [CrossRef]
- Mimura, H.; Yumoto, H.; Matsuyama, S.; Koyama, T.; Tono, K.; Inubushi, Y.; Togashi, T.; Sato, T.; Kim, J.; Fukui, R.; et al. Generation of 1020 W cm−2 hard X-ray laser pulses with two-stage reflective focusing system. Nat. Commun. 2014, 5, 3539. [Google Scholar] [CrossRef]
- Ping, Y.; Fernandez-Panella, A.; Sio, H.; Correa, A.; Shepherd, R.; Landen, O.; London, R.A.; Sterne, P.A.; Whitley, H.D.; Fratanduono, D.; et al. Differential heating: A versatile method for thermal conductivity measurements in high-energy-density matter. Phys. Plasmas 2015, 22, 092701. [Google Scholar] [CrossRef]
- Zastrau, U.; Sperling, P.; Harmand, M.; Becker, A.; Bornath, T.; Bredow, R.; Dziarzhytski, S.; Fennel, T.; Fletcher, L.B.; Förster, E.; et al. Resolving Ultrafast Heating of Dense Cryogenic Hydrogen. Phys. Rev. Lett. 2014, 112, 105002. [Google Scholar] [CrossRef]
- Chung, H.K.; Chen, M.H.; Morgan, W.L.; Ralchenko, Y.; Lee, R.W. Flychk: Generalized population kinetics and spectral model for rapid spectroscopic analysis for all elements. High Energy Density Phys. 2005, 1, 3–12. [Google Scholar] [CrossRef]
- Chung, H.K.; Chen, M.H.; Lee, R.W. Extension of atomic configuration sets of the Non-LTE model in the application to the Kα diagnostics of hot dense matter. High Energy Density Phys. 2007, 3, 57–64. [Google Scholar] [CrossRef]
- Chung, H.K.; Cho, B.I.; Ciricosta, O.; Vinko, S.M.; Wark, J.S.; Lee, R.W. Atomic processes modeling of X-ray free electron laser produced plasmas using SCFLY code. AIP Conf. Proc. 2017, 1811, 020001. [Google Scholar]
- Lewis, G.N.; Lipkin, D.; Magel, T.T. Reversible Photochemical Processes in Rigid Media. A Study of the Phosphorescent State. J. Am. Chem. Soc. 1941, 63, 3005–3018. [Google Scholar] [CrossRef]
- Wood, G.L.; Clark, W.W., III; Miller, M.J.; Salamo, G.J.; Sharp, E.J. Evaluation Of Passive Optical Limiters And Switches; SPIE 1989 Technical Symposium on Aerospace Sensing; SPIE: Bellingham, WA, USA, 1989; Volume 1105. [Google Scholar]
- Zhang, B.; Li, Y.; Liu, R.; Pritchett, T.M.; Haley, J.E.; Sun, W. Extending the bandwidth of reverse saturable absorption in platinum complexes using two-photon-initiated excited-state absorption. ACS Appl. Mater. Interfaces 2013, 5, 565–572. [Google Scholar] [CrossRef]
- He, G.S.; Tan, L.S.; Zheng, Q.; Prasad, P.N. Multiphoton absorbing materials: Molecular designs, characterizations, and applications. Chem. Rev. 2008, 108, 1245–1330. [Google Scholar] [CrossRef]
- Nagler, B.; Zastrau, U.; Faustlin, R.R.; Vinko, S.M.; Whitcher, T.; Nelson, A.J.; Sobierajski, R.; Krzywinski, J.; Chalupsky, J.; Abreu, E.; et al. Turning solid aluminium transparent by intense soft X-ray photoionization. Nat. Phys. 2009, 5, 693–696. [Google Scholar]
- Inubushi, Y.; Yoneda, H.; Higashiya, A.; Ishikawa, T.; Kimura, H.; Kumagai, T.; Morimoto, S.; Nagasono, M.; Ohashi, H.; Sato, F.; et al. Measurement of saturable absorption by intense vacuum ultraviolet free electron laser using fluorescent material. Rev. Sci. Instrum. 2010, 81, 036101. [Google Scholar] [CrossRef]
- Yoneda, H.; Inubushi, Y.; Sato, F.; Morimoto, S.; Kumagaya, T.; Nagasono, M.; Higashiya, A.; Yabashi, M.; Ishikawa, T.; Ohashi, H.; et al. Observation of Saturable Absorption of Sn Metal Film with Intense EUV Laser Pulse; Ultrafast Nonlinear Optics; SPIE: Bellingham, WA, USA, 2009; Volume 7501. [Google Scholar]
- Rackstraw, D.S.; Ciricosta, O.; Vinko, S.M.; Barbrel, B.; Burian, T.; Chalupsky, J.; Cho, B.I.; Chung, H.K.; Dakovski, G.L.; Engelhorn, K.; et al. Saturable absorption of an x-ray free-electron-laser heated solid-density aluminum plasma. Phys. Rev. Lett. 2015, 114, 015003. [Google Scholar] [CrossRef]
- Cho, M.S.; Chung, H.K.; Cho, B.I. Intensity-dependent resonant transmission of x-rays in solid-density aluminum plasma. Phys. Plasmas 2018, 25, 053301. [Google Scholar] [CrossRef]
- Cho, B.I.; Cho, M.S.; Kim, M.; Chung, H.K.; Barbrel, B.; Engelhorn, K.; Burian, T.; Chalupsky, J.; Ciricosta, O.; Dakovski, G.L.; et al. Observation of Reverse Saturable Absorption of an X-ray Laser. Phys. Rev. Lett. 2017, 119, 075002. [Google Scholar] [CrossRef] [PubMed]
- Yoneda, H.; Inubushi, Y.; Nagamine, K.; Michine, Y.; Ohashi, H.; Yumoto, H.; Yamauchi, K.; Mimura, H.; Kitamura, H.; Katayama, T.; et al. Atomic inner-shell laser at 1.5-ångström wavelength pumped by an X-ray free-electron laser. Nature 2015, 524, 446. [Google Scholar] [CrossRef] [PubMed]
- Strickland, D.; Mourou, G. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 56, 219–221. [Google Scholar] [CrossRef]
- Mourou, G. The ultrahigh-peak-power laser: Present and future. Appl. Phys. B 1997, 65, 205–211. [Google Scholar] [CrossRef]
- Forsman, A.; Ng, A.; Chiu, G.; More, R.M. Interaction of femtosecond laser pulses with ultrathin foils. Phys. Rev. E 1998, 58, R1248–R1251. [Google Scholar] [CrossRef]
- Audebert, P.; Shepherd, R.; Fournier, K.B.; Peyrusse, O.; Price, D.; Lee, R.; Springer, P.; Gauthier, J.C.; Klein, L. Heating of Thin Foils with a Relativistic-Intensity Short-Pulse Laser. Phys. Rev. Lett. 2002, 89, 265001. [Google Scholar] [CrossRef]
- Ng, A.; Ao, T.; Perrot, F.; Dharma-Wardana, M.W.C.; Foord, M.E. Idealized slab plasma approach for the study of warm dense matter. Laser Part. Beams 2005, 23, 527–537. [Google Scholar] [CrossRef]
- Ao, T.; Ping, Y.; Widmann, K.; Price, D.F.; Lee, E.; Tam, H.; Springer, P.T.; Ng, A. Optical properties in nonequilibrium phase transitions. Phys. Rev. Lett. 2006, 96, 055001. [Google Scholar] [CrossRef]
- Spitzer, L., Jr. Physics of Fully Ionized Gases; Dover Publications: Wiley, NY, USA, 1956. [Google Scholar]
- Cho, B.I.; Engelhorn, K.; Correa, A.A.; Ogitsu, T.; Weber, C.P.; Lee, H.J.; Feng, J.; Ni, P.A.; Ping, Y.; Nelson, A.J.; et al. Electronic structure of warm dense copper studied by ultrafast x-ray absorption spectroscopy. Phys. Rev. Lett. 2011, 106, 167601. [Google Scholar] [CrossRef]
- Cho, B.I.; Ogitsu, T.; Engelhorn, K.; Correa, A.A.; Ping, Y.; Lee, J.W.; Bae, L.J.; Prendergast, D.; Falcone, R.W.; Heimann, P.A. Measurement of Electron.-Ion. Relaxation in Warm Dense Copper. Sci. Rep. 2016, 6, 18843. [Google Scholar] [CrossRef]
- Dyer, G.; Sheppherd, R.; Kuba, J.; Fill, E.; Wootton, A.; Patel, P.; Price, D.; Ditmire, T. Isochoric heating of solid aluminium with picosecond X-ray pulses. J. Mod. Opt. 2003, 50, 2495–2505. [Google Scholar] [CrossRef]
- Tschentscher, T.; Toleikis, S. Investigations of ultrafast phenomena in high-energy density physicsusing X-ray FEL radiation. Eur. Phys. J. D At. Mol. Opt. Plasma Phys. 2005, 36, 193–197. [Google Scholar]
- Cho, B.I.; Engelhorn, K.; Vinko, S.M.; Chung, H.K.; Ciricosta, O.; Rackstraw, D.S.; Falcone, R.W.; Brown, C.R.; Burian, T.; Chalupsky, J.; et al. Resonant Kalpha spectroscopy of solid-density aluminum plasmas. Phys. Rev. Lett. 2012, 109, 245003. [Google Scholar] [CrossRef] [PubMed]
- Vinko, S.M.; Ciricosta, O.; Preston, T.R.; Rackstraw, D.S.; Brown, C.R.D.; Burian, T.; Chalupský, J.; Cho, B.I.; Chung, H.K.; Engelhorn, K.; et al. Investigation of femtosecond collisional ionization rates in a solid-density aluminium plasma. Nat. Commun. 2015, 6, 6397. [Google Scholar] [CrossRef]
- Lévy, A.; Audebert, P.; Shepherd, R.; Dunn, J.; Cammarata, M.; Ciricosta, O.; Deneuville, F.; Dorchies, F.; Fajardo, M.; Fourment, C.; et al. The creation of large-volume, gradient-free warm dense matter with an x-ray free-electron laser. Phys. Plasmas 2015, 22, 030703. [Google Scholar] [CrossRef]
- Williams, G.O.; Künzel, S.; Daboussi, S.; Iwan, B.; Gonzalez, A.I.; Boutu, W.; Hilbert, V.; Zastrau, U.; Lee, H.J.; Nagler, B.; et al. Tracking the ultrafast XUV optical properties of x-ray free-electron-laser heated matter with high-order harmonics. Phys. Rev. A 2018, 97, 023414. [Google Scholar] [CrossRef]
- Stewart, J.C.; Pyatt, K.D., Jr. Lowering of Ionization Potentials in Plasmas. Astrophys. J. 1966, 144, 1203. [Google Scholar] [CrossRef]
- Ciricosta, O.; Vinko, S.M.; Chung, H.K.; Cho, B.I.; Brown, C.R.; Burian, T.; Chalupsky, J.; Engelhorn, K.; Falcone, R.W.; Graves, C.; et al. Direct measurements of the ionization potential depression in a dense plasma. Phys. Rev. Lett. 2012, 109, 065002. [Google Scholar] [CrossRef]
- Ciricosta, O.; Vinko, S.M.; Chung, H.K.; Jackson, C.; Lee, R.W.; Preston, T.R.; Rackstraw, D.S.; Wark, J.S. Detailed model for hot-dense aluminum plasmas generated by an x-ray free electron laser. Phys. Plasmas 2016, 23, 022707. [Google Scholar] [CrossRef]
- Ecker, G.; Kröll, W. Lowering of the Ionization Energy for a Plasma in Thermodynamic Equilibrium. Phys. Fluids 1963, 6, 62–69. [Google Scholar] [CrossRef]
- Hoarty, D.J.; Allan, P.; James, S.F.; Brown, C.R.D.; Hobbs, L.M.R.; Hill, M.P.; Harris, J.W.O.; Morton, J.; Brookes, M.G.; Shepherd, R.; et al. The first data from the Orion laser; measurements of the spectrum of hot, dense aluminium. High Energy Density Phys. 2013, 9, 661–671. [Google Scholar] [CrossRef]
- Hoarty, D.J.; Allan, P.; James, S.F.; Brown, C.R.D.; Hobbs, L.M.R.; Hill, M.P.; Harris, J.W.O.; Morton, J.; Brookes, M.G.; Shepherd, R.; et al. Observations of the Effect of Ionization-Potential Depression in Hot Dense Plasma. Phys. Rev. Lett. 2013, 110, 265003. [Google Scholar] [CrossRef] [PubMed]
- Son, S.-K.; Thiele, R.; Jurek, Z.; Ziaja, B.; Santra, R. Quantum-Mechanical Calculation of Ionization-Potential Lowering in Dense Plasmas. Phys. Rev. X 2014, 4, 031004. [Google Scholar] [CrossRef]
- Vinko, S.M.; Ciricosta, O.; Wark, J.S. Density functional theory calculations of continuum lowering in strongly coupled plasmas. Nat. Commun. 2014, 5, 3533. [Google Scholar] [CrossRef] [PubMed]
- Crowley, B.J.B. Continuum lowering—A new perspective. High Energy Density Phys. 2014, 13, 84–102. [Google Scholar] [CrossRef]
- Lin, C.; Röpke, G.; Kraeft, W.-D.; Reinholz, H. Ionization-potential depression and dynamical structure factor in dense plasmas. Phys. Rev. E 2017, 96, 013202. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, B.I. X-ray Spectroscopies of High Energy Density Matter Created with X-ray Free Electron Lasers. Appl. Sci. 2019, 9, 4812. https://doi.org/10.3390/app9224812
Cho BI. X-ray Spectroscopies of High Energy Density Matter Created with X-ray Free Electron Lasers. Applied Sciences. 2019; 9(22):4812. https://doi.org/10.3390/app9224812
Chicago/Turabian StyleCho, Byoung Ick. 2019. "X-ray Spectroscopies of High Energy Density Matter Created with X-ray Free Electron Lasers" Applied Sciences 9, no. 22: 4812. https://doi.org/10.3390/app9224812
APA StyleCho, B. I. (2019). X-ray Spectroscopies of High Energy Density Matter Created with X-ray Free Electron Lasers. Applied Sciences, 9(22), 4812. https://doi.org/10.3390/app9224812



