Photon Enhanced Interaction and Entanglement in Semiconductor Position-Based Qubits
Abstract
1. Introduction
2. Statement of the Problem
3. Position-Based Semiconductor Qubits in the Frame of Semiconductor Photon Communication
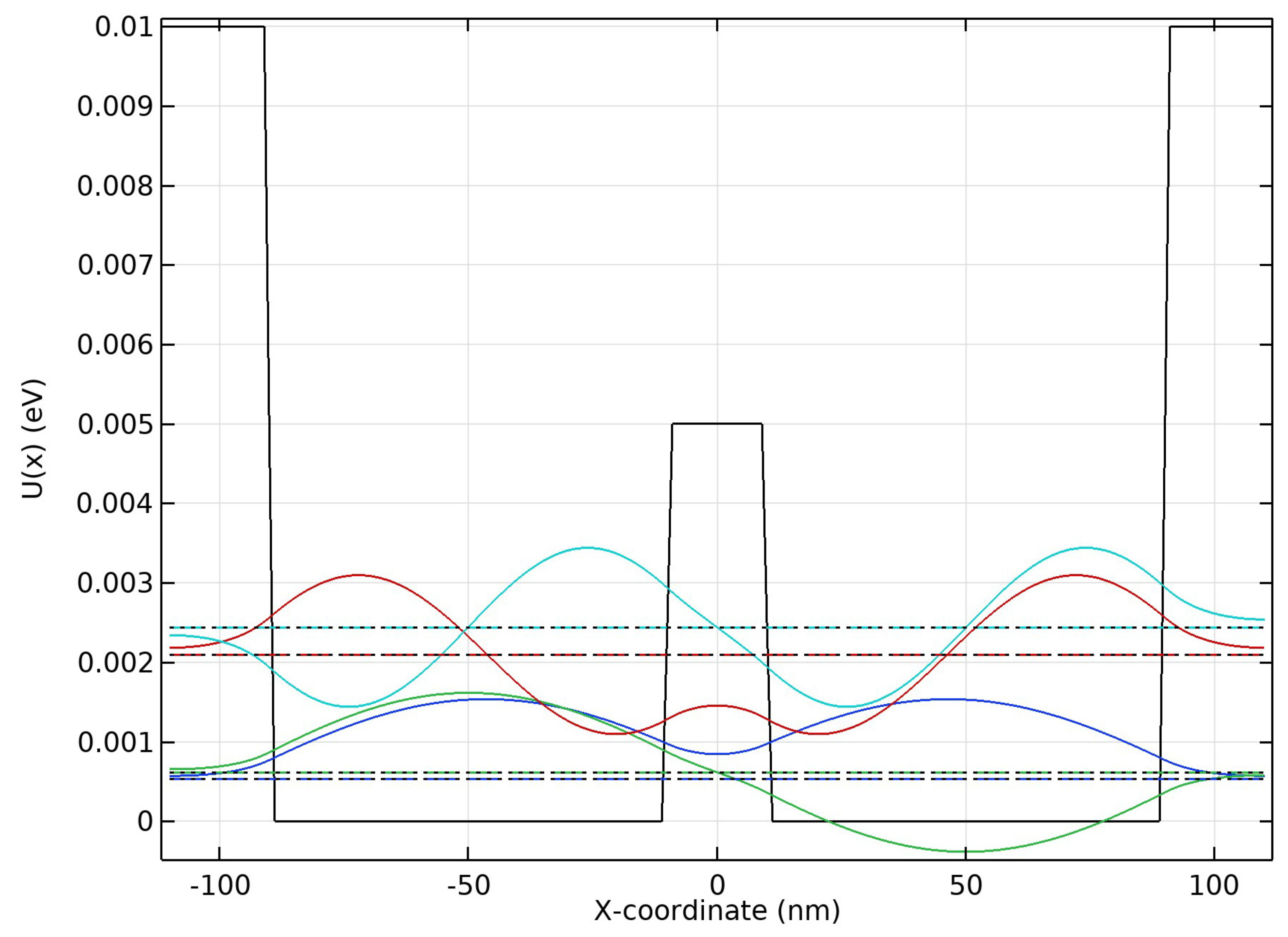
3.1. Rabi Flopping Frequency of a Position-Based Qubit
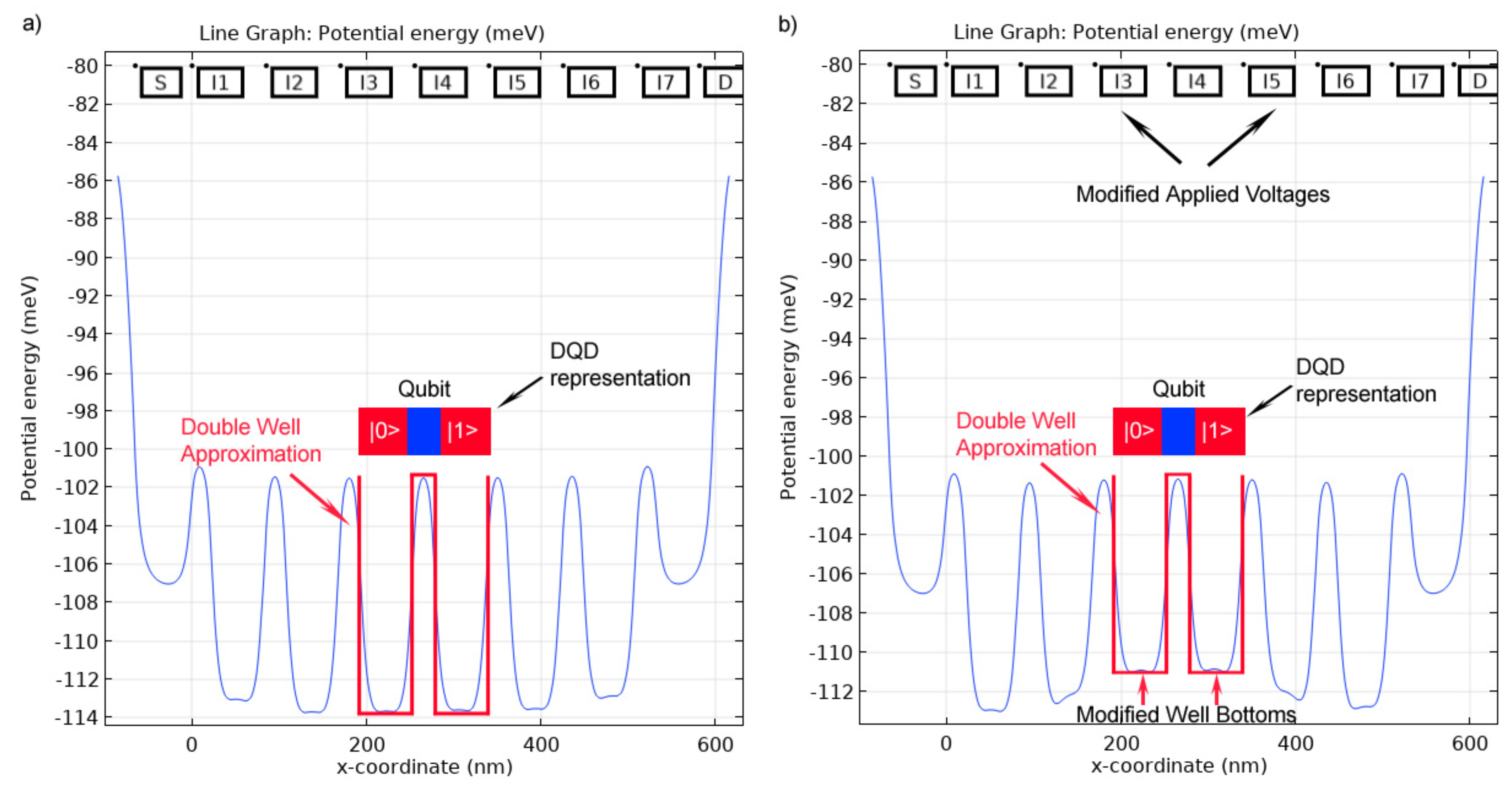
3.2. Representation of the System in a Position Basis
4. Photon Emission Due to Transitions in a Semiconductor Position-Based Qubit—Description Based on a Jaynes–Cummings–Hubbard Formalism
4.1. Description of the System of Coupled Position-Based Qubit with a Cavity
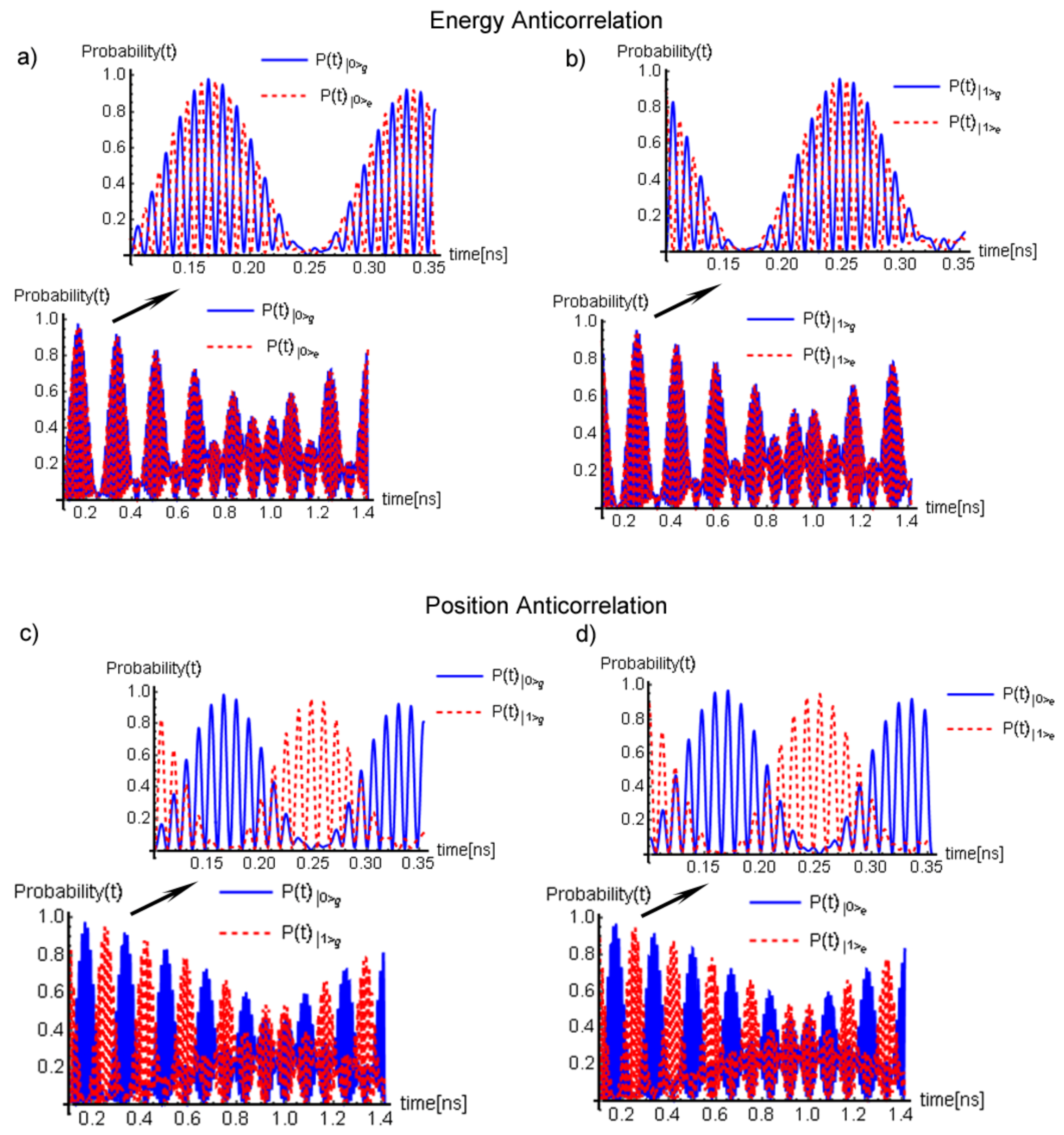
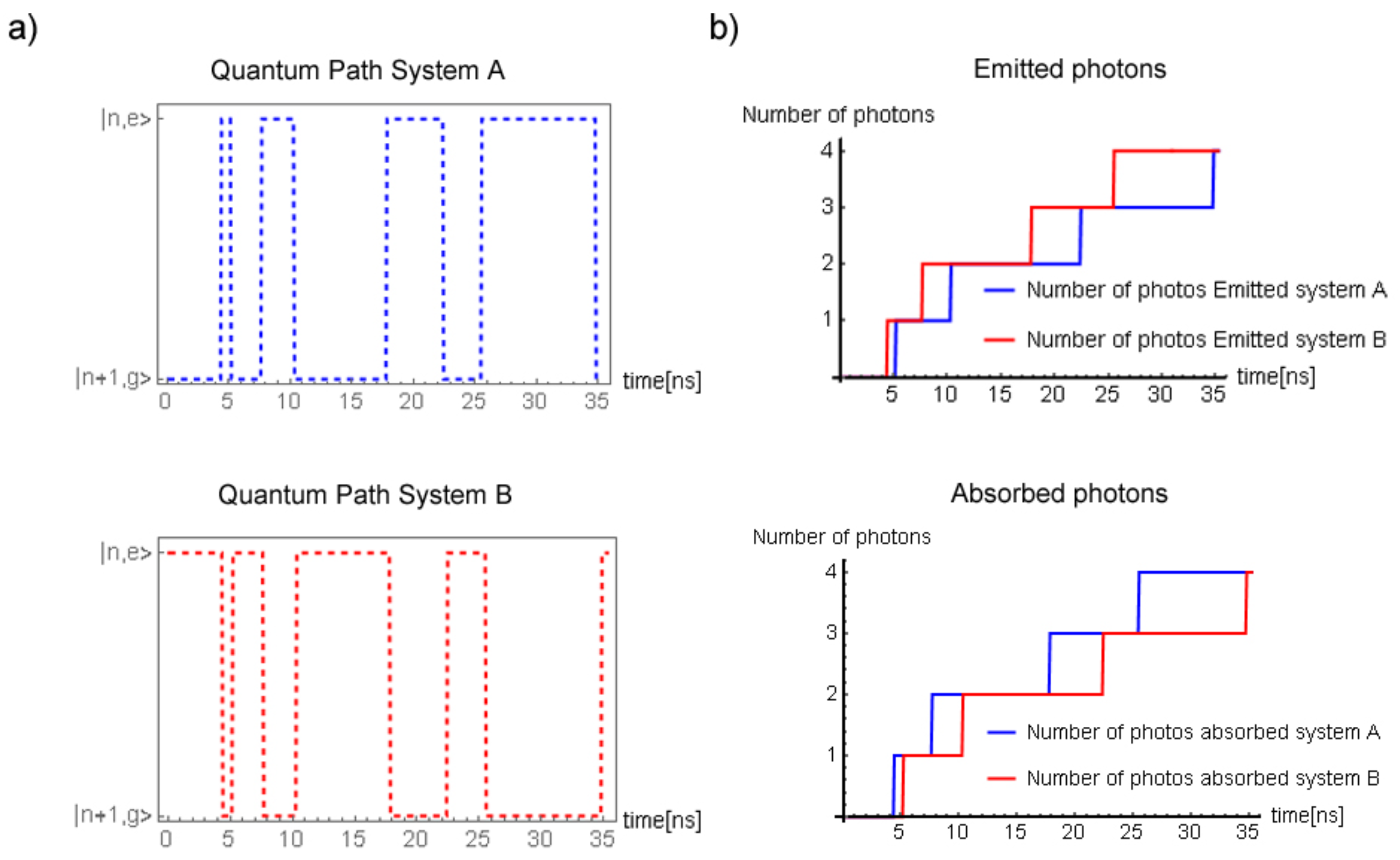
4.2. Simulation Results
4.3. Description of System of Two Entangled Coupled Position-Based Qubits with a Cavity
4.4. Maximally Entangled States and Entanglement Entropy
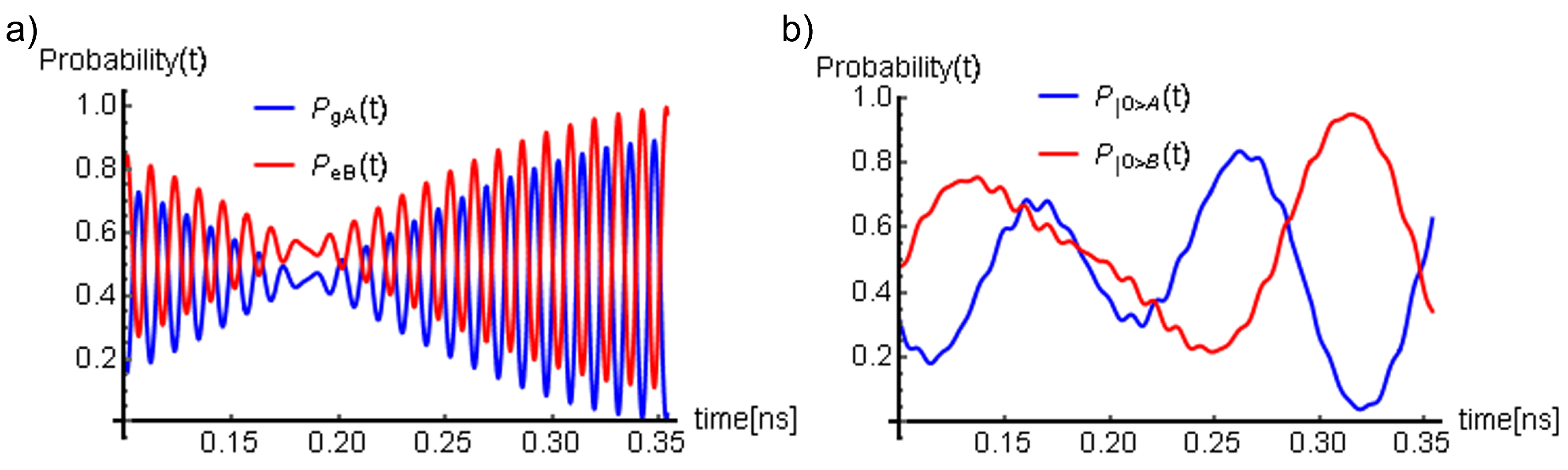
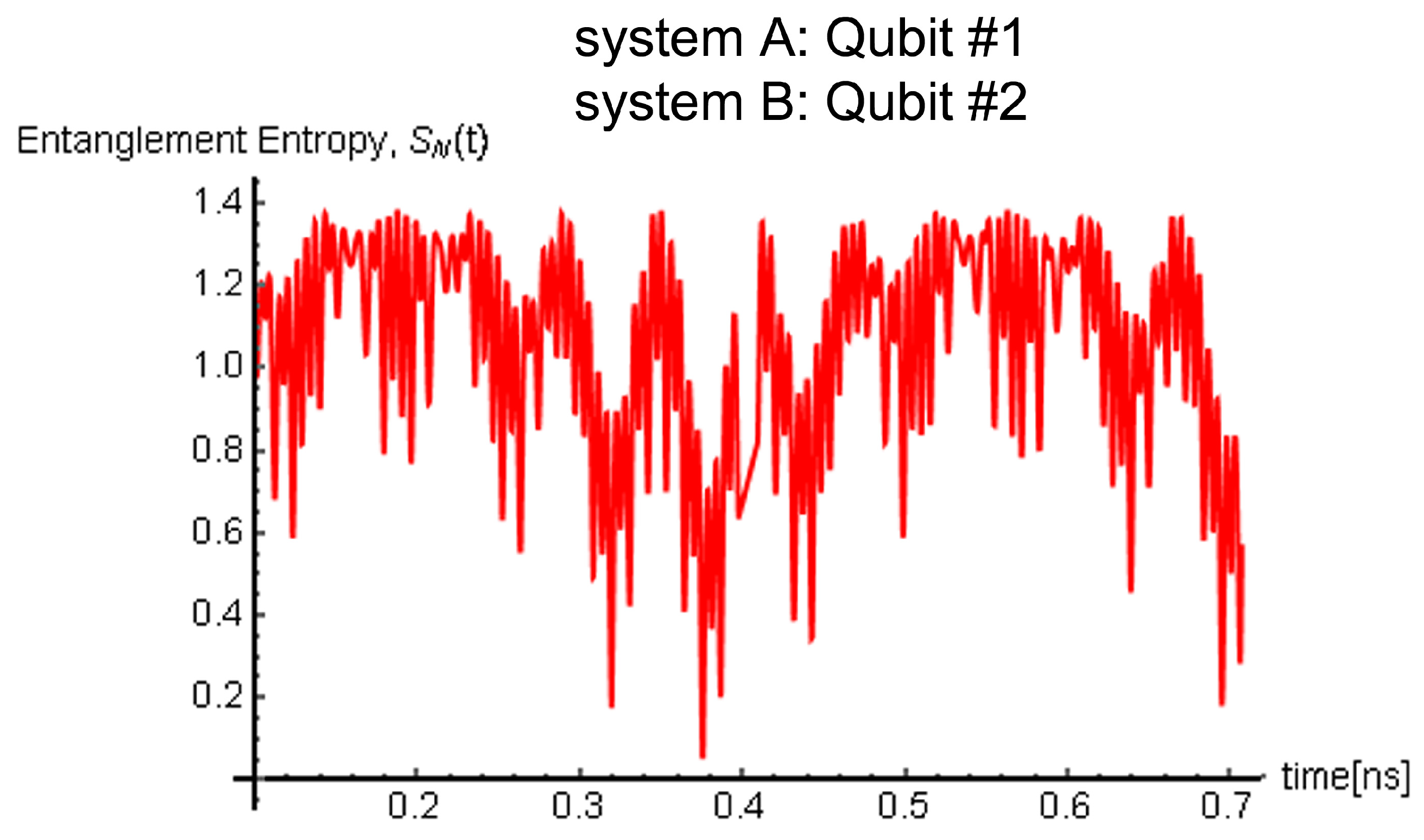
4.5. Simulation Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bashir, I.; Asker, M.; Cetintepe, C.; Leipold, D.; Esmailiyan, A.; Wang, H.; Siriburanon, T.; Giounanlis, P.; Blokhina, E.; Pomorski, K.; et al. A mixed-signal control core for a fully integrated semiconductor quantum computer system-on-chip. In Proceedings of the IEEE European Solid-State Circuits Conference (ESSCIRC), Poland, Krakow, 23–26 September 2019; pp. 125–128. [Google Scholar]
- Leipold, D. Fully integrated quantum computing SOC in 22nm FD-SOI. In Proceedings of the International Workshop on Cryogenic Electronics for Quantum Systems, Fermilab, Chicago, IL, USA, 17–20 June 2019. [Google Scholar]
- Bluhm, H.; Schreiber, L.R. Semiconductor Spin Qubits-A Scalable Platform for Quantum Computing? In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar]
- Lehmann, T. Cryogenic Support Circuits and Systems for Silicon Quantum Computers. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar]
- Pakkiam, P.; Timofeev, A.; House, M.; Hogg, M.; Kobayashi, T.; Koch, M.; Rogge, S.; Simmons, M. Single-shot single-gate rf spin readout in silicon. Phys. Rev. X 2018, 8, 041032. [Google Scholar] [CrossRef]
- Ekanayake, S.R.; Lehmann, T.; Dzurak, A.S.; Clark, R.G.; Brawley, A. Characterization of SOS-CMOS FETs at low temperatures for the design of integrated circuits for quantum bit control and readout. IEEE Trans. Electron Devices 2010, 57, 539–547. [Google Scholar] [CrossRef]
- Bonen, S.; Alakusu, U.; Duan, Y.; Gong, M.; Dadash, M.; Lucci, L.; Daughton, D.; Adam, G.; Iordănescu, S.; Pǎşteanu, M.; et al. Cryogenic Characterization of 22-nm FDSOI CMOS Technology for Quantum Computing ICs. IEEE Electron Device Lett. 2018, 40, 127–130. [Google Scholar]
- Patra, B.; Incandela, R.M.; Van Dijk, J.P.; Homulle, H.A.; Song, L.; Shahmohammadi, M.; Staszewski, R.B.; Vladimirescu, A.; Babaie, M.; Sebastiano, F.; et al. Cryo-CMOS circuits and systems for quantum computing applications. IEEE J. Solid-State Circuits 2018, 53, 309–321. [Google Scholar] [CrossRef]
- Lutchyn, R.M.; Sau, J.D.; Sarma, S.D. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 2010, 105, 077001. [Google Scholar] [CrossRef]
- Maurand, R.; Jehl, X.; Kotekar-Patil, D.; Corna, A.; Bohuslavskyi, H.; Laviéville, R.; Hutin, L.; Barraud, S.; Vinet, M.; Sanquer, M. A CMOS silicon spin qubit. Nat. Commun. 2016, 7, 13575. [Google Scholar] [CrossRef]
- Crippa, A.; Maurand, R.; Bourdet, L.; Kotekar-Patil, D.; Amisse, A.; Jehl, X.; Sanquer, M.; Laviéville, R.; Bohuslavskyi, H.; Hutin, L.; et al. Electrical spin driving by g-matrix modulation in spin-orbit qubits. Phys. Rev. Lett. 2018, 120, 137702. [Google Scholar] [CrossRef]
- Corna, A.; Bourdet, L.; Maurand, R.; Crippa, A.; Kotekar-Patil, D.; Bohuslavskyi, H.; Laviéville, R.; Hutin, L.; Barraud, S.; Jehl, X.; et al. Electrically driven electron spin resonance mediated by spin–valley–orbit coupling in a silicon quantum dot. Quantum Inf. 2018, 4, 6. [Google Scholar] [CrossRef]
- Shinkai, G.; Hayashi, T.; Ota, T.; Fujisawa, T. Correlated Coherent Oscillations in Coupled Semiconductor Charge Qubits. Phys. Rev. Lett. 2009, 103, 056802. [Google Scholar] [CrossRef]
- Mills, A.; Zajac, D.; Gullans, M.; Schupp, F.; Hazard, T.; Petta, J.R. Shuttling a single charge across a one-dimensional array of silicon quantum dots. Nat. Commun. 2019, 10, 1063. [Google Scholar] [CrossRef]
- Hensgens, T.; Fujita, T.; Janssen, L.; Li, X.; Van Diepen, C.; Reichl, C.; Wegscheider, W.; Sarma, S.D.; Vandersypen, L.M. Quantum simulation of a Fermi–Hubbard model using a semiconductor quantum dot array. Nature 2017, 548, 70. [Google Scholar] [CrossRef] [PubMed]
- Van der Wiel, W.G.; De Franceschi, S.; Elzerman, J.M.; Fujisawa, T.; Tarucha, S.; Kouwenhoven, L.P. Electron transport through double quantum dots. Rev. Mod. Phys. 2002, 75, 1. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Petersson, K.; Stehlik, J.; Taylor, J.M.; Petta, J.R. Photon emission from a cavity-coupled double quantum dot. Phys. Rev. Lett. 2014, 113, 036801. [Google Scholar] [CrossRef]
- Bose, R.; Cai, T.; Choudhury, K.R.; Solomon, G.S.; Waks, E. All-optical coherent control of vacuum Rabi oscillations. Nat. Photonics 2014, 8, 858. [Google Scholar] [CrossRef]
- Fink, J.; Göppl, M.; Baur, M.; Bianchetti, R.; Leek, P.; Blais, A.; Wallraff, A. Climbing the Jaynes–Cummings ladder and observing its nonlinearity in a cavity QED system. Nature 2008, 454, 315. [Google Scholar] [CrossRef]
- Akopian, N.; Lindner, N.; Poem, E.; Berlatzky, Y.; Avron, J.; Gershoni, D.; Gerardot, B.; Petroff, P. Entangled photon pairs from semiconductor quantum dots. Phys. Rev. Lett. 2006, 96, 130501. [Google Scholar] [CrossRef]
- Deppe, F.; Mariantoni, M.; Menzel, E.; Marx, A.; Saito, S.; Kakuyanagi, K.; Tanaka, H.; Meno, T.; Semba, K.; Takayanagi, H.; et al. Two-photon probe of the Jaynes–Cummings model and controlled symmetry breaking in circuit QED. Nat. Phys. 2008, 4, 686. [Google Scholar] [CrossRef]
- Araneda, G.; Higginbottom, D.B.; Slodička, L.; Colombe, Y.; Blatt, R. Interference of single photons emitted by entangled atoms in free space. Phys. Rev. Lett. 2018, 120, 193603. [Google Scholar] [CrossRef]
- Lee, C.J. Photon Emission Dynamics of a Two-Level Atom in a Cavity. arXiv 2015, arXiv:1512.08607. [Google Scholar]
- Luo, Y.; Liu, N.; Li, X.; Hone, J.C.; Strauf, S. Single photon emission in WSe2 up 160 K by quantum yield control. 2D Mater. 2019, 6, 035017. [Google Scholar] [CrossRef]
- Liu, Y.x.; Miranowicz, A.; Koashi, M.; Imoto, N. Realization of symmetric sharing of entanglement in semiconductor microcrystallites coupled by a cavity field. Phys. Rev. A 2002, 66, 062309. [Google Scholar] [CrossRef]
- Giounanlis, P.; Blokhina, E.; Pomorski, K.; Leipold, D.; Staszewski, R.B. Modeling of semiconductor electrostatic qubits realized through coupled quantum dots. IEEE Access 2019, 7, 49262–49278. [Google Scholar] [CrossRef]
- Giounanlis, P.; Blokhina, E.; Leipold, D.; Staszewski, R.B. Occupancy oscillations and electron transfer in multiple–quantum–dot qubits and their circuit representation. In Proceedings of the 25th IEEE International Conf. on Electronics Circuits and Systems (ICECS), Bordeaux, France, 9–12 December 2018; pp. 153–156. [Google Scholar]
- Gerry, C.; Knight, P. Introductory Quantum Optics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Orlando, T. Two-Level System with Static and Dynamic Coupling; Department of Electrical Engineering and Computer Science Massachusetts Institute of Technology. 2004. Available online: https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-728-applied-quantum-and-statistical-physics-fall-2006/study-materials/twolevel04.pdf (accessed on 20 July 2019).
- Dubbers, D.; Stöckmann, H.J. Quantum Physics: The Bottom-up Approach: From the Simple Two-Level System to Irreducible Representations; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Terhal, B.M. Bell inequalities and the separability criterion. Phys. Lett. A 2000, 271, 319–326. [Google Scholar] [CrossRef]
- Anaya-Contreras, J.A.; Moya-Cessa, H.M.; Zúñiga-Segundo, A. The von Neumann entropy for mixed states. Entropy 2019, 21, 49. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giounanlis, P.; Blokhina, E.; Leipold, D.; Staszewski, R.B. Photon Enhanced Interaction and Entanglement in Semiconductor Position-Based Qubits. Appl. Sci. 2019, 9, 4534. https://doi.org/10.3390/app9214534
Giounanlis P, Blokhina E, Leipold D, Staszewski RB. Photon Enhanced Interaction and Entanglement in Semiconductor Position-Based Qubits. Applied Sciences. 2019; 9(21):4534. https://doi.org/10.3390/app9214534
Chicago/Turabian StyleGiounanlis, Panagiotis, Elena Blokhina, Dirk Leipold, and Robert Bogdan Staszewski. 2019. "Photon Enhanced Interaction and Entanglement in Semiconductor Position-Based Qubits" Applied Sciences 9, no. 21: 4534. https://doi.org/10.3390/app9214534
APA StyleGiounanlis, P., Blokhina, E., Leipold, D., & Staszewski, R. B. (2019). Photon Enhanced Interaction and Entanglement in Semiconductor Position-Based Qubits. Applied Sciences, 9(21), 4534. https://doi.org/10.3390/app9214534




