Properties of Phase Solitons in an Optically Driven Semiconductor Ring Laser

Abstract

A semiconductor ring laser with a long cavity supports propagating localised structures with a chiral charge, named phase solitons. In this paper we study the dependence of the velocity and of the duration of the phase solitons on the characteristic time scales of the laser, namely the photon lifetime and the carrier lifetime. We show numerically that phase solitons are stable over a large range of those parameters and verify that the propagation velocity decreases linearly with the ratio of the carrier lifetime to the photon lifetime, while the duration is proportional to the ratio of the carrier lifetime to the cavity roundtrip time.

1. Introduction

Dissipative temporal solitons are light pulses moving round and round indeterminately inside a nonlinear optical cavity [1,2,3,4]. They can be found in mode locked lasers, where they are usually modelled by means of delay differential equations [5] or of the cubic-quintic Ginzburg-Landau [6], as well as in driven passive resonators such as fibers [7] or microcavities [8], where they are interpreted as localised solutions of the Lugiato-Lefever equation [9]. The interest in dissipative temporal solitons is related to their use as frequency combs, with several applications for instance in spectroscopy, metrology and astronomy [10].

Recently a novel kind of dissipative temporal soliton was found in a highly multimode semiconductor ring laser with a long cavity driven by a coherent field [11]. Unlike solitons in passive media, these solitons are not locked to the driving field. During a roundtrip the complex electric field performs a full rotation of $2\pi$ in such a way that at the end it still satisfies the boundary condition imposed by the forcing beam. The motion is not a pure rotation since the amplitude also varies considerably giving rise to a pulse. Nevertheless these structure are named dissipative phase solitons because phase dynamics plays a major role. In principle the rotation in the complex plane could be either clockwise or anticlockwise and we can associate, respectively, a chiral charge of $-1$ or $+1$ to it. Yet, both experiments and numerical simulations showed that only the phase solitons with positive chiral charge are stable due to the inertia of the active medium [12]. Consequently during a roundtrip time the phase evolves as a positive kink from 0 to $2\pi$. Further studies have shown that phase solitons display long range interaction and can form complexes with multiple chiral charge [13] or give rise to complex dynamics and extreme or abnormal events [14,15].

Phase solitons are common in spatially extended oscillatory systems to which a nearly resonant forcing is applied [16]. In our case it is the mismatch between the frequency of the free running laser and that of the injected field that leads to the formation of $2\pi$ phase kinks. Therefore phase solitons are intrinsically different from the dissipative temporal solitons mentioned above.

So far the study of phase solitons was limited to a very small set of parameters. The aim of this paper is to study how their stability and main properties depend on the relevant time scales of a laser, that is, the photon lifetime and the the gain recovery time or carrier lifetime in a semiconductor laser.

In Section 2 we present the simplest laser model that can account for the existence and stability of phase solitons in a ring semiconductor laser with optical injection and recall the main properties of such solitons. In Section 3 we present the results of our numerical simulations which allow to determine simple linear laws that relate the propagation velocity of the phase solitons and their duration with the time scales of the laser. In the final Section 4 we summarize our results and suggest the possibility of miniaturizing the experiment using a quantum cascade laser instead of a diode laser.

2. Methods

We consider a semiconductor ring laser made by an antireflection coated semiconductor medium (few mm long) placed in a long ring resonator of length L (about 1 m). The semiconductor medium is pumped electrically and the laser is driven by a coherent field injected into the cavity.

The long cavity combined with the large gainwidth allow highly multimode operation. In Reference [11] the system was studied using a set of effective Maxwell-Bloch equation where the coherent dynamics of the active medium was described by an effective macroscopic polarisation variable. However, very soon it was realised that as long as phase solitons are concerned a rate equation model suffices, where the polarisation variable is adiabatically eliminated [12]. The equations are

$$\begin{array}{ccc}\hfill \frac{\partial E}{\partial z}+\frac{\partial E}{\partial t}& =& \sigma \left[E_I-\left(1+i\theta \right)E+\left(1-i\alpha \right)DE\right],\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill \frac{\partial D}{\partial t}& =& b\left[\mu -\left(1+{\left|E\right|}^2\right)D\right].\hfill \end{array}$$

(2)

The dynamical variables are the dimensionless slowly varying envelope of the electric field E, which obeys a periodic boundary condition and the gain $D=\zeta (N/N_0-1)$, where $\zeta$ is a dimensionless parameter of order 1 [17], N is the carrier density and $N_0$ its transparency value, hence D is proportional to the excess of carriers with respect to transparency. We neglect the dependence of E and D on the transverse coordinates.

The parameters are the mismatch $\theta =({\omega }_c-{\omega }_I){\tau }_p$ between the cavity frequency ${\omega }_c$ and the frequency of the injected field ${\omega }_I$ multiplied by the photon lifetime, the dimensionless amplitude $E_I$ of the injected field, the linewidth enhancement $\alpha$ and the pump parameter $\mu =\zeta (I/I_0-1)$, where I is the injected current and $I_0$ its transparency value. At the lasing threshold we have ${\mu }_{\mathrm{thr}}=1$, which means that the threshold current is $I_{\mathrm{thr}}=I_0(1+{\zeta }^{-1})$. The longitudinal coordinate z is scaled to the length of the active medium and time is scaled to the cavity roundtrip time ${\tau }_R=L/c$, being L the cavity length and c the light speed in vacuum. Consequently the decay rates of the electric field and of the population variable are defined as

$$\sigma =\frac{{\tau }_R}{{\tau }_p},b=\frac{{\tau }_R}{{\tau }_e},$$

(3)

where ${\tau }_p$ and ${\tau }_e$ are, respectively, the photon and carrier lifetimes. Since the photon lifetime is by definition equal to the roundtrip time ${\tau }_R$ divided by cavity losses, the parameter $\sigma$ coincides with the cavity losses. The carrier lifetime ${\tau }_e$ for a semiconductor laser is of the order of 0.1–1 ns and the roundtrip time is on the order of some ns for a cavity length on the order of 1 m, hence the parameter b is on the order of 10–100. For suitable values of $\mu$, $\alpha$ and $\theta$ the stationary homogeneous solution is bistable. In this paper we fix the values $\mu =1.1$, which means that the laser is 10% above threshold, $\alpha =3$, which is a typical value for semiconductor lasers and $\theta =-2.7$, so that $\theta +\alpha =0.3$. Since $\theta +\alpha =({\omega }_L-{\omega }_I){\tau }_p$, where ${\omega }_L$ is the laser frequency [18], the latter choice means that the frequency of the driving field is some GHz larger than that of the nearest empty cavity resonance but smaller than the lasing frequency.

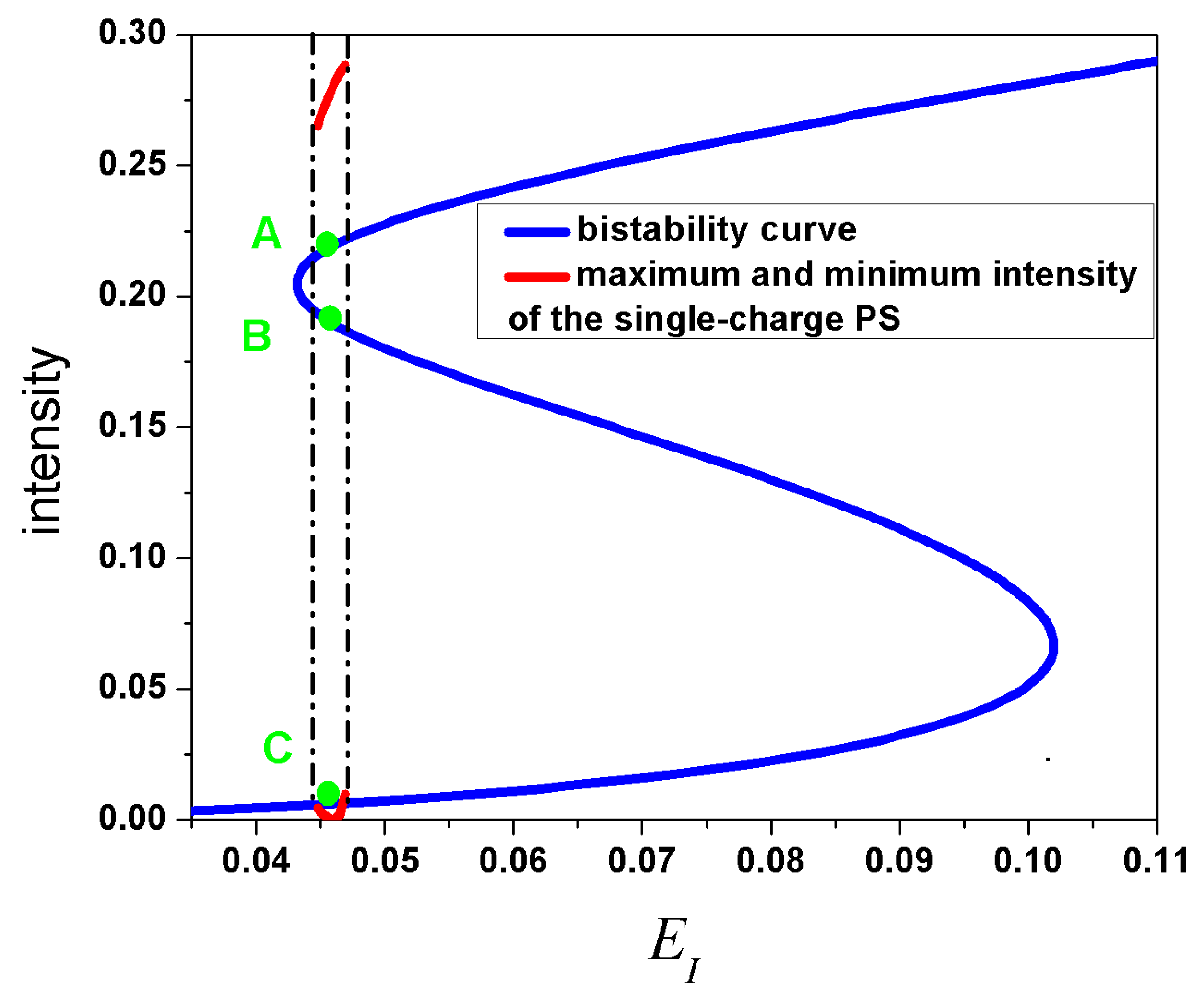
In Figure 1 we show the S-shaped homogeneous solution together with the branch of stable phase solitons obtained with that choice of the parameters and setting also $\sigma =0.3$, $b=50$.

The phase solitons are obtained letting the system evolve from an initial state whose amplitude is that of the state A but to which a phase profile in the form of a positive phase kink from 0 to $2\pi$ is superimposed. In the extended system where the dynamical variables are allowed to depend on the longitudinal coordinate z the homogeneous state A is still stable but it coexists with the phase soliton, that is, a state in which the phase varies by $2\pi$. The stability of the phase soliton is checked as usual by adding dynamical noise to the equations. In Reference [13] the stability and the properties of the phase solitons were studied assuming that all the parameters but the amplitude $E_I$ of the injected field are fixed. In other words the different phase solitons that can be observed varying one experimental parameter in a given laser configuration were considered. Here we take a different approach and, by fixing the amplitude $E_I$ of the injected field, we study how the stability and the properties of the phase solitons change for different laser configurations, defined by the fundamental time scales associated with the active material $\left({\tau }_e\right)$ and with the cavity $({\tau }_R,{\tau }_p)$.

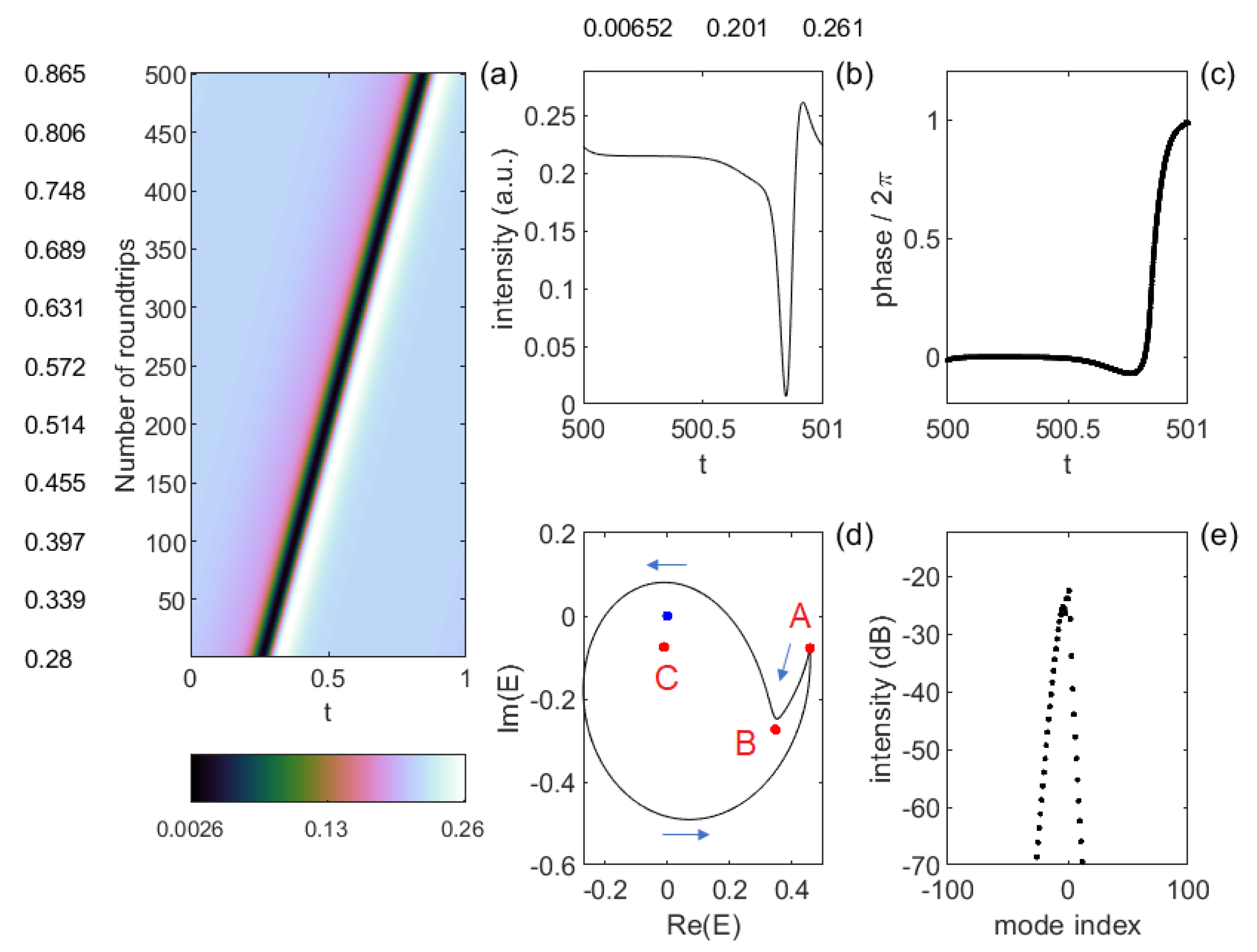
Precisely, in the following we set $E_I=0.0445$ and let $\sigma$ and b vary, which means that for a fixed cavity length we assume to vary the photon lifetime ${\tau }_R$ and the carrier lifetime ${\tau }_e$. Figure 2 shows a typical example of phase soliton obtained for our initial choice of the parameters $\sigma =0.3$ and $b=50$.

Panel (a) is a space-time intensity plot where the horizontal axis is time scaled to the roundtrip time and the vertical axis counts the number of roundtrips. Here we assume to observe the field intensity at a fixed position inside the cavity (for instance at the exit of the active medium). We could as well imagine to fix time and follow the evolution of the spatial profile of the intensity one roundtrip after the other. In that case, however, the horizontal axis should be reversed, so that an image symmetric with respect to the vertical axis would be obtained. In our false-color plots, the abscissa represents time in a frame moving at velocity c, thus a rightward (leftward) tilted evolution corresponds to $v<c$ ($v>c$). All stable phase solitons propagate at a velocity smaller than c, so that a stable phase soliton is described by a line inclined to the right. The larger is the inclination, the slower is the phase soliton.

Panels (b) and (c) show the time evolution of the field intensity and phase, respectively, over the last roundtrip. The phase soliton displays a deep minimum followed by a small maximum in the intensity and a positive $2\pi$ phase kink in the phase.

Panel (d) shows the evolution of the complex electric field during one roundtrip time. The labels A, B and C denote the three fixed points of the homogeneous stationary curve. The trajectory starts and terminates in A, which is the stable fixed point on the upper branch of the bistable curve, it is repelled by B, which is the unstable fixed point on the negative slope branch and circles around the origin O and around C, which is the unstable focus on the lower branch of the bistable curve. The tip of the complex electric field moves anticlockwise along the trajectory, apart for the small portion between A and B. This motion results in the positive phase kink of $2\pi$ shown in (c). The phase soliton with a negative phase kink is always unstable [11,12]. Finally, panel (e) shows the power spectrum of the phase soliton that is, the intensities of the longitudinal modes that compose the phase soliton. The central mode ($n=0$), which is always largely dominant because pumped by the external field, is not shown. The spectra are asymmetric, with a prevalence of modes with negative index.

3. Results

Starting from the choice of the parameters $\sigma$ and b of Figure 2 we investigated how the properties of the phase solitons depend on those two parameters. For fixed $b=50$ we varied $\sigma$ from 0.1 to 0.9 by steps of 0.1 and for fixed $\sigma =0.3$ we varied b from 10 to 100 by steps of 10. In our study we focused mainly on two properties of the phase solitons: their velocity and their width or duration.

As mentioned above, the propagation velocity of the phase soliton is related to the inclination of the straight line that depicts the phase soliton in the space-time diagrams. We calculate the propagation velocity in the following way [13]. Let us call $\Delta \tau$ the delay accumulated during N roundtrips. Then the velocity is

$$v=\frac{NL}{N{\tau }_c+\Delta \tau }=\frac{L/{\tau }_c}{1+\Delta \tau /\left(N{\tau }_c\right)}=\frac{c}{1+\Delta \tau /\left(N{\tau }_c\right)}$$

(4)

and

$$\frac{v}{c}\approx 1-\frac{\Delta \tau }{N{\tau }_c},$$

(5)

since $\Delta \tau \ll N{\tau }_c$. As shown in panel (b) of Figure 2 in presence of a phase soliton the field intensity is approximately uniform for most of the time and approximately equal to the intensity of the stable fixed point A. This intensity level is the background for the phase soliton and we call it $I_{\mathrm{bg}}$. The phase soliton consists of a deep negative pulse where the intensity reaches its minimum value $I_{min}$ followed by a small positive pulse where the intensity reaches its maximum value $I_{max}$. If we introduce the intensities

$$I_1=\frac{I_{min}+I_{\mathrm{bg}}}{2},I_2=\frac{I_{max}+I_{\mathrm{bg}}}{2},$$

(6)

we can define the duration of the phase soliton or its width, ${\tau }_{ps}={\tau }_2-{\tau }_1$ as the interval between the instant ${\tau }_1$ when the intensity reaches for the first time the value $I_1$ and the instant ${\tau }_2$ when the intensity reaches for the second time the value $I_2$.

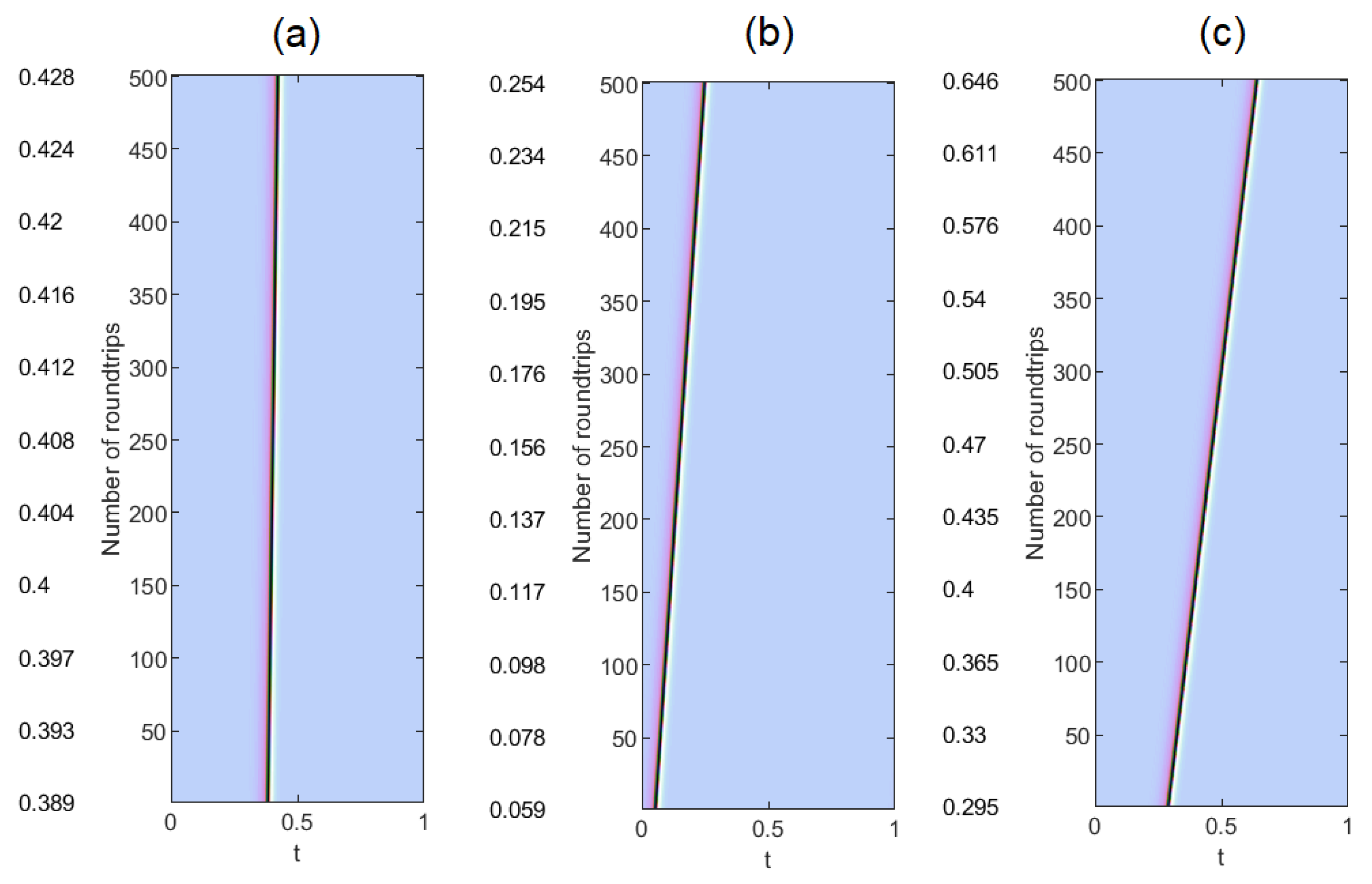
As a first result we found that when b is fixed and $\sigma$ is varied the only property of the phase soliton that changes is its velocity. In Figure 3 we show the space-time plots for $b=50$ fixed and three values of $\sigma$: $\sigma =0.1$ in (a), $\sigma =0.5$ in (b) and $\sigma =0.9$ in (c). The propagation velocity of the phase soliton decreases with $\sigma$, while its shape, spectrum and trajectory in the complex plane remain unchanged.

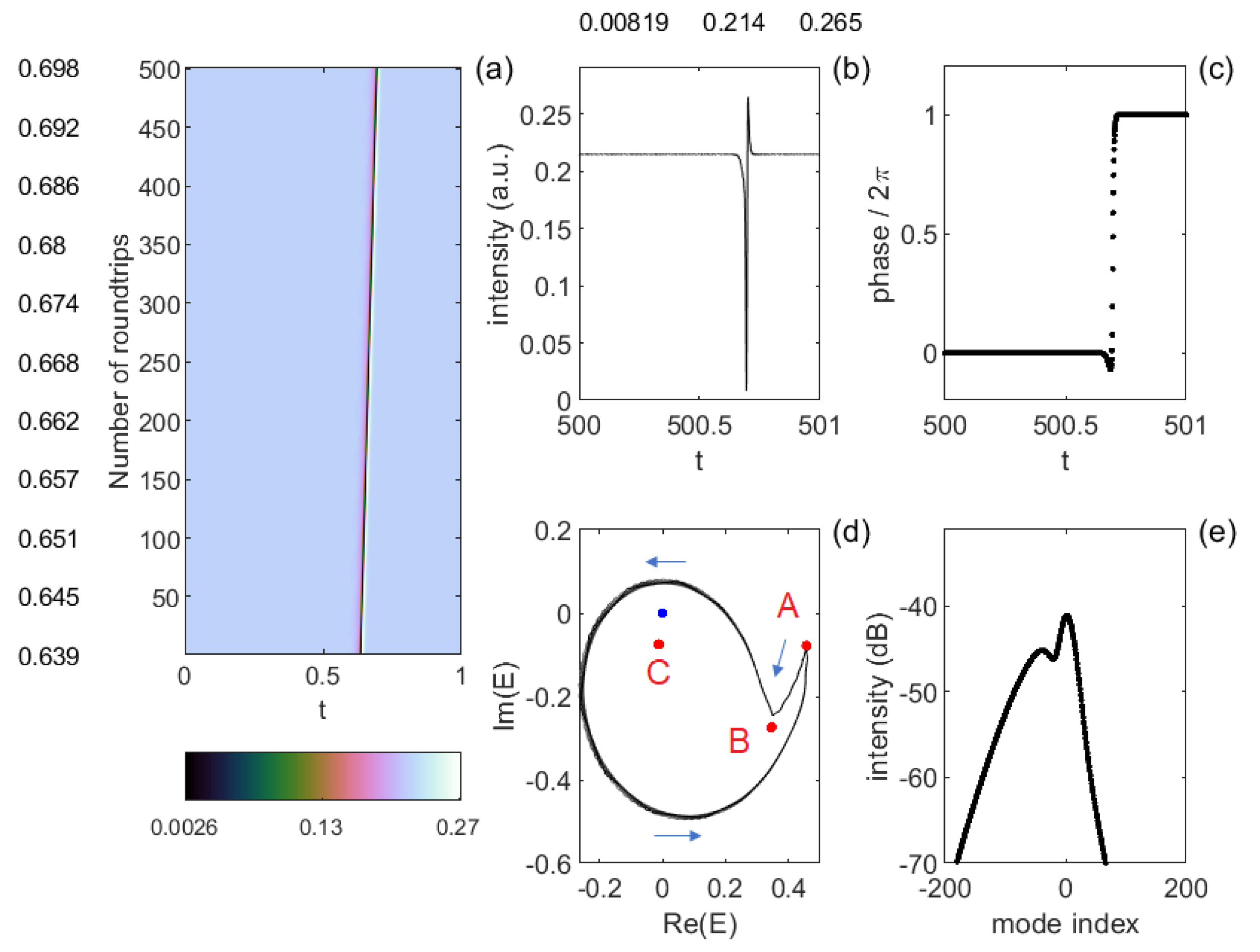
The situation is different when $\sigma$ is kept fixed and b is varied. Figure 4 and Figure 5 show the phase solitons for the same value $\sigma =0.3$ as in Figure 2 but $b=10$ in Figure 4 and $b=100$ in Figure 5. Here both the velocity and the shape of the phase soliton change considerably and consequently also the spectrum. The phase soliton is much narrower and much faster for $b=100$ and the phase kink is also much steeper. Only the shape of the trajectory in the complex plane is the same in the two cases but it must be considered that in Figure 5 the representative point remains close to the fixed point A for almost all the roundtrip time and the trajectory around the origin is travelled much faster.

The change in shape of the phase solitons is accompanied by a different modal composition. We can compare the panels (e) of Figure 4 and Figure 5. The number of modes with intensity larger than −70 dB is 39 for $b=10$ and 247 for $b=100$.

An explanation for the above results can be found looking at the structure of the dynamical Equations (1) and (2). We see that the equations can be made to depend just on the ratio $\sigma /b$ by defining the new spatial and temporal variables $z^{\prime }=bz$ and $t^{\prime }=bt$

$$\begin{array}{ccc}\hfill \frac{\partial E}{\partial z^{\prime }}+\frac{\partial E}{\partial t^{\prime }}& =& \frac{\sigma }{b}\left[E_I-\left(1+i\theta \right)E+\left(1-i\alpha \right)DE\right],\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill \frac{\partial D}{\partial t^{\prime }}& =& \mu -\left(1+{\left|E\right|}^2\right)D.\hfill \end{array}$$

(8)

Therefore, the velocity of the phase soliton can depend only on that ratio, while their duration scales with b. More precisely, if we look for a solution of Equations (7) and (8) of the form $E=E\left(w\right)$, $D=D\left(w\right)$ with $w=zc/v-t$, that is, a pulse propagating at velocity v, we obtain from Equation (7)

$$E^{\prime }\left(\frac{c}{v}-1\right)=\frac{\sigma }{b}{f}_E,$$

(9)

where we have denoted by $f_E$ the content of the square brackets at the right hand side of Equation (7) and by $E^{\prime }$ the derivative of E with respect to w. This equation can be made independent of the ratio $\sigma /b$ by setting

$$\frac{c}{v}-1=K_1\frac{\sigma }{b}.$$

(10)

Since v is very close to c this is equivalent to $v/c=1-K_1\sigma /b$.

From this discussion it follows that the propagation velocity of the phase soliton decreases linearly with the ratio $\sigma /b={\tau }_e/{\tau }_p$, while its width is inversely proportional to the parameter $b={\tau }_R/{\tau }_e$. Two phenomena concur in slowing down the phase solitons—the inertia of the active medium, which is proportional to ${\tau }_e$ and the escape of photons from the cavity, which is inversely proportional to ${\tau }_p$. The width of the phase soliton, instead, is determined only by inertia of the active medium.

The above assumptions were fully confirmed by the plots shown in Figure 6a,b, where we collected all the results obtained by varying independently $\sigma$ and b. The numerical data admit the linear fits

$$\frac{v}{c}=1-K_1\frac{\sigma }{b},{\tau }_{ps}=\frac{K_2}{b}.$$

(11)

The constants $K_1$ and $K_2$ depend on all the parameters of the system. Here we found $K_1=0.03908\pm 0.00006$ and $K_2=1.48285\pm 0.00266$.

The above consideration, however, do not allow to determine the range of values of $\sigma$ and b for which the phase solitons exist and are stable. A complete analysis is beyond the scope of this paper but from our simulations we can at least state that in order for the phase solitons to be stable the ratio $\sigma /b$ must be sufficiently small, that is, we must be in the class-A laser limit. For fixed $\sigma =0.3$ the smallest value of b for which we found a stable phase soliton is stable is $b=5$, that is, $\sigma /b=0.06$. If the medium is too slow, the laser cannot support stable phase solitons. Assuming that the roundtrip time is ${\tau }_c=3.6$ ns as in the experiment of Reference [11] this means that the phase soliton is stable for ${\tau }_e\le 0.72$ ns.

Figure 7a–e shows that before loosing stability the phase soliton changes considerably with respect to the typical shape shown in Figure 2. Here the soliton is much wider and slower and now its trajectory in the complex plane never touches the stable fixed point A. Panel (f) of the same figure shows the process of destabilization of the phase soliton as we lower the parameter b to $b=4$ starting from the stable solution of $b=5$. The electric field evolves in a complex dynamical state over 2000 roundtrip times.

4. Conclusions

In this paper we have investigated how the stability, velocity, duration and modal composition of phase solitons depend on the dimensionless decay rates $\sigma ={\tau }_R/{\tau }_p$ and $b={\tau }_R/{\tau }_e$. We have interpreted our results having in mind the experiment of Reference [11] where the cavity length L is on the order of 1 m and the carrier lifetime ${\tau }_e$ on the order of 0.1–1 ns. We could however imagine an experiment in which the active medium is much faster. For instance, for a quantum cascade laser, the carrier lifetime on the order of 1 ps. Since $b={\tau }_c/{\tau }_e$ and ${\tau }_R=L/c$, we have $L=bc{\tau }_e$. With fixed cavity losses $\sigma =0.3$ we have found stable phase solitons for b of the order of 10 to 100. This suggests the interesting possibility of miniaturizing the experiment down to the scale of the cm. This means that the cavity roundtrip time is on the order of 0.1 ns and therefore the duration of the phase solitons would be on the order of 10 ps.