Development of an ANN-Based Lumped Plasticity Model of RC Columns Using Historical Pseudo-Static Cyclic Test Data
Abstract
Featured Application
Abstract
1. Introduction
2. Data Collection
- The shape of the cross section of the RC columns should be rectangular; others like circular columns are not included in this study.
- The RC columns only sustained constant axial loading and unidirectional cyclic lateral force. Cyclic tests of the RC column under biaxial lateral or variable axial loads are excluded.
- A complete loading process was applied to the specimens until failure; the load carrying capacity of the specimen decreased by more than 20% compared to the peak strength.
- Details of the specimens are available, such as the geometrical size and reinforcement, as well as experimental results of the hysteretic curves.
- Normal concrete was used in the manufacture of the specimens, without additives such as steel fiber.
3. ANN Model
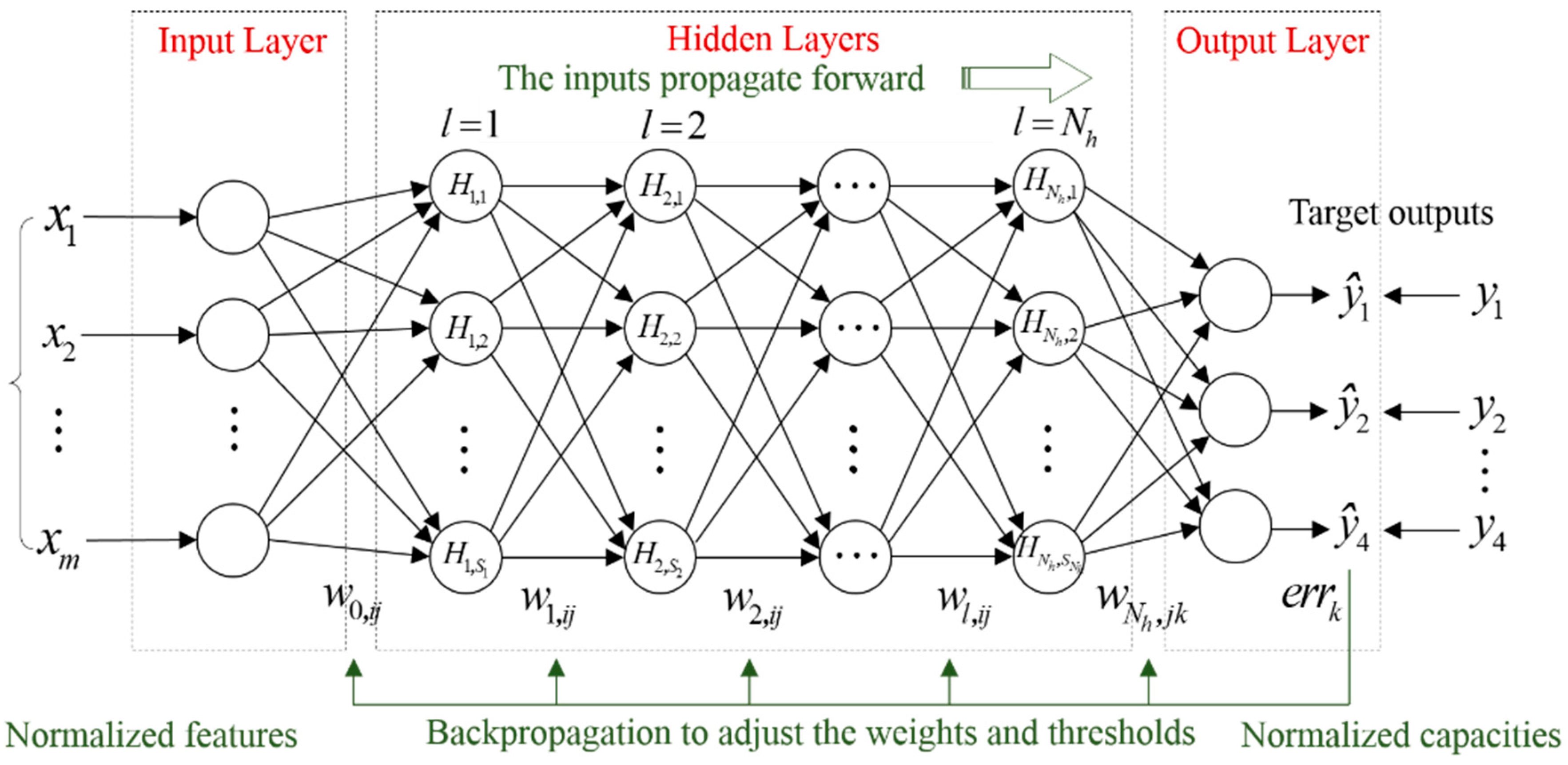
3.1. Architecture of the ANN Model
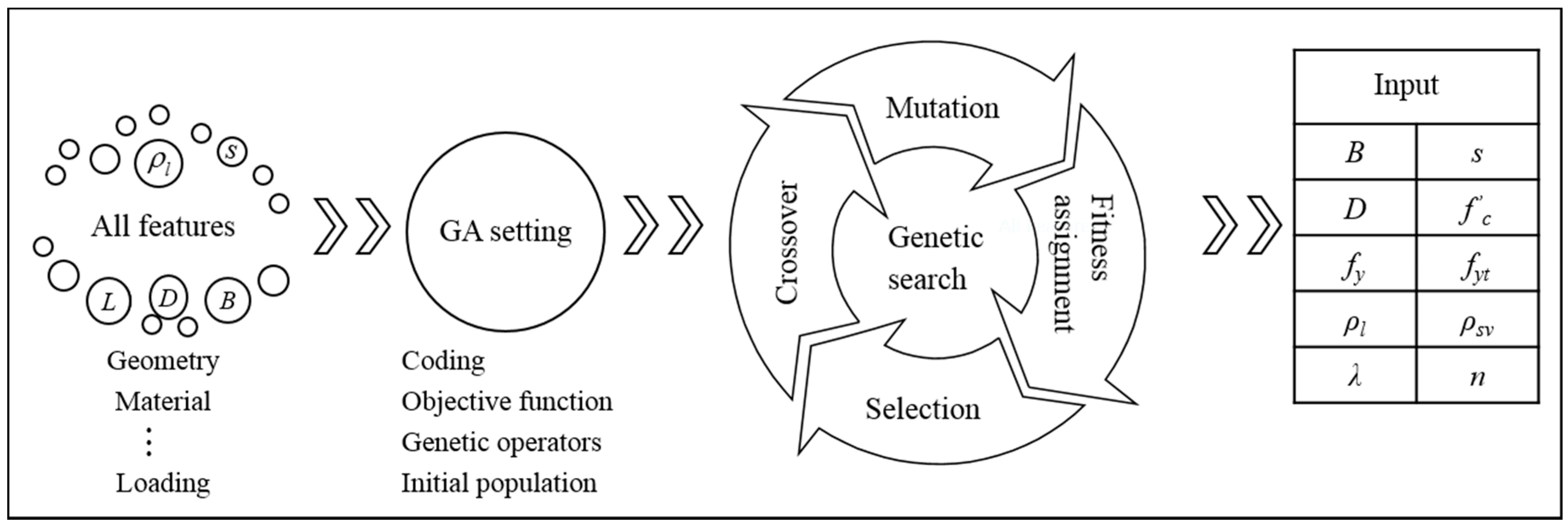
3.2. Input and Output Layer
4. Results and Discussion
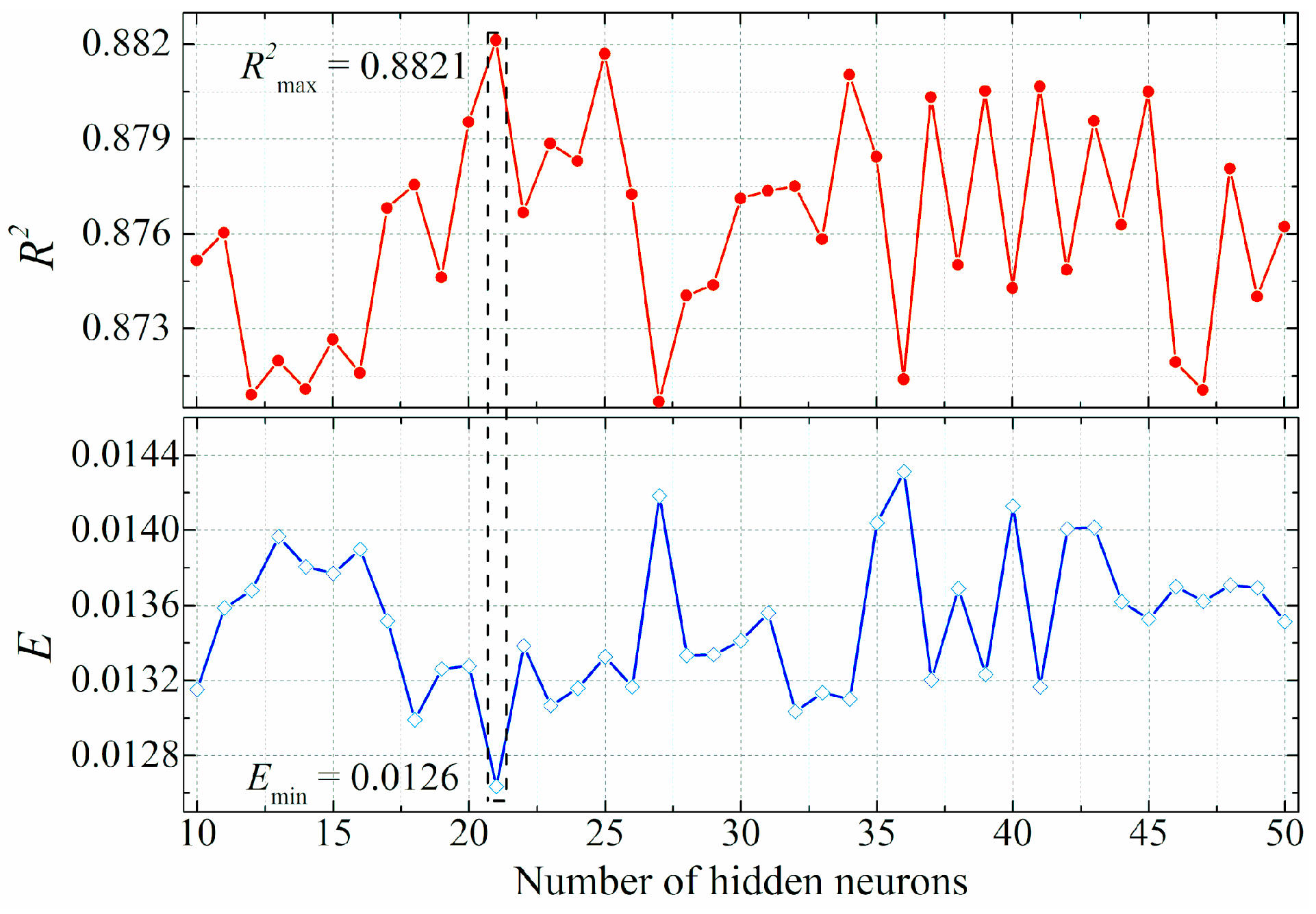
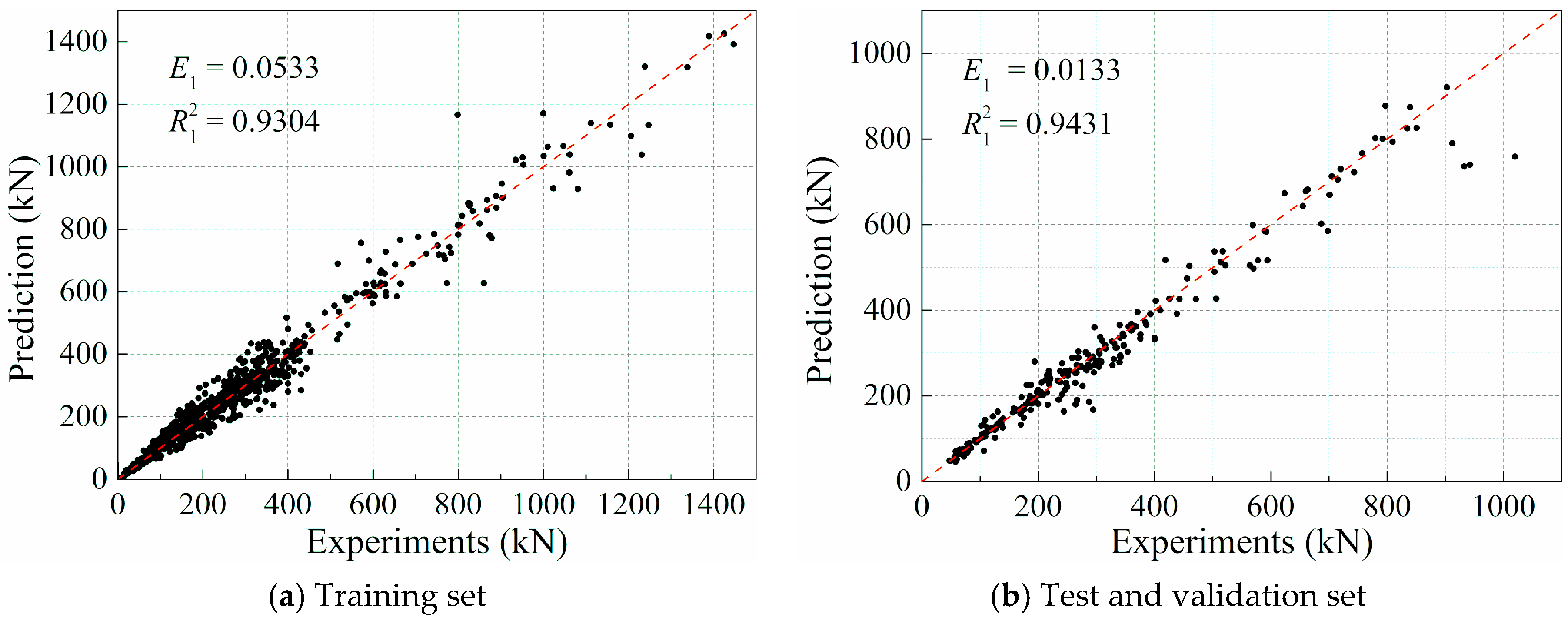
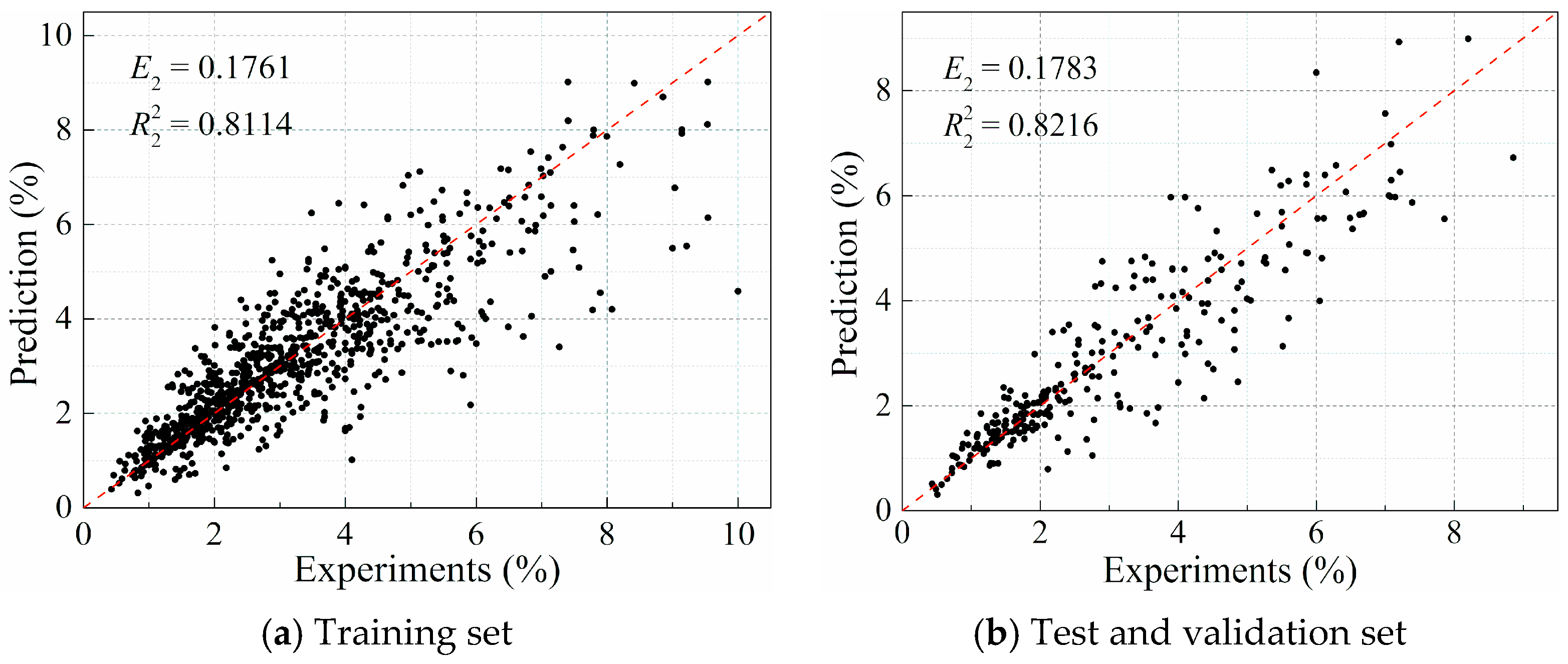
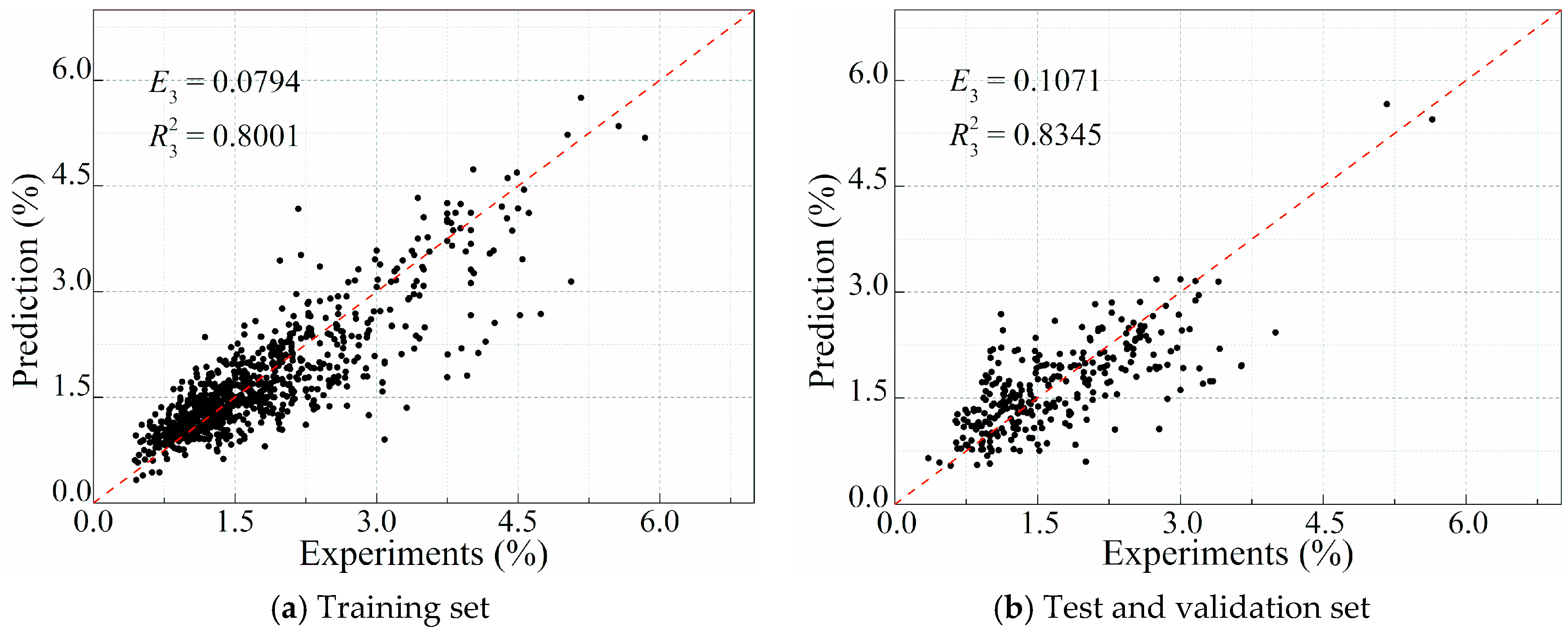
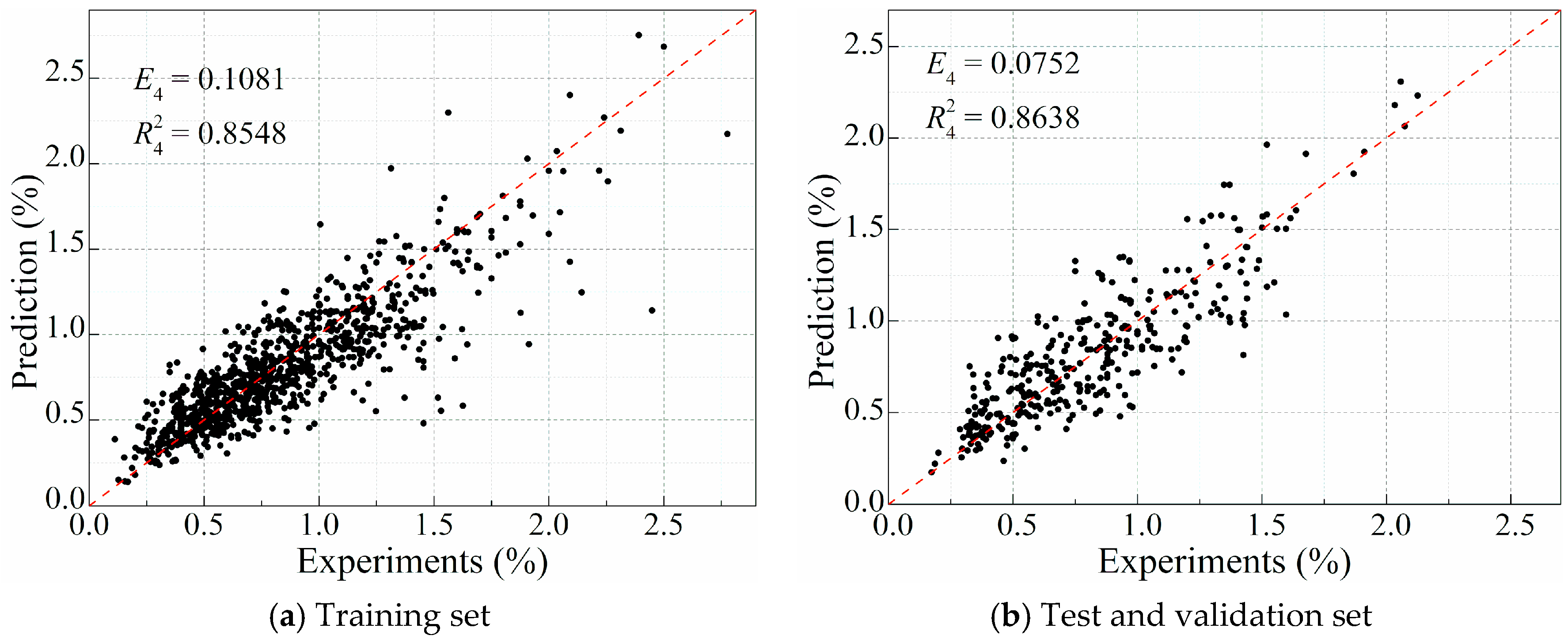
4.1. Training of the ANN Model
4.2. Validation
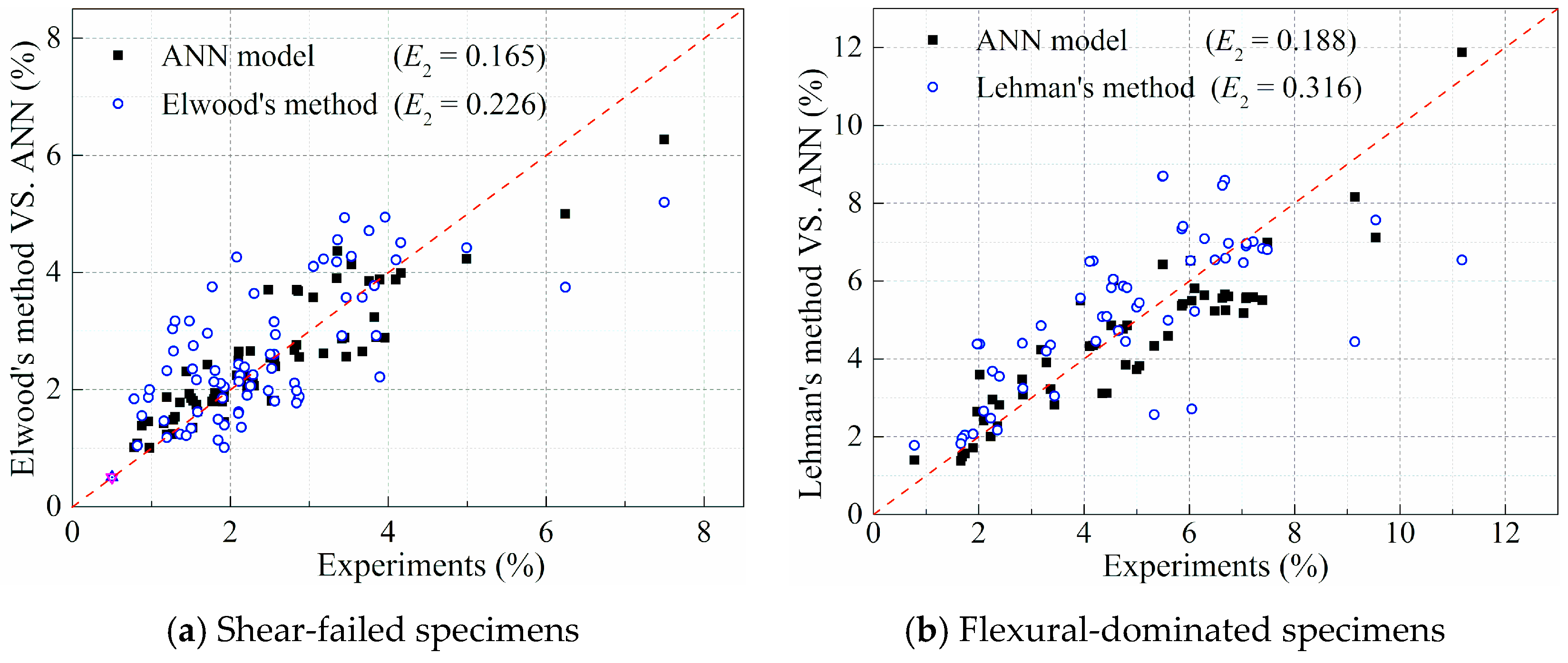
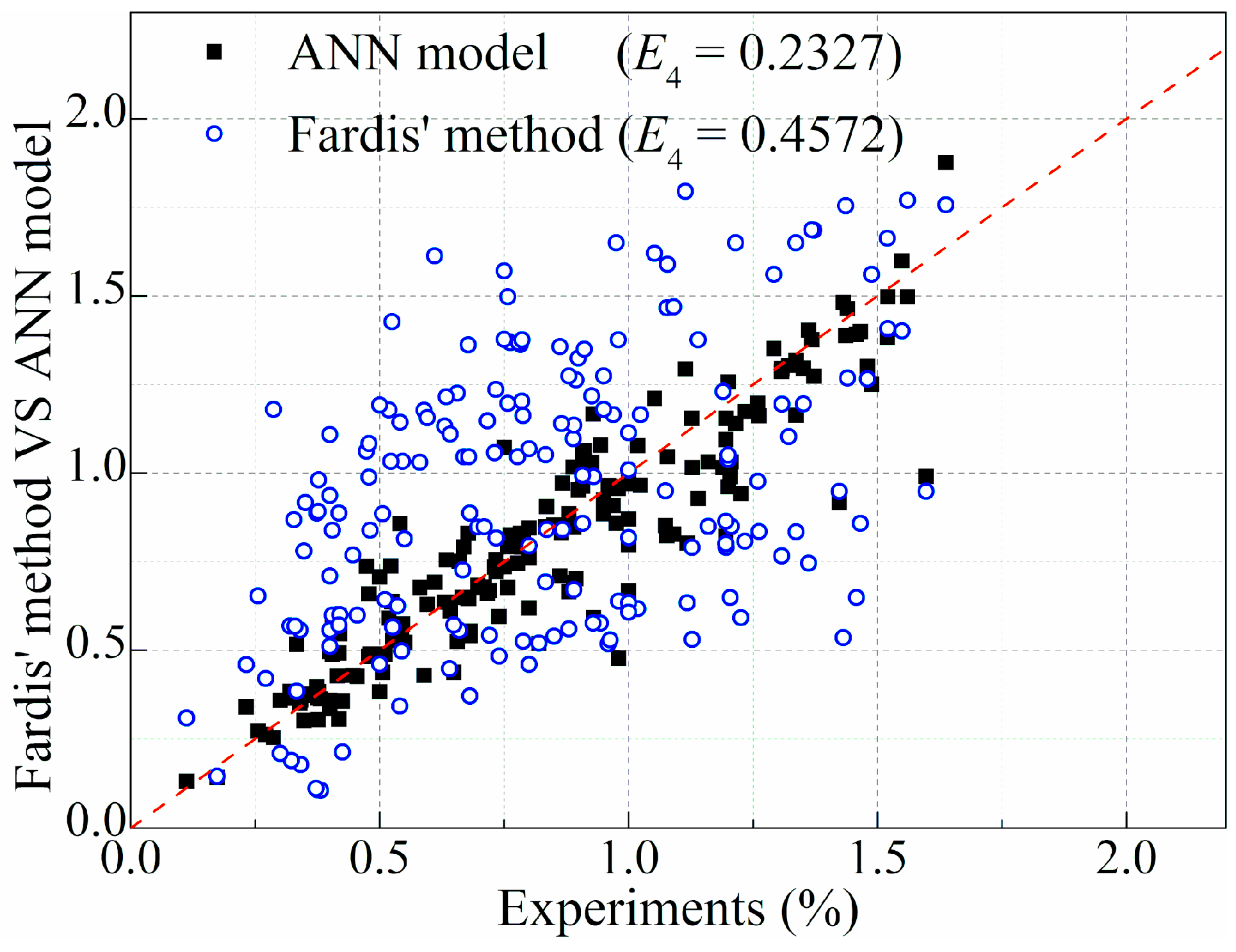
4.3. Evaluation of the ANN-Based LP Model
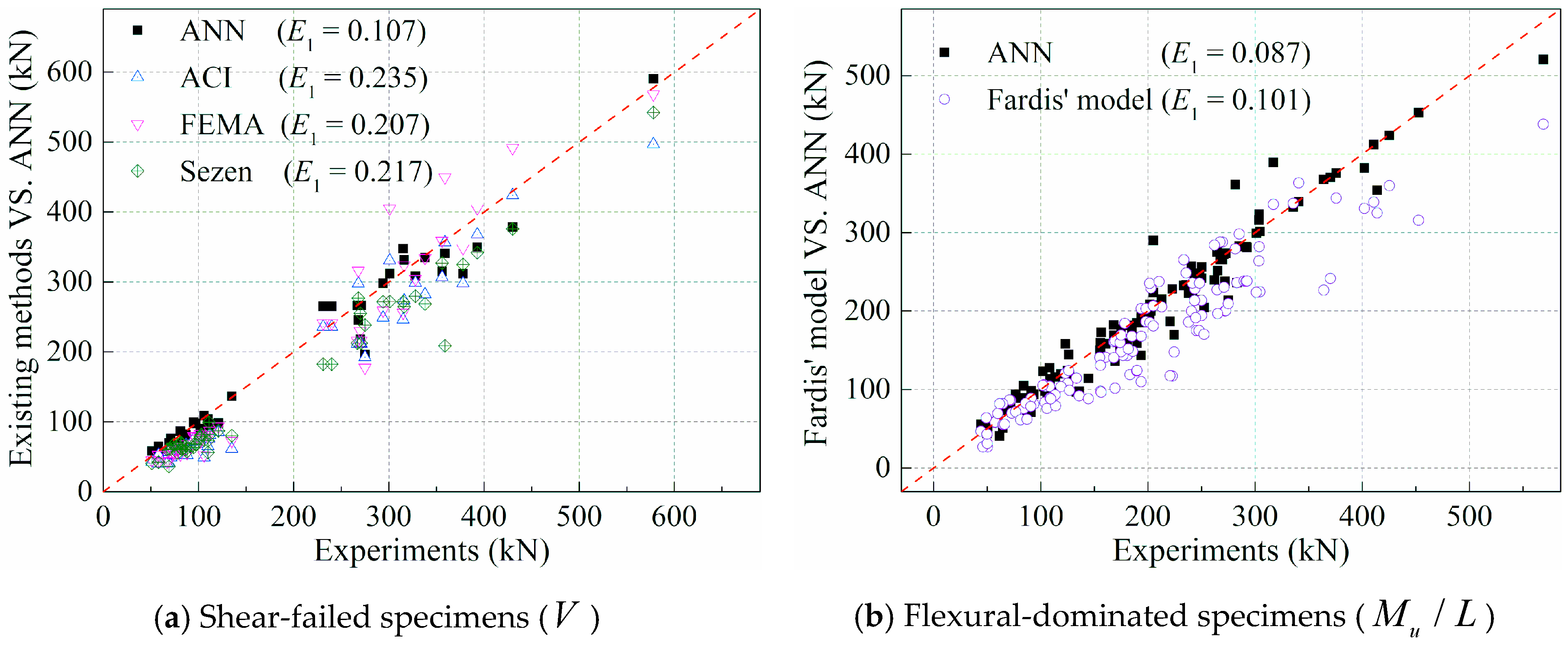
4.3.1. Comparison with the Pseudo-Static Test
4.3.2. Comparison with Shake Table Test
5. Conclusions
- On the basis of a large historical experimental database and advanced humanlike information processing algorithm, the proposed model-free method in this study can rapidly get more accurate input parameters for any bilinear and tri-linear LP model than current explicit formulas. The accuracy of the proposed method can also have been improved with the increment of the sample quantity of the database.
- The validation results through both the collected experimental data and several existing functions indicate that the ANN-based method can be effectively used to predict the most important characteristics of RC columns, which are also critical for the further modeling of structures. In addition, another advantage of the proposed model-free method is that the quantity of the input features could be easily changed according to the requirement of an arbitrary multi-linear model.
- The ANN-based LP model can help reduce the subjective and experimental errors. The prediction results of the RC frame structures using the well-trained ANN-based LP model show a good agreement with both the quasi-static and shaking table test results, especially for the pre-collapse stage. Thus, the model-free method based on the machine learning theory will be an innovative and promising approach for a fast seismic performance evaluation of the buildings and bridges in the future.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
| References | Number of Specimens | Width (mm) | Shear Span (mm) | Concrete Strength (MPa) | Axial Load Ratio |
|---|---|---|---|---|---|
| Berry and Eberhard [44] | 132 | 150~550 | 160~2200 | 16~160 | 0.0~0.8 |
| Browning et al. [26] | 168 | 80~800 | 80~2500 | 13~116 | 0.0~0.9 |
| Yun [45] | 6 | 510 | 1778 | 62.1~64.1 | 0.20~0.34 |
| Ho and Johnny [46] | 20 | 325 | 1515 | 56.5~111.1 | 0.11~0.55 |
| Ongsupankul et al. [47] | 4 | 400 | 1550 | 29.61~32.36 | 0.07~0.08 |
| Woodward and Jirsa [48] | 5 | 300 | 455 | 31~41 | 0.0~0.21 |
| Bayrak [49] | 24 | 250~350 | 1473 | 70.8~112.1 | 0.31~0.53 |
| Mo and Wang [50] | 9 | 400 | 1400 | 24.9~27.5 | 0.1~0.21 |
| Paultre et al. [51] | 8 | 305 | 2150 | 78.7~110 | 0.35~0.53 |
| Xiao and Yun [52] | 6 | 510 | 1778 | 62.1, 64.1 | 0.2~0.34 |
| Lam et al. [53] | 9 | 160~267 | 400~480 | 42, 47 | 0.4~0.65 |
| Hwang and Yun [54] | 8 | 200 | 300 | 68.3~70.3 | 0.3 |
| Moretti and Tassios [7] | 8 | 250 | 250~750 | 35~49 | 0.3,0.6 |
| Ahn and Shin [55] | 20 | 240 | 500 | 32~70 | 0.3~0.5 |
| Woods et al. [56] | 7 | 203 | 625 | 69 | 0.16 |
| Marefat et al. [57] | 7 | 150~200 | 750 | 20~28 | 0.16~0.31 |
| Xiao et al. [58] | 6 | 200 | 850 | 60, 90 | 0.38~0.54 |
| Bae [59] | 5 | 610, 440 | 2630 | 29.6~43.4 | 0.2, 0.5 |
| Cao [60] | 10 | 250, 350 | 600, 850 | 22.6~32.5 | 0.2~0.5 |
| Ou et al. [61] | 8 | 600 | 900 | 92.5~121 | 0.1, 0.2 |
| Abdelsamie et al. [62] | 7 | 250 | 700, 1050 | 26.6~151.4 | 0 |
| Martirossyan and Xiao [63] | 6 | 254 | 508 | 76, 86 | 0.1, 0.2 |
| Li et al. [64] | 8 | 300 | 250~500 | 23.4~27.5 | 0.09~0.29 |
| Nakamura et al. [65] | 6 | 450 | 450, 700 | 25, 28 | 0.16~0.18 |
| Popa et al. [66] | 7 | 300 | 450 | 18~29 | 0.2~0.4 |
| Jin et al. [67] | 8 | 150 | 495~660 | 34~73 | 0.09, 0.13 |
| Bechtoula et al. [68] | 10 | 325~520 | 813~1300 | 80, 130 | 0.3 |
| El-Attar et al. [69] | 7 | 150 | 870 | 141 | 0~0.35 |
| Personal communications | 626 | 150~900 | 150~3500 | 20~180 | 0~0.9 |
References
- Guo, A.; Liu, Z.; Li, S.; Li, H. Seismic performance assessment of highway bridge networks considering post-disaster traffic demand of a transportation system in emergency conditions. Struct. Infrastruct. Eng. 2017, 13, 1523–1537. [Google Scholar] [CrossRef]
- Eurocode 8: Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings; European Committee for Standardization: Brussels, Belgium, 2005.
- American Society of Civil Engineers. Prestandard and Commentary for the Seismic Rehabilitation of Buildings; FEMA 356: Washington, DC, USA, 2000.
- Priestley, M.N.; Verma, R.; Xiao, Y. Seismic shear strength of reinforced concrete columns. J. Struct. Eng. 1994, 120, 2310–2329. [Google Scholar] [CrossRef]
- Sezen, H.; Moehle, J.P. Shear Strength Model for Lightly Reinforced Concrete Columns. J. Struct. Eng. 2004, 130, 1692–1703. [Google Scholar] [CrossRef]
- Elwood, K.J.; Moehle, J.P. Drift Capacity of Reinforced Concrete Columns with Light Transverse Reinforcement. Earthq. Spectra 2005, 21, 71–89. [Google Scholar] [CrossRef]
- Moretti, M.; Tassios, T.P. Behaviour of short columns subjected to cyclic shear displacements: Experimental results. Eng. Struct. 2007, 29, 2018–2029. [Google Scholar] [CrossRef]
- Taheri, A.; Moghadam, A.S.; Tasnimi, A.A. Critical factors in displacement ductility assessment of high-strength concrete columns. Int. J. Adv. Struct. Eng. 2017, 9, 325–340. [Google Scholar] [CrossRef]
- Mostafaei, H.; Vecchio, F.J.; Kabeyasawa, T. Deformation Capacity of Reinforced Concrete Columns. ACI Struct. J. 2009, 106, 187–195. [Google Scholar]
- Wibowo, A.; Wilson, J.L.; Lam, N.T.K.; Gad, E.F. Drift Capacity of Lightly Reinforced Concrete Columns. Aust. J. Struct. Eng. 2011, 15, 131–150. [Google Scholar] [CrossRef]
- Ferdous, W.; Manalo, A.; Aravinthan, T.; Fam, A. Flexural and shear behaviour of layered sandwich beams. Const. Build. Mater. 2018, 173, 429–442. [Google Scholar] [CrossRef]
- Ferdous, W.; Manalo, A.; Erp, G.V.; Aravinthan, T.; Ghabraie, K. Evaluation of an Innovative Composite Railway Sleeper for a Narrow-Gauge Track under Static Load. J. Compos. Const. 2018, 22, 04017050. [Google Scholar] [CrossRef]
- Kim, S.-H.; Han, S.-J.; Kim, K.S. Nonlinear Finite Element Analysis Formulation for Shear in Reinforced Concrete Beams. Appl. Sci. 2019, 9, 3503. [Google Scholar] [CrossRef]
- Szcześniak, A.; Stolarski, A. Dynamic Relaxation Method for Load Capacity Analysis of Reinforced Concrete Elements. Appl. Sci. 2018, 8, 396. [Google Scholar] [CrossRef]
- Lucchini, A.; Franchin, P.; Kunnath, S. Failure simulation of shear-critical RC columns with non-ductile detailing under lateral load. Earthq. Eng. Struct. Dyn. 2017, 46, 855–874. [Google Scholar] [CrossRef]
- Lu, X.; Ye, L.; Pan, P.; Zhao, Z.; Ji, X.; Qian, J. Pseudo-static collapse experiments and numerical prediction competition of RC frame structure І:RC frame experiment. Build. Struct. 2012, 42, 23–26. [Google Scholar]
- Ibarra, L.F.; Medina, R.A.; Krawinkler, H. Hysteretic models that incorporate strength and stiffness deterioration. Earthq. Eng. Struct. Dyn. 2005, 34, 1489–1511. [Google Scholar] [CrossRef]
- Haselton, C.B.; Liel, A.B.; Deierlein, G.G. Simulation structural collapse due to earthquakes: Model calibration, and numerical solution algorithms. In Proceedings of the Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN), Rhodes, Greece, 22–24 June 2009. [Google Scholar]
- Liel Abbie, B.; Haselton Curt, B.; Deierlein Gregory, G. Seismic Collapse Safety of Reinforced Concrete Buildings. II: Comparative Assessment of Nonductile and Ductile Moment Frames. J. Struct. Eng. 2011, 137, 492–502. [Google Scholar] [CrossRef]
- Lucchi, E. Non-invasive method for investigating energy and environmental performances in existing buildings. In Proceedings of the PLEA—Architecture and Sustainable Development, Louvain-la-Neuve, Belgium, 13–15 July 2011. [Google Scholar]
- Kawashima, K.; Oreta, A.W.C. Neural Network Modeling of Confined Compressive Strength and Strain of Circular Concrete Columns. J. Struct. Eng. 2003, 129, 554–561. [Google Scholar]
- Iztok, P.; Karmen, P.; Fajfar, P. Flexural deformation capacity of rectangular RC columns determined by the CAE method. Earthq. Eng. Struct. Dyn. 2006, 35, 1453–1470. [Google Scholar]
- Chou, J.-S.; Ngo, N.-T.; Pham, A.-D. Shear Strength Prediction in Reinforced Concrete Deep Beams Using Nature-Inspired Metaheuristic Support Vector Regression. J. Comput. Civ. Eng. 2016, 30, 04015002. [Google Scholar] [CrossRef]
- González, M.P.; Zapico, J.L. Seismic damage identification in buildings using neural networks and modal data. Comput. Struct. 2008, 86, 416–426. [Google Scholar] [CrossRef]
- Reza, S.M.; Alam, M.S.; Tesfamariam, S. Lateral load resistance of bridge piers under flexure and shear using factorial analysis. Eng. Struct. 2014, 59, 821–835. [Google Scholar] [CrossRef]
- Browning, J.A.; Pujol, S.; Eigenmann, R.; Ramirez, J.A. NEEShub Databases. Concrete International. 2013, Volume 35. Available online: https: //datacenterhub.org/ resources/databases (accessed on 4 April 2013).
- University of Washington. The UW-PEER Reinforced Concrete Column Test Database. Available online: http://www.ce.washington.edu/∼peera1/: (accessed on 1 January 2004).
- Mckenna, F.; Fenves, G.L. Open system for earthquake engineering simulation (OpenSees). In Pacific Earthquake Engineering Research Center; University of California: California, CA, USA, 2013. [Google Scholar]
- Haselton, C.B. Beam-Column Element Model Calibrated for Predicting Flexural Response Leading to Global Collapse of RC Frame Buildings; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2008. [Google Scholar]
- Dimitrios, L. Sidesway Collapse of Deteriorating Structural Systems under Seismic Excitations; Stanford University: Standford, CA, USA, 2009. [Google Scholar]
- Ziegel, E.R. The Elements of Statistical Learning; World Publishing Corporation: New York, NY, USA, 2015. [Google Scholar]
- Flood, I. Neural networks in civil engineering: A review. Civil and Structural Engineering Computing; Saxe-Coburg Publications: Stirling, UK, 2001; pp. 185–209. [Google Scholar]
- Booker, L.B.; Goldberg, D.E.; Holland, J.H. Classifier systems and genetic algorithms. Artif. Intell. 1989, 40, 235–282. [Google Scholar] [CrossRef]
- Shafti, L.S.; Pérez, E. Fitness Function Comparison for GA-Based Feature Construction. In Proceedings of the Current Topics in Artificial Intelligence, Conference of the Spanish Association for Artificial Intelligence, Caepia, Salamanca, Spain, 12–16 November 2007; pp. 249–258. [Google Scholar]
- Oliveira, A.L.I.; Braga, P.L.; Lima, R.M.F.; Lio, M.; Rcio, L. GA-based method for feature selection and parameters optimization for machine learning regression applied to software effort estimation. Inf. Softw. Technol. 2010, 52, 1155–1166. [Google Scholar] [CrossRef]
- Li, D.; Jin, L.; Du, X.; Fu, J.; Lu, A. Size effect tests of normal-strength and high-strength RC columns subjected to axial compressive loading. Eng. Struct. 2016, 109, 43–60. [Google Scholar] [CrossRef]
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- ACI 318-05. Building Code Requirements for Structural Concrete; Farmington Hills: Oakland, MI, USA, 2002; pp. 16–17. [Google Scholar]
- FEMA, F. NEHRP Guidelines for the Seismic Rehabilitation of Buildings: FEMA 273; Federal Emergency Management Agency: Washington, DC, USA, 1997. [Google Scholar]
- Telemachos, B.P.; Michael, N.F. Deformations of Reinforced Concrete Members at Yielding and Ultimate. Aci Struct. J. 2001, 98, 135–147. [Google Scholar] [CrossRef]
- Moehle, J.P.; Lehman, D.E. Seismic Performance of Well-confined Confined Concrete Bridge Columns. Spec. Publ. 2000, 238. [Google Scholar] [CrossRef]
- Tekeli, H.; Aydin, A. An experimental study on the seismic behavior of infilled RC frames with opening. Sci. Iran. 2017. [Google Scholar] [CrossRef]
- Wu, C.L.; Yang, Y.S.; Hwang, S.J.; Loh, C.H. Dynamic collapse of reinforced concrete columns. In Proceedings of the 9th U.S. National and 10th Canadian Conference on Earthquake Engineering, Toronto, ON, Canada, 25–29 July 2010. [Google Scholar]
- Berry, M.; Eberhard, M. Performance Models for Flexural Damage in Reinforced Concrete Columns; University of Califorlia Berkeley: Berkeley, CA, USA, 2003. [Google Scholar]
- Yun, H.W. Full-Scale Experimental and Analytical Studies on High-Strength Concrete Columns. Ph.D. Thesis, University of Southern California, Los Angeles, CA, USA, 2003. [Google Scholar]
- Ho, J.C.M. Inelastic Design of Reinforced Concrete Beams and Limited Ductilehigh-Strength Concrete Columns. Ph.D. Thesis, The University of Hong Kong, Hong Kong, China, 2003. [Google Scholar]
- Ongsupankul, S.; Kanchanalai, T.; Kawashima, K. Behavior of reinforced concrete bridge pier columns subjected to moderate seismic load. ScienceAsia 2007, 33, 175–185. [Google Scholar] [CrossRef]
- Woodward, K.A.; Jirsa, J.O. Influence of Reinforcement on RC Short Column Lateral Resistance. J. Struct. Eng. 1984, 110, 90–104. [Google Scholar] [CrossRef]
- Bayrak, O. Seismic Performance of Rectilinearly Confined High Strength Concrete Columns. Ph.D. Thesis, University of Toronto, Toronto, OT, Canada, 1999. [Google Scholar]
- Mo, Y.L.; Wang, S.J. Seismic Behavior of RC Columns with Various Tie Configurations. J. Struct. Eng. 2000, 126, 1122–1130. [Google Scholar] [CrossRef]
- Paultre, P.; Légeron, F.; Mongeau, D. Influence of concrete strength and transverse reinforcement yield strength on behavior of high-strength concrete columns. ACI Struct. J. 2001, 98, 490–501. [Google Scholar]
- Xiao, Y.; Yun, H.W. Experimental studies on full-scale high-strength concrete columns. ACI Struct. J. 2002, 99, 199–207. [Google Scholar]
- Lam, S.S.E.; Wang, Z.Y.; Liu, Z.Q.; Wong, Y.L.; Li, C.S.; Wu, B. Drift Capacity of Rectangular Reinforced Concrete Columns with Low Lateral Confinement and High-Axial Load. J. Struct. Eng. 2003, 129, 733–742. [Google Scholar] [CrossRef]
- Hwang, S.K.; Yun, H.D. Effects of transverse reinforcement on flexural behaviour of high-strength concrete columns. Eng. Struct. 2004, 26, 1–12. [Google Scholar] [CrossRef]
- Ahn, J.M.; Shin, S.W. An evaluation of ductility of high-strength reinforced concrete columns subjected to reversed cyclic loads under axial compression. Mag. Concr. Res. 2007, 59, 29–44. [Google Scholar] [CrossRef]
- Woods, J.M.; Kiousis, P.D.; Ehsani, M.R.; Saadatmanesh, H.; Fritz, W. Bending ductility of rectangular high strength concrete columns. Eng. Struct. 2007, 29, 1783–1790. [Google Scholar] [CrossRef]
- Marefat, M.S.; Khanmohammadi, M.; Bahrani, M.K.; Goli, A. Experimental Assessment of Reinforced Concrete Columns with Deficient Seismic Details under Cyclic Load. Adv. Struct. Eng. 2008, 9, 337–347. [Google Scholar] [CrossRef]
- Xiao, X.; Guan, F.L.; Yan, S. Use of ultra-high-strength bars for seismic performance of rectangular high-strength concrete frame columns. Mag. Concr. Res. 2008, 60, 253–259. [Google Scholar] [CrossRef]
- Bae, S. Seismic performance of full-scale reinforced concrete columns. Aci Struct. J. 2008, 105, 123–133. [Google Scholar]
- Cao, T.N.T. Experimental and Analytical Studies on the Seismic Behavior of Reinforced Concrete Columns with Light Transverse Reinforcement. Ph.D. Thesis, Nanyang Technological University, Singapore, 2010. [Google Scholar]
- Ou, Y.C.; Kurniawan, D.P.; Handika, N. Shear Behavior of Reinforced Concrete Columns with High-Strength Steel and Concrete under Low Axial Load. ACI Mater. J. 2015, 112, 35–45. [Google Scholar]
- Abdelsamie, E.; Tom, B.; Salah, E. Plastic Hinge Length Considering Shear Reversal in Reinforced Concrete Elements. J. Earthq. Eng. 2012, 16, 188–210. [Google Scholar]
- Martirossyan, A.; Xiao, Y. Flexural-Shear Behavior of High-Strength Concrete Short Columns. Earthq. Spectra 2012, 17, 679–695. [Google Scholar] [CrossRef]
- Li, Y.A.; Huang, Y.T.; Hwang, S.J. Seismic Response of Reinforced Concrete Short Columns Failed in Shear. Aci Struct. J. 2014, 111, 945–954. [Google Scholar] [CrossRef]
- Nakamura, T.; Yoshimura, M. Gravity load collapse of reinforced concrete columns with decreased axial load. In Proceedings of the 2nd European Conference on Earthquake Engineering and Seismology, Istanbul, Turkey, 25–29 August 2014. [Google Scholar]
- Popa, V.; Cotofana, D.; Vacareanu, R. Effective stiffness and displacement capacity of short reinforced concrete columns with low concrete quality. Bull. Earthq. Eng. 2014, 12, 2705–2721. [Google Scholar] [CrossRef]
- Jin, C.; Pan, Z.; Meng, S.; Qiao, Z. Seismic Behavior of Shear-Critical Reinforced High-Strength Concrete Columns. J. Struct. Eng. 2015, 141, 04014198. [Google Scholar] [CrossRef]
- Bechtoula, H.; Kono, S.; Watanabe, F.; Mehani, Y.; Kibboua, A.; Naili, M. Performance of HSC columns under severe cyclic loading. Bull. Earthq. Eng. 2015, 13, 503–538. [Google Scholar] [CrossRef]
- El-Attar, M.M.; El-Karmoty, H.Z.; El-Moneim, A.A. The behavior of ultra-high-strength reinforced concrete columns under axial and cyclic lateral loads. HBRC J. 2016, 12, 284–295. [Google Scholar] [CrossRef][Green Version]
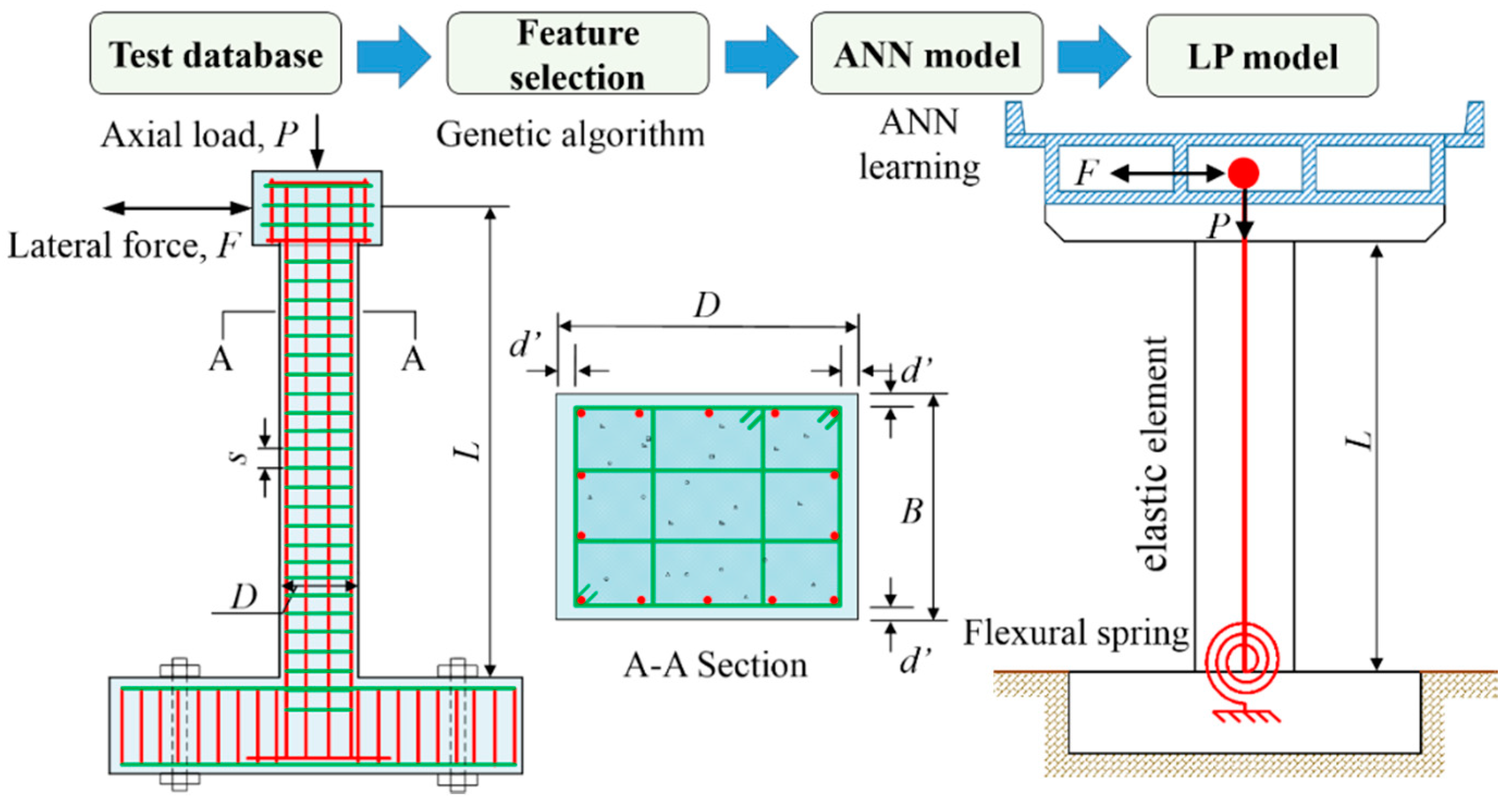
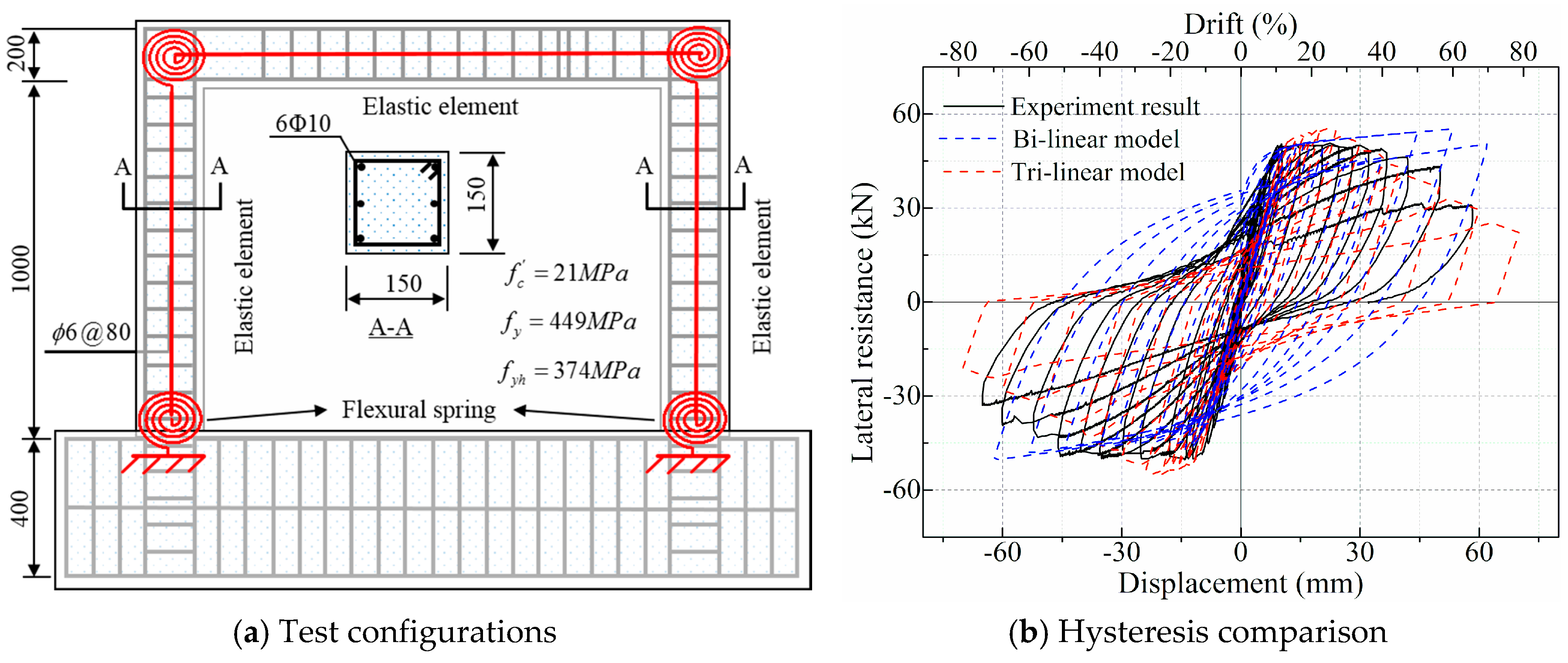
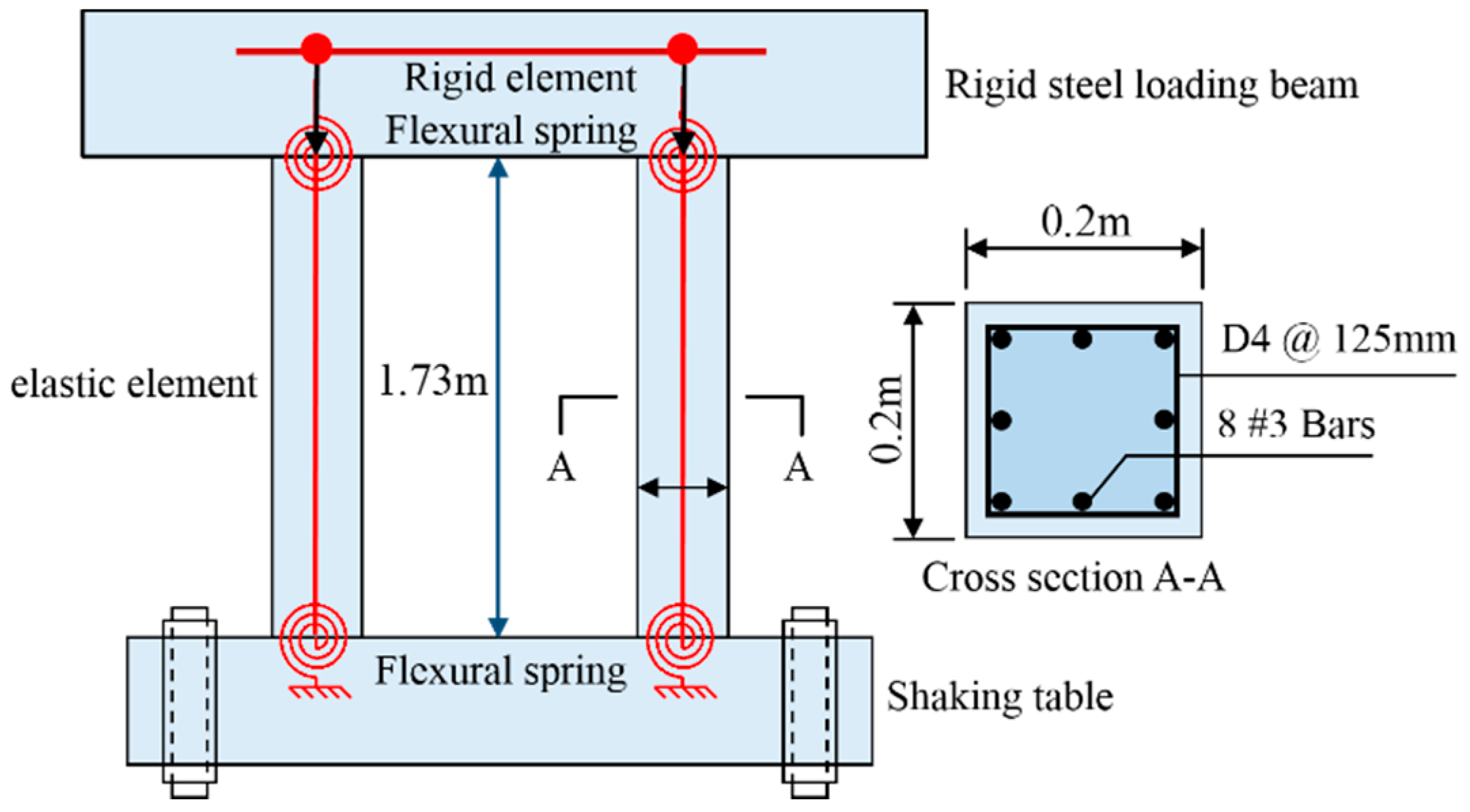
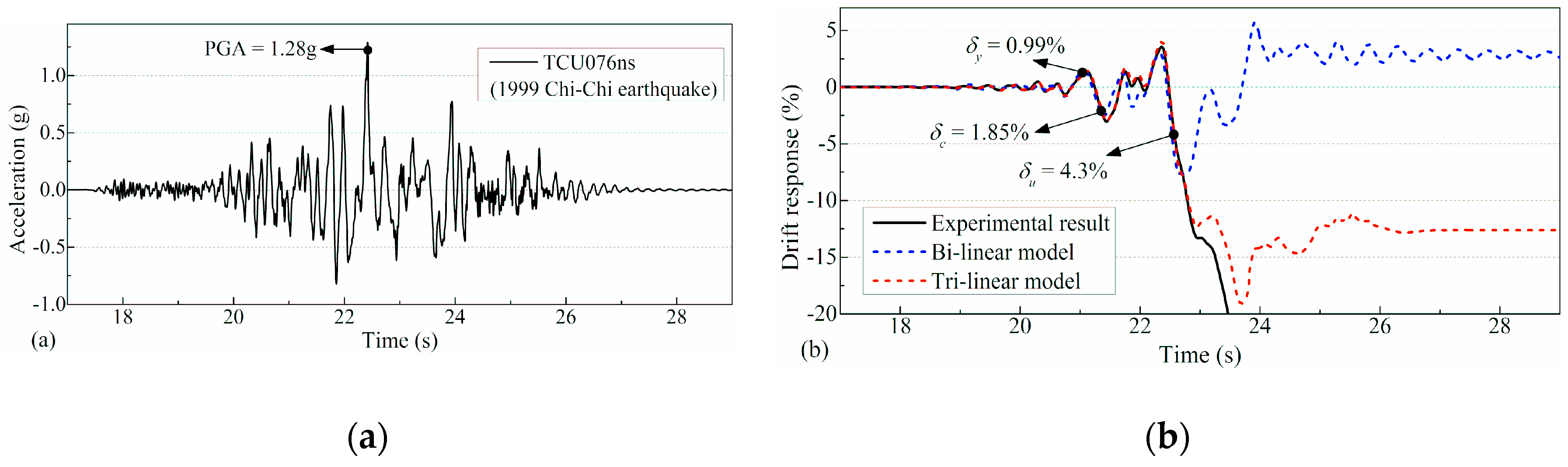
| Category | Feature | Category | Feature | ||
|---|---|---|---|---|---|
| Cross Section | B | Width of column section | Long bars | ρl | Longitudinal reinforcement ratio |
| D | Depth of column section | fyl | Yield strength of longitudinal bar | ||
| Ac | Gross area of column section | ful | Ultimate strength of longitudinal bar | ||
| Ic | Moment of inertia of column section | dl | Diameter of longitudinal bar | ||
| de | Effective depth of column section | Asl | Area of a single longitudinal bar | ||
| d′ | Effective cover thickness | Nl | Number of longitudinal bars | ||
| Span | L | Effective height of specimen | Trans. bars | fyt | Yield strength of transverse steel |
| λ | Span-to-depth ratio | fut | Ultimate strength of transverse steel | ||
| Vertical loading | P | Applied axial load | dst | Diameter of transverse reinforcement bar | |
| n | Axial compression ratio | Ast | Area of one transverse reinforcement bar | ||
| Concrete | 28-day concrete compressive strength | s | Spacing of transverse reinforcement | ||
| Ec | Elastic modulus of concrete | ρsv | Transverse reinforcement volumetric ratio | ||
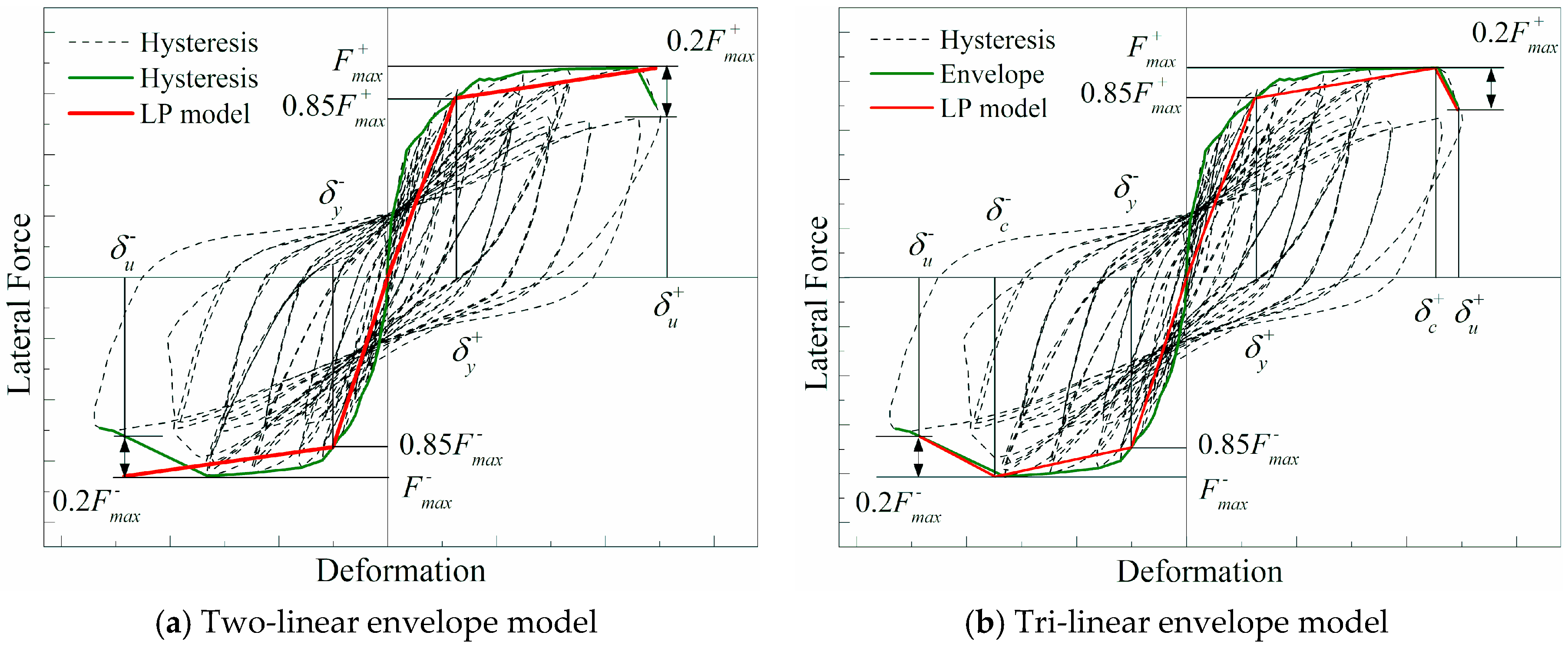
| Parameter | Description | Calculation |
|---|---|---|
| the initial stiffness of the linear segment | ||
| the yielding moment | ||
| the hardening ratio | , |
| Parameter | Description | Calculation |
|---|---|---|
| the initial stiffness of the linear segment | ||
| the yielding moment | ||
| the pre-capping hardening ratio | , | |
| the post-capping hardening ratio | , | |
| the capping moment to the yielding moment | , |
| Reference | ||
|---|---|---|
| Sezen and Moehle [5] FEMA 356 [3] | ||
| ACI 318-05 [38] | ||
| FEMA 273 [39] |
| Model | Parameters |
|---|---|
| ANN model | , , , |
| Bi-linear model | , , |
| Tri-linear model | , , , , |
| Model | Parameters |
|---|---|
| ANN model | , , , |
| Bi-linear model | , , |
| Tri-linear model | , , , , |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Li, S. Development of an ANN-Based Lumped Plasticity Model of RC Columns Using Historical Pseudo-Static Cyclic Test Data. Appl. Sci. 2019, 9, 4263. https://doi.org/10.3390/app9204263
Liu Z, Li S. Development of an ANN-Based Lumped Plasticity Model of RC Columns Using Historical Pseudo-Static Cyclic Test Data. Applied Sciences. 2019; 9(20):4263. https://doi.org/10.3390/app9204263
Chicago/Turabian StyleLiu, Zhenliang, and Suchao Li. 2019. "Development of an ANN-Based Lumped Plasticity Model of RC Columns Using Historical Pseudo-Static Cyclic Test Data" Applied Sciences 9, no. 20: 4263. https://doi.org/10.3390/app9204263
APA StyleLiu, Z., & Li, S. (2019). Development of an ANN-Based Lumped Plasticity Model of RC Columns Using Historical Pseudo-Static Cyclic Test Data. Applied Sciences, 9(20), 4263. https://doi.org/10.3390/app9204263





