Optimal Estimation of Parameters Encoded in Quantum Coherent State Quadratures
Abstract
1. Introduction
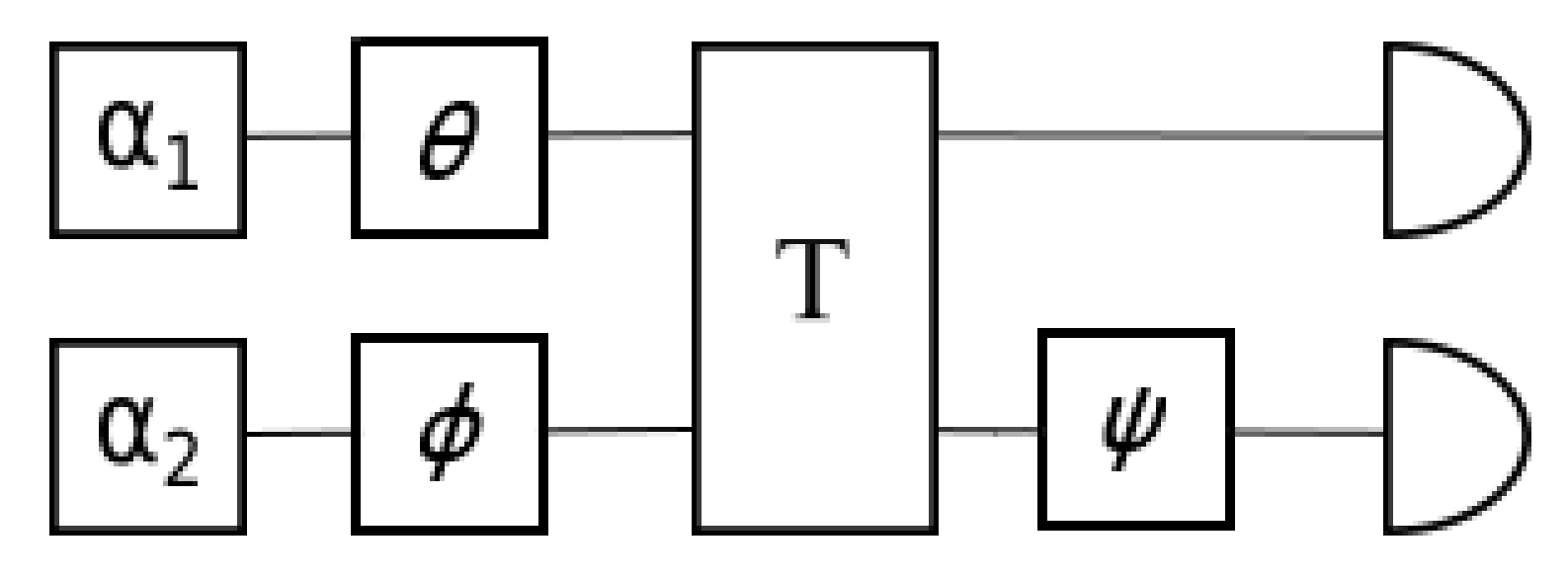
2. Two-Mode Coherent-State Parameter Communication Scheme with Linear Encoding
3. Parameter Estimation
3.1. Quantum Cramér–Rao Bound
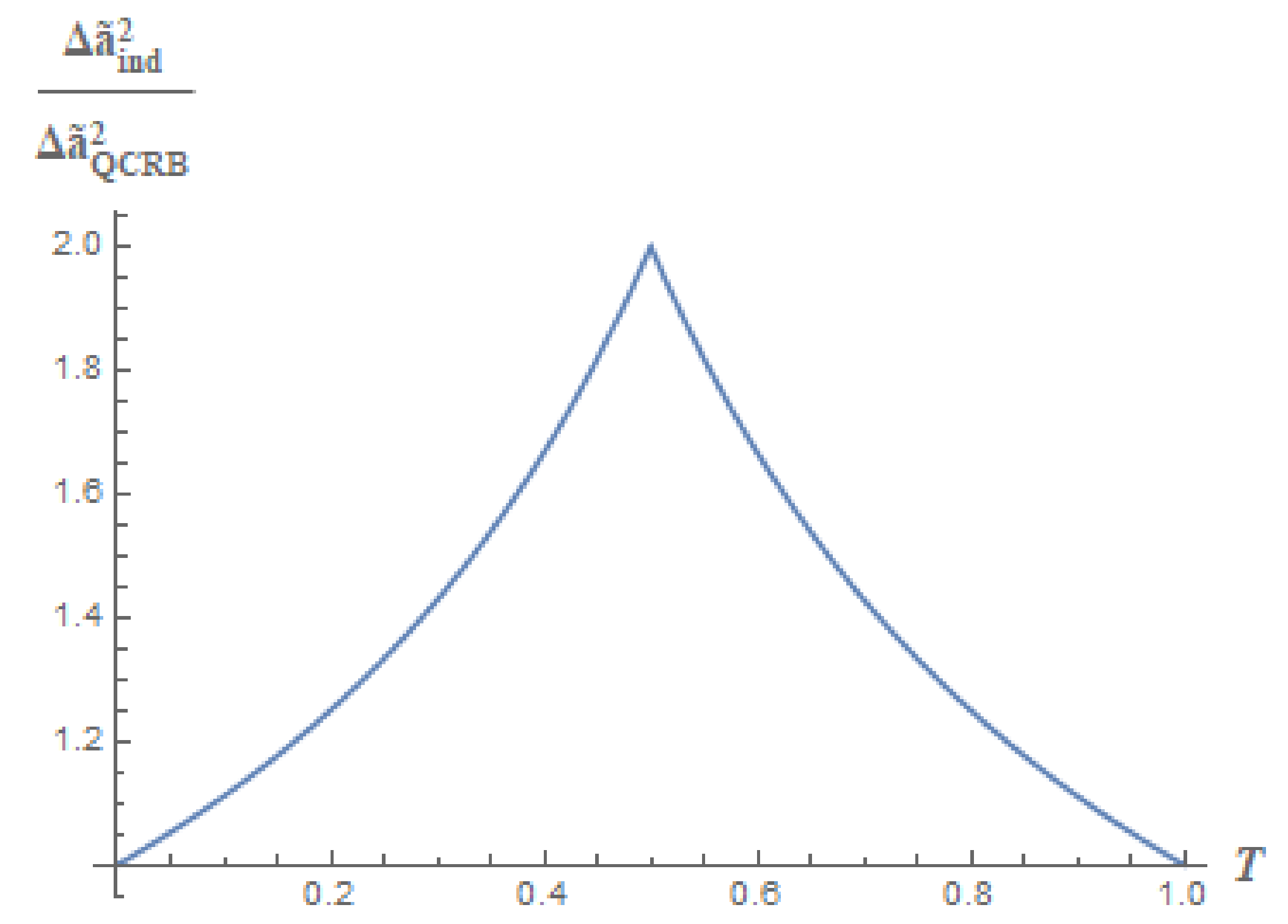
3.2. Optimal Lower Bound
3.3. Attainability of the Quantum Cramér–Rao Bound
4. Two-Mode Encoding and Estimation Schemes
4.1. Identical Encoding
4.2. Optimal Scheme
5. Arbitrary Number of Modes
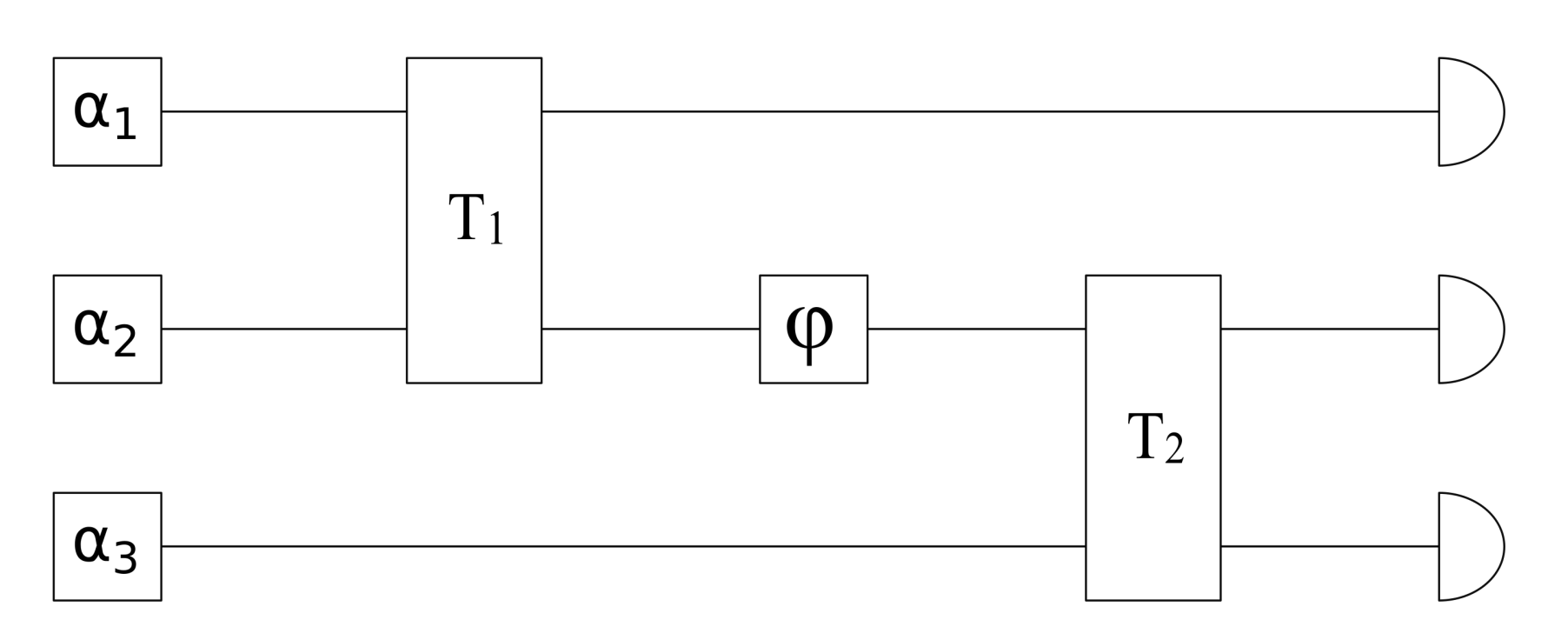
5.1. Three-Mode Encoding and Estimation Scheme
5.2. n-Mode Extension
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- Alice chooses real a, b, and by imposing that energies of the “optimal input states” given by Equation (29) are equal to the energies of the given coherent states in corresponding modes. This leads to the following equations:The two equations contain three unknown variables, a, b, and T. Although a and b are related by the energy conservation in Equation (2), it is linearly dependent on the two equations above. Indeed, the above system is obviously equivalent towhere the first equation is, in fact, the energy constraint. If the energies of the given coherent states 1 and 2 are equal, then satisfies the second equation and we are free to choose any a and b on the circle determined by the first equation. Another valid option is to choose and take an arbitrary T.If the energies of the given coherent states are not equal, we can replace the second equation byso that T becomes a function of the ratio between the differences of the number of photon in the input and output modes. Equation (A3) further limits the choice of x and p because , meaning thatOnce x and p are chosen, T becomes
- In both cases considered above, Equation (29) determines the parameters of two input states, which would provide the desired optimal measurement,By our construction, the energies of the optimal input states are equal to the energies of the given states in corresponding input modes. Then, the given and optimal input states are related by simple rotation in phase space by angles and , which can be easily found from the vector algebrawhere and .
- After performing the calculations described above, Alice provides to Bob with the measurement settings and the given coherent states.
- Upon receiving the measurement settings, Bob applies local rotations to the input modes followed by the beam splitter transformation and homodyne measurements in the output modes, thus realizing an optimal extraction of encoded x and p variable.
References
- Helstrom, C.W. Quantum Detection and Estimation Theory. J. Stat. Phys. 1969, 1, 231. [Google Scholar] [CrossRef]
- Pinel, O.; Fade, J.; Braun, D.; Jian, P.; Treps, N.; Fabre, C. Ultimate sensitivity of precision measurements with intense Gaussian quantum light: A multimodal approach. Phys. Rev. A 2012, 85, 010101. [Google Scholar] [CrossRef]
- Pinel, O.; Jian, P.; Treps, N.; Fabre, C.; Braun, D. Quantum parameter estimation using general single-mode Gaussian states. Phys. Rev. A 2013, 88, 040102(R). [Google Scholar] [CrossRef]
- Humphreys, P.C.; Barbieri, M.; Datta, A.; Walmsley, I.A. Quantum Enhanced Multiple Phase Estimation. Phys. Rev. Lett. 2013, 111, 070403. [Google Scholar] [CrossRef] [PubMed]
- Sparaciari, C.; Olivares, S.; Paris, M.G.A. Bounds to precision for quantum interferometry with Gaussian states and operations. J. Opt. Soc. Am. B 2015, 32, 1354. [Google Scholar] [CrossRef]
- Gagatsos, C.N.; Branford, D.; Datta, A. Gaussian systems for quantum-enhanced multiple phase estimation. Phys. Rev. A 2016, 94, 042342. [Google Scholar] [CrossRef]
- Genoni, M.G.; Paris, M.G.A.; Adesso, G.; Nha, H.; Knight, P.L.; Kim, M.S. Optimal estimation of joint parameters in phase space. Phys. Rev. A 2013, 87, 012107. [Google Scholar] [CrossRef]
- Gao, Y.; Lee, H. Bounds on quantum multiple-parameter estimation with Gaussian state. Eur. Phys. J. D 2014, 68, 347. [Google Scholar] [CrossRef]
- Baumgratz, T.; Datta, A. Quantum Enhanced Estimation of a multidimensional Field. Phys. Rev. Lett. 2016, 116, 030801. [Google Scholar] [CrossRef]
- Bradshaw, M.; Assad, S.M.; Lam, P.K. A tight Cramér-Rao bound for joint parameter estimation with a pure two-mode squeezed probe. Phys. Lett. A 2017, 381, 2598–2607. [Google Scholar] [CrossRef][Green Version]
- Bradshaw, M.; Assad, S.M.; Lam, P.K. Ultimate precision of joint quadrature parameter estimation with a Gaussian probe. Phys. Rev. A 2018, 97, 012106. [Google Scholar] [CrossRef]
- Albarelli, F.; Friel, J.F.; Datta, A. Evaluating the Holevo Cramér-Rao bound for multi-parameter quantum metrology. arXiv 2019, arXiv:1906.05724. [Google Scholar]
- Demkowicz-Dobrzański, R.; Jarzyna, M.; Kołodyński, J. Chapter Four—Quantum Limits in Optical Interferometry. Prog. Opt. 2015, 60, 345–435. [Google Scholar]
- Cerf, N.J.; Iblisdir, S. Phase conjugation of continuous quantum variables. Phys. Rev. A 2001, 64, 032307. [Google Scholar] [CrossRef]
- Niset, J.; Acin, A.; Andersen, U.L.; Cerf, N.J.; Garcia-Patron, R.; Navascues, M.; Sabuncu, M. Superiority of Entangled Measurements over All Local Strategies for the Estimation of Product Coherent States. Phys. Rev. Lett. 2007, 98, 260404. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Caves, C.M. Statistical Distance and the Geometry of Quantum States. Phys. Rev. Lett. 1994, 72, 3439. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Caves, C.M.; Milburn, G.J. Generalized uncertainty relations: Theory, examples and Lorentz invariance. Ann. Phys. 1995, 247, 135–173. [Google Scholar] [CrossRef]
- Paris, M.G.A. Quantum Estimation for Quantum Technology. Int. J. Quant. Inf. 2009, 7, 125–137. [Google Scholar] [CrossRef]
- Matsumoto, K. A new approach to the Cramér-Rao-type bound of the pure-state model. J. Phys. A Math. Gen. 2002, 35, 3111. [Google Scholar] [CrossRef]
- Ragy, S.; Jarzyna, M.; Demkowicz-Dobrański, R. Compatibility in multiparameter quantum metrology. Phys. Rev. A 2016, 94, 052108. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arnhem, M.; Karpov, E.; Cerf, N.J. Optimal Estimation of Parameters Encoded in Quantum Coherent State Quadratures. Appl. Sci. 2019, 9, 4264. https://doi.org/10.3390/app9204264
Arnhem M, Karpov E, Cerf NJ. Optimal Estimation of Parameters Encoded in Quantum Coherent State Quadratures. Applied Sciences. 2019; 9(20):4264. https://doi.org/10.3390/app9204264
Chicago/Turabian StyleArnhem, Matthieu, Evgueni Karpov, and Nicolas J. Cerf. 2019. "Optimal Estimation of Parameters Encoded in Quantum Coherent State Quadratures" Applied Sciences 9, no. 20: 4264. https://doi.org/10.3390/app9204264
APA StyleArnhem, M., Karpov, E., & Cerf, N. J. (2019). Optimal Estimation of Parameters Encoded in Quantum Coherent State Quadratures. Applied Sciences, 9(20), 4264. https://doi.org/10.3390/app9204264



