Simulation of Metro Congestion Propagation Based on Route Choice Behaviors Under Emergency-Caused Delays
Abstract
Featured Application
Abstract
1. Introduction
2. Literature Review
3. Route Choice Modeling
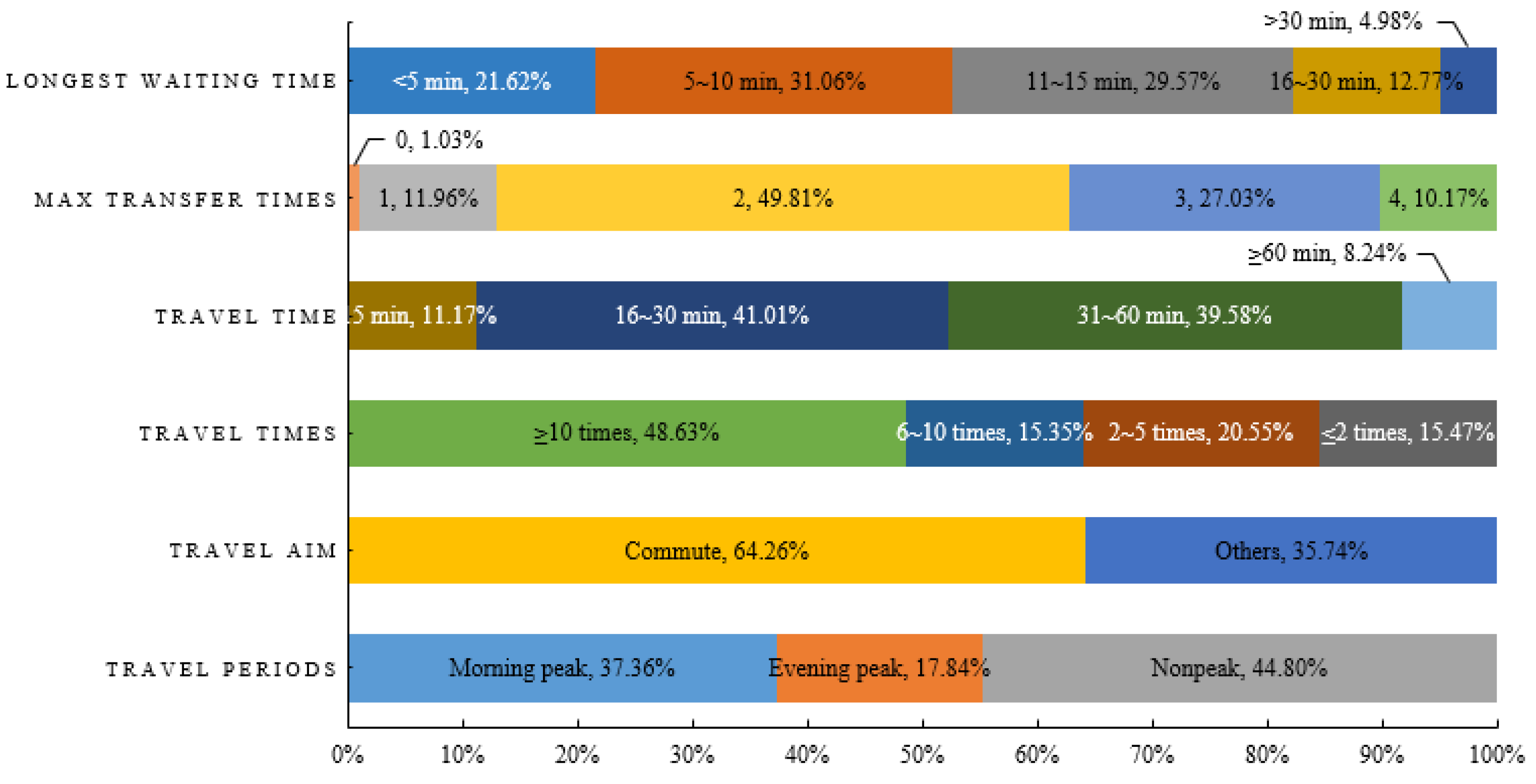
3.1. Data
3.2. Explanatory Variables
3.3. Model Description
3.4. Estimation Result
4. Simulation Model of Metro Congestion Propagation Process
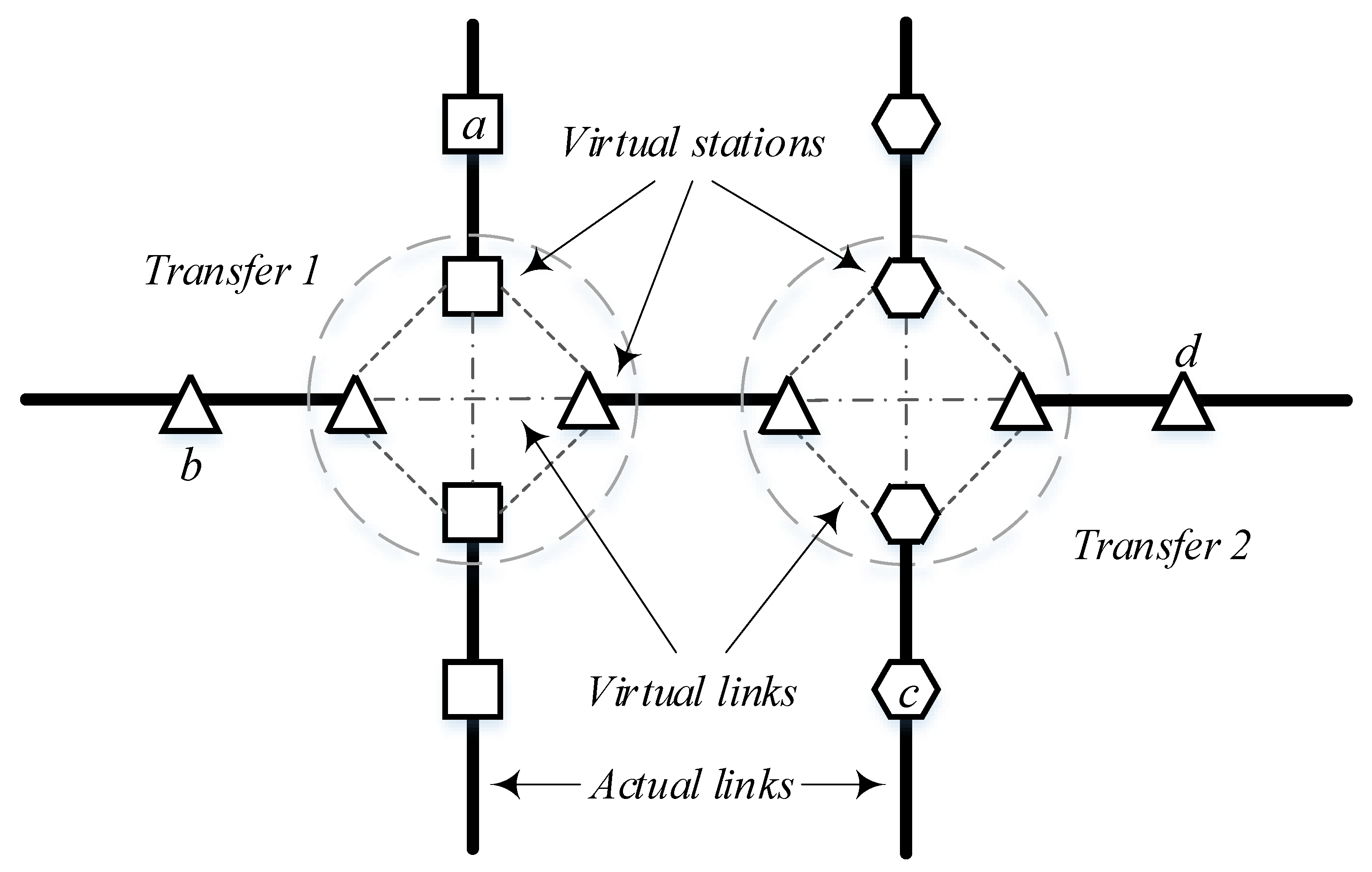
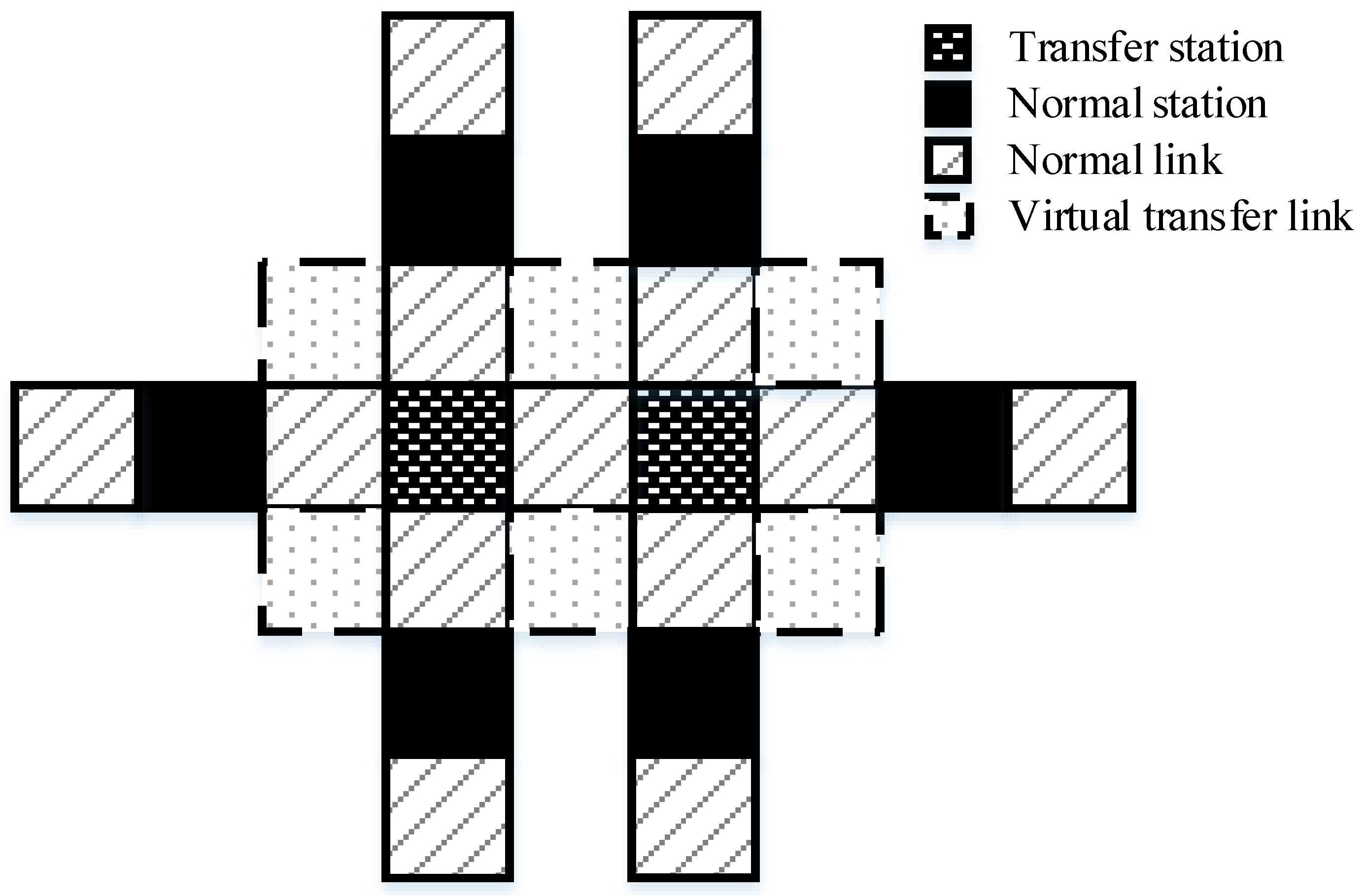
4.1. Augmented Metro Network
- (a)
- Stations at both ends of a metro line shared with other metro lines as ends are not regarded as transfer stations, for there are fewer transfer passengers in these stations, such as Guangzhou south railway station on line 2 and line 7.
- (b)
- The metro network is a directed graph, but as the distance and travel time are similar between link lij and lji, it is regarded as an undirected graph in the simulation and the only difference lies in the directions of the links.
4.2. Metro Network with Graph Cellular Automata
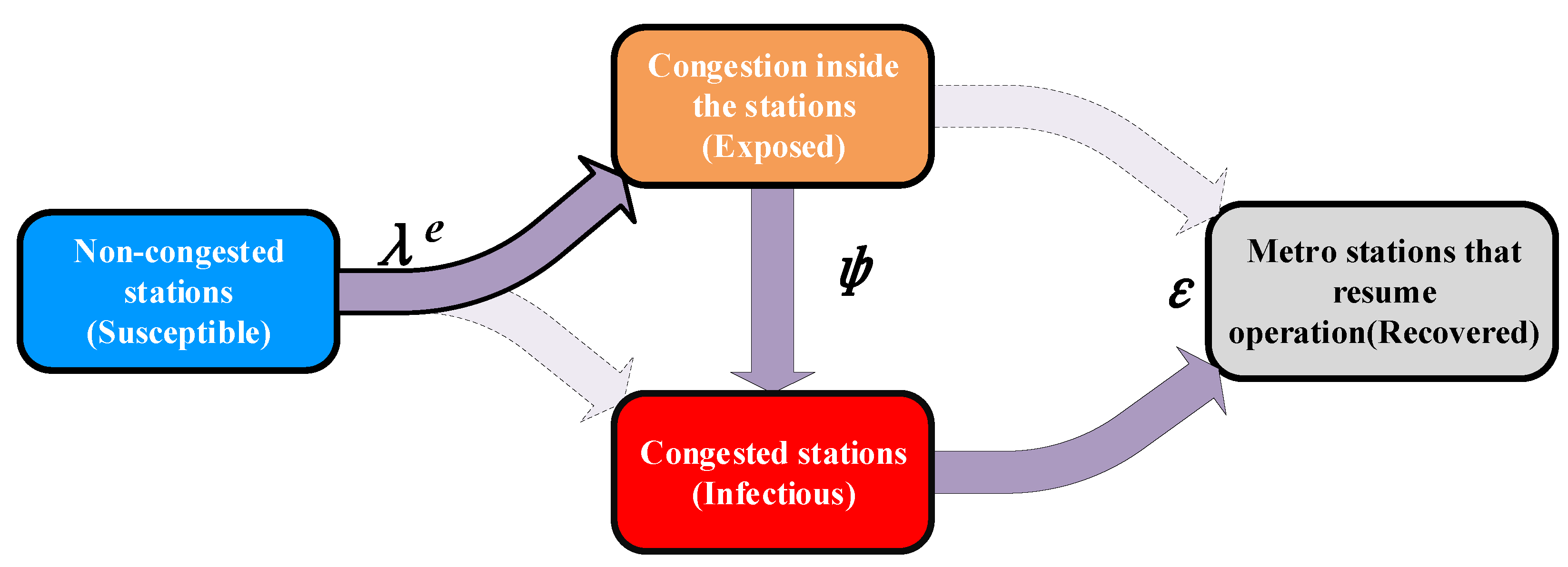
4.3. ASEIR Model with Time Delays
4.4. Quantify Method for Congestion Propagation Rate
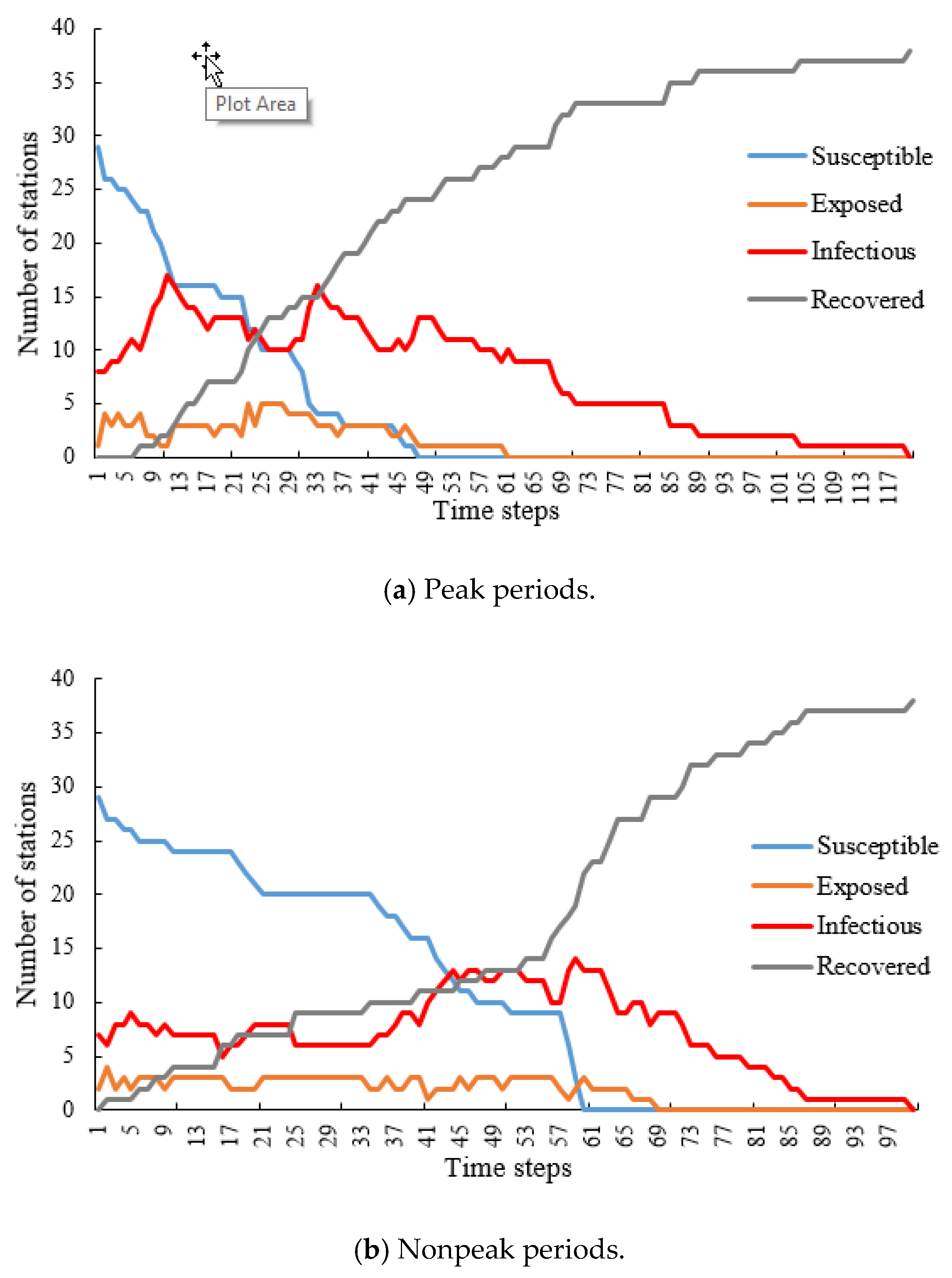
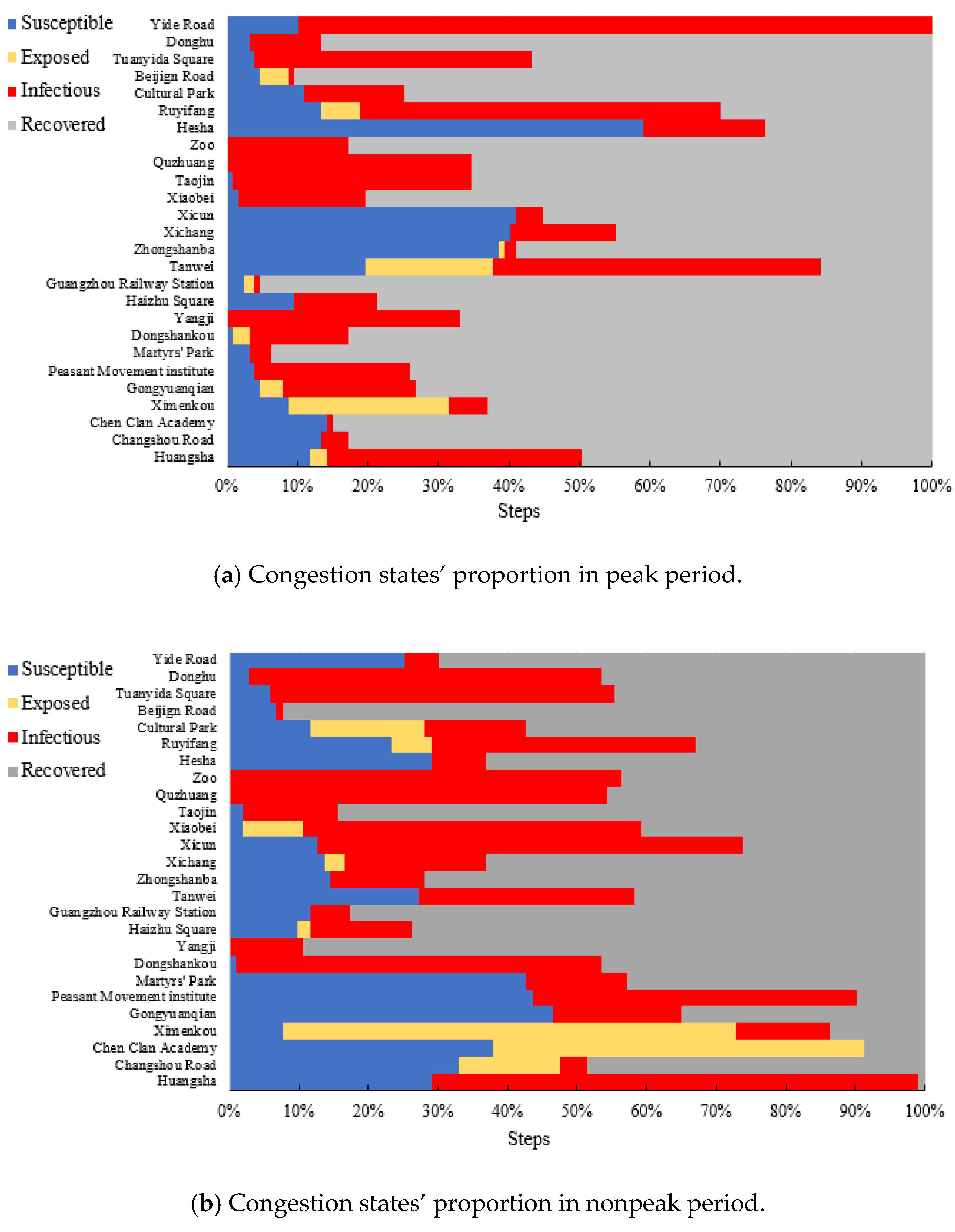
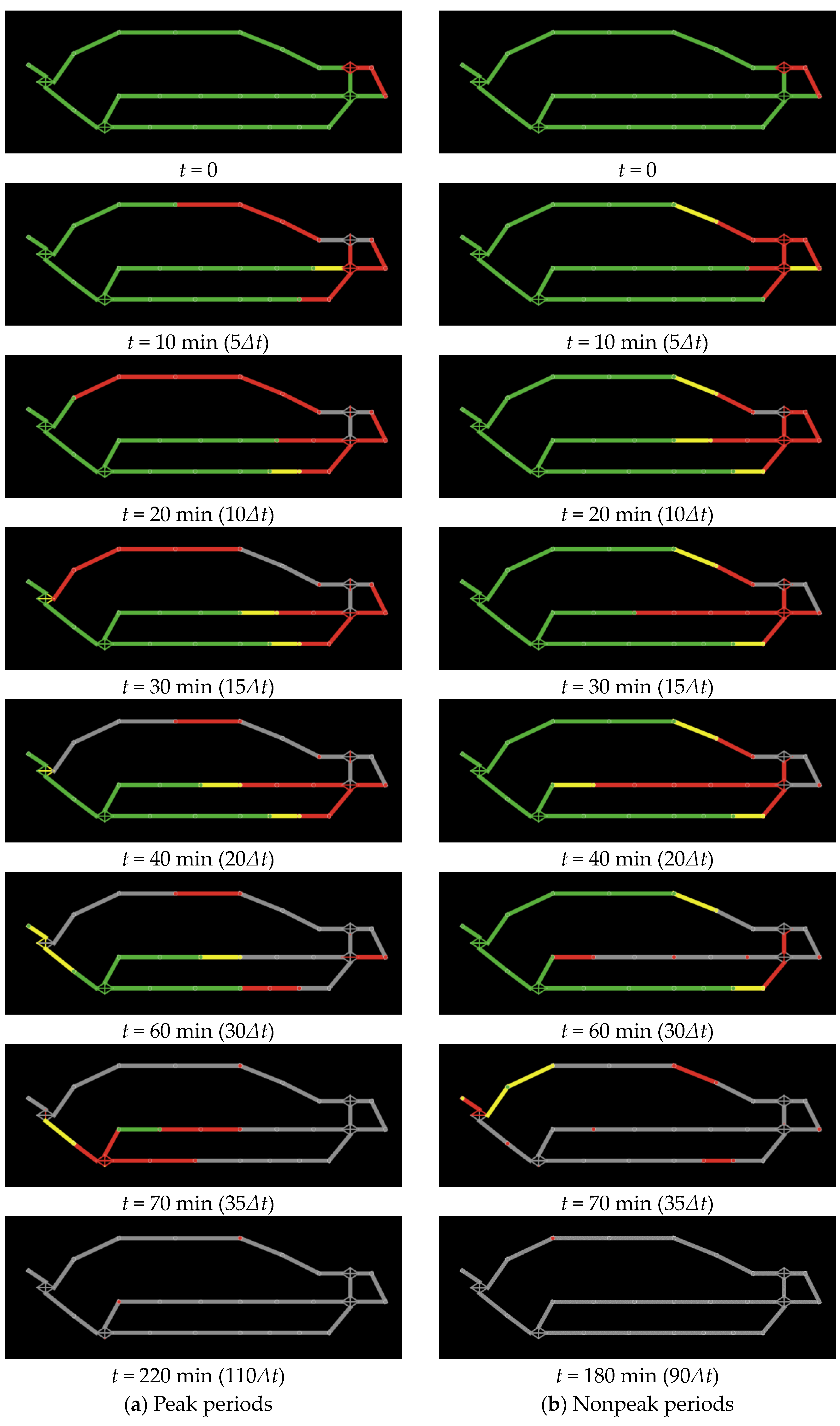
5. Empirical Study
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hu, Y. Study on the Network Characteristics of Urban Rail Transit in Beijing Based on Intelligent Card Data—A Case Study of Beijing; Beijing Jiaotong University: Beijing, China, 2017. [Google Scholar]
- Wu, Y.; Xu, J.; Jia, L.; Qin, Y. Estimation of emergency evacuation capacity for subway stations. J. Transp. Saf. Secur. 2018, 10, 586–601. [Google Scholar] [CrossRef]
- Sandeep, M.; Kaan, O.; Bekir, B. Evaluating the resilience and recovery of public transit system using big data: Case study from New Jersey. J. Transp. Saf. Secur. 2018. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, Y.; Mohammad, K.; Zhao, G. Risk analysis on Beijing metro operation initiated by human factors. J. Transp. Saf. Secur. 2018. [Google Scholar] [CrossRef]
- Mcfadden, D. The revealed preferences of a government bureaucracy: Theory. Bell. J. Econ. 1975, 6, 401–416. [Google Scholar] [CrossRef]
- Sheffi, C.F.D. On Stochastic Models of Traffic Assignment. Transp. Sci. 1977, 11, 253–274. [Google Scholar]
- Heiss, F. Specification(s) of Nested Logit Models; MEA Discussion Paper Series; MEA: New Delhi, India, 2002. [Google Scholar]
- Yang, Y.; Yao, E.; Yang, Z.; Zhang, R. Modeling the charging and route choice behavior of BEV drivers. Transp. Res. Part C Emerg. Technol. 2016, 65, 190–204. [Google Scholar] [CrossRef]
- Daniel, M.K.T. Mixed MNL Models for Discrete Response. J. Appl Econ. 2000, 15, 447–470. [Google Scholar]
- Lee, B.J.; Fujiwara, A.; Zhang, J.; Sugie, Y. Analysis of Mode Choice Behaviors based on Latent Class Models. In Proceedings of the 10th International Conference on Travel Behaviour Research Lucerne, Lucerne, Switzerland, 10–15 August 2003. [Google Scholar]
- Hess, S.; Stathopoulos, A. Linking response quality to survey engagement: A combined random scale and latent variable approach. J. Choice Model. 2013, 7, 1–12. [Google Scholar] [CrossRef]
- Sun, Z.; Arentze, T.; Timmermans, H. A heterogeneous latent class model of activity rescheduling, route choice and information acquisition decisions under multiple uncertain events. Transp. Res. Part C Emerg. Technol. 2012, 25, 46–60. [Google Scholar] [CrossRef]
- Tian, H.; Gao, S.; Fisher, D.L.; Brian, K.P. A Mixed-Logit Latent-Class Model of Strategic Route Choice Behavior with Real-time Information. In Proceedings of the Transportation Research Board Meeting, Washington, DC, USA, 22–26 January 2012. [Google Scholar]
- Hoogendoorn, S. A State-of-the-Art Review: Developments in Utility Theory, Prospect Theory and Regret Theory to Investigate Travelers’ Behavior in Situations Involving Travel Time Uncertainty. Transp. Rev. 2014, 34, 46–67. [Google Scholar]
- Chorus, C.G.; Arentze, T.A.; Timmermans, H.J.P. A Random Regret-Minimization model of travel choice. Transp. Res. Part B 2008, 42, 1–18. [Google Scholar] [CrossRef]
- Chorus, C.G. A new model of random regret minimization. Eur. J. Transp. Infrastruct. Res. 2010, 10, 181–196. [Google Scholar]
- Charoniti, E.; Rasouli, S.; Timmermans, H.J.P. Context-driven regret-based model of travel behavior under uncertainty: A latent class approach. Transp. Res. Procedia 2017, 24, 89–96. [Google Scholar] [CrossRef]
- Jing, P.; Zhao, M.; He, M.; Chen, L. Travel Mode and Travel Route Choice Behavior Based on Random Regret Minimization: A Systematic Review. Sustainability 2018, 10, 1185. [Google Scholar] [CrossRef]
- Thiene, M.; Boeri, M.; Chorus, C.G. Random Regret Minimization: Exploration of a New Choice Model for Environmental and Resource Economics. Environ. Resour. Econ. 2012, 51, 413–429. [Google Scholar] [CrossRef]
- Kaplan, S.; Prato, C.G. The application of the random regret minimization model to drivers’ choice of crash avoidance maneuvers. Transp. Res. Part F Traffic Psychol. Behav. 2012, 15, 699–709. [Google Scholar] [CrossRef]
- Hensher, D.A.; Greene, W.H.; Chorus, C.G. Random regret minimization or random utility maximization: An exploratory analysis in the context of automobile fuel choice. J. Adv. Transp. 2013, 47, 667–678. [Google Scholar] [CrossRef]
- Rasouli, S.; Timmermans, H. Specification of regret-based models of choice behaviour: Formal analyses and experimental design based evidence. Transportation 2016, 44, 1555–1576. [Google Scholar] [CrossRef]
- Jang, S.; Rasouli, S.; Timmermans, H. Incorporating psycho-physical mapping into random regret choice models: Model specifications and empirical performance assessments. Transportation 2016, 44, 999–1019. [Google Scholar] [CrossRef]
- Toffoli, T.; Margolus, N.H. Invertible Cellular Automata: A Review; Cellular Automata; MIT Press: Cambridge, MA, USA, 1990; Volume 45, pp. 229–253. [Google Scholar]
- Santé, I.; García, A.M.; Miranda, D.; Crecente, R. Cellular automata models for the simulation of real-world urban processes: A review and analysis. Landsc. Urban Plan. 2010, 96, 1–122. [Google Scholar] [CrossRef]
- Li, K.; Gao, Z.; Ning, B. Cellular automaton model for railway traffic. J. Comput. Phys. 2005, 209, 179–192. [Google Scholar] [CrossRef]
- Zheng, Y.; Xi, X.; Zhuang, Y.; Zhang, Y. Dynamic Parameters Cellular Automaton Model for Passengers in Subway. Tsinghua Sci. Technol. Int. J. Inf. Sci. 2015, 20, 594–601. [Google Scholar] [CrossRef]
- Stevens, D.; Dragicevic, S. A GIS-based irregular cellular automata model of land-use change. Environ. Plan. B Plan. Des. 2007, 34, 708–724. [Google Scholar] [CrossRef]
- Dahal, K.R.; Chow, T.E. Characterization of neighborhood sensitivity of an irregular cellular automata model of urban growth. Int. J. Geogr. Inf. Syst. 2015, 29, 475–497. [Google Scholar] [CrossRef]
- Shi, W.; Pang, M.Y.C. Development of Voronoi-based cellular automata -an integrated dynamic model for Geographical Information Systems. Int. J. Geogr. Inf. Syst. 2000, 14, 455–474. [Google Scholar] [CrossRef]
- White, R.; Engelen, G. Cellular automata and fractal urban form: A cellular modelling approach to the evolution of urban land-use patterns. Environ. Plan. A 1993, 25, 1175–1199. [Google Scholar] [CrossRef]
- Osullivan, D. Graph-Cellular Automata: A Generalised Discrete Urban and Regional Model. Environ. Plan. B Plan. Des. 2001, 28, 687–705. [Google Scholar] [CrossRef]
- Martinez, M.J.; Merino, E.G.; Sanchez, E.G.; Sánchez, J.E.G.; del Rey, A.M.; Sánchez, G.R. A graph cellular automata model to study the spreading of an infectious disease. In Proceedings of the Mexican International Conference on Artificial Intelligence, San Luis Potosi, Mexico, 27 October–4 November 2012; pp. 458–468. [Google Scholar]
- Rin, P.R.; Dalp, D.D.; Ven, M.J.; Clausse, A. Graph-based Cellular Automata for Simulation of Surface Flows in Large Plains. Asian J. Appl. Sci. 2012, 5, 224–231. [Google Scholar]
- Krzysztof, M.; Jarosław, J.; Rokita, M. Application of Graph Cellular Automata in Social Network Based Recommender System. In Proceedings of the International Conference on Computational Collective Intelligence, Craiova, Romania, 11–13 September 2013. [Google Scholar]
- Tretyakova, A.; Seredynski, F.; Bouvry, P. Cellular Automata Approach to Maximum Lifetime Coverage Problem in Wireless Sensor Networks. Simul. Trans. Soc. Model. Simul. Int. 2014, 92, 153–164. [Google Scholar]
- Małecki, K. Graph Cellular Automata with Relation-Based Neighborhoods of Cells for Complex Systems Modelling: A Case of Traffic Simulation. Symmetry 2017, 9, 322. [Google Scholar] [CrossRef]
- Bodo, A.; Katona, G.Y.; Simon, P.L. SIS Epidemic Propagation on Hypergraphs. Bull. Math. Biol. 2016, 78, 713–735. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, T. Epidemic spreading of an SEIRS model in scale-free networks. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 3375–3384. [Google Scholar] [CrossRef]
- Raveau, S.; Guo, Z.; Munoz, J.C.; Wilson, N.H.M. A behavioural comparison of route choice on metro networks: Time, transfers, crowding, topology and socio-demographics. Transp. Res. Part A Policy Pract. 2014, 66, 185–195. [Google Scholar] [CrossRef]
- Raveau, S.; Munoz, J.C.; De Grange, L. A topological route choice model for metro. Transp. Res. Part A Policy Pract. 2011, 45, 138–147. [Google Scholar] [CrossRef]
- Zhang, Y.; Yao, E.; Dai, H. Transfer volume forecasting method for the metro in networking conditions. J. China Railw. Soc. 2013, 35, 1–6. [Google Scholar]
- Newman, M. Networks: An Introduction. Astron. Nachr. 2010, 327, 741–743. [Google Scholar]
- Daniel, S.; Yuhan, Z.; Qing-Chang, L. Vulnerability Analysis of Urban Rail Transit Networks: A Case Study of Shanghai, China. Sustainability 2015, 7, 6919–6936. [Google Scholar]
- Mcfadden, D. Quantitative Methods for Analyzing Travel Behaviour of Individuals: Some Recent Developments; Cowles Foundation Discussion Papers; Yale University: New Haven, CT, USA, 1978. [Google Scholar]
- Si, B.; Zhong, M.; Sun, H.; Gao, Z. Equilibrium model and algorithm of urban transit assignment based on augmented network. Sci. China Technol. Sci. 2009, 52, 3158–3167. [Google Scholar] [CrossRef]
- Wu, J.; Sun, H.; Gao, Z.; Han, L.; Si, B. Risk-based stochastic equilibrium assignment model in augmented urban railway network. J. Adv. Transp. 2014, 48, 332–347. [Google Scholar]
- Si, B.; Zhong, M.; Yang, X.; Gao, Z. Urban transit assignment model based on augmented network with in-vehicle congestion and transfer congestion. J. Syst. Sci. Syst. Eng. 2011, 20, 155–172. [Google Scholar] [CrossRef]
- Zhang, Y.; Yao, E.; Zhang, J.; Zhang, K. Estimating metro passengers’ path choices by combining self-reported revealed preference and smart card data. Transp. Res. Part C Emerg. Technol. 2018, 92, 76–89. [Google Scholar] [CrossRef]
- Wilensky, U. Center for Connected Learning and Computer-Based Modeling. In NetLogo; Northwestern University: Evanston, IL, USA, 1999; Available online: http://ccl.northwestern.edu/netlogo/ (accessed on 7 January 2019).
- Wilensky, U. NetLogo 6.1.0. User Manual. Available online: http://ccl.northwestern.edu/netlogo/docs/ (accessed on 13 May 2019).
- Xiong, Z.H.; Yao, S.Z. Congestion Propagation Quantization Model about Rail Transit System. J. Transp. Syst. Eng. Inf. Technol. 2018, 18, 146–151. [Google Scholar]
- Zeng, Z. Analyzing Congestion Propagation on Urban Rail Transit Oversaturated Conditions: A Framework Based on SIR Epidemic Model. Urban Rail Transit 2018, 4, 130–140. [Google Scholar] [CrossRef]


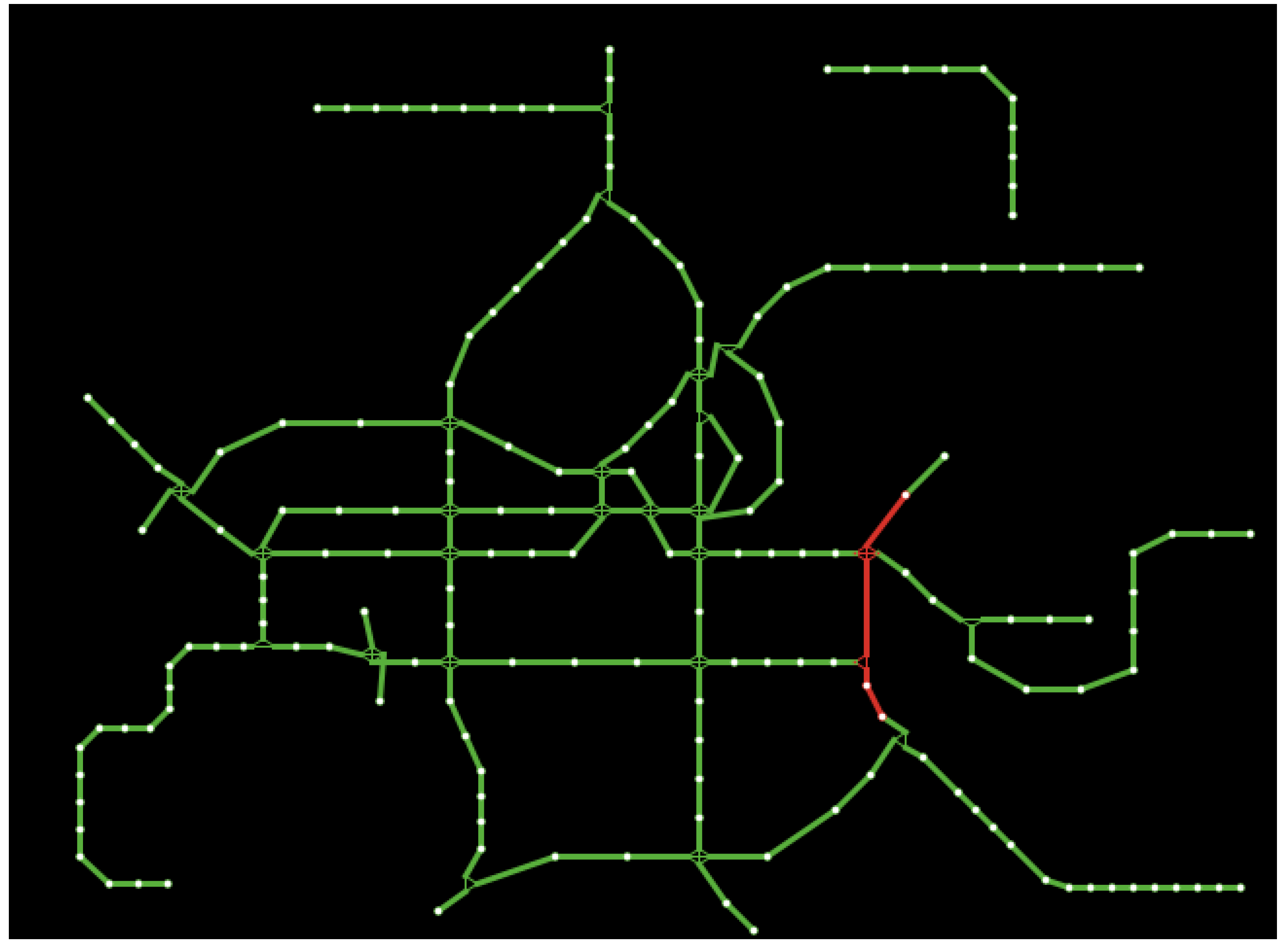
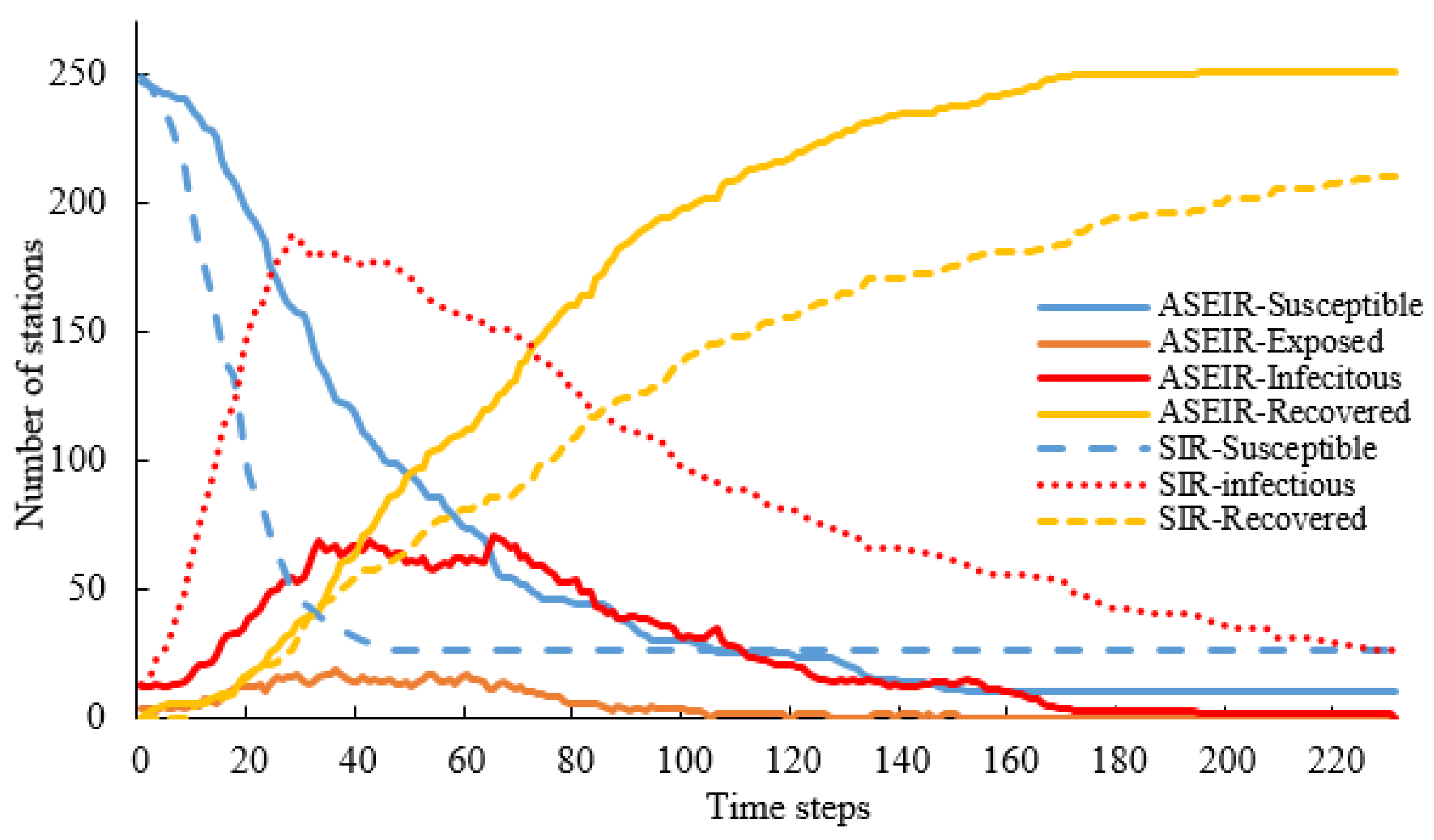
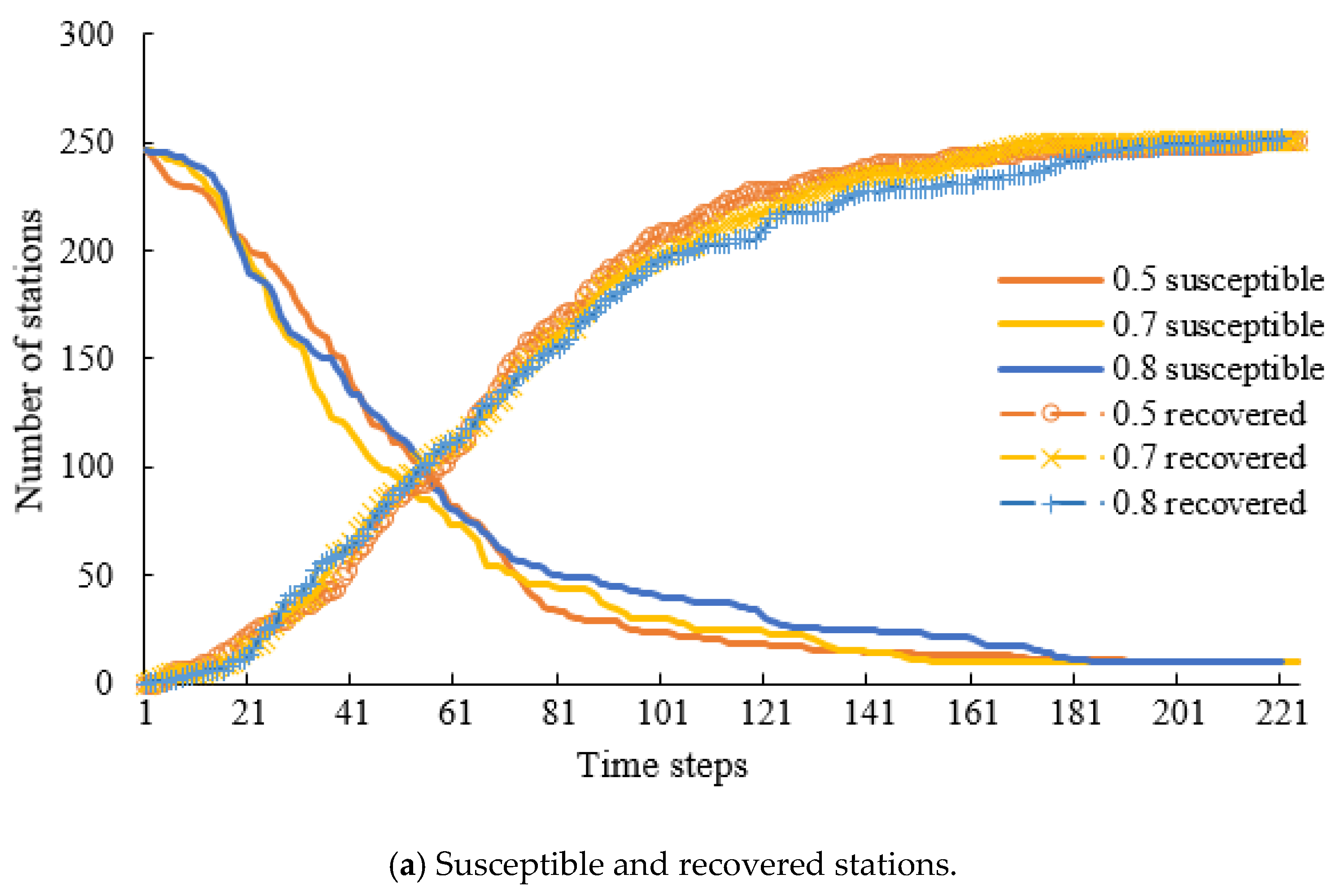
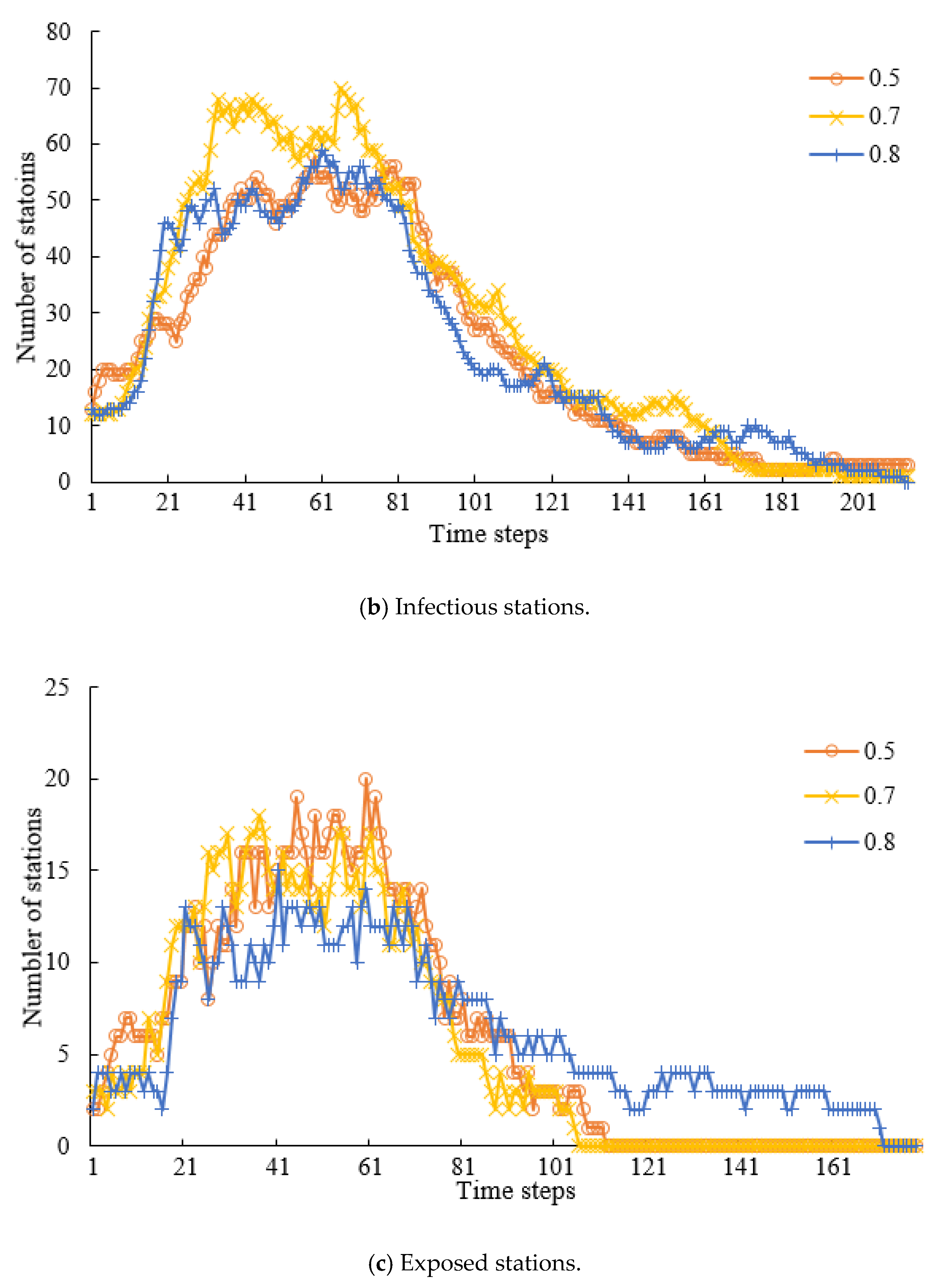
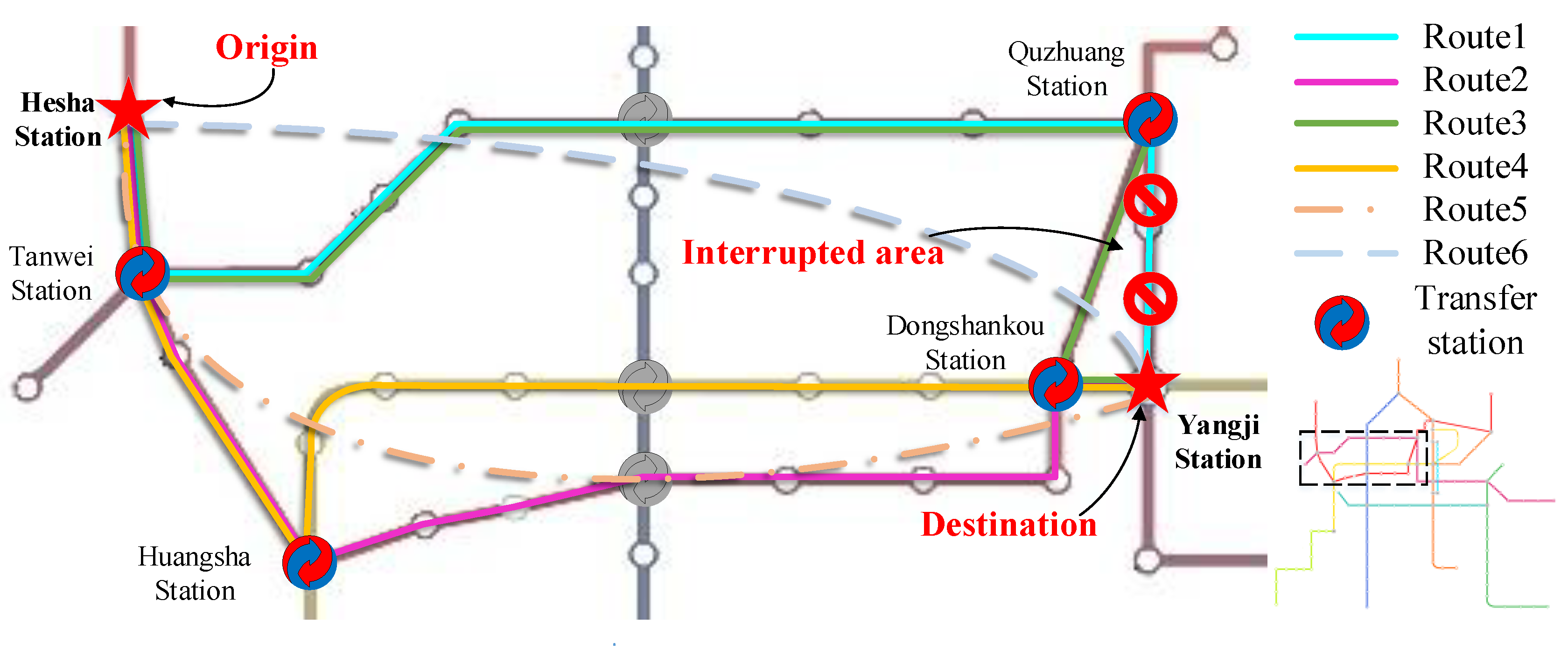
| Route | Traffic Mode | Route Property | Delay Time |
|---|---|---|---|
| 1 | Metro | The time shortest route before the metro emergency occurs. | 3 to 20 min |
| 2 | Metro, metro & bus or taxi | Detour routes in metro alone or combined with ground traffic modes like bus or taxi, travel time is longer than route 1. | 0 |
| 3 | 0 | ||
| 4 | 0 | ||
| 5 | Bus | Passengers abandon the metro because of the emergency-caused delays and switch to ground traffic modes like buses or taxis. Travel time or travel cost may be higher than the metro routes. | 0 |
| 6 | Taxi | 0 |
| Models | Alternatives | M1 | M2 | M3 |
|---|---|---|---|---|
| Parameters | Value (t-Test) | Value (t-Test) | Value (t-Test) | |
| ASC1 | Route 1 | 7.790 (114.770) | 7.630 (83.200) | 7.930 (77.080) |
| AC/m | 0.178 (13.210) | 0.167 (8.750) | 0.190 (9.870) | |
| BC | −0.204 (−3.890) | −0.143 (−1.950) | −0.273 (−3.630) | |
| RSC | −0.059 (−5.460) | −0.076 (−3.400) | −0.049 (−3.900) | |
| Travel cost/CNY | −6.49 × 10−4 (−0.620) | 3.69 × 10−3 (2.610) | −6.67 × 10−3 (−4.030) | |
| Travel time/min | −0.030 (−33.490) | −0.032 (−26.210) | −0.027 (−20.940) | |
| Transfer times | 0.087 (5.220) | 0.089 (3.730) | 0.085 (3.580) | |
| ASC2 | Route 2 Route 3 Route 4 | 5.990 (85.450) | 6.050 (64.730) | 5.910 (54.820) |
| ASC3 | 5.640 (56.290) | 5.850 (41.650) | 5.400 (37.080) | |
| ASC4 | 3.610 (37.940) | 3.590 (26.730) | 3.670 (26.770) | |
| AC/m | 0.178 (13.210) | 0.167 (8.750) | 0.190 (9.870) | |
| BC | −0.204 (−3.890) | −0.143 (−1.950) | −0.273 (−3.630) | |
| Travel cost/CNY | −6.49 × 10−4 (−0.620) | 3.69 × 10−3 (2.610) | −6.67 × 10−3 (−4.030) | |
| Travel time/min | −0.030 (−33.490) | −0.032 (−26.210) | −0.027 (−20.940) | |
| Transfer times | 0.087 (5.220) | 0.089 (3.730) | 0.085 (3.580) | |
| ASC5 | Route 5 Route 6 | 2.040 (22.250) | 2.310 (18.310) | 1.730 (12.710) |
| Travel cost/CNY | −6.49 × 10−4 (−0.620) | 3.69 × 10−3 (2.610) | −6.67 × 10−3 (−4.030) | |
| Travel time/min | −0.030 (−33.490) | −0.032 (−26.210) | −0.027 (−20.940) | |
| Transfer times | 0.087 (5.220) | 0.089 (3.730) | 0.085 (3.580) | |
| Sample size | 10,128 | 5591 | 4537 | |
| Log likelihood | −12,415.973 | −6738.605 | −5619.129 | |
| Rho-square | 0.217 | 0.230 | 0.210 | |
| Adjusted rho-square | 0.217 | 0.229 | 0.208 | |
| Route | AC/m | BC | RSC | Travel Time/min | Transfer Times | Travel Cost/CNY |
|---|---|---|---|---|---|---|
| 1 | 2770.73 | 0.92 | 1 | 23.72 | 1 | 5 |
| 2 | 2888.46 | 0.81 | 0.43 | 23.93 | 1 | 5 |
| 3 | 3219.03 | 1.01 | 0.58 | 30.88 | 3 | 5 |
| 4 | 3020.31 | 0.79 | 0.49 | 26.75 | 1 | 5 |
| 5 | - | - | 2.25 | 63 | 0 | 2 |
| 6 | - | - | 0.64 | 33 | 0 | 33 |
| Route | M1 | M2 | M3 |
|---|---|---|---|
| 1 | 8.61% | 6.75% | 10.86% |
| 2 | 49.83% | 48.16% | 51.28% |
| 3 | 34.03% | 37.59% | 30.13% |
| 4 | 3.91% | 3.41% | 4.73% |
| 5 | 0.89% | 0.72% | 1.10% |
| 6 | 2.73% | 3.37% | 1.91% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Yao, E.; Liu, S. Simulation of Metro Congestion Propagation Based on Route Choice Behaviors Under Emergency-Caused Delays. Appl. Sci. 2019, 9, 4210. https://doi.org/10.3390/app9204210
Wang X, Yao E, Liu S. Simulation of Metro Congestion Propagation Based on Route Choice Behaviors Under Emergency-Caused Delays. Applied Sciences. 2019; 9(20):4210. https://doi.org/10.3390/app9204210
Chicago/Turabian StyleWang, Xingchuan, Enjian Yao, and Shasha Liu. 2019. "Simulation of Metro Congestion Propagation Based on Route Choice Behaviors Under Emergency-Caused Delays" Applied Sciences 9, no. 20: 4210. https://doi.org/10.3390/app9204210
APA StyleWang, X., Yao, E., & Liu, S. (2019). Simulation of Metro Congestion Propagation Based on Route Choice Behaviors Under Emergency-Caused Delays. Applied Sciences, 9(20), 4210. https://doi.org/10.3390/app9204210




