Advanced Adaptive Cruise Control Based on Operation Characteristic Estimation and Trajectory Prediction †
Abstract
:1. Introduction
2. Overview
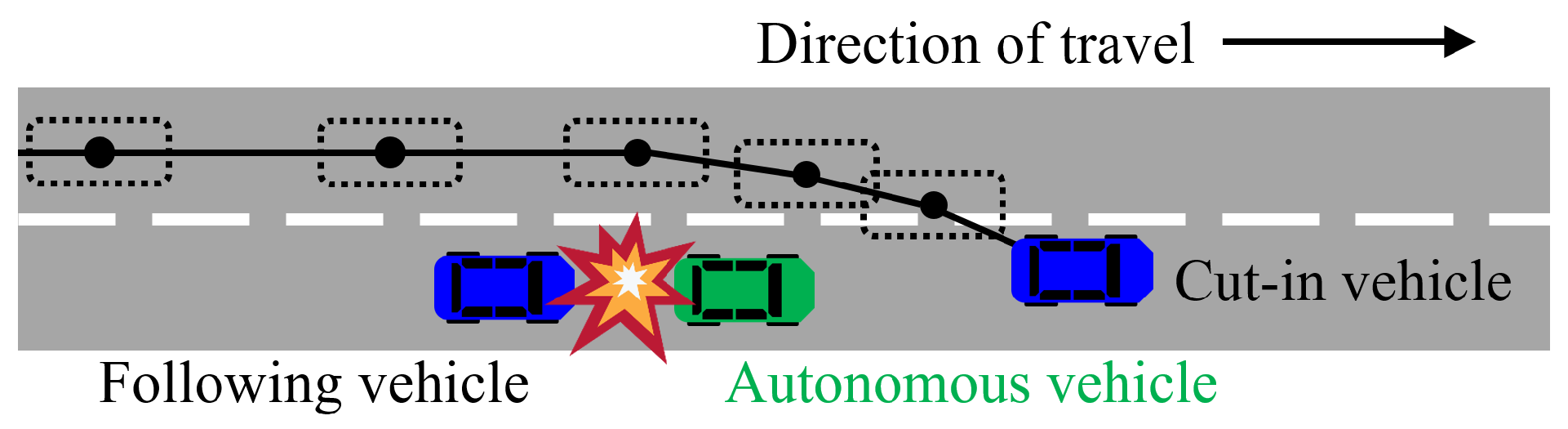
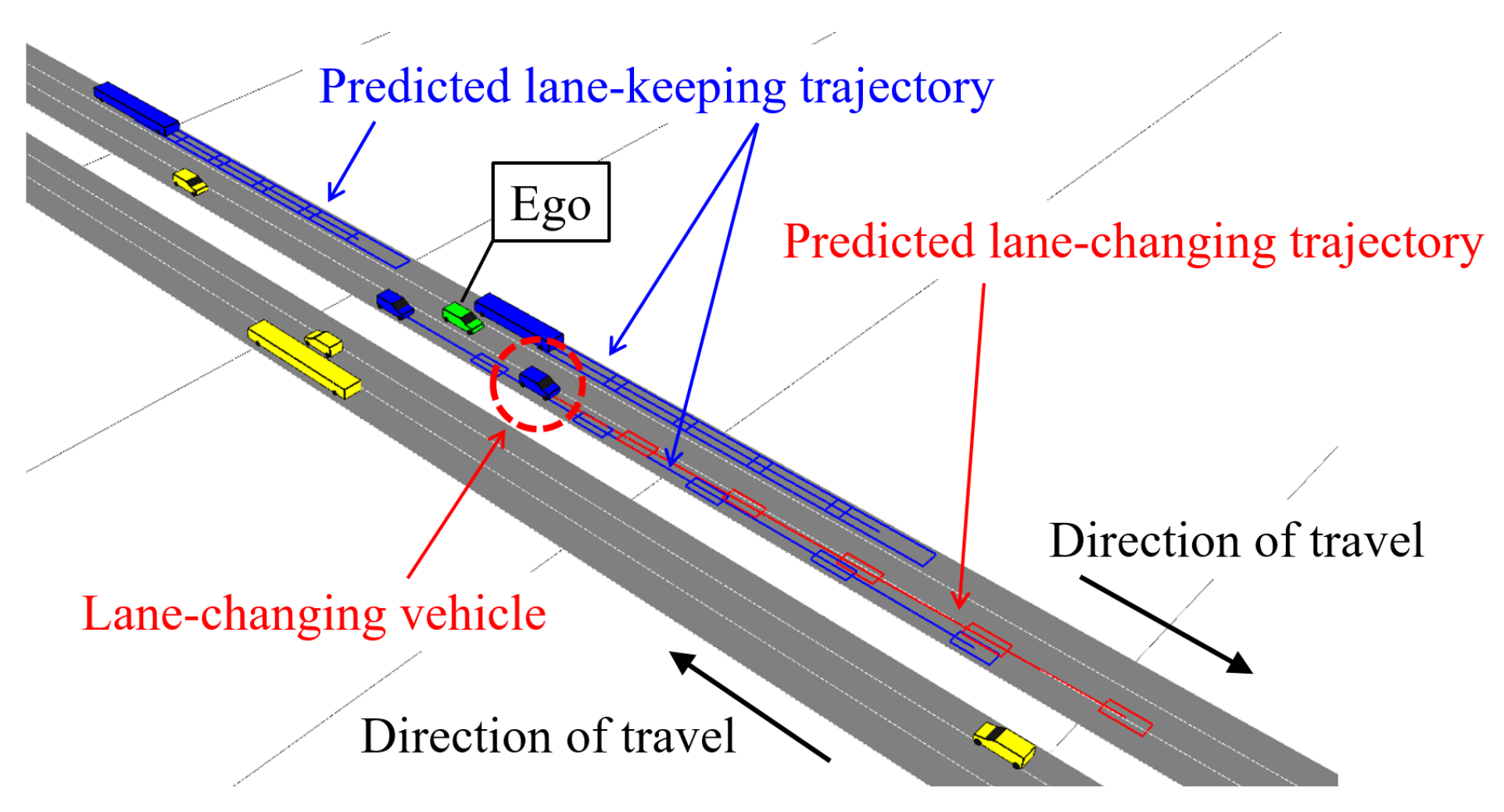
2.1. Problem Definition
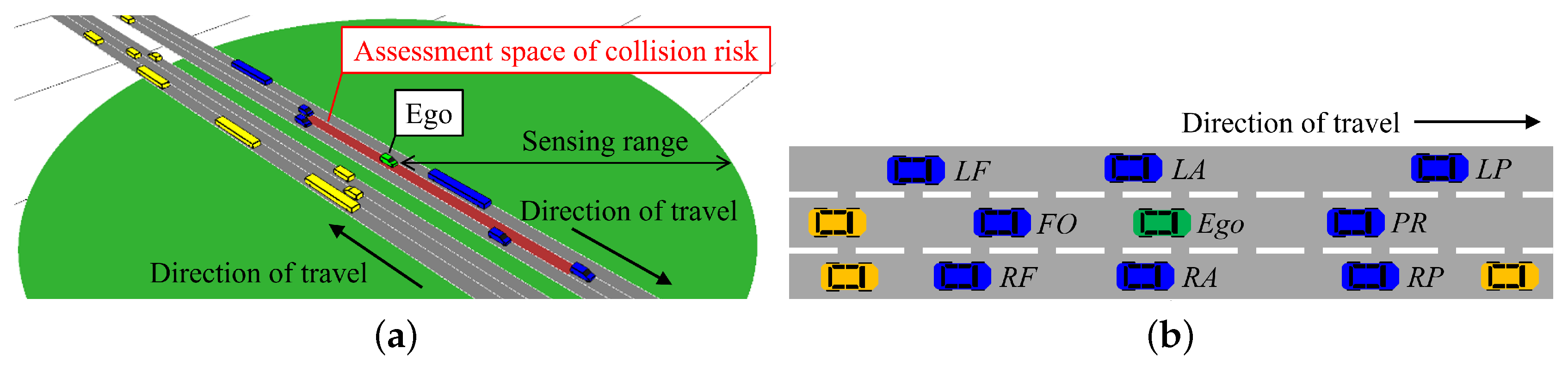
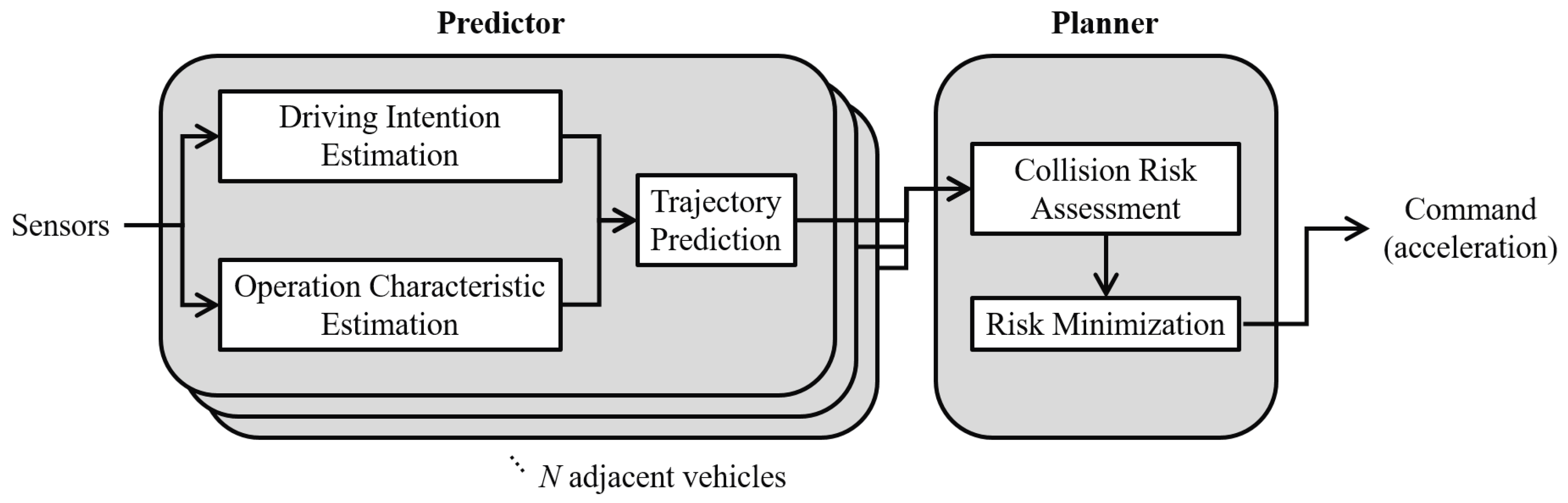
2.2. Overview of the Proposed Method
3. Proposed Method
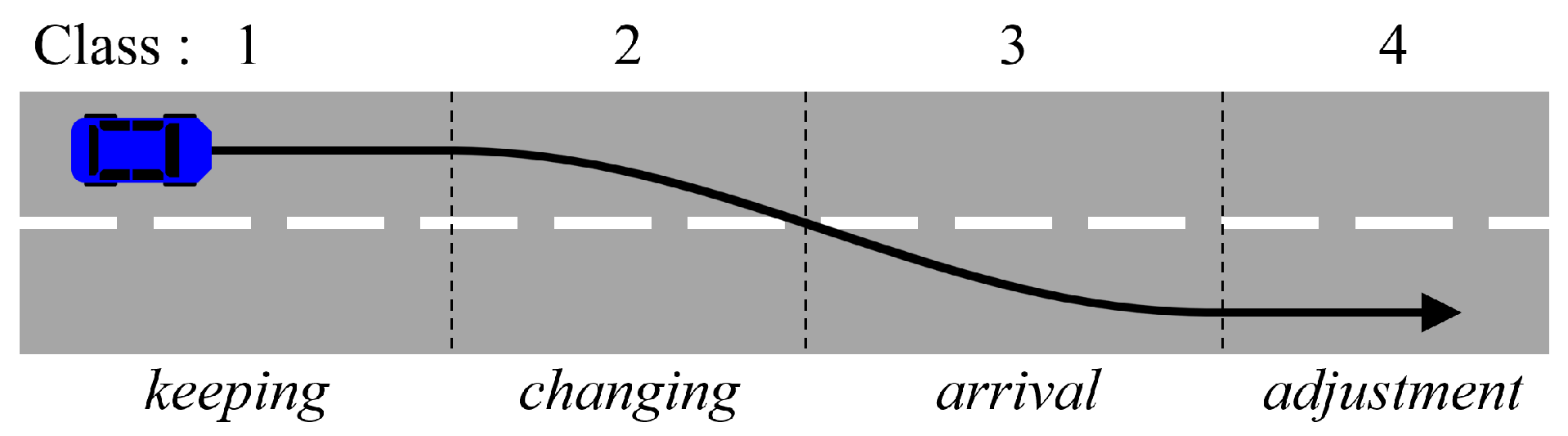
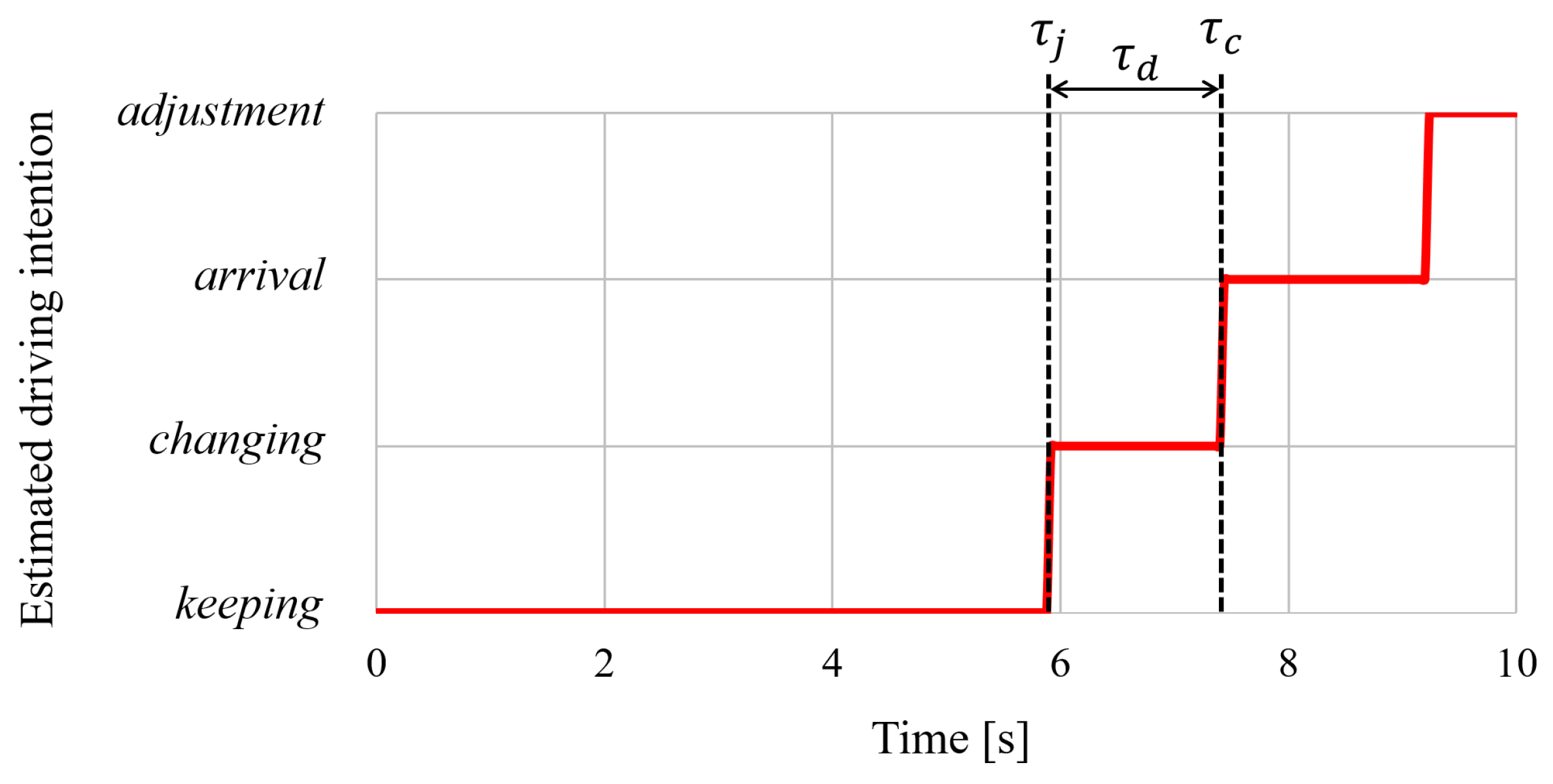
3.1. Driving Intention Estimation
3.2. Operation Characteristic Estimation
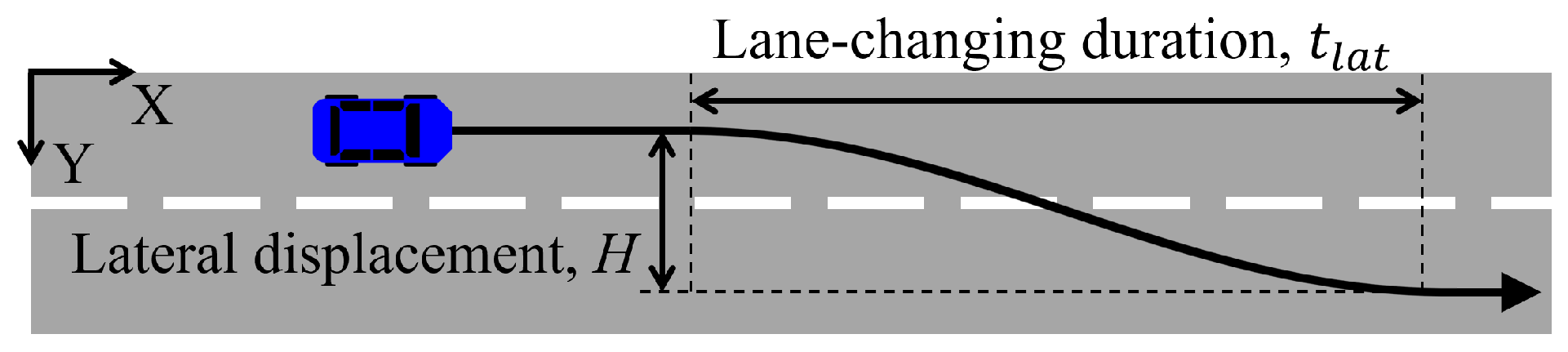
3.3. Trajectory Prediction
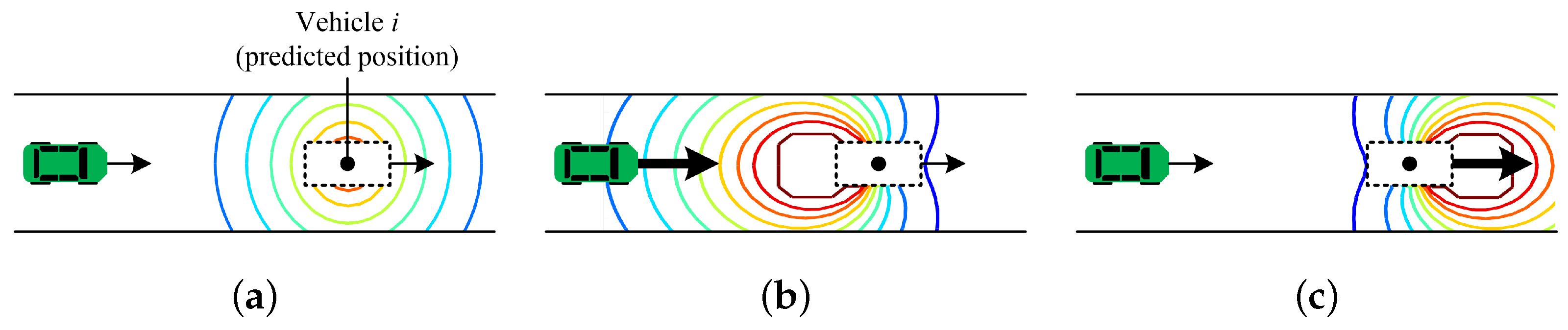
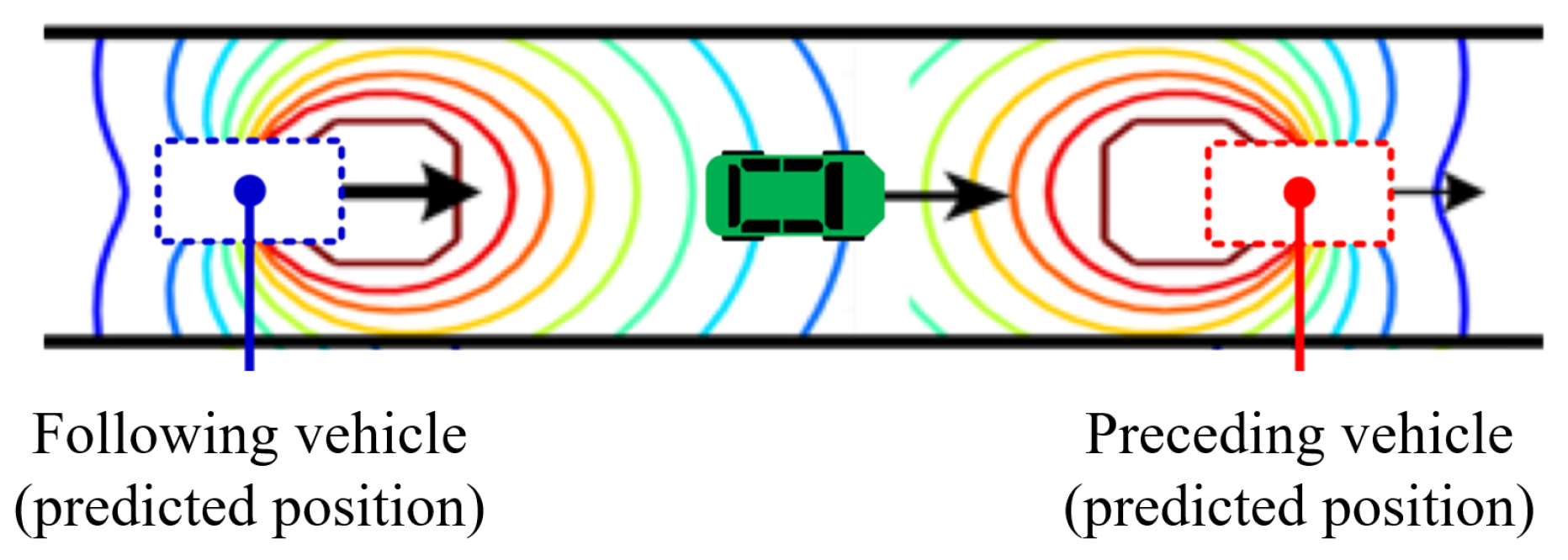
3.4. Collision Risk Assessment
3.5. Risk Minimization
4. Evaluation
4.1. Dataset
4.2. Performance of the Driving Intention Estimation
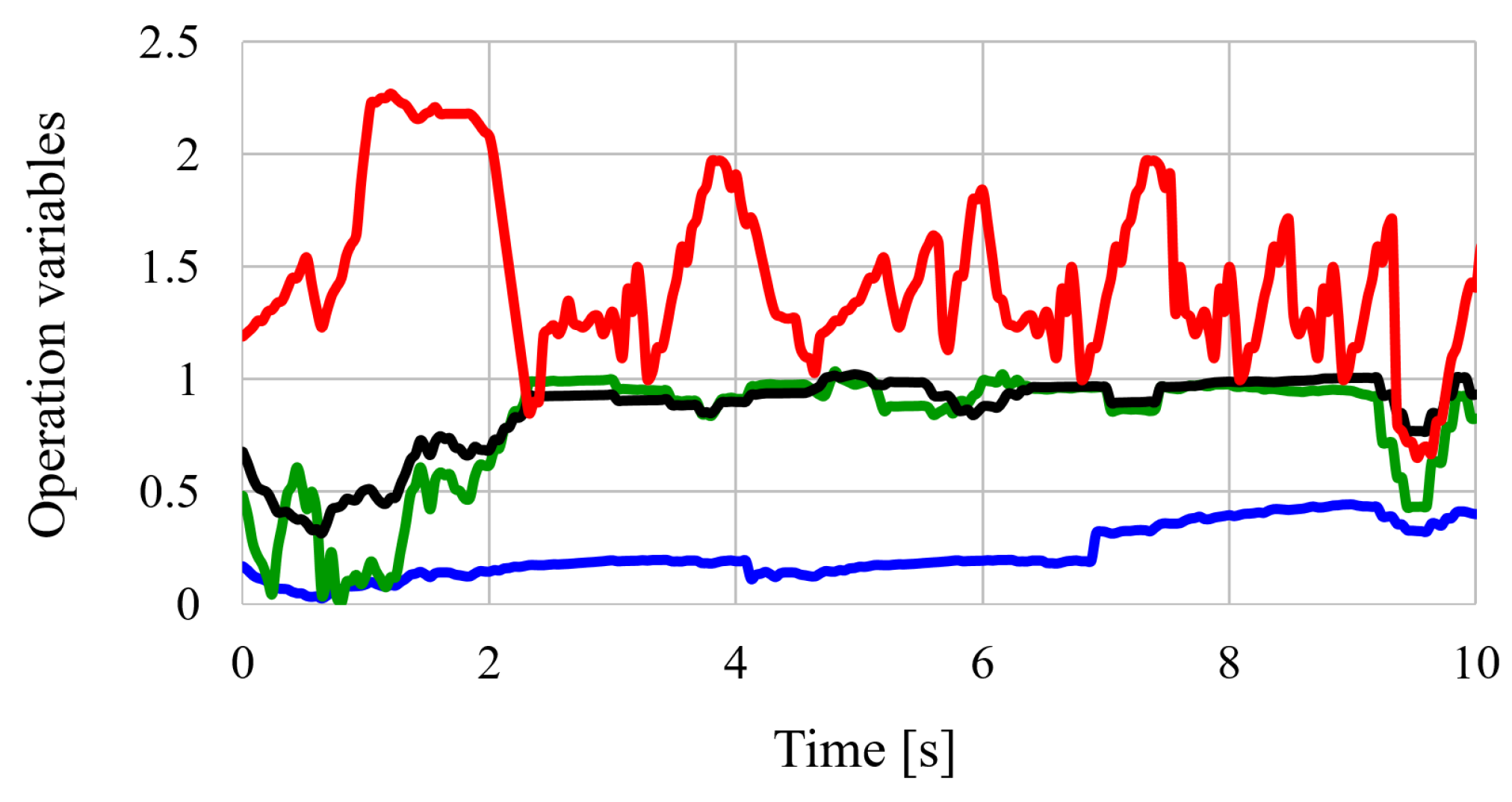
4.3. Results of the Operation Characteristic Estimation
4.4. Performance of Trajectory Prediction
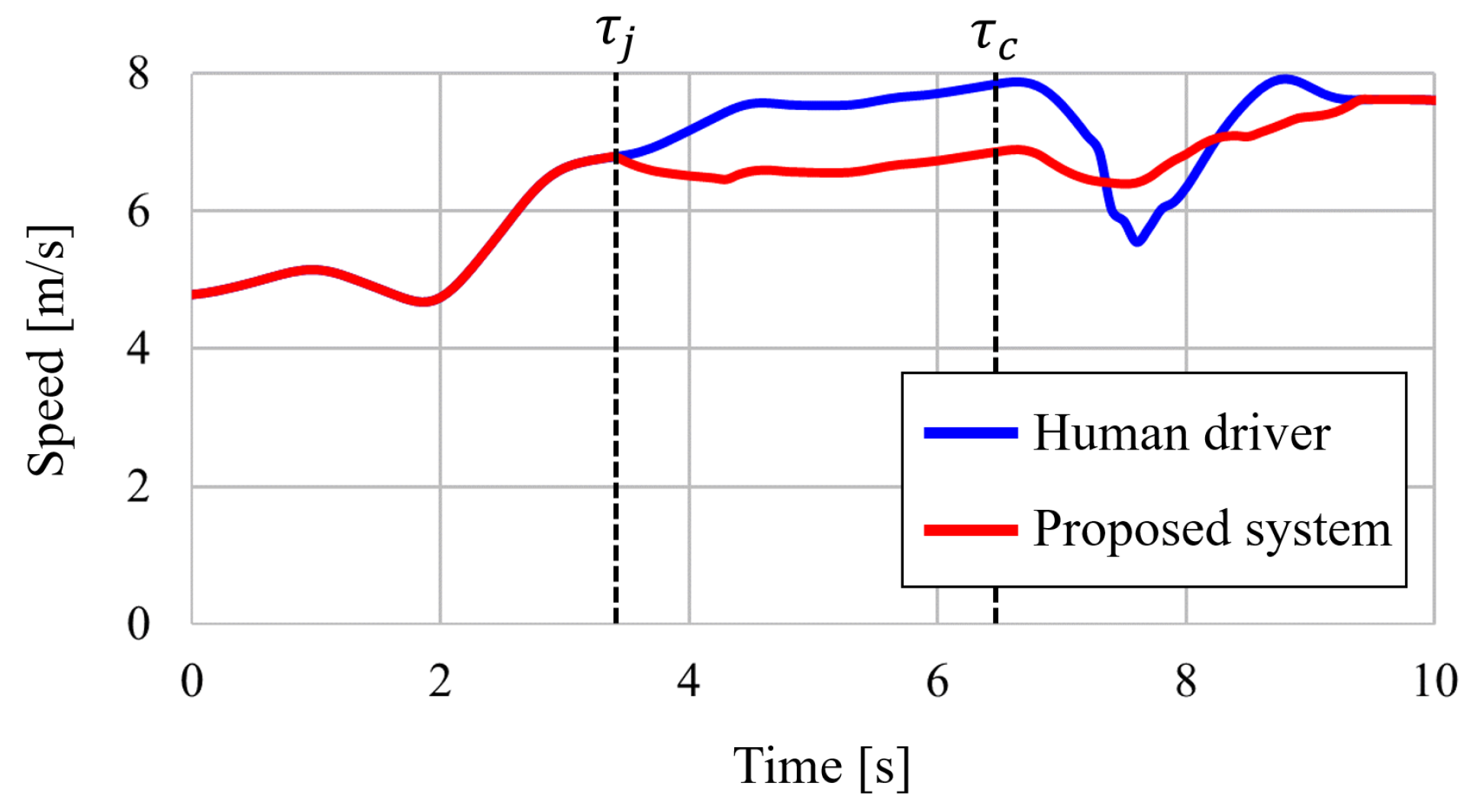
4.5. Performance of Collision Risk Minimization
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- U.S. Department of Transportation. Critical Reasons for Crashes Investigated in the National Motor Vehicle Crash Causation Survey; Report No. DOT HS 812 115; USDOT: Washington, DC, USA, 2015.
- Federal Highway Administration, Roadway Departure Safety. Available online: https://safety.fhwa.dot.gov/roadway_dept/ (accessed on 3 April 2019).
- Chandler, R.E.; Herman, R.E.; Montrol, W. Traffic dynamics: Studies in car-following. Oper. Res. 1958, 6, 165–184. [Google Scholar] [CrossRef]
- Gazis, D.C.; Herman, R.; Rothery, R.W. Nonlinear follow-the-leader models of traffic flow. Oper. Res. 1961, 9, 545–567. [Google Scholar] [CrossRef]
- Bexelius, S. An extended model for car-following. Transp. Res. 1968, 2, 13–21. [Google Scholar] [CrossRef]
- Daganzo, C.F. The cell transimission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory. Transp. Res. Part B Methodol. 1994, 28, 269–287. [Google Scholar] [CrossRef]
- Higgs, B.; Abbas, M.M.; Medina, A. Analysis of the Wiedemann Car Following Model Over Different Speeds Using Naturalistic Data. 2011. Available online: http://onlinepubs.trb.org/onlinepubs/conferences/2011/RSS/3/Higgs,B.pdf (accessed on 11 November 2019).
- Green, M. How long does it take to stop?: Methodological analysis of driver perception-brake times. Transp. Hum. Factors 2000, 2, 195–216. [Google Scholar] [CrossRef]
- Woo, H.; Ji, Y.; Tamura, Y.; Kuroda, Y.; Sugano, T.; Yamamoto, Y.; Yamashita, A.; Asama, H. Advanced adaptive cruise control based on collision risk assessment. In Proceedings of the 21th IEEE International Conference on Intelligent Transportation Systems, Maui, HI, USA, 4–7 November 2018; pp. 939–944. [Google Scholar]
- Mehmood, A.; Saccomanno, F.; Hellinga, B. Evaluation of a car-following model using systems dynamics. In Proceedings of the 19th International System Dynamics Conference, Atlanta, GA, USA, 23–27 July 2001; pp. 1–23. [Google Scholar]
- You, C.; Lu, J.; Tsiotras, P. Driver parameter estimation using joint E-/UKF and dual E-/UKF under nonlinear state inequality constraints. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics, Budapest, Hungary, 9–12 October 2016; pp. 1215–1220. [Google Scholar]
- Filev, D.; Lu, J.; Prakah-Asante, K.; Tseng, F. Real-time driving behavior identification based on driver-in-the-loop vehicle dynamics and control. In Proceedings of the 2009 IEEE International Conference on Systems, Man, and Cybernetics, San Antonio, TX, USA, 11–14 October 2018; pp. 2089–2094. [Google Scholar]
- Zhu, M.; Wang, X.; Wang, Y. Human-like autonomous car-following model with deep reinforcement learning. Transp. Res. Part C Emerg. Technol. 2018, 97, 348–368. [Google Scholar] [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2000, 62, 1805–1824. [Google Scholar] [CrossRef]
- Kesting, A.; Treiber, M.; Helbing, D. Enhanced intelligent driver model to access the impact of driving strategies on traffic capacity. Philos. Trans. R. Soc. A 2010, 368, 4585–4605. [Google Scholar] [CrossRef]
- Davis, C. Effect of adaptive cruise control systems on traffic flow. Phys. Rev. E 2004, 69, 1–8. [Google Scholar] [CrossRef]
- Milanés, V.; Shladover, S.E. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data. Transp. Res. Part C 2014, 48, 285–300. [Google Scholar] [CrossRef]
- Lu, C.; Aakre, A. A new adaptive cruise control strategy and its stabilization effect on traffic flow. Eur. Transp. Res. Rev. 2018, 10, 49. [Google Scholar] [CrossRef]
- Touran, A.; Brackstone, M.A.; McDonald, M. A collision model for safety evaluation of autonomous intelligent cruise control. Accid. Anal. Prev. 1999, 31, 567–578. [Google Scholar] [CrossRef]
- Woo, H.; Ji, Y.; Tamura, Y.; Kuroda, Y.; Sugano, T.; Yamamoto, Y.; Yamashita, A.; Asama, H. Dynamic state estimation of driving style based on driving risk feature. Int. J. Automot. Eng. 2018, 9, 31–38. [Google Scholar]
- Heyes, M.P.; Ashworth, R. Further research on car-following models. Transp. Res. 1972, 6, 287–291. [Google Scholar] [CrossRef]
- Ozaki, H. Reaction and anticipation in the car-following behaviour. In Proceedings of the 13th International Symposium on Traffic and Transportation Theory, Lyon, France, 24–26 July 1993; pp. 349–366. [Google Scholar]
- Aron, M. Car-following in an urban network: Simulation and experiments. In Proceedings of the Seminar D, 16th Planning and Transport, Research and Computation Meeting, Warwick, UK, 13–16 July 1988; pp. 27–39. [Google Scholar]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An algorithm for least-squares estimation of nonlinear parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Woo, H.; Ji, Y.; Kono, H.; Tamura, Y.; Kuroda, Y.; Sugano, T.; Yamamoto, Y.; Yamashita, A.; Asama, H. Automatic detection method of lane-changing intentions based on relationship with adjacent vehicles using artificial potential fields. Int. J. Automot. Eng. 2016, 7, 127–134. [Google Scholar]
- Gazis, D.C.; Herman, R.; Potts, R.B. Car-following theory of steady-state traffic flow. Oper. Res. 1959, 7, 499–505. [Google Scholar] [CrossRef]
- Butakov, V.A.; Ioannou, P. Personalized driver/vehicle lane change models for ADAS. IEEE Trans. Veh. Technol. 2014, 64, 4422–4431. [Google Scholar] [CrossRef]
- Guo, L.; Ge, P.; Yue, M.; Zhao, Y. Lane changing trajectory planning and tracking controller design for intelligent vehicle running on curved road. Mat. Probl. Eng. 2014, 2014, 478573. [Google Scholar] [CrossRef]
- Krajewski, R.; Bock, J.; Kloeker, L.; Eckstein, L. The highD dataset: A drone dataset of naturalistic vehicle trajectories on German highways for validation of highly automated driving systems. In Proceedings of the 21th IEEE International Conference on Intelligent Transportation Systems, Maui, HI, USA, 4–7 November 2018; pp. 2118–2125. [Google Scholar]
- Kasper, D.; Weidl, G.; Dang, T.; Breuel, G.; Tamke, A.; Wedel, A. Object-oriented bayesian networks for detection of lane change maneuvers. In Proceedings of the 2011 IEEE International Conference on Intelligent Vehicle Symposium, Baden-Baden, Germany, 5–9 June 2011; pp. 673–678. [Google Scholar]
- Woo, H.; Ji, Y.; Tamura, Y.; Kuroda, Y.; Sugano, T.; Yamamoto, Y.; Yamashita, A.; Asama, H. Lane-change detection based on individual driving style. Adv. Robot. 2019, 33, 1087–1098. [Google Scholar] [CrossRef]


| Location ID | Heyes [21] | Ozaki [22] | Aron [23] | Proposed |
|---|---|---|---|---|
| 1 | 0.159 m | 0.215 m | 0.211 m | 0.065 m |
| 2 | 0.130 m | 0.178 m | 0.181 m | 0.062 m |
| 3 | 0.093 m | 0.150 m | 0.133 m | 0.055 m |
| 4 | 0.115 m | 0.165 m | 0.148 m | 0.062 m |
| 5 | 0.180 m | 0.216 m | 0.218 m | 0.079 m |
| 6 | 0.155 m | 0.202 m | 0.195 m | 0.070 m |
| Average | 0.139 m | 0.189 m | 0.183 m | 0.065 m |
| Standard deviation | 0.032 m | 0.028 m | 0.034 m | 0.008 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woo, H.; Madokoro, H.; Sato, K.; Tamura, Y.; Yamashita, A.; Asama, H. Advanced Adaptive Cruise Control Based on Operation Characteristic Estimation and Trajectory Prediction. Appl. Sci. 2019, 9, 4875. https://doi.org/10.3390/app9224875
Woo H, Madokoro H, Sato K, Tamura Y, Yamashita A, Asama H. Advanced Adaptive Cruise Control Based on Operation Characteristic Estimation and Trajectory Prediction. Applied Sciences. 2019; 9(22):4875. https://doi.org/10.3390/app9224875
Chicago/Turabian StyleWoo, Hanwool, Hirokazu Madokoro, Kazuhito Sato, Yusuke Tamura, Atsushi Yamashita, and Hajime Asama. 2019. "Advanced Adaptive Cruise Control Based on Operation Characteristic Estimation and Trajectory Prediction" Applied Sciences 9, no. 22: 4875. https://doi.org/10.3390/app9224875
APA StyleWoo, H., Madokoro, H., Sato, K., Tamura, Y., Yamashita, A., & Asama, H. (2019). Advanced Adaptive Cruise Control Based on Operation Characteristic Estimation and Trajectory Prediction. Applied Sciences, 9(22), 4875. https://doi.org/10.3390/app9224875






