Hemodynamic Interference of Serial Stenoses and Its Impact on FFR and iFR Measurements
Abstract
1. Introduction
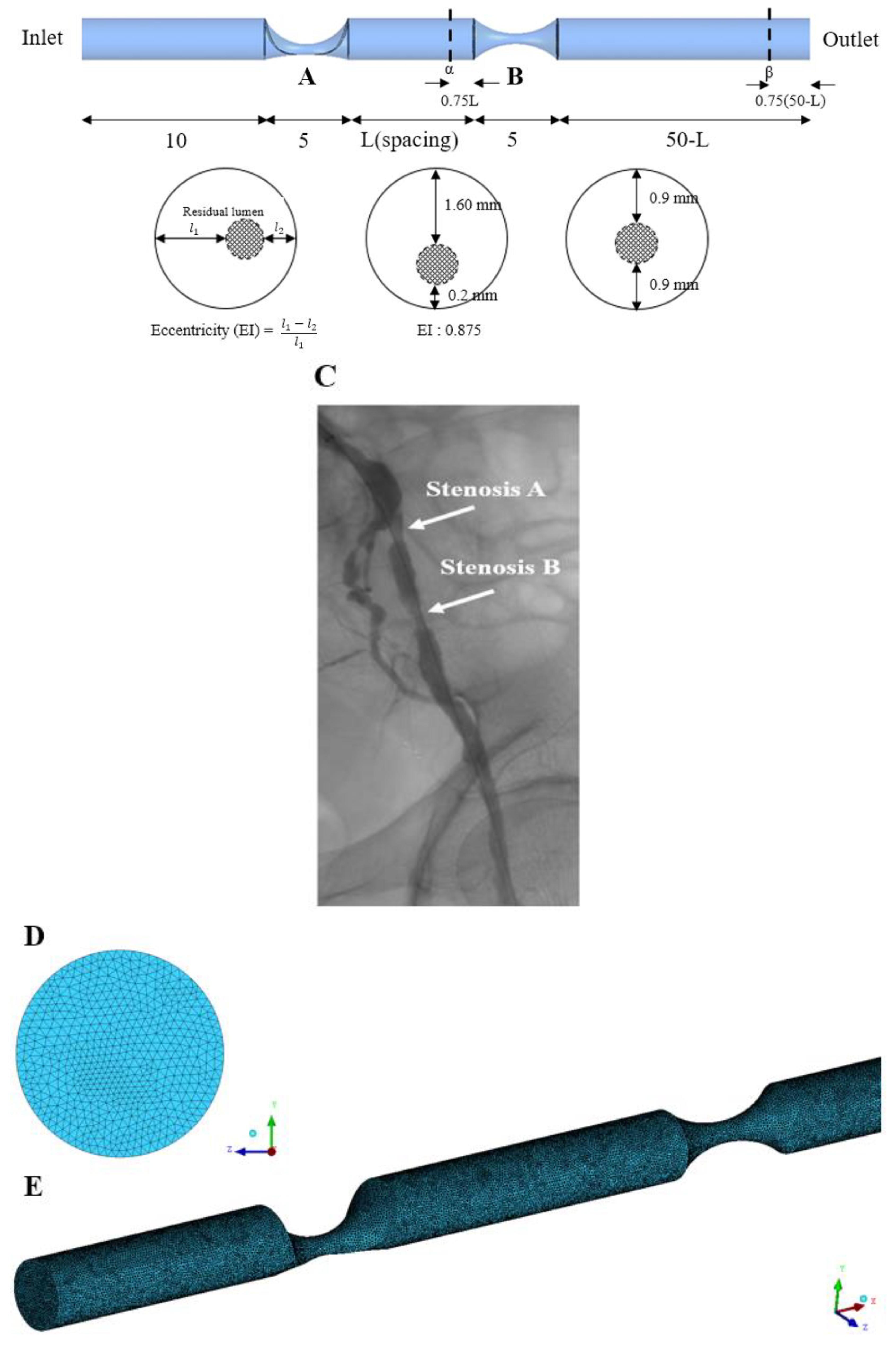
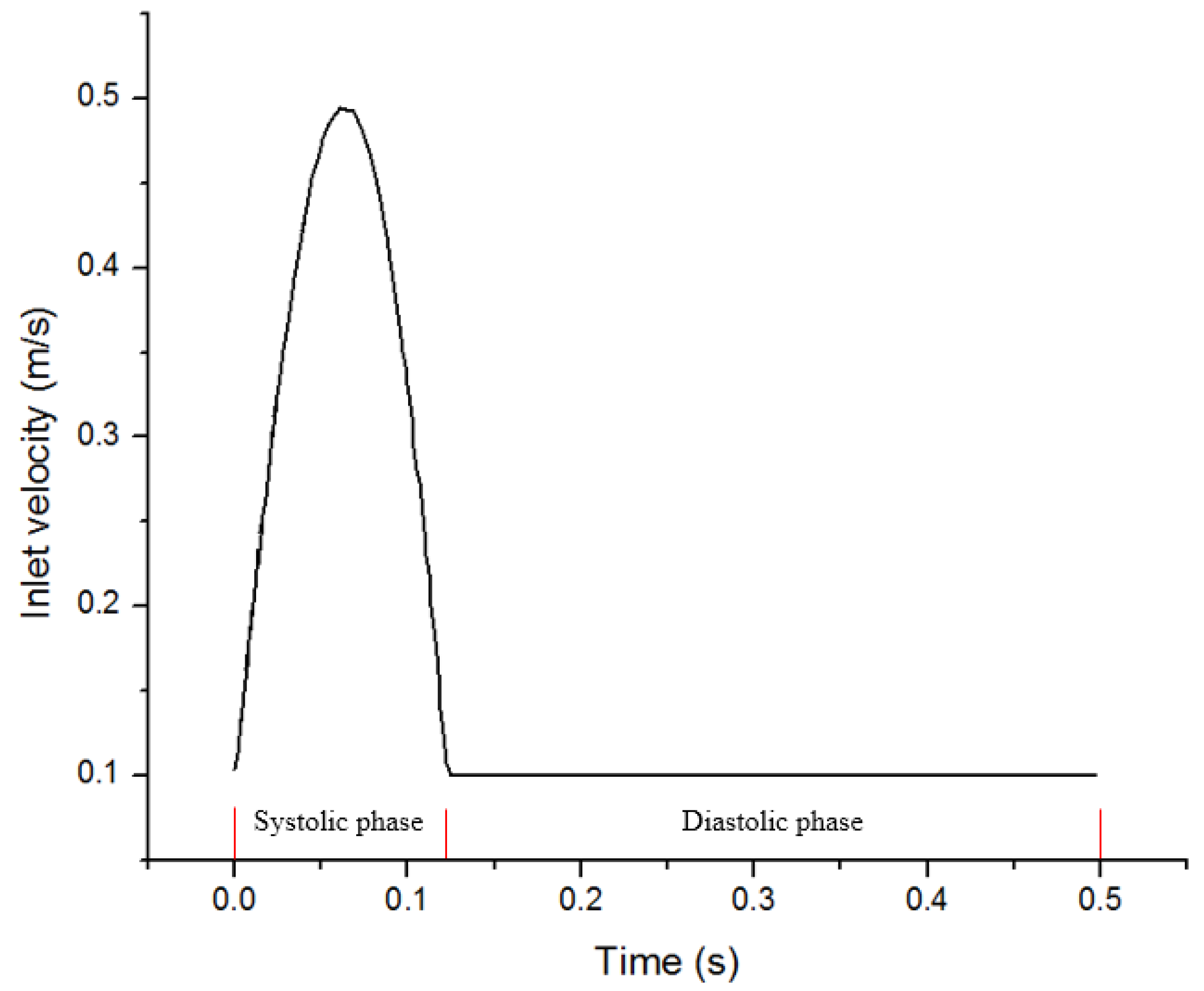
2. Materials and Methods
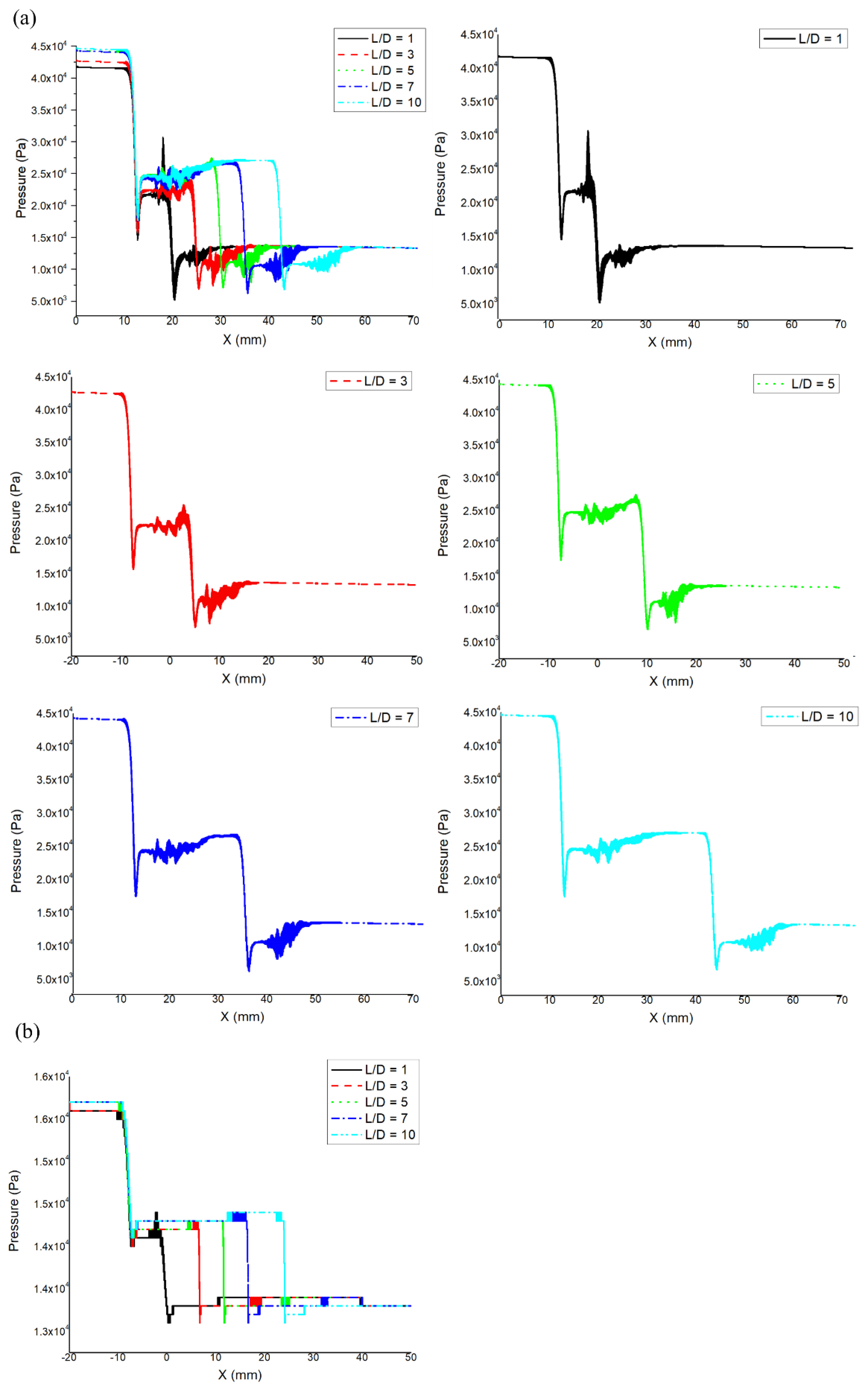
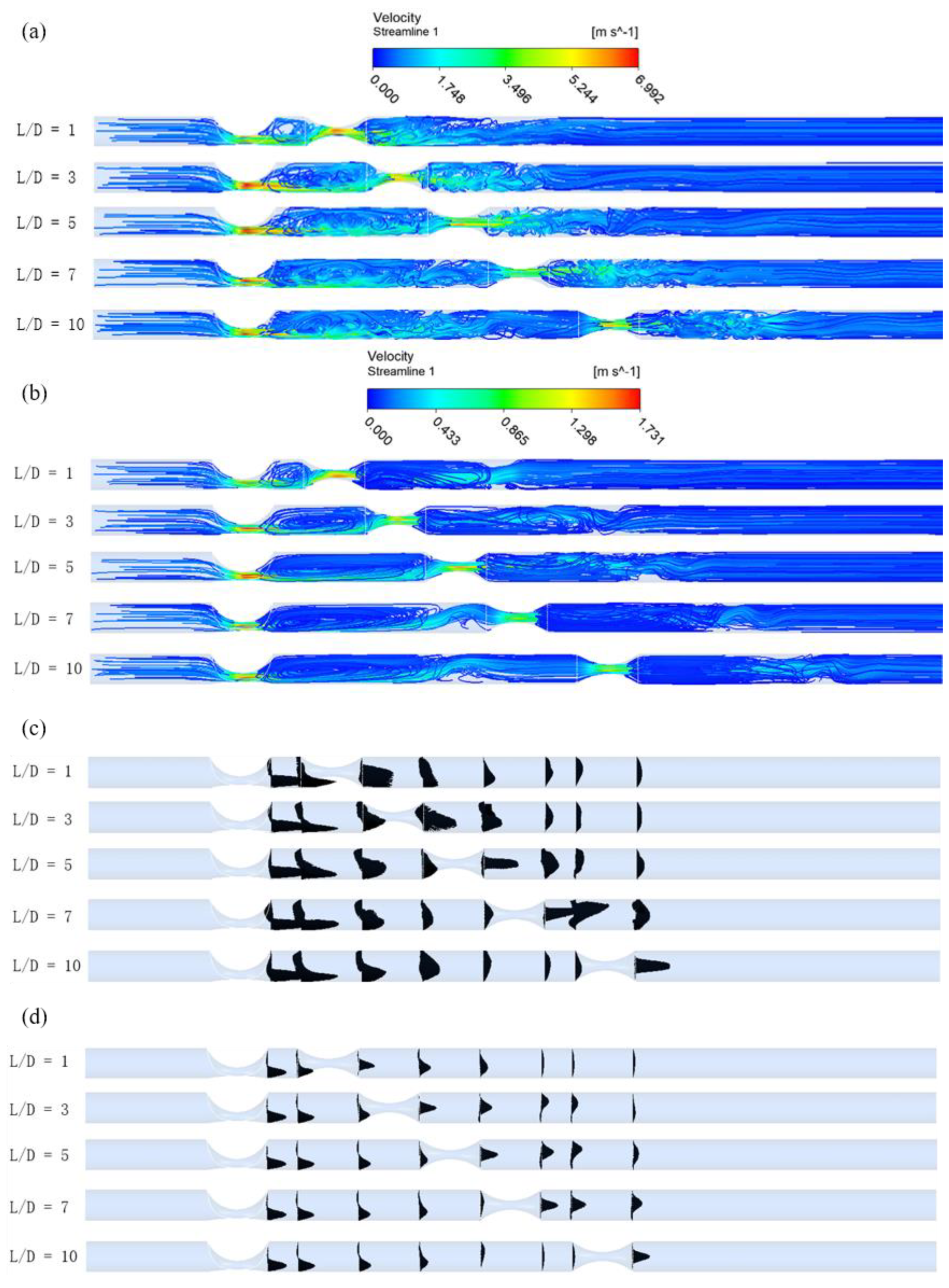
3. Results
4. Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gordon, G.R.; Mulligan, S.J.; MacVicar, B.A. Astrocyte control of the cerebrovasculature. Glia 2007, 55, 1214–1221. [Google Scholar] [CrossRef] [PubMed]
- Pijls, N.H.; Fearon, W.F.; Tonino, P.A.; Siebert, U.; Ikeno, F.; Bornschein, B.; van’t Veer, M.; Klauss, V.; Manoharan, G.; Engstrøm, T.; et al. Fractional flow reserve versus angiography for guiding percutaneous coronary intervention in patients with multivessel coronary artery disease: 2-year follow-up of the FAME (Fractional Flow Reserve Versus Angiography for Multivessel Evaluation) study. J. Am. Coll. Cardiol. 2010, 56, 177–184. [Google Scholar] [CrossRef] [PubMed]
- Tebaldi, M.; Campo, G.; Biscaglia, S. Fractional flow reserve: Current applications and overview of the available data. World J. Clin. Cases 2015, 3, 678–681. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, K.; Bezerra, H.G.; Gaur, S.; Attizzani, G.F.; Bøtker, H.E.; Costa, M.A.; Rogers, C.; Nørgaard, B.L. Comparison between non-invasive (coronary computed tomography angiography derived) and invasive-fractional flow reserve in patients with serial stenoses within one Coronary artery: A NXT trial substudy. Ann. Biomed. Eng. 2016, 44, 580–589. [Google Scholar] [CrossRef] [PubMed]
- De Bruyne, B.; Pijls, N.H.; Heyndrickx, G.R.; Hodeige, D.; Kirkeeide, R.; Gould, K.L. Pressure-derived fractional flow reserve to assess serial epicardial stenoses: Theoretical basis and animal validation. Circulation 2000, 101, 1840–1847. [Google Scholar] [CrossRef]
- Siebert, U.; Arvandi, M.; Gothe, R.M.; Bornschein, B.; Eccleston, D.; Walters, D.L.; Rankin, J.; De Bruyne, B.; Fearon, W.F.; Pijls, N.H.; et al. Improving the quality of percutaneous revascularisation in patients with multivessel disease in Australia: Cost-effectiveness, public health implications, and budget impact of FFR-guided PCI. Heart Lung Circ. 2014, 23, 527–533. [Google Scholar] [CrossRef] [PubMed]
- Modi, B.; Chattersingh, A.; Ryan, M.; Ellis, H.; Lee, J.; Gaddum, N.; Chowienczyk, P.; Perera, D. P3322Optimising physiological assessment of serial coronary artery lesions using an in vitro model of tandem stenoses. Eur. Heart J. 2017, 38 (Suppl. 1). [Google Scholar] [CrossRef]
- Sen, S.; Asrress, K.N.; Nijjer, S.; Petraco, R.; Malik, I.S.; Foale, R.A.; Mikhail, G.W.; Foin, N.; Broyd, C.; Hadjiloizou, N.; et al. Diagnostic classification of the instantaneous wave-free ratio is equivalent to fractional flow reserve and is not improved with adenosine administration: Results of CLARIFY (Classification Accuracy of Pressure-Only Ratios Against Indices Using Flow Study). J. Am. Coll. Cardiol. 2013, 61, 1409–1420. [Google Scholar] [CrossRef] [PubMed]
- Nijjer, S.S.; Sen, S.; Petraco, R.; Escaned, J.; Echavarria-Pinto, M.; Broyd, C.; Al-Lamee, R.; Foin, N.; Foale, R.A.; Malik, I.S.; et al. Pre-angioplasty instantaneous wave-free ratio pullback provides virtual intervention and predicts hemodynamic outcome for serial lesions and diffuse coronary artery disease. JACC Cardiovasc. Interv. 2014, 7, 1386–1396. [Google Scholar] [CrossRef] [PubMed]
- De Rosa, S.; Polimeni, A.; Petraco, R.; Davies, J.E.; Indolfi, C. Diagnostic performance of the instantaneous wave-free ratio: Comparison with fractional flow reserve. Circ. Cardiovasc. Interv. 2018, 11, e004613. [Google Scholar] [CrossRef] [PubMed]
- Modi, B.N.; De Silva, K.; Rajani, R.; Curzen, N.; Perera, D. Physiology-guided management of serial coronary artery disease: A review. JAMA Cardiol. 2018, 3, 432–438. [Google Scholar] [CrossRef] [PubMed]
- Sen, S.; Escaned, J.; Malik, I.S.; Mikhail, G.W.; Foale, R.A.; Mila, R.; Tarkin, J.; Petraco, R.; Broyd, C.; Jabbour, R.; et al. Development and validation of a new adenosine-independent index of stenosis severity from coronary wave-intensity analysis: Results of the ADVISE (ADenosine Vasodilator Independent Stenosis Evaluation) study. J. Am. Coll. Cardiol. 2012, 59, 1392–1402. [Google Scholar] [CrossRef] [PubMed]
- Nijjer, S.S.; Sen, S.; Petraco, R.; Mayet, J.; Francis, D.P.; Davies, J.E. The Instantaneous wave-Free Ratio (iFR) pullback: A novel innovation using baseline physiology to optimise coronary angioplasty in tandem lesions. Cardiovasc. Revasc. Med. 2015, 16, 167–171. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.; Liao, W.; Low, H. Numerical simulation of turbulent flow through series stenoses. Int. J. Numer. Methods Fluids 2003, 42, 717–740. [Google Scholar] [CrossRef]
- Liu, X.; Peng, C.; Xia, Y.; Gao, Z.; Xu, P.; Wang, X.; Xian, Z.; Yin, Y.; Jiao, L.; Wang, D.; et al. Hemodynamics analysis of the serial stenotic coronary arteries. Biomed. Eng. Online 2017, 16, 127. [Google Scholar] [CrossRef]
- Chen, X.; Gao, Y.; Lu, B.; Jia, X.; Zhong, L.; Kassab, G.S.; Tan, W.; Huo, Y. Hemodynamics in coronary arterial tree of serial stenoses. PLoS ONE 2016, 11, e0163715. [Google Scholar] [CrossRef] [PubMed]
- Hunt, J.C.; Wray, A.A.; Moin, P. Eddies, Streams, and Convergence Zones in Turbulent Flows. In Proceedings of the Summer Program 1988; Center for Turbulence Research: Stanford, CA, USA, 1988. [Google Scholar]
- Waller, B.F. The eccentric coronary atherosclerotic plaque: Morphologic observations and clinical relevance. Clin. Cardiol. 1989, 12, 14–20. [Google Scholar] [CrossRef]
- Pijls, N.H.; De Bruyne, B.; Bech, G.J.; Liistro, F.; Heyndrickx, G.R.; Bonnier, H.J.; Koolen, J.J. Coronary pressure measurement to assess the hemodynamic significance of serial stenoses within one coronary artery: Validation in humans. Circulation 2000, 102, 2371–2377. [Google Scholar] [CrossRef]
- Ohara, T.; Toyoda, K.; Otsubo, R.; Nagatsuka, K.; Kubota, Y.; Yasaka, M.; Naritomi, H.; Minematsu, K. Eccentric stenosis of the carotid artery associated with ipsilateral cerebrovascular events. Am. J. Neuroradiol. 2008, 29, 1200–1203. [Google Scholar] [CrossRef] [PubMed]
- Kern, M.J.; Lerman, A.; Bech, J.W.; De Bruyne, B.; Eeckhout, E.; Fearon, W.F.; Higano, S.T.; Lim, M.J.; Meuwissen, M.; Piek, J.J.; et al. Physiological assessment of coronary artery disease in the cardiac catheterization laboratory. Circulation 2006, 114, 1321–1341. [Google Scholar] [CrossRef]
- Sinnott, M.; Cleary, P.W.; Prakash, M. An investigation of pulsatile blood flow in a bifurcation artery using a grid-free method. In Proceedings of the Fifth International Conference on CFD in the Process Industries (CSIRO), Melbourne, Australia, 13–15 December 2006. [Google Scholar]
- Gribbin, B.; Pickering, T.G.; Sleight, P.; Peto, R. Effect of age and high blood pressure on barorefiex sensitivity in man. Circ. Res. 1971, 29, 424–431. [Google Scholar] [CrossRef] [PubMed]
- Olufsen, M.S.; Peskin, C.S.; Kim, W.Y.; Pedersen, E.M.; Nadim, A.; Larsen, J. Numerical simulation and experimental validation of blood flow in arteries with structured-tree outflow conditions. Ann. Biomed. Eng. 2000, 28, 1281–1299. [Google Scholar] [CrossRef]
- Perktold, K.; Peter, R.O.; Resch, M.; Langs, G. Pulsatile non-Newtonian blood flow in three-dimensional carotid bifurcation models: A numerical study of flow phenomena under different bifurcation angles. J. Biomed. Eng. 1991, 13, 507–515. [Google Scholar] [CrossRef]
- Noutchie, S.C.O. Flow of a Newtonian Fluid: The Case of Blood in Large Arteries. Master’s Thesis, University of South Africa, Pretoria, South Africa, November 2005. [Google Scholar]
- Temam, R. Navier—Stokes Equations; North-Holland: Amsterdam, The Netherlands, 1984; Volume 2. [Google Scholar]
- Mouza, A.; Skordia, O.D.; Tzouganatos, I.D.; Paras, S.V. A simplified model for predicting friction factors of laminar blood flow in small-caliber vessels. Fluids 2018, 3, 75. [Google Scholar] [CrossRef]
- Kapoor, N.; Fahsah, I.; Karim, R.; Jevans, A.J.; Leesar, M.A. Physiological assessment of renal artery stenosis: Comparisons of resting with hyperemic renal pressure measurements. Catheter. Cardiovasc. Interv. 2010, 76, 726–732. [Google Scholar] [CrossRef] [PubMed]
- Toth, G.G.; Johnson, N.P.; Jeremias, A.; Pellicano, M.; Vranckx, P.; Fearon, W.F.; Barbato, E.; Kern, M.J.; Pijls, N.H.; De Bruyne, B. Standardization of fractional flow reserve measurements. J. Am. Coll. Cardiol. 2016, 68, 742–753. [Google Scholar] [CrossRef]
- Bach, D.S. Echo/Doppler evaluation of hemodynamics after aortic valve replacement: Principles of interrogation and evaluation of high gradients. JACC Cardiovasc. Imaging 2010, 3, 296–304. [Google Scholar] [CrossRef]
- Barker, A.J.; van Ooij, P.; Bandi, K.; Garcia, J.; Albaghdadi, M.; McCarthy, P.; Bonow, R.O.; Carr, J.; Collins, J.; Malaisrie, S.C.; et al. Viscous energy loss in the presence of abnormal aortic flow. Magn. Reson. Med. 2014, 72, 620–628. [Google Scholar] [CrossRef]
- Gould, K.L. Pressure-flow characteristics of coronary stenoses in unsedated dogs at rest and during coronary vasodilation. Circ. Res. 1978, 43, 242–253. [Google Scholar] [CrossRef]
- Buchmann, N.A.; Jermy, M.C. Blood flow measurements in idealised and patient specific models of the human carotid artery. In Proceedings of the 14th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 7–10 July 2008. [Google Scholar]
- Govindaraju, K.; Viswanathan, G.N.; Badruddin, I.A.; Kamangar, S.; Salman Ahmed, N.J.; Al-Rashed, A.A. The influence of artery wall curvature on the anatomical assessment of stenosis severity derived from fractional flow reserve: A computational fluid dynamics study. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 1541–1549. [Google Scholar] [CrossRef]
- Lin, S.; Han, X.; Bi, Y.; Ju, S.; Gu, L. Fluid-structure interaction in abdominal aortic aneurysm: Effect of modeling techniques. BioMed Res. Int. 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Zheng, J.; Bach, R.; Tang, D. Influence of model boundary conditions on blood flow patterns in a patient specific stenotic right coronary artery. Biomed. Eng. Online 2015, 14, S6. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, Y.; Johnson, N.P.; Berry, C.; De Bruyne, B.; Gould, K.L.; Jeremias, A.; Oldroyd, K.G.; Pijls, N.H.J.; Fearon, W.F. CONTRAST Study Investigators. The influence of lesion location on the diagnostic accuracy of adenosine-free coronary pressure wire measurements. JACC Cardiovasc. Interv. 2016, 9, 2390–2399. [Google Scholar] [CrossRef] [PubMed]
- Pisters, R.; Ilhan, M.; Veenstra, L.F.; Gho, B.C.G.; Stein, M.; Hoorntje, J.C.A.; Rasoul, S. Instantaneous wave-free ratio and fractional flow reserve in clinical practice. Neth. Heart J. 2018, 1–8. [Google Scholar] [CrossRef] [PubMed]

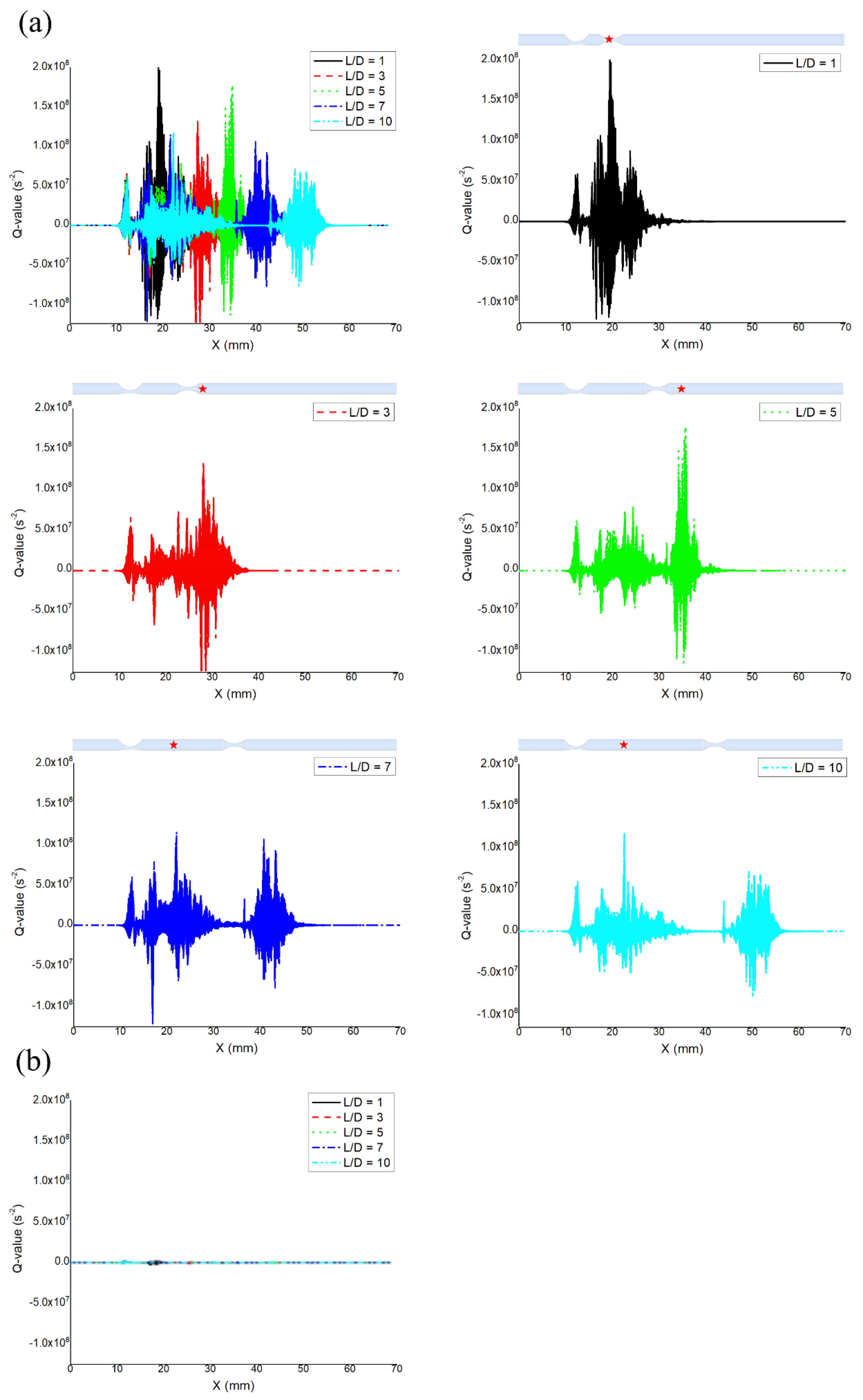
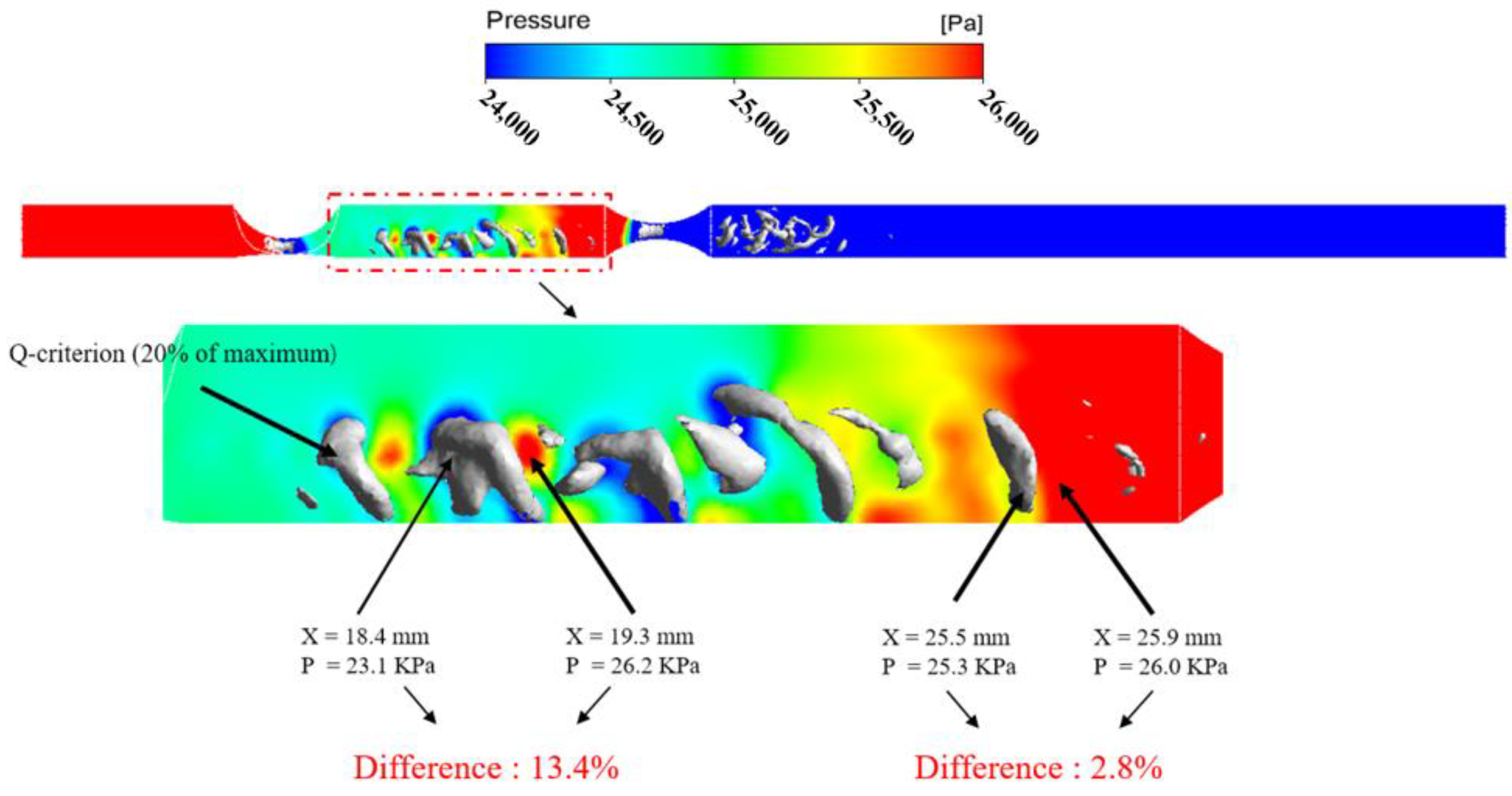
| Spacing Ratio (L/D) | FFR (1st Lesion/2nd Lesion) | iFR (1st Lesion/2nd Lesion) |
|---|---|---|
| 1 | 0.517/0.618 | 0.904/0.943 |
| 3 | 0.503/0.618 | 0.910/0.936 |
| 5 | 0.577/0.520 | 0.911/0.930 |
| 7 | 0.599/0.500 | 0.911/0.930 |
| 10 | 0.606/0.490 | 0.917/0.923 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, S.; Gu, L. Hemodynamic Interference of Serial Stenoses and Its Impact on FFR and iFR Measurements. Appl. Sci. 2019, 9, 279. https://doi.org/10.3390/app9020279
Ju S, Gu L. Hemodynamic Interference of Serial Stenoses and Its Impact on FFR and iFR Measurements. Applied Sciences. 2019; 9(2):279. https://doi.org/10.3390/app9020279
Chicago/Turabian StyleJu, Siyeong, and Linxia Gu. 2019. "Hemodynamic Interference of Serial Stenoses and Its Impact on FFR and iFR Measurements" Applied Sciences 9, no. 2: 279. https://doi.org/10.3390/app9020279
APA StyleJu, S., & Gu, L. (2019). Hemodynamic Interference of Serial Stenoses and Its Impact on FFR and iFR Measurements. Applied Sciences, 9(2), 279. https://doi.org/10.3390/app9020279






