Short-Term Deformability of Three-Dimensional Printable EVA-Modified Cementitious Mortars
Abstract
1. Introduction
2. Summary of the Author’s Previous Research
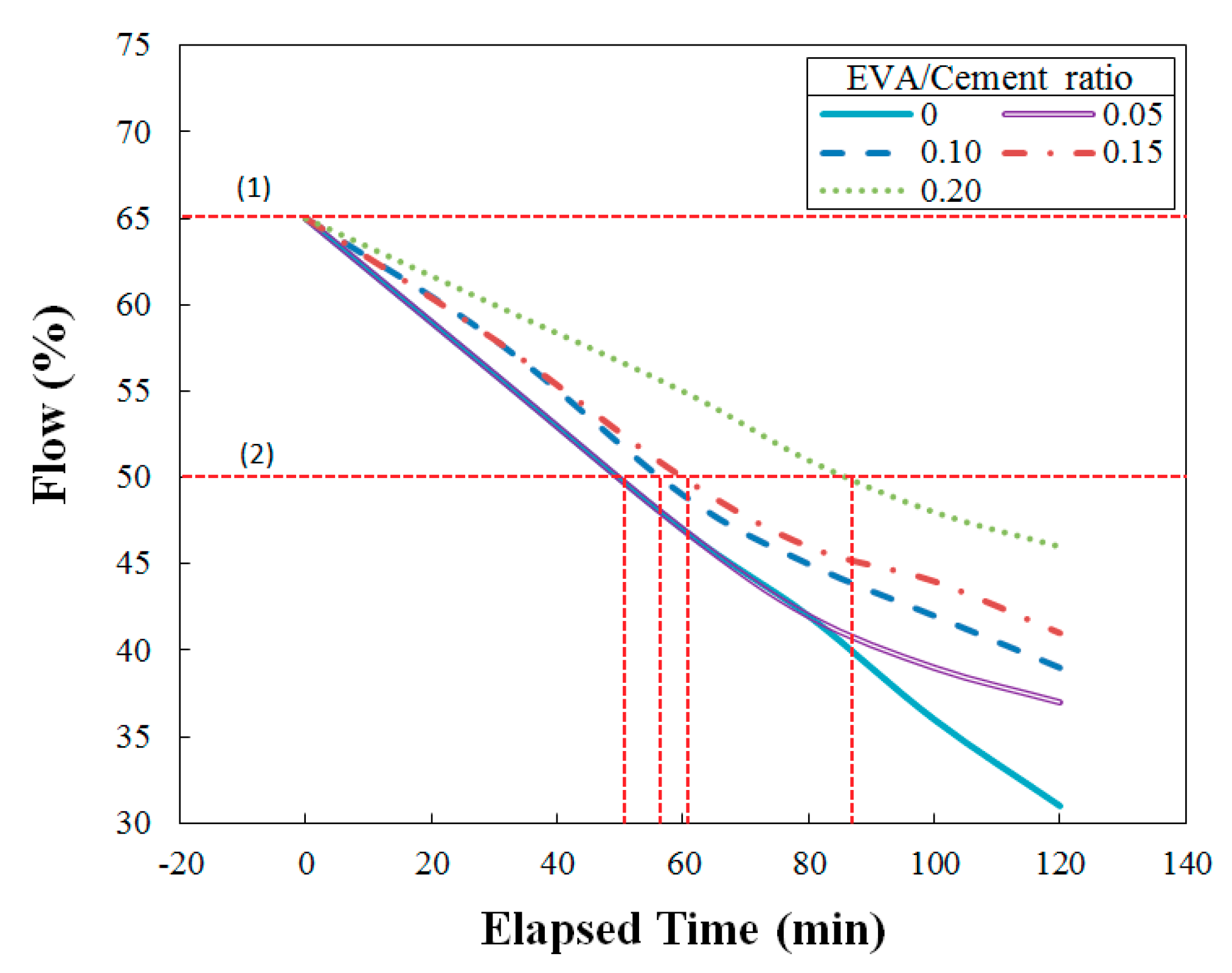
2.1. Flowability and Open Time
2.2. Buildability
3. Materials and Methods
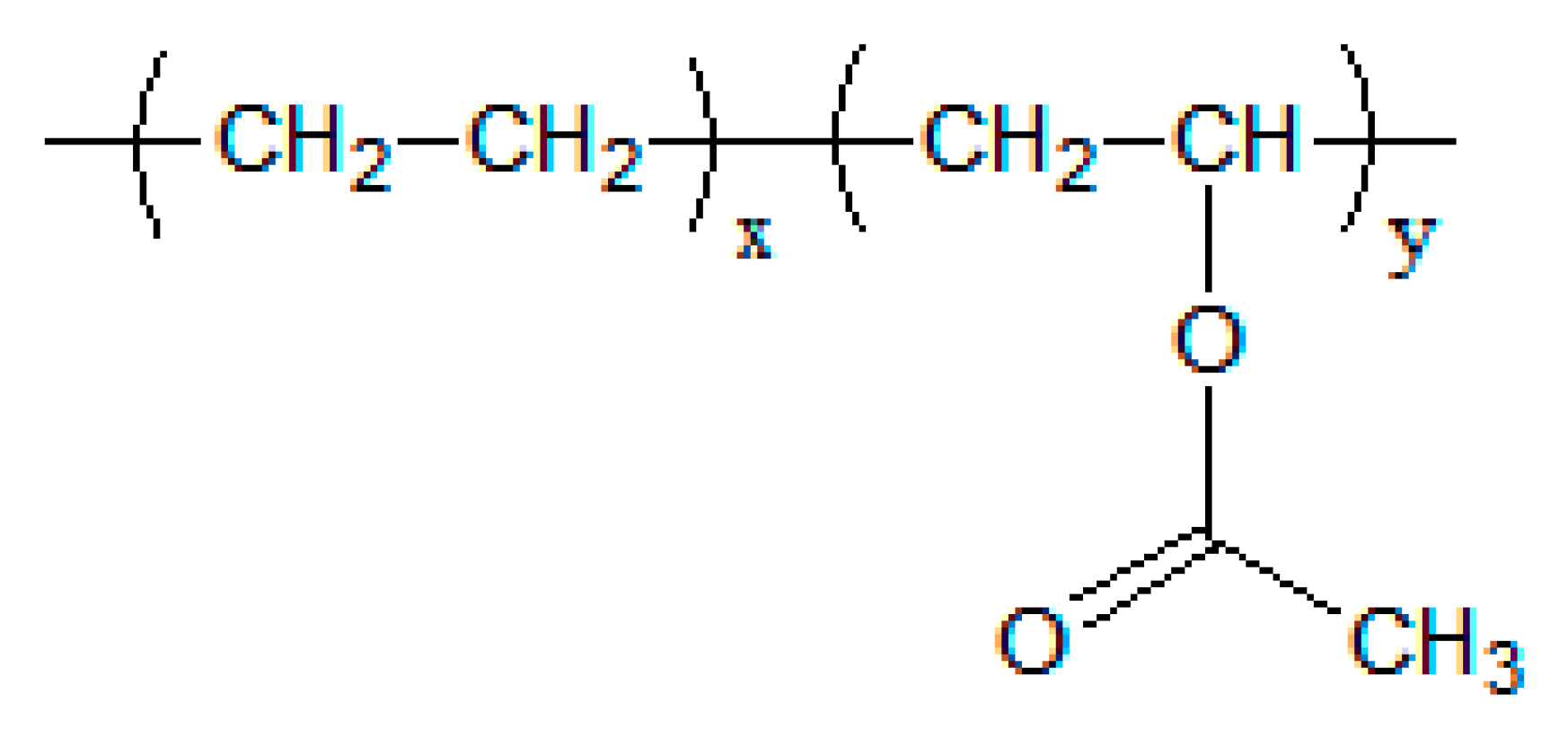
3.1. Materials
3.2. Method
3.2.1. Mixture
3.2.2. Preparation of Specimens
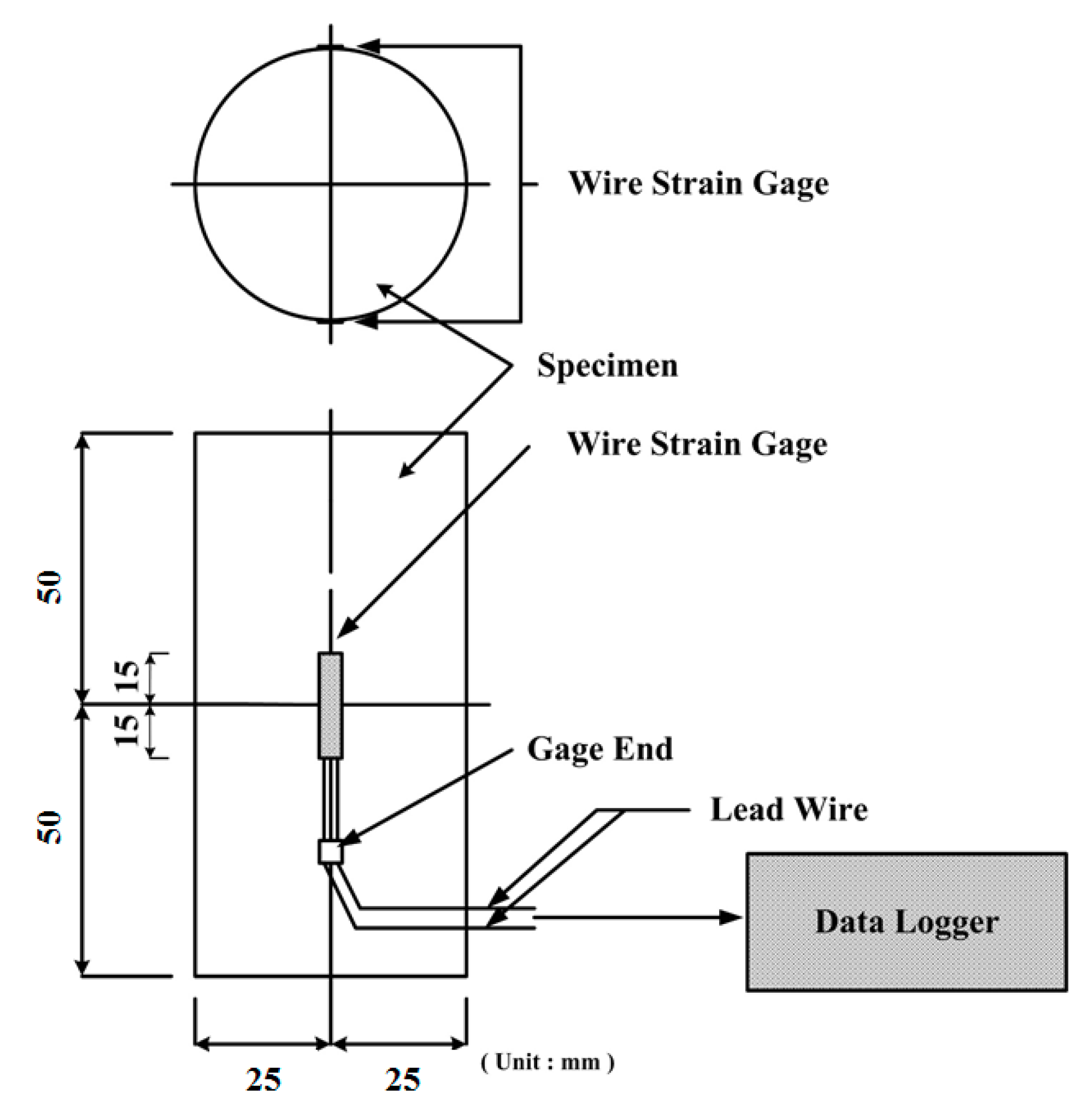
3.2.3. Test of Modulus of Elasticity
3.2.4. Test of Drying Shrinkage
3.2.5. Test of Thermal Expansion
4. Results and Discussion
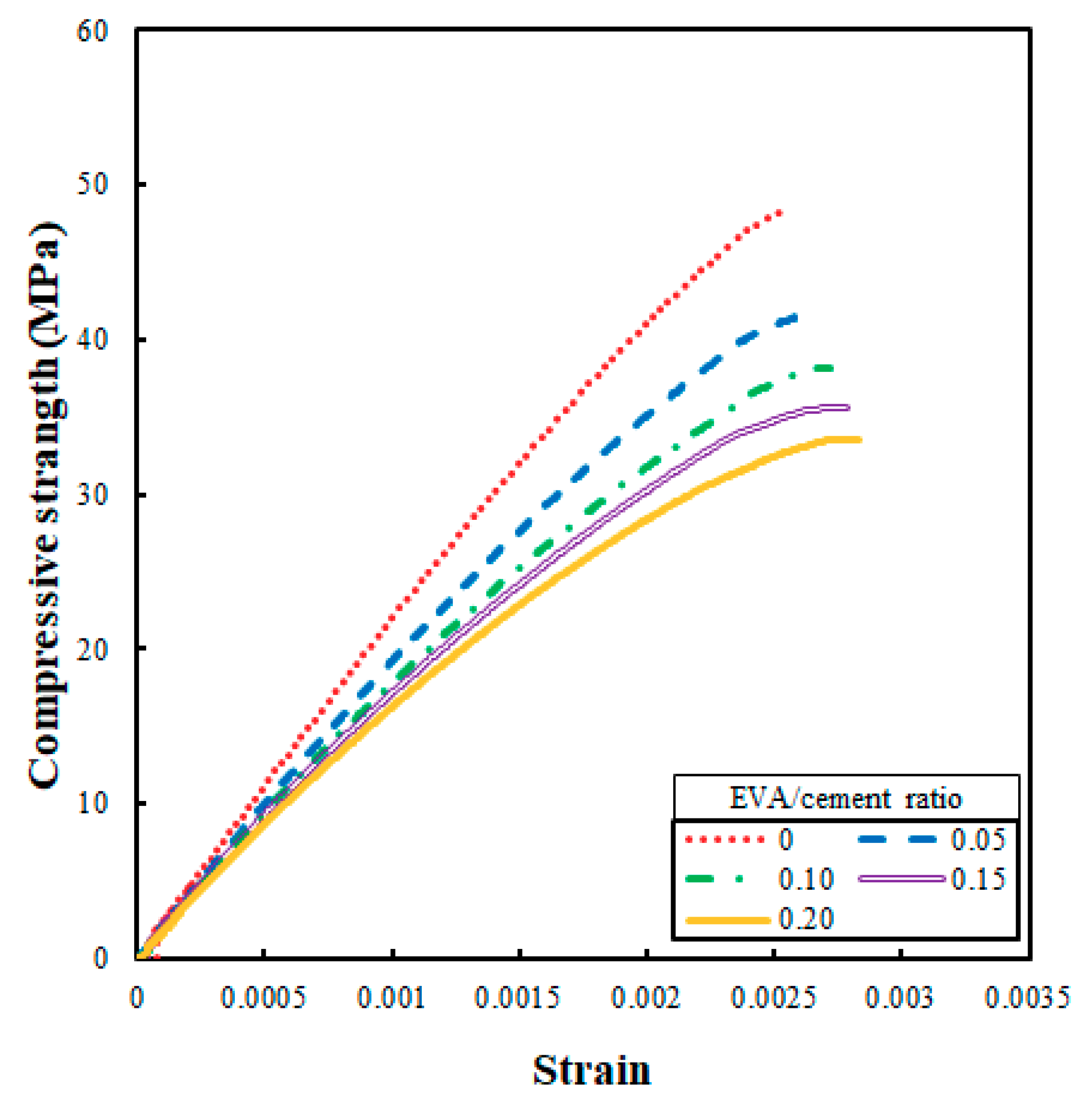
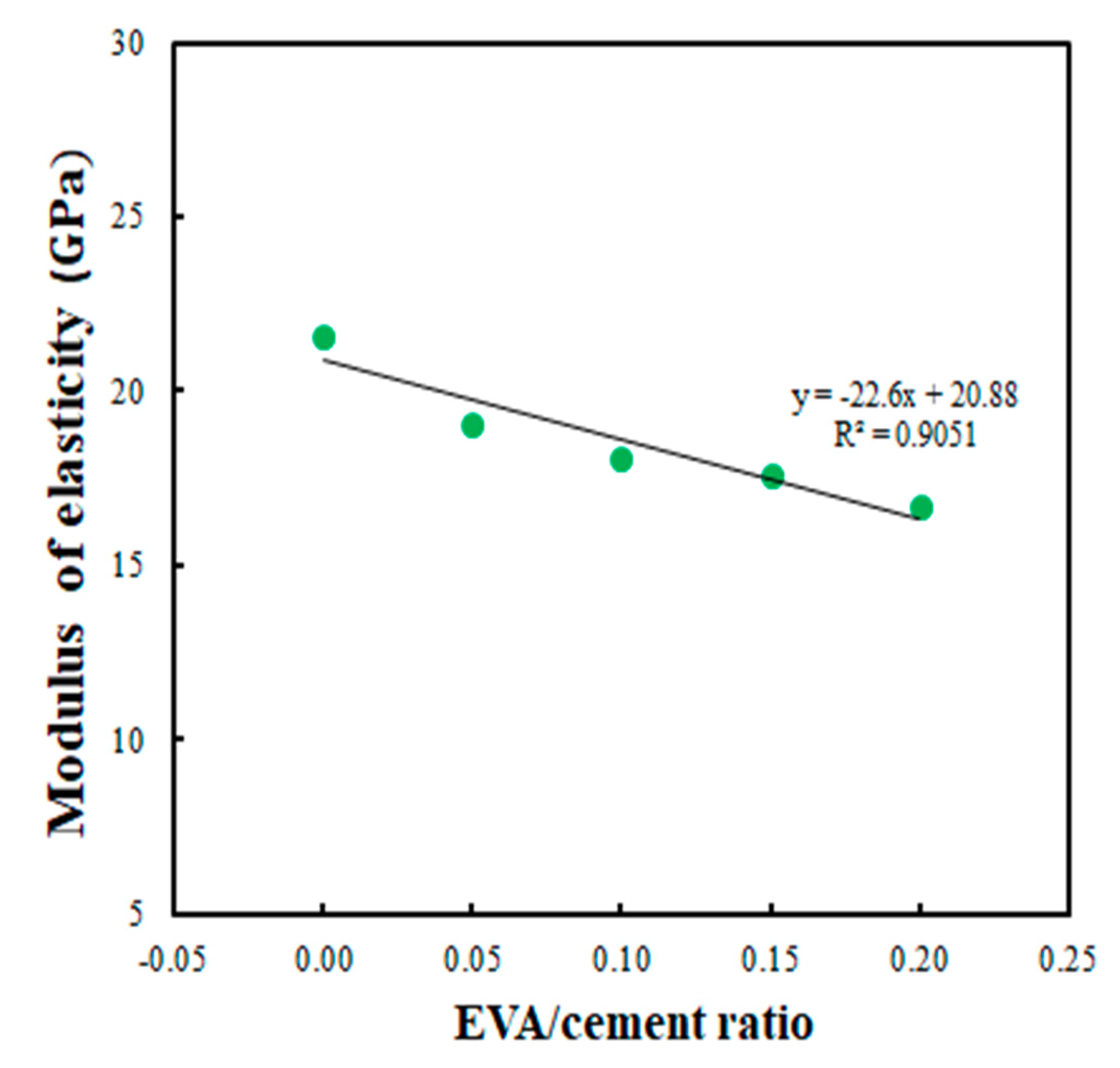
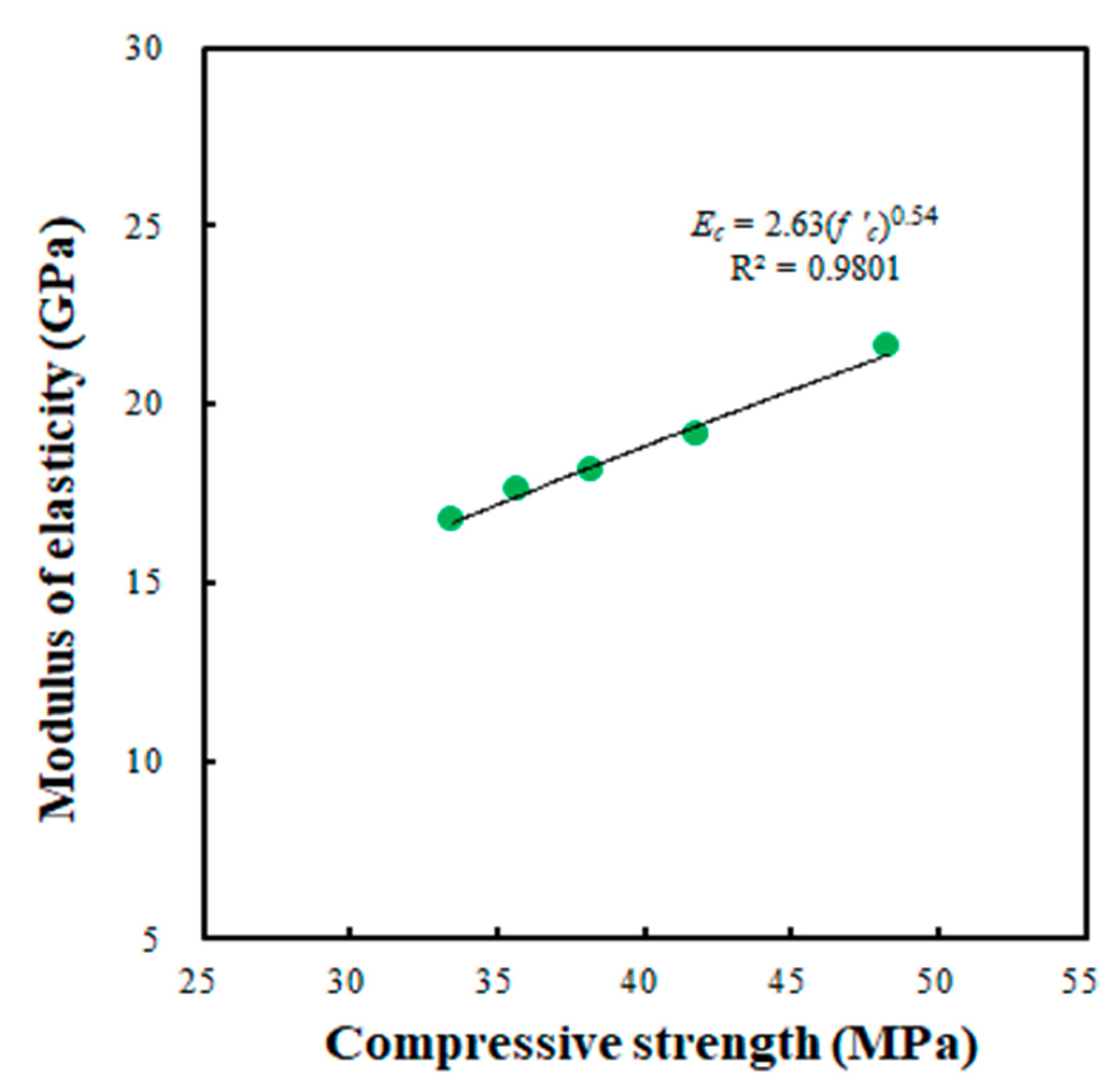
4.1. Stress–Strain Relationship and Modulus of Elasticity
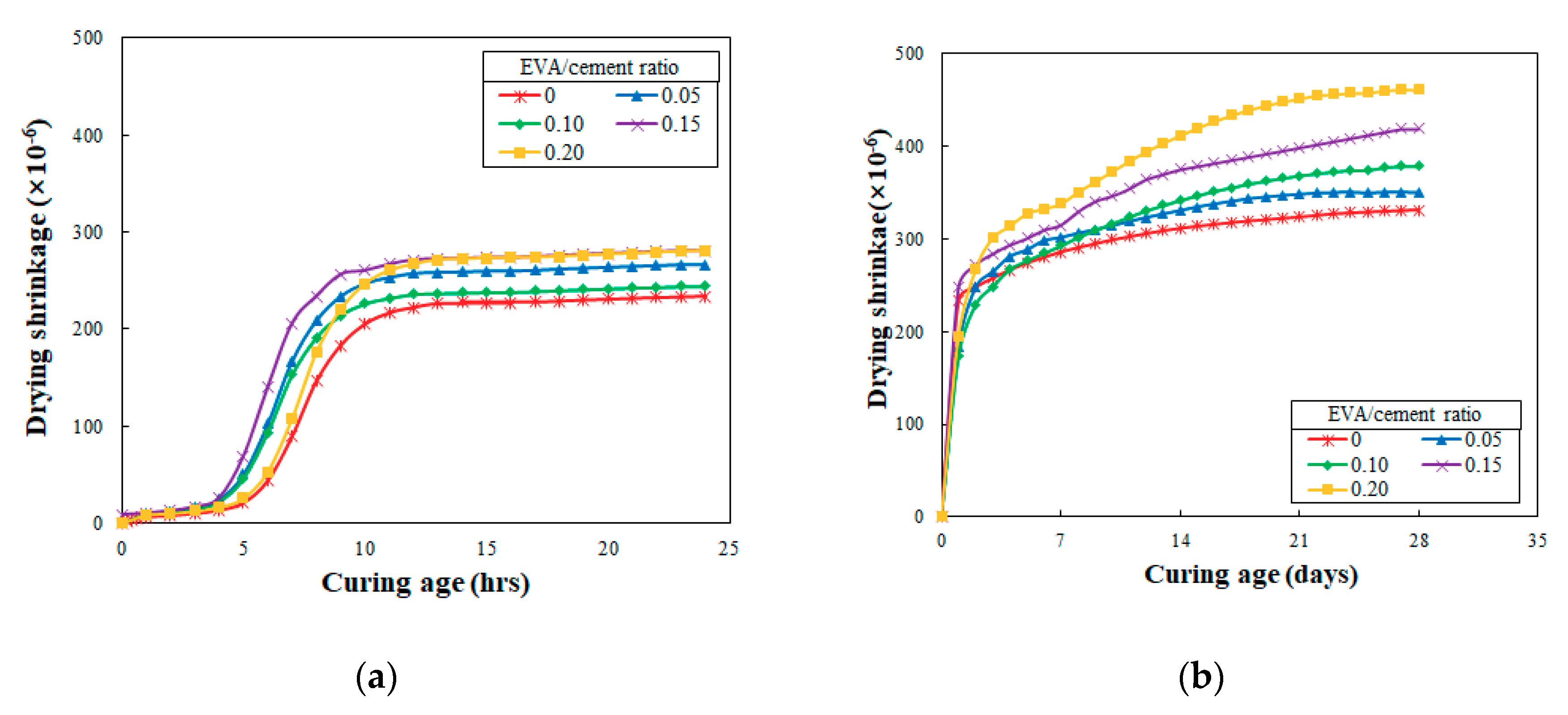
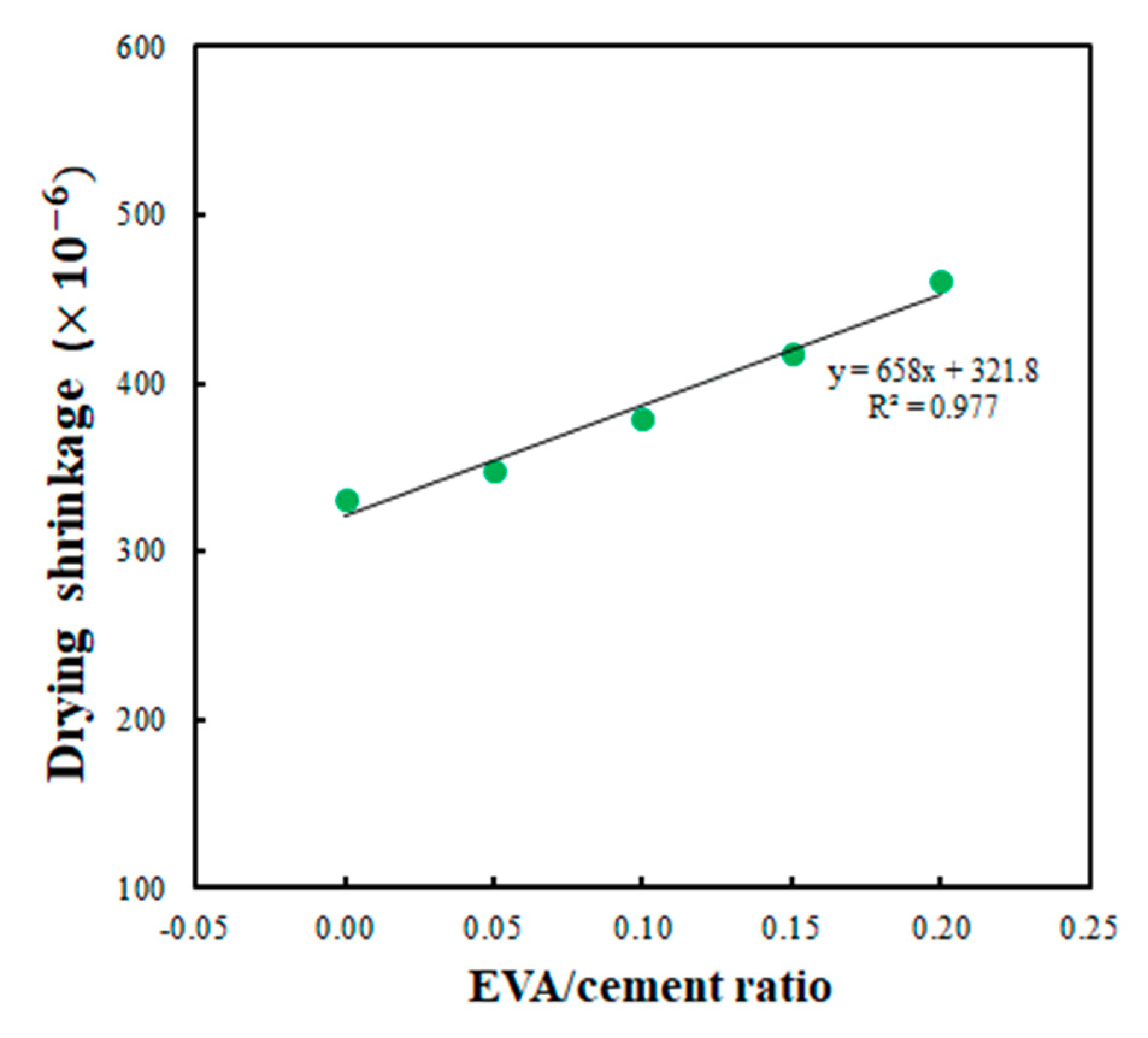
4.2. Drying Shrinkage
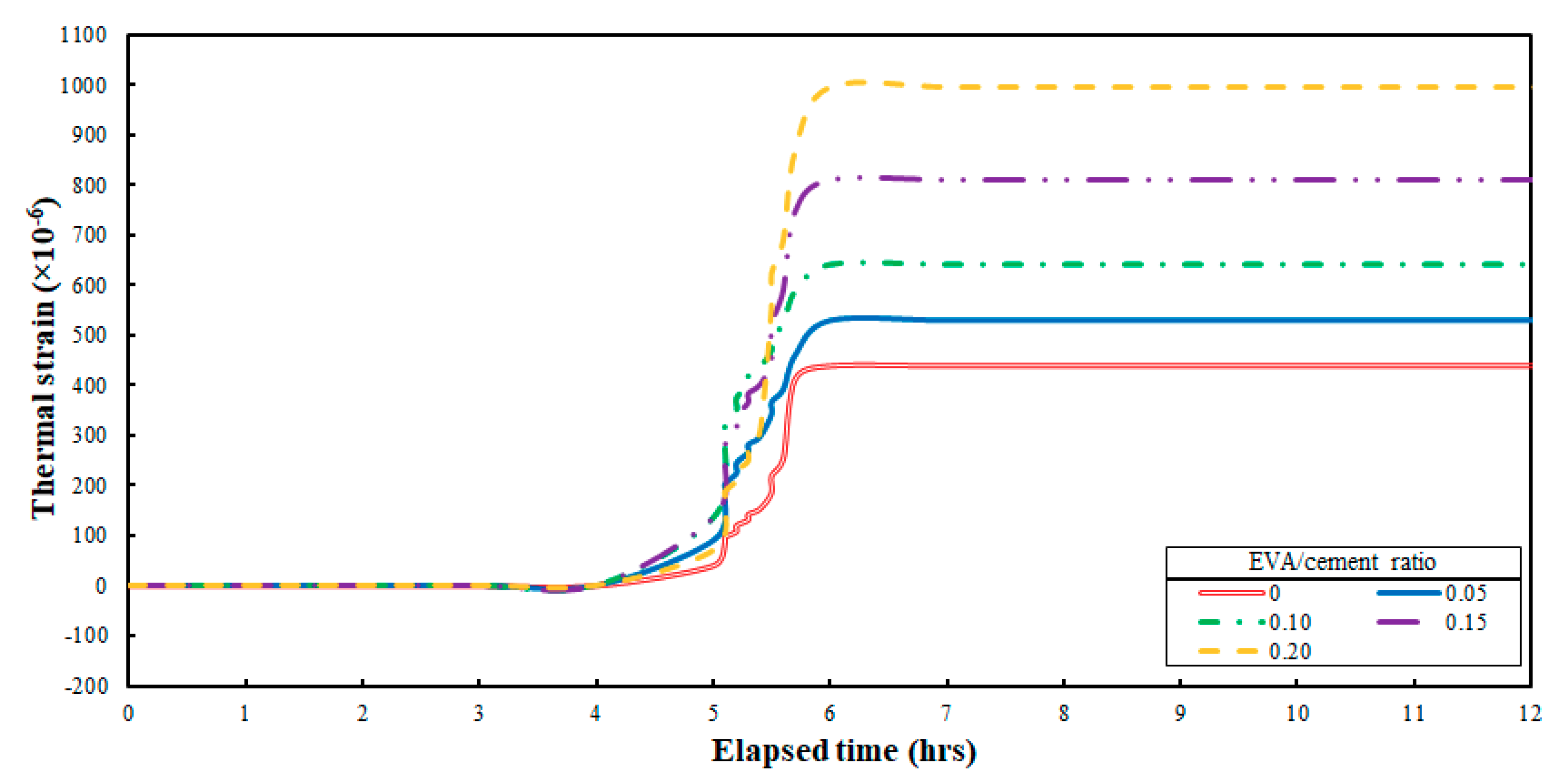
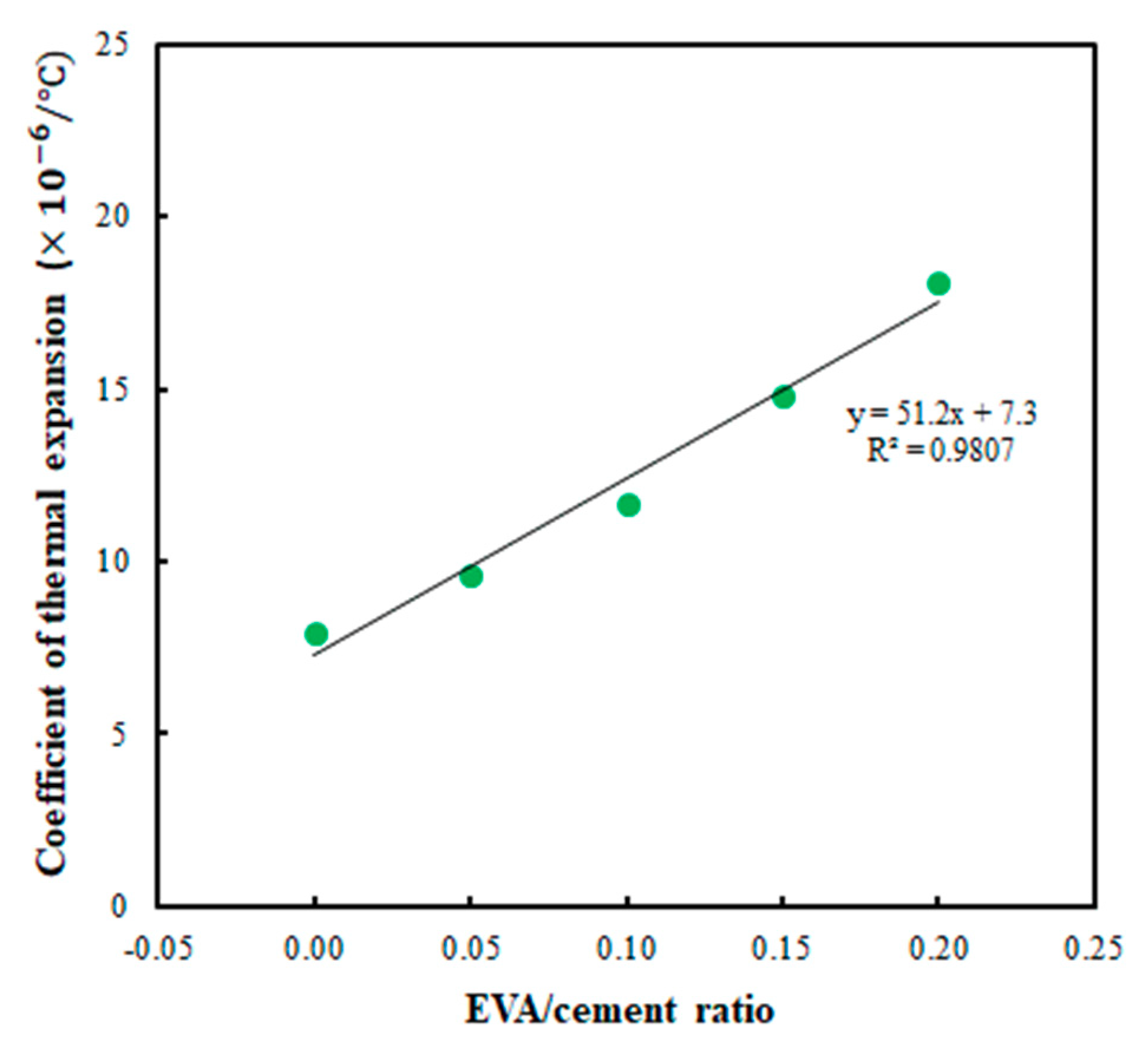
4.3. Coefficient of Thermal Expansion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Chinese Company Assembles 10 3D-Printed Concrete Houses in a Day for Less Than $5,000 Each. Available online: https://inhabitat.com/chinese-company-assembles-ten-3d-printed-concrete-houses-in-one-day-for-less-than-5000-each/ (accessed on 1 September 2019).
- Apis Cor and Gerdau to Print Homes Together on Earth and Beyond. Available online: https://www.apis-cor.com/apiscor-and-gerdau (accessed on 1 September 2019).
- TU/e and BAM Infra Get to Work on 3D Printed Concrete Bicycle Bridge. Available online: https://3dprint.com/178462/eindhoven-3d-printed-bridge/ (accessed on 1 September 2019).
- Nerella, V.N.; Mechtcherine, V. Studying the printability of fresh concrete for formwork-free concrete onsite 3D printing technology (CONPrint3D). In 3D Concrete Printing Technology, 1st ed.; Sanjayan, J.G., Nazari, A., Nematollahi, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 16, pp. 333–347. [Google Scholar]
- Rushing, T.S.; Stynoski, P.B.; Barna, L.A.; Al-Chaar, G.K.; Burroughs, J.F.; Shannon, J.D.; Kreiger, M.A.; Case, M.P. Investigation of concrete mixtures for additive construction. 3D concrete printing technology. In 3D Concrete Printing Technology, 1st ed.; Sanjayan, J.G., Nazari, A., Nematollahi, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 7, pp. 137–160. [Google Scholar]
- Khoshnevis, B. Automated Construction by Contour Crafting—Related Robotics and Information Technologies. Autom. Constr. 2004, 13, 5–19. [Google Scholar] [CrossRef]
- Tay, Y.W.D.; Panda, B.; Paul, S.C.; Noor Mohamed, N.A.; Tan, M.J.; Leong, K.F. 3D Printing Trends in Building and Construction Industry: A Review. Virtual Phys. Prot. 2017, 12, 261–276. [Google Scholar] [CrossRef]
- Hager, I.; Golonka, A.; Putanowicz, R. 3D Printing of Buildings and Building Components as the Future of Sustainable Construction? Proc. Eng. 2016, 151, 292–299. [Google Scholar] [CrossRef]
- Yeon, K.S.; Kim, K.K.; Yeon, J. Feasibility study of the use of polymer-modified cement composites as 3D concrete printing material. In Proceedings of the International Congress in Polymers in Concrete, Washington, DC, USA, 29 April–1 May 2018; Taha, M.R., Ed.; Springer: Berlin, Germany, 2018. [Google Scholar]
- Bentz, D.P.; Jones, S.Z.; Bentz, I.R.; Peltz, M.A. Towards the formulation of robust and sustainable cementitious binders for 3D additive construction by extrusion. In 3D Concrete Printing Technology, 1st ed.; Sanjayan, J.G., Nazari, A., Nematollahi, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 15, pp. 307–331. [Google Scholar]
- Kazmian, A.; Yuan, X.; Meier, R.; Khoshnevis, B. Performance-based testing portland cement concrete for construction-scale 3D printing. In 3D Concrete Printing Technology, 1st ed.; Sanjayan, J.G., Nazari, A., Nematollahi, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 2, pp. 13–35. [Google Scholar]
- Li, Z.; Wang, L.; Ma, G. Method for the enhancement of buildability and bending resistance of three-dimensional-printable tailing mortar. In 3D Concrete Printing Technology, 1st ed.; Sanjayan, J.G., Nazari, A., Nematollahi, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 8, pp. 161–180. [Google Scholar]
- Weng, Y.; Li, M.; Tan, M.J.; Qian, S. Design 3D printing cementitious materials via Fuller Thompson Theory and Marson-Percy Model. In 3D Concrete Printing Technology, 1st ed.; Sanjayan, J.G., Nazari, A., Nematollahi, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 14, pp. 281–306. [Google Scholar]
- Wu, Y.Y.; Ma, B.G.; Wang, J.; Zhang, F.C.; Jian, S.W. Study on Interface Properties of EVA-Modified Cement Mortar. Adv. Mater. Res. 2011, 250–253, 875–880. [Google Scholar] [CrossRef]
- Yeon, K.; Kim, K.K.; Yeon, J.; Lee, H.J. Fresh Properties of EVA-Modified Cementitious Mixtures for Use in Additive Construction via Extrusion. Materials 2019, 12, 2292. [Google Scholar] [CrossRef] [PubMed]
- Ohama, Y. Handbook of Polymer-Modified Concrete and Mortars, 1st ed.; Noyes Publications: Park Ridge, NJ, USA, 1995. [Google Scholar]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstructure, Properties, and Materials, 3rd ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- ASTM C109/C109M-02. Standard Test Method for Compressive Strength of Hydraulic Cement Mortars. Available online: https://www.astm.org/DATABASE.CART/HISTORICAL/C109C109M-02.htm (accessed on 1 September 2019).
- Ohama, Y.; Kan, S. Effects of Specimen Size on Strength and Drying Shrinkage of Polymer-Modified Concrete. Int. J. Cem. Compos. Lightweight Concr. 1982, 4, 229–233. [Google Scholar] [CrossRef]
- ASTM C469/C469M-14. Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression. Available online: https://www.astm.org/Standards/C469 (accessed on 1 September 2019).
- ASTM C596-01. Standard Test Method for Drying Shrinkage of Mortar Containing Hydraulic Cement. Available online: https://www.astm.org/DATABASE.CART/HISTORICAL/C596-01.htm (accessed on 1 September 2019).
- ASTM C531–18. Standard Test Method for Linear Shrinkage and Coefficient of Thermal Expansion of Chemical-Resistant Mortars, Grouts, Monolithic Surfacings, and Polymer Concretes. Available online: https://www.astm.org/Standards/C531.htm (accessed on 1 September 2019).
- Neville, A.M. Properties of Concrete, 4th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Chandra, S.; Ohama, Y. Polymers in Concrete, 1st ed.; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Buswell, R.A.; Leal de Silva, W.R.; Jones, S.Z.; Dirrenberger, J. 3D Printing Using Concrete Extrusion: A Road Map for Research. Cem. Concr. Res. 2018, 112, 37–49. [Google Scholar] [CrossRef]
- Lea, F.M. The Chemistry of Cement and Concrete, 3rd ed.; Chemical Publishing Company: New York, NY, USA, 1970. [Google Scholar]
- Weng, T.L.; Lin, W.T.; Li, C.H. Properties Evaluation of Repair Mortars Containing EVA and VA/VeoVa Polymer Powders. Polym. Polym. Compos. 2017, 25, 77–86. [Google Scholar] [CrossRef]
- Kardon, J.B. Polymer-Modified Concrete: Review. J. Mater. Civ. Eng. 1997, 9, 85–92. [Google Scholar] [CrossRef]
- Kawano, T. Studies on the mechanism of reducing drying shrinkage of cement mortar modified by rubber latex. In Proceedings of the Third International Congress on Polymers in Concrete, Koriyama, Japan, 13–15 May 1981; Transport Research Laboratory: Wokingham, UK, 1981. [Google Scholar]
- Kim, W.; Ohama, Y.; Demura, K. Drying Shrinkage Reduction of Polymer-Modified Mortars Using Redispersible Polymer Powder by Use of Shrinkage-Reducing Agents. J. Soc. Mater. Sci. Jap. 1997, 46, 84–88. [Google Scholar] [CrossRef]




| Density (g/cm3) | Specific Surface (cm2/g) | Chemical Composition (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| CaO | SiO2 | Al2O3 | Fe2O3 | SO3 | MgO | Ig. loss | ||
| 3.14 | 3630 | 64.10 | 17.00 | 4.44 | 3.88 | 2.97 | 2.34 | 2.76 |
| Size(mm) | Apparent Density | Purity (%) | Water Content (%) |
|---|---|---|---|
| 0.08 | 1.57 | 97.3 | ≤0.1 |
| Density (g/cm3) | Specific Surface (cm2/g) | Chemical Composition (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| SiO2 | Al2O3 | CaO | Fe2O3 | SO3 | MgO | Ig. loss | ||
| 2.22 | 3651 | 51.90 | 21.80 | 8.25 | 6.93 | 1.02 | 0.89 | 3.20 |
| Bulk Density-Densified (kg/m3) | Specific Surface (cm2/g) | Chemical Composition (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| SiO2 | Al2O3 | CaO | MgO | Fe2O3 | SO3 | Ig. loss | ||
| 600–700 | 157,700 | 96.70 | 0.29 | 0.25 | 0.15 | 0.10 | - | 2.39 |
| Specific Gravity (20 °C) | pH | Alkali (%) | Chloride (%) |
|---|---|---|---|
| 1.05 ± 0.05 | 5.0 ± 2.0 | ≤0.01 | ≤0.01 |
| Appearance | Bulk Density (kg/m3) | Moisture Content (%) | Particle Size (0.074 mm, %) |
|---|---|---|---|
| White powder | 430 | ≤12 | ≥95 |
| Solids Content (%) | Ash Content (%) | Bulk Density (kg/m3) | Particle Size after Redispersion (μm) | Minimum Film Forming Temp (°C) | Protective Colloid |
|---|---|---|---|---|---|
| 98–100 | 9–13 | 470–570 | 0.5–8.0 | 4 | Polyvinyl alcohol (PVA) |
| EVA/Cement Ratio | W/C Ratio | EVA | Cement | Water | Silica Sand | Fly Ash | Silica Fume | Super- Plasticizer | Viscosity Modifying Agent |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.45 | 0 | 642 | 289 | 1377 | 184 | 92 | 6 | 0.3 |
| 0.05 | 0.46 | 32 | 638 | 294 | 1368 | 182 | 91 | 6 | 0.3 |
| 0.10 | 0.51 | 63 | 635 | 324 | 1360 | 181 | 91 | 6 | 0.3 |
| 0.15 | 0.52 | 95 | 631 | 328 | 1351 | 180 | 90 | 6 | 0.3 |
| 0.20 | 0.55 | 125 | 627 | 345 | 1343 | 179 | 90 | 6 | 0.3 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeon, J. Short-Term Deformability of Three-Dimensional Printable EVA-Modified Cementitious Mortars. Appl. Sci. 2019, 9, 4184. https://doi.org/10.3390/app9194184
Yeon J. Short-Term Deformability of Three-Dimensional Printable EVA-Modified Cementitious Mortars. Applied Sciences. 2019; 9(19):4184. https://doi.org/10.3390/app9194184
Chicago/Turabian StyleYeon, Jaeheum. 2019. "Short-Term Deformability of Three-Dimensional Printable EVA-Modified Cementitious Mortars" Applied Sciences 9, no. 19: 4184. https://doi.org/10.3390/app9194184
APA StyleYeon, J. (2019). Short-Term Deformability of Three-Dimensional Printable EVA-Modified Cementitious Mortars. Applied Sciences, 9(19), 4184. https://doi.org/10.3390/app9194184





