Optimal Strokes of Low Reynolds Number Linked-Sphere Swimmers
Abstract
1. Introduction
2. Swimming at LRN by Shape Changes-the Exterior Problem
Given a cyclic shape deformation that is specified by , solve the Stokes equations subject to:
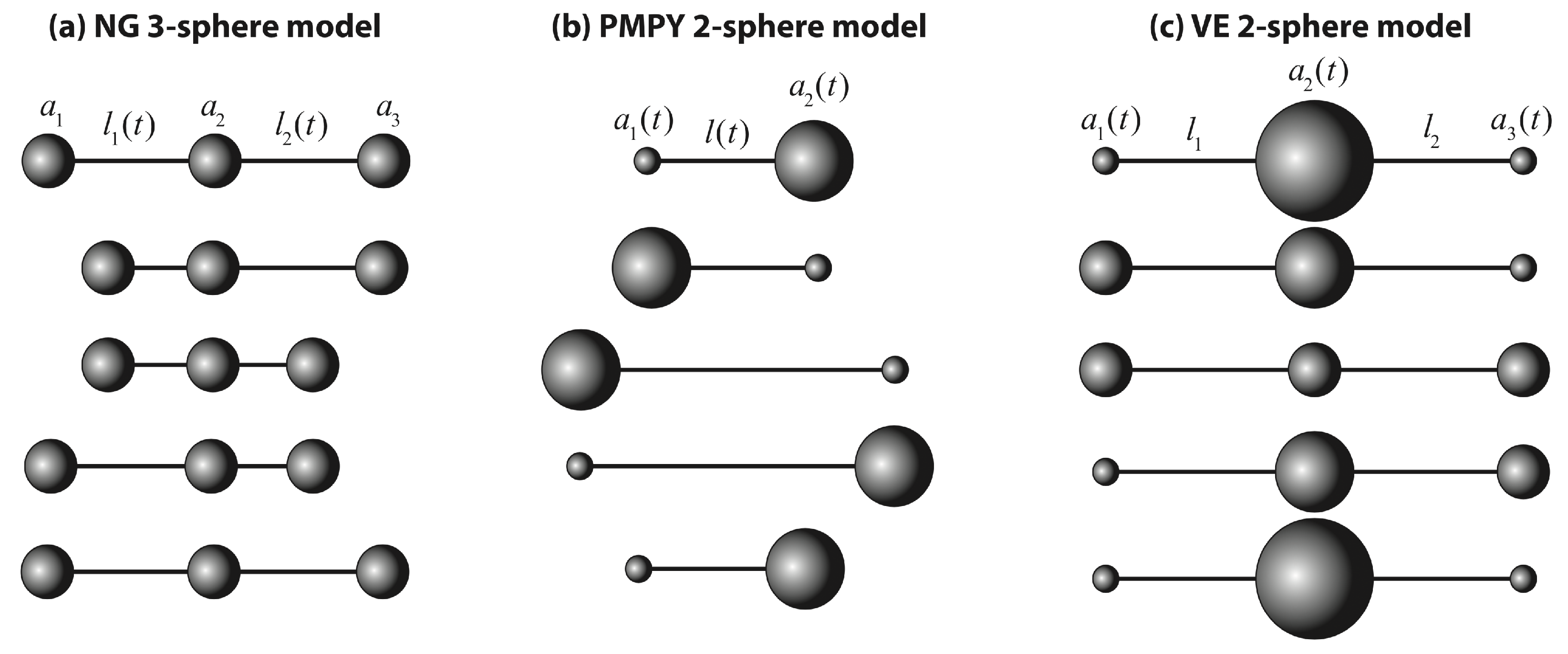
3. Linked-Sphere LRN Swimmers
3.1. Fundamental Solutions for Translating and Radially Deforming Spheres
3.2. Non-Dimensionalization of the System
3.3. NG 3-Sphere Swimmer
3.4. PMPY 2-Sphere Swimmer
3.5. VE 3-Sphere Swimmer
4. Optimal Strokes of NG, PMPY and VE Swimmers
4.1. Euler–Lagrange Equation for Optimal Strokes of LRN Swimmers
Given an initial shape and a net translation , find the stroke in that minimizes the energy dissipation :
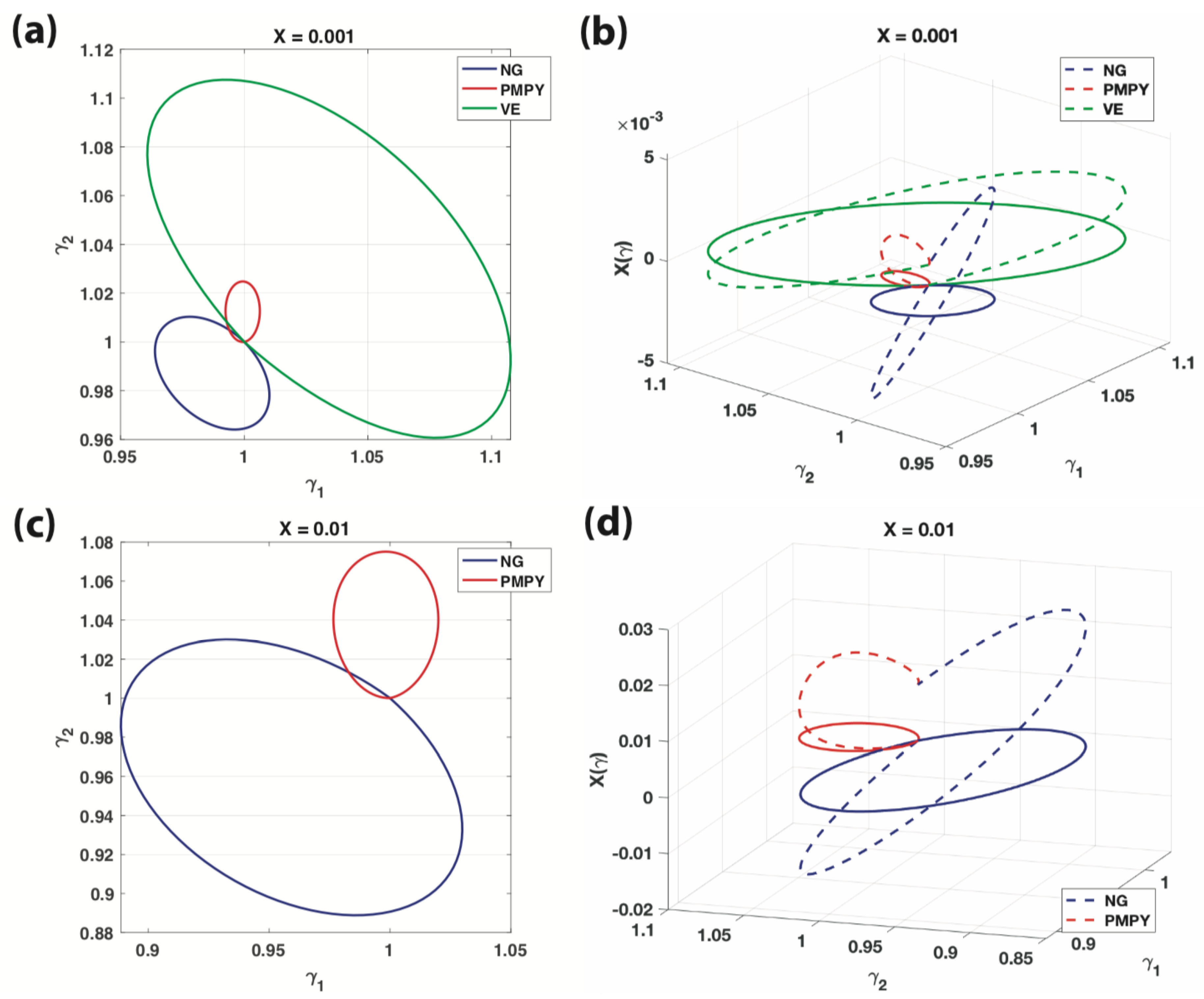
4.2. Numerical Results
- A PMPY model that adopts a mixed-mode of shape deformations is the most efficient among the three; next is NG and the last is VE, both of which adopt a single-mode of shape deformations (see Remark below).
- Single-loop geodesic strokes are more efficient than multi-loop geodesic strokes.
- The efficiency of a given LRN swimmer is almost the same for different X, as long as the optimal stroke is single-looped.
Comparing to single-mode shape deformations, mixed-modes of shape deformations, i.e., body stretching combined with mass transportation is more efficient when swimming at LRN.
5. Optimal Strokes of -Linked-Sphere LRN Swimmers
5.1. -Linked-Sphere NG Swimmers
5.2. -Linked-Sphere PMPY Swimmers
5.3. -Linked-Sphere NG and PMPY Swimmers with Widely Separated Spheres
6. Discussion
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| LRN | Low Reynolds Number |
| NG | Najafi-Golestanian 3-sphere model |
| PMPY | Pushmepullyou 2-sphere model |
| VE | Volume-exchange 3-sphere model |
| SM | Shooting method |
Appendix A. Shooting Method
Given initial shape and a net translation , find , s.t. .
| Algorithm 1:(Shooting Method) |
Let , choose a parameter N. Make an initial guess .
|
Appendix B. Geodesic Strokes
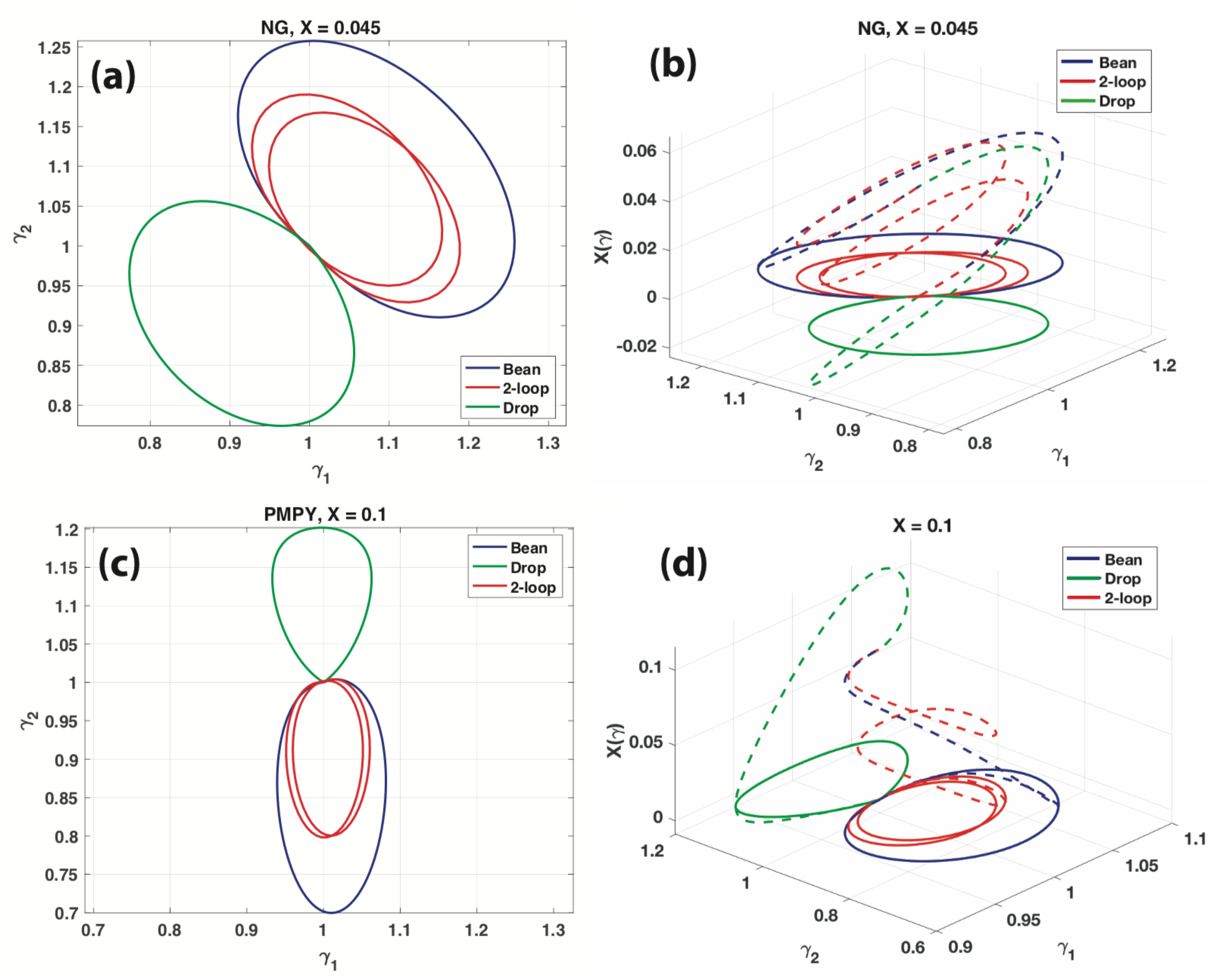
| NG 3-Sphere | Eff | |
|---|---|---|
| Bean | ||
| Drop | ||
| 2-loop (pretzel) |
| PMPY 2-Sphere | Eff | |
|---|---|---|
| Bean | ||
| Drop | ||
| 2-loop (pretzel) |

| PMPY 2-Sphere | Eff | |
|---|---|---|
| 1-loop | ||
| 3-loop | ||
| 5-loop |
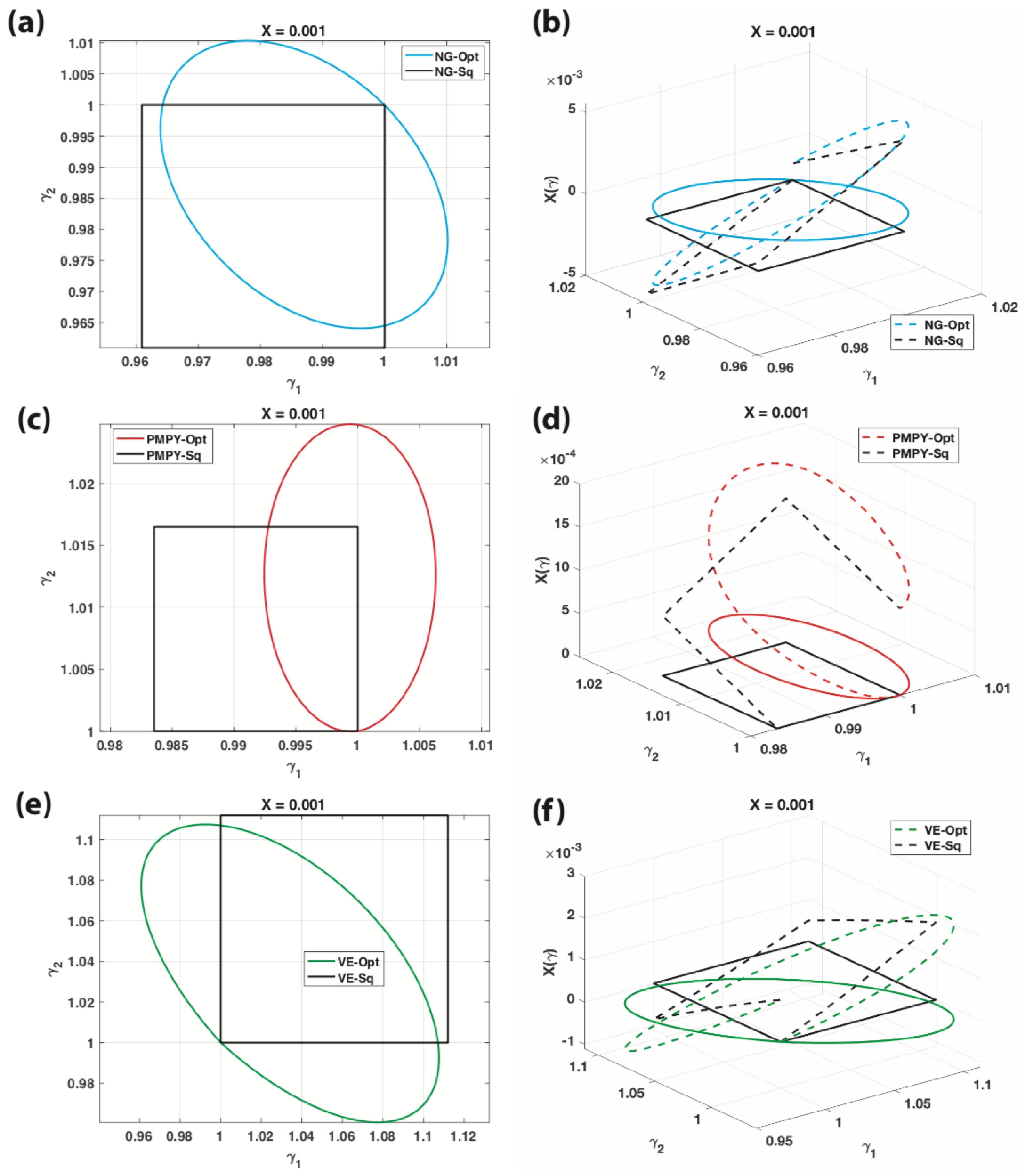
Appendix C. Comparison between Optimal and Square Strokes
| NG 3-Sphere | PMPY 2-Sphere | VE 3-Sphere | ||||
|---|---|---|---|---|---|---|
| Eff | Eff | Eff | ||||
| Optimal strokes () | ||||||
| Square strokes () | ||||||
References
- Purcell, E.M. Life at low Reynolds number. Am. J. Phys. 1977, 45, 3–11. [Google Scholar] [CrossRef]
- Lauga, E.; Willow, R.; DiLuzio, G.M. Whitesides, and Howard A. Stone. Swimming in circles: Motion of bacteria near solid boundaries. Biophys. J. 2006, 90, 400–412. [Google Scholar] [CrossRef]
- Rafaï, S.; Levan, J.; Philippe, P. Effective viscosity of microswimmer suspensions. Phys. Rev. Lett. 2010, 104, 098102. [Google Scholar] [CrossRef]
- Riedel, I.H.; Karsten, K.; Jonathon, H. A self-organized vortex array of hydrodynamically entrained sperm cells. Science 2005, 309, 300–303. [Google Scholar] [CrossRef]
- Sokolov, A.; Apodaca, M.M.; Grzybowski, B.A.; Aranson, I.S. Swimming bacteria power microscopic gears. Proc. Natl. Acad. Sci. USA 2010, 107, 969–974. [Google Scholar] [CrossRef]
- Van Haastert, P.J. Amoeboid cells use protrusions for walking, gliding and swimming. PLoS ONE 2011, 6, e27532. [Google Scholar] [CrossRef]
- Barry, N.P.; Mark, S.B. Dictyostelium amoebae and neutrophils can swim. Proc. Natl. Acad. Sci. USA 2010, 107, 11376–11380. [Google Scholar] [CrossRef]
- Franz, A.; Wood, W.; Martin, P. Fat body cells are motile and actively migrate to wounds to drive repair and prevent infection. Dev. Cell 2018, 44, 460–470. [Google Scholar] [CrossRef]
- Nelson, B.J.; Kaliakatsos, I.K.; Abbott, J.J. Microrobots for minimally invasive medicine. Annu. Rev. Biomed. Eng. 2010, 12, 55–85. [Google Scholar] [CrossRef]
- Najafi, A.; Golestanian, R. Simple swimmer at low Reynolds number: Three linked spheres. Phys. Rev. E 2004, 69, 062901. [Google Scholar] [CrossRef]
- Alexander, G.P.; Pooley, C.M.; Yeomans, J.M. Hydrodynamics of linked sphere model swimmers. J. Phys.-Condens. Matter 2008, 21, 204108. [Google Scholar] [CrossRef]
- Golestanian, R.; Ajdari, A. Analytic results for the three-sphere swimmer at low Reynolds number. Phys. Rev. E 2008, 77, 036308. [Google Scholar] [CrossRef]
- Curtis, M.P.; Gaffney, E.A. Three-sphere swimmer in a nonlinear viscoelastic medium. Phy. Rev. E 2013, 87, 043006. [Google Scholar] [CrossRef]
- Alouges, F.; Di Fratta, G. Parking 3-sphere swimmer I. Energy minimizing strokes. Discret. Contin. Dyn. B 2018, 23, 1797–1817. [Google Scholar] [CrossRef]
- Avron, J.E.; Kenneth, O.; Oaknin, D.H. Pushmepullyou: An efficient micro-swimmer. New J. Phys. 2005, 7, 234. [Google Scholar] [CrossRef]
- Rizvi, M.S.; Farutin, A.; Misbah, C. Three-bead steering microswimmers. Phys. Rev. E 2018, 97, 023102. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, J.; Othmer, H. Natural Locomotion in Fluids and on Surfaces: Swimming, Flying, and Sliding; chapter Models of low reynolds number swimmers inspired by cell blebbing; Springer: Berlin, Germany, 2012; pp. 185–195. [Google Scholar]
- Zhang, S.; Or, Y.; Murray, R.M. Experimental demonstration of the dynamics and stability of a low Reynolds number swimmer near a plane wall. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 1013–1041. [Google Scholar]
- Or, Y.; Zhang, S.; Murray, R.M. Dynamics and stability of low-Reynolds-number swimming near a wall. Siam J. Appl. Dyn. Syst. 2011, 10, 1013–1041. [Google Scholar] [CrossRef][Green Version]
- Saadat, M.; Mirzakhanloo, M.; Shen, J.; Tomizuka, M.; Alam, M.R. The Experimental Realization of an Artificial Low-Reynolds-Number Swimmer with Three-Dimensional Maneuverability. arXiv 2019, arXiv:1905.05893. [Google Scholar]
- Kadam, S.; Joshi, K.; Gupta, N.; Katdare, P.; Banavar, R. Trajectory tracking using motion primitives for the purcell’s swimmer. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 3246–3251. [Google Scholar]
- Alouges, F.; Antonio, D.; Aline, L. Optimal strokes for low Reynolds number swimmers: An example. J. Nonlinear Sci. 2008, 18, 277–302. [Google Scholar] [CrossRef]
- Alouges, F.; Antonio, D.; Lefebvre, A. Optimal strokes for axisymmetric microswimmers. Eur. Phys. J. E 2009, 28, 279–284. [Google Scholar] [CrossRef]
- Alouges, F.; DeSimone, A.; Heltai, L. Numerical strategies for stroke optimization of axisymmetric microswimmers. Math. Mod. Meth. Appl. Sci. 2011, 21, 361–387. [Google Scholar] [CrossRef]
- Avron, J.E.; Gat, O.; Kenneth, O. Optimal swimming at low Reynolds numbers. Phys. Rev. Lett. 2004, 93, 186001. [Google Scholar] [CrossRef] [PubMed]
- Avron, J.E.; Raz, O. A geometric theory of swimming: Purcell’s swimmer and its symmetrized cousin. New J. Phys. 2008, 10, 063016. [Google Scholar] [CrossRef]
- Blake, J.R. Self propulsion due to oscillations on the surface of a cylinder at low Reynolds number. B Aust. Math. Soc. 1971, 5, 255–264. [Google Scholar] [CrossRef]
- Chambrion, T.; Giraldi, L.; Munnier, A. Optimal strokes for driftless swimmers: A general geometric approach. ESAIM Control Optim. Calc. 2019, 25, 6. [Google Scholar] [CrossRef]
- Ishimoto, K.; Gaffney, E.A. Swimming efficiency of spherical squirmers: Beyond the Lighthill theory. Phys. Rev. E 2014, 90, 012704. [Google Scholar] [CrossRef]
- Lighthill, M.J. On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Math. 1952, 5, 109–118. [Google Scholar] [CrossRef]
- Lohéac, J.; Scheid, J.-F.; Tucsnak, M. Controllability and time optimal control for low Reynolds numbers swimmers. Acta Appl. Math. 2013, 123, 175–200. [Google Scholar] [CrossRef]
- Lohéac, J.; Munnier, A. Controllability of 3D low Reynolds number swimmers. ESAIM Control Optim. Cacl. 2014, 20, 236–268. [Google Scholar] [CrossRef]
- Shapere, A.; Wilczek, F. Efficiencies of self-propulsion at low Reynolds number. J. Fluid Mech. 1989, 198, 587–599. [Google Scholar] [CrossRef]
- Tsang, A.C.H.; Tong, P.W.; Nallan, S.; Pak, O.S. Self-learning how to swim at low Reynolds number. arXiv 2019, arXiv:1808.07639. [Google Scholar]
- Shapere, A.; Wilczek, F. Geometry of self-propulsion at low Reynolds number. J. Fluid Mech. 1989, 198, 557–585. [Google Scholar] [CrossRef]
- Pozrikidis, C. Boundary Integral and Singularity Methods for Linearized Viscous Flow; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Kim, S.; Karrila, S.J. Microhydrodynamics: Principles and Selected Applications; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Liang, Z.; Gimbutas, Z.; Greengard, L.; Huang, J.; Jiang, S. A fast multipole method for the Rotne–Prager–Yamakawa tensor and its applications. J. Comput. Phys. Mech. 2014, 234, 133–139. [Google Scholar] [CrossRef]
- Wajnryb, E.; Mizerski, K.A.; Zuk, P.J.; Szymczak, P. Generalization of the Rotne–Prager–Yamakawa mobility and shear disturbance tensors. J. Fluid Mech. 2013, 731, R3. [Google Scholar] [CrossRef]
- Wang, Q.; Othmer, H.G. Analysis of a model microswimmer with applications to blebbing cells and mini-robots. J. Math. Biol. 2018, 76, 1699–1763. [Google Scholar] [CrossRef] [PubMed]
- Yamakawa, H. Transport properties of polymer chains in dilute solution: Hydrodynamic interaction. J. Chem. Phys. 1970, 53, 436–443. [Google Scholar] [CrossRef]
- Zuk, P.J.; Wajnryb, E.; Mizerski, K.A.; Szymczak, P. Rotne–Prager–Yamakawa approximation for different-sized particles in application to macromolecular bead models. J. Fluid Mech. 2014, 741, 436–443. [Google Scholar] [CrossRef]
- Cherman, A.; Delgado, J.; Duda, F.; Ehlers, K.; Koiller, J.; Montgomery, R. Low Reynolds number swimming in two dimensions. In Hamiltonian Systems and Celestial Mechanics: (HAMSYS–98); World Scientific: Singapore, 2000; pp. 32–62. [Google Scholar]
- Leshansky, A.M.; Kenneth, O.; Gat, O.; Avron, J.E. A frictionless microswimmer. New J. Phys. 2007, 9, 145. [Google Scholar] [CrossRef]
- Nasouri, B.; Vilfan, A.; Golestanian, R. Efficiency limits of the three-sphere swimmer. arXiv 2019, arXiv:1905.06510. [Google Scholar] [CrossRef]
- Elgeti, J.; Winkler, R.G.; Gompper, G. Physics of microswimmers—Single particle motion and collective behavior: A review. Rep. Prog. Phys. 2015, 78, 056601. [Google Scholar] [CrossRef]
- Hancock, G.J. The self-propulsion of microscopic organisms through liquids. Proc. R. Soc. Lond. A 1953, 217, 96–121. [Google Scholar]
- Higdon, J.J.L. The hydrodynamics of flagellar propulsion: Helical waves. J. Fluid Mech. 1979, 94, 331–351. [Google Scholar] [CrossRef]
- Lauga, E.; Powers, T.R. The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 2009, 72, 096601. [Google Scholar] [CrossRef]
- Patteson, A.E.; Gopinath, A.; Goulian, M.; Arratia, P.E. Running and tumbling with E. coli in polymeric solutions. Sci. Rep. 2015, 5, 15761. [Google Scholar] [CrossRef] [PubMed]
- Phan-Thien, N.; Tran-Cong, T.; Ramia, M. A boundary-element analysis of flagellar propulsion. J. Fluid Mech. 1987, 184, 533–549. [Google Scholar] [CrossRef]
- Sowa, Y.; Richard, M.B. Bacterial flagellar motor. Q. Rev. Biophys. 2008, 41, 103–132. [Google Scholar] [CrossRef] [PubMed]
- Taylor, G.I. The action of waving cylindrical tails in propelling microscopic organisms. Proc. R. Soc. Lond. 1952, 211, 225–239. [Google Scholar]
- Bae, A.J.; Eberhard, B. On the swimming of Dictyostelium amoebae. Proc. Natl. Acad. Sci. USA 2010, 107, E165–E166. [Google Scholar] [CrossRef]
- Wang, Q.; Othmer, H.G. The performance of discrete models of low reynolds number swimmers. Math. Biosci. Eng. 2015, 12, 1303–1320. [Google Scholar] [CrossRef]
- Farutin, A.; Rafaï, S.; Dysthe, D.K.; Duperray, A.; Peyla, P.; Misbah, C. Amoeboid swimming: A generic self-propulsion of cells in fluids by means of membrane deformations. Phy. Rev. L 2013, 111, 228102. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; Springer: Berlin, Germany, 2013. [Google Scholar]
- Wang, Q.; Othmer, H.G. Computational analysis of amoeboid swimming at low Reynolds number. J. Math. Biol. 2016, 72, 1893–1926. [Google Scholar] [CrossRef] [PubMed]


| NG 3-Sphere | PMPY 2-Sphere | VE 3-Sphere | ||||
|---|---|---|---|---|---|---|
| Eff | Eff | Eff | ||||
(Figure 2a,b) | ||||||
(Figure 2c,d) | - | - | ||||
| - | - | |||||
| - | - | |||||
| - | - | - | - | |||
| - | - | - | - | |||
| NG | PMPY | |
|---|---|---|
| 4-Sphere ( 3) | 2-Sphere ( 1) | |
| NG 21-Spheres | PMPY 21-Spheres | |
|---|---|---|
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q. Optimal Strokes of Low Reynolds Number Linked-Sphere Swimmers. Appl. Sci. 2019, 9, 4023. https://doi.org/10.3390/app9194023
Wang Q. Optimal Strokes of Low Reynolds Number Linked-Sphere Swimmers. Applied Sciences. 2019; 9(19):4023. https://doi.org/10.3390/app9194023
Chicago/Turabian StyleWang, Qixuan. 2019. "Optimal Strokes of Low Reynolds Number Linked-Sphere Swimmers" Applied Sciences 9, no. 19: 4023. https://doi.org/10.3390/app9194023
APA StyleWang, Q. (2019). Optimal Strokes of Low Reynolds Number Linked-Sphere Swimmers. Applied Sciences, 9(19), 4023. https://doi.org/10.3390/app9194023





