Abstract
Ultrasonic multi-angle plane-wave (PW) coherent compounding relies on delay-and-sum (DAS) beamforming of two-dimensional (2D) echo matrix in both the dimensions PW transmit angle and receiving channel to construct each image pixel. Due to the characteristics of DAS beamforming, PW coherent compounding may suffer from high image clutter when the number of transmit angles is kept low for ultrafast image acquisition. Delay-multiply-and-sum (DMAS) beamforming exploits the spatial coherence of the receiving aperture to suppress clutter interference. Previous attempts to introduce DMAS beamforming into multi-angle PW imaging has been reported but only in either dimension of the 2D echo matrix. In this study, a novel DMAS operation is proposed to extract the 2D spatial coherence of echo matrix for further improvement of image quality. The proposed 2D-DMAS method relies on a flexibly tunable p value to manipulate the signal coherence in the beamforming output. For p = 2.0 as an example, simulation results indicate that 2D-DMAS outperforms other one-dimensional DMAS methods by at least 9.3 dB in terms of ghost-artifact suppression. Experimental results also show that 2D-DMAS provides the highest improvement in lateral resolution by 32% and in image contrast by 15.6 dB relative to conventional 2D-DAS beamforming. Nonetheless, since 2D-DMAS emphasizes signal coherence more than its one-dimensional DMAS counterparts, it suffers from the most elevated speckle variation and the granular pattern in the tissue background.
1. Introduction
In medical ultrasound imaging, delay-and-sum (DAS) beamforming is the standard technique to produce image outputs. However, DAS beamforming intrinsically suffers from limited image resolution and insufficient rejection of off-axis clutter interference. The loss of image quality is particularly evident in the case of plane-wave (PW) imaging due to the lack of transmit focusing [1]. In PW imaging, an unfocused wave is transmitted to illuminate a wide field-of-view, and then the backscattered echoes in the receiving array are coherently summed after time compensation of geometric paths to generate low-quality images at frame rates on the order of kHz. To improve the image quality of PW imaging, coherent plane wave compounding (CPWC) uses multi-angle PW transmissions to achieve synthetic transmit focusing [2,3]. Unlike incoherent compounding, which combines the envelope image without phase information to reduce speckle variation, CPWC depends on the summation of image data with phase information to achieve synthetic focusing. In other words, low-quality images are firstly obtained with different PW transmit angles and then combined coherently to form the final high-quality image. Therefore, each image pixel in CPWC imaging is actually constructed by the two-dimensional (2D) DAS beamforming of the corresponding echo matrix of which the dimensions are the PW transmit angle and the receiving channel. Though CPWC imaging provides a trade-off between the frame rate and the image quality, its image quality heavily depends on the number of PW transmit angles. With only a few PW transmit angles, the suppression of side-lobe clutter and axial-lobe artifacts is generally unsatisfactory, and thus leads to ghost artifact in the image [4].
In order to improve image quality, many adaptive imaging methods have been proposed to process the echo matrix in multi-angle PW imaging. One of the widely used methods is minimum variance (MV) beamforming. Joint transmitting-receiving (JTR) beamforming calculates both the transmit and the receiving MV weights and then applies them to the echo matrix after sub-matrix averaging [5]. In double MV [6], adaptive weights of received channel data are firstly applied to each PW image, and then the second weights in the PW dimension are estimated from the resultant image data with different transmit angles. Spatial-coherence-based MV (DCT-MV and DCR-MV) beamforming is also feasible in which the covariance matrix is estimated through different combinations of the echo matrix [7]. Other methods mainly rely on adaptive weighting to suppress the image artifacts in multi-angle PW imaging. The coherence factor (CF) can represent the focusing quality, which is defined as the ratio between the coherent power and the total power in the channel data [8]. The CF weighting can also be combined with MV beamforming as suggested in References [9,10]. In multi-angle PW imaging, it can be calculated from the output of JTR-MV beamforming in both the transmit and receive dimensions [11]. Other definitions of focusing factor include generalized coherence factor (GCF) [12], short-lag spatial coherence (SLSC) [13,14], normalized autocorrelation factor (NAF) [15], and cross-coherence factor [4]. These factors are calculated using received echoes from multi-angle PW transmissions and then applied to the final CPWC image output to suppress low-quality pixels. Singular value decomposition (SVD) filter is also proposed for side-lobe suppression of CPWC by transforming the multi-angle PW image data into a 2D spatio-angular matrix before applying the SVD filter to extract the high-coherence component [16].
Recently, a novel nonlinear beamforming has been proposed for ultrasound imaging by multiplying radiofrequency (RF) echoes between every possible channel pair after time compensation. It is referred to as the delay-multiply-and-sum (DMAS) beamforming [17,18]. The purpose of channel-domain multiplication is to introduce spatial coherence in the channel data into the beamforming process. Consequently, the side-lobe clutter and ghost artifact can be suppressed in the beamforming output due to their lower coherence relative to the main-lobe signal. DMAS beamforming in combination with adaptive weighting has been adopted not only in medical ultrasound but also in photoacoustic imaging [19]. Note that, though the original form of DMAS beamforming is computationally demanding due to the multiplication between every possible channel pair, a low computational cost formulation has been exploited and implemented in real time on a research scanner [20]. However, since DMAS imaging is based on the multiplicative coupling of RF channel signals, it demands oversampling to avoid aliasing the corresponding spectral components for imaging. We have previously developed an alternative high-order baseband DMAS beamforming (BB-DMAS) [21] to avoid the aforementioned oversampling because the multiplication of baseband channel data does not lead to undesired spectral components at high frequencies. When the order of baseband DMAS beamforming is represented as a rational p value larger than unity, the magnitude of time-delayed channel signals is scaled by pth root and then restored by pth power after channel sum. Note that a higher p value corresponds to higher spatial coherence in BB-DMAS beamforming and thus leads to higher image contrast ratios. Note that an improved RF version of DMAS beamforming has recently been developed as the p-DAS [22], which is also capable of flexibly tuning the image quality by the p value but still at the cost of oversampling. Similar to other coherence-based beamforming, the downside of DMAS beamforming includes the loss of image magnitude in the speckle region [23] and also dark-region artifacts [24] around wire reflectors and hyperechoic cysts.
Previous attempts to introduce DMAS beamforming into multi-angle PW imaging has been reported but only in either dimension of the echo matrix. For example, the echo matrix can be firstly summed in the dimension of the PW transmit angle to achieve synthetic transmit focusing before applying DMAS processing in the dimension of the receiving channel, as in Reference [25]. On the contrary, when the echo matrix is firstly summed in the dimension of the receiving channel to render the low-quality image as in CPWC imaging, DMAS processing can be performed to extract signal coherence in the dimension of the PW transmit angle [26]. In this study, a novel 2D-DMAS beamforming is proposed to further boost the image quality of multi-angle PW imaging. Baseband multiplicative coupling in both the dimensions of PW transmit angle and receiving channel is used to extract 2D spatial coherence of the echo matrix. Note that the original CPWC imaging can be regarded as 2D-DAS since the echo matrix is coherently summed in both the dimensions of PW transmit angle and receiving channel. Using 2D-DAS as a reference, image quality of 2D-DMAS beamforming will be compared to that of one-dimensional DMAS beamforming for multi-angle PW imaging.
2. Theory
2.1. BB-DMAS Beamforming for Single-Angle PW Imaging
Baseband beamforming achieves high focusing accuracy by firstly demodulating the channel waveforms down to baseband and then by applying coarser time delays without oversampling. Under the assumption that the sound speed of the imaged object is constant, the time delay for beamforming is calculated using the propagating path from the transmit PW wave front to a given pixel in the image in combination with the backscattered path from this pixel position back to the receiving channels, as described in Reference [22]. Finally, to correct the phase error produced in the demodulation process among different channels, phase rotation would be performed by including an additional phase term for each time-delayed channel before coherent summation. Representing the received baseband channel data of the nth channel in the N-element array for this pixel as () after time compensation and phase rotation, its magnitude-scaled version is obtained by pth rooting the magnitude of channel data while keeping the phase unchanged. Then, the output of the BB-DMAS beamformer for this pixel is defined as the pth power of the summation of magnitude-scaled channel data:
Note that BB-DMAS is similar to that in Reference [22] but that the sign operation is not required. BB-DMAS provides a lower side-lobe level and a narrower main-lobe width in the lateral direction when the p value increases. Moreover, the signal processing of BB-DMAS remains unchanged for any p value and, thus, simplifies its implementation together with flexible manipulation of image quality.
2.2. 2D-DMAS Processing for Multi-Angle PW Imaging
Multi-angle PW imaging can be understood as 2D signal processing of the received echo matrix of which the dimensions are the receiving channel and the PW transmit angle. Each PW transmission with specified a transmit angle corresponds to one transmit event, and thus, the echoes after time delay and phase rotation can be represented as a three-dimensional signal with the dimensions of image width, image depth, and receiving channel. Therefore, for each pixel (x, z) in the image where x and z are respectively the lateral and axial positions, a 2D echo matrix comprising the received channel signal from every transmit event of different PW transmit angles can be constructed. The echo matrix can be processed to produce the final B-mode output by any combination of DAS and DMAS beamforming in the two dimensions of PW transmit angle and receiving channel. CPWC imaging depends on the 2D coherent summation of the echo matrix to achieve both receive and transmit focusing and is referred to as 2D-DAS in this study. Given the baseband channel data in multi-angle PW imaging after time compensation and phase rotation as where n is the index of receiving channel (n = 1, 2,…, N) and k is the index of PW transmit angle (k = 1, 2,…, M), the 2D-DAS beamforming (i.e., CPWC) can be formulated as follows:
On the contrary, the proposed 2D-DMAS method extracts the 2D signal coherence by directly applying the DMAS process on the echo matrix. In other words, each entry in the echo matrix is magnitude-scaled by pth rooting while maintaining its phase. Then, the signal dimensionality is restored by pth power after 2D summation, as shown in the following:
Other DMAS beamforming methods proposed in the literatures for multi-angle PW imaging are considered for comparison, and they are referred to as Rx-DMAS [25] and Tx-DMAS [26]. Rx-DMAS and Tx-DMAS also consider the spatial coherence of the echo matrix but in only one dimension. In other words, the DMAS operation is performed in the dimension of either the PW transmit angle or the receiving channel. For Rx-DMAS, the echo matrix is firstly summed in the dimension of the PW transmit angle for synthetic transmit focusing. Then, the DMAS processing is applied on the channel data to estimate the spatial coherence in the dimension of the receiving channel. For Tx-DMAS, on the contrary, the echo matrix is firstly summed in the dimension of the receiving channel to achieve dynamic receive focusing before the DMAS processing is applied in the dimension of the PW transmit angle to emphasize the signal coherence from distinct PW transmissions. Specifically, Tx-DMAS beamforming can be understood as the pth-root magnitude-scaling of low-quality images from several PW transmit angles, coherently summing these images to produce a high-quality image but with pth-power restoring of signal dimensionality. Using the same representation of baseband echo matrix in Equation (2), Rx-DMAS and Tx-DMAS can be formulated in Equations (4) and (5), respectively:
2.3. Relationship between 2D-DMAS and 2D-DAS
With the assumption that the magnitude variation within the echo matrix can be ignored (i.e., for n = 1, 2,…, N and k = 1, 2,…, M), the relation between 2D-DMAS beamforming and 2D-DAS beamforming can be formulated as follows:
The aforementioned assumption of constant channel magnitude is valid for a coherent target without focusing errors. In other words, 2D-DMAS beamforming in multi-angle PW imaging can be understood as 2D-DAS beamforming weighted by the (p − 1)-th power of the phase coherence factor derived from the corresponding echo matrix. Note that the absolute value of the phase coherence factor always ranges from 0 to 1. Consequently, when p becomes larger, the phase coherence weighting value gets even smaller due to the operation of the (p − 1)-th power and, thus, the low-coherence component is further attenuated. When p is close to one, as a special case, the phase coherence weighting approaches unity so 2D-DMAS beamforming performs similar to 2D-DAS beamforming.
3. Research Method
The aforementioned four beamforming methods for multi-angle PW imaging are compared using the data on the PICMUS platform established for IEEE IUS 2016 [27] to quantitatively evaluate the resolution and contrast on two simulated phantoms and two experimental phantoms, respectively. In vivo data of a carotid artery in both the transverse and longitudinal views are also included. The data are acquired using a 128-element linear array with a pitch of 0.3 mm. The transmit waveform is a 2.5-cycle sinusoid at 5.2 MHz. The received echo is digitized at a sampling frequency of 20.8 MHz. The detailed parameters of the PICMUS dataset are listed in Table 1. The performances are evaluated with seven PW compounding (7 PW), uniformly tilted from −16° to +16° with spacing of 5.3°. The mean resolutions of the image are automatically measured by the PICMUS program using Matlab (R2018b, The MathWorks, Natick, MA, USA) in terms of the full widths at half maximum (FWHM) of wire reflectors in Figure 1a–d and Figure 3a–d. The FWHMs in the axial and lateral directions are respectively referred to axial width (AW) and lateral width (LW) in this paper. The ghost-artifact level is estimated as the image magnitude in the background area (red rectangle) in Figure 1a. Note that the ghost artifact in this study mainly comes from the axial lobes and grating lobes of the horizontal wire reflectors at depths of 20 mm. The contrast ratio (CR) and contrast-to-noise ratio (CNR) are calculated using the image magnitude before log-compression inside the cyst (green circle) and in the background region (blue rectangle) in Figure 1e and Figure 3e as follows:
where , , , and are the averaged values and the standard deviations of image magnitude, respectively, in the cyst and the background. In addition to the conventional CR and CNR, the generalized CNR (GCNR) as suggested in Reference [28] is also included for evaluation of image contrast. The GCNR is estimated from the overlap area of the probability density function of the background and the cyst regions subtracted from unity.

Table 1.
Imaging parameters of PICMUS data.

Figure 1.
Simulated B-mode images of wire reflectors and anechoic cysts for two-dimensional delay-and-sum (2D-DAS), Rx-DMAS, Tx-DMAS, and two-dimensional delay-multiply-and-sum (2D-DMAS) beamforming: The p value in DMAS beamforming is fixed to 2.0.
In order to perform baseband beamforming, the IQ channel data and corresponding program are adopted on the PICMUS platform. Specifically, the received channel waveforms are firstly demodulated and then down-sampled by a factor of four. Given the baseband IQ channel data from individual PW transmissions, time compensations and phase rotations are performed for every image pixel. Then, all phase-aligned channel data from seven PW transmissions are concatenated to construct the echo matrix. For 2D-DAS beamforming, the echo matrix is sequentially summed in the dimension of the PW transmit angle and then in the dimension of the receiving channel to generate the final image. For 2D-DMAS, Rx-DMAS, and Tx-DMAS beamforming, they are implemented according to Equations (3)–(5) in Section 2, respectively. Since the output of either beamforming method is still a baseband signal, the B-mode image in this study is reconstructed by simply taking the absolute value of the beamforming output to retrieve the envelope before log-compression with a dynamic range of 60 dB. In this study, p values of 1.5, 2.0, 2.5, and 3.0 are considered for all DMAS beamforming for quantitative comparison of image quality. For illustration of B-mode imaging, the p value of DMAS beamforming is selected to be 2.0 in order to compare with the original DMAS in the RF domain [17,25].
4. Results
4.1. Phantom Simulations
Simulated B-mode images of wire reflectors in Figure 1a–d show that the 2D-DMAS, Rx-DMAS, and Tx-DMAS beamforming methods can effectively suppress side-lobe and ghost artifact compared to conventional CPWC imaging (i.e., 2D-DAS). The p value of DMAS beamforming in Figure 1 is set to be 2.0 as an example. Visual comparison reveals that 2D-DMAS provides the lowest side-lobe and ghost-artifact levels among all three DMAS methods. B-mode images of anechoic cysts in Figure 1e–h also show that these DMAS beamforming methods lead to noticeably lower clutter artifacts within the cyst, especially in the depth ranging from 15 mm to 35 mm. This is because the presence of ghost artifacts in 2D-DAS beamforming is relatively obvious in the shallow depth while spatial-coherence-based beamforming like DMAS is capable of alleviating the ghost artifact in the case of short transmit pulse [29]. On the other hand, speckle variation in the background region is also noticeably higher due to the emphasis of signal coherence in these DMAS beamforming methods. This is particularly evident for 2D-DMAS and Rx-DMAS. Nonetheless, it should be noted that 2D-DMAS beamforming appears to provide the lowest clutter within the cysts compared to the Rx-DMAS and Tx-DMAS counterparts.
Quantitative analyses of each beamforming method with p values ranging from 1.5 to 3.0 are shown in Figure 2. Though Figure 2a,b shows that the image resolution generally improves with p value for all DMAS methods, it should be noted that the change of AW with p value is minor for Rx-DMAS and Tx-DMAS. On the contrary, only the AW in 2D-DMAS significantly decreases from 0.38 mm to 0.33 mm when the p value increases from 1.5 to 3.0. For LW, on the other hand, all 2D-DMAS, Rx-DMAS, and Tx-DMAS demonstrate a lower LW with the increase of p value. Among them, note that 2D-DMAS consistently provides the lowest LW when the same p value is considered. Figure 2c also shows that the resultant ghost-artifact level decreases with p value for all DMAS methods but that 2D-DMAS consistently outperforms the other two. For p = 2.0 as an example, the corresponding ghost-artifact levels are −90.8, −81.5, and −73.5 dB, respectively, for 2D-DMAS, Rx-DMAS, and Tx-DMAS. For image contrast, Figure 2d shows that the CR markedly improves with p value, especially for 2D-DMAS and Rx-DMAS. However, it should be indicated in Figure 2e that the conventional 2D-DAS still provides the highest CNR while 2D-DMAS has the lowest due to the elevated granular pattern in the speckle background. Note that the difference in CNR between 2D-DMAS and the other DMAS counterparts becomes relatively minor with decreasing p value. For example, the CNRs are respectively 0.59, 0.69, and 0.89 for 2D-DMAS, Rx-DMAS, and Tx-DMAS when p = 3.0. This corresponds to a CNR difference of 0.3 between 2D-DMAS and Tx-DMAS. However, when p decreases to 2.0, the CNR becomes respectively 0.89, 0.96, and 1.02 for 2D-DMAS, Rx-DMAS, and Tx-DMAS. In other words, the CNR difference between 2D-DMAS and Tx-DMAS now decreases to 0.13. When the GCNR is considered, however, it should be noted that 2D-DMAS and Rx-DMAS outperforms 2D-DAS. In other words, 2D-DMAS and Rx-DMAS indeed provide improvements in image contrast even with the elevated speckle variation.
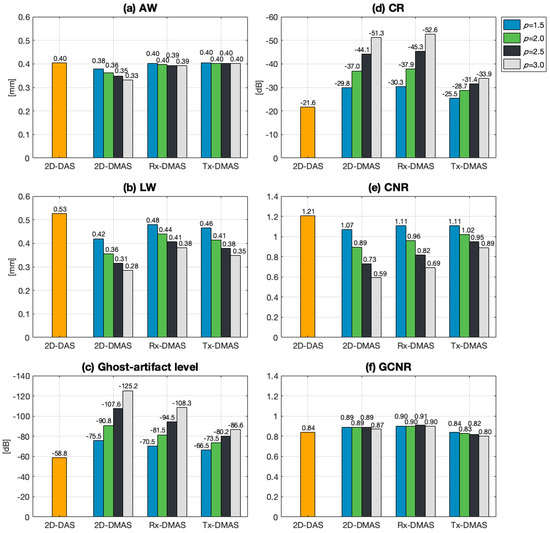
Figure 2.
Quantitative analysis of image resolution, ghost-artifact level, and image contrast for the simulated B-mode images in Figure 1.
4.2. Phantom Experiments
The experimental B-mode images in Figure 3a–d with p = 2.0 show that, compared to the 2D-DAS counterpart, all three DMAS beamforming can make the wire reflectors stand out from the speckle background. This is expected since the echoes from the wire reflectors have much higher signal coherences than those from speckle scatterers. Consequently, the image magnitude of the speckle background appears to be relatively suppressed in any DMAS beamforming. Note that, among the three DMAS beamforming methods, the suppression of speckle background is the most obvious for 2D-DMAS and is the least for Tx-DMAS. Moreover, both 2D-DMAS and Rx-DMAS exhibit noticeable dark-region artifacts around the wire reflectors and the hyperechoic cyst while the dark-region artifacts are relatively alleviated for Tx-DMAS. Figure 3e–h further shows that the edge of cysts gets clearer in all three DMAS beamforming methods due to the lower clutter artifacts within the anechoic regions. The 2D-DMAS exhibits the lowest clutter level compared to the Rx-DMAS and Tx-DMAS beamforming but at the cost of reduced magnitude and elevated variation of speckle background. These observations are consistent with those in the simulation results.

Figure 3.
Experimental B-mode images of wire reflectors and various contrast cysts in speckle background for 2D-DAS, Rx-DMAS, Tx-DMAS, and 2D-DMAS beamforming: The p value in DMAS beamforming is fixed to 2.0.
Quantitative analyses of experimental B-mode images for the DMAS beamforming method with different p values are shown in Figure 4. The experimental results are generally similar to those in the simulations. Figure 4a,b shows that the image resolution is the highest for 2D-DMAS when the same p value is considered. For example, the LW decreases from 0.53 mm for the 2D-DAS reference to 0.36 mm for 2D-DMAS with p = 2.0. This corresponds to an improvement of 32% in lateral resolution. In Figure 4c, it is also demonstrated that the image CR of the anechoic cyst significantly improves for 2D-DMAS and Rx-DMAS respectively by 15.6 dB and 13.7 dB relative to the 2D-DAS reference. Nonetheless, the results in Figure 4d indicate that the conventional 2D-DAS still provides a higher CNR than all three DMAS beamforming methods. For p = 2.0, the CNRs are respectively 0.82, 0.86, and 0.86 for 2D-DMAS, Rx-DMAS, and Tx-DMAS while that for 2D-DAS is 0.99. On the other hand, all DMAS beamforming methods result in higher GCNR than 2D-DAS especially for 2D-DMAS and Rx-DMAS.
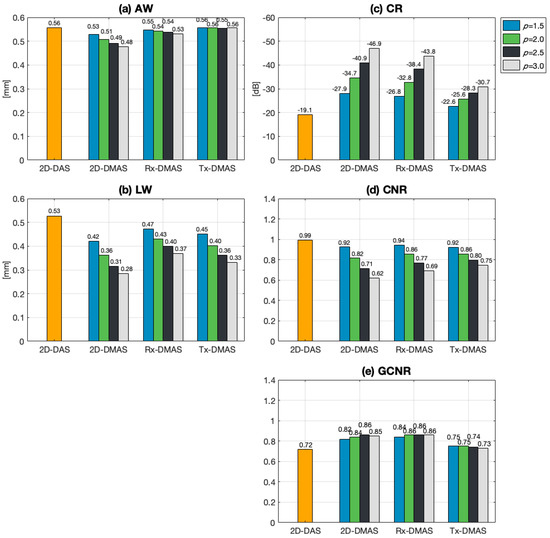
Figure 4.
Quantitative analyses of image resolution and image contrast for the experimental B-mode images in Figure 3.
4.3. In Vivo Experiments
B-mode images of the in vivo carotid artery in longitudinal and transverse views are respectively demonstrated in Figure 5a–d and in Figure 5e–h. All DMAS beamforming methods show noticeable suppression of clutter artifacts so that their corresponding images appear to be less foggy than the 2D-DAS reference. However, it should be noted that the performance of Tx-DMAS is marginal in terms of removal of acoustic reverberation within the vessel and in the peripheral tissue structure. In the longitudinal view, for example, the reverberation artifacts beneath the upper wall of the vessel at about 15 mm of the lateral position (i.e., green rectangle in Figure 5a) remain apparent with Tx-DMAS beamforming while they are suppressed most effectively by 2D-DMAS beamforming. In the transverse view, the CRs evaluated using the image magnitude inside the carotid region (green circle) and in the tissue background (blue rectangle) of Figure 5e are −26.8 dB, −47.1 dB, −46.1 dB, and −29.5 dB respectively for 2D-DAS, 2D-DMAS, Rx-DMAS, and Tx-DMAS. Though 2D-DMAS produces the highest CR, it still has the lowest CNR of 0.63 while 2D-DAS has the highest CNR of 1.10. Nonetheless, it should be noted that both the GCNRs of 2D-DMAS and 2D-DAS are 0.94. Moreover, visual comparison among all beamforming methods in Figure 5 also suggests the superior image resolution of 2D-DMAS to that of the one-dimensional DMAS counterparts. These observations agree with those of the simulations and phantom experiments.
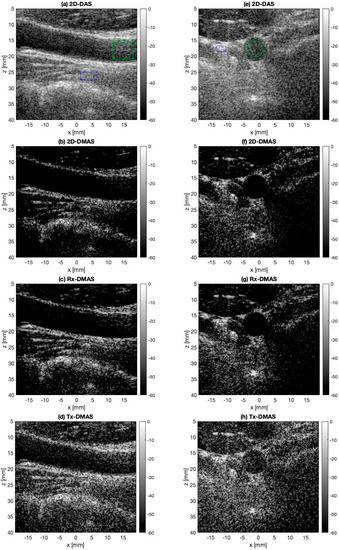
Figure 5.
Experimental B-mode images of in vivo carotid artery for 2D-DAS, Rx-DMAS, Tx-DMAS, and 2D-DMAS beamforming: The p value in DMAS beamforming is fixed to 2.0.
5. Discussions and Conclusions
In this study, DMAS beamforming has been extended to use 2D spatial coherence in multi-angle PW imaging. The 2D spatial coherence is derived from the echo matrix of every image pixel in both the dimensions of PW transmit angle and receiving channel. Specifically, the proposed 2D-DMAS method extracts the 2D signal coherence by magnitude-scaling every entry in the echo matrix by pth root operation while maintaining its phase. After 2D summation of the magnitude-scaled echo matrix, pth power operation is used to restore the dimensionality of the final image output. Here, the aforementioned p value determines the extent of 2D signal coherence included in the beamforming output, and thus provides a flexibly tunable manipulation of image quality. Moreover, due to the baseband nature of the proposed 2D-DMAS beamforming, its implementation does not demand for oversampling as the original DMAS in the RF domain.
Simulated and experimental B-mode images of wire reflectors and speckle phantom from PICMUS data indicate that, compared to other one-dimensional DMAS methods such as Rx-DMAS and Tx-DMAS, the proposed 2D-DMAS beamforming is capable of the most effective improvement not only in image resolution but also in ghost-artifact suppression in multi-angle PW imaging. For image contrast, both 2D-DMAS and Rx-DMAS lead to higher image CRs and GCNRs than the Tx-DMAS counterpart. B-mode images of in vivo carotid artery further indicate that, in clinical scenarios, 2D-DMAS beamforming provides the most apparent suppression of image artifacts within the vessel even in the presence of acoustic reverberations. Nonetheless, in terms of image CNR, all DMAS beamforming methods remain inferior to the conventional CPWC image (i.e., 2D-DAS) due to the noticeably elevated speckle variation, especially for 2D-DMAS. This observation is as expected since the speckle variation has been known to increase with the extent of spatial coherence considered in B-mode imaging. Since 2D-DMAS emphasizes the signal coherence in the beamforming output more than the other one-dimensional DMAS counterparts, it suffers from more noticeable increases of speckle variation. Nonetheless, it is noticeable that 2D-DMAS also provides higher or at least comparable GCNRs to the 2D-DAS. To improve the image CNR in DMAS beamforming, either frequency compounding [30] or receive aperture compounding [31] can be a feasible solution to smoothing the granular speckle appearance of B-mode image. Though 2D-DMAS effectively improves the image contrast and resolution in B-mode imaging, its application in motion or blood flow estimation may be limited due to the low signal coherence of moving objects in the dimension of the PW transmit angle.
The 2D-DMAS beamforming in this study is implemented as described in Equation (3) by firstly accumulating the received channel data from distinct PW transmit angles to construct the echo matrix before applying 2D-DMAS processing. Consequently, it demands for huge memory allocation for the echo matrix, especially when the number of PW transmit angles is high. This is also why the number of PW transmit angles is currently limited to only seven in this study. Nonetheless, note that the formulation of 2D-DMAS can be rewritten in an alternative form as follows:
In this alternative form of 2D-DMAS implementation, the received channel data from each PW transmit angle is firstly magnitude-scaled by pth root operation and then combined to fulfill the inner summation in Equation (7). In other words, for each PW transmit angle, the received channel data has been summed with magnitude-scaling to a single value for the corresponding image pixel. This produces one magnitude-scaled low-quality image for each PW transmit angle. Therefore, similar to the real-time implementation of CPWC imaging, 2D-DMAS imaging can be also constructed by sequentially combining these magnitude-scaled low-quality images from distinct PW transmit angles and then by restoring the signal dimensionality of the high-quality image with a final pth power operation. In this way, 2D-DMAS beamforming can be efficiently implemented without the need for memory allocation for the huge echo matrix. Though Rx-DMAS may provide similar performances in lateral resolution, image CR, and ghost-artifact suppression to the proposed 2D-DMAS by selecting a p value higher than that of 2D-DMAS, the implementation of Rx-DMAS can be relatively complicated. Specifically, for Rx-DMAS, the echoes from all PW transmit angles have to be firstly synthesized before the DMAS processing in the receiving channels. Consequently, unlike the alternative form of 2D-DMAS in Equation (9), Rx-DMAS inevitably suffers from huge memory allocations for the echo matrix. Moreover, the axial resolution of 2D-DMAS is always higher than that of Rx-DMAS regardless of the p value of Rx-DMAS. This is because the spatial coherence of 2D-DMAS in the dimension of the PW transmit angle also helps to reduce the axial length of pulse responses by comparing the phase coherence among different PW transmit angles. Due to the aforementioned observations, the proposed 2D-DMAS appears to be a superior beamforming method to Rx-DMAS in terms of both implementation and overall performance in image quality. In future work, 2D-DMAS will be studied using the implementation in Equation (9) for its performance with a higher number of PW transmit angles.
Author Contributions
Che-Chou Shen is the supervisor of this research who proposes the idea of 2D-DMAS beamforming. Pei-Ying Hsieh performs the simulations and the experiments to validate the efficacy of the 2D-DMAS beamforming.
Funding
This research was funded by Ministry of Science and Technology of Taiwan under Grant No. 108-2221-E-011-072-MY3 and 108-2221-E-011-071-MY3.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sandrin, L.; Catheline, S.; Tanter, M.; Hennequin, X.; Fink, M. Time-resolved pulsed elastography with ultrafast ultrasonic imaging. Ultrason. Imaging 1999, 21, 259–272. [Google Scholar] [CrossRef]
- Tanter, M.; Fink, M. Ultrafast imaging in biomedical ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 102–119. [Google Scholar] [CrossRef] [PubMed]
- Montaldo, G.; Tanter, M.; Bercoff, J.; Benech, N.; Fink, M. Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 489–506. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Guo, Y.; Lee, W.N. Ultrafast ultrasound imaging using combined transmissions with cross-coherence-based reconstruction. IEEE Trans. Med. Imaging 2018, 37, 337–348. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Wang, Y.; Zeng, X.; Yu, J.; Yiu, B.Y.S.; Yu, A.C.H. Plane wave compounding based on a joint transmitting-receiving adaptive beamformer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 1440–1452. [Google Scholar] [CrossRef] [PubMed]
- Rindal, O.M.H.; Austeng, A. Double adaptive plane-wave imaging. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016. [Google Scholar]
- Nguyen, N.Q.; Prager, R.W. A spatial coherence approach to minimum variance beamforming for plane-wave compounding. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 522–534. [Google Scholar] [CrossRef]
- Hollman, K.W.; Rigby, K.W.; O’Donnell, M. Coherence factor of speckle from a multi-row probe. In Proceedings of the 1999 IEEE International Ultrasonics Symposium (IUS), Lake Tahoe, NV, USA, 17–20 October 1999. [Google Scholar]
- Asl, B.M.; Mahloojifar, A. Minimum variance beamforming combined with adaptive coherence weighting applied to medical ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 1923–1931. [Google Scholar] [CrossRef]
- Nilsen, C.-I.C.; Holm, S. Wiener beamforming and the coherence factor in ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 1329–1346. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Wang, Y.; Guo, W. Joint subarray coherence and minimum variance beamformer for multitransmission ultrasound Imaging modalities. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 1600–1617. [Google Scholar] [CrossRef]
- Li, P.C.; Li, M.L. Adaptive imaging using the generalized coherence factor. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 128–141. [Google Scholar]
- Lediju, M.A.; Trahey, G.E.; Byram, B.C.; Dahl, J.J. Short-lag spatial coherence of backscattered echoes: Imaging characteristics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1377–1388. [Google Scholar] [CrossRef] [PubMed]
- Pinton, G.F.; Trahey, G.E.; Dahl, J.J. Spatial coherence in human tissue: Implications for imaging and measurement. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1976–1987. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wang, Y.; Zheng, C.; Peng, H.; Zhang, C. Coherent plane-wave compounding based on normalized autocorrelation factor. IEEE Access 2018, 6, 36927–36938. [Google Scholar] [CrossRef]
- Guo, W.; Wang, Y.; Yu, J. A sibelobe suppressing beamformer for coherent plane wave compounding. Appl. Sci. 2016, 6, 359. [Google Scholar] [CrossRef]
- Matrone, G.; Savoia, A.S.; Caliano, G.; Magenes, G. The delay multiply and sum beamforming algorithm in ultrasound B-mode medical imaging. IEEE Trans. Med. Imaging 2015, 34, 940–949. [Google Scholar] [CrossRef] [PubMed]
- Matrone, G.; Ramalli, A. Spatial coherence of backscattered signals in multi-line transmit ultrasound imaging and its effect on short-lag filtered-delay multiply and sum beamforming. Appl. Sci. 2018, 8, 486. [Google Scholar] [CrossRef]
- Jeon, S.; Park, E.Y.; Choi, W.; Managuli, R.; Lee, K.; Kim, C. Real-time delay-multiply-and-sum beamforming with coherence factor for in vivo clinical photoacoustic imaging of humans. Photoacoustics 2019, 15, 100136. [Google Scholar] [CrossRef] [PubMed]
- Ramalli, A.; Scaringella, M.; Matrone, G.; Dallai, A.; Boni, E.; Savoia, A.S.; Bassi, L.; Hine, G.E.; Tortoli, P. High dynamic range ultrasound imaging with real-time filtered-delay multiply and sum beamforming. In Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS), Washington, DC, USA, 6–9 September 2017. [Google Scholar]
- Shen, C.C.; Hsieh, P.Y. Ultrasound baseband delay-multiply-and-sum (BB-DMAS) nonlinear beamforming. Ultrasonics 2019, 96, 165–174. [Google Scholar] [CrossRef]
- Polichetti, M.; Varray, F.; Béra, J.C.; Cachard, C.; Nicolas, B. A nonlinear beamformer based on p-th root compression—Application to plane wave ultrasound imaging. Appl. Sci. 2018, 8, 599. [Google Scholar] [CrossRef]
- Prieur, F.; Rindal, O.M.H.; Austeng, A. Signal coherence and image amplitude with the filtered delay multiply and sum beamformer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 1133–1140. [Google Scholar] [CrossRef]
- Rindal, O.M.H.; Rodriguez-Molares, A.; Austeng, A. The dark region artifact in adaptive ultrasound beamforming. In Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS), Washington, DC, USA, 6–9 September 2017. [Google Scholar]
- Matrone, G.; Savoia, A.S.; Caliano, G.; Magenes, G. Ultrasound plane-wave imaging with delay multiply and sum beamforming and coherent compounding. In Proceedings of the 2016 IEEE Conference of Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 17–20 August 2016. [Google Scholar]
- Go, D.; Kang, J.; Yoo, Y. A new compounding method for high contrast ultrafast ultrasound imaging based on delay multiply and sum. In Proceedings of the 2018 IEEE International Ultrasonics Symposium (IUS), Kobe, Japan, 22–25 October 2018. [Google Scholar]
- Liebgott, H.; Rodriguez-Molares, A.; Cervenansky, F.; Jensen, J.A.; Bernard, O. Plane-wave imaging challenge in medical ultrasound. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016. [Google Scholar]
- Rodriguez-Molares, A.; Rindal, O.M.H.; D’Hooge, J.; Måsøy, S.E.; Austeng, A.; Torp, H. The generalized contrast-to-noise ratio. In Proceedings of the 2018 IEEE International Ultrasonics Symposium (IUS), Kobe, Japan, 22–25 October 2018. [Google Scholar]
- Camacho, J.; Parrilla, M.; Fritsch, C. Phase coherence imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 958–974. [Google Scholar] [CrossRef] [PubMed]
- Matrone, G.; Ramalli, A.; Tortoli, P.; Magenes, G. Experimental evaluation of ultrasound higher-order harmonic imaging with Filtered-Delay Multiply and Sum (F-DMAS) non-linear beamforming. Ultrasonics 2018, 86, 59–68. [Google Scholar] [CrossRef] [PubMed]
- Jensen, A.C.; Nasholm, S.P.; Nilsen, C.C.; Austeng, A.; Holm, S. Applying Thomson’s multitaper approach to reduce speckle in medical ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 2178–2185. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).