Spatial-Temporal Self-Focusing of Partially Coherent Pulsed Beams in Dispersive Medium
Abstract
Featured Application
Abstract
1. Introduction
2. Theory
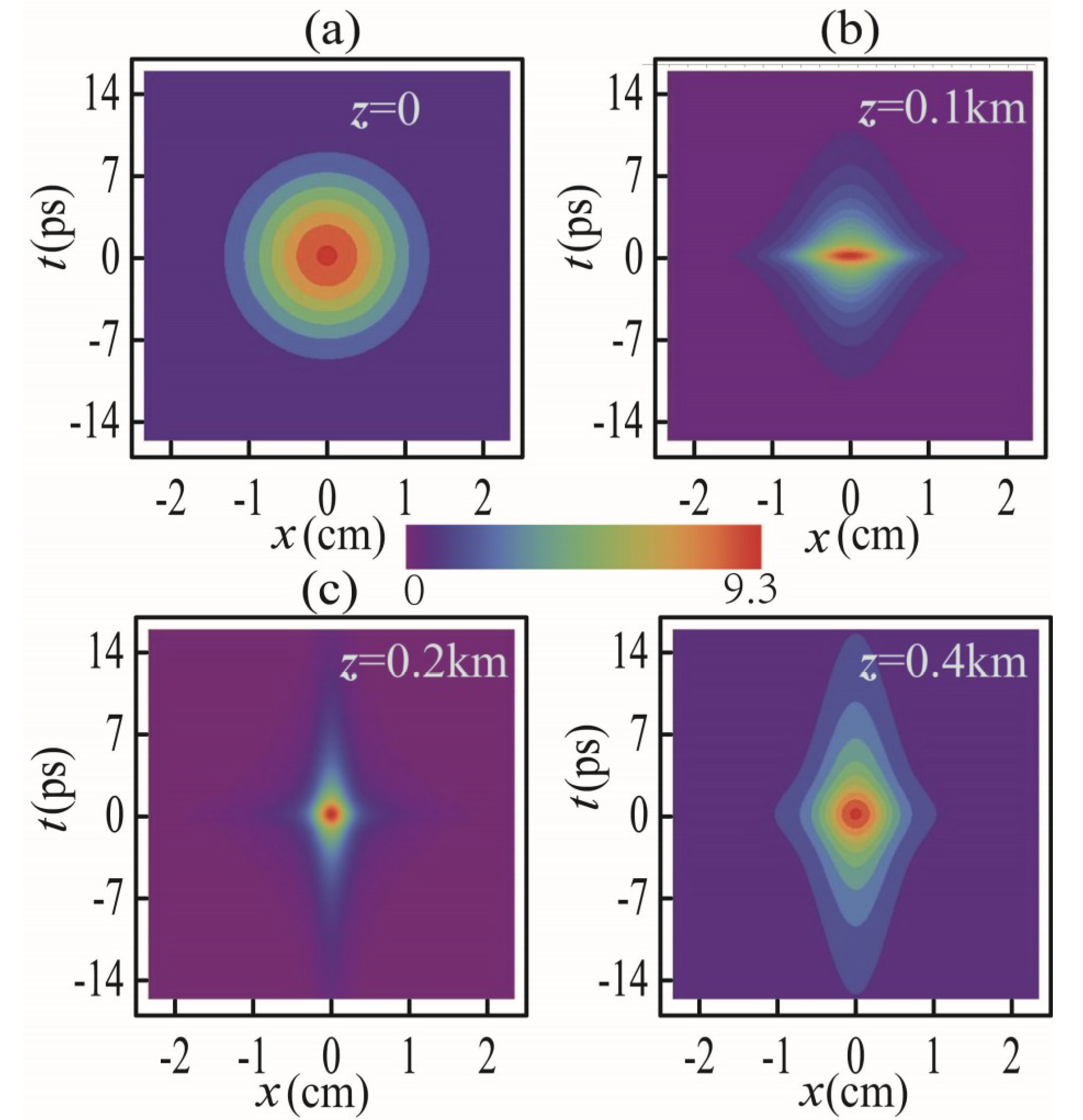
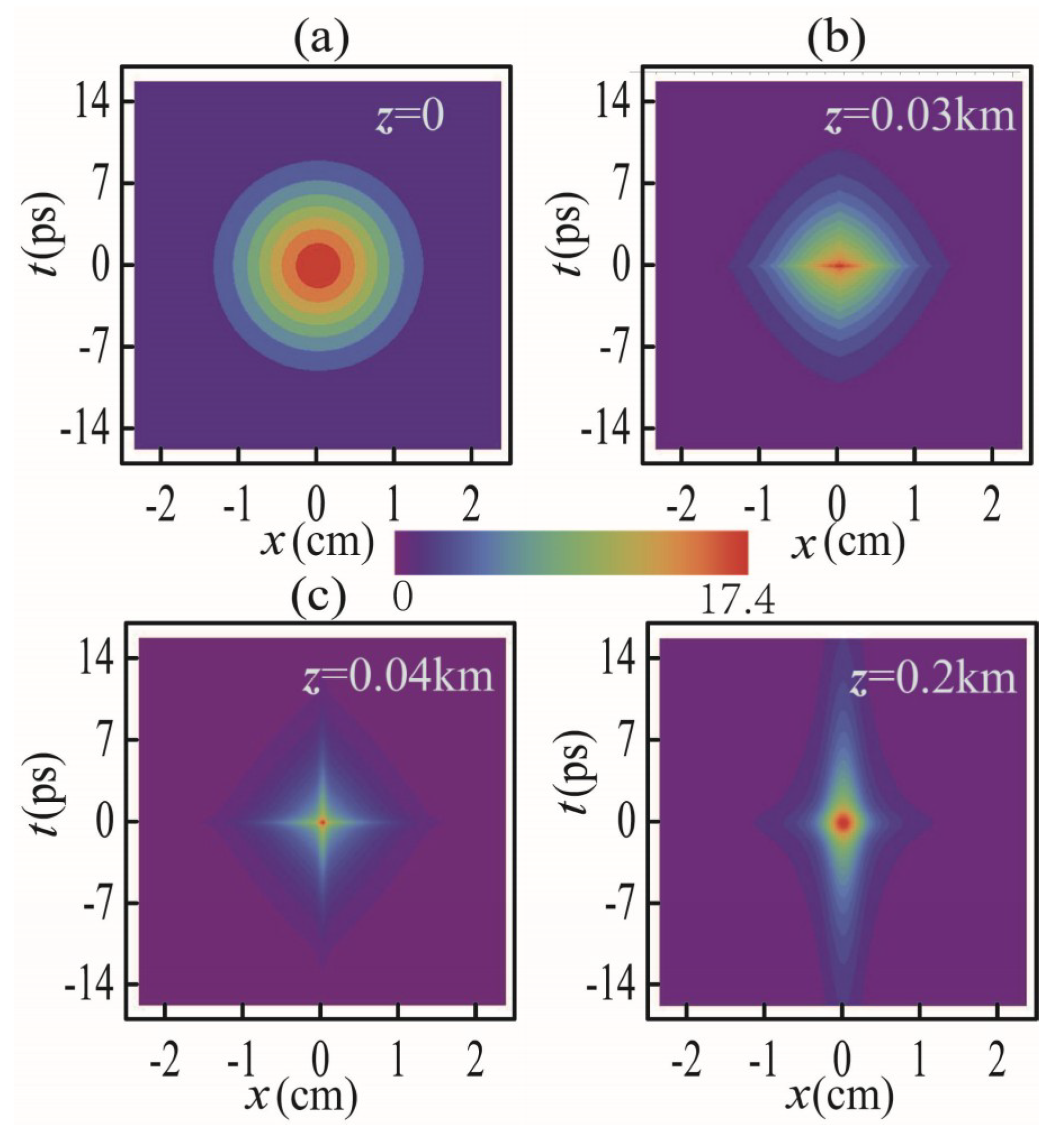
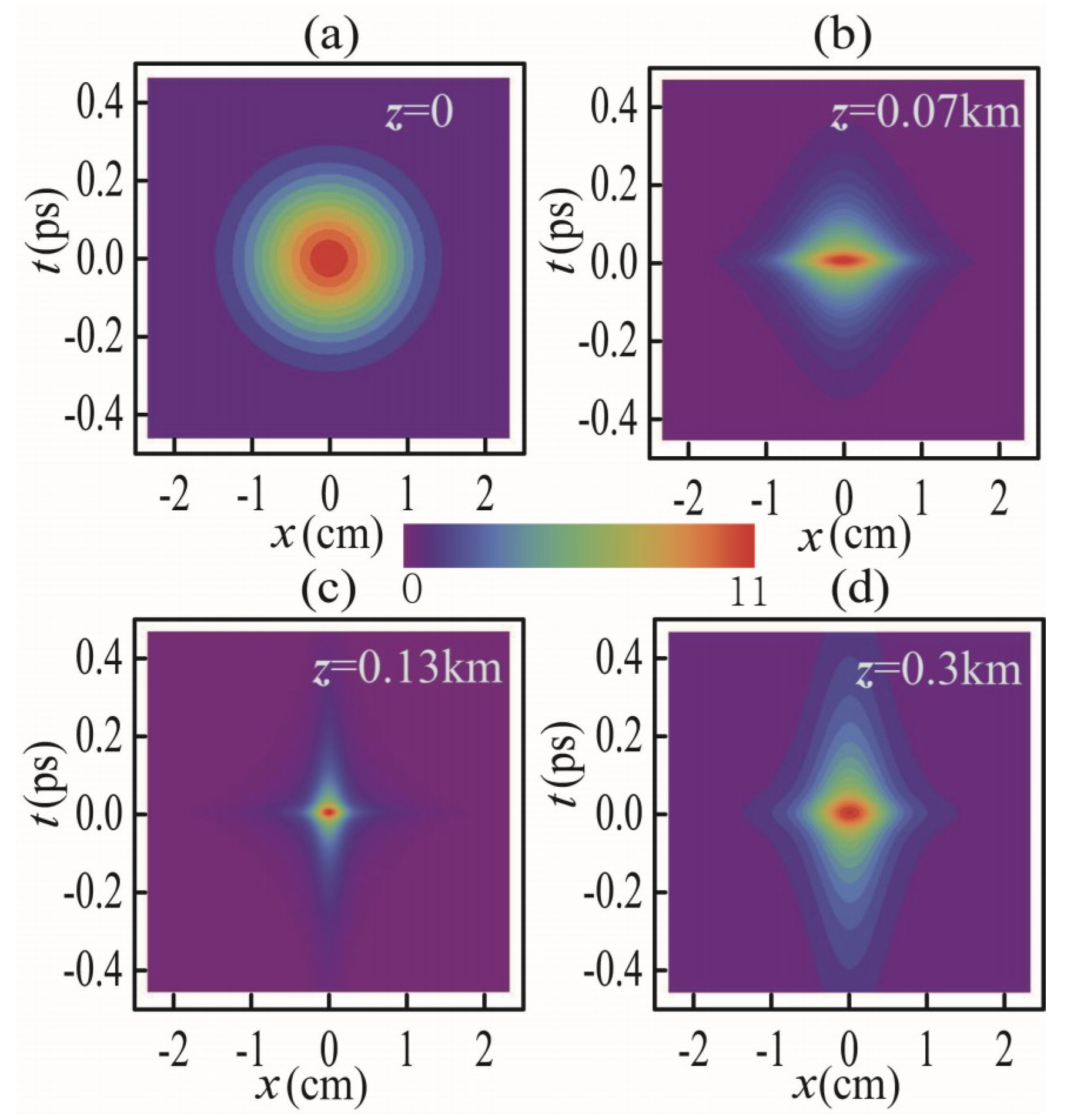
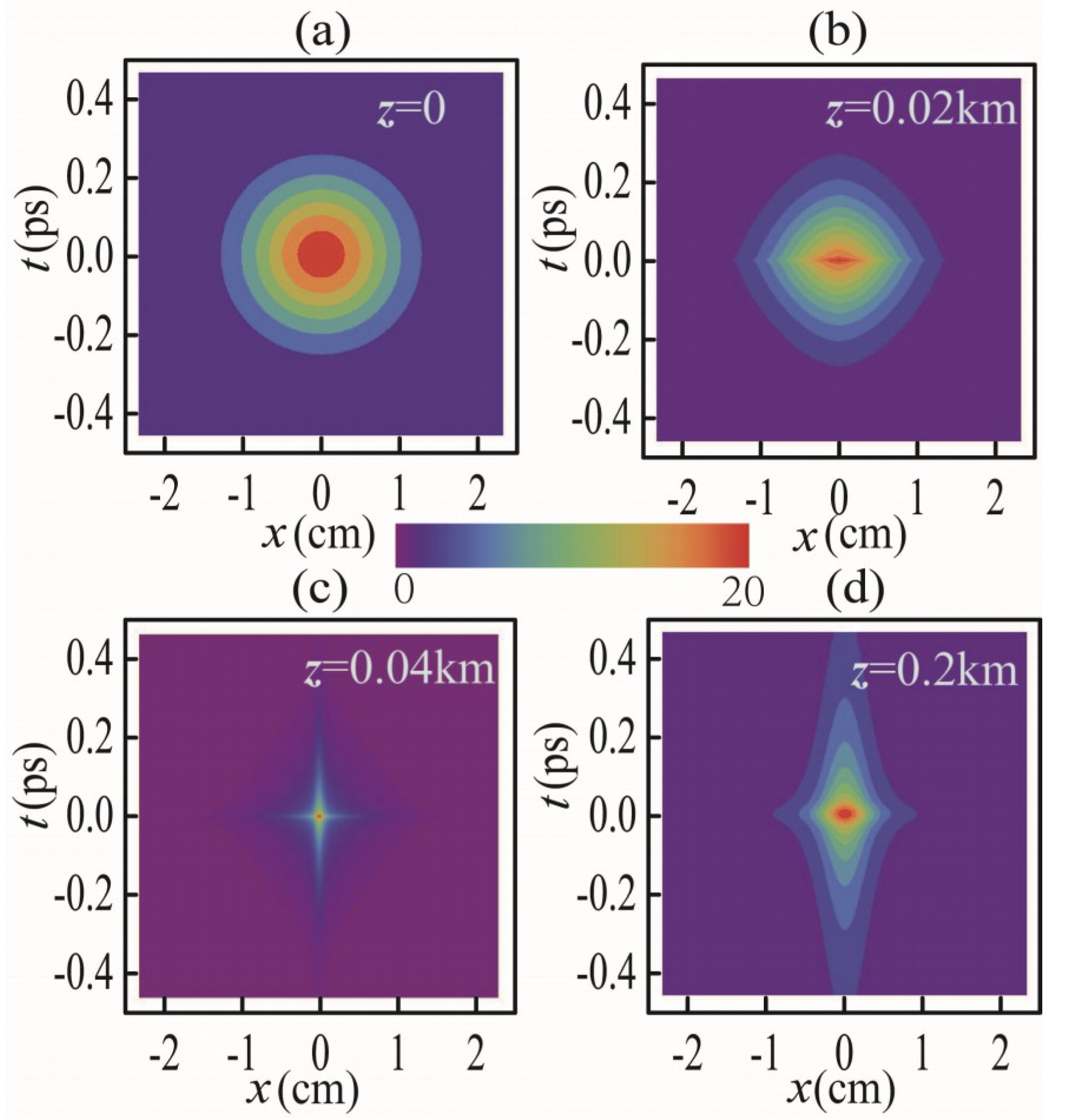
3. Spatial-Temporal Self-Focusing of PCP Beams in Dispersive Medium
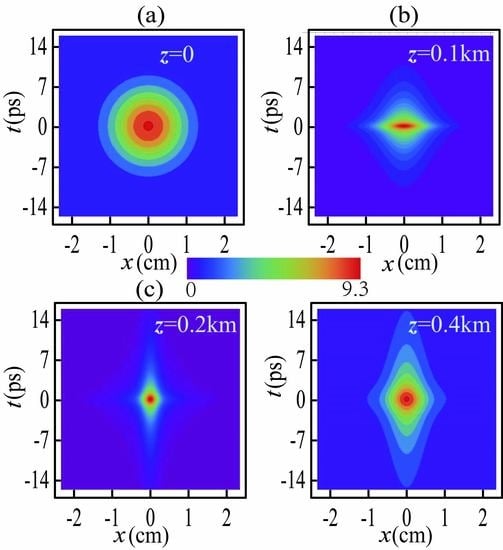
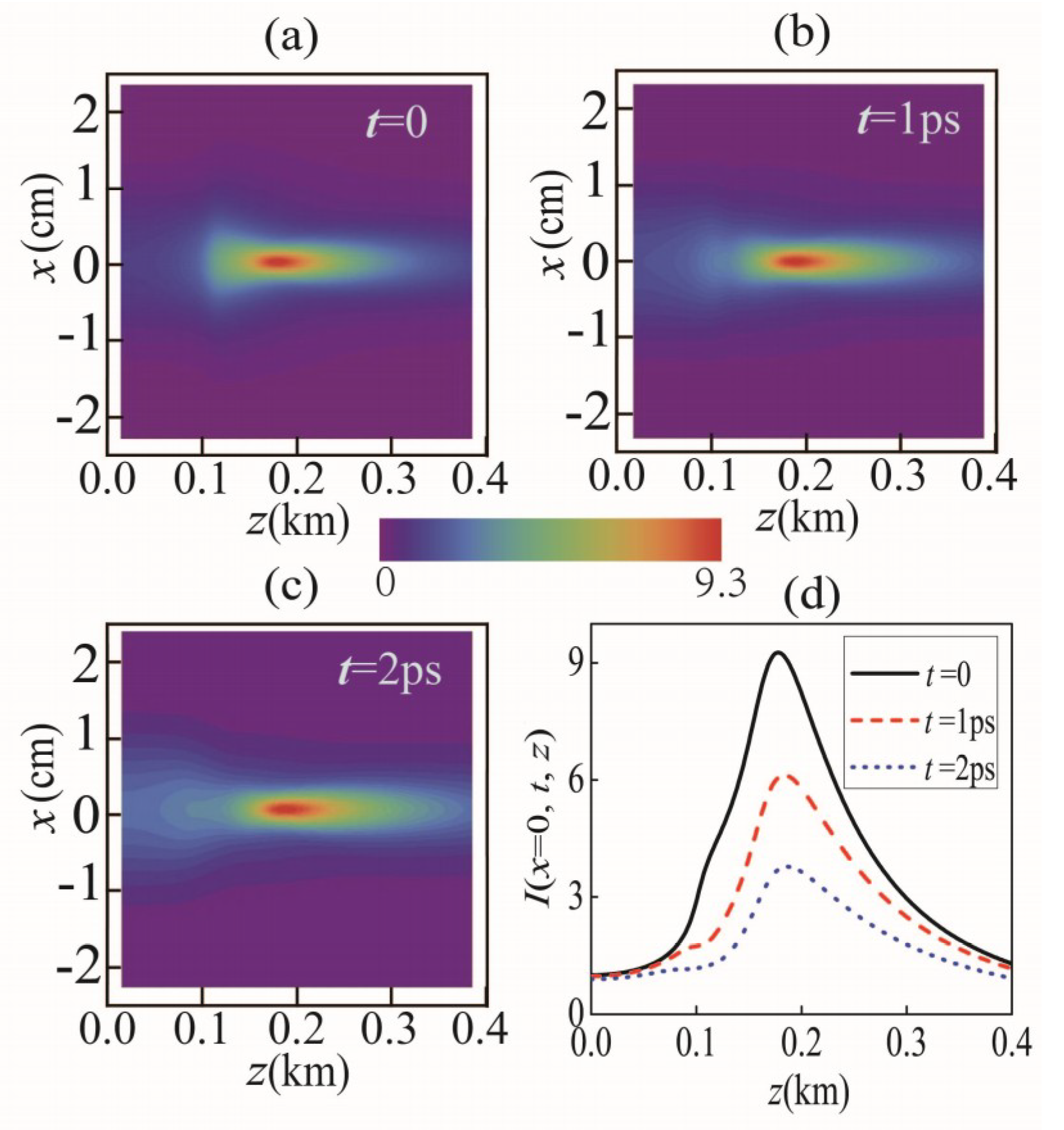
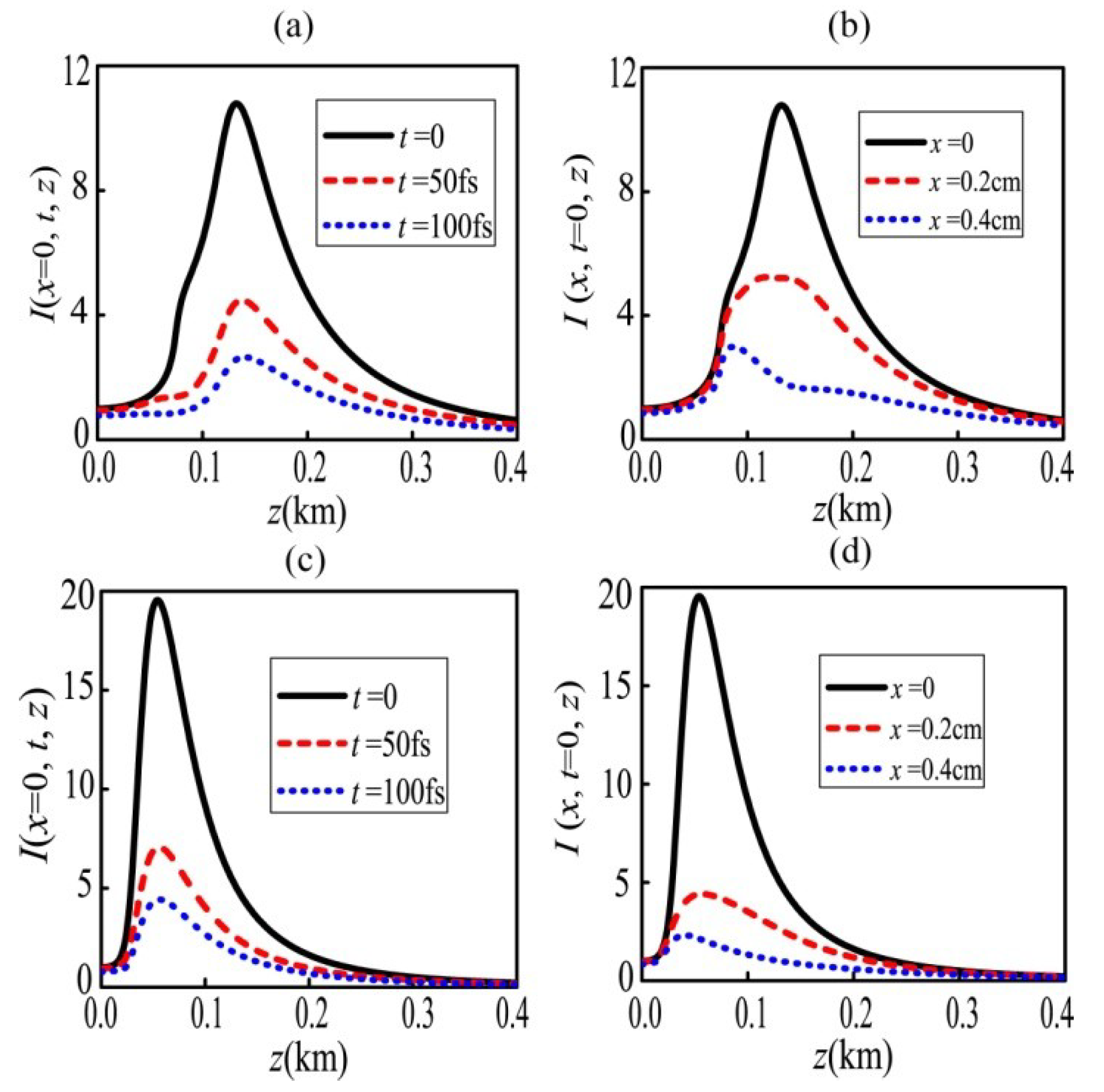
3.1. Water Case
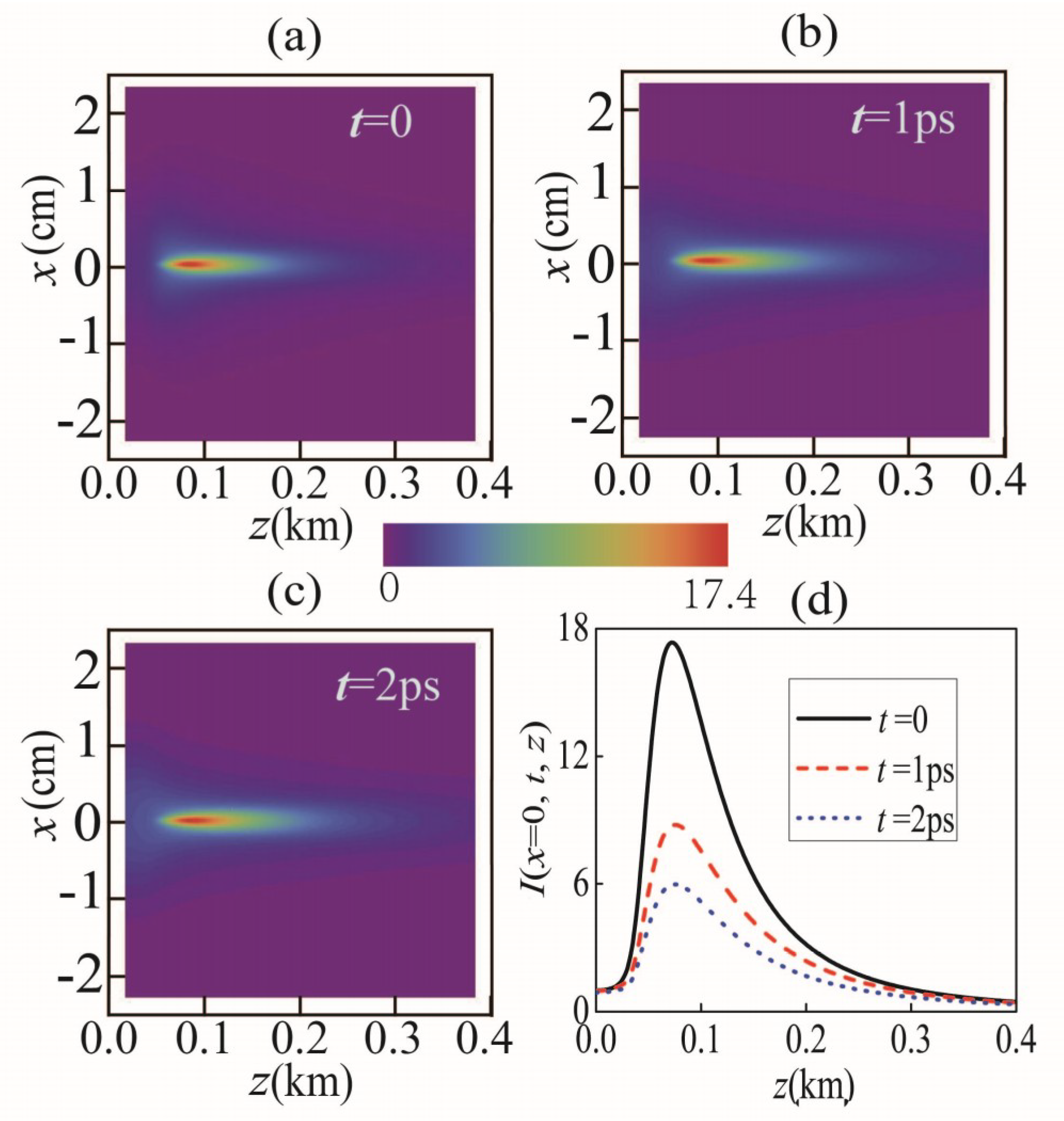
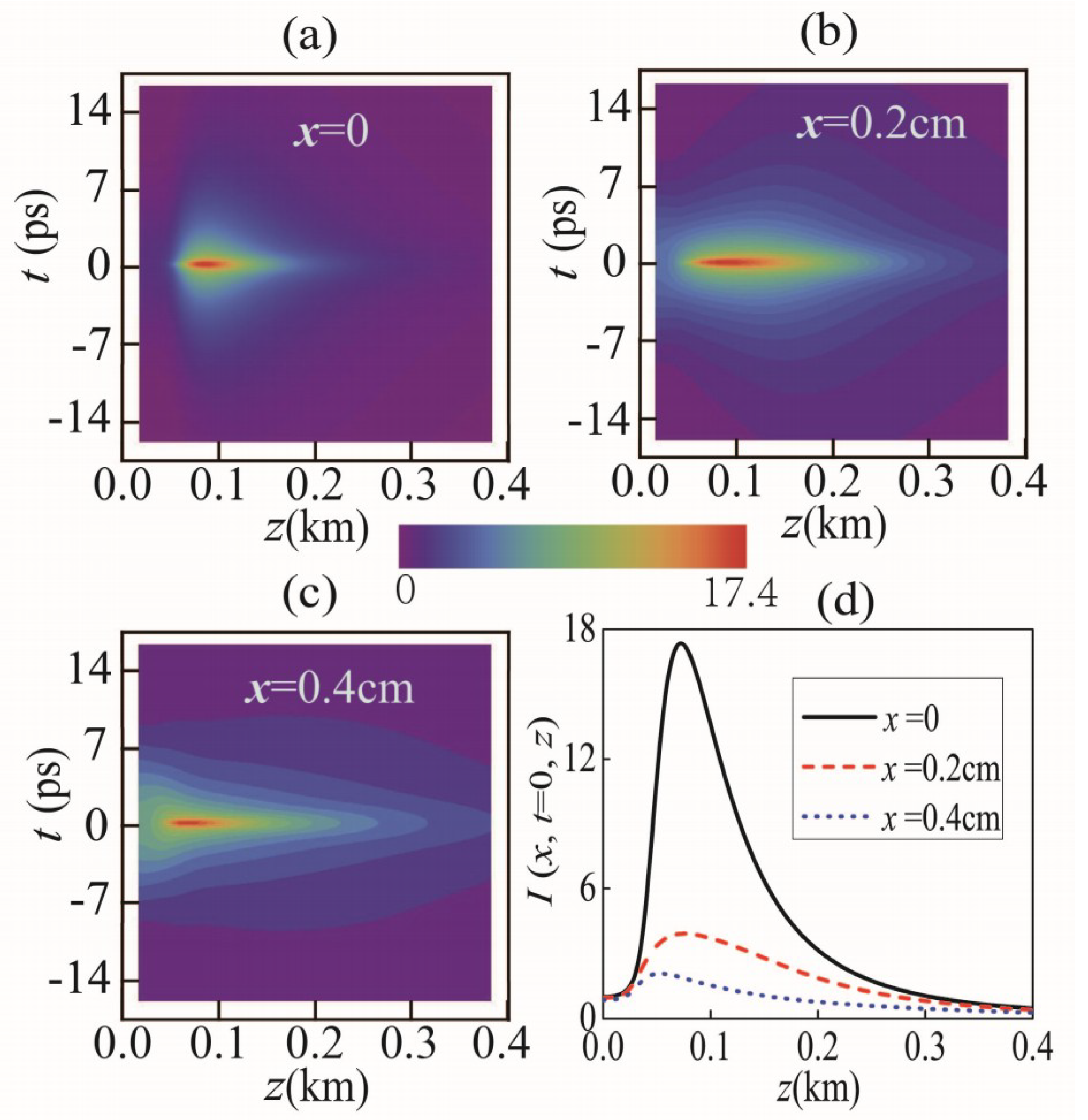
3.2. Air Case
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University: Cambridge, UK, 1995. [Google Scholar]
- Wolf, E. Introduction to the Theory of Coherence and Polarization of Light, 1st ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Gbur, G.; Visser, T.D. Can spatial coherence effects produce a local minimum of intensity at focus? Opt. Lett. 2003, 28, 1627–1629. [Google Scholar] [CrossRef]
- Pu, J.; Nemoto, S.; Liu, X. Beam shaping of focused partially coherent beams by use of the spatial coherence effect. Appl. Opt. 2004, 43, 5281–5286. [Google Scholar] [CrossRef]
- Van Dijk, T.; Fischer, D.G.; Visser, T.D.; Wolf, E. Effects of Spatial Coherence on the Angular Distribution of Radiant Intensity Generated by Scattering on a Sphere. Phys. Rev. Lett. 2010, 104, 173902. [Google Scholar] [CrossRef]
- Sahin, S.; Korotkova, O. Light sources generating far fields with tunable flat profiles. Opt. Lett. 2012, 37, 2970–2972. [Google Scholar] [CrossRef]
- Mei, Z.; Korotkova, O. Random sources generating ring-shaped beams. Opt. Lett. 2013, 38, 91–93. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, Y.; Wang, F. Generation and propagation of partially coherent beams with nonconventional correlation functions: A review. J. Opt. Soc. Am. A 2014, 31, 2083–2096, (invited). [Google Scholar] [CrossRef]
- Cai, Y.; Chen, Y.; Yu, J.; Liu, X.; Liu, L. Generation of Partially Coherent Beams. In Progress in Optics; Elsevier BV: Amsterdam, The Netherlands, 2017; Volume 62, pp. 157–223. [Google Scholar]
- Korotkova, O. Random sources for rectangular far fields. Opt. Lett. 2014, 39, 64–67. [Google Scholar] [CrossRef]
- Li, J.; Wang, F.; Korotkova, O. Random sources for cusped beams. Opt. Express 2016, 24, 17779–17791. [Google Scholar] [CrossRef]
- Wang, F.; Korotkova, O. Random sources for beams with azimuthal intensity variation. Opt. Lett. 2016, 41, 516–519. [Google Scholar] [CrossRef]
- Mei, Z.; Korotkova, O. Random sources for rotating spectral densities. Opt. Lett. 2017, 42, 255–258. [Google Scholar] [CrossRef]
- Reddy, S.G.; Kumar, A.; Prabhakar, S.; Singh, R.P. Experimental generation of ring-shaped beams with random sources. Opt. Lett. 2013, 38, 4441–4444. [Google Scholar] [CrossRef]
- Wang, F.; Liang, C.; Yuan, Y.; Cai, Y. Generalized multi-Gaussian correlated Schell-model beam: From theory to experiment. Opt. Express 2014, 22, 23456–23464. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, L.; Wang, F.; Zhao, C.; Cai, Y. Elliptical Laguerre-Gaussian correlated Schell-model beam. Opt. Express 2014, 22, 13975–13987. [Google Scholar] [CrossRef]
- Liang, C.; Wang, F.; Liu, X.; Cai, Y.; Korotkova, O. Experimental generation of cosine-Gaussian-correlated Schell-model beams with rectangular symmetry. Opt. Lett. 2014, 39, 769–772. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, F.; Liu, L.; Zhao, C.; Cai, Y.; Korotkova, O. Generation and propagation of a partially coherent vector beam with special correlation functions. Phys. Rev. A 2014, 89, 013801. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, F.; Zhao, C.; Cai, Y. Experimental demonstration of a Laguerre-Gaussian correlated Schell-model vortex beam. Opt. Express 2014, 22, 5826–5838. [Google Scholar] [CrossRef]
- Iv, M.W.H.; Basu, S.; Xiao, X.; Voelz, D.G. Producing any desired far-field mean irradiance pattern using a partially-coherent Schell-model source. J. Opt. 2015, 17, 055607. [Google Scholar]
- Milo, W.H.I.V.; Santasri, B.; David, G.V.; Xifeng, X. Experimentally generating any desired partially coherent Schell-model source using phase-only control. J. Appl. Phys. 2015, 118, 093102. [Google Scholar]
- Chen, Y.; Gu, J.; Wang, F.; Cai, Y. Self-splitting properties of a Hermite-Gaussian correlated Schell-model beam. Phys. Rev. A 2015, 91, 013823. [Google Scholar] [CrossRef]
- Chen, Y.H.; Ponomarenko, A.S.; Cai, Y.J. Experimental generation of optical coherence lattices. Appl. Phys. Lett. 2016, 109, 061107. [Google Scholar] [CrossRef]
- Hyde, M.W.; Bose-Pillai, S.; Voelz, D.G.; Xiao, X. Generation of Vector Partially Coherent Optical Sources Using Phase-Only Spatial Light Modulators. Phys. Rev. Appl. 2016, 6, 064030. [Google Scholar] [CrossRef]
- Chen, Y.; Ponomarenko, S.A.; Cai, Y. Self-steering partially coherent beams. Sci. Rep. 2017, 7, 39957. [Google Scholar] [CrossRef] [PubMed]
- Hyde IV, M.W.; Bose-Pillai, S.; Voelz, D.G.; Xiao, X. A fast and efficient method for producing partially coherent sources. J. Opt. 2017, 19, 025601. [Google Scholar] [CrossRef]
- Hyde, M.W.; Bose-Pillai, S.R.; Wood, R.A. Synthesis of non-uniformly correlated partially coherent sources using a deformable mirror. Appl. Phys. Lett. 2017, 111, 101106. [Google Scholar] [CrossRef]
- Wan, L.P.; Zhao, D.M. Optical coherence grids and their propagation characteristics. Opt. Express 2018, 26, 2168–2180. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Zhou, X.; Chen, Z.; Sasaki, O.; Li, Y.; Pu, J. Tight focusing properties of a circular partially coherent Gaussian beam. J. Opt. Soc. Am. A 2018, 35, 1974–1980. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Cai, Y.; Gbur, G. Rectangular Hermite non-uniformly correlated beams and its propagation properties. Opt. Express 2018, 26, 27894–27906. [Google Scholar] [CrossRef] [PubMed]
- de Sande, J.C.G.; Martínez-Herrero, R.; Piquero, G.; Santarsiero, M.; Gori, F. Pseudo-Schell model sources. Opt. Express 2019, 27, 3963–3977. [Google Scholar] [CrossRef] [PubMed]
- Liang, C.; Khosravi, R.; Liang, X.; Kacerovská, B.; Monfared, Y.E.; Khosrav, R. Standard and elegant higher-order Laguerre–Gaussian correlated Schell-model beams. J. Opt. 2019, 21, 085607. [Google Scholar] [CrossRef]
- Wu, G.F.; Cai, Y.J. Detection of a semirough target in turbulent atmosphere by a partially coherent beam. Opt. Lett. 2011, 36, 1939–1941. [Google Scholar] [CrossRef]
- Singh, M.; Lajunen, H.; Tervo, J.; Turunen, J. Imaging with partially coherent light: Elementary-field approach. Opt. Express 2015, 23, 28132. [Google Scholar] [CrossRef] [PubMed]
- Gbur, G. Partially coherent beam propagation in atmospheric turbulence. J. Opt. Soc. Am. A 2014, 31, 2038–2045, (invited). [Google Scholar] [CrossRef] [PubMed]
- Santarsiero, M.; Martínez-Herrero, R.; Maluenda, D.; De Sande, J.C.G.; Piquero, G.; Gori, F. Partially coherent sources with circular coherence. Opt. Lett. 2017, 42, 1512–1515. [Google Scholar] [CrossRef] [PubMed]
- Santarsiero, M.; Martínez-Herrero, R.; Maluenda, D.; De Sande, J.C.G.; Piquero, G.; Gori, F. Synthesis of circularly coherent sources. Opt. Lett. 2017, 42, 4115–4118. [Google Scholar] [CrossRef] [PubMed]
- Iv, M.W.H.; Bose-Pillai, S.R. Partially coherent sources with circular coherence: Comment. Opt. Lett. 2017, 42, 3084. [Google Scholar]
- Ding, C.; Koivurova, M.; Turunen, J.; Pan, L. Self-focusing of a partially coherent beam with circular coherence. J. Opt. Soc. Am. A 2017, 34, 1441–1447. [Google Scholar] [CrossRef]
- Torres-Company, V.; Lancis, J.; Andrés, P. Incoherent frequency-to-time mapping: Application to incoherent pulse shaping. J. Opt. Soc. Am. A 2007, 24, 888–894. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 4th ed.; Academic: New York, NY, USA, 2007. [Google Scholar]
- Nan, S.; Bai, Y.; Shi, X.; Shen, Q.; Qu, L.; Li, H.; Fu, X. Experimental investigation of ghost imaging of reflective objects with different surface roughness. Photonics Res. 2017, 5, 372–376. [Google Scholar] [CrossRef]
- Turunen, J. Low-Coherence Laser Beams. In Laser Beam Propagation: Generation and Propagation of Customized Light; Forbes, A., Ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Pääkkönen, P.; Turunen, J.; Vahimaa, P.; Friberg, A.T.; Wyrowski, F. Partially coherent Gaussian pulses. Opt. Commun. 2002, 204, 53–58. [Google Scholar] [CrossRef]
- Wang, L.; Lin, Q.; Zhu, S. Partially coherent light pulse and its propagation. Opt. Commun. 2003, 219, 65–70. [Google Scholar]
- Lajunen, H.; Tervo, J.; Vahimaa, P. Theory of spatially and spectrally partially coherent pulses. J. Opt. Soc. Am. A 2005, 22, 1536–1545. [Google Scholar] [CrossRef]
- Lancis, J.; Torres-Company, V.; Silvestre, E.; Andrés, P. Space–time analogy for partially coherent plane-wave-type pulses. Opt. Lett. 2005, 30, 2973–2975. [Google Scholar] [CrossRef] [PubMed]
- Torres-Company, V.; Mínguez-Vega, G.; Lancis, J.; Friberg, A.T. Controllable generation of partially coherent light pulses with direct space-to-time pulse shaper. Opt. Lett. 2007, 32, 1608–1610. [Google Scholar] [CrossRef] [PubMed]
- Torres-Company, V.; Lajunen, H.; Lancis, J.; Friberg, A.T. Ghost interference with classical partially coherent light pulses. Phys. Rev. A 2008, 77, 043811. [Google Scholar] [CrossRef]
- Ding, C.; Cai, Y.; Korotkova, O.; Zhang, Y.; Pan, L. Scattering-induced changes in the temporal coherence length and the pulse duration of a partially coherent plane-wave pulse. Opt. Lett. 2011, 36, 517–519. [Google Scholar] [CrossRef] [PubMed]
- Mokhtarpour, L.; Ponomarenko, S.A. Complex area correlation theorem for statistical pulses in coherent linear absorbers. Opt. Lett. 2012, 37, 3498–3500. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Dutta, R.; Korhonen, M.; Friberg, A.T.; Genty, G.; Turunen, J. Broadband spatiotemporal Gaussian Schell-model pulse trains. J. Opt. Soc. Am. A 2014, 31, 637–643. [Google Scholar] [CrossRef] [PubMed]
- Dutta, R.; Friberg, A.T.; Genty, G.; Turunen, J. Two-time coherence of pulse trains and the integrated degree of temporal coherence. J. Opt. Soc. Am. A 2015, 32, 1631–1637. [Google Scholar] [CrossRef]
- Dutta, R.; Turunen, J.; Friberg, A.T. Michelson’s interferometer and the temporal coherence of pulse trains. Opt. Lett. 2015, 40, 166–169. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, X.; Zhang, H.; Li, X.; Wang, T.; Wang, H.; Deng, Y. Self-focusing and group-velocity dispersion of pulsed laser beams in the inhomogeneous atmosphere. Opt. Express 2018, 26, 14617–14625. [Google Scholar] [CrossRef]
- Lajunen, H.; Saastamoinen, T. Non-uniformly correlated partially coherent pulses. Opt. Express 2013, 21, 190–195. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.L.; Cai, Y.J.; Zhang, Y.T.; Wang, H.X.; Zhao, Z.G.; Pan, L.Z. Stochastic electromagnetic plane-wave pulse with non-uniform correlation distribution. Phys. Lett. A 2013, 377, 1563–1565. [Google Scholar] [CrossRef]
- Ding, C.; Korotkova, O.; Pan, L. The control of pulse profiles with tunable temporal coherence. Phys. Lett. A 2014, 378, 1687–1690. [Google Scholar] [CrossRef]
- Ding, C.; Korotkova, O.; Zhang, Y.; Pan, L. Cosine-Gaussian correlated Schell-model pulsed beams. Opt. Express 2014, 22, 931–942. [Google Scholar] [CrossRef] [PubMed]
- Ding, C.; Koivurova, M.; Turunen, J.; Pan, L. Temporal self-splitting of optical pulses. Phys. Rev. A 2018, 97, 053838. [Google Scholar] [CrossRef]
- Liu, X.Y.; Zhao, D.M.; Tian, K.H.; Pan, W.Q.; Zhang, K.W. Gaussian temporal modulation for the behavior of multi-sinc Schell-model pulses in dispersive media. Opt. Commun. 2018, 416, 160–165. [Google Scholar] [CrossRef]
- Luo, M.L.; Zhao, D.M. Characterizing the polarization and cross-polarization of electromagnetic vortex pulses in the space-time and space-frequency domain. Opt. Express 2015, 23, 4153–4162. [Google Scholar] [CrossRef]
- Lajunen, H.; Turunen, J.; Vahimaa, P.; Tervo, J.; Wyrowski, F. Spectrally partially coherent pulse trains in dispersive media. Opt. Commun. 2005, 255, 12–22. [Google Scholar] [CrossRef]
- Lajunen, H.; Saastamoinen, T. Propagation characteristics of partially coherent beams with spatially varying correlations. Opt. Lett. 2011, 36, 4104–4106. [Google Scholar] [CrossRef]
- Jing, C.; Qi, X.; Wang, Z.; Ma, B.; Ding, C. Comparative study of femtosecond filamentation properties in the classical model and the full model for different incident pulse durations. J. Opt. 2019, 21, 065503. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Ding, C.; Zhang, Y.; Pan, L. Spatial-Temporal Self-Focusing of Partially Coherent Pulsed Beams in Dispersive Medium. Appl. Sci. 2019, 9, 3616. https://doi.org/10.3390/app9173616
Zhao Z, Ding C, Zhang Y, Pan L. Spatial-Temporal Self-Focusing of Partially Coherent Pulsed Beams in Dispersive Medium. Applied Sciences. 2019; 9(17):3616. https://doi.org/10.3390/app9173616
Chicago/Turabian StyleZhao, Zhiguo, Chaoliang Ding, Yongtao Zhang, and Liuzhan Pan. 2019. "Spatial-Temporal Self-Focusing of Partially Coherent Pulsed Beams in Dispersive Medium" Applied Sciences 9, no. 17: 3616. https://doi.org/10.3390/app9173616
APA StyleZhao, Z., Ding, C., Zhang, Y., & Pan, L. (2019). Spatial-Temporal Self-Focusing of Partially Coherent Pulsed Beams in Dispersive Medium. Applied Sciences, 9(17), 3616. https://doi.org/10.3390/app9173616