Abstract
All real-world systems are affected by the saturation phenomenon due to inherent physical limitations of actuators. These limitations should be taken into account in the controller’s design to prevent a possibly severe deterioration of the system’s performance, and may even lead to instability of the closed-loop system. Contrarily to most of the control strategies, which assume that the saturation limits are constant in time, this paper considers the problem of designing a state-feedback controller for a system affected by time-varying saturation limits with the objective to improve the performance. In order to tie variations of the saturation function to changes in the performance of the closed-loop system, the shifting paradigm is used, that is, some parameters scheduled by the time-varying saturations are introduced to schedule the performance criterion, which is considered to be the instantaneous guaranteed decay rate. The design conditions are obtained within the framework of linear parameter varying (LPV) systems using quadratic Lyapunov functions with constant Lyapunov matrices and they consist in a linear matrix inequality (LMI)-based feasibility problem, which can be solved efficiently using available solvers. Simulation results obtained using an illustrative example demonstrate the validity and the main characteristics of the proposed approach.
1. Introduction
The phenomenon of saturation affects all real-world systems due to the inherent physical limitations of actuation devices. Designing a control system without taking into account the presence of saturation may lead to severe deterioration of the performance and even to instability of the closed-loop system. For this reason, this issue has been investigated by several control theorists, with recent results such as those reported in References [1,2,3,4,5,6,7]. Existing solutions may be divided into two categories—anti-windup compensation [8], where a compensator is added to an already designed controller in order to handle the saturation constraints and direct control design [9], in which the input constraints are considered at the controller design stage.
In the vast literature addressing the saturation problem, the assumption that the saturation limits are constant in time is made, to the best of the authors’ knowledge. For example, this assumption can be found in Reference [10], where the region of attraction of a saturated linear parameter varying (LPV) system with bounded parameter variations is optimized by means of parameter-dependent Lyapunov functions, generalized sector conditions and a static output-feedback controller. The same assumption holds in Reference [11], where the idea is to approximate the region of attraction using the concept of quadratic boundedness, such that off-line optimization algorithms are presented to design a saturated dynamic output feedback controller for an LPV system with bounded disturbance. On other hand, in Reference [12] the saturation phenomenon is included in the design problem of an dynamic output-feedback controller for a class of uncertain discrete stochastic nonlinear time-varying systems using the recursive linear matrix inequality (RLMI) approach, thus obtaining a suitable algorithm for online applications.
However, from a practical viewpoint, it makes sense to consider time-varying saturation limits. They could arise in control systems due to several reasons, such as the natural wear of engines and devices, that would provide a progressively decreasing actuation signal or temporary shortages in the availability of electrical or pneumatic power. Moreover, in trajectory tracking problems, the control signal is usually obtained as the sum of a feedforward and a feedback component. When a time-varying trajectory is considered, the feedforward component changes in time, which would be perceived by the feedback controller as a time-varying saturation.
The main goal of this paper is to propose a methodology for designing state-feedback controllers that take into account time-varying input saturations. It makes sense that a change in the saturation function should be tied to a change in the performance achieved by the closed-loop control system (e.g., if the maximum possible input decreases, the system’s response should become slower). For this reason, the time-varying saturation limits are addressed using shifting specifications, following some ideas found, for example, in References [13,14]. This means that some parameters are introduced which, on the one hand, they are scheduled by the time-varying saturations and, on the other hand, they schedule the performance criteria in such a way that different values of these parameters imply different performances (in this paper, we will consider the guaranteed decay rate but the developed results can be extended straightforwardly to other criteria, for example, pole clustering or / guaranteed bounds).
The direct consequence of introducing the above mentioned scheduling parameters is that the closed-loop system becomes a parameter-varying system and the design conditions can be determined within the framework of linear parameter varying (LPV) systems [15,16]. Notably, many nonlinearities can be represented as varying parameters that depend on endogenous signals, for example, states and inputs [17], which broadens the applicability of the design methodology to nonlinear plants. Examples of successful applications of the LPV paradigm are—wind turbines [18], vehicles [19,20] and drones [21].
As in Reference [13], the proposed approach is obtained using quadratic Lyapunov functions with constant matrices and, therefore, the results might be somehow conservative when compared to other types of Lyapunov functions, for example, parameter-dependent [22] or piecewise [23], which lead to more complex mathematical calculations and are beyond the scope of this paper. The final design procedure is developed using the theory of ellipsoidal invariant sets [24]. It consists on a linear matrix inequality (LMI)-based feasibility problem, which can be solved efficiently using available solvers (the reader is referred to Reference [25] for a tutorial on the application of LMIs to LPV analysis and design problems).
This paper is structured as follows. In Section 2, the problem statement is introduced. In Section 3, the procedure for controller design with constant saturation is given. In Section 4, the proposed methodology is adapted to the case of time-varying input saturation. Section 5 presents an illustrative example with simulation results. Finally, Section 6 summarizes the main conclusions and discusses possible future work.
2. Problem Statement
Let us consider a continuous-time LPV system
where is the state vector, is the input vector and is the scheduling parameter vector, with known, closed and bounded set. Matrices , , and are the parameter-dependent state, input, output and feedforward matrices, respectively.
The polytopic representation of (1) is used throughout this paper. In this representation, the system’s matrices are defined as a weighted sum of matrices that represent the system in the N vertices of a polytope that contains
where matrices , , and define the so-called vertex systems and are the coefficients of the polytopical decomposition that satisfy
The time dependency of x, , y and u is dropped from now on and it will only be made explicit when necessary. Also, without loss of generality, we consider the behaviour of the system starting from a time instant . The extension to the case where is straightforward by means of a simple translation of the time axis.
The following assumptions are made on (2):
Assumption 1.
The state variables and the scheduling variables are measurable or can be estimated online.
Assumption 2.
The input and output matrices are constant.
Assumption 3.
System disturbances are not considered.
Assumption 4.
The system (2) is stabilizable.
Remark 1.
Note that Assumptions 1–3 are only made for the sake of keeping the mathematical complexity somehow simpler and could be removed by extending the results presented in this paper taking into account existing techniques in the literature. For instance, inexactly measured parameters were considered by Reference [26]; the complexity arising from parameter-varying input and output matrices can be dealt with using conditions based on Polya’s theorems [27]; disturbances can be considered under a quadratic boundedness framework, see for example, Reference [28]. On the other hand, Assumption 4 is a necessary (not sufficient) condition in order to solve the controller design problem described in this paper. Note that recent work has suggested a practical test to assess this property in systems described by a polytopic representation [29].
Considering the above assumptions, the output equation can be neglected and (2) becomes
In this paper, we consider the case in which the input signal is affected by a nonlinearity, such that the change arises in (4), with denoting a symmetric saturation
where > and ≤ are meant element-wise and is the saturation limit value, which is considered constant in Section 3 and time-varying within the interval in Section 4.
The contribution of this work lies in proposing conditions to design an LPV state-feedback controller that ensures the stability of the system (4). In order to obtain these conditions, three ellipsoidal regions are established in the state domain—region contains the set of allowed initial conditions of the system; region is defined by a quadratic Lyapunov function, whose unit level curve contains ; and, finally, region corresponds to an ellipsoidal subset of the region of the state space , in which the input u is not saturated. These four regions satisfy the relation
On the basis of (6) a set of LMIs that provide conditions for the design of the LPV state-feedback controller is obtained.
Remark 2.
Note that the proposed design methodology considers the input to work only in its linear region, which introduces additional conservativeness. This drawback could be alleviated by scheduling the controller also with saturation indicator parameters, as suggested by Reference [30].
3. Design with Constant Input Saturation
Let us define the state-feedback control law for (4) as
where is the parameter-dependent gain matrix and , denotes the gain matrix for each vertex i.
Let us also define the region as the one that determines the allowed initial states. It is defined by means of matrix as follows
In order to consider exactly (5) within the design, polyhedral Lyapunov functions should be considered, which adds computational complexity since the arising design conditions cannot be expressed as LMIs. For this reason, let us consider an ellipsoidal maximal volume region contained in the hyper-rectangle described by (5), as follows
where , , W is a rotation matrix that describes the axes orientation of the ellipsoid and
Hereinafter, without loss of generality, we assume that since in most of the cases the axes of the ellipsoidal region are aligned with the axes of the input space.
Note that the ellipsoid , although defined in the input space, is mapped onto the state space as a parameter-varying ellipsoid by means of the state-feedback control law, as follows
The following theorem provides the conditions to obtain the vertex gains that ensure the closed-loop stability with guaranteed decay rate of the system obtained as the interconnection of (4) and (7).
Theorem 1.
Consider the continuous time LPV system (4), the control law (7) and the regions and defined in (8) and (11), respectively, with given matrices and , and a desired . If , there exist a symmetric matrix and matrices such that the following set of LMIs is feasible
and the vertex gains of the LPV state-feedback controller are calculated as . Then the closed-loop system obtained as the interconnection of (4) and (7) is stable and has a guaranteed decay rate α. Moreover, the control law computed as (7) is such that .
Proof.
By defining the quadratic Lyapunov function, , where , the closed-loop stability inequality is obtained for each vertex i from the condition
where is obtained by means of a change of variable, as follows
The term can be added to the inequalities (16) to ensure a guaranteed decay rate of the derivative of the Lyapunov function, which can be used to tune the closed-loop transient properties [24], thus obtaining (13).
Thereupon, let us introduce the ellipsoidal region , which corresponds to the unit level curve of the Lyapunov function
By introducing an inclusion relation between and , one can guarantee that, as long as the system is working in the linear region of the saturation function, any state trajectory which starts from an initial state contained in will necessarily remain inside region . In particular, the inclusion can be expressed by the following inequality
which, by means of appropriate manipulations, leads to
and, by means of Schur complements, leads to (14).
Finally, taking into account the inclusion , we can guarantee that any state trajectory contained in the unit level curve of the Lyapunov function will also lie in the region of linearity of the actuators, such that no saturation occurs and, hence, convergence of x to 0 when is ensured for any (hence, for any ). In particular, the above inclusion is described by
Remark 3.
Note that the quadratic Lyapunov function used in the proof of the Theorem 1 introduces conservativeness due to the constant matrix P. The conservativeness can be decreased by modifying through a parameter-dependent matrix , although such modification would add computational complexity to the LMI problem.
4. Design with Time-Varying Input Saturation
Following some ideas that appeared in Reference [13], we adapt the controller’s design to deal with time-varying input saturation limits. In the proposed method, we add a new scheduling parameter vector to describe changes in time of the saturation function and we use it to schedule both the controller and the achieved performance. More specifically, the vector of varying parameters in (4), is augmented with another vector that is linked to by the following relation
Note that the values of , calculated as in (23) are constrained to belong to the interval . Also note that (23) can be used to express as a function of , as follows
As a consequence, the expression for in the input space becomes
and, taking into account the new scheduling parameters, let us modify (7) as follows
Similar to the previous section, the region is mapped onto the state domain as a parameter-varying ellipsoid by means of the new state-feedback control law (26), as follows
The following theorem, akin to Theorem 1, provides the conditions to obtain the vertex gains of the LPV state-feedback controller (26) that ensure the closed-loop stability of the system (4) and the ability to change the guaranteed decay rate according to changes in the time-varying saturation limits.
Theorem 2.
Consider the continuous time LPV system (4), the control law (26) and the regions and of the state space described by (8) and (27), respectively, with given matrices and , and a desired parameter-varying decay rate that varies within the interval . Assume that parameter-dependent matrix and the function can be expressed in polytopic form as follows
where M is the number of vertices of Φ . If , there exist a symmetric matrix and matrices such that the following set of LMIs is feasible
and the vertex gains of the LPV state-feedback controller are calculated as . Then the closed-loop system obtained as the interconnection of (4) and (26) is stable and has guaranteed decay rate . Moreover, the control law computed as (26) is such that .
Proof.
Theorem 2 ensures the closed-loop system’s stability in the same way as Theorem 1, adding the adaptive capacity of the controller to decrease the closed-loop performance when the saturation limits decrease. Hereunder, a sketch of this proof is presented.
By defining the same quadratic Lyapunov function of Theorem 1 with the constraint (30) and the control law (26), the closed-loop stability inequality is obtained for each value of and from the condition
where .
Additionally, (29) is added to (34) through the parameter-dependent term in order to adjust online the closed-loop performance depending on the instantaneous saturation limits. As a consequence, we ensure a guarantee decay rate of that varies within the interval , thus obtaining
that can be described by (31) for each vertex and of and , respectively.
Thereupon, let us consider the regions (8) and (18) and the inclusion described by (19) to obtain (32).
Finally, by means of appropiate manipulations and the application of Schur complements, the inclusion leads to the following inequality
that can be described by (33) for each vertex as mentioned above. □
Note that the polytopical representation of described by (28) is valid for given by the following
Additionally, the vertex coefficients of can be obtained as follows
where and denotes the cardinality of the set .
Remark 4.
Note that, in this paper, for illustrative purposes and to maintain the overall formulation simple, we have decided to consider a scheduled guaranteed decay rate as performance criterion but the results could be generalized to other criteria, for example, sector clusters in the complex plane to avoid undesired oscillations [31].
5. Illustrative Example
In this section, an illustrative example is introduced to show the closed-loop performance of an LPV state-feedback controller, designed with Theorem 2, under time-varying input saturation limits. Note that the results corresponding to an LPV controller designed using Theorem 1 are omitted because they can be considered a particular case of Section 4 in which the saturation scheduling variables are frozen.
Figure 1 presents the followed control-loop scheme throughout the example.
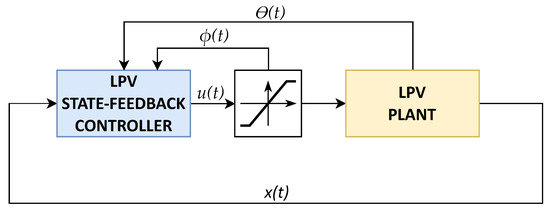
Figure 1.
Control scheme.
Let us consider the LPV plant modelled as in (1) with the following state-space matrices (note that the system is open-loop unstable for every frozen value of )
where B, C and D are constant due to Assumptions 2 and 3, and the parameter-varying state matrix can be written in the polytopic form (2) with vertex state matrices
Let us consider a time-varying input saturation, where the saturation limits of and are and respectively.
Following the method described in Section 4, the LPV state-feedback controller is scheduled by the following parameters
The controller’s design is obtained solving the LMIs (30)–(33) of Theorem 2, which are particularized as follows
where and R has been chosen as
so that the expected initial condition for the system lies in a circle centered in the origin of the state space, with radius 0.1. On the other hand the polytopical expression of (29) for is
and it is chosen to vary within the interval obtaining the following coefficients through (40)
Finally, taking into account the variability of and , the matrices are given by
By using the SeDuMi solver [32] and the YALMIP [33] toolbox, we find a solution of (45) that, through , allows us to calculate the eight controller vertex gains.
Hereafter, two different scenarios are used to show that the designed LPV state-feedback controller is able to guarantee the closed-loop system stability and its capacity to adapt its performance taking into account the time-varying limits of the input saturation.
5.1. Scenario I
The purpose of Scenario I is to evaluate the closed-loop system stability and its closed-loop performance for a given initial condition with three different constant values of the control input saturation. To do this, we simulate the closed-loop response from an initial state and . Finally, fixing the frozen values of , and , thus obtaining instantaneous saturation limits values and , and and and , respectively.
As shown in Figure 2, the closed-loop system stability is guaranteed for all the values of and that were mentioned. Moreover, note that the system’s response that was evaluated with the scheduling parameters , corresponds to the maximum allowed limit values of and , obtaining the fastest system response and showing that the designed LPV state-feedback controller is able to adjust the system’s performance depending on the different values taken by .
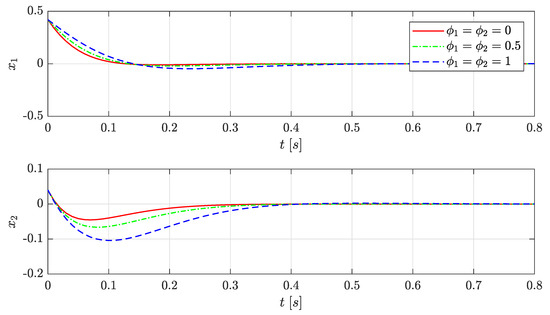
Figure 2.
Scenario I: closed-loop system response.
Figure 3 shows the instantaneous values of the saturation limit of and for the three frozen values of and and the evolution of the control signals. For illustrative purposes, since the signal takes only negative values during the system’s response, only the lower bound of the saturation is plotted. As a variation of the saturation limit occurs, the input signal changes as a result of the adaptability capacity of the designed controller. For example, the interval of linearity of the control signal corresponds to when and to when . Note that if the controller gain corresponding to had been used for the case in which , then saturation would have occurred.
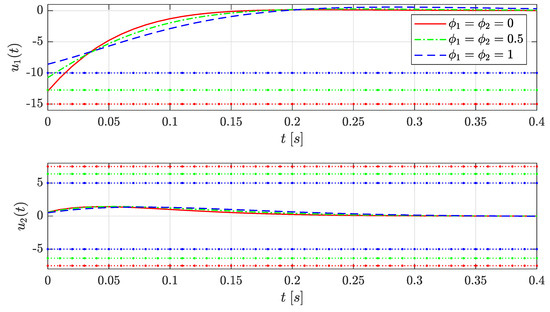
Figure 3.
Scenario I: control input responses (the saturation limits are shown as dotted lines).
Figure 4 shows the evolution of the Lyapunov function for the three frozen values of and , which correspond to guaranteed decay rates of 10, 5.5 and 1 respectively. It can be seen that the largest decay rate corresponds to the fastest closed-loop system response, whose saturation scheduling parameters are and . Also, all the functions are under the unit value, hence it is guaranteed by design that none of the control inputs saturates, as already shown in Figure 3.
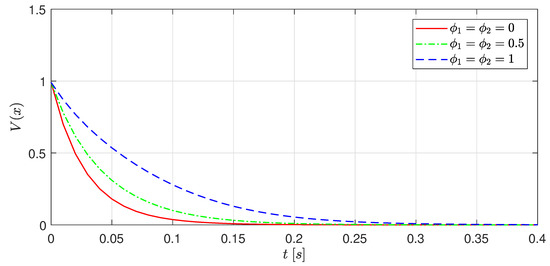
Figure 4.
Scenario I: Lyapunov functions evolution.
5.2. Scenario II
Scenario II shows the adaptability of the designed controller to changes in along the transient response of the closed-loop. We consider and . Also, we fix and we vary such that it switches between its known limits and .
Figure 5 shows that the designed LPV state-feedback controller is able to adapt the generated control signal taking into account the changes in .
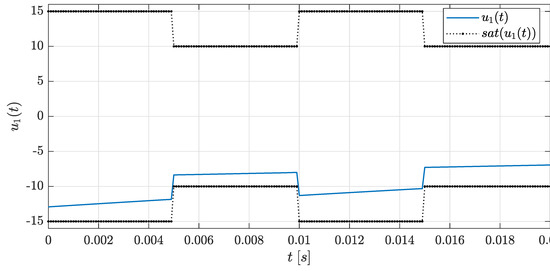
Figure 5.
Scenario II: adaptability of control signal .
Figure 6 shows the evolution of the Lyapunov function , which decreases slower when the guaranteed decay rate , as a result of fixing and faster when . As a consequence, the closed-loop system performance is modified online according to changes in the saturation limits.
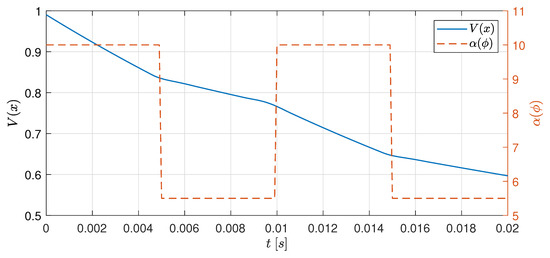
Figure 6.
Scenario II: Lyapunov function and guaranteed decay rate.
6. Conclusions and Future Work
In this paper, the problem of designing an LPV state-feedback controller that takes into account the time-varying saturation limits has been investigated. The design procedure corresponds to checking the feasibility of an appropriate set of LMIs, which can be solved efficiently using available solvers. Finally, the results obtained in the illustrative example correspond to the case where the LPV state-feedback controller designed following the proposed methodology is evaluated in an LPV mathematical system with time-varying boundaries, showing that the controller guarantees the closed-loop stability and its capacity of adjusting the system’s performance in front of the variability of the saturation limits.
Future work will focus on applying the procedure described in this paper to design an LPV controller using robust control techniques combined with a model reference control for UAV vehicles. Moreover, in order to deal with exogenous disturbances, for example, wind gusts in the application of UAV control, the results presented in this paper will be extended to the case where disturbance rejection is considered.
Author Contributions
Conceptualization, Methodology, Supervision and Writing—original draft, review & editing, A.R., D.R. and B.M.
Funding
This work has been partially funded by the Spanish State Research Agency (AEI) and the European Regional Development Fund (ERFD) through the project SCAV (ref. MINECO DPI2017-88403-R). This work has also been partially funded by AGAUR of Generalitat de Catalunya through the Advanced Control Systems (SAC) group grant (2017 SGR 482) and by the Spanish State Research Agency through the Maria de Maeztu Seal of Excellence to IRI (MDM-2016-0656). Adrián Ruiz is also supported by Formació Personal Investigador a la Universitat Politècnica de Catalunya under an FPI-UPC 2018 grant (ref. 20 FPI-UPC 2018). Damiano Rotondo is also supported by Juan de la Cierva - Formacion grant (FJCI-2016-29019).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tarbouriech, S.; Garcia, G.; Gomes da Silva, J.M., Jr.; Queinnec, I. Stability and Stabilization of Linear Systems with Saturating Actuators; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Corradini, M.L.; Cristofaro, A.; Orlando, G. Robust stabilization of multi input plants with saturating actuators. IEEE Trans. Autom. Control 2010, 55, 419–425. [Google Scholar] [CrossRef]
- Corradini, M.L.; Cristofaro, A.; Orlando, G. Sliding-mode control of discrete-time linear plants with input saturation: Application to a twin-rotor system. Int. J. Control 2014, 87, 1523–1535. [Google Scholar] [CrossRef]
- Rotondo, D.; Ponsart, J.C.; Theilliol, D.; Nejjari, F.; Puig, V. A virtual actuator approach for the fault tolerant control of unstable linear systems subject to actuator saturation and fault isolation delay. Annu. Rev. Control 2015, 39, 68–80. [Google Scholar] [CrossRef]
- Rotondo, D.; Rizzello, G.; Naso, D. Robust control of systems with output hysteresis and input saturation using a finite time stability approach. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami Beach, FL, USA, 17–19 December 2018; pp. 3830–3835. [Google Scholar]
- Jeyasenthil, R.; Choi, S.B. A new anti-windup compensator based on quantitative feedback theory for an uncertain linear system with input saturation. Appl. Sci. 2019, 9, 10. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, H.; Hao, F. Decentralized integral-based event-triggered stabilization for linear plant with actuator saturation and output feedback. Appl. Sci. 2017, 7, 11. [Google Scholar] [CrossRef]
- Hussain, M.; Rehan, M.; Ahn, C.K.; Zheng, Z. Static anti-windup compensator design for nonlinear time-delay systems subjected to input saturation. Nonlinear Dyn. 2018, 95, 1879–1901. [Google Scholar] [CrossRef]
- Aouaouda, S.; Chadli, M. Robust fault tolerant controller design for Takagi-Sugeno systems under input saturation. Int. J. Syst. Sci. 2019, 50, 1163–1178. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Chevrel, P.; Claveau, F. Gain-scheduled static output feedback control for saturated LPV systems with bounded parameter variations. Automatica 2018, 89, 420–424. [Google Scholar] [CrossRef]
- Ping, X.; Wang, P.; Li, Z. Quadratic boundedness of LPV systems via saturated dynamic output feedback controller. Optim. Control Appl. Methods 2017, 38, 1239–1248. [Google Scholar] [CrossRef]
- Wang, Z.; Ho, D.W.; Dong, H.; Gao, H. Robust H∞ finite-horizon control for a class of stochastic nonlinear time-varying systems subject to sensor and actuator saturations. IEEE Trans. Autom. Control 2010, 55, 1716–1722. [Google Scholar] [CrossRef]
- Rotondo, D.; Nejjari, F.; Puig, V. Design of parameter-scheduled state-feedback controllers using shifting specifications. J. Frankl. Inst. 2015, 352, 93–116. [Google Scholar] [CrossRef]
- Sánchez, H.S.; Rotondo, D.; Puig Cayuela, V.; Quevedo Casín, J.J. A shifting pole placement approach for the design of performance-varying multivariable PID controllers via BMIs. In Proceedings of the PID 2018: 3rd IFAC Conference on Advances in Proportional-Integral-Derivative Control, Ghent, Belgium, 9–11 May 2018; pp. 256–261. [Google Scholar]
- Rotondo, D. Advances in Gain-Scheduling and Fault Tolerant Control Techniques; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Yang, Z.; Chai, Y.; Yin, H.; Tao, S. LPV model based sensor fault diagnosis and isolation for permanent magnet synchronous generator in wind energy conversion systems. Appl. Sci. 2018, 8, 1816. [Google Scholar] [CrossRef]
- Hoffmann, C.; Werner, H. A survey of linear parameter-varying control applications validated by experiments or high-fidelity simulations. IEEE Trans. Control Syst. Technol. 2014, 23, 416–433. [Google Scholar] [CrossRef]
- Pérez-Estrada, A.J.; Osorio-Gordillo, G.L.; Alma, M.; Darouach, M.; Olivares-Peregrino, V.H. H∞ generalized dynamic unknown inputs observer design for discrete LPV systems. Application to wind turbine. Eur. J. Control 2018, 44, 40–49. [Google Scholar] [CrossRef]
- Lopez Estrada, F.R.; Zaragoza, C.M.A.; Palomo, G.V.; Rojas, C.R.; Gonzalez, C.G.; Gomez, E.E. Observer-based LPV stabilization system for a riderless bicycle. IEEE Lat. Am. Trans. 2018, 16, 1076–1083. [Google Scholar] [CrossRef]
- Morato, M.M.; Nguyen, M.Q.; Sename, O.; Dugard, L. Design of a fast real-time LPV model predictive control system for semi-active suspension control of a full vehicle. J. Frankl. Inst. 2019, 356, 1196–1224. [Google Scholar] [CrossRef]
- Trapiello, C.; Puig, V.; Morcego, B. Position-heading quadrotor control using LPV techniques. IET Control Theory Appl. 2019, 13, 783–794. [Google Scholar] [CrossRef]
- Cox, P.B.; Weiland, S.; Tóth, R. Affine parameter-dependent Lyapunov functions for LPV systems with affine dependence. IEEE Trans. Autom. Control 2018, 63, 3865–3872. [Google Scholar] [CrossRef]
- Johansson, M.; Rantzer, A.; Arzen, K.E. Piecewise quadratic stability of fuzzy systems. IEEE Trans. Fuzzy Syst. 1999, 7, 713–722. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994; Volume 15. [Google Scholar]
- Rotondo, D.; Sanchez, H.S.; Nejjari, F.; Puig, V. Analysis and design of linear parameter varying systems using LMIs. Rev. Iberoam. Autom. Inform. Ind. 2019, 16, 1–14. [Google Scholar] [CrossRef]
- Daafouz, J.; Bernussou, J.; Geromel, J.C. On inexact LPV control design of continuous-time polytopic systems. IEEE Trans. Autom. Control 2008, 53, 1674–1678. [Google Scholar] [CrossRef]
- Sala, A.; Arino, C. Asymptotically necessary and sufficient conditions for stability and performance in fuzzy control: Applications of Polya’s theorem. Fuzzy Sets Syst. 2007, 158, 2671–2686. [Google Scholar] [CrossRef]
- Cayero, J.; Rotondo, D.; Morcego, B.; Puig, V. Optimal state observation using quadratic boundedness: Application to UAV disturbance estimation. Int. J. Appl. Math. Comput. Sci. 2019, 29, 99–109. [Google Scholar] [CrossRef]
- Witczak, M.; Rotondo, D.; Puig, V.; Witczak, P. A practical test for assessing the reachability of discrete-time Takagi–Sugeno fuzzy systems. J. Frankl. Inst. 2015, 352, 5936–5951. [Google Scholar] [CrossRef]
- Wu, F.; Grigoriadis, K.M.; Packard, A. Anti-windup controller design using linear parameter-varying control methods. Int. J. Control 2000, 73, 1104–1114. [Google Scholar] [CrossRef]
- Chilali, M.; Gahinet, P. H∞ Design with pole placement constraints: An LMI approach. IEEE Trans. Autom. Control 1996, 41, 358–367. [Google Scholar] [CrossRef]
- Sturm, J.F. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optim. Methods Softw. 1999, 11, 625–653. [Google Scholar] [CrossRef]
- Löfberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the CACSD Conference, Taipei, Taiwan, 2–4 September 2004; Volume 3. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).