The Photovoltaic Output Prediction Based on Variational Mode Decomposition and Maximum Relevance Minimum Redundancy
Abstract
1. Introduction
2. Methodology
- (1)
- The VMD proposed by Dragomiretskiy K in 2014 is the new kind of non-stationary signal adaptive decomposition estimation method [31], which aims to decompose the original complex non-stationary photovoltaic sequence into sub-sequences with different characteristics. Compared with wavelet decomposition, EMD decomposition and EEMD decomposition, VMD decomposition can suppress modal aliasing more effectively.
- (2)
- The mRMR was proposed by Peng, HC. et al. in 2005, and is a feature selection method that uses mutual information and correlation distance to calculate correlation [32]. It has the feature of maximizing the correlation between features and categorical variables, and minimizing the correlation between features and features, mainly used to solve the redundancy of feature variables.
- (3)
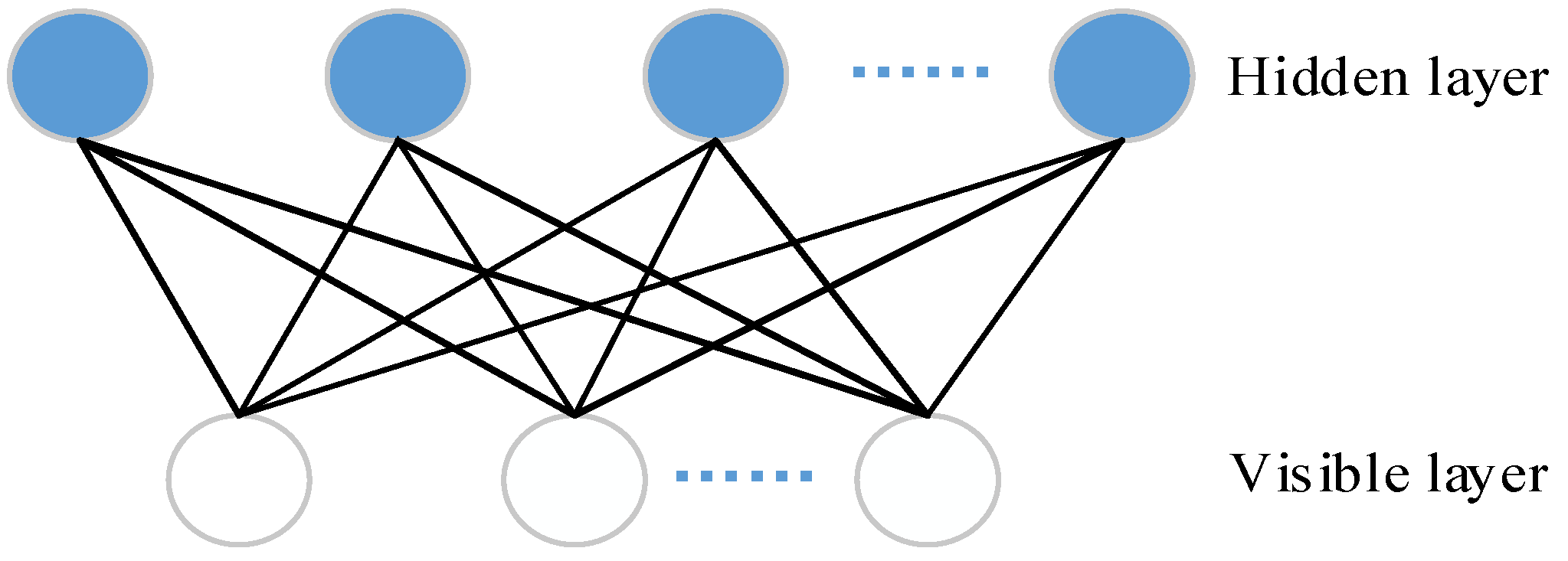
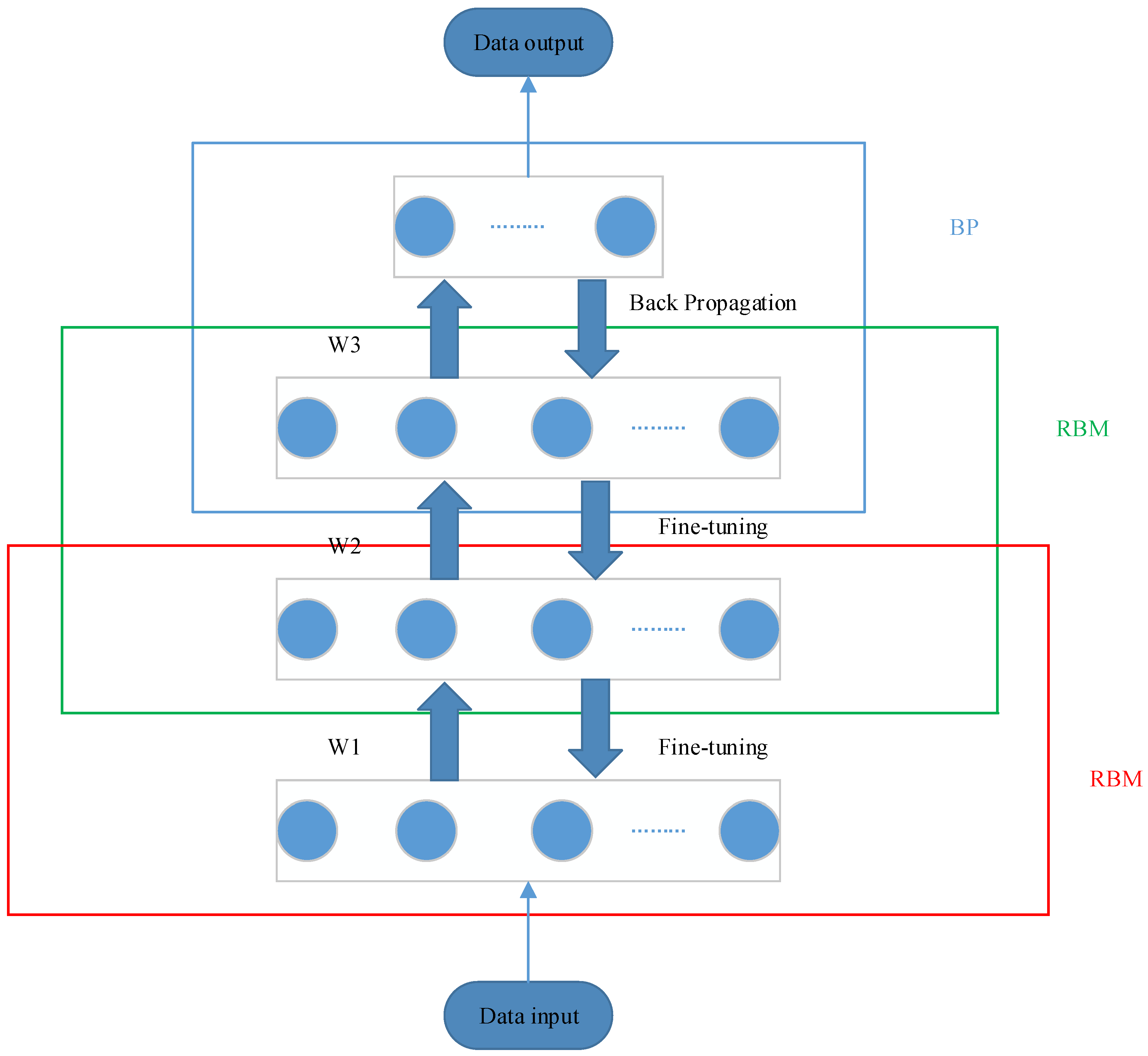
- DBN is a deep network efficient learning algorithm proposed by Hinton et al., with adaptive and self-learning capabilities, mainly used to deal with high-dimensional, large-scale data problems [33]. A DBN network consists of several layers of unsupervised restricted Boltzmann machine (RBM) and a supervised back-propagation (BP). RBM is a probability graph model consisting of visible layers and hidden layers, two layers of neurons are connected by weights. In general, visible layer units are used to describe the characteristics of data, while hidden layer units can be regarded as feature extraction layers. The structure of the RBM is shown in Figure 1.
3. Case Study
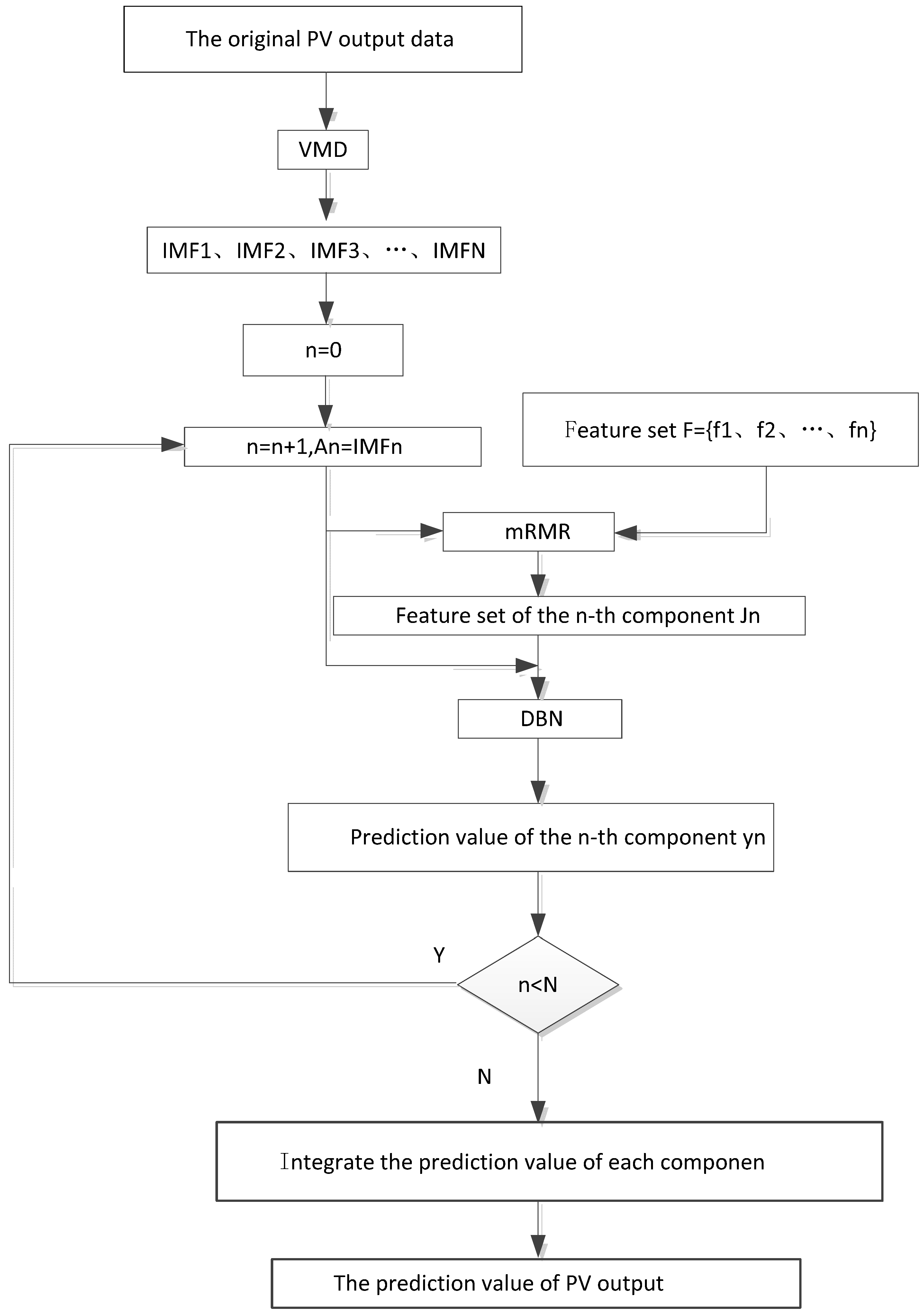
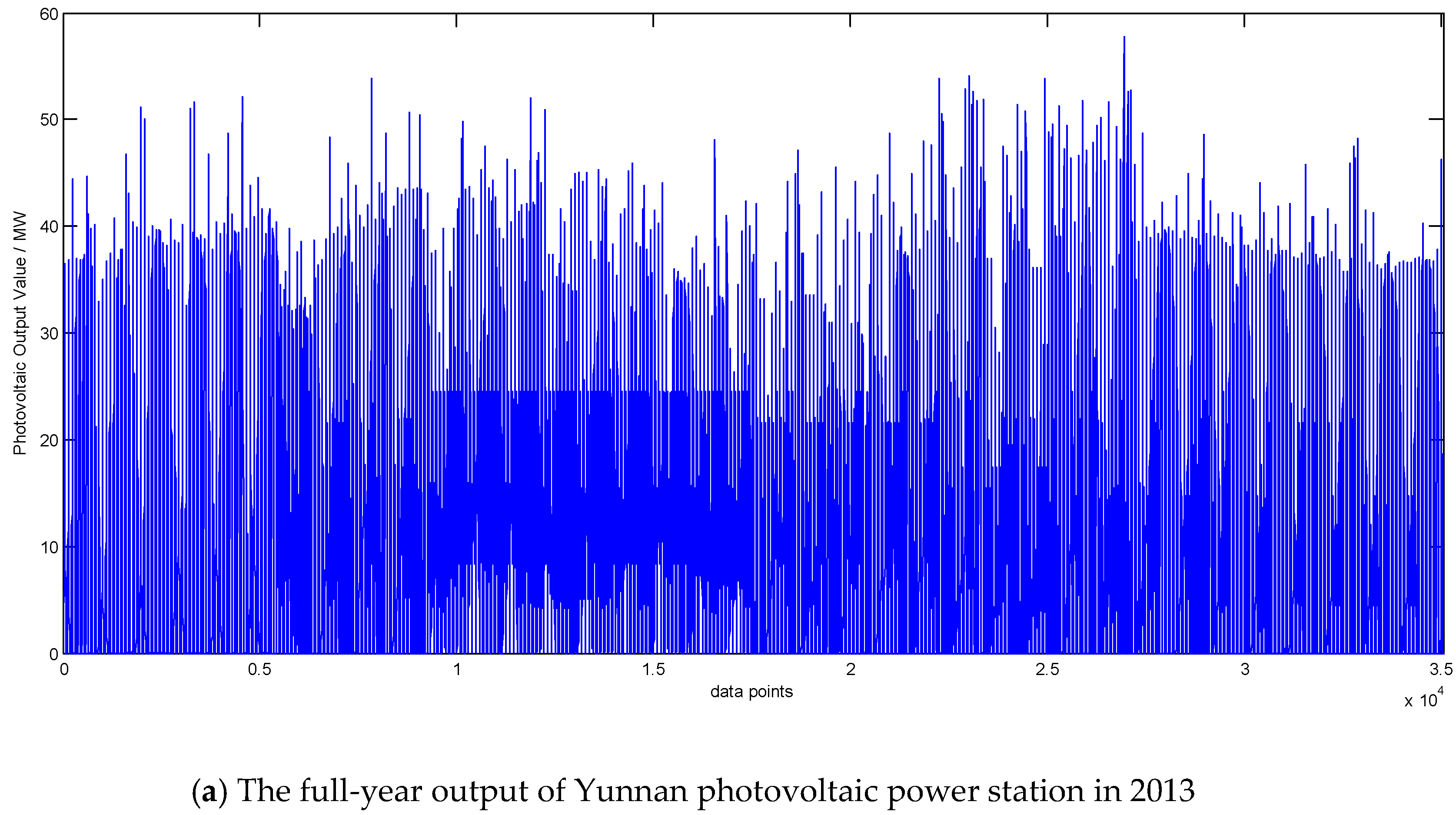
3.1. Analysis and Decomposing the Photovoltaic Output
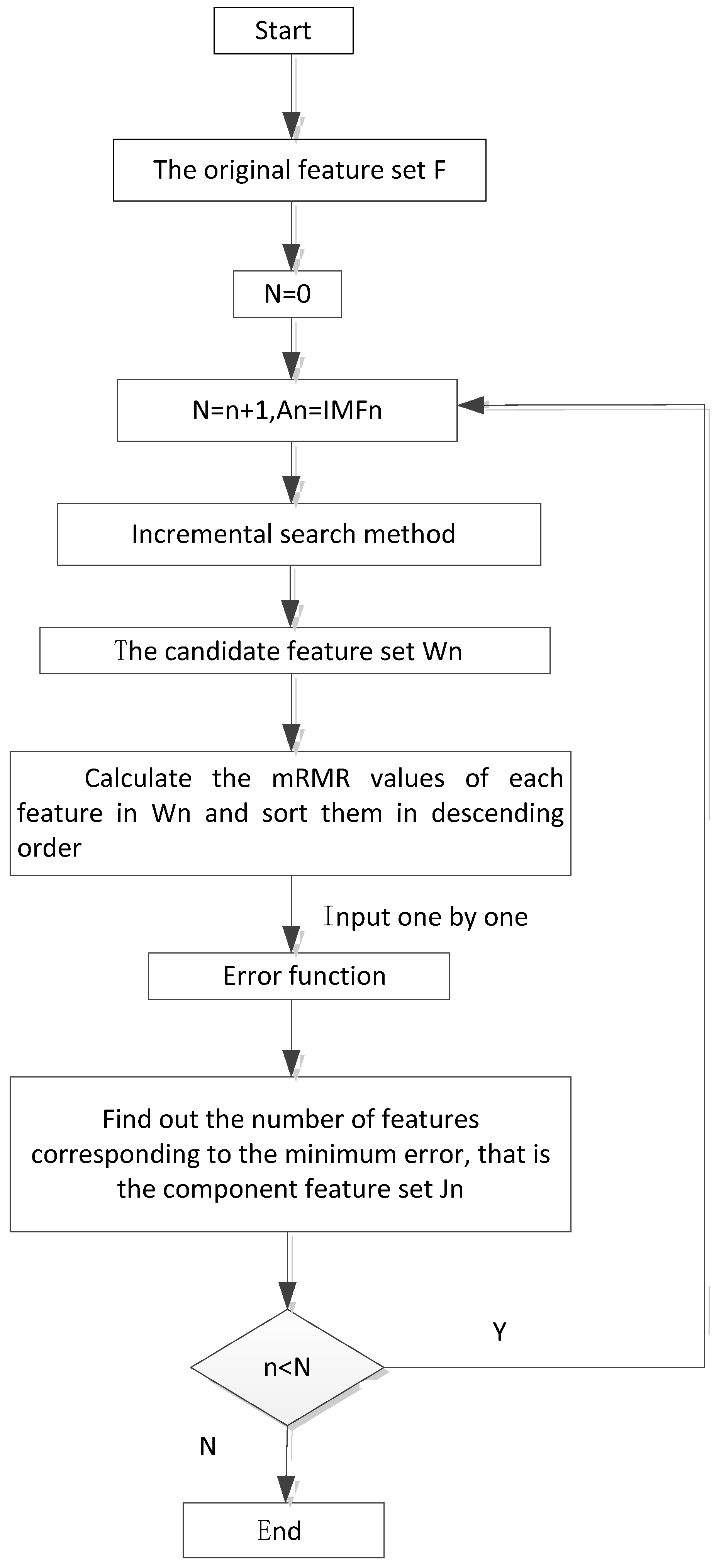
3.2. Establish Feature Sets of Each Component
- Use an incremental search method to establish a candidate feature set of the component;
- Calculate the mRMR values of each feature in and arrange them in descending order according to the magnitude of the mRMR value, and then input them into error function one by one to obtain the error;
- Take the number of features corresponding to the minimum error to establish a component feature set.
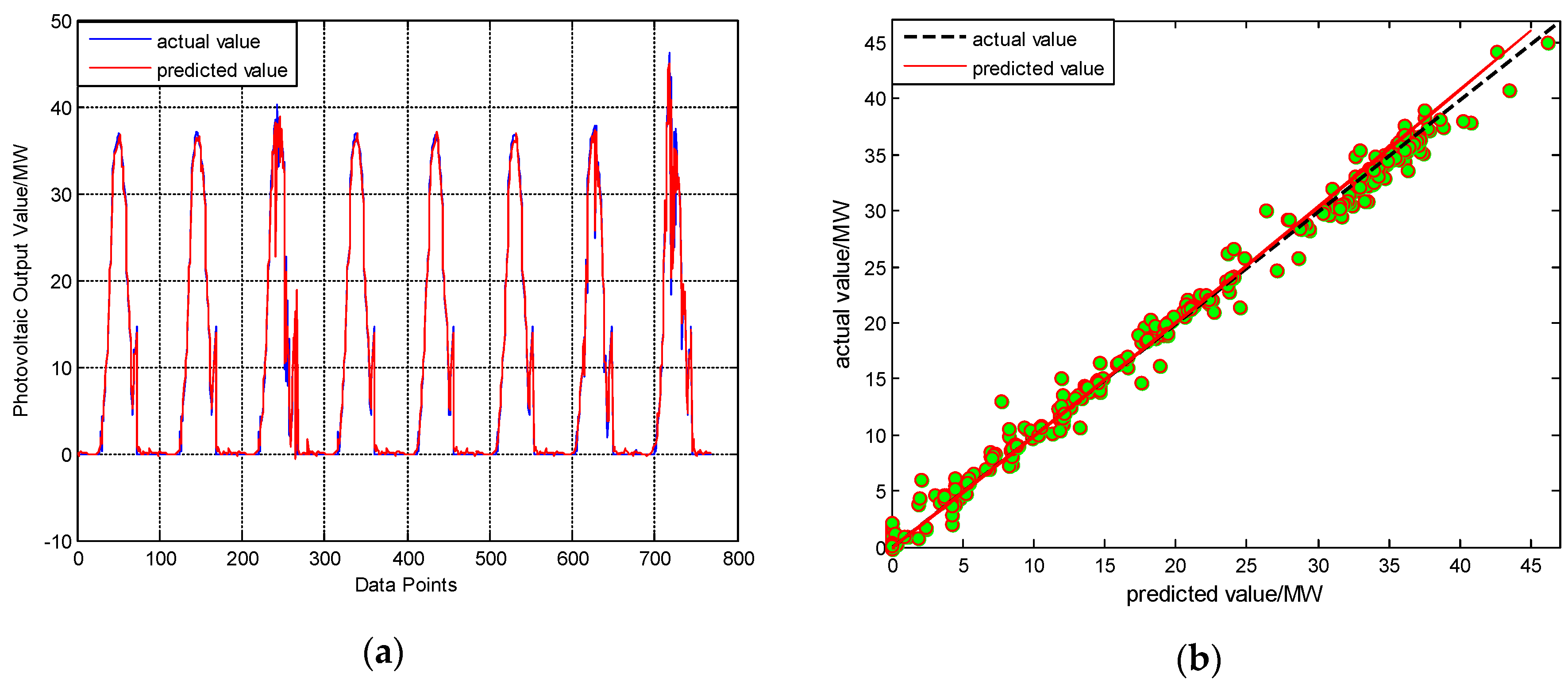
3.3. The Components and Photovoltaic Output Prediction
3.4. The Comparison
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, J.P.; Long, Y.; Song, X.H. A Study on the Conduction Mechanism and Evaluation of the Comprehensive Efficiency of Photovoltaic Power Generation in China. Energies 2017, 10, 22. [Google Scholar]
- Sen, S.; Ganguly, S. Opportunities, barriers and issues with renewable energy development—A discussion. Renew. Sust. Energ. Rev. 2017, 69, 1170–1181. [Google Scholar] [CrossRef]
- Zang, H.; Cheng, L.; Ding, T.; Cheung, K.W.; Liang, Z.; Wei, Z.; Sun, G. Hybrid method for short-term photovoltaic power forecasting based on deep convolutional neural network. IET Gener. Transm. Distrib. 2018, 12, 4557–4567. [Google Scholar] [CrossRef]
- Voyant, C.; Motte, F.; Fouilloy, A.; Notton, G.; Paoli, C.; Nivet, M.-L. Forecasting method for global radiation time series without training phase: Comparison with other well-known prediction methodologies. Energy 2017, 120, 199–208. [Google Scholar] [CrossRef]
- Watanabe, T.; Nohara, D. Prediction of time series for several hours of surface solar irradiance using one-granule cloud property data from satellite observations. Sol. Energy 2019, 186, 113–125. [Google Scholar] [CrossRef]
- Chantana, J.; Kawano, Y.; Kamei, A.; Minemoto, T. Description of degradation of output performance for photovoltaic modules by multiple regression analysis based on environmental factors. Optik 2019, 179, 1063–1070. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Niu, J. Forecast of power generation for grid-connected photovoltaic system based on grey theory and verification model. In Proceedings of the Fourth International Conference on Intelligent Control and Information Processing, Beijing, China, 9–11 June 2013; pp. 129–133. [Google Scholar]
- Persson, C.; Bacher, P.; Shiga, T.; Madsen, H. Multi-site solar power forecasting using gradient boosted regression trees. Sol. Energy 2017, 150, 423–436. [Google Scholar] [CrossRef]
- Yang, C.; Thatte, A.A.; Xie, L. Multitime-Scale Data-Driven Spatio Temporal Forecast of Photovoltaic Generation. IEEE Trans. Sustain. Energy 2015, 6, 104–112. [Google Scholar] [CrossRef]
- Guan, L.; Zhao, Q.; Zhou, B.; Lyu, Y.; Zhao, W.; Yao, W. Multi-scale Clustering Analysis Based Modeling of Photovoltaic Power Characteristics and Its Application in Prediction. Autom. Electr. Power Syst. 2018, 42, 24–30. [Google Scholar]
- Wang, Y.; Fu, Y.; Sun, L.; Xue, H. Ultra-Short Term Prediction Model of Photovoltaic Output Power Based on Chaos-RBF Neural Network. Power Syst. Technol. 2018, 42, 1110–1116. [Google Scholar]
- Andrews, R.W.; Pearce, J.M. Prediction of energy effects on photovoltaic systems due to snow fall events. In Proceedings of the 38th IEEE Photovoltaic Specialists Conference, Austin, TX, USA, 3–8 June 2012; pp. 3386–3391. [Google Scholar]
- Long, H.; Zhang, Z.; Su, Y. Analysis of daily solar power prediction with data-driven approaches. Appl. Energy 2014, 126, 29–37. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, J.; Cheng, H.; Xue, F.; Xie, Q.; Li, P. Study of Short-Term Photovoltaic Power Forecast Based on Error Calibration under Typical Climate Categories. Energies 2016, 9, 523. [Google Scholar] [CrossRef]
- Zhu, Y.; Tian, J. Application of Least square Support Vector Machine in Photovoltaic Power Forecasting. Power Syst. Technol. 2011, 35, 54–59. [Google Scholar]
- Mittal, M.; Bora, B.; Saxena, S.; Gaur, A.M. Performance prediction of PV module using electrical equivalent model and artificial neural network. Sol. Energy 2018, 176, 104–117. [Google Scholar] [CrossRef]
- Ding, M.; Xu, N. A Method to Forecast Short-Term Output Power of Photovoltaic Generation System Based on Markov Chain. Power Syst. Technol. 2011, 35, 152–157. [Google Scholar]
- Eseye, A.T.; Zhang, J.; Zheng, D. Short-term photovoltaic solar power forecasting using a hybrid Wavelet-PSO-SVM model based on SCADA and Meteorological information. Renew. Energy 2018, 118, 357–367. [Google Scholar] [CrossRef]
- Marquez, R.; Coimbra, C.F.M. Forecasting of global and direct solar irradiance using stochastic learning methods, ground experiments and the NWS database. Sol. Energy 2011, 85, 746–756. [Google Scholar] [CrossRef]
- Li, J.; Huang, Q.; Wei, S.; Huang, Y. Improved Deep Learning Algorithm Based on S-BGD and Gradient Pile Strategy and Its Application in PV Power Forecasting. Power Syst. Technol. 2017, 41, 3292–3300. [Google Scholar]
- Malvoni, M.; DeGiorgi, M.G.; Congedo, P.M. Photovoltaic forecast based on hybrid PCA-LSSVM using dimensionality reducted data. Neurocomputing 2016, 211, 72–83. [Google Scholar] [CrossRef]
- Li, F.-F.; Wang, S.-Y.; Wei, J.-H. Long term rolling prediction model for solar radiation combining empirical mode decomposition (EMD) and artificial neural network (ANN) techniques. J. Renew. Sustain. Energy 2018, 10, 013704. [Google Scholar] [CrossRef]
- Wang, H.; Sun, J.; Wang, W. Photovoltaic Power Forecasting Based on EEMD and a Variable-Weight Combination Forecasting Model. Sustainability 2018, 10, 2627. [Google Scholar] [CrossRef]
- Mao, M.; Gong, W.; Chang, L.; Cao, Y.; Xu, H. Short-term Photovoltaic Generation Forecasting Based on EEMD-SVM Combined Method. Proc. Chin. Soc. Electr. Eng. 2013, 33, 17–24. [Google Scholar]
- Xie, T.; Zhang, G.; Liu, H.; Liu, F.; Du, P. A Hybrid Forecasting Method for Solar Output Power Based on Variational Mode Decomposition, Deep Belief Network sand Auto-Regressive Moving Average. Appl. Sci. 2018, 8, 1901. [Google Scholar] [CrossRef]
- He, X.; Luo, J.; Zuo, G.; Xie, J. Daily Run off Forecasting Using a Hybrid Model Based on Variational Mode Decomposition and Deep Neural Networks. Water Resour. Manag. 2019, 33, 1571–1590. [Google Scholar] [CrossRef]
- Xie, T.; Zhang, G.; Hou, J.; Xie, J.; Lv, M.; Liu, F. Hybrid forecasting model for non-stationary daily run off series: A case study in the Han River Basin, China. J. Hydrol. 2019, 577, 123915. [Google Scholar] [CrossRef]
- Han, Y.; Wang, N.; Ma, M.; Zhou, H.; Dai, S.; Zhu, H. A PV power interval forecasting based on seasonal model and nonparametric estimation algorithm. Sol. Energy 2019, 184, 515–526. [Google Scholar] [CrossRef]
- Kim, G.G.; Choi, J.H.; Park, S.Y.; Bhang, B.G.; Nam, W.J.; Cha, H.L.; Park, N.; Ahn, H.-K. Prediction Model for PV Performance with Correlation Analysis of Environmental Variables. IEEE J. Photovolt. 2019, 9, 832–841. [Google Scholar] [CrossRef]
- Liu, J.; Sun, H.; Chang, P.; Jiao, Z.; Wei, P.; Ke, X.; Sun, X.; Cheng, L. Research of Photovoltaic Power Forecasting Based on Big Data and mRMR Feature Reduction. In Proceedings of the2018 IEEE Power & Energy Society General Meeting, Portland, OR, USA, 5–9 August 2018. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.-R.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Patrick, N.; Sainath, T.N.; et al. Deep Neural Networks for A coustic Modeling in Speech Recognition. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Cui, J.; Yu, R.; Zhao, D.; Yang, J.; Ge, W.; Zhou, X. Intelligent load pattern modeling and denoising using improved variational mode decomposition for various calendar periods. Appl. Energy 2019, 247, 480–491. [Google Scholar] [CrossRef]
- Alshamaa, D.; Chehade, F.M.; Honeine, P. A hierarchical classification method using belief functions. Signal Process. 2018, 148, 68–77. [Google Scholar] [CrossRef]
- Fu, G. Deep belief network based ensemble approach for cooling load forecasting of air-conditioning system. Energy 2018, 148, 269–282. [Google Scholar] [CrossRef]
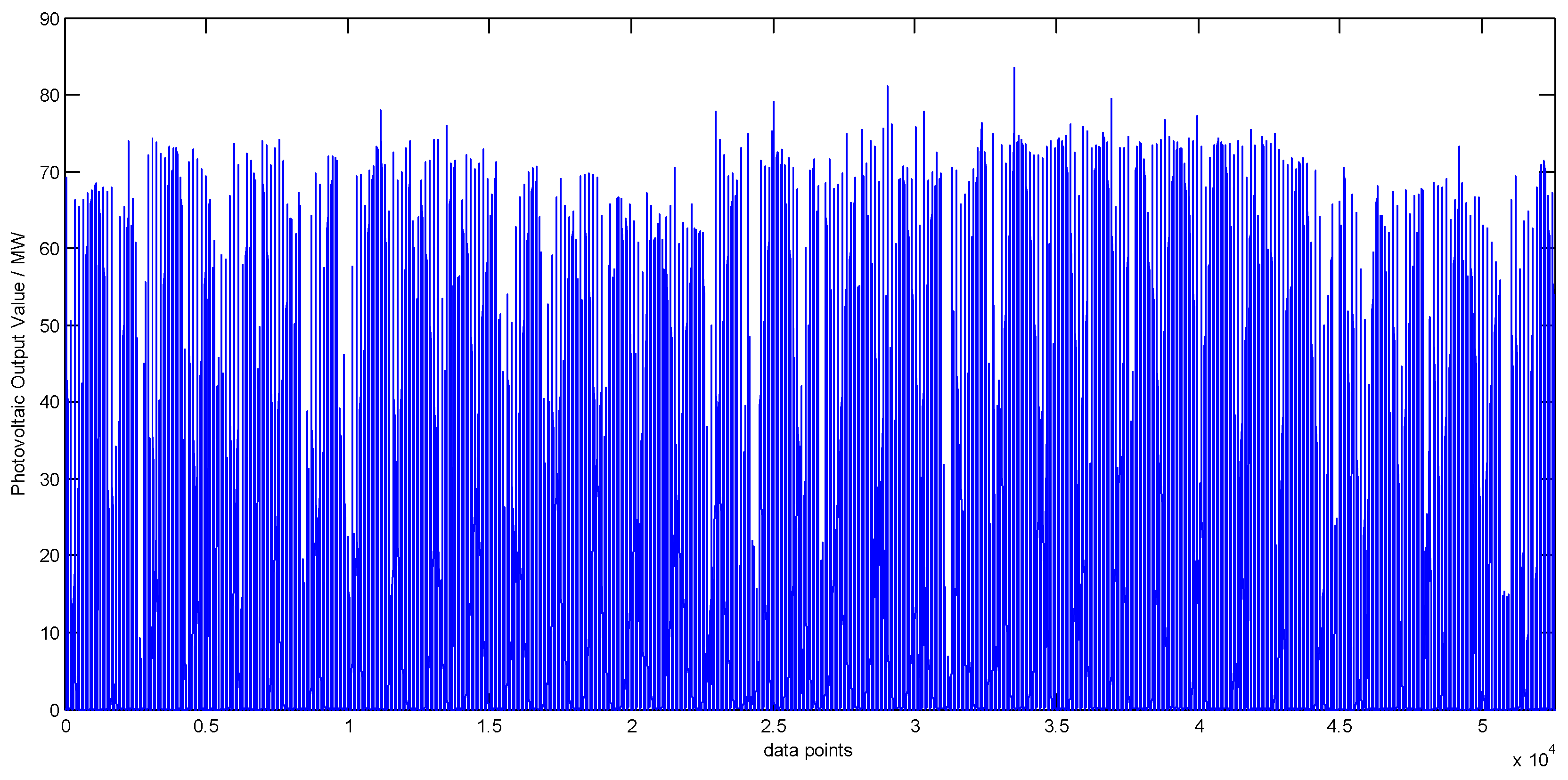



| Region | Yunnan | Gansu | ||||||
|---|---|---|---|---|---|---|---|---|
| Month | Index (MW) | |||||||
| Max | Min | Average | Standard Deviation | Max | Min | Average | Standard Deviation | |
| 1 | 51.0880 | 0 | 8.5451 | 12.9116 | 74.3600 | 0 | 15.3126 | 23.8975 |
| 2 | 52.1515 | 0 | 10.1411 | 14.0405 | 74.0806 | 0 | 15.4304 | 22.9636 |
| 3 | 53.8360 | 0 | 10.5843 | 12.7793 | 78.0693 | 0 | 17.0654 | 23.7851 |
| 4 | 50.6495 | 0 | 14.4332 | 12.2235 | 76.0156 | 0 | 18.5160 | 23.8937 |
| 5 | 52.0025 | 0 | 14.4195 | 10.9419 | 70.4691 | 0 | 18.6636 | 22.8334 |
| 6 | 48.1051 | 0 | 13.8450 | 10.3952 | 79.0193 | 0 | 17.9615 | 23.4606 |
| 7 | 47.1511 | 0 | 8.5261 | 9.9922 | 81.0183 | 0 | 17.6143 | 22.8236 |
| 8 | 54.0445 | 0 | 9.9151 | 12.4363 | 83.4411 | 0 | 18.7014 | 24.9872 |
| 9 | 53.8485 | 0 | 8.9923 | 12.0795 | 79.5083 | 0 | 20.0493 | 26.4243 |
| 10 | 57.7775 | 0 | 10.0323 | 13.2926 | 77.3358 | 0 | 18.9459 | 26.1223 |
| 11 | 45.7834 | 0 | 9.5029 | 13.0666 | 71.6986 | 0 | 14.1018 | 21.9549 |
| 12 | 48.2302 | 0 | 9.0874 | 12.7911 | 73.2493 | 0 | 13.0200 | 21.3749 |
| IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 | IMF9 | IMF10 |
|---|---|---|---|---|---|---|---|---|---|
0.0887 | 0.0927 | 0.0842 | 0.0877 | 0.0806 | 0.1612 | 0.0561 | 0.1239 | 0.3889 | 0.0522 |
0.0531 | 0.0452 | 0.0903 | 0.0863 | 0.1178 | 0.1229 | 0.1697 | 0.1537 | 0.2397 | 0.0307 |
0.0254 | 0.0717 | 0.0773 | 0.1167 | 0.1080 | 0.1532 | 0.1387 | 0.1092 | 0.2474 | 0.0540 |
0.0714 | 0.0949 | 0.0862 | 0.0902 | 0.0783 | 0.1336 | 0.1766 | 0.2308 | 0.1507 | 0.0685 |
0.0908 | 0.0753 | 0.1006 | 0.0833 | 0.1090 | 0.1462 | 0.0629 | 0.1287 | 0.3041 | 0.0387 |
0.0752 | 0.0738 | 0.0834 | 0.1198 | 0.0876 | 0.0493 | 0.1163 | 0.1662 | 0.2194 | 0.0751 |
0.0701 | 0.0557 | 0.0754 | 0.0725 | 0.0921 | 0.0537 | 0.1427 | 0.0750 | 0.3341 | 0.0574 |
0.0404 | 0.0602 | 0.0787 | 0.1037 | 0.0904 | 0.0687 | 0.1066 | 0.0992 | 0.3742 | 0.0892 |
0.0635 | 0.0598 | 0.1097 | 0.1044 | 0.1165 | 0.1120 | 0.1312 | 0.1469 | 0.2239 | 0.0211 |
0.0493 | 0.0855 | 0.0797 | 0.1063 | 0.0993 | 0.0494 | 0.1310 | 0.2960 | 0.2478 | 0.0619 |
0.0623 | 0.0720 | 0.1324 | 0.0753 | 0.0930 | 0.1404 | 0.1218 | 0.2115 | 0.1322 | 0.0726 |
0.0868 | 0.0827 | 0.1219 | 0.1567 | 0.0893 | 0.0794 | 0.1466 | 0.2605 | 0.3907 | 0.0314 |
| Component | Feature |
|---|---|
| IMF1 | |
| IMF2 | |
| IMF3 | |
| IMF4 | |
| IMF5 | |
| IMF6 | |
| IMF7 | |
| IMF8 | |
| IMF9 | |
| IMF10 |
| Component | Structure |
|---|---|
| IMF1 | 3-24-12-1 |
| IMF2 | 3-16-6-4-1 |
| IMF3 | 3-20-6-1 |
| IMF4 | 3-20-8-1 |
| IMF5 | 3-16-8-1 |
| IMF6 | 3-24-6-1 |
| IMF7 | 3-16-4-1 |
| IMF8 | 3-12-6-1 |
| IMF9 | 3-12-8-1 |
| IMF10 | 3-8-1 |
| Index | Model | |||||
|---|---|---|---|---|---|---|
| ARMA | DBN | EMD + DBN | EEMD + DBN | VMD + DBN | This Paper | |
| MAE(MW) | 4.6721 | 3.9642 | 2.3263 | 1.7331 | 1.0147 | 0.4063 |
| RMSE(MW) | 6.1381 | 5.3763 | 2.5324 | 2.0972 | 1.1364 | 0.7345 |
| 0.1359 | 0.1268 | 0.0572 | 0.0361 | 0.0092 | 0.0053 | |
| Index | Model | |||||
|---|---|---|---|---|---|---|
| ARMA | DBN | EMD + DBN | EEMD + DBN | VMD + DBN | This Paper | |
| MAE(MW) | 5.2794 | 4.4682 | 2.1984 | 1.7069 | 1.0510 | 0.4414 |
| RMSE(MW) | 6.8934 | 5.9792 | 2.4728 | 2.1421 | 1.2316 | 0.7816 |
| 0.1894 | 0.1659 | 0.0643 | 0.0579 | 0.0096 | 0.0061 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, P.; Zhang, G.; Li, P.; Li, M.; Liu, H.; Hou, J. The Photovoltaic Output Prediction Based on Variational Mode Decomposition and Maximum Relevance Minimum Redundancy. Appl. Sci. 2019, 9, 3593. https://doi.org/10.3390/app9173593
Du P, Zhang G, Li P, Li M, Liu H, Hou J. The Photovoltaic Output Prediction Based on Variational Mode Decomposition and Maximum Relevance Minimum Redundancy. Applied Sciences. 2019; 9(17):3593. https://doi.org/10.3390/app9173593
Chicago/Turabian StyleDu, Peidong, Gang Zhang, Pingli Li, Meng Li, Hongchi Liu, and Jinwang Hou. 2019. "The Photovoltaic Output Prediction Based on Variational Mode Decomposition and Maximum Relevance Minimum Redundancy" Applied Sciences 9, no. 17: 3593. https://doi.org/10.3390/app9173593
APA StyleDu, P., Zhang, G., Li, P., Li, M., Liu, H., & Hou, J. (2019). The Photovoltaic Output Prediction Based on Variational Mode Decomposition and Maximum Relevance Minimum Redundancy. Applied Sciences, 9(17), 3593. https://doi.org/10.3390/app9173593





