Phase Extraction from Single Interferogram Including Closed-Fringe Using Deep Learning
Abstract
1. Introduction
2. Fourier-Transform Method
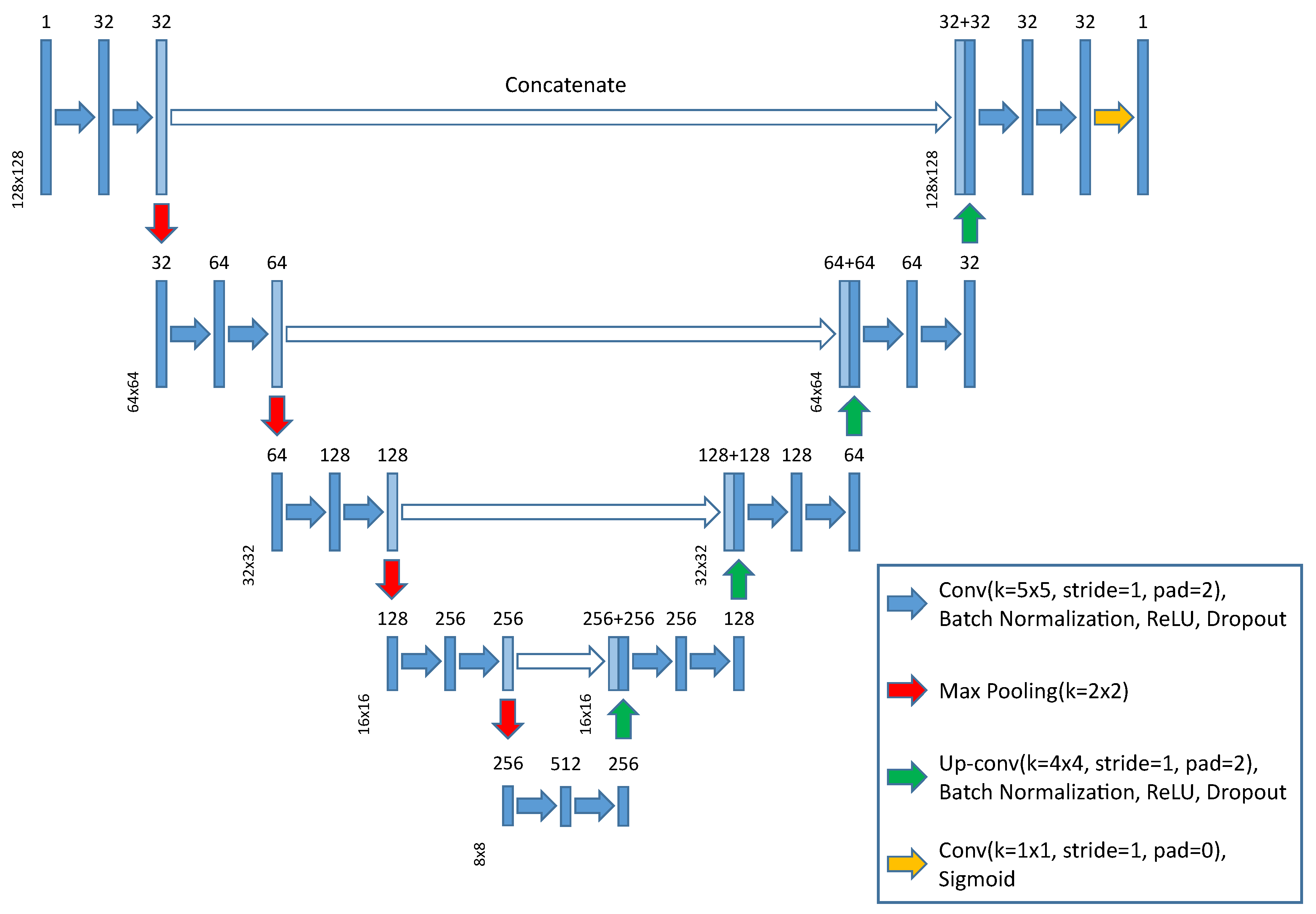
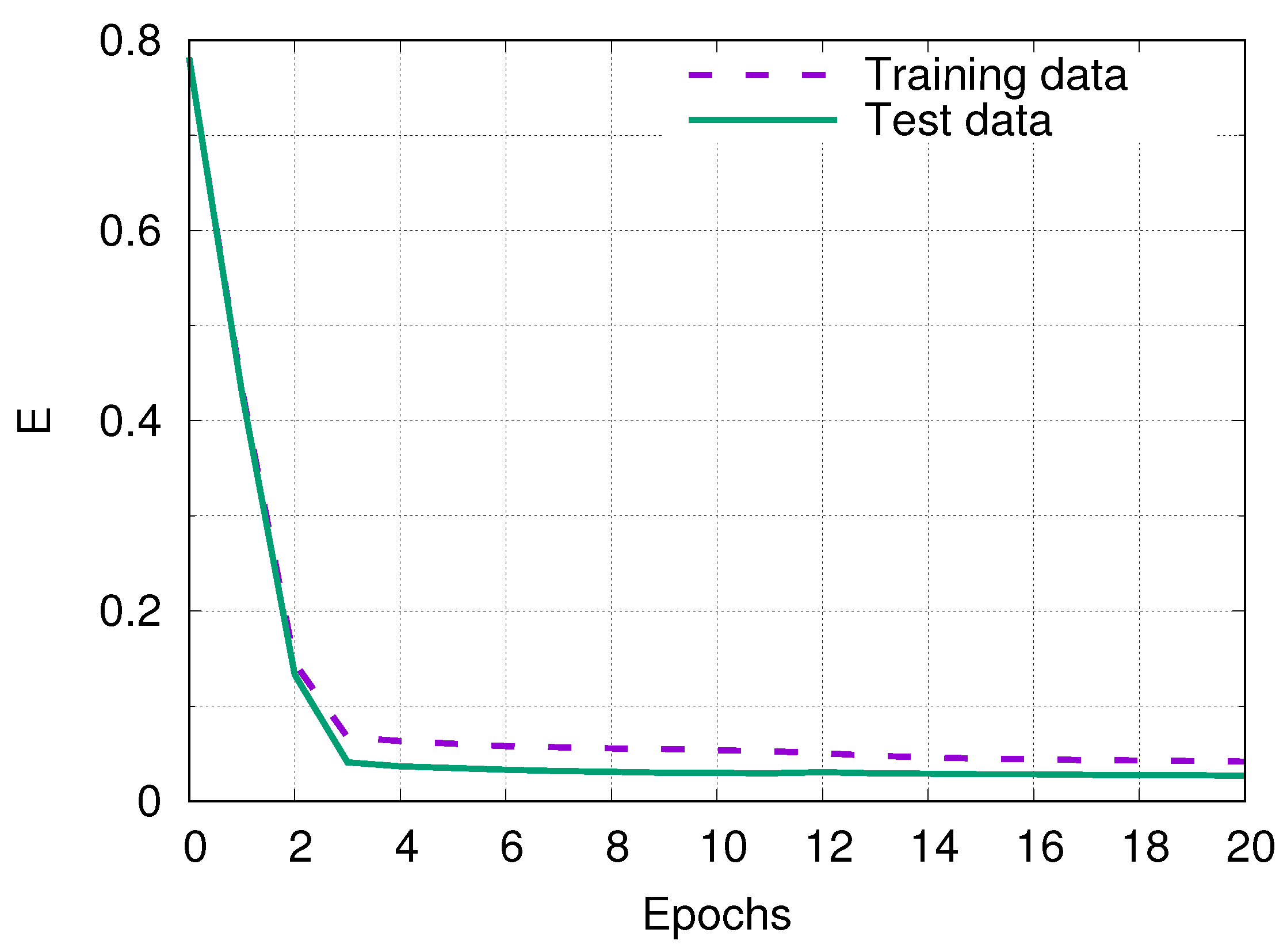
3. Deep Learning
4. Results and Discussion
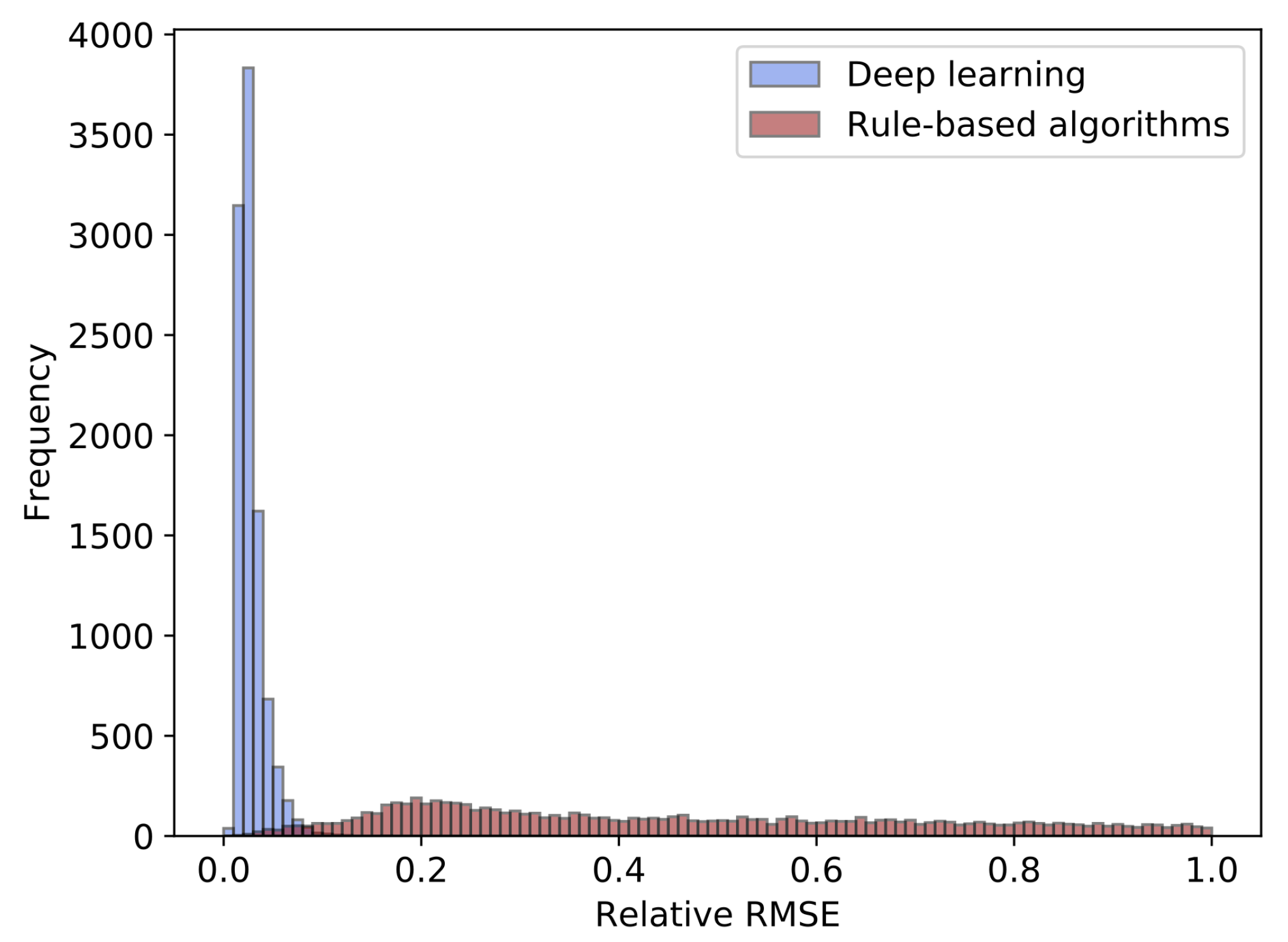
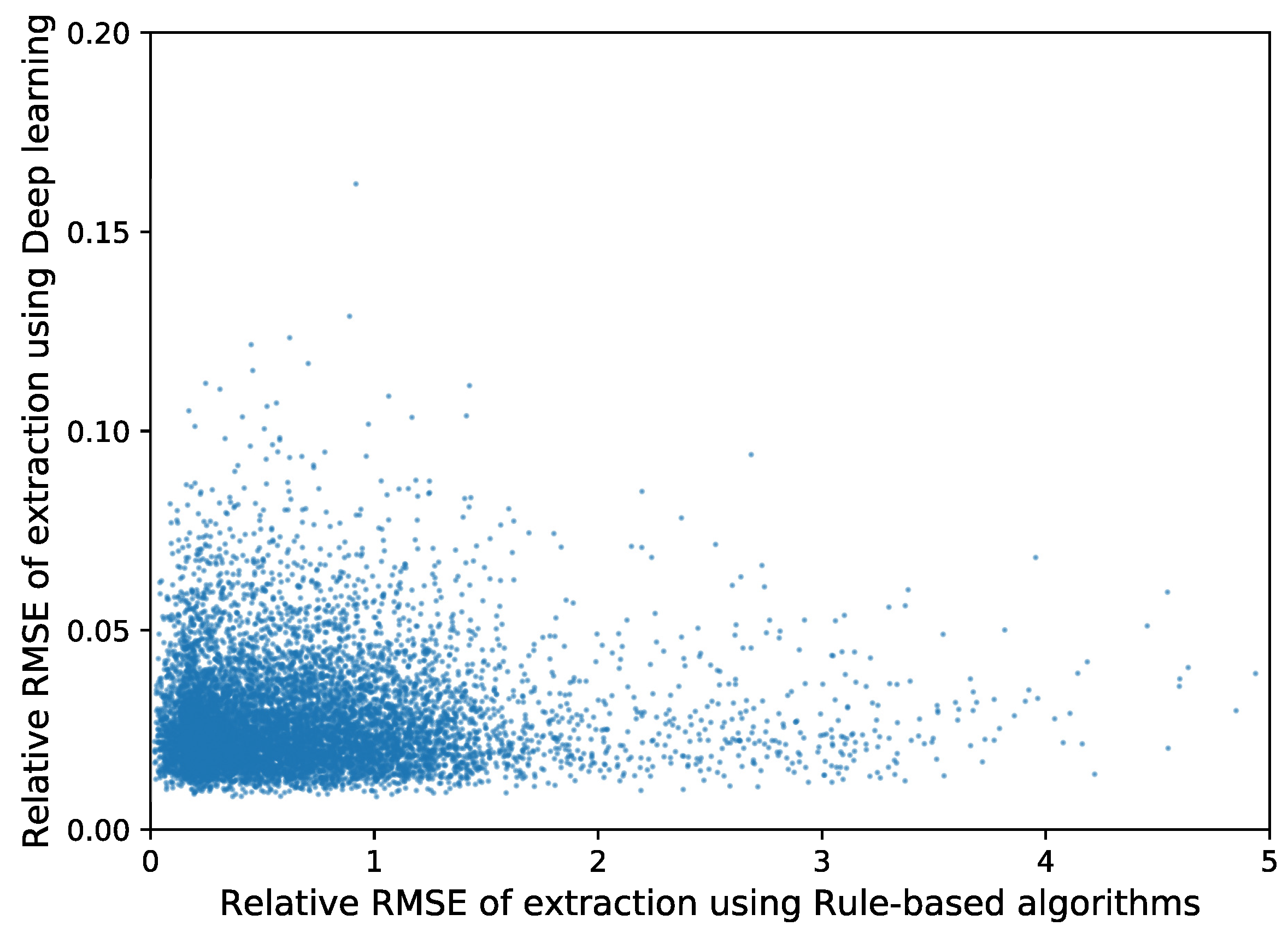
4.1. Extracted Phase-Shift from Simulated Interferogram
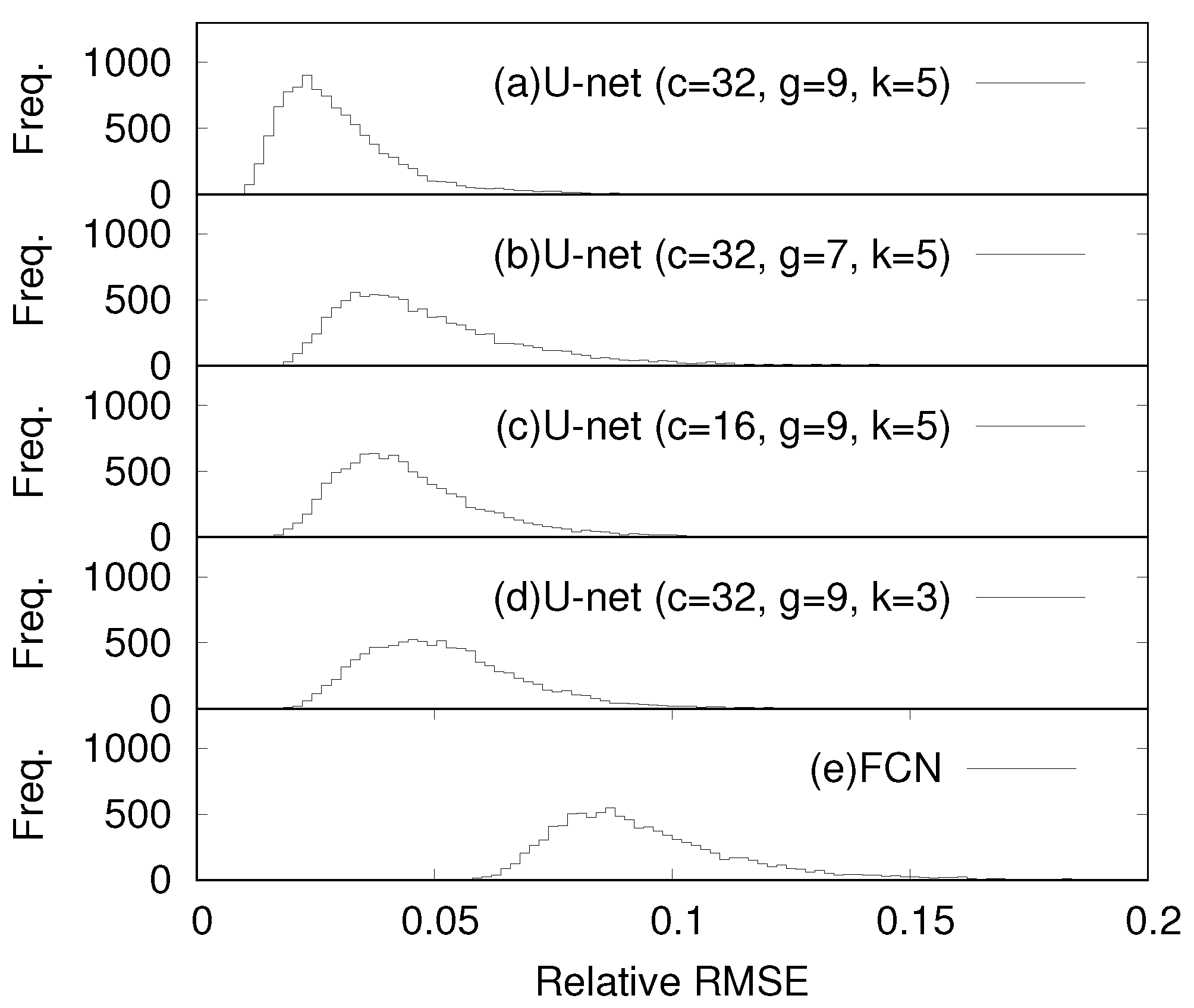
- (a):
- the estimation errors, , by both the deep learning and the Fourier-transform method from the interferogram, , belong to the maximum of the histogram shown in Figure 5; which are called a mode,
- (b):
- of the Fourier-transform method is smaller than the mode, by both the deep learning and the rule-based algorithm are the mode of the histogram shown in Figure 5,
- (c):
- and (d): the interferograms include closed-fringes.
4.2. Extracted Phase-Shift from Interferogram Obtained by an Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef]
- Huang, W.; Xiao, L.; Wei, Z.; Liu, H.; Tang, S. A new pan-sharpening method with deep neural networks. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1037–1041. [Google Scholar] [CrossRef]
- Vinyals, O.; Toshev, A.; Bengio, S.; Erhan, D. Show and tell: A neural image caption generator. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3156–3164. [Google Scholar]
- Gatys, L.A.; Ecker, A.S.; Bethge, M. A neural algorithm of artistic style. arXiv 2015, arXiv:1508.06576. [Google Scholar] [CrossRef]
- Tomioka, S.; Nishiyama, S.; Heshmat, S.; Hashimoto, Y.; Kurita, K. Three-dimensional gas temperature measurements by computed tomography with incident angle variable interferometer. Proc. SPIE 2015, 9401, 94010J. [Google Scholar] [CrossRef]
- Tomioka, S.; Nishiyama, S.; Miyamoto, N.; Kando, D.; Heshmat, S. Weighted reconstruction of three-dimensional refractive index in interferometric tomography. Appl. Opt. 2017, 56, 6755–6764. [Google Scholar] [CrossRef] [PubMed]
- Perry, K.E., Jr.; McKelvie, J. A Comparison of Phase Shifting and Fourier Methods in the Analysis of Discontinuous Fringe Patterns. Opt. Lasers Eng. 1993, 19, 269–284. [Google Scholar] [CrossRef]
- Bruning, J.H.; Herriott, D.R.; Gallagher, J.E.; Rosenfeld, D.P.; White, A.D.; Brangaccio, D.J. Digital Wavefront Measuring Interferometer for Testing Optical Surfaces and Lenses. Appl. Opt. 1974, 13, 2693–2703. [Google Scholar] [CrossRef]
- Breuckmann, B.; Thieme, W. Computer-aided analysis of holographic interferograms using the phase-shift method. Appl. Opt. 1985, 24, 2145–2149. [Google Scholar] [CrossRef]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- Cuche, E.; Marquet, P.; Depeursinge, C. Spatial Filtering for Zero-Order and Twin-Image Elimination in Digital Off-Axis Holography. Appl. Opt. 2000, 39, 4070–4075. [Google Scholar] [CrossRef]
- Bone, D.J.; Bachor, H.A.; Sandeman, R.J. Fringe-pattern analysis using a 2-D Fourier transform. Appl. Opt. 1986, 25, 1653–1660. [Google Scholar] [CrossRef]
- Tomioka, S.; Nishiyama, S.; Heshmat, S. Carrier peak isolation from single interferogram using spectrum shift technique. Appl. Opt. 2014, 53, 5620–5631. [Google Scholar] [CrossRef] [PubMed]
- Fried, D.L. Least-square fitting a wave-front distortion estimate to an array of phase-difference measurements. J. Opt. Soc. Am. 1977, 67, 370–375. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- Flynn, T.J. Two-dimensional phase unwrapping with minimum weighted discontinuity. JOSA A 1997, 14, 2692–2701. [Google Scholar] [CrossRef]
- Tomioka, S.; Heshmat, S.; Miyamoto, N.; Nishiyama, S. Phase unwrapping for noisy phase maps using rotational compensator with virtual singular points. Appl. Opt. 2010, 49, 4735–4745. [Google Scholar] [CrossRef] [PubMed]
- Heshmat, S.; Tomioka, S.; Nishiyama, S. Reliable phase unwrapping algorithm based on rotational and direct compensators. Appl. Opt. 2011, 50, 6225–6233. [Google Scholar] [CrossRef]
- Tomioka, S.; Nishiyama, S. Phase unwrapping for noisy phase map using localized compensator. Appl. Opt. 2012, 51, 4984–4994. [Google Scholar] [CrossRef]
- Ge, Z.; Kobayashi, F.; Matsuda, S.; Takeda, M. Coordinate-Transform Technique for Closed-Fringe Analysis by the Fourier-Transform Method. Appl. Opt. 2001, 40, 1649–1657. [Google Scholar] [CrossRef]
- Heshmat, S.; Tomioka, S.; Nishiyama, S. Performance Evaluation of Phase Unwrapping Algorithms for Noisy Phase Measurements. Int. J. Optomech. 2014, 8, 260–274. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Shenzhen, China, 13–17 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Yao, W.; Zeng, Z.; Lian, C.; Tang, H. Pixel-wise regression using U-Net and its application on pansharpening. Neurocomputing 2018, 312, 364–371. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kando, D.; Tomioka, S.; Miyamoto, N.; Ueda, R. Phase Extraction from Single Interferogram Including Closed-Fringe Using Deep Learning. Appl. Sci. 2019, 9, 3529. https://doi.org/10.3390/app9173529
Kando D, Tomioka S, Miyamoto N, Ueda R. Phase Extraction from Single Interferogram Including Closed-Fringe Using Deep Learning. Applied Sciences. 2019; 9(17):3529. https://doi.org/10.3390/app9173529
Chicago/Turabian StyleKando, Daichi, Satoshi Tomioka, Naoki Miyamoto, and Ryosuke Ueda. 2019. "Phase Extraction from Single Interferogram Including Closed-Fringe Using Deep Learning" Applied Sciences 9, no. 17: 3529. https://doi.org/10.3390/app9173529
APA StyleKando, D., Tomioka, S., Miyamoto, N., & Ueda, R. (2019). Phase Extraction from Single Interferogram Including Closed-Fringe Using Deep Learning. Applied Sciences, 9(17), 3529. https://doi.org/10.3390/app9173529




