Real-Time City-Scale Time-History Analysis and Its Application in Resilience-Oriented Earthquake Emergency Responses
Abstract
1. Introduction
2. Real-Time City-Scale Nonlinear Time-History Analysis
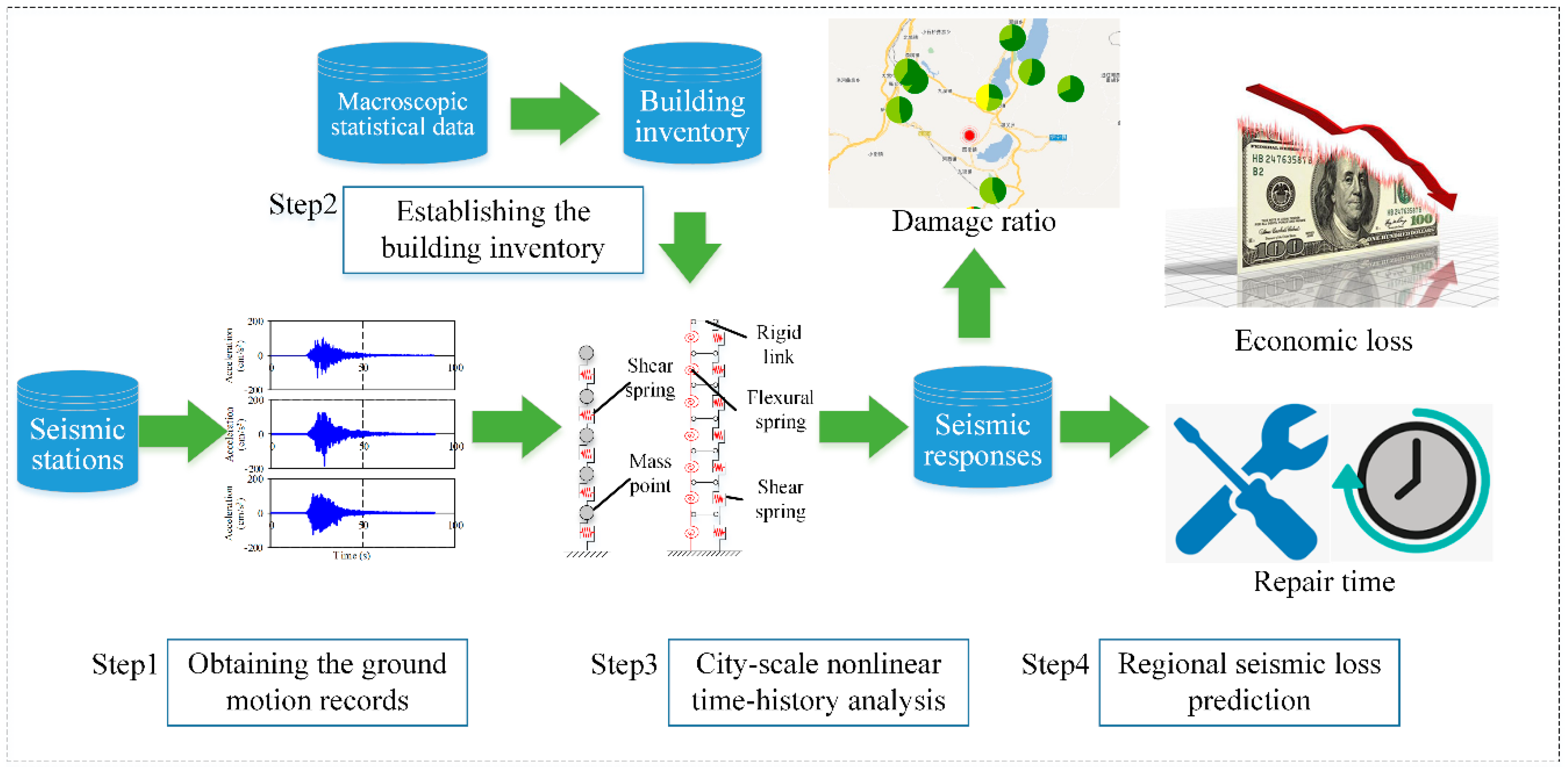
2.1. Framework
- (1)
- Obtaining the real-time ground motion records from the seismic stations;
- (2)
- Establishing the building inventory database for the target region;
- (3)
- Conducting the city-scale nonlinear time-history analysis to predict the seismic damage of the target region; and
- (4)
- Performing the regional seismic loss prediction to assess the seismic economic loss and repair time of the target region.
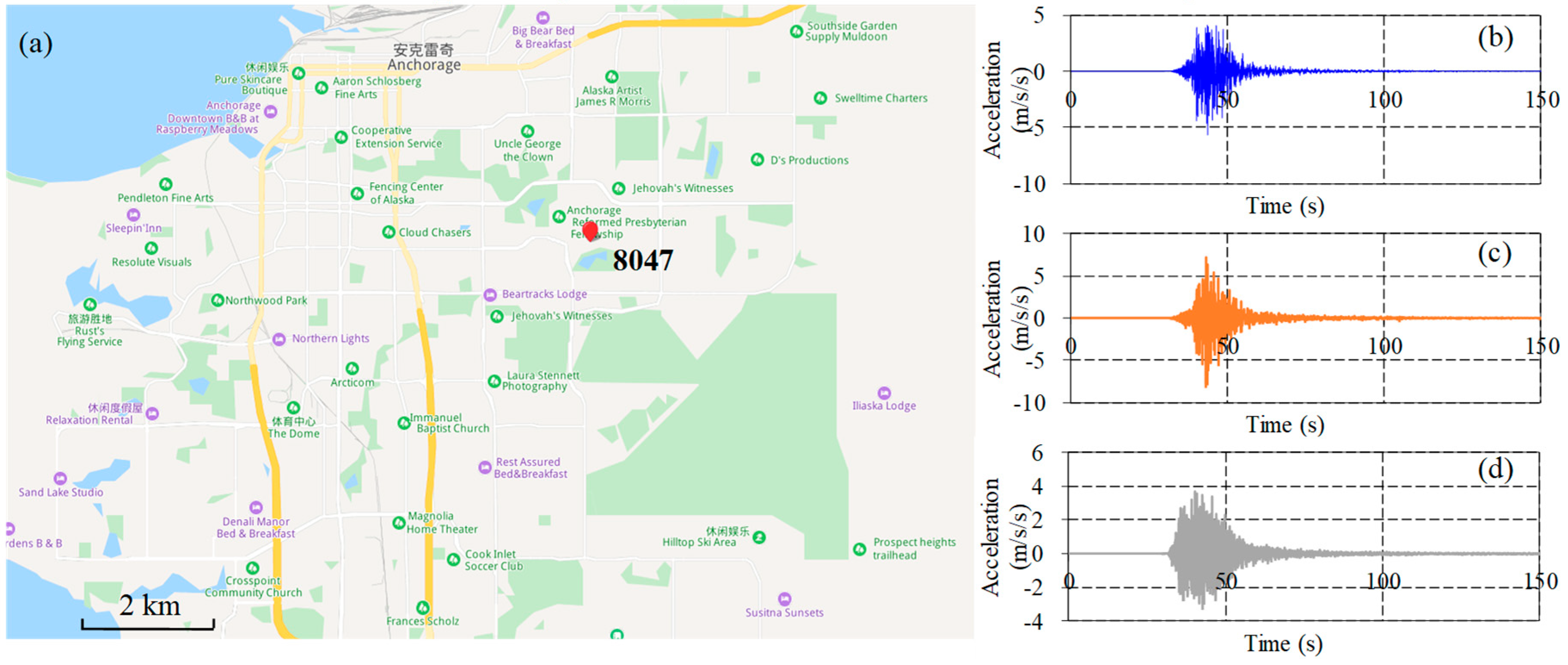
2.2. Real-Time Recorded Ground Motions
2.3. Building Inventory Database
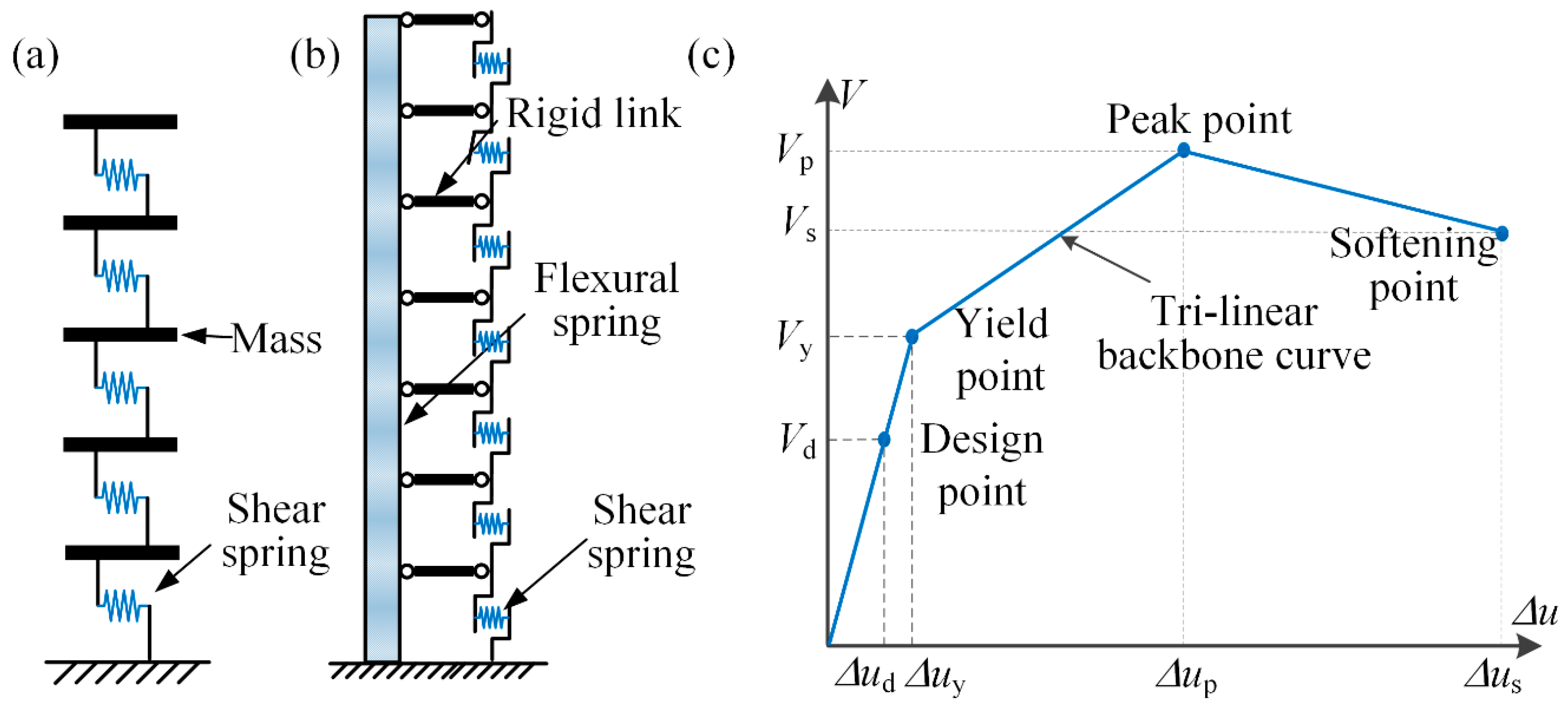
2.4. City-Scale Nonlinear Time-History Analysis
2.4.1. Parameter Determination Method for Buildings in China
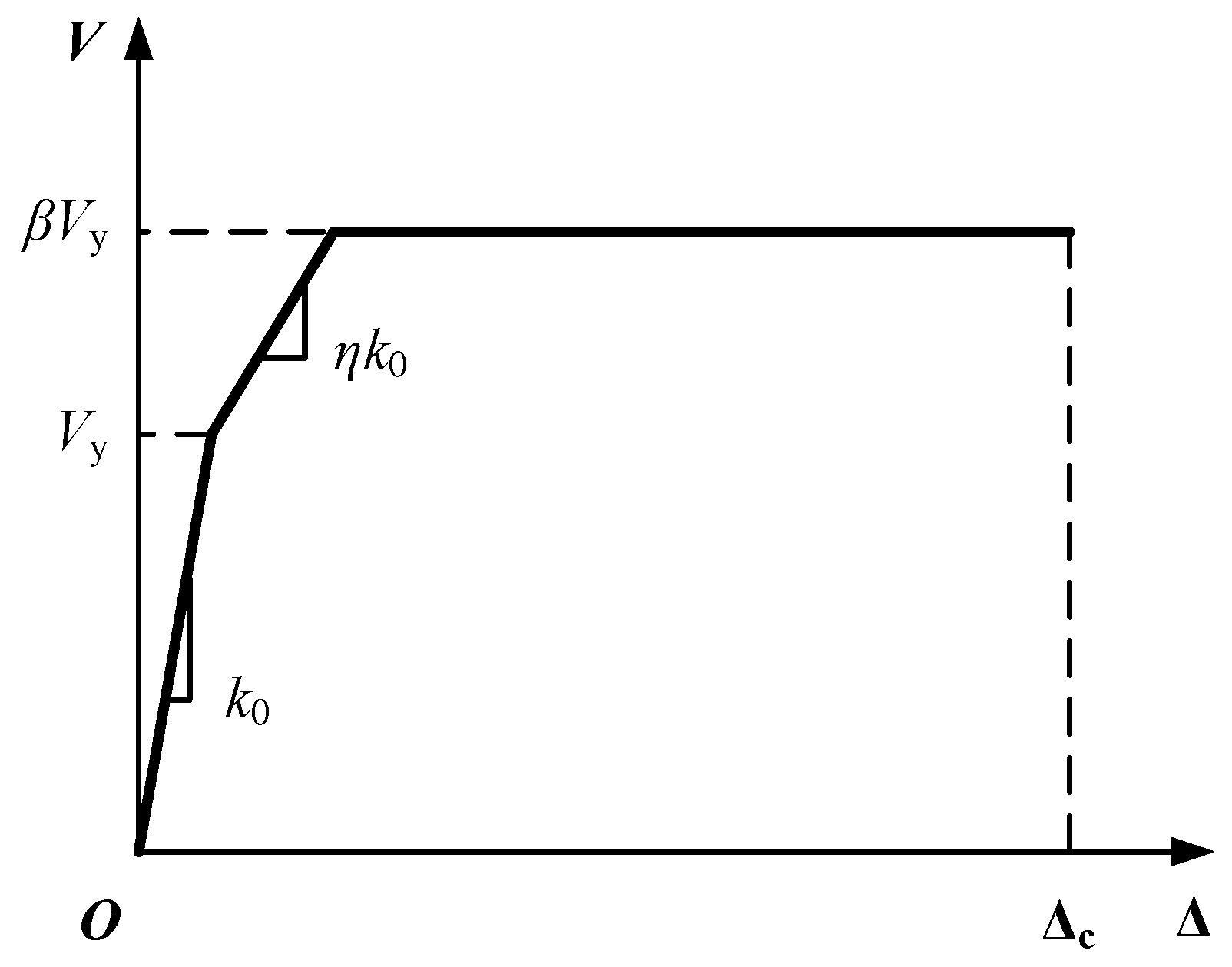
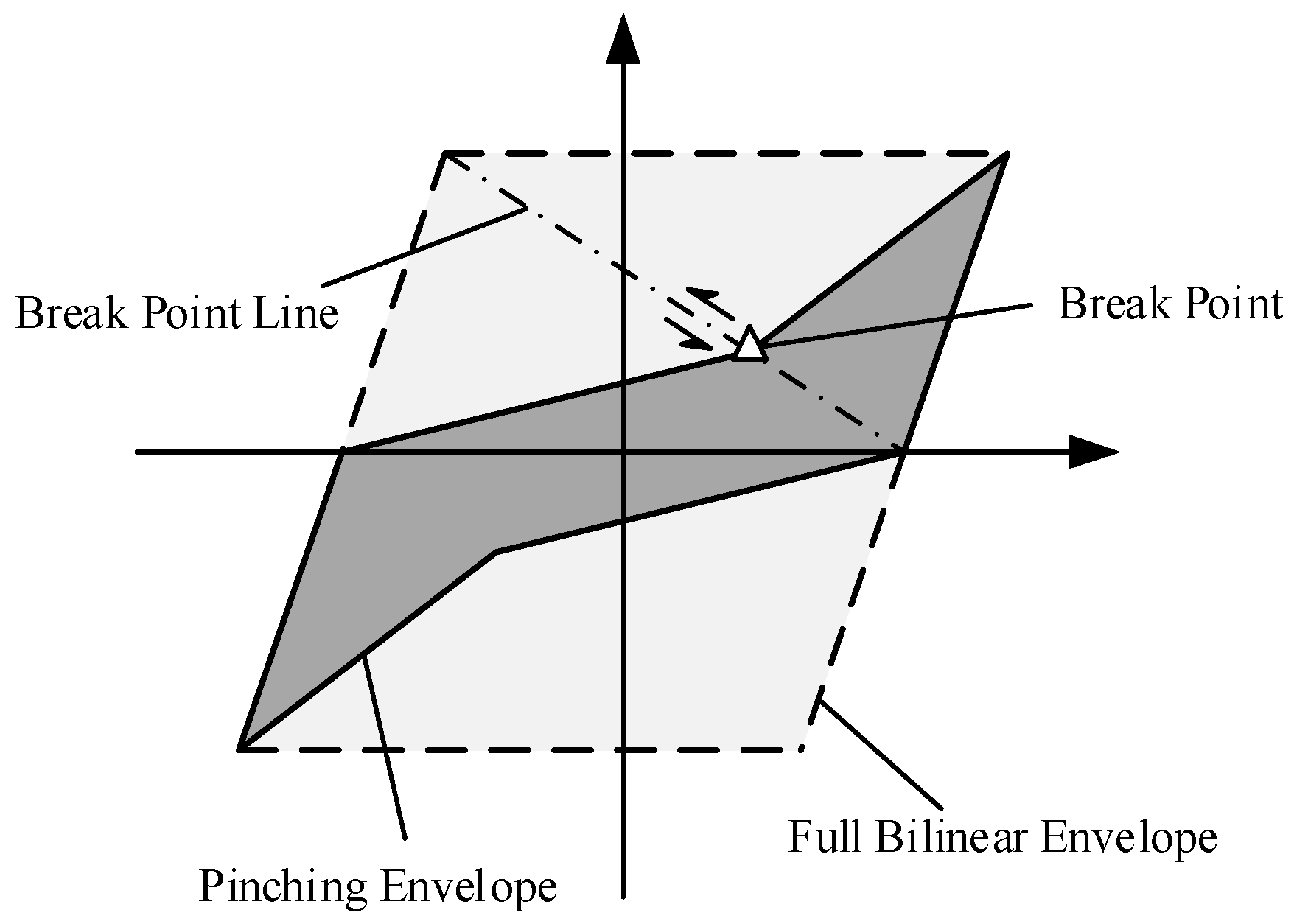
2.4.2. Parameter Determination for Backbone Curve Based on the HAZUS Data
2.5. Regional Seismic Loss Prediction and Resilience Assessment
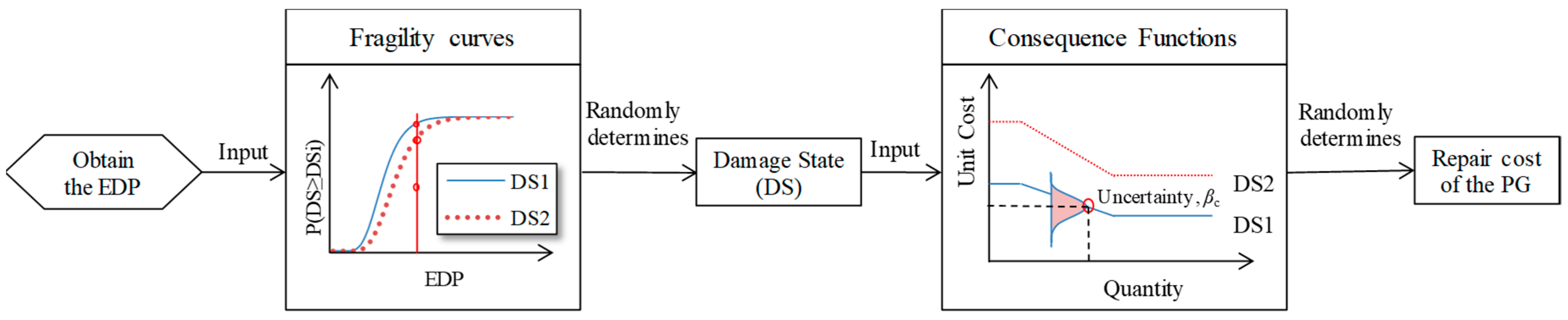
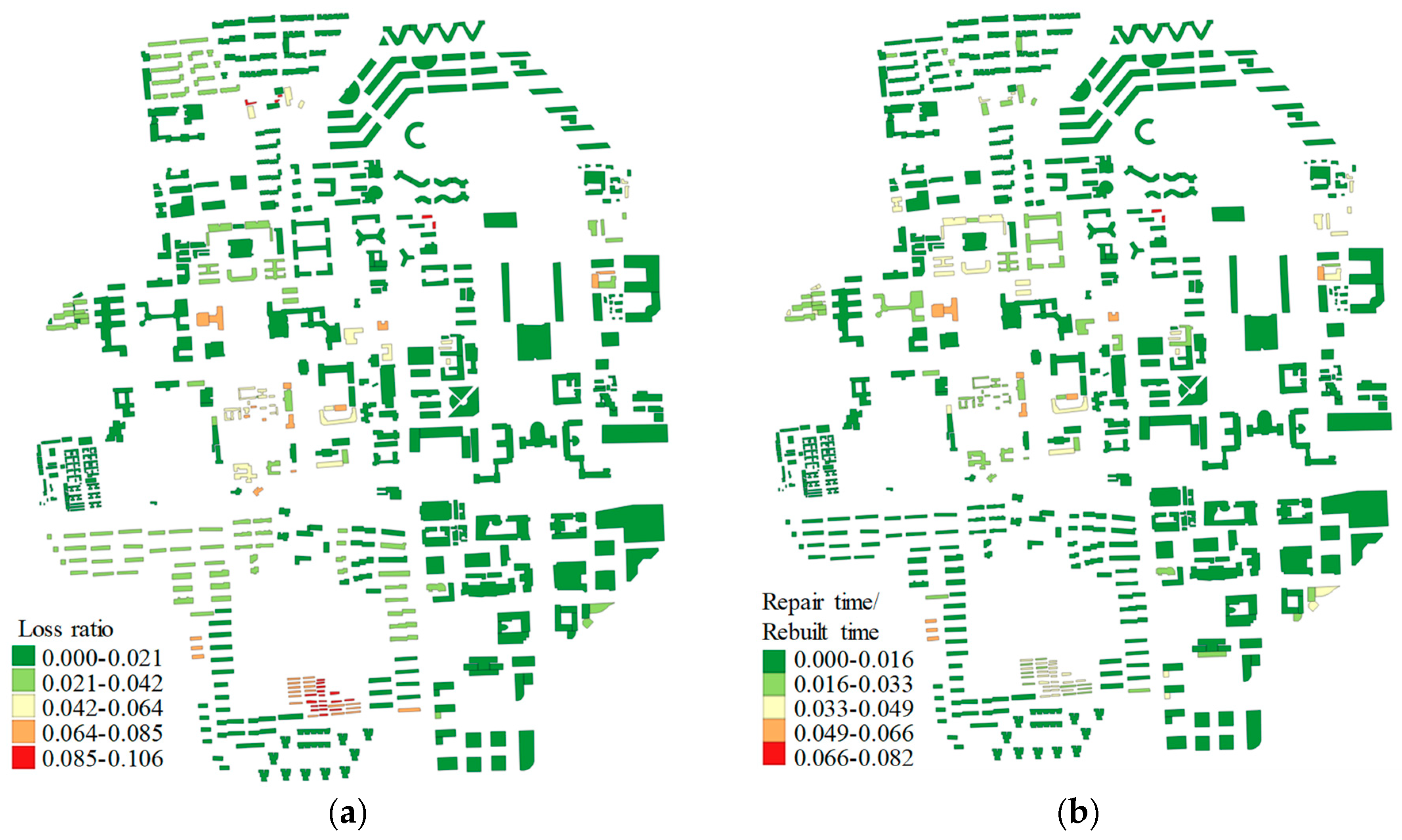
2.5.1. Regional Seismic Loss Prediction Using Conventional Method
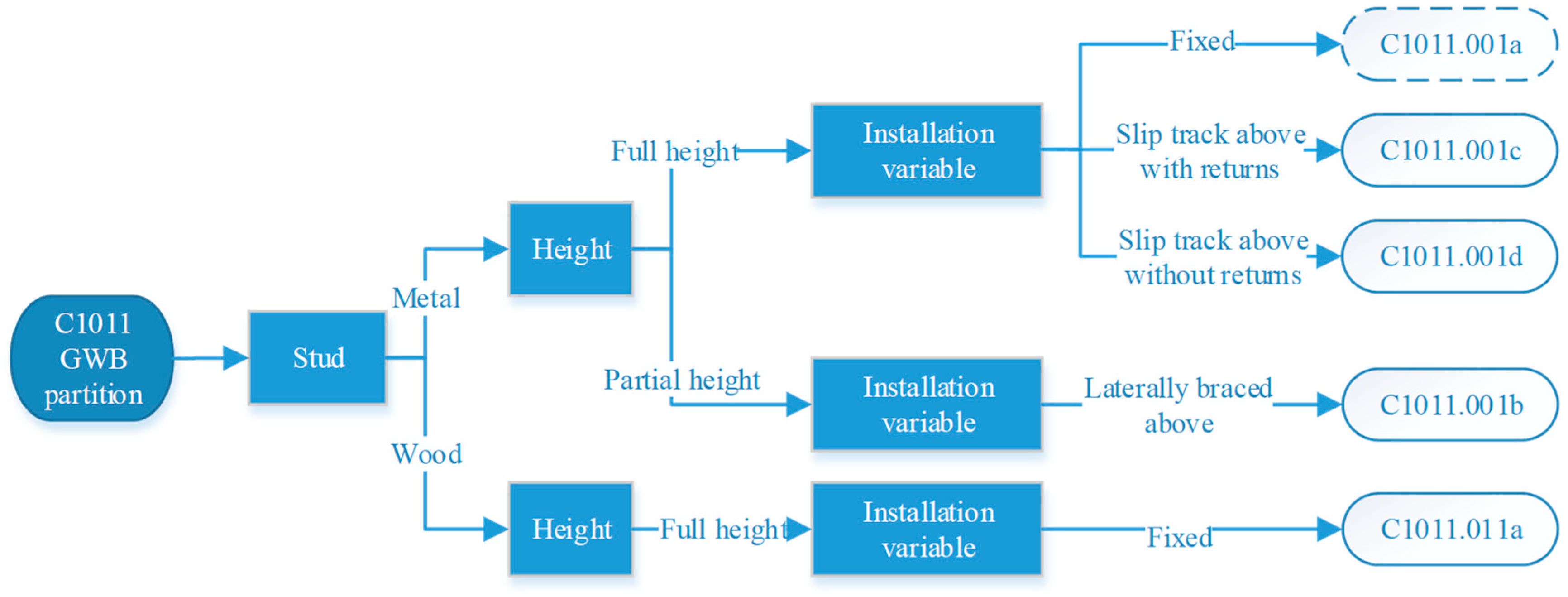
2.5.2. Regional Resilience Assessment Using FEMA P-58
- (a)
- Field survey data and building design drawings
- (b)
- Building information models
- (c)
- GIS database
2.6. High-Performance Computing for Post-Earthquake Emergency Response
3. Applications in Earthquake Emergency Response
3.1. Overview of the Applications
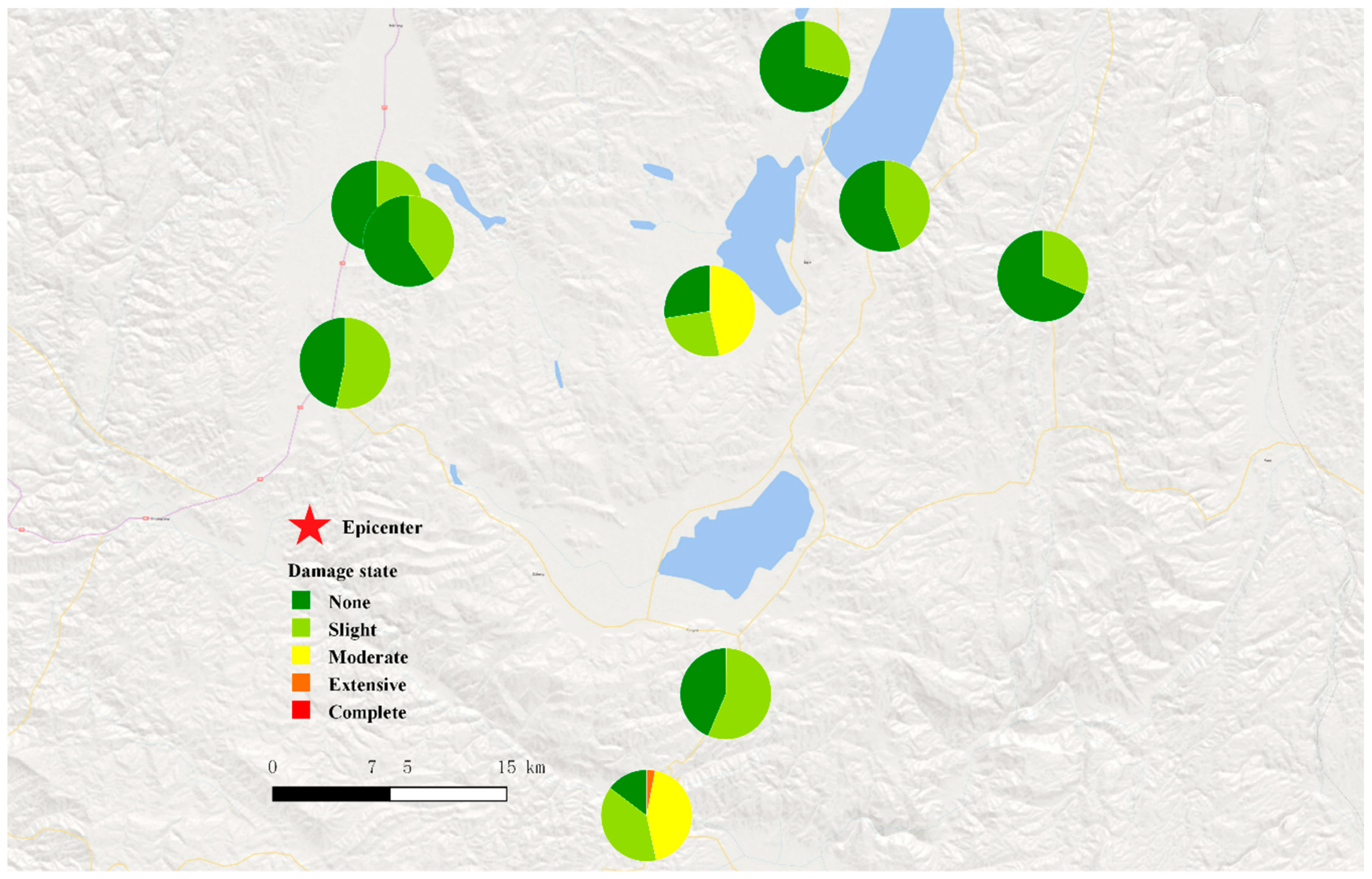
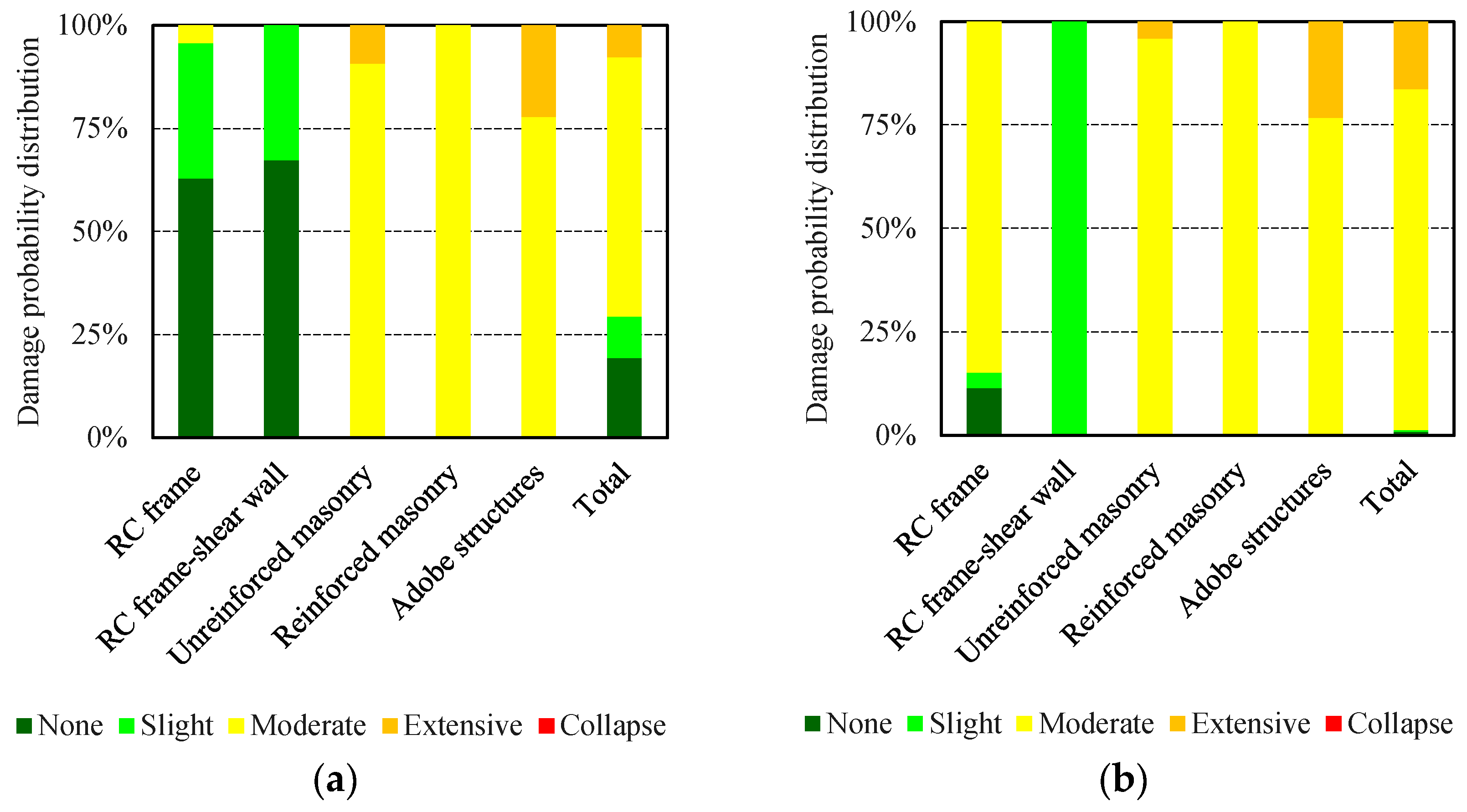
3.2. 2017 M7.0 Jiuzhaigou Earthquake
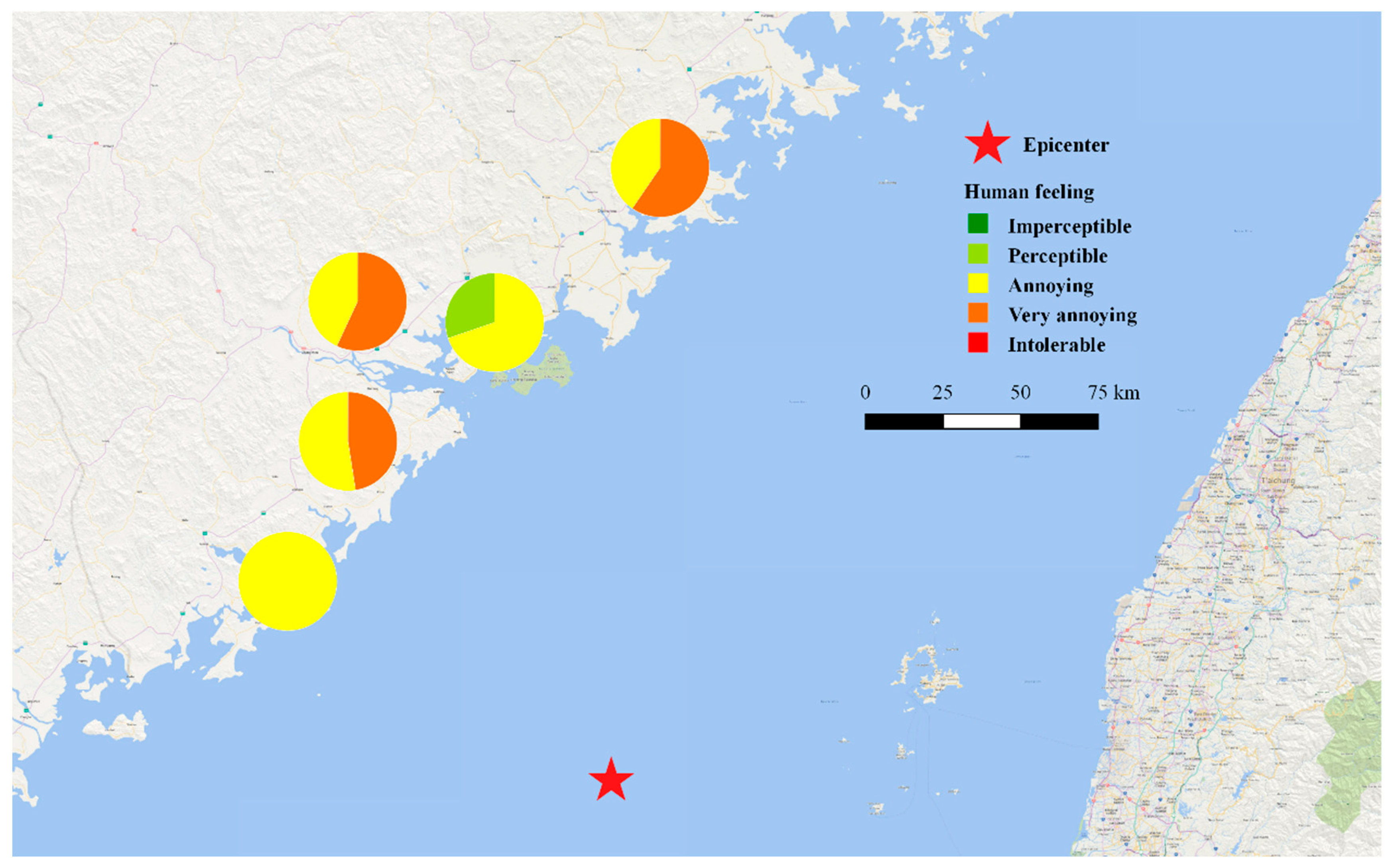
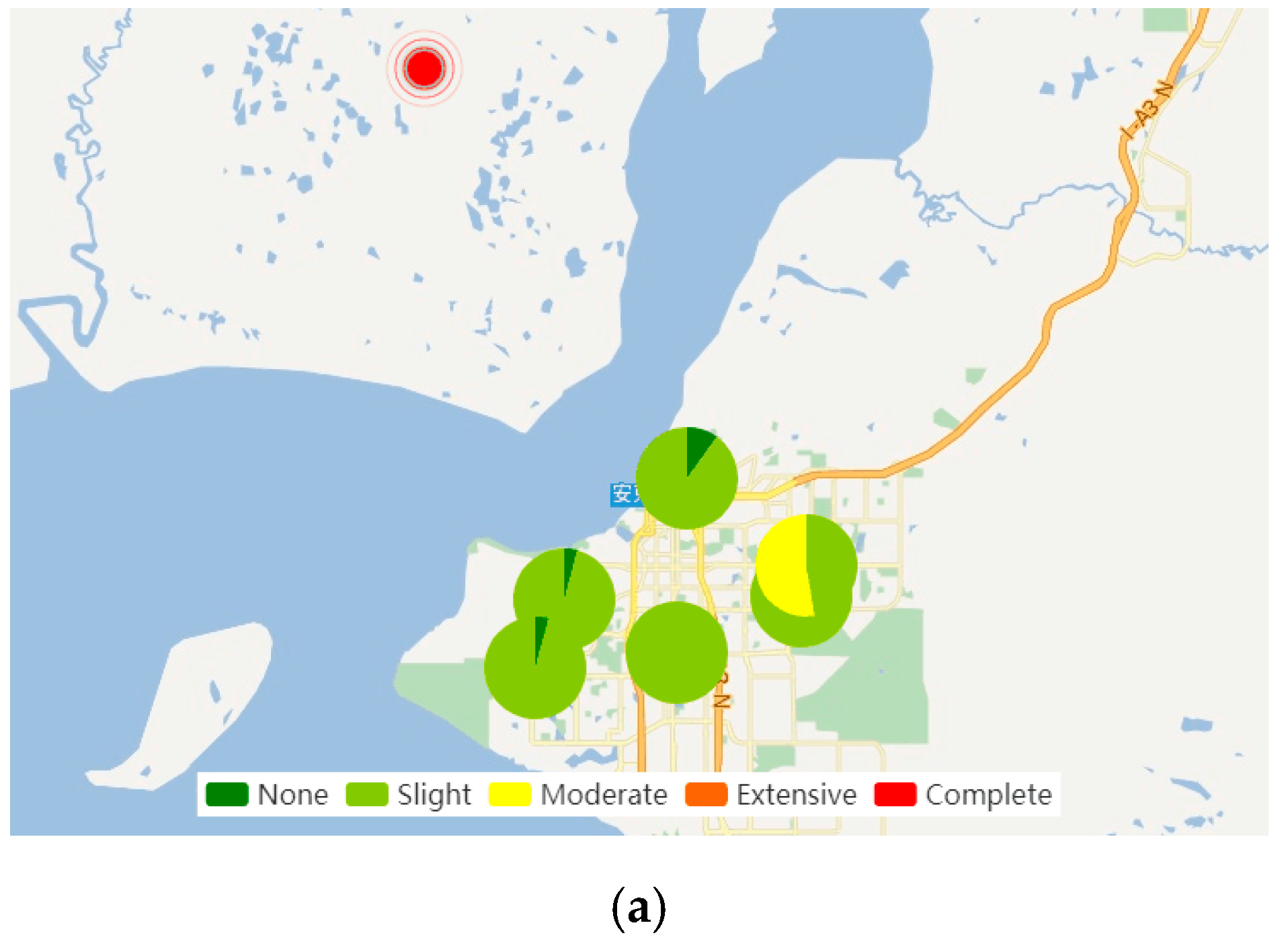
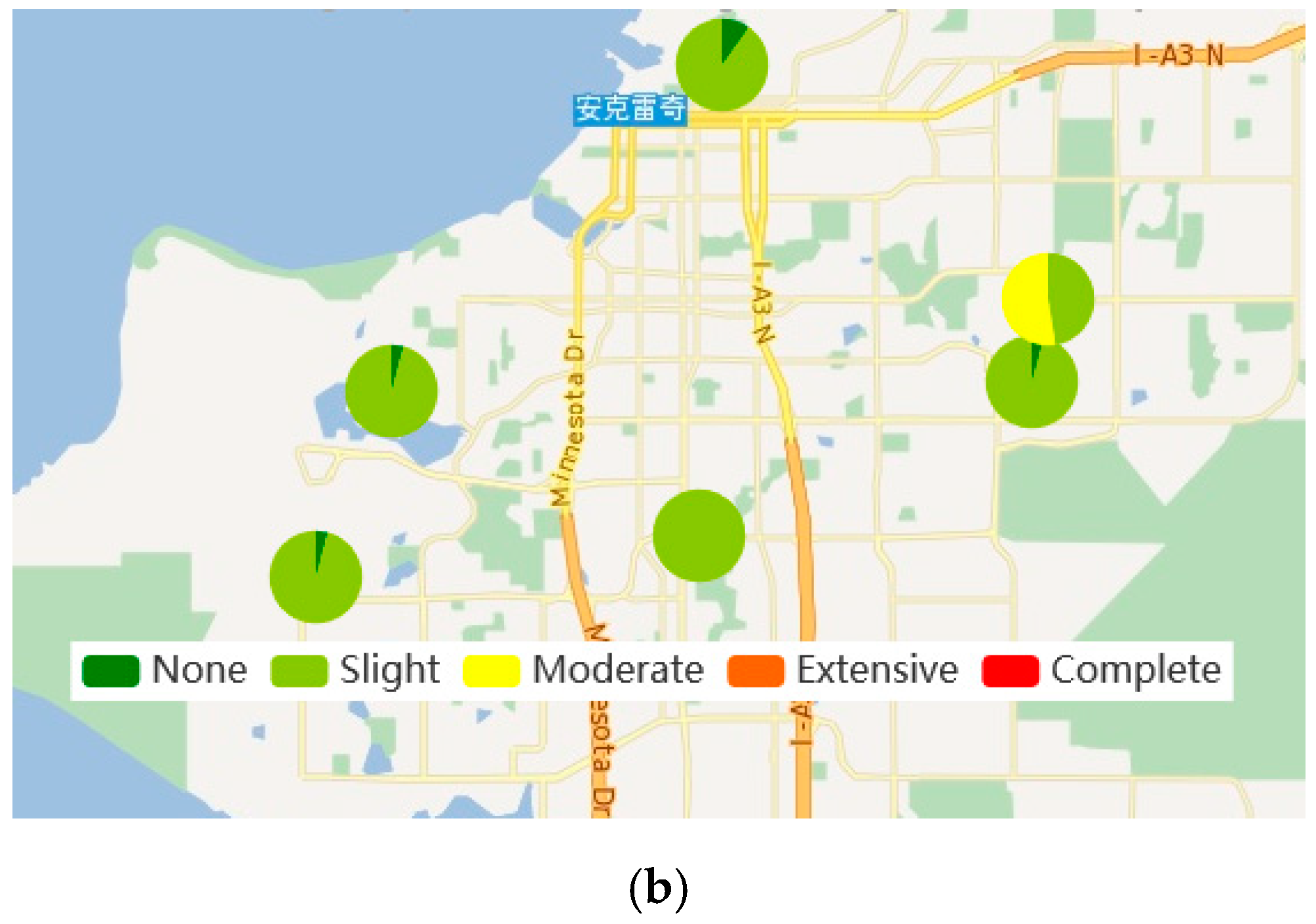
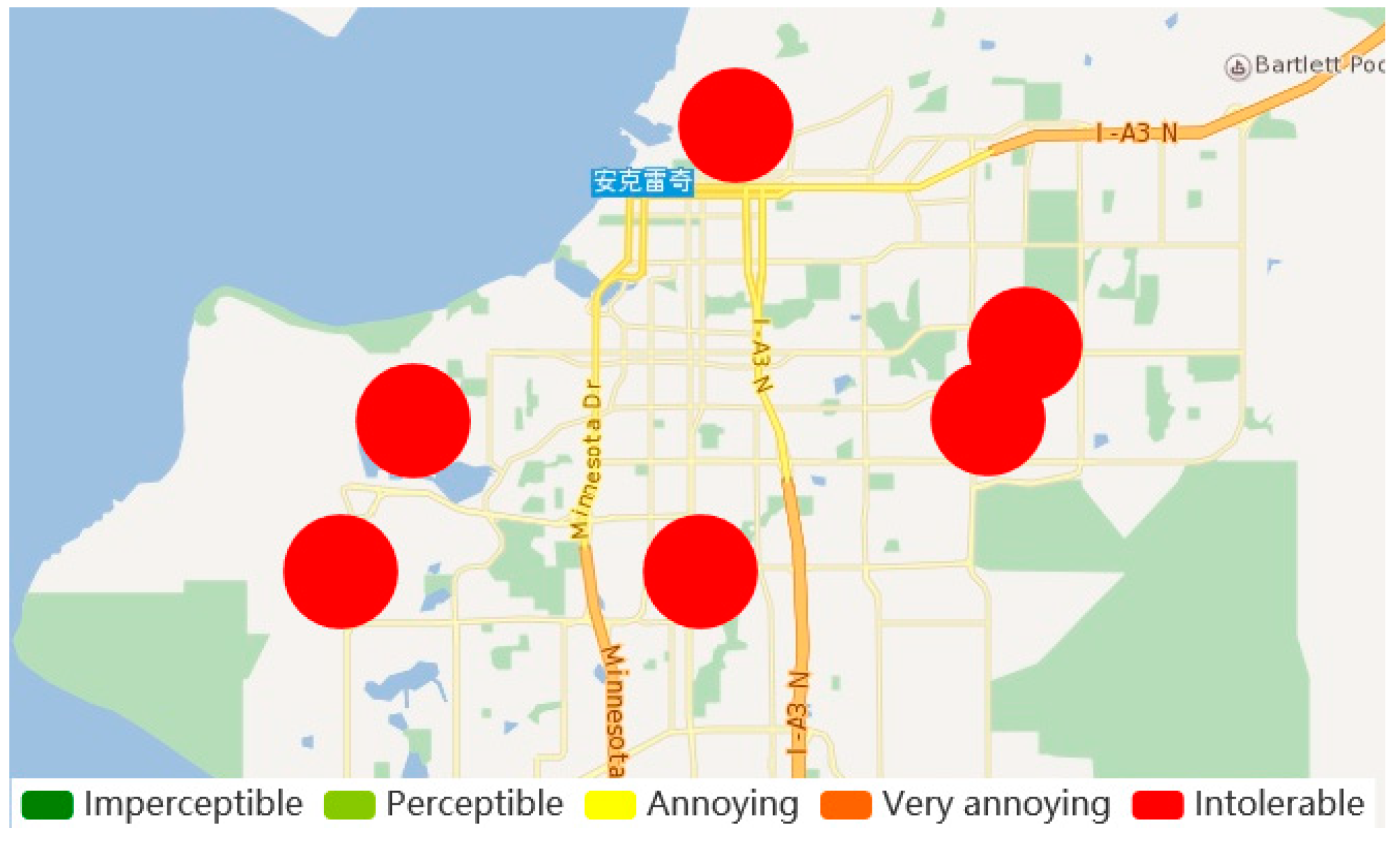
3.3. 2018 Mw 7.0 Anchorage Earthquake
4. Conclusions
- (1)
- The uncertainty problem of ground motion input is solved properly with the proposed method based on the real-time ground motion obtained from the seismic stations;
- (2)
- The amplitude, spectrum, and duration characteristics of ground motions, as well as the stiffness, strength, and deformation characteristics of different buildings are fully considered in this method, based on the nonlinear time-history analysis and MDOF models;
- (3)
- Using the real-time city-scale time-history analysis and the corresponding report system, the assessment of the earthquake’s destructive power, repair time, and economic loss can be obtained shortly after an earthquake event, which provides a useful reference for scientific decision-making for earthquake disaster relief. This work is highly significant to enhancing the resilience of earthquake-stricken areas.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Erdik, M.; Şeşetyan, K.; Demircioğlu, M.B.; Hancılar, U.; Zülfikar, C. Rapid earthquake loss assessment after damaging earthquakes. Soil Dyn. Earthq. Eng. 2011, 31, 247–266. [Google Scholar] [CrossRef]
- Wald, D.J.; Jaiswal, K.; Marano, K.D.; Bausch, D.B.; Hearne, M.G. PAGER—Rapid Assessment of an Earthquake’s Impact; U.S. Geological Survey Fact Sheet 2010–3036; U.S. Geological Survey: Reston, VA, USA, 2010.
- GDACS. Global Disaster Alert and Coordination System. Available online: http://www.gdacs.org (accessed on 11 August 2019).
- Trendafiloski, G.; Wyss, M.; Rosset, P. Loss estimation module in the second generation software QLARM. In Human Casualties in Earthquakes; Springer: Dordrecht, The Netherlands, 2011; pp. 95–106. [Google Scholar]
- Erdik, M.; Fahjan, Y. Damage scenarios and damage evaluation. In Assessing and Managing Earthquake Risk; Springer: Dordrecht, The Netherlands, 2008; pp. 213–237. [Google Scholar]
- Applied Technology Council (ATC). Earthquake Damage Evaluation Data for California; ATC-13; Applied Technology Council: Redwood City, CA, USA, 1985. [Google Scholar]
- Federal Emergency Management Agency (FEMA). Multi-hazard Loss Estimation Methodology-Earthquake Model Technical Manual (HAZUS-MH 2.1); Final Report; Federal Emergency Management Agency: Washington, DC, USA, 2012.
- Morfidis, K.; Kostinakis, K. Approaches to the rapid seismic damage prediction of r/c buildings using artificial neural networks. Eng. Struct. 2018, 165, 120–141. [Google Scholar] [CrossRef]
- De Lautour, O.R.; Omenzetter, P. Prediction of seismic-induced structural damage using artificial neural networks. Eng. Struct. 2009, 31, 600–606. [Google Scholar] [CrossRef]
- Population Census Office under the State Council, Department of Population and Employment Statistics of National Bureau of Statistics. Tabulation on the 2010 Population Census of the People’s Republic of China; China Statistics Press: Beijing, China, 2012. (In Chinese)
- Lu, X.Z.; Guan, H. Nonlinear MDOF Models for Earthquake Disaster Simulation of Urban Buildings. In Earthquake Disaster Simulation of Civil Infrastructures: From Tall Buildings to Urban Areas; Springer: Singapore, 2017; pp. 257–301. [Google Scholar]
- Xiong, C.; Lu, X.Z.; Guan, H.; Xu, Z. A nonlinear computational model for regional seismic simulation of tall buildings. Bull. Earthq. Eng. 2016, 14, 1047–1069. [Google Scholar] [CrossRef]
- Xiong, C.; Lu, X.Z.; Lin, X.C.; Xu, Z.; Ye, L.P. Parameter determination and damage assessment for THA-based regional seismic damage prediction of multi-story buildings. J. Earthq. Eng. 2017, 21, 461–485. [Google Scholar] [CrossRef]
- Hori, M. Introduction to Computational Earthquake Engineering; Imperial College Press: London, UK, 2006. [Google Scholar]
- Lu, X.Z.; Han, B.; Hori, M.; Xiong, C.; Xu, Z. A coarse-grained parallel approach for seismic damage simulations of urban areas based on refined models and GPU/CPU cooperative computing. Adv. Eng. Softw. 2014, 70, 90–103. [Google Scholar] [CrossRef]
- Sobhaninejad, G.; Hori, M.; Kabeyasawa, T. Enhancing integrated earthquake simulation with high performance computing. Adv. Eng. Softw. 2011, 42, 286–292. [Google Scholar] [CrossRef]
- GB50009-2012. Load Code for Design of Building Structures (GB 50009-2012); Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD): Beijing, China, 2012.
- American Society of Civil Engineers (ASCE). Minimum Design Loads for Buildings and Other Structures (ASCE/SEI 7-10); American Society of Civil Engineers (ASCE): Reston, VA, USA, 2010. [Google Scholar]
- GB50011-2010. Code for Seismic Design of Buildings (GB50011-2010); Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD): Beijing, China, 2010.
- GB50010-2010. Code for Seismic Design of Concrete Structures (GB50010-2010); Ministry of Housing and Urban-Rural Development of the People’s Republic of China (MOHURD): Beijing, China, 2010.
- Steelman, J.S.; Hajjar, J.F. Influence of inelastic seismic response modeling on regional loss estimation. Eng. Struct. 2009, 31, 2976–2987. [Google Scholar] [CrossRef]
- Lu, X.Z.; Tian, Y.; Guan, H.; Xiong, C. Parametric sensitivity study on regional seismic damage prediction of reinforced masonry buildings based on time-history analysis. Bull. Earthq. Eng. 2017, 15, 4791–4820. [Google Scholar] [CrossRef]
- Simiu, E.; Scanlan, R.H. Wind Effects on Structures: Fundamentals and Applications to Design, 3rd ed.; John Wiley: New York, NY, USA, 1996; p. 512. [Google Scholar]
- GB/T18208. Post-Earthquake Field Works—Part 4: Assessment of Direct Loss (GB/T 18208.4-2011); Standardization Administration of China: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Zeng, X.; Lu, X.Z.; Yang, T.Y.; Xu, Z. Application of the FEMA-P58 methodology for regional earthquake loss prediction. Nat. Hazards 2016, 83, 177–192. [Google Scholar] [CrossRef]
- Xu, Z.; Lu, X.Z.; Zeng, X.; Xu, Y.J.; Li, Y. Seismic loss assessment for buildings with various-LOD BIM data. Adv. Eng. Inf. 2019, 39, 112–126. [Google Scholar] [CrossRef]
- Zeng, X. Direct Seismic Loss Assessment and Fire Following Earthquake Simulation of Urban Buildings. Ph.D. Thesis, Tsinghua University, Beijing, China, 2018. (In Chinese). [Google Scholar]
- Federal Emergency Management Agency (FEMA). Seismic Performance Assessment of Buildings; Methodology; Technical Report FEMA-P58; Federal Emergency Management Agency (FEMA): Washington, DC, USA, 2012; Volume 1.
- Xu, X.; Ding, L.Y.; Luo, H.B.; Ma, L. From building information modeling to city information modeling. J. Inf. Technol. Constr. 2014, 19, 292–307. [Google Scholar]
- Chandra, R.; Dagum, L.; Kohr, D.; Menon, R.; Maydan, D.; McDonald, J. Parallel Programming in OpenMP; Morgan Kaufmann: San Diego, CA, USA,, 2001; pp. 8–14. [Google Scholar]
- Lu, X.Z.; Gu, D.L.; Lin, X.C.; Cheng, Q.L.; Zhang, L.; Tian, Y.; Zeng, X. Seismic damage assessment of the ground motion near the epicenter of the 7.0 earthquake in Jiuzhaigou, Sichuan. Stand. Eng. Constr. 2017, 68–73. (In Chinese) [Google Scholar]
- Dai, J.W.; Sun, B.T.; Li, S.Y.; Tao, Z.R.; Ma, Q.; Zhang, L.X.; Lin, J.Q. Engineering Damage in Jiuzhaigou M 7.0 Earthquake; Seismological Press: Beijing, China, 2018; p. 18. (In Chinese) [Google Scholar]
- Lu, X.Z. Damage Capacity of the Ground Motions of the Dec. 1, Alaska Earthquake; Research Group Report; Tsinghua University: Beijing, China, 2018. [Google Scholar]
- Structural Extreme Event Reconnaissance Network (StEER), Earthquake Engineering Research Institute (EERI). Alaska Earthquake Preliminary Virtual Assessment Team (P-VAT) Joint Report; Earthquake Engineering Research Institute: Oakland, CA, USA, 2018. [Google Scholar]
- Center for Engineering Strong Motion Data (CESMD). Available online: https://www.strongmotioncenter.org/cgi-bin/CESMD/iqrStationMap.pl?ID=us1000hyfh (accessed on 26 January 2019).
| Number of stories | 1 | 2–3 | 4–6 | 7–9 | >9 |
| Proportions | 20.6% | 10.6% | 36.3% | 4.9% | 27.6% |
| Year built | <1990 | 1990–1999 | >1999 | ||
| Proportions | 30.3% | 29.8% | 39.9% | ||
| Structural type | Steel and reinforced concrete | Masonry | Wood | Other structures | |
| Proportions | 47.9% | 40.3% | 11.6% | 0.2% | |
| ID | Earthquake Name | ID | Earthquake Name |
|---|---|---|---|
| 1 | 12/08/2016 M6.2 Xinjiang Hutubi earthquake | 18 | 11/26/2018 M6.2 Taiwan Strait earthquake |
| 2 | 12/18/2016 M4.3 Shanxi Qingxu earthquake | 19 | 12/08/2018 M4.5 Xinjiang Changji earthquake |
| 3 | 03/27/2017 M5.1 Yunnan Yangbi earthquake | 20 | 12/16/2018 M5.7 Sichuan Yibin earthquake |
| 4 | 08/08/2017 M7.0 Sichuan Jiuzhaigou earthquake | 21 | 12/20/2018 M5.2 Xinjiang Kizilsu earthquake |
| 5 | 09/30/2017 M5.4 Sichuan Qingchuan earthquake | 22 | 01/03/2019 M5.3 Sichuan Yibin earthquake |
| 6 | 02/06/2018 M6.5 Taiwan Hualien earthquake | 23 | 01/07/2019 M4.8 Xinjiang Jiashi earthquake |
| 7 | 02/12/2018 M4.3 Hebei Yongqing earthquake | 24 | 04/16/2016 M7.3 Japan Kumamoto earthquake |
| 8 | 05/28/2018 M5.7 Jilin Songyuan earthquake | 25 | 08/24/2016 M6.2 Italy earthquake |
| 9 | 08/13/2018 M5.0 Yunnan Tonghai earthquake | 26 | 11/13/2016 M8.0 New Zealand earthquake |
| 10 | 08/14/2018 M5.0 Yunnan Tonghai earthquake | 27 | 09/20/2017 M7.1 Mexico earthquake |
| 11 | 09/04/2018 M5.5 Xinjiang Jiashi earthquake | 28 | 11/23/2017 M7.8 Iraq earthquake |
| 12 | 09/08/2018 M5.9 Yunnan Mojiang earthquake | 29 | 06/18/2018 M6.1 Japan Osaka earthquake |
| 13 | 09/12/2018 M5.3 Shanxi Ningqiang earthquake | 30 | 09/06/2018 M6.9 Japan Hokkaido earthquake |
| 14 | 10/16/2018 M5.4 Xinjiang Jinghe earthquake | 31 | 10/26/2018 M5.4 Japan Hokkaido earthquake |
| 15 | 10/31/2018 M5.1 Sichuan Xichang earthquake | 32 | 12/01/2018 M7.0 Alaska earthquake |
| 16 | 11/04/2018 M5.1 Xinjiang Atushi earthquake | 33 | 01/03/2019 M6.2 Japan Kumamoto earthquake |
| 17 | 11/25/2018 M5.1 Xinjiang Bole earthquake |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Cheng, Q.; Xu, Z.; Xu, Y.; Sun, C. Real-Time City-Scale Time-History Analysis and Its Application in Resilience-Oriented Earthquake Emergency Responses. Appl. Sci. 2019, 9, 3497. https://doi.org/10.3390/app9173497
Lu X, Cheng Q, Xu Z, Xu Y, Sun C. Real-Time City-Scale Time-History Analysis and Its Application in Resilience-Oriented Earthquake Emergency Responses. Applied Sciences. 2019; 9(17):3497. https://doi.org/10.3390/app9173497
Chicago/Turabian StyleLu, Xinzheng, Qingle Cheng, Zhen Xu, Yongjia Xu, and Chujin Sun. 2019. "Real-Time City-Scale Time-History Analysis and Its Application in Resilience-Oriented Earthquake Emergency Responses" Applied Sciences 9, no. 17: 3497. https://doi.org/10.3390/app9173497
APA StyleLu, X., Cheng, Q., Xu, Z., Xu, Y., & Sun, C. (2019). Real-Time City-Scale Time-History Analysis and Its Application in Resilience-Oriented Earthquake Emergency Responses. Applied Sciences, 9(17), 3497. https://doi.org/10.3390/app9173497





