Handover-Driven Interference Management for Co-Channel Deployment of Femto- and Macro-Cells

Abstract

Femtocell technology has been gaining popularity as an inexpensive means of enhancing cellular coverage and capacity. However, under co-channel deployment—expected to be commonplace due to high spectrum costs—femtocells may incur harmful interference to existing macrocells, and vice versa. To alleviate this problem, This paper proposes a new architecture called HandOver-driven Femtocell Interference Management (HO-FIM) that offloads macrocells by handing macrocell users over to “hybrid-access” femtocells that allow the access of both subscribed and unsubscribed users. This use of handovers adds a new degree-of-freedom for solving the interference problem, thus overcoming the capacity limit of the existing approaches that exploit radio resource coordination only. A new challenge associated with this approach is how to minimize handovers while reaching a desired system condition due to the inevitable service interruptions that accompany handovers. This paper proposes to overcome this challenge by triggering handovers only when needed and, once triggered, to find an optimal sequence to reach a target system condition with minimal handovers. This paper designs a greedy per-user control algorithm that has a fine control granularity and thus enables convergence to an optimal solution. The in-depth evaluation of the paper shows that HO-FIM improves the service quality of both macro- and femtocell users; in an example simulation scenario, HO-FIM is shown to improve the signal-to-interference and noise ratios (SINRs) of macro- and femtocell users by up to 23.3 and 2.9 dB, respectively, on average, compared to the case of no handovers.

1. Introduction

Recently, there has been a growing interest in femtocell technology, which promises cost-effective enhancement of indoor network coverage and capacity to meet increasing demands for bandwidth-hungry data services within home or enterprise environments [1]. A femtocell is a small indoor area covered by a low-power base station (BS), referred to as a femto BS in this paper. A significant capacity improvement is expected to be achieved with femtocells via their enhanced spatial reuse of spectrum resources. In addition, femtocells can offload macrocells and improve indoor coverage at low capital and operational costs. Femto BSs are installed on the subscriber’s premise without the operator’s lengthy planning and are typically connected to an operator’s core network via public Internet connections, such as DSL and cable modems.

A key challenge faced by femtocell technology is how to protect macrocell user services from femtocell interference when macro- and femtocells are allocated the same frequency band for economic reasons, called co-channel deployment, while exploiting spatial reuse of channel resources within femtocells. Co-channel deployment of macro- and femtocells is expected to be commonplace due to the high cost of the licensed spectrum. Under this co-channel deployment, transmissions within femtocells may cause harmful interference to user services within macrocells, and vice versa, as reported by many researchers [2]. The resultant performance degradation has become a major obstacle to market penetration of the femtocell technology, since the deteriorated service to existing users will increase the churn rate.

There have been many proposals to resolve the femtocell interference problem based mostly on radio resource coordination between macro- and femtocells, but their achievable capacity is limited. To overcome the capacity limit of existing approaches by adding a degree-of-freedom (DoF) when solving the interference problem, a new solution architecture called HandOver-driven Femtocell Interference Management (HO-FIM) is proposed. HO-FIM mitigates the interference problem and offloads the overall heterogeneous networks by exploiting handovers between macrocells and hybrid-access femtocells based on the users’ measurement reports. A new challenge associated with this approach is how to minimize the number of triggered handovers and suppress ping-pong handovers while reaching a desired system condition, since handovers accompany inevitable interruptions of ongoing user services being handed over. This paper proposes to meet this challenge by triggering handovers only when absolutely needed and, once triggered, to find an optimal handover sequence to reach a target system condition with minimal handovers. HO-FIM accompanies a greedy per-user control algorithm which has a fine control granularity and thus enables convergence to an optimal solution. HO-FIM is composed of the following three interacting controllers:

• Master controller: Makes decisions on whether to activate/deactivate the handover controller based on the current status of radio resource usage;
• Handover controller: Determines a sequence of handovers to be made to reach a target system condition with minimal handovers while avoiding ping-pong handovers;
• Radio resource controller: Handles intra-cell scheduling of frequency, time and power resources to meet users’ target service levels.

The approach of HO-FIM is also applicable to the general concept of heterogeneous networks (HetNets) that represents cellular deployments with heterogeneous types of cells of different sizes and overlapping coverage areas including femto and small (hotzone) cells.

The evaluation results show that HO-FIM improves the performance of both macro- and femtocell users under various environmental settings. In an example scenario with 30 macrocell users and 50 femtocell users within a macrocell, more than 90% of macrocell users achieved higher signal-to-interference and noise ratios (SINRs) by 23.3 dB on average than in a case without using handovers; the entire cohort of femtocell users achieved 2.9 dB higher SINRs.

The rest of this paper is organized as follows. Section 2 and Section 3 describe the motivation of this work and the system model, respectively. Section 4 presents the HO-FIM architecture, and Section 5 describes the control algorithm. Section 6 evaluates the HO-FIM architecture using detailed simulations, and Section 7 concludes the paper.

2. Motivation

The use of handovers for interference mitigation is first advocated. Then, the requirements of a new interference management architecture is discussed and the limitations in applying existing techniques to femtocell networks is identified.

2.1. Why Handover for Interference Mitigation?

A main challenge associated with femtocell technology is how to protect macrocell user services against femtocell users’ interference when macro- and femtocells use the same frequency band, while exploiting high spatial reuse of spectrum resources within each femtocell. Due to the high cost of the licensed spectrum, operators may wish to allocate both macro- and femtocells the same frequency channel, called co-channel deployment. Under this co-channel deployment, however, transmissions of femtocell users (those being served by femtocells) may cause interference to the ongoing transmissions of macrocell users (those being served by macrocells), and vice versa, in both downlink (DL) and uplink (UL) communications.

As briefly reviewed below in this section, there have been numerous research efforts to tackle this problem based on radio resource coordination; these approaches can be classified into orthogonal resource block (RB) assignment (a resource block (RB) is a group of subcarriers and also the minimum scheduling granule in OFDMA systems; for example, in 3GPP Long-Term Evolution (LTE), 12 contiguous subcarriers compose an RB (5 RBs in a 900 kHz band)), power control or combinations thereof. 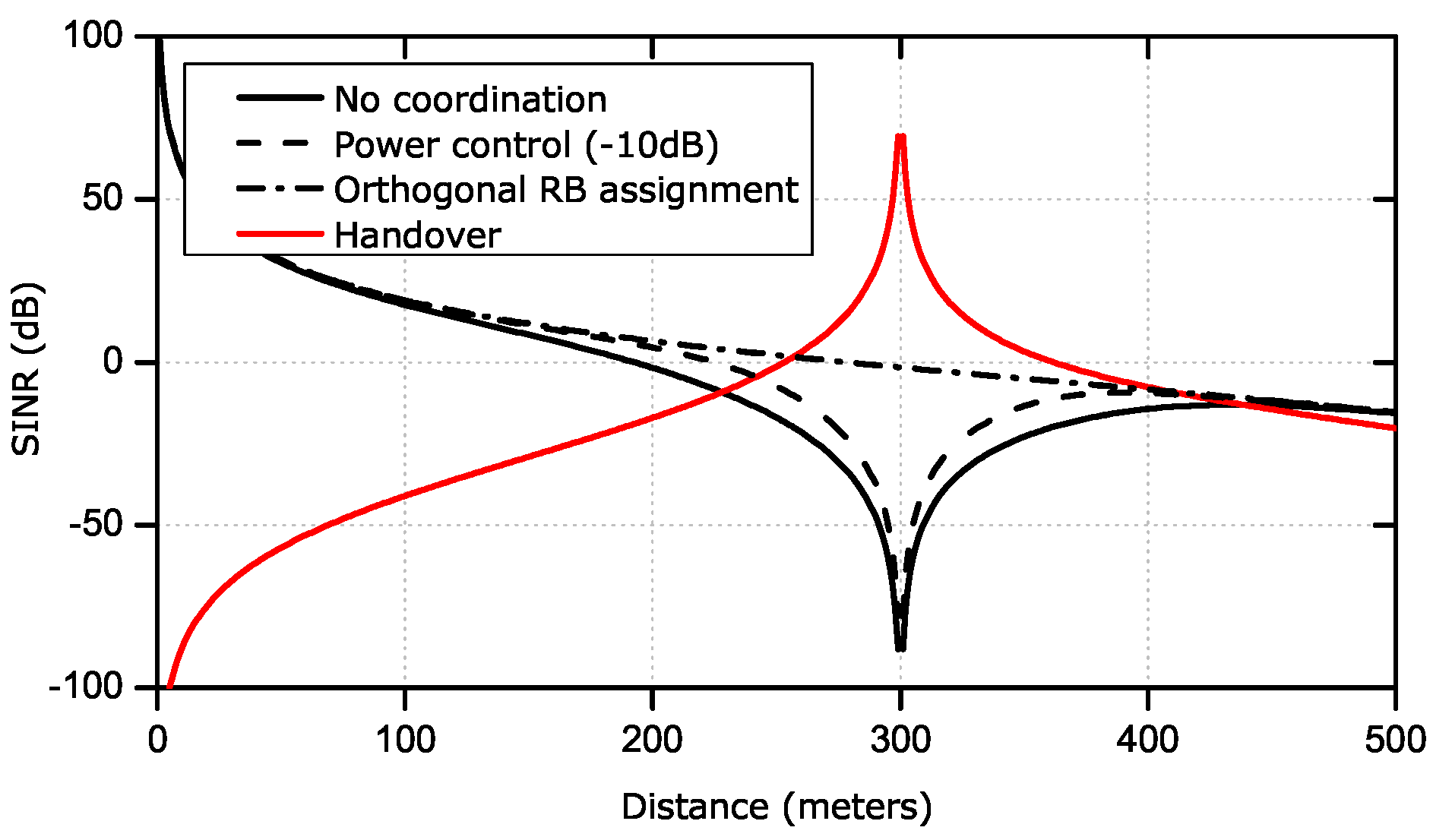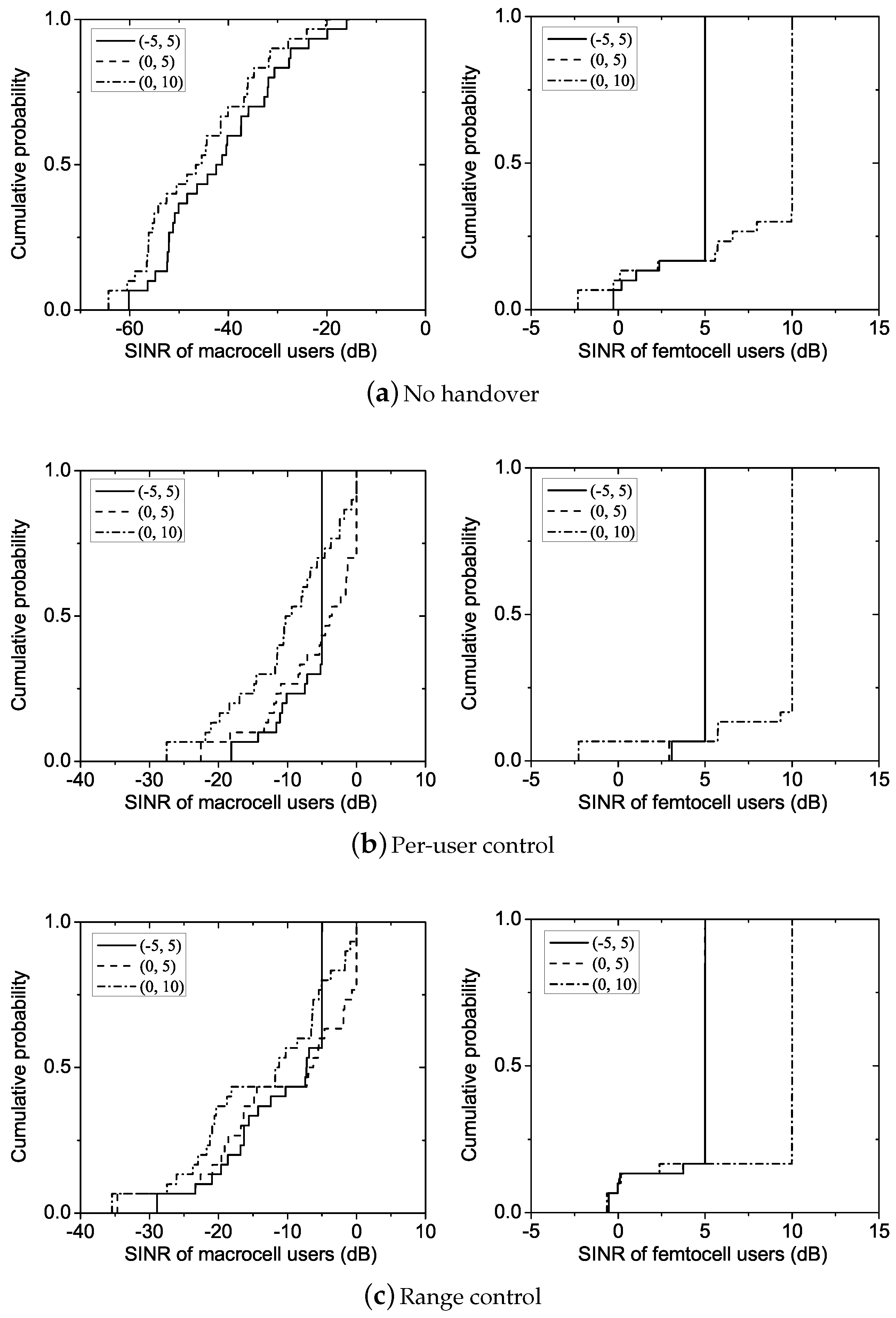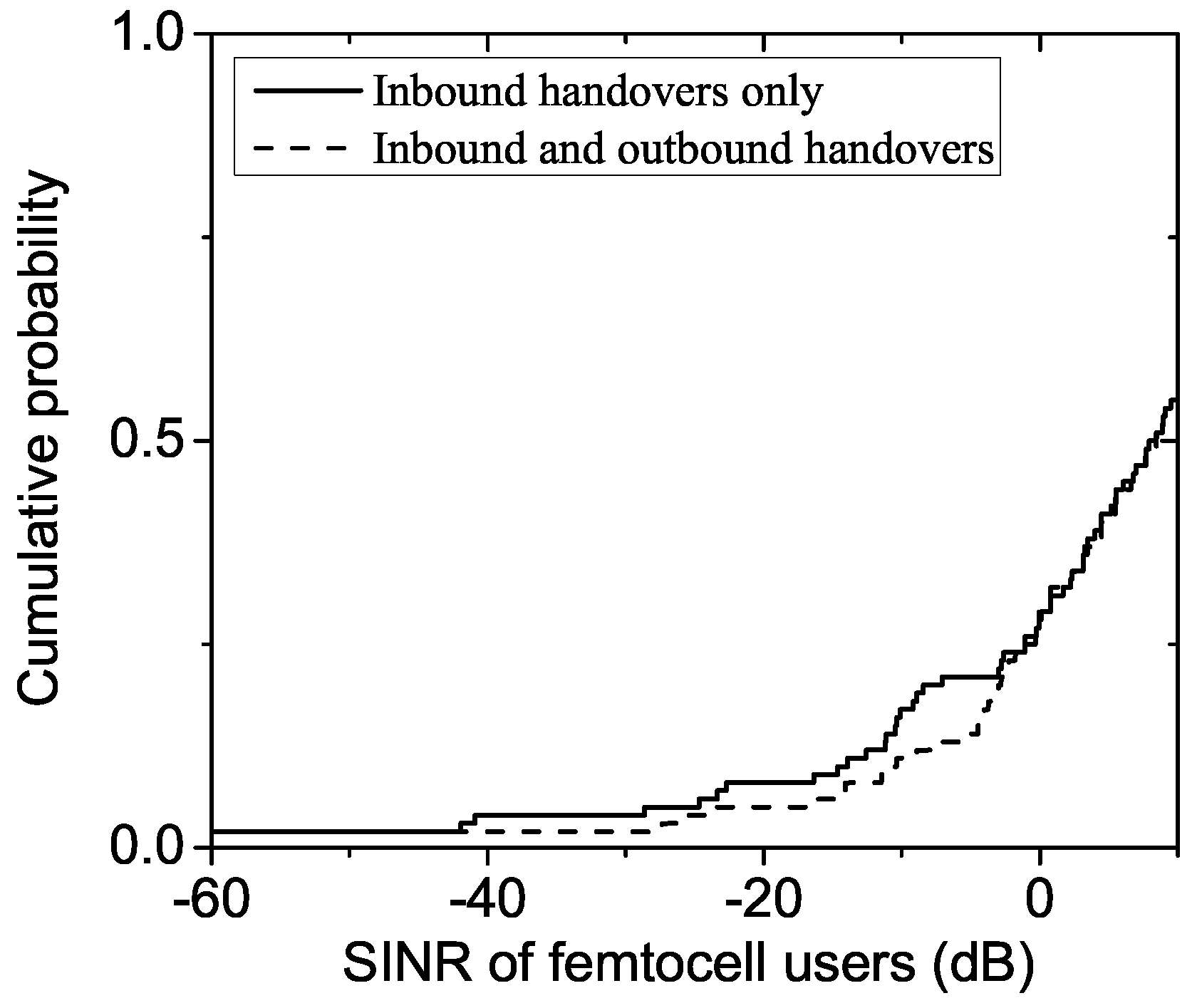Figure 1 compares the achieved DL SINR of a macrocell user under different approaches, showing that radio resource coordination can mitigate the interference problem to some degree. As a macrocell user passes by a femto BS located 300 m away, his SINR gets deteriorated considerably. To protect the nearby macrocell users’ communications, the femto BS can reduce its transmitting power (power control) or use a different RB from that allocated to the macrocell user (orthogonal RB assignment). However, both approaches, if operated dynamically, require the detailed (e.g., per-RB) and real-time information of the macrocell’s resource usage, and, moreover, their achievable gain is  limited.

Another solution that can be combined with radio resource coordination is to hand the macrocell user over to the interfering femtocell if the femtocell has spare resources to serve the user. Figure 1 shows that the handover approach can not only mitigate the interference problem but also improve the achievable capacity significantly. The performance gain of the handover approach comes from: (1) reduced interference (due to reduced path losses and enabled coordination within the same serving cell); and (2) load-balancing, as explained next. A macrocell user may experience high DL interference from, and produce high UL interference to, a nearby femtocell. If the macrocell user is handed over to the femtocell, he may experience reduced loss of paths to his serving cell (i.e., the femtocell), thus achieving a better SINR with the same radio resources or a target SINR with less radio resources. Moreover, both macro- and femtocell users—previously interfered with by each other—will be served by the same femtocell with their interference coordination enabled. In many cases, femtocells are also likely to be less loaded than macrocells, as they typically serve fewer users. Thus, a macrocell user, if handed over to a femtocell, will likely be allocated more radio resources. However, the standard handover decisions based on the strongest signal power are not suitable for realizing the above benefits, since, due to the overlaid cell deployment, a macrocell’s signal strength could still be strong within a femtocell’s coverage area. Therefore, the handover-based approach requires a new method of making handover decisions, tailored to femtocell networks. It should determine which user should be handed over to which femtocell and when.

Handovers from macrocells to femtocells may not always be supported due to the different access modes of target femtocells:

• Open Subscriber Group (OSG) femtocells, where all users are allowed to connect;
• Closed Subscriber Group (CSG) femtocells, where only subscribed users are allowed to establish connections; and
• Hybrid-access femtocells: Unsubscribed users are allowed to access if there are idle/spare resources.

In general, a femtocell can support only a small number of concurrent sessions (e.g., eight or eight data sessions) due to its limited processing power. Thus, private femtocells are likely to operate in the CSG mode, although OSG mode may provide a higher capacity if interference is mitigated. Therefore, a hybrid of the two access modes may maximize capacity while preserving the privileged access of subscribed users. Thus, the use of hybrid access for all femtocells is assumed.

2.2. Requirements of a New Architecture

Due to the use of handovers and other salient features of femtocells, the following requirements have to be considered when designing a handover-based interference management architecture.

• Minimization of handovers: Current OFDMA-based cellular systems (e.g., 3GPP LTE and 5G NR) support hard handovers only. Thus, a user’s handover accompanies a temporary interruption of his ongoing voice or data service as well as a signaling overhead. To minimize users’ performance degradation, handovers should be triggered only when service deterioration for users would otherwise be inevitable or if a significant reduction of the interference to macro- and femtocell users is expected. Moreover, any solution algorithm should be able to reach a desired system condition with the minimum number of handovers. Ping-pong handovers must be avoided as well.
• Low computation complexity: This is an important design requirement due to the expected large number of users to be supported by a single BS in forthcoming cellular networks (resulting from the increased bandwidth) and multiple femtocells to be deployed within a macrocell. The Next Generation Mobile Networks (NGMN), an alliance of cellular operators, specifies that a 5G network should support up to 150 thousand concurrent user sessions per square kilometer [3]. To meet such a high connection density, the number of femtocells to be installed within a macrocell coverage area could be up to several thousands in the future. Consequently, the search space of a handover-decision algorithm will be widened significantly.
• No special hardware: For cost-efficiency, femto BSs and user devices should not be required to have special hardware.

2.3. Limitations of Existing Techniques

There is a rich body of research that has attempted to resolve the femtocell interference problem based on radio resource (power, frequency, and time) management. Ma et al. [4] proposed a hybrid overlay and underlay spectrum access mechanism and solved a subchannel allocation problem as a coalition formation game among femtocell users. Yun et al. [5] proposed an asynchronous coordination scheme of co-channel femtocells based on delayed signaling and asynchronous update behavior and derived the condition of configuration parameters that guarantees convergence to a global optimum. DACA [6] is an intra- and inter-cell resource coordination framework associated with control algorithms for full-duplex heterogeneous cellular networks.

Recently, there have been an increasing number of proposals exploiting hybrid-access femtocells. AbdelNabi et al. [7] analyzed the performance of hybrid access schemes in the perspective of MIMO array configurations. Kim et al. [8] proposed a scheme to jointly optimize the ratio of dedicated resources for femtocells in open and hybrid-access femtocells. Zhang et al. [9] proposed a spectrum allocation method for hybrid-access femtocells where a macro BS allocates a portion of subchannels to femtocells with which each femtocell guarantees the throughput of served macrocell users. Deng et al. [10] proposed a similar framework and designed an auction-based algorithm where each femtocell receives additional macro users as bidders while the macro BS acts as the auctioneer. Thakur et al. [11] developed a QoS-aware cell selection scheme that assigns mobile users to femtocells, incorporating the energy consumption of backhaul links. Game-theoretic incentive frameworks to motivate femtocells to adopt a hybrid access policy by pricing accessed macrocell users’ resource usages were proposed in [12,13]. However, most studies focused on intra-cell resource management combined with BS assignment, and none considered the optimality and convergence of dynamic handover management.

Some research works focused on the cell selection problem (also known as the BS assignment problem) that is used to find optimal pairs of users and serving cells. The system energy efficiency of small cell networks was considered for cell selection in [14,15]. There are numerous proposals to solve the problem in general cellular networks. Yates and Huang [16] proposed synchronous and asynchronous distributed algorithms that find the optimal power vector and BS assignment. Lee et al. [17] developed a pricing-based BS assignment algorithm considering the congestion level of BSs. The use of iterative algorithms based on linear programming (LP) to solve the BS assignment problem was presented in [18]. Alorainy and Hossain [19] considered a coordinated multipoint dynamic cell selection problem. However, they all focused on the optimality of resultant BS assignments only, and none of them considered the handover overhead. Some heuristic approaches that consider the handover overhead exist, but they do not guarantee the optimality [20].

Range extension, which expands the handover ranges of overlaid cells [21], was discussed in 3GPP as a solution to address the interference problem. The use of cell ranges for distributing users is advantageous in that it can be implemented within a conventional cell-selection framework of existing cellular systems without modifying user devices or an air interface. To fully realize the benefit of the range extension, vendors need an algorithm to control the handover ranges. There has been a notable attempt at optimal range control for hybrid-access femtocells. 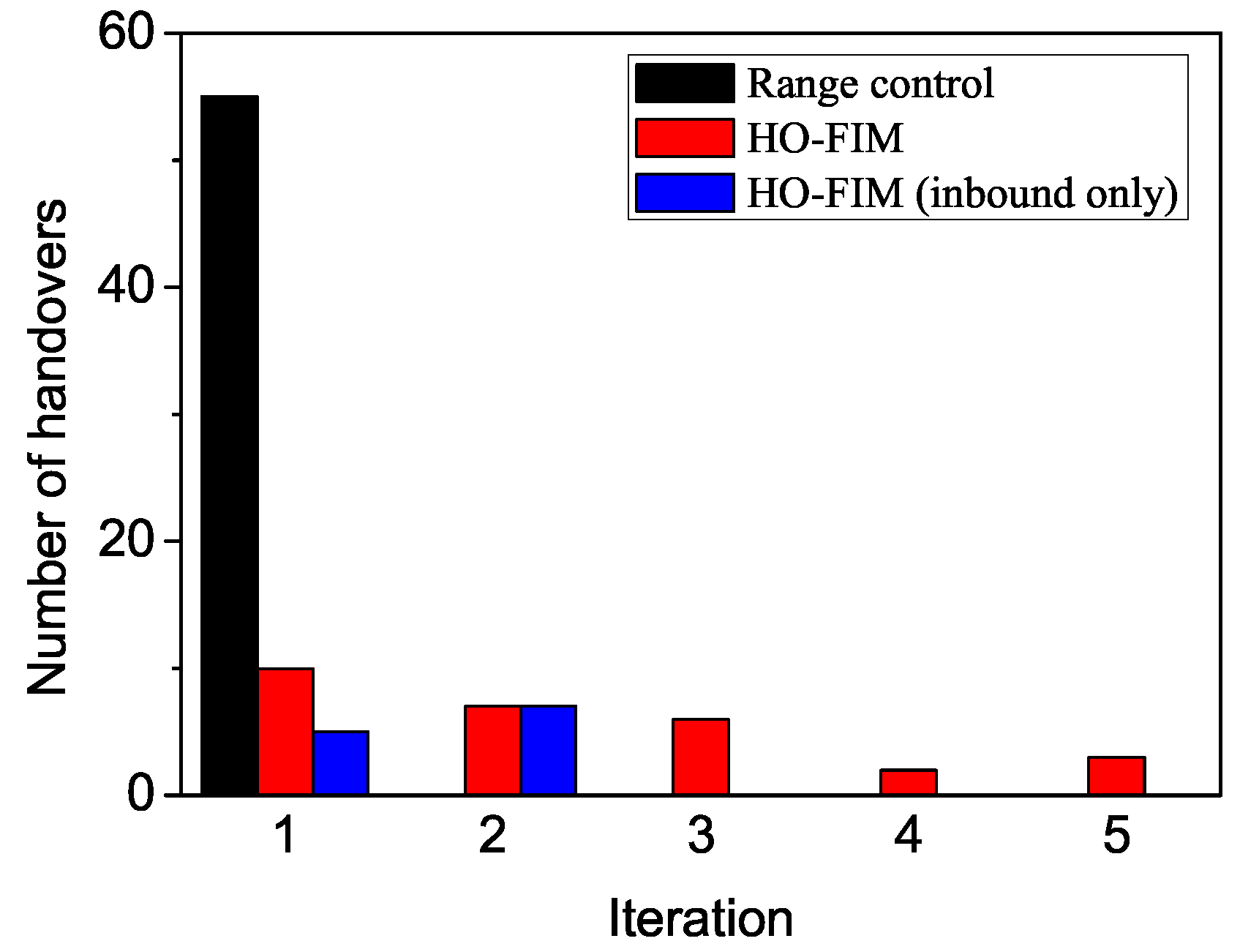ARCHoN [22] allocates radio resources (frequency, time, and power) and distributes/assigns users among overlapping cells by controlling hotzone cell ranges such that the overall DL and UL loads of a HetNet are minimized while per-user rate constraints are met. The proposed scheme of this paper outperforms ARCHoN due to its finer control granularity (as compared in the evaluation section).

3. System Model

This section describes the network architecture under consideration, including the implementation details of the user measurement. The typical handover procedure that is assumed in this paper is described as well.

3.1. Network Architecture

A typical two-tier femtocell network architecture where femtocells are overlaid on a macrocell is considered. The number of macrocell users and that of femtocells are denoted by M and F, respectively. The macrocell and the set of femtocells $\mathcal{F}=\{1,\dots ,F\}$ use an identical frequency band. Cell i operates under the control of BS i. Macro and femto BSs are assumed to use identical OFDMA technology. The set of users $\mathcal{U}=\{1,\dots ,N\}$ is divided into the set ${\mathcal{U}}_M=\{1,\dots ,M\}$ of macrocell users, and the set ${\mathcal{U}}_i$ of femtocell users being served by femtocell $i\in \mathcal{F}$. All femtocells are configured to use the hybrid access mode, i.e., both subscribed and unsubscribed macrocell and femtocell users are allowed to access all femtocells.

3.2. Handover Procedure

Figure 2 illustrates the procedure of a macrocell-to-femtocell handover considered in this paper, which is analogous to that of 5G NR [23]. A user measures the pilot signal strength of neighbor cells and reports the measurement to his serving macrocell according to the rules set by the system information (SI). If a target femtocell is not uniquely identified due to physical cell ID confusion (due to the typical cell size of femtocells being much smaller than macrocells, there can be multiple femtocells within the coverage of the source macrocell that have the same physical cell ID, which leads to a condition referred to as physical cell ID confusion, where the source macrocell is unable to determine the correct target femtocell for handover [24]), the macrocell requests the user to report the femtocell’s global cell ID by acquiring the SI of the femtocell. This operation requires the user to suspend reception and transmission with the source macrocell for a certain time duration, thus degrading the user’s performance. Based on a new measurement report, the source macro BS makes a handover decision and sends a handover request to the target femtocell. Upon reception of the acknowledgment (Ack) for the handover request from the femtocell, the macro BS transmits a handover command to the user, which triggers his service interruption immediately. The user accesses the target femtocell via a random access channel and gets allocated new radio resources from it. This implies the user experiences a performance loss due to a handover, which is further aggravated by the additional SI acquisition step.

3.3. Users’ Measurement Reports

As shown in the handover procedure, existing cellular systems allow a user to acquire the target cell’s SI and report the required information within the SI to his serving cell to retrieve the target cell’s detailed information to make a better handover decision. Within this framework, a macro BS is assumed to be able to obtain knowledge of the transmit power and DL and UL cell load statuses of femtocells close to its users all from the users’ measurement reports. However, since users’ measurements consume battery and possibly deteriorate performance (when a single transceiver per user is assumed), a tradeoff exists between the freshness (and, thus, the accuracy) of the measurement and the users’ performance.

4. The HO-FIM Architecture

The architecture of HO-FIM and its basic concept and design rationale are presented first. Then, the problems for the design of a control algorithm for the HO-FIM architecture are formulated.

4.1. Overview of HO-FIM

The objective of HO-FIM is to offload both DLs and ULs to mitigate the interference between macro- and femtocells while preserving the users’ quality of service (a load is defined in the next subsection). To meet this objective, HO-FIM hands over users dynamically between macro- and femtocells. Basically, HO-FIM is required to make the following important decisions:

• when to trigger handovers;
• which macrocell users to be handed over; and
• which femtocell to hand a selected user over to.

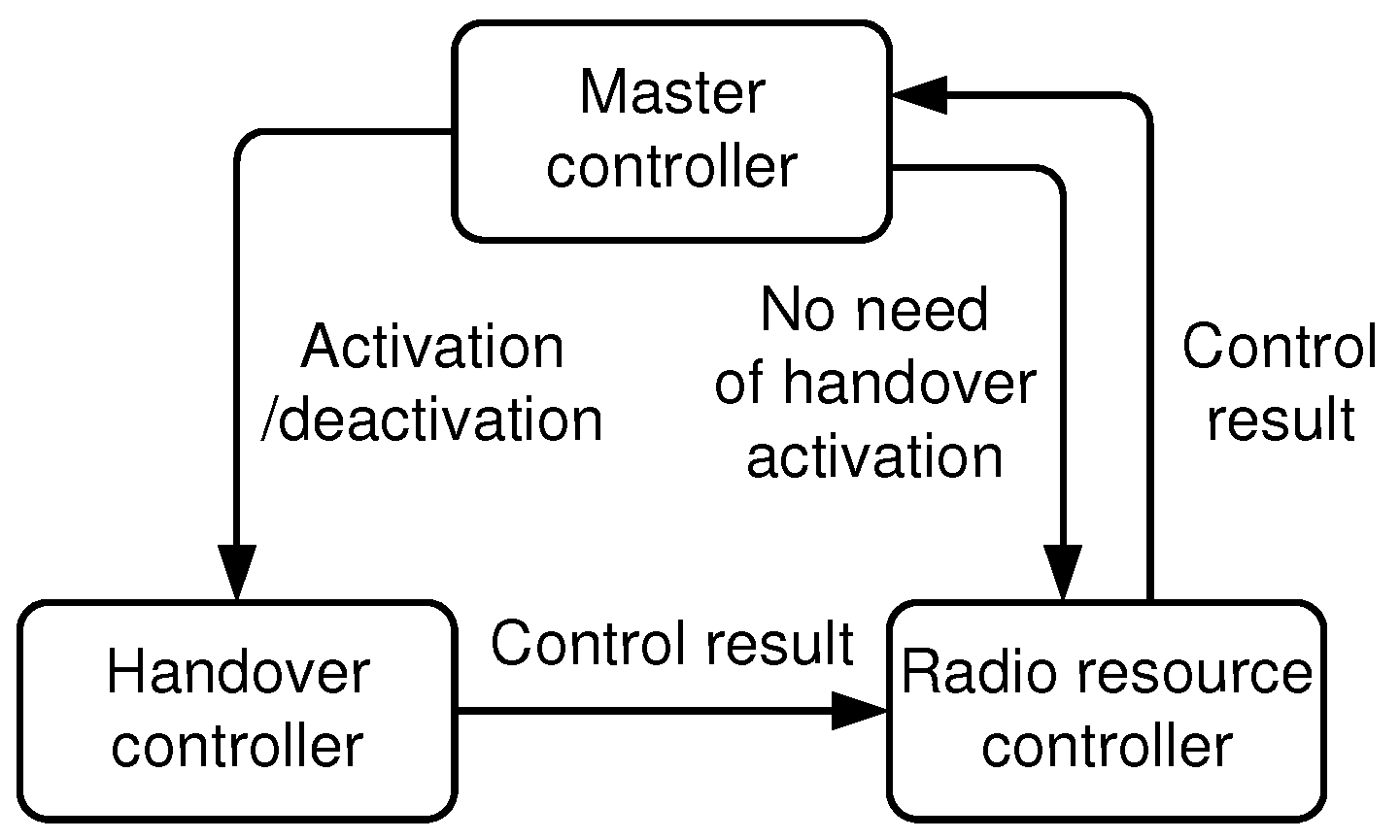
Besides, HO-FIM needs to minimize the number of triggered handovers and suppress ping-pong handovers while reaching a desired system condition. HO-FIM is composed of three interacting decision-making controllers, as illustrated in Figure 3. In what follows, each of these controllers and their complementary interactions are described.

4.1.1. Master Controller

The master controller decides to activate the handover controller only when needed to minimize handovers; a decision is made based on the current status of radio resource usage reported by the radio resource controller, i.e., when a macrocell’s load exceeds a certain threshold (activation threshold). The master controller stops the handover controller running if the network load status gets: (1) close enough to an optimum; or (2) lower than a certain point (deactivation threshold). The latter will go through fewer handovers.

4.1.2. Handover Controller

The handover controller, once activated, finds a handover sequence to reach a target system condition with minimal handovers. The past handover history also needs to be taken into account for a user not to suffer from repeated (or ping-pong) handovers; once a user is handed over, he will not be considered again as a candidate for handover for a certain duration. The algorithm designed for the handover controller’s decision determines handovers iteratively in a greedy manner.

4.1.3. Radio Resource Controller

This controller schedules the frequency and handles time and power resources to meet the users’ target SINRs. It is assumed that the allocation of frequency (resource block, RB) and time resources is done by conventional schedulers. It is also assumed that the target SINR of a user is given on a per-RB basis. Transmit power is controlled to meet the per-RB target SINR.

4.2. Definition of Cell and System Loads

The load to measure the degree of crowdedness of a cell or the entire system is defined. It is assumed that the power resource allocated to a user at a RB is zero unless the RB is assigned to him. Then, the load can be modeled as a function of allocated power as follows:

• Load ${\rho }_i$ of cell i measures the resource usage status of cell i. It depends on the power allocations of the users being served by cell i.
• System load $\rho$ measures the resource usage status of all users in the entire system. It depends on the power allocations of all users.

The macrocell load is denoted by ${\rho }_m$ and the activation and deactivation thresholds of the handover controller are denoted by ${\rho }_m^{(+)}$ and ${\rho }_m^{(-)}$, respectively.

Two properties of the load function are assumed: (1) the cell and system loads are monotonically increasing in the transmit power vector; and (2) the cell load function is additive, i.e., ${\rho }_i\left({\sum }_j{\mathbf{p}}_j\right)={\sum }_j{\rho }_i\left({\mathbf{p}}_j\right)$ when ${\mathbf{p}}_j$ is the transmit power vector assigned to user j. The monotonicity is straightforward. The additivity is acceptable if the cell load is defined as a sum or an average of the per-RB load since RB assignments are orthogonal between users within a cell (${\rho }_i\left(\mathbf{p}\right)={\rho }_i\left({\sum }_j{\mathbf{p}}_j\right)$).

4.3. Problem Formulation

To simplify the exposition, a single RB is assumed while formulating problems and describing algorithms. Extension to multiple RBs is straightforward.

Let $n_j$ be the serving cell of user j and $p_j$ and $q_j$ be the DL transmitting power to, and the UL transmitting power from, user j, respectively. ${\gamma }_j$ is the minimum target SINR. For the user set $\mathcal{U}$, the following vectors are defined:

• Serving cell vector $\mathbf{n}=[n_1,n_2,\dots ,n_N];$
• DL transmit power vector $\mathbf{p}=[p_1,p_2,\dots ,p_N];$
• UL transmit power vector $\mathbf{q}=[q_1,q_2,\dots ,q_N];$ and
• Minimum target SINR vector $\mathsf{\Gamma }=[{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_N].$

Then, HO-FIM aims to find $\mathbf{n}$ (by the handover controller), $\mathbf{p}$, and $\mathbf{q}$ (by the radio resource controller) that minimize the DL and UL loads of the entire network. The handover-based load minimization problem denoted by $P1$ is stated as (the curled inequality symbol ⪰ (and its strict form ≻) represents component-wise inequality):

Definition 1

(Handover-based load minimization problem).

$$\begin{array}{l}P1:\underset{\mathbf{n}}{\min }(\rho \left(\mathbf{p}\right)+\rho \left(\mathbf{q}\right))\\ \mathit{subject} \mathit{to}\mathbf{p},\mathbf{q}⪰0\end{array}$$

(1)

When solving $P1$, $\mathbf{p}$ and $\mathbf{q}$ are given by the radio resource controller. It is said that $p_j$ is feasible when a SINR higher than ${\gamma }_j$ is achieved, i.e., $h_{n_j,j}{p}_j/I_{DL,j}\ge {\gamma }_j$ where $h_{n_j,j}$ is a DL channel gain and $I_{DL,j}$ is the DL interference experienced by user j; $\mathbf{p}$ is feasible when $p_j$ is feasible for all $j\in \mathcal{U}$. The feasibility of $q_j$ and $\mathbf{q}$ is defined likewise. The feasibility conditions of $\mathbf{p}$ and $\mathbf{q}$ can be written using matrix notation as $\mathbf{p}⪰{\mathbf{G}}_{DL}\mathbf{p}+\eta$ and $\mathbf{q}⪰{\mathbf{G}}_{UL}\mathbf{q}+\eta$, respectively, when the elements of the normalized channel gain matrices ${\mathbf{G}}_{DL}$ and ${\mathbf{G}}_{UL}$ are defined as $G_{DL}(j,j^{\prime })={\gamma }_j{h}_{n_{j^{\prime }},j}/h_{n_j,j}(j\ne j^{\prime })$ or $0(j=j^{\prime })$ and $G_{UL}(j,j^{\prime })={\gamma }_j{h}_{j^{\prime },n_j}/h_{j,n_j}(j\ne j^{\prime })$ or $0(j=j^{\prime })$. $\eta$ is the thermal noise.

The handover overhead is considered in a separate problem. Let ${\mathbf{n}}_0$ and ${\mathbf{n}}_{\infty }$ denote the initial and limit points of the serving cell assignment, respectively. Let $\mathbf{x}$ be a handover sequence to reach ${\mathbf{n}}_{\infty }$ from ${\mathbf{n}}_0$ and ${\Delta }_m^{\left(\mathbf{x}\right)}\left(t\right)$ be the load update step of a macrocell at the tth iteration when $\mathbf{x}$ is applied. Then, to minimize the number of handovers: (1) ${\sum }_{t=1}^T{N}_{ho}\left(t\right)$ should be minimized when $N_{ho}\left(t\right)$ is the number of triggered handovers at the tth iteration and T is the number of iterations required to reach ${\rho }_m^{(-)}$; and (2) the gap between ${\rho }_m\left(T\right)$ and ${\rho }_m^{(-)}$ should be minimized as well. Thus, the handover minimization problem can be defined as follows:

Definition 2

(Handover minimization problem).

$$\begin{array}{l}P2.1:\underset{\mathbf{x}}{\min }T\\ P2.2:\underset{\mathbf{x}}{\min }({\rho }_m^{(-)}-{\rho }_m\left(T\right))\\ \mathit{subject} \mathit{to}{\rho }_m^{(-)}\ge {\rho }_m\left(T\right)\end{array}$$

(2)

Where

$${\rho }_m\left(k\right)={\rho }_m\left(0\right)-{\sum }_{t=1}^k{\Delta }_m^{\left(\mathbf{x}\right)}\left(t\right).$$

(3)

5. Control Algorithm

A handover control algorithm to solve $P1$ and $P2$ is now presented. The proposed algorithm operates in a greedy manner, i.e., it makes a decision at each iteration without considering achievable gains at subsequent iterations. This greedy strategy enables the design of a simple algorithm and the analysis of its convergence behavior. The pseudo code of the algorithm is given in Algorithm 1.

Algorithm 1 Handover control algorithm.

1: t : Slot index 2: $T_{HO}$ : Interval of handover-controller activation (in terms of slots) 3: ${\mathcal{U}}_{HO}$ : User set to be handed over in the current iteration 4: $N_{HO}$ : Maximum allowed number of handovers per iteration 5: for slot t do 6:  Update radio resource allocation for all user $j\in \mathcal{U}$ 7:  if $t\mathrm{mod}{T}_{HO}==0$ then 8:   ${\mathcal{U}}^{\prime }\leftarrow \mathcal{U}$ 9:   ${\mathcal{U}}_{HO}\leftarrow \left\{\right\}$ 10:   for $|{\mathcal{U}}_{HO}|<N_{HO}$ do 11:    Obtain $j^{*}\in {\mathcal{U}}^{\prime }$ according to Equation (12) 12:    if ${\Delta }_{m,DL}^{\left(n_{j^{*}}\right)}\left(\mathbf{p}\right)+{\Delta }_{m,UL}^{\left(n_{j^{*}}\right)}\left(\mathbf{q}\right)>0$ then 13:     ${\mathcal{U}}_{HO}\leftarrow {\mathcal{U}}_{HO}+\left\{j^{*}\right\}$ 14:    end if 15:   16:    ${\mathcal{U}}^{\prime }\leftarrow {\mathcal{U}}^{\prime }-\left\{j^{*}\right\}$ 17:   end for 18:   Perform handover for all user $j\in {\mathcal{U}}_{HO}$ 19:  end if 20:  $t\leftarrow t+1$ 21: end for

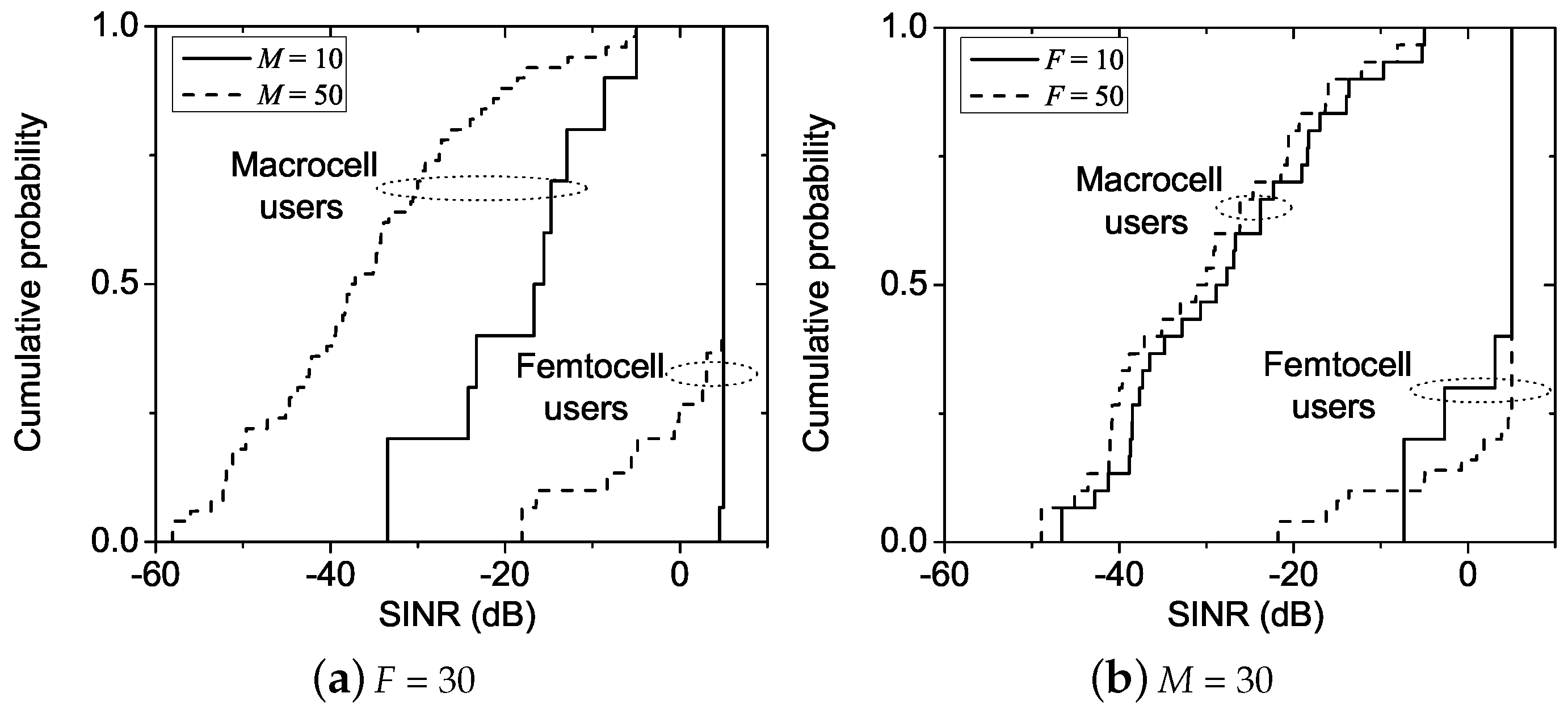
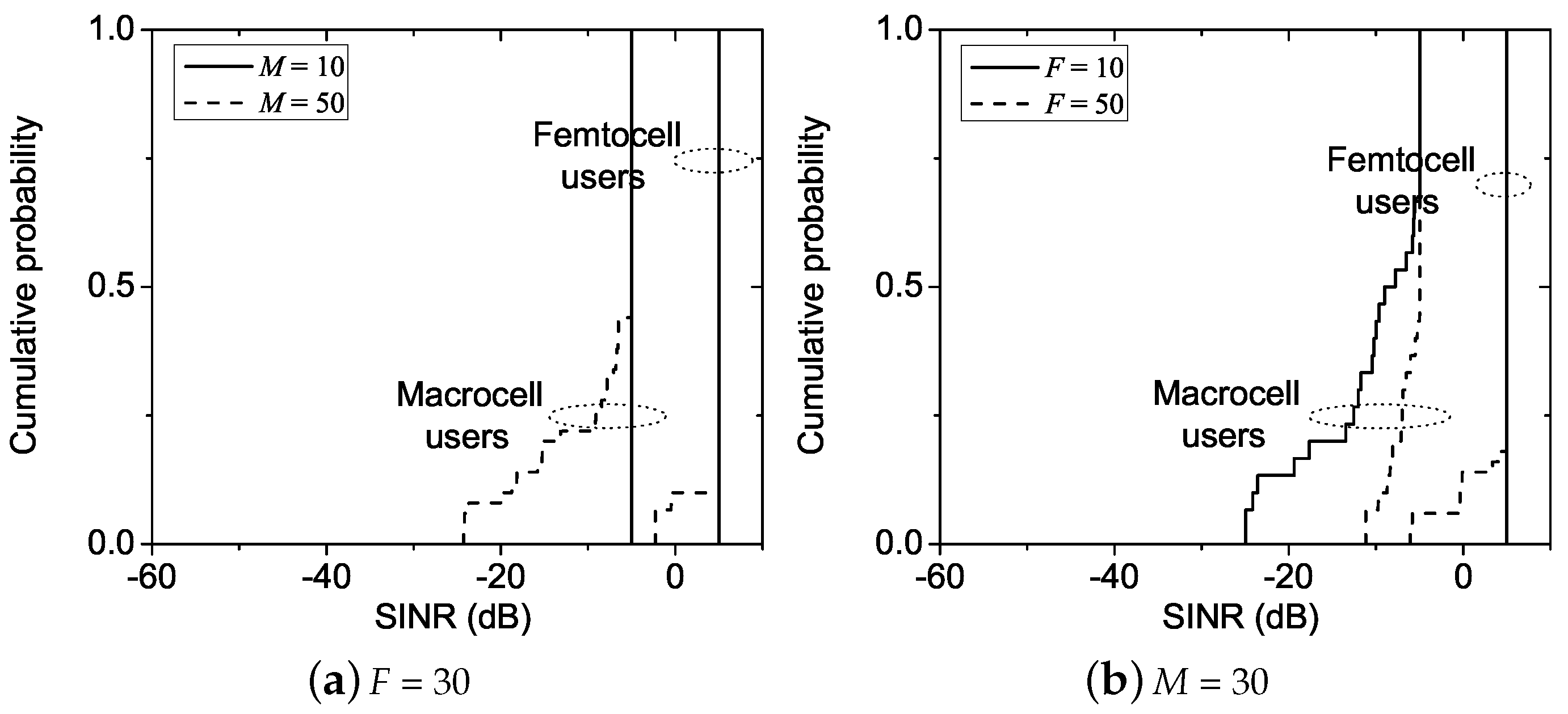
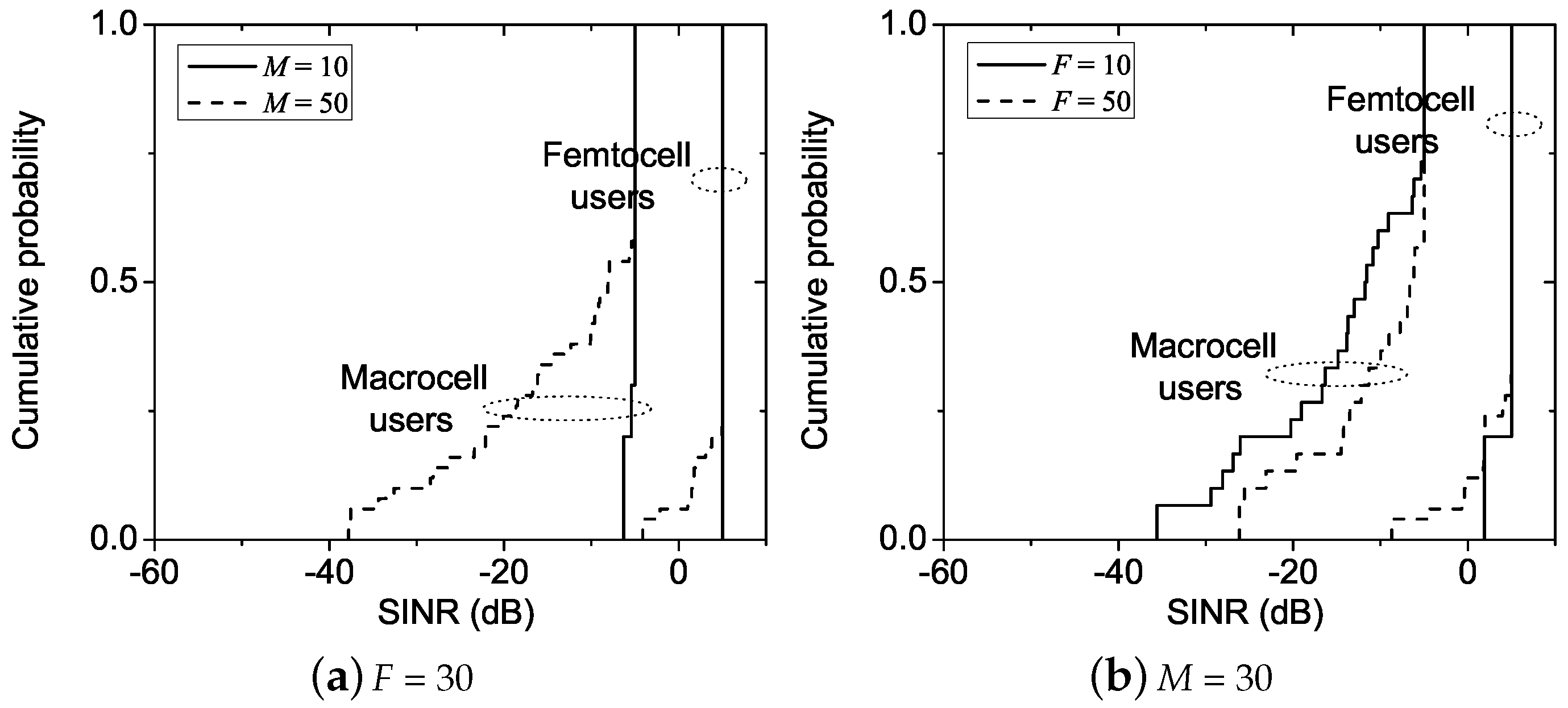
For a greedy algorithm to reduce the number of handovers, it is beneficial to trigger more gainful handovers at each iteration than those of other sequences as well as those at subsequent iterations. That is, it chooses $\mathbf{x}$ such that: (1) ${\Delta }_m^{\left(\mathbf{x}\right)}\left(t\right)\ge {\Delta }_m^{\left({\mathbf{x}}^{\prime }\right)}\left(t\right)$ for any feasible sequence ${\mathbf{x}}^{\prime }$; and (2) ${\Delta }_m^{\left(\mathbf{x}\right)}\left(t\right)\ge {\Delta }_m^{\left(\mathbf{x}\right)}(t+1)$. The rationale behind this strategy is as follows: First, consider two sequences ${\mathbf{x}}_1$ and ${\mathbf{x}}_2$ such that ${\Delta }_m^{\left({\mathbf{x}}_1\right)}\left(t\right)\ge {\Delta }_m^{\left({\mathbf{x}}_2\right)}\left(t\right)$. Then, it is probable that, for arbitrary ${\rho }_m^{(-)}$, ${\mathbf{x}}_2$ does not reach ${\rho }_m^{(-)}$ at the tth iteration while ${\mathbf{x}}_1$ does. Second, suppose that ${\Delta }_m^{\left({\mathbf{x}}_1\right)}\left(t\right)\ge {\Delta }_m^{\left({\mathbf{x}}_1\right)}(t+1)$ and ${\Delta }_m^{\left({\mathbf{x}}_2\right)}\left(t\right)={\Delta }_m^{\left({\mathbf{x}}_1\right)}(t+1)\le {\Delta }_m^{\left({\mathbf{x}}_2\right)}(t+1)={\Delta }_m^{\left({\mathbf{x}}_1\right)}\left(t\right)$. Similarly, for arbitrary ${\rho }_m^{(-)}$, ${\mathbf{x}}_1$ is likely to reach ${\rho }_m^{(-)}$ earlier than ${\mathbf{x}}_2$. Note that these conditions are meaningful because a greedy algorithm is assumed (there could be a sequence requiring less handovers while not meeting these conditions). An algorithm called per-user control is designed so as to meet the above conditions.

The handover of multiple users or only one user may be allowed at each iteration. The former will speed up convergence at the expense of more handovers than the latter due to the coarser control granularity. It is shown that both converge to a unique optimal assignment ${\mathbf{n}}^{*}$.

At each iteration, a macrocell first calculates the expected transmit power of its users when each of them is handed over to a candidate target femtocell while keeping the others in the macrocell. When user $j\in {\mathcal{U}}_m$ is handed over to femtocell $n\in \mathcal{F}$, his minimum transmit power needed to meet the target SINR ${\gamma }_j$ within cell n, denoted by $P_j^{\left(n\right)}$ and $Q_j^{\left(n\right)}$ for DL and UL, respectively, is obtained as

$$\begin{array}{c}{P}_j^{\left(n\right)}\left(\mathbf{p}\right)={\gamma }_j(I_{DL}^{\left(n\right)}\left(\mathbf{p}\right)+\eta )/h_{n,j},\\ Q_j^{\left(n\right)}\left(\mathbf{p}\right)={\gamma }_j(I_{UL}^{\left(n\right)}\left(\mathbf{q}\right)+\eta )/h_{j,n}\end{array}$$

(4)

where $I_{DL}^{\left(n\right)}\left(\mathbf{p}\right)$ and $I_{UL}^{\left(n\right)}\left(\mathbf{q}\right)$ are the average levels of DL and UL interference experienced by user j at a RB after user j is handed over to cell n. It is expected in general that the path loss of a user to a femtocell is smaller than that to a macrocell, so there may exist femtocell n enabling user j to have lower $P_j^{\left(n\right)}$ and $Q_j^{\left(n\right)}$ than those with the macrocell, thus leading to reduced interference. This is one reason why the handover approach achieves enhanced performance. After this handover, for downlink (uplink), the macrocell (other macrocell users) becomes a new interference source while femtocell n (its users) no longer causes interference due to the orthogonal RB allocation within the cell. Let the expected DL interference from the source cell (macrocell m) after the handover be denoted by $\Delta I_{DL,src}^{\left(m\right)}$ and that from the target femtocell n before the handover be denoted by $\Delta I_{DL,trgt}^{\left(n\right)}$. That is, by the handover, the new interference term $\Delta I_{DL,src}^{\left(m\right)}$ is added to and the existing term $\Delta I_{DL,trgt}^{\left(n\right)}$ is removed from the total DL interference experienced by user j, which can be interpreted as load adjustment (load-balancing) between the cells. If femtocell n is selected such that $\Delta I_{DL,src}^{\left(m\right)}<\Delta I_{DL,trgt}^{\left(n\right)}$, i.e., appropriate load-balancing is applied, the resulting DL interference experienced by user j is reduced, which is another reason why the handover approach obtains performance gain. Assume that the long-term probabilities for a user to be allocated each RB are evenly distributed. Then, $I_{DL}^{\left(n\right)}\left(\mathbf{p}\right)$ is rewritten as

$$\begin{array}{cc}{I}_{DL}^{\left(n\right)}\left(\mathbf{p}\right)& =I_{DL}^{\left(m\right)}\left(\mathbf{p}\right)+\Delta I_{DL,src}^{\left(m\right)}-\Delta I_{DL,trgt}^{\left(n\right)}\hfill \\ & =I_{DL}^{\left(m\right)}\left(\mathbf{p}\right)+h_{m,j}E\left[p_{j^{\prime }}\right|j^{\prime }\in {\mathcal{U}}_m-\left\{j\right\}]-h_{n,j}E\left[p_{j^{\prime }}\right|j^{\prime }\in {\mathcal{U}}_n]\hfill \end{array}$$

(5)

where m indicates the source macrocell. If cell n broadcasts $E\left[p_{j^{\prime }}\right|j^{\prime }\in {\mathcal{U}}_n]$ (the average per-RB DL transmit power) in SI, the macrocell can obtain the information by commanding users to report it. Similarly, it is also assumed that $I_{UL}^{\left(n\right)}\left(\mathbf{p}\right)$ is broadcast by cell n and reported by users to the macrocell. Thus, the macrocell has all the information required to calculate $P_j^{\left(n\right)}$ and $Q_j^{\left(n\right)}$. Using this calculation result, the transmit-power vectors are defined as ${\mathbf{P}}^{\left(n_j\right)}\left(\mathbf{p}\right)\triangleq [p_1,\dots ,P_j^{\left(n_j\right)}\left(\mathbf{p}\right),\dots ,p_N]$ and ${\mathbf{Q}}^{\left(n_j\right)}\left(\mathbf{q}\right)\triangleq [q_1,\dots ,Q_j^{\left(n_j\right)}\left(\mathbf{q}\right),\dots ,q_N]$.

Next, the macrocell determines the target femtocell of user j such that a maximum decrease of its cell load is obtained at this iteration. This is expressed as

$$\begin{array}{c}{\displaystyle n_j^{*}=arg\underset{n_j}{max}\{{\Delta }_{m,DL}^{\left(n_j\right)}\left(\mathbf{p}\right)+{\Delta }_{m,UL}^{\left(n_j\right)}\left(\mathbf{q}\right)\}}\hfill \end{array}$$

(6)

where

$$\begin{array}{c}{\Delta }_{m,DL}^{\left(n_j\right)}\left(\mathbf{p}\right)\triangleq {\rho }_m\left(\mathbf{p}\right)-{\rho }_m\left({\mathbf{P}}^{\left(n_j\right)}\left(\mathbf{p}\right)\right),\\ {\Delta }_{m,UL}^{\left(n_j\right)}\left(\mathbf{q}\right)\triangleq {\rho }_m\left(\mathbf{q}\right)-{\rho }_m\left({\mathbf{Q}}^{\left(n_j\right)}\left(\mathbf{q}\right)\right).\end{array}$$

The above problem should be solved for each user. Thus, the search space size of the per-user handover control problem is $M\times F$. Finally, the serving cells and transmit powers at $t+1$ are determined as

$$\begin{array}{cc}\mathbf{n}(t+1)=& {\mathbf{n}}^{*}\triangleq [n_1^{*},\dots ,n_M^{*},n_{M+1},\dots ,n_N]\hfill \\ \mathbf{p}(t+1)=& {\mathbf{P}}^{\left({\mathbf{n}}^{*}\right)}\left(\mathbf{p}\right)\triangleq [P_1^{\left(n_1^{*}\right)}\left(\mathbf{p}\right),\dots ,P_M^{\left(n_M^{*}\right)}\left(\mathbf{p}\right),\hfill \\ & P_{M+1}^{\left(n_{M+1}\right)}\left(\mathbf{p}\right),\dots ,P_N^{\left(n_N\right)}\left(\mathbf{p}\right)]\hfill \\ \mathbf{q}(t+1)=& {\mathbf{Q}}^{\left({\mathbf{n}}^{*}\right)}\left(\mathbf{q}\right)\triangleq [Q_1^{\left(n_1^{*}\right)}\left(\mathbf{q}\right),\dots ,Q_M^{\left(n_M^{*}\right)}\left(\mathbf{q}\right),\hfill \\ & Q_{M+1}^{\left(n_{M+1}\right)}\left(\mathbf{q}\right),\dots ,Q_N^{\left(n_N\right)}\left(\mathbf{q}\right)].\hfill \end{array}$$

(7)

If the determined serving cell of a user differs from the current one, his transfer will be triggered. Here, only inbound (from macrocell to femtocell) handovers are considered, and, thus, femtocell users stay within their serving femtocells while their power allocations are updated. When outbound (from femtocell to macro- or other femtocell) handovers are allowed as well, femtocells make handover decisions on their users in the same way as the macrocell does. It is now shown that the above algorithm converges to an optimum.

Proposition 1.

A unique system load ${\rho }^{*}$ exists such that ${\rho }^{*}\le {\rho }^{\left(\mathbf{n}\right)}$ for $\forall \mathbf{n}$.

Proof. 

Due to the monotonicity of $\rho$ in $\mathbf{p}$, a sufficient condition is the existence of a unique power vector $({\mathbf{p}}^{*},{\mathbf{q}}^{*})$ such that $({\mathbf{p}}^{*},{\mathbf{q}}^{*})⪯({\mathbf{p}}^{\left(\mathbf{n}\right)},{\mathbf{q}}^{\left(\mathbf{n}\right)})$ $\forall \mathbf{n}$, i.e., ${\rho }^{*}=\rho ({\mathbf{p}}^{*},{\mathbf{q}}^{*})$. When DL was considered only, the existence and uniqueness of ${\mathbf{p}}^{*}$ were proved in Theorem 1 of [16] under the same feasibility condition as defined earlier on $\mathbf{p}$. A new power vector $\mathbf{y}\triangleq (\mathbf{p},\mathbf{q})$ can be defined and then the actual problem is transformed into one with an analogous structure to the DL-only problem. Thus, the above proposition follows. □

Proposition 2.

Starting from any feasible power vectors $\mathbf{p}$ and $\mathbf{q}$, the per-user control algorithm makes the system load ρ converge to ${\rho }^{*}$.

Proof. 

The proof follows a procedure similar to the one used in [16]. Consider a condition where, if $\mathbf{p}\left(t\right)$ and $\mathbf{q}\left(t\right)$ are feasible power vectors, $\left(\mathbf{p}\right(t+1),\mathbf{q}(t+1\left)\right)⪯\left(\mathbf{p}\right(t),\mathbf{q}(t\left)\right)$, and $\mathbf{p}(t+1)$ and $\mathbf{q}(t+1)$ are feasible. If this condition is met, $\left(\mathbf{p}\right(0),\mathbf{q}(0\left)\right)⪰\cdots ⪰\left(\mathbf{p}\right(t),\mathbf{q}(t\left)\right)$, and $\mathbf{p}\left(t\right)$ and $\mathbf{q}\left(t\right)$ are feasible. Hence, the sequence of $\left(\mathbf{p}\right(t),\mathbf{q}(t\left)\right)$ is decreasing and always feasible. Since $\rho$ is monotonic and bounded below by ${\rho }^{*}$, the sequence of $\rho \left(\mathbf{p}\right(t),\mathbf{q}(t\left)\right)$ converges to ${\rho }^{*}$.

In what follows, it is shown that the proposed algorithm meets the above condition. Equation (6) can be rewritten as

$$\begin{array}{l}\underset{n_j}{\max }\{{\Delta }_{i,DL}^{\left(n_j\right)}\left(\mathbf{p}\right)+{\Delta }_{i,UL}^{\left(n_j\right)}\left(\mathbf{q}\right)\}\\ ={\rho }_i(\mathbf{p},\mathbf{q})-\underset{n_j}{\min }{\rho }_i({\mathbf{P}}^{\left(n_j\right)}\left(\mathbf{p}\right),{\mathbf{Q}}^{\left(n_j\right)}\left(\mathbf{q}\right))\\ ={\displaystyle \sum _{j^{\prime }\in {\mathcal{U}}_i}}{\rho }_i(p_{j^{\prime }},q_{j^{\prime }})\\ -\underset{n_j}{\min }\left\{{\displaystyle \sum _{j^{\prime }\in {\mathcal{U}}_i-\left\{j\right\}}}{\rho }_i(p_{j^{\prime }},q_{j^{\prime }})+{\rho }_i(P_j^{\left(n_j\right)}\left(\mathbf{p}\right),Q_j^{\left(n_j\right)}\left(\mathbf{q}\right))\right\}\\ ={\rho }_i(p_j,q_j)-\underset{n_j}{\min }{\rho }_i(P_j^{\left(n_j\right)}\left(\mathbf{p}\right),Q_j^{\left(n_j\right)}\left(\mathbf{q}\right))\end{array}$$

(8)

where the second equality follows from the additivity of the cell load function. That is, the algorithm minimizes

$${\rho }_i(P_j^{\left(n_j\right)}\left(\mathbf{p}\right),Q_j^{\left(n_j\right)}\left(\mathbf{q}\right))\forall j,\mathrm{so}{\rho }_i(P_j^{\left(n_j^{*}\right)}\left(\mathbf{p}\right),Q_j^{\left(n_j^{*}\right)}\left(\mathbf{q}\right))\le {\rho }_i(P_j^{\left(n_j\right)}\left(\mathbf{p}\right),Q_j^{\left(n_j\right)}\left(\mathbf{q}\right)).$$

Therefore,

$$\begin{array}{cc}\hfill {\displaystyle {\rho }_i(\mathbf{p}(t+1),\mathbf{q}(t+1))}& ={\rho }_i({\mathbf{P}}^{\left({\mathbf{n}}^{*}\right)}\left(\mathbf{p}\left(t\right)\right),{\mathbf{Q}}^{\left({\mathbf{n}}^{*}\right)}\left(\mathbf{q}\left(t\right)\right))\hfill \\ & =\sum _j{\rho }_i(P_j^{\left(n_j^{*}\right)}\left(\mathbf{p}\left(t\right)\right),Q_j^{\left(n_j^{*}\right)}\left(\mathbf{q}\left(t\right)\right))\hfill \\ & \le \sum _j{\rho }_i(P_j^{\left(n_j\right)}\left(\mathbf{p}\left(t\right)\right),Q_j^{\left(n_j\right)}\left(\mathbf{q}\left(t\right)\right))\hfill \\ & ={\rho }_i({\mathbf{P}}^{\left(\mathbf{n}\right)}\left(\mathbf{p}\left(t\right)\right),{\mathbf{Q}}^{\left(\mathbf{n}\right)}\left(\mathbf{q}\left(t\right)\right))\hfill \\ & \le {\rho }_i(\mathbf{p}\left(t\right),\mathbf{q}\left(t\right))\hfill \end{array}$$

(9)

where the last inequality is obtained by the defined monotonicity of the cell load function and the assumed feasibility of $\left(\mathbf{p}\right(t),\mathbf{q}(t\left)\right)$. Equation (9) shows that the cell load decreases monotonically as the algorithm runs through iterations. If $\mathbf{p}\left(t\right)$ is feasible, $p_j(t+1)={\mathbf{G}}_{j,DL}^{\left(n\right)}\mathbf{p}\left(t\right)+\eta \ge {\mathbf{G}}_{j,DL}^{\left(n\right)}\mathbf{p}(t+1)$ since $\mathbf{p}\left(t\right)⪰\mathbf{p}(t+1)$, thus $\mathbf{p}(t+1)$ is also feasible and the same holds for $\mathbf{q}(t+1)$ (${\mathbf{G}}_{j,DL}^{\left(n\right)}$ is jth row vector of ${\mathbf{G}}_{DL}^{\left(n\right)}$). Thus, the above condition is met. □

Proposition 3.

The load gap monotonically decreases as the algorithm runs through iterations.

Proof. 

First, a power gap is defined as

$$\begin{array}{cc}{\delta }_{DL}\left(\mathbf{p}\left(t\right)\right)& \triangleq \mathbf{p}\left(t\right)-\mathbf{p}(t+1)\hfill \\ & =\mathbf{p}\left(t\right)-{\mathbf{P}}^{\left({\mathbf{n}}^{*}\right)}\left(\mathbf{p}\left(t\right)\right)\hfill \\ & =\mathbf{p}\left(t\right)-({\mathbf{G}}_{DL}^{\left({\mathbf{n}}^{*}\right)}\mathbf{p}\left(t\right)+{\eta }^{\left({\mathbf{n}}^{*}\right)})\hfill \\ & =(I-{\mathbf{G}}_{DL}^{\left({\mathbf{n}}^{*}\right)})\mathbf{p}\left(t\right)-{\eta }^{\left({\mathbf{n}}^{*}\right)}\hfill \\ & \triangleq {\widehat{\mathbf{G}}}_{DL}^{\left({\mathbf{n}}^{*}\right)}\mathbf{p}\left(t\right)-{\eta }^{\left({\mathbf{n}}^{*}\right)}.\hfill \end{array}$$

(10)

It has been shown for fixed ${\mathbf{G}}_{DL}^{\left({\mathbf{n}}^{*}\right)}$ that, if the largest eigenvalue of ${\mathbf{G}}_{DL}^{\left({\mathbf{n}}^{*}\right)}$ is less than unity, the power update procedure converges at a geometric rate [25]. Therefore, ${\delta }_{DL}$ is a monotonically increasing function in $\mathbf{p}$. Similarly, so is ${\delta }_{UL}$. Let $\mathbf{n}\left(t\right)$ be the BS assignment at t, then

$$\begin{array}{l}\delta \left(t\right)-\delta (t+1)=[{\widehat{\mathbf{G}}}_{DL}^{\left(\mathbf{n}\right(t\left)\right)}\mathbf{p}(t-1)-{\widehat{\mathbf{G}}}_{DL}^{\left(\mathbf{n}\right(t+1\left)\right)}\mathbf{p}\left(t\right)]\\ +{\widehat{\mathbf{G}}}_{UL}^{\left(\mathbf{n}\right(t\left)\right)}\mathbf{q}(t-1)-{\widehat{\mathbf{G}}}_{UL}^{\left(\mathbf{n}\right(t+1\left)\right)}\mathbf{q}\left(t\right)\\ \ge {\widehat{\mathbf{G}}}_{DL}^{\left(\mathbf{n}\right(t\left)\right)}\mathbf{p}(t-1)-{\widehat{\mathbf{G}}}_{DL}^{\left(\mathbf{n}\right(t+1\left)\right)}\mathbf{p}(t-1)\\ +{\widehat{\mathbf{G}}}_{UL}^{\left(\mathbf{n}\right(t\left)\right)}\mathbf{q}(t-1)-{\widehat{\mathbf{G}}}_{UL}^{\left(\mathbf{n}\right(t+1\left)\right)}\mathbf{q}(t-1)\\ ={\mathbf{G}}_{DL}^{\left(\mathbf{n}\right(t+1\left)\right)}\mathbf{p}(t-1)-{\mathbf{G}}_{DL}^{\left(\mathbf{n}\right(t\left)\right)}\mathbf{p}(t-1)\\ +{\mathbf{G}}_{UL}^{\left(\mathbf{n}\right(t+1\left)\right)}\mathbf{q}(t-1)-{\mathbf{G}}_{UL}^{\left(\mathbf{n}\right(t\left)\right)}\mathbf{q}(t-1)\\ ={\mathbf{P}}^{\left(\mathbf{n}\right(t+1\left)\right)}\left(\mathbf{p}(t-1)\right)-{\mathbf{P}}^{\left(\mathbf{n}\right(t\left)\right)}\left(\mathbf{p}(t-1)\right)\\ +{\mathbf{Q}}^{\left(\mathbf{n}\right(t+1\left)\right)}\left(\mathbf{q}(t-1)\right)-{\mathbf{Q}}^{\left(\mathbf{n}\right(t\left)\right)}\left(\mathbf{q}(t-1)\right)\end{array}$$

(11)

where the first inequality follows from the monotonicity of $\delta$ and $\mathbf{p}\left(t\right)⪯\mathbf{p}(t-1)$. From Equation (6), ${\mathbf{P}}^{\left(\mathbf{n}\right(t\left)\right)}\left(\mathbf{p}(t-1)\right)+{\mathbf{Q}}^{\left(\mathbf{n}\right(t\left)\right)}\left(\mathbf{q}(t-1)\right)⪯{\mathbf{P}}^{\left({\mathbf{n}}^{\prime }\right)}\left(\mathbf{p}(t-1)\right)+{\mathbf{Q}}^{\left({\mathbf{n}}^{\prime }\right)}\left(\mathbf{q}(t-1)\right)$ for all ${\mathbf{n}}^{\prime }$, and, thus, Equation (11) is non-negative. Therefore, $\delta \left(t\right)$ monotonically decreases as t increases. □

Proposition 4.

If handed-over users are excluded from consideration for further handovers at subsequent iterations, the system load converges to a sub-optimal solution ${\rho }^{\prime }$ such that $\rho \left(0\right)\ge {\rho }^{\prime }\ge {\rho }^{*}$.

Proof. 

The power update procedure under a fixed serving cell assignment is known to converge. That is, even after user j is handed over, its transmit power at subsequent iterations satisfies $p_j\left(t\right)\ge p_j(t+1)$, but $p_j(t+1)\ge P_j^{\left(n_j^{*}\right)}\left(\mathbf{p}\left(t\right)\right)$ due to a lack of further handovers. The remaining part of the proof is the same as shown above and is hence omitted. □

Allowing handover of an unlimited number of users at each iteration may speed up convergence but trigger excessive handover overhead at once. To limit handover overhead per iteration, allowing only a configured number of users to be handed over at each iteration is considered. The modified algorithm selects a user to be handed over as

$$\begin{array}{c}{\displaystyle j^{*}=arg\underset{j\in {\mathcal{U}}^{\prime }}{max}\left(\underset{n_j}{max}\{{\Delta }_{m,DL}^{\left(n_j\right)}\left(\mathbf{p}\right)+{\Delta }_{m,UL}^{\left(n_j\right)}\left(\mathbf{q}\right)\}\right).}\hfill \end{array}$$

(12)

where ${\mathcal{U}}^{\prime }$ is the user set excluding previously-selected ones. User selection is repeated (a user producing the next largest gain is selected next) until the configured number of users to hand over per iteration is reached.

6. Performance Evaluation

6.1. Evaluation Model

The evaluation model of the simulation was based on the evaluation methodologies of 3GPP and ITU, and similar to the ones used in prior research works on femtocell [26,27,28]. The simulation assumptions are described in the following and summarized in

Table 1. Simulation parameters.

Parameter	Value
Network deployment	Femtocell: random deployment within a macrocell
	User: random placement within each’s initial serving cell
Carrier frequency	2.5 GHz
System bandwidth	5 MHz (10 resource blocks)
Number of macrocell users in a macrocell at initialization	[10, 20, 50]
Number of femtocell users in a macrocell at initialization	[10, 30, 50, 100]
Number of femtocells in a macrocell	[10, 30, 50, 100]
Transmit power range of a user	−50∼25 dBm
Fading	Frequency-selective Rayleigh fading with a maximum doppler spread of 30 Hz
Shadowing	Lognormal shadowing with a standard deviation of 8 dB
Minimum distance	30 m
between a macro BS and its user
Thermal noise density	−174 dBm/Hz
User antenna gain	0 dBi
Slot interval	1 ms
Scheduling algorithm	Wong et al.’s [29]

.

6.1.1. System and Network Model

We follow the simulation scenario of 3GPP [30] for macro- and femtocell deployment. A single-sector macrocell on which multiple femtocells are overlaid is considered. The radius of the macrocell is 500 m and macrocell users are randomly distributed in the macrocell; the angle and the distance of each to the macro BS are randomly chosen with a uniform probability distribution. Femto BSs are randomly distributed within a macrocell and each of them serves a single subscribed user who is also randomly distributed within 50 m of it.

Both macro and femto BSs operate in the frequency band of 2.5 GHz with a channel bandwidth of 5 MHz. A slot is defined as one unit of time and each slot interval is 1 ms. Transmit power changes at a slot time scale. For RB allocation, a scheme proposed by Wong et al. [29] is used; first, it sequentially allocates each user the best resource block in terms of the expected capacity. The remaining RBs are then allocated to users in descending order of the ratio of the expected capacity to the pre-determined user weight. In the simulation, all users within a cell are given an identical weight. The minimum and maximum transmit powers inherently given to user devices are assumed to be $-50$ and 25 dBm, respectively. The handover controller, if activated, makes handover decisions (at most 10 handovers at once) every 100 slots. The performance of HO-FIM (denoted by per-user control) was compared with the range control (named ARCHoN) of Yun and Shin [22]. The system load is defined as the sum of the transmitting powers of all users.

6.1.2. Channel Model

The path losses of a user to BSs are determined based on the ITU and COST231, models which are described as [31,32]:

• Macrocell user to macro BS (outdoor link):

  $${\displaystyle h={10}^{4.9}{\left(\frac{r}{1000}\right)}^4{f}^3{10}^{S/10}}$$

  (13)
• Macrocell user to femto BS, femtocell user to macro BS (outdoor-to-indoor or indoor-to-outdoor link):

  $${\displaystyle h={10}^{4.9}{\left(\frac{r}{1000}\right)}^4{f}^3{10}^{S/10}{10}^{(L_i+L_e)/10}}$$

  (14)
• Femtocell user to femto BS (indoor link):

  $$\begin{array}{c}{\displaystyle h={10}^3{r}^{3.7}{10}^{S/10}{10}^{L_i/10}}\hfill \end{array}$$

  (15)

where r is the transmitter–receiver separation distance in meters; f is the carrier frequency in MHz; S is the log-normal shadowing factor with a standard deviation of 8 dB; and $L_i$ and $L_e$ are internal and external wall losses that are set to 2 and 7 dB, respectively, in the simulation. The frequency selective multipath channel is modeled to consist of six independent Rayleigh multipaths, with an exponentially decaying profile. A maximum doppler spread of 30 Hz is assumed.

6.2. Numerical Results

Figure 4 shows the sample-time evolutions of the UL interference at the macrocell and three example femtocells: (a) without handover; (b) with per-user handover control (HO-FIM); and (c) with range control. Thirty macrocell users and thirty femtocells are distributed in the macrocell. The target SINR of macrocell users is set to $-5$ dB while that of femtocell users is 5 dB (it is assumed that indoor femtocell users tend to use data-centric services requiring a higher data-rate). As shown in Figure 4, without handover, the macrocell’s interference is $-83.9$ dBm. When the per-user handover control is applied, however, a significant reduction of the interference is obtained every 100 slots (i.e., when handovers are triggered), and the macrocell’s interference converges to $-114.4$ dBm. The range control also results in a considerably reduced interference ($-103.2$ dBm), but the achieved gain is smaller than the per-user control due to the reduced optimality, as explained above. Figure 4a reveals that the UL interference at some femtocells (depending on the presence of a nearby macrocell or femtocell user) could be serious ($-67.1$ dBm at Femtocell 3). With HO-FIM, a similar result is observed for femtocells, i.e., convergence of the interferences at femtocells to significantly reduced levels.

The achieved SINRs of different handover mechanisms are compared in Figure 5 for macrocell users (top) and femtocell users (bottom) when the target SINRs of macrocell and femtocell users are set to 0 and 10 dB, respectively. First, it is shown that the conventional handover control based on the strongest received power achieves much better SINRs of macrocell users than the case without using handovers. This result encourages exploitation of handovers to solve the femtocell interference problem, since even a non-optimal control of handovers improves performance. Such an improvement comes from: (1) reduced loss of path to serving cells; and (2) macrocell offloading. Either per-user (HO-FIM) or range control, as expected from the ability to reduce interference, further improves the achieved SINRs of macrocell users by making handover decisions towards the minimum system load. HO-FIM also improves the achieved SINRs of femtocell users. That is, HO-FIM benefits both macrocell and femtocell users, instead of sacrificing femtocell users to protect macrocell users, as many of the existing approaches do.

The effects of the number of macrocell users (M) and femtocells (F) are explored in Figure 6 (no handover), Figure 7 (per-user control), and Figure 8 (range control). The results show a common trend that the increasing number of macrocell users deteriorates the SINRs of all users due to the increase in the number of interference sources. As the number of femtocells increases, the users’ achieved SINRs get deteriorated when handovers are not used, while the SINRs are improved with HO-FIM. Figure 6 clearly shows a degradation of macrocell users’ performance when F is increased from 10 to 50. In contrast, in Figure 7, the increase in F improves the SINRs of macrocell users with HO-FIM. This results from the increased possibility for macrocell users to be served by local femtocells, thus further offloading the macrocell and enhancing spatial reuse of channel resources. When 30 macrocell users and 50 femtocell users within a macrocell are considered, more than 90% of macrocell users achieve higher SINRs with HO-FIM than the case without using handovers by 23.3 dB on average, which is 3.7 dB higher than the range control. The entire cohort of femtocell users with HO-FIM is shown to achieve 2.9 dB higher SINRs, on average.

Next, the effect of the target SINR is studied. The corresponding simulation results are plotted in Figure 9 when M = 30 and F = 30. According to the considered power control mechanism described in Equation (4), the transmitting power of a user is proportional to his target SINR. Thus, it is clear that a higher target SINR will generate a larger interference and thus degrade the performance of the users having insufficient room to increase their transmit power. However, a change in macrocell users’ target SINR and a change in femtocell users do not result in the same level of performance degradation. When the target SINR of macrocell users is changed from $-5$ dB to 0 dB, some macrocell users achieve better SINRs (due to the increased target SINR) and others achieve lower ones, but femtocell users are unaffected. This is because macrocell users are likely to experience larger path losses to their serving cells (either macro- or femtocells) than femtocell users and thus, they are less robust against interference.

Two different handover options in the per-user control are investigated in Figure 10 (M = 50, F = 100): (1) allowing macrocell-to-femtocell (inbound) handovers of macrocell users only; and (2) allowing femtocell-to-macrocell (outbound) handovers of femtocell users as well. Most femtocell users are expected to be better served by femtocells, since they may experience smaller wall losses to their own femtocells (as can be inferred from the considered channel models). However, it is also probable that some femtocell users, when handed over to a macrocell, achieve better SINRs if they happen to be closer to a macro BS or their serving femtocells experience significant interference from nearby macro- and femtocell users. Accordingly, as shown in the figure, allowing outbound handovers makes a slight improvement of users’ performance. However, this phenomenon is difficult to observe when the level of interference is low due to a small number of users.

Finally, the number of handovers is shown for different schemes in Figure 11 (M = 30, F = 50). The range control triggers a large number of handovers at the first iteration, thus incurring significant handover overhead at once. Thanks to the finer control granularity, HO-FIM triggers a smaller number of handovers at each iteration, which even decreases over iterations. HO-FIM with inbound handovers triggers an even smaller number of handovers, but at the expense of reduced performance gain (as seen in Figure 10).

7. Conclusions

In this paper, a novel handover-based interference management framework, called HO-FIM, is presented for two-tier femtocell networks. HO-FIM is composed of three complementary controllers—master, handover, and radio resource controllers—which activate/deactivate the handover controller, make handover decisions, and handle radio resource scheduling. HO-FIM activates the handover controller only when needed and finds a control sequence to minimize handovers while reaching a desired system condition. The handover controller iteratively controls users’ handovers in a greedy manner. HO-FIM successfully overcomes the performance limit of existing radio resource coordination approaches and benefits both macro- and femtocell users thanks to the introduction of an additional degree-of-freedom when solving the interference problem.