A Novel Combined Evolutionary Algorithm for Optimal Planning of Distributed Generators in Radial Distribution Systems
Abstract
1. Introduction
2. Details and Performance Analysis of QODELFA
2.1. Main Procedures of QODELFA
2.1.1. Procedures of DE
2.1.2. LF Perturbation:
2.1.3. Concept of QOBL
2.2. The QODELFA
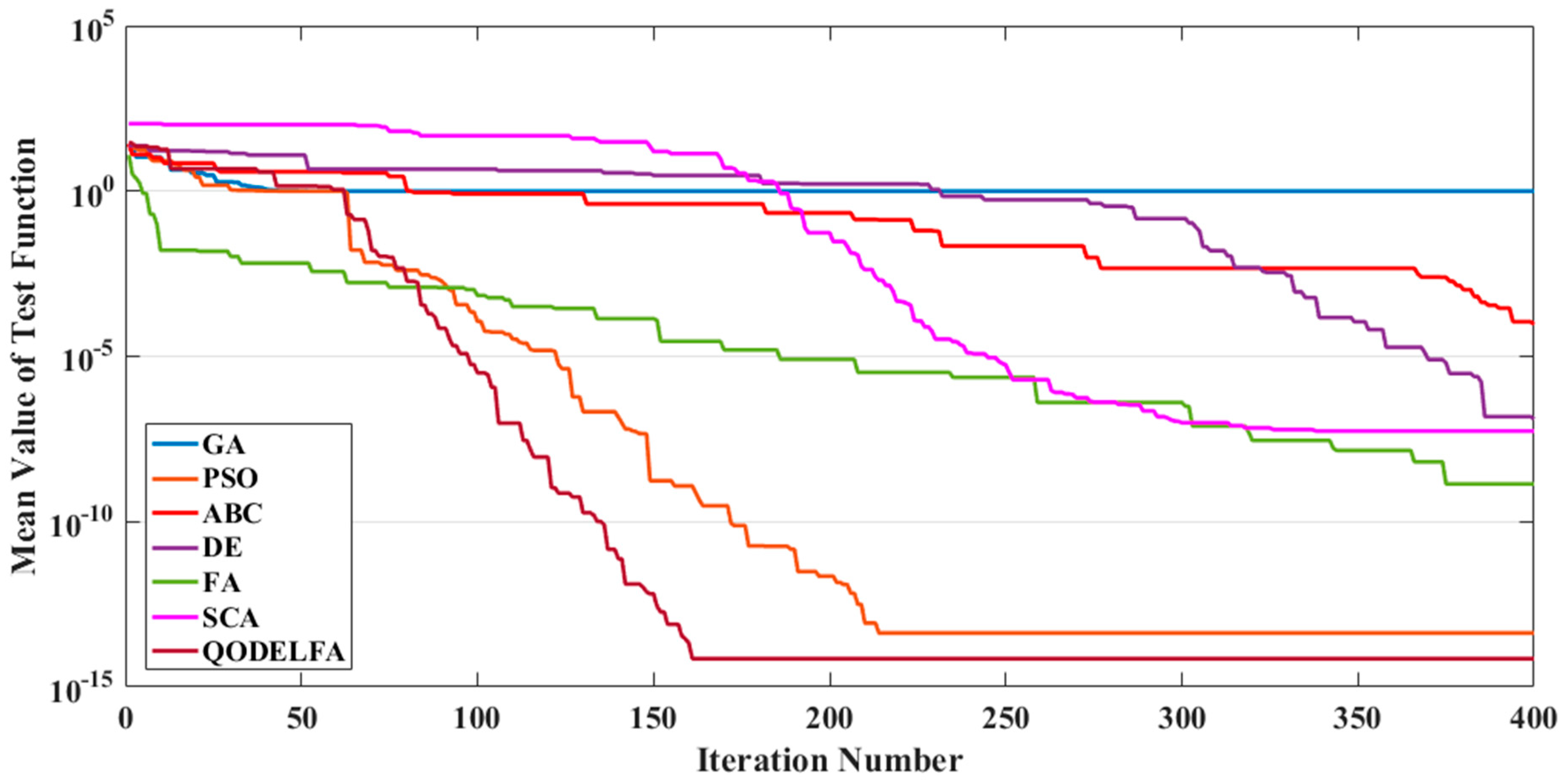
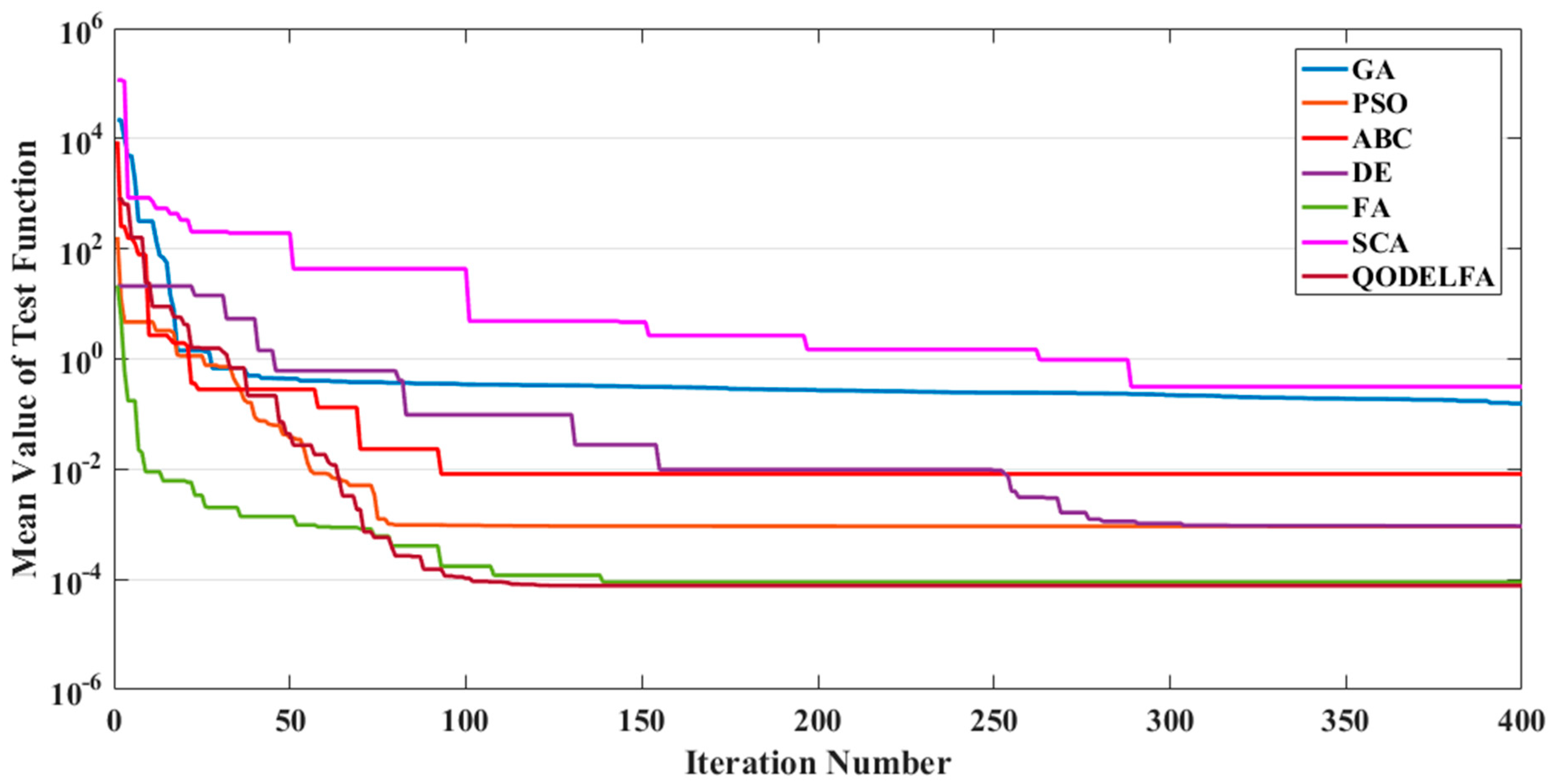
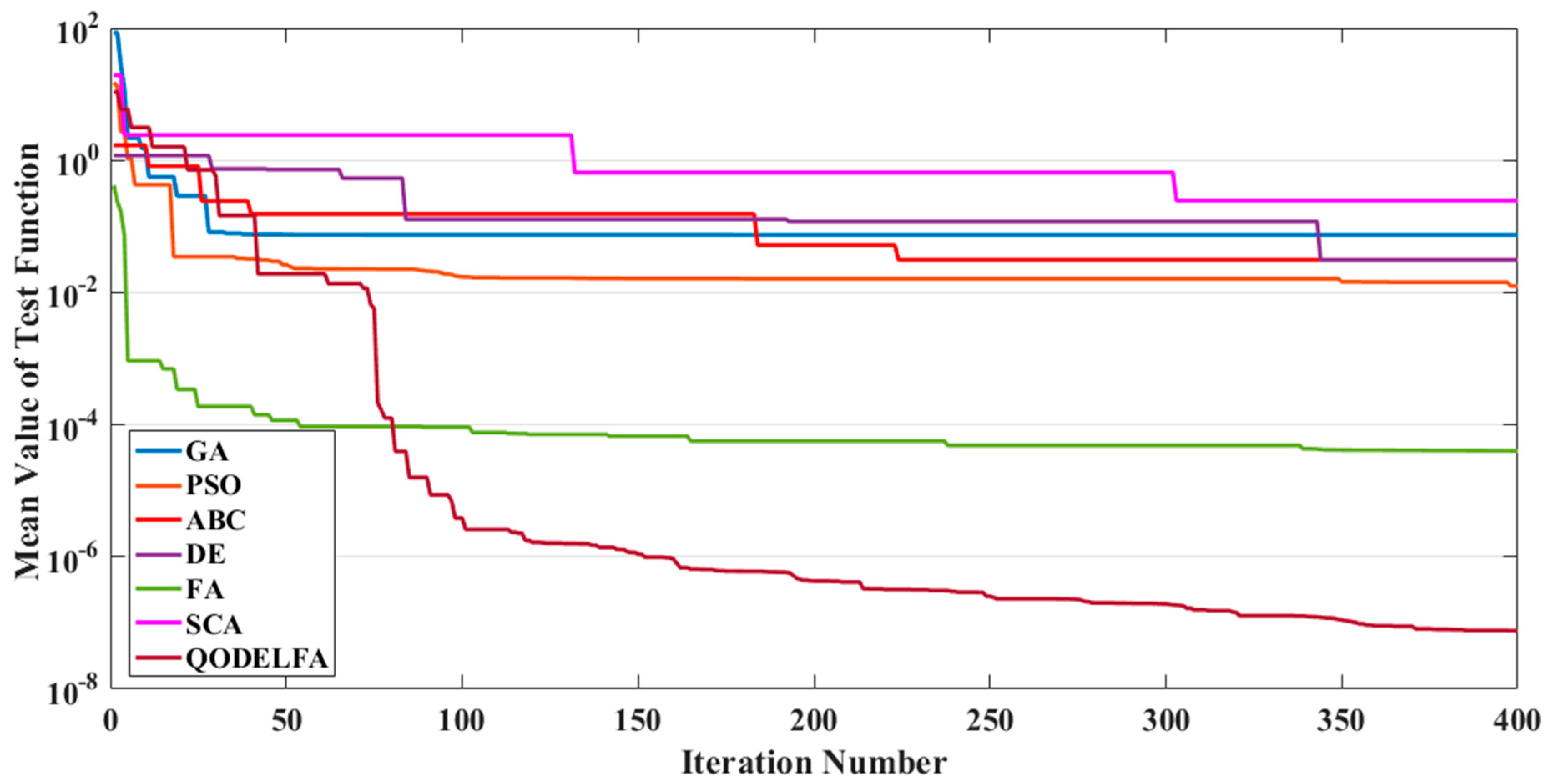
2.3. Performance Comparison by Solving Benchmark Functions
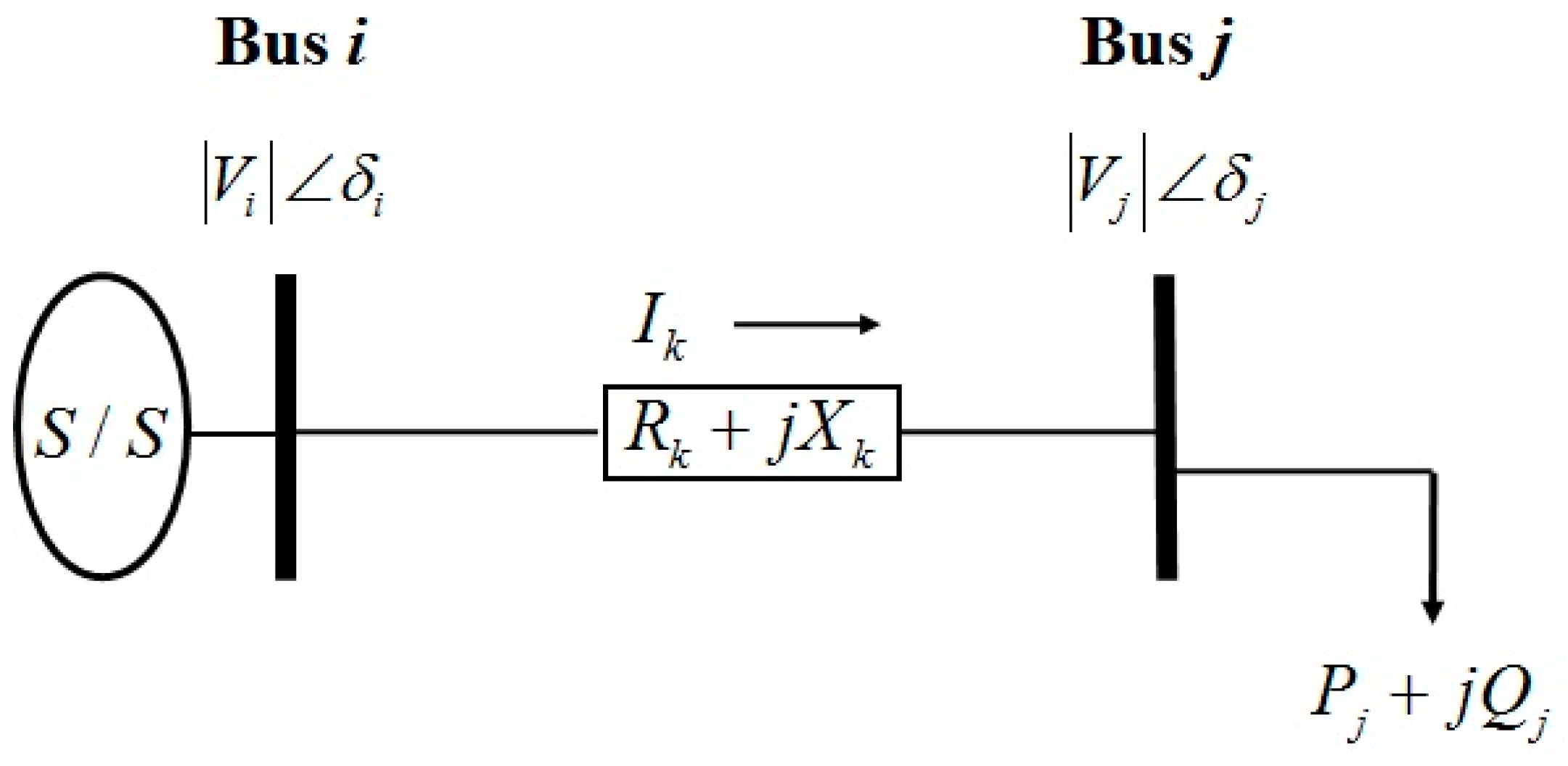
3. OPDG Problem Formulation
3.1. Objective Functions
3.1.1. Minimization of Active Power Loss
3.1.2. Minimization of Voltage Deviation
3.1.3. Maximization of Voltage Stability Index
3.2. Constraints
3.2.1. Power Balance
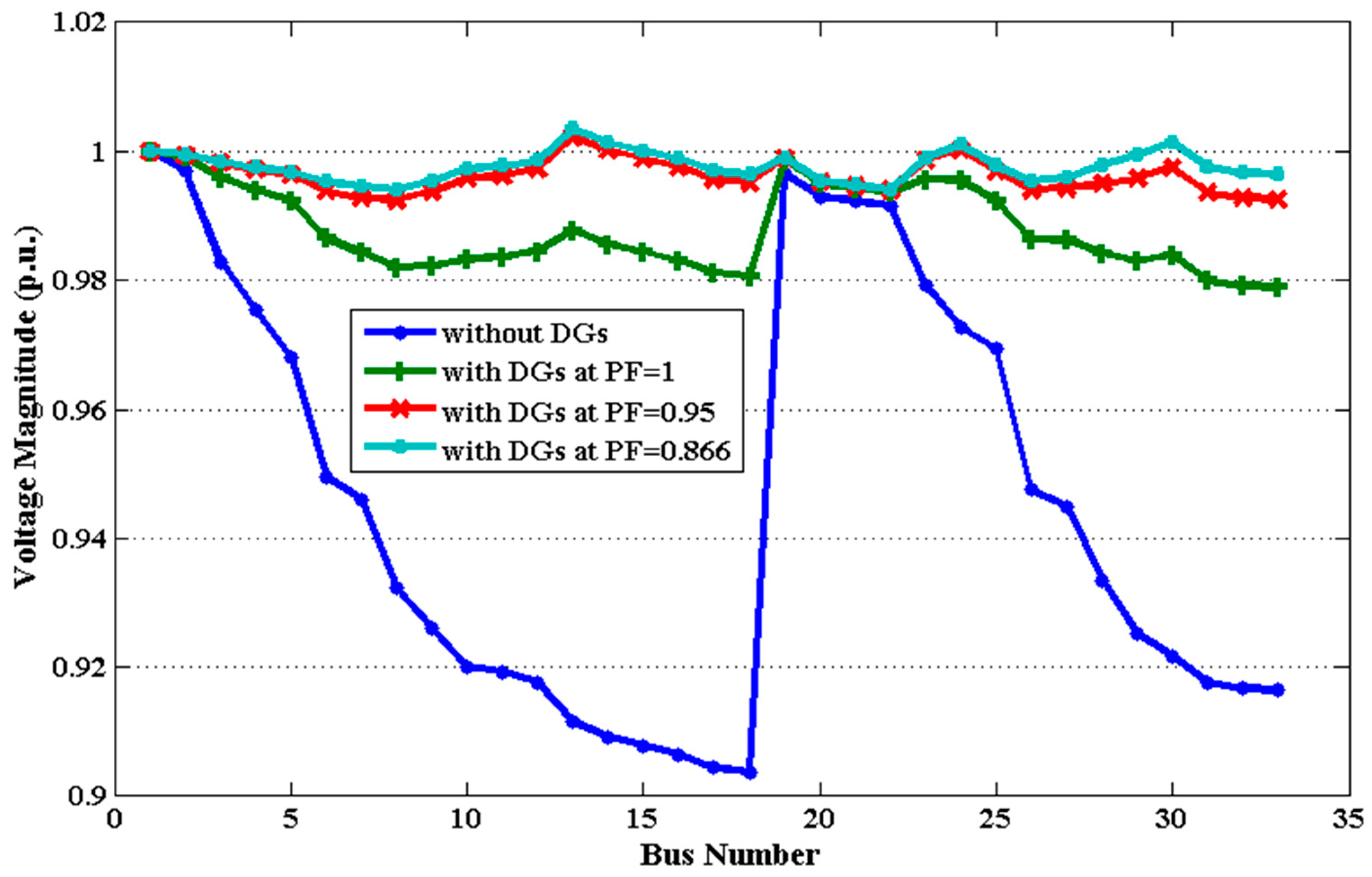
3.2.2. Voltage Limits
3.2.3. Active and Reactive Power Limits of DG
3.2.4. Permissible Limit of DG Penetration
4. Implementation of QODELFA on the OPDG Problem
| Algorithm: QODELFA for solving the OPDG problem. | |
| A: Input load and line data for the RDS, and set required parameters for the algorithm: maximum number of iterations (M), population size (PS), total number of variables (N), cr, and . B: Run the power flow program to record the base-case values of the system’s characteristics and the objective functions. C: QOBL Initialization 1: Create initial population (IP) of random solutions by generating a (PS × N) matrix, where every row of this matrix contains the sizes and locations of DGs. 2: Evaluate the IP by the objective function (OF) given in (19) after adding penalties in case of violating the constraints as 3: Regenerate the IP based on the QOBL technique given in (11). 4: Evaluate the QOBL-based IP by the given in (27). 5: Apply the greedy selection (GS) to compare both IPs evaluated in steps 2 and 4 and save the best population. 6: Assign the QOBL-based population saved in step 5 as the IP of the DELF’s main loop. | D: Main loop: 7: while stopping criterion is not satisfied, do 8: Apply the mutation of DE on the population according to (2) considering the limits on sizes and locations of DGs. 9: Evaluate the mutant solution by the given in (27). 10: Execute the crossover on the mutant solution according to (4), then evaluate it by the given in (27). 11: Apply the GS to keep the superior population by comparing both solutions evaluated in steps 9 and 10. 12: Apply the LF perturbation on the superior solution saved in step 11 according to (5) considering the limits on sizes and locations of DGs. 13: Evaluate the new solution by the given in (27). 14: perform the crossover on the new solution according to (4), then evaluate it by the given in (27). 15: Apply the GS to keep the new superior solution by comparing both solutions evaluated in steps 13 and 14. 16: end while E: Display the final obtained solutions and save the results. |
5. Results and Discussions
5.1. System 1: The IEEE 33-Bus
5.1.1. Case 1: APL Minimization
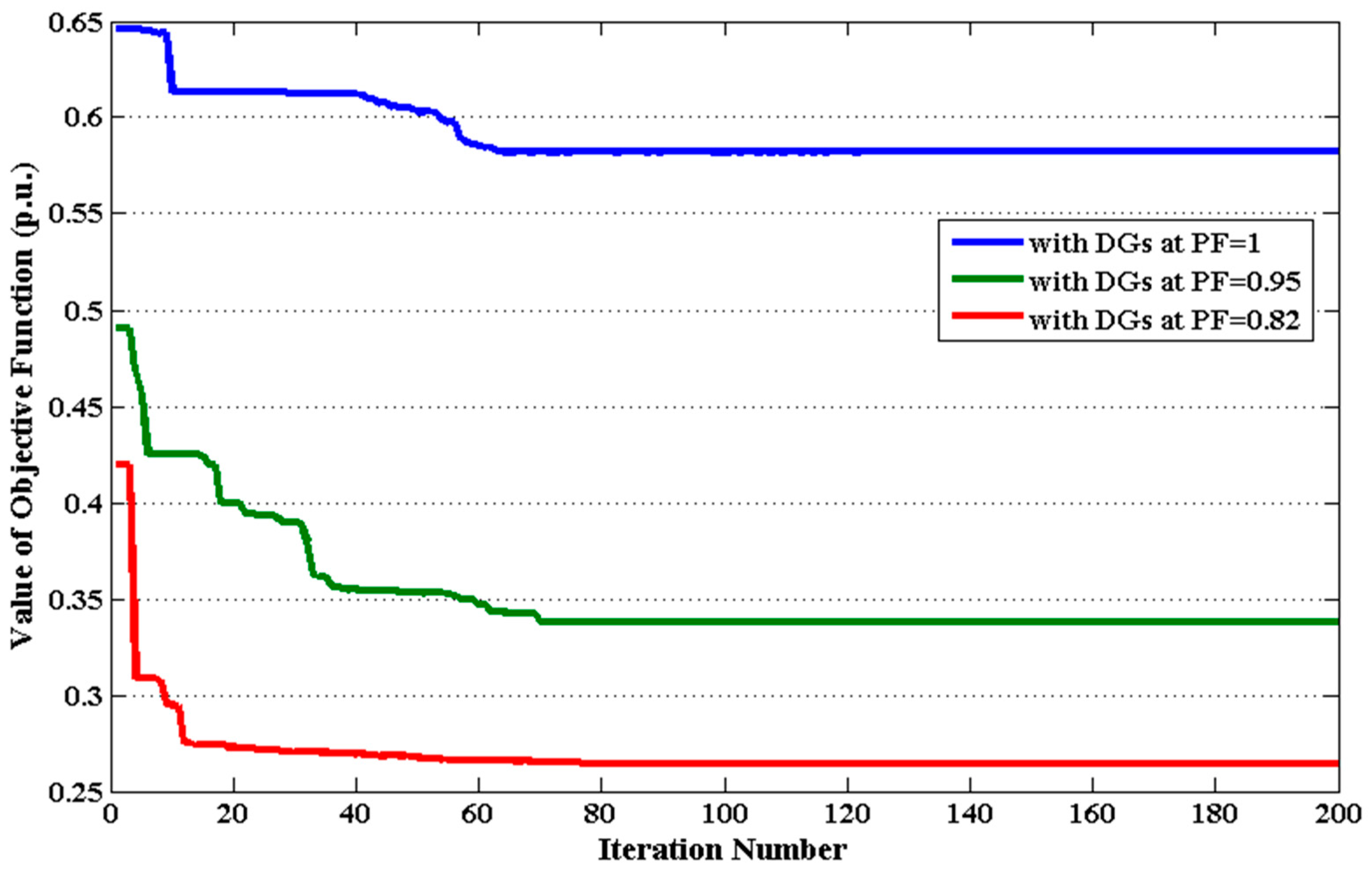
5.1.2. Case 2: Simultaneous Minimization of APL and VD
5.1.3. Case 3: Simultaneous Minimization of APL, VD, and VSI−1
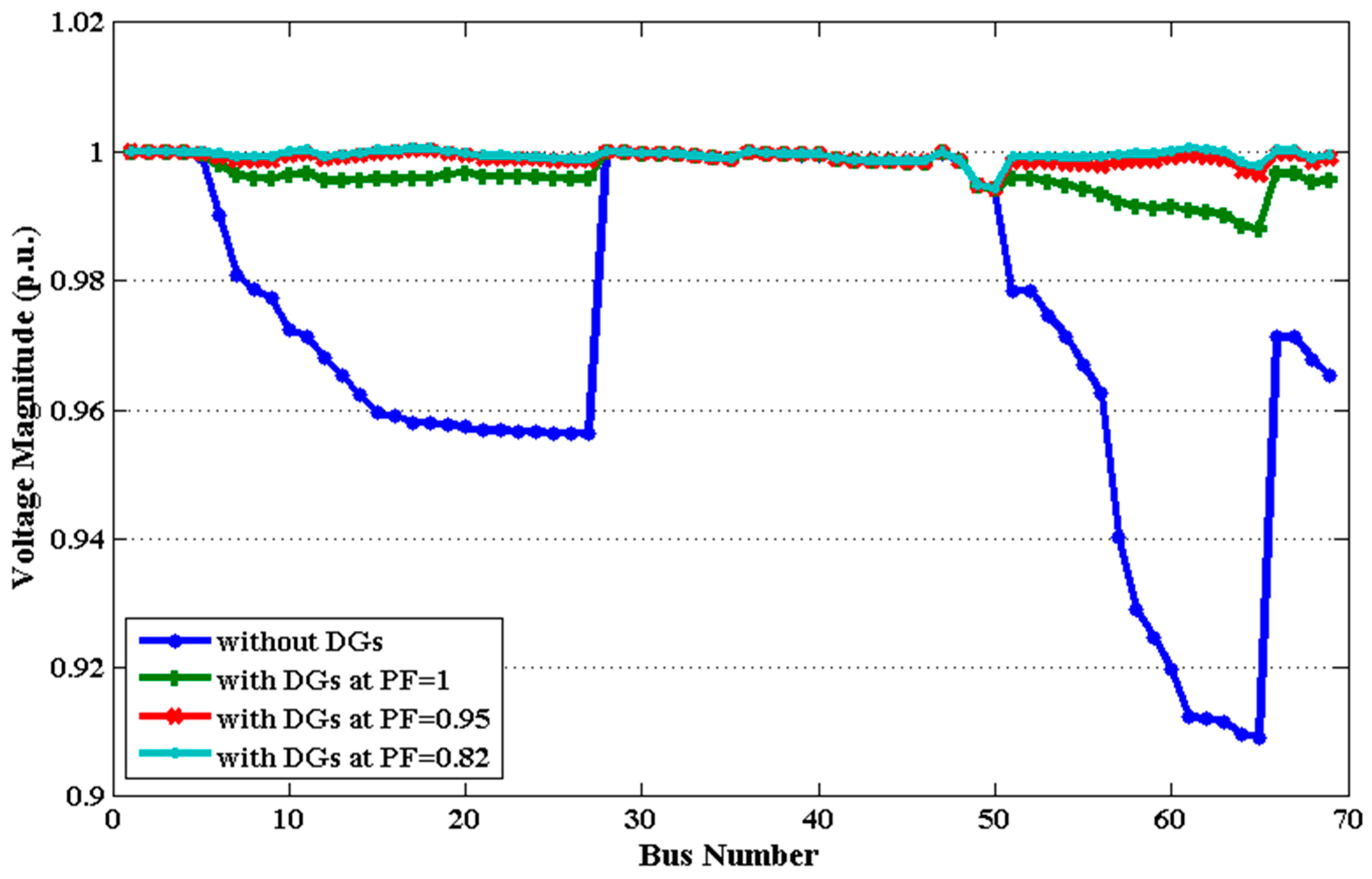
5.2. System 2: The IEEE 69-Bus
5.2.1. Case 1: APL Minimization
5.2.2. Case 2: Simultaneous Minimization of APL and VD
5.2.3. Case 3: Simultaneous Minimization of APL, VD, and VSI−1
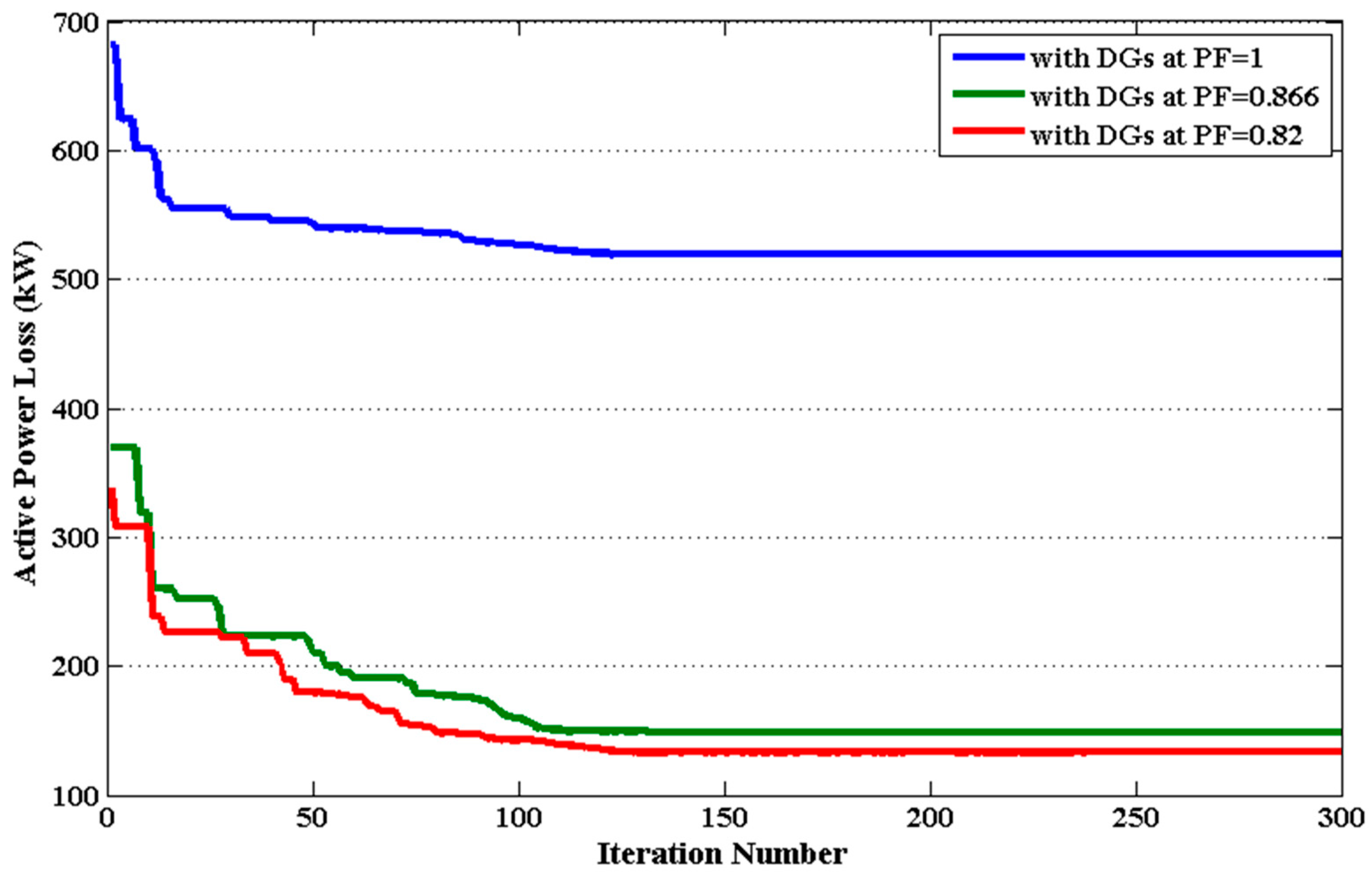
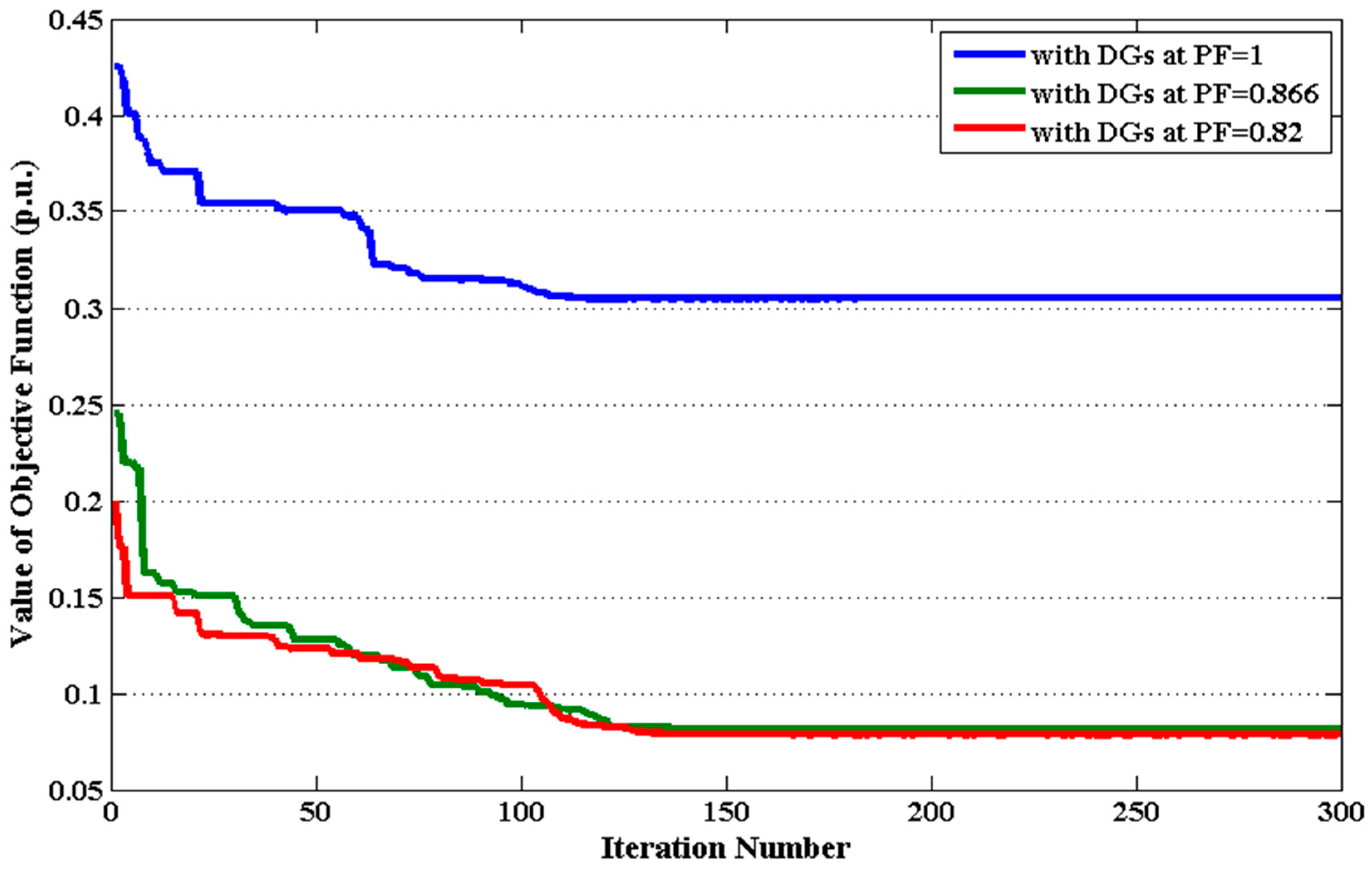
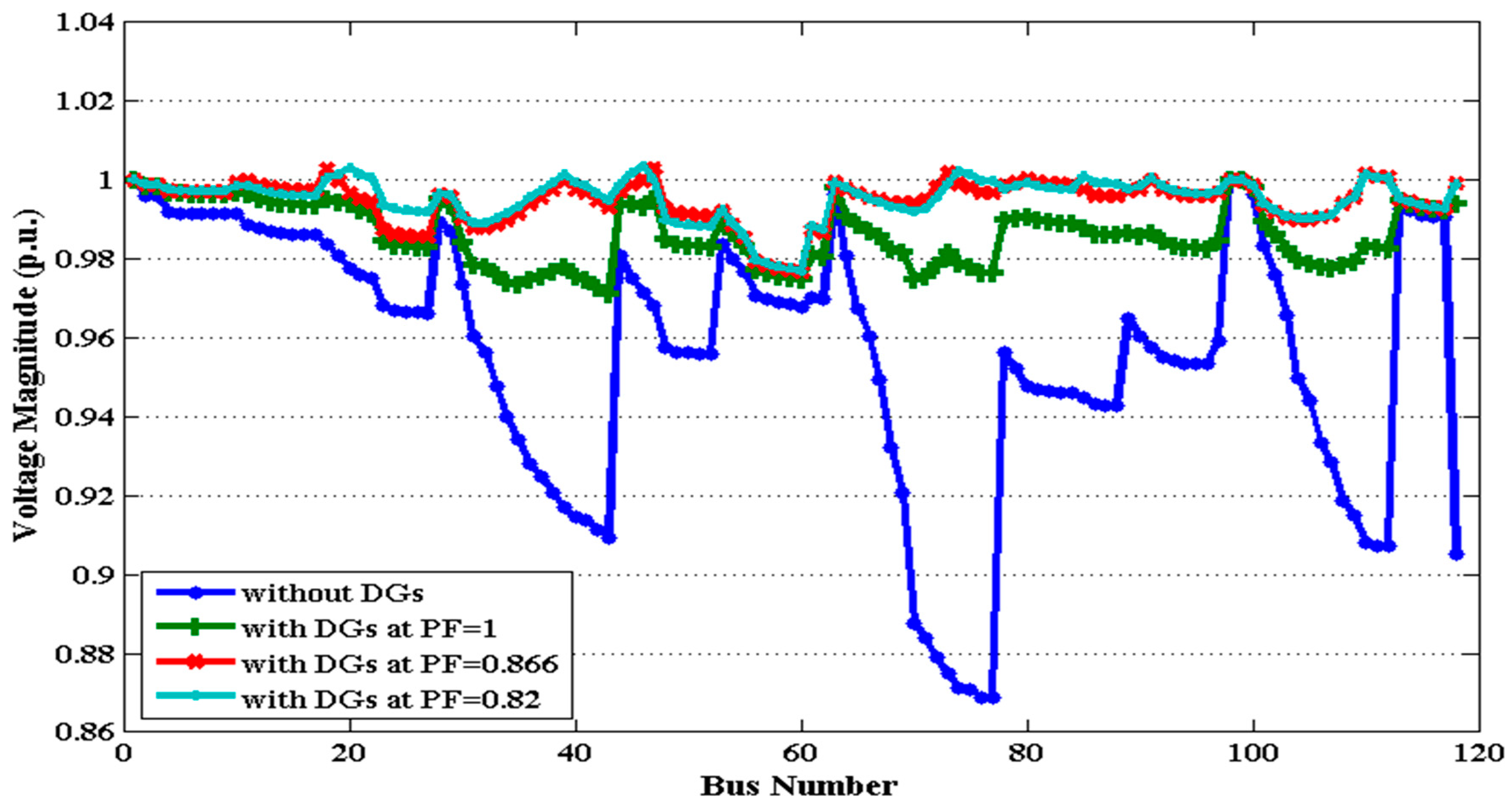
5.3. System 3: The IEEE 118-Bus
5.3.1. Case 1: APL Minimization
5.3.2. Case 2: Simultaneous Minimization of APL and VD
5.3.3. Case 3: Simultaneous Minimization of APL, VD, and VSI−1
- Two main mechanisms are combined to construct the proposed QODELFA; the former finds the global optimum solution using DE, whereas, the latter implements a local permutation using LF. Furthermore, the initial population of the combined DELF is generated by applying the QOBL concept, which consequently increases the diversity and exploration of the initial solutions. As a result, the implementation of the proposed QODELFA ensures the convergence towards the optimum rapidly and reliably. In addition, the elite solutions are elected in each generation, which guarantees the efficient and flexible flow of solutions to the optimal region inside the search space.
- The obtained results presented in this paper show that the SDs are quite small. Hence, the proposed algorithm’s performance stability and robustness are validated.
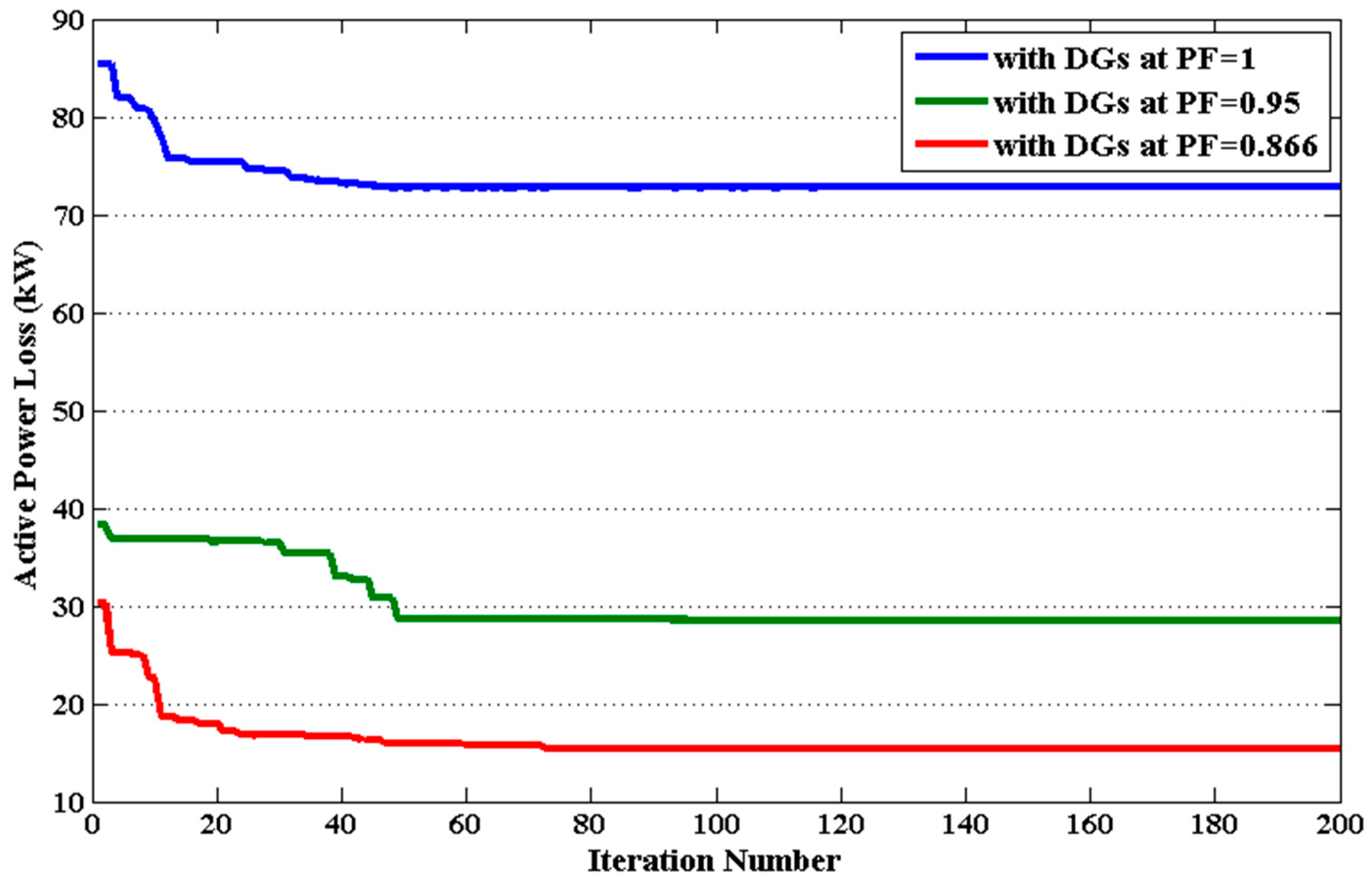
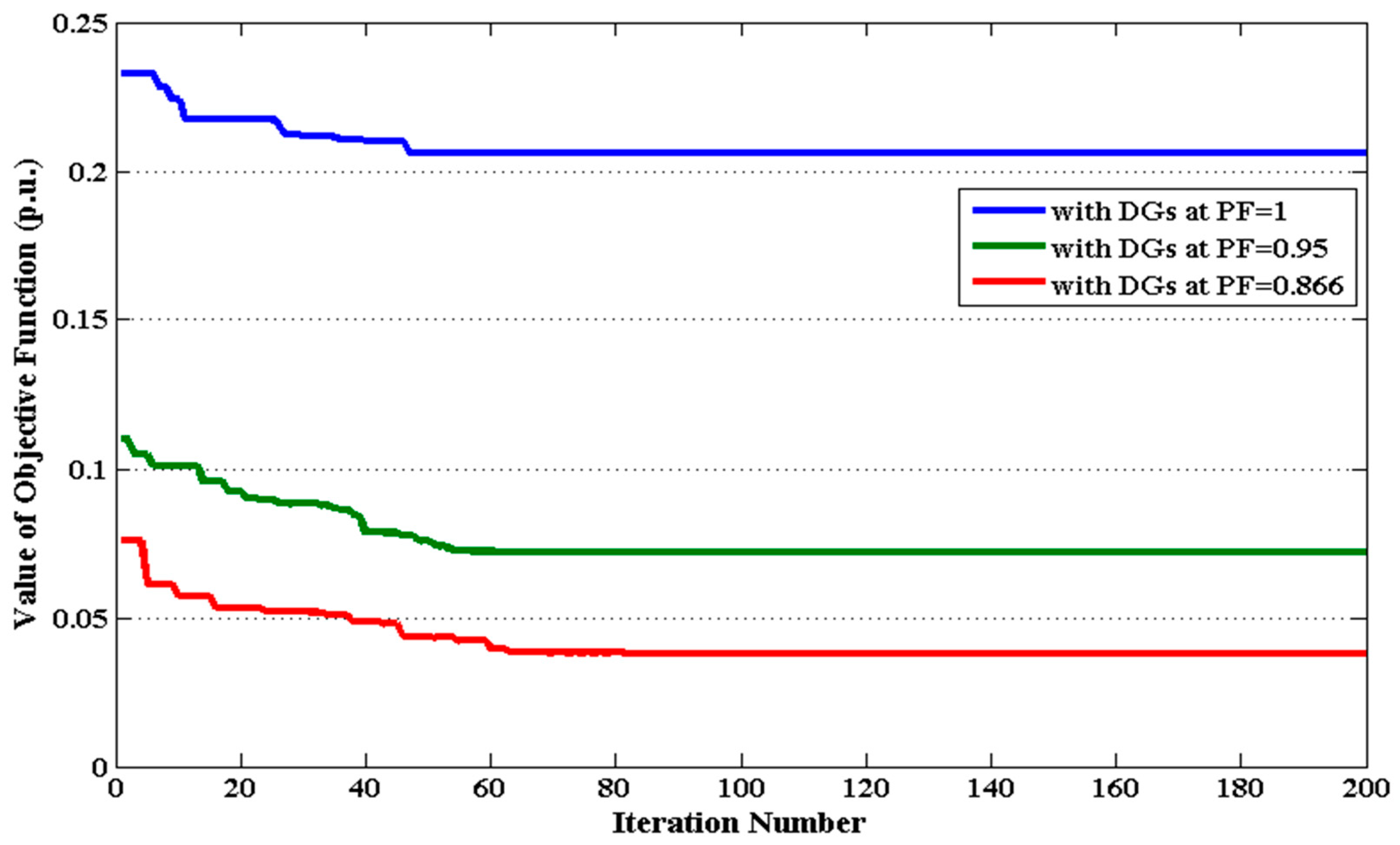
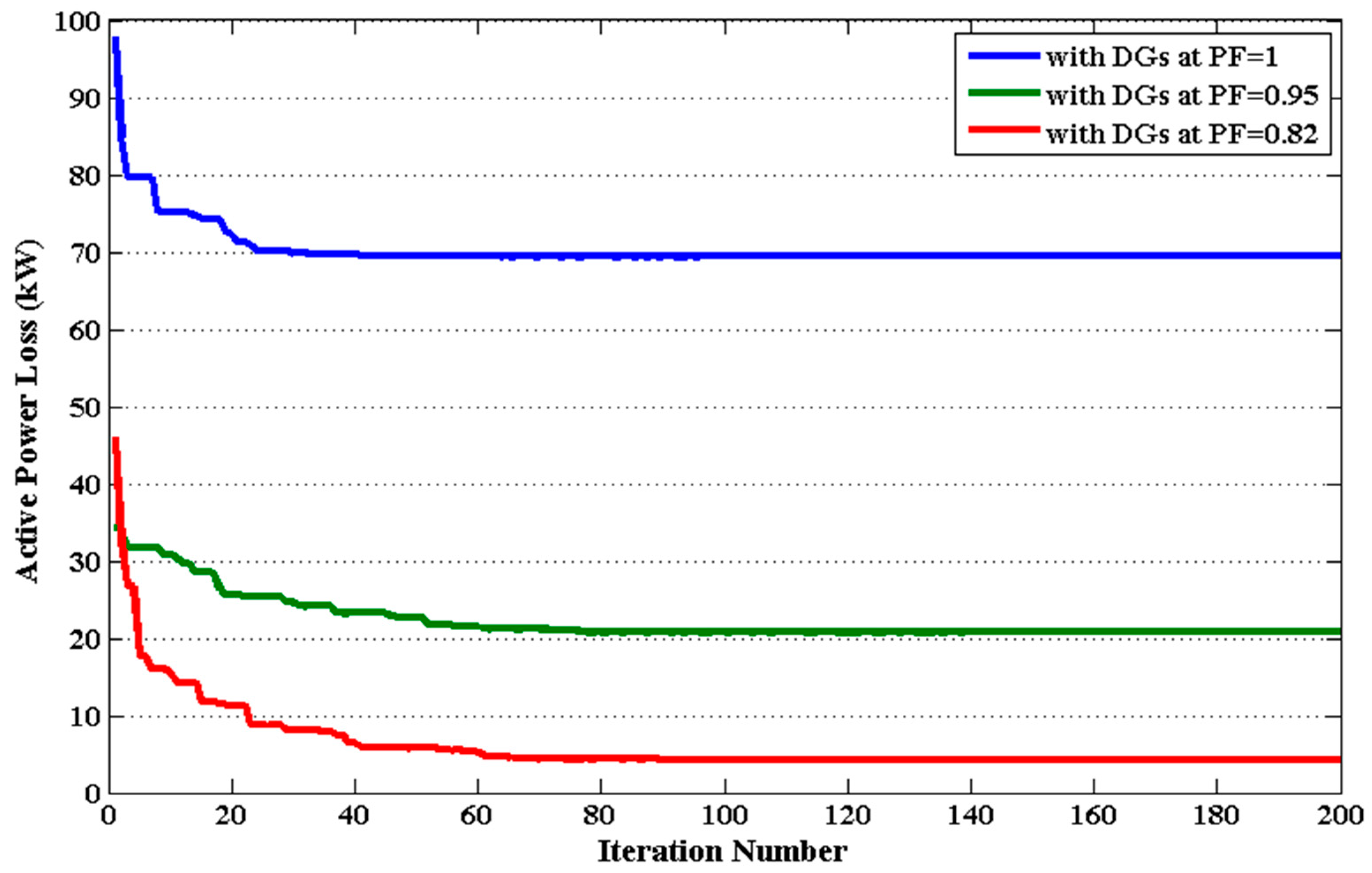
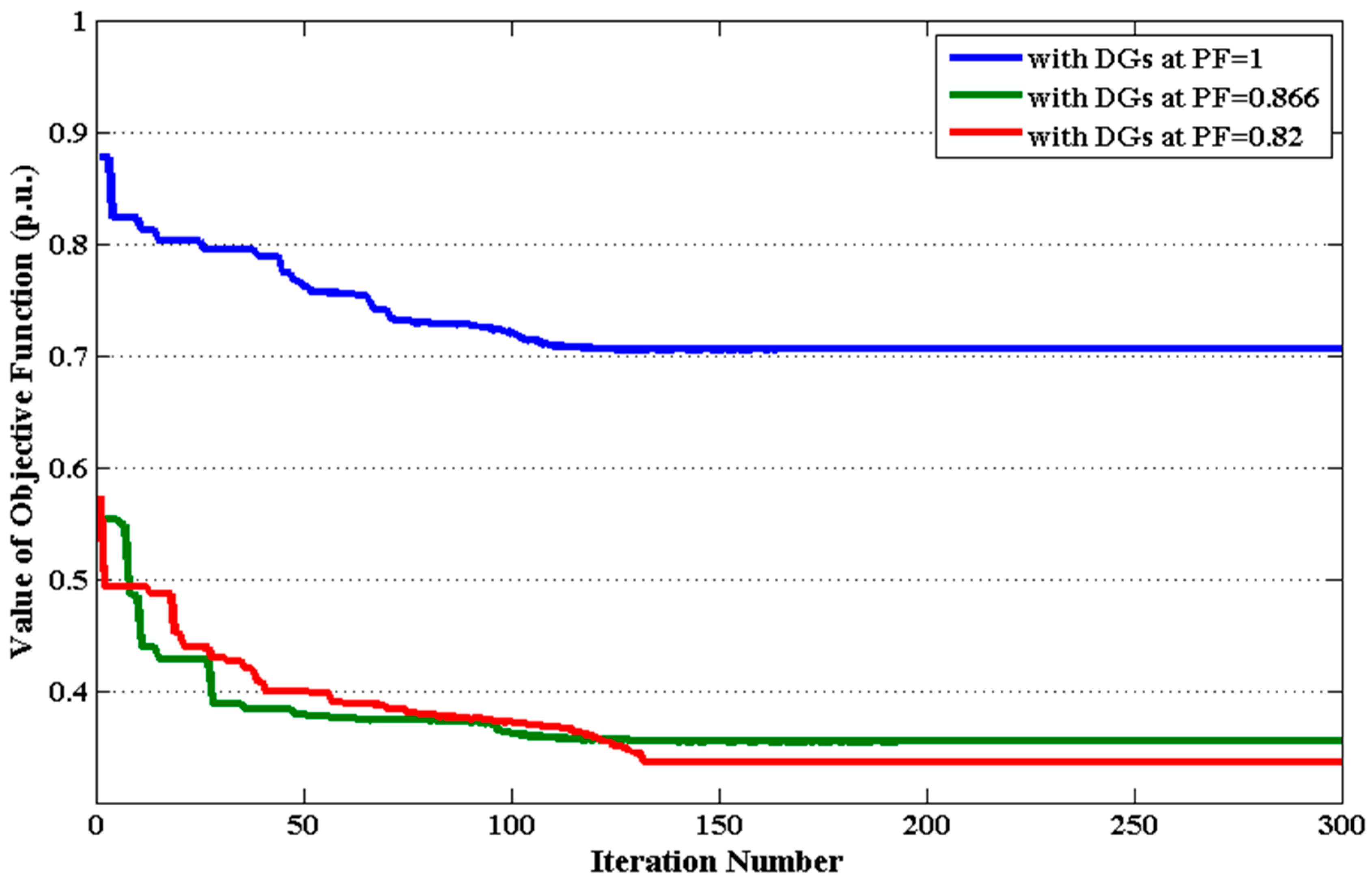
- The effectiveness of the QODELFA is also verified by demonstrating the convergence characteristics of the proposed algorithm as given in this paper. Apparently, the optimal solutions are obtained with a small number of iterations.
- The computational time for QODELFA is slightly more than some original algorithms discussed in the literature and the paper. This is mainly because of the combined framework of three powerful search mechanisms together; namely, QOBL, DE, and LF, in addition to the implementation of crossover and selection many times during the execution of the proposed algorithm. Nevertheless, using a relatively more powerful computer can overcome this problem. Also, a slight additional computational time can be neglected when much better solutions are obtained.
- The proposed algorithm has been tested using well-known benchmark functions, including, many minima, bowl-shaped, valley-shaped, and other difficult objective functions besides the OPDG problem solved in this paper. Hence, it is recommended here, to further investigate the performance of the algorithm in other engineering applications.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sultana, U.; Khairuddin, A.B.; Aman, M.M.; Mokhtar, A.S.; Zareen, N. A review of optimum DG placement based on minimization of power losses and voltage stability enhancement of distribution system. Renew. Sustain. Energy Rev. 2016, 63, 363–378. [Google Scholar] [CrossRef]
- Napis, N.F.; Khatib, T.; Hassan, E.E.; Sulaima, M.F. An improved method for reconfiguring and optimizing electrical active distribution network using evolutionary particle swarm optimization. Appl. Sci. 2018, 8, 804. [Google Scholar] [CrossRef]
- Yaprakdal, F.; Baysal, M.; Anvari-Moghaddam, A. Optimal operational scheduling of reconfigurable microgrids in presence of renewable energy sources. Energies 2019, 12, 1858. [Google Scholar] [CrossRef]
- Abd El-salam, M.F.; Beshr, E.; Eteiba, M.B. A new hybrid technique for minimizing power losses in a distribution system by optimal sizing and siting of distributed generators with network reconfiguration. Energies 2018, 11, 3351. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, J.; Wang, W.; Jing, T.; Zhang, M. Optimal operation analysis of the distribution network comprising a micro energy grid based on an improved grey wolf optimization algorithm. Appl. Sci. 2018, 8, 923. [Google Scholar] [CrossRef]
- Aman, M.M.; Jasmon, G.B.; Mokhlis, H.; Bakar, A.H.A. Optimal placement and sizing of a DG based on a new power stability index and line losses. Int. J. Electr. Power Energy Syst. 2012, 43, 1296–1304. [Google Scholar] [CrossRef]
- Murty, V.V.S.N.; Kumar, A. Optimal placement of DG in radial distribution systems based on new voltage stability index under load growth. Int. J. Electr. Power Energy Syst. 2015, 69, 246–256. [Google Scholar] [CrossRef]
- Kumar, A.; Vijay Babu, P.; Murty, V.V.S.N. Distributed generators allocation in radial distribution systems with load growth using loss sensitivity approach. J. Inst. Eng. India Ser. B 2017, 98, 275–287. [Google Scholar] [CrossRef]
- Murty, V.V.S.N.; Kumar, A. Comparison of optimal DG allocation methods in radial distribution systems based on sensitivity approaches. Int. J. Electr. Power Energy Syst. 2013, 53, 450–467. [Google Scholar] [CrossRef]
- Viral, R.; Khatod, D.K. An analytical approach for sizing and siting of DGs in balanced radial distribution networks for loss minimization. Int. J. Electr. Power Energy Syst. 2015, 67, 191–201. [Google Scholar] [CrossRef]
- Atwa, Y.M.; El-Saadany, E.F.; Salama, M.M.A.; Seethapathy, P. Optimal renewable resources mix for distribution system energy loss minimization. IEEE Trans. Power Syst. 2010, 25, 360–370. [Google Scholar] [CrossRef]
- Khalesi, N.; Rezaei, N.; Haghifam, M.R. DG allocation with application of dynamic programming for loss reduction and reliability improvement. Int. J. Electr. Power Energy Syst. 2011, 33, 288–295. [Google Scholar] [CrossRef]
- Kaur, S.; Kumbhar, G.; Sharma, J. A MINLP technique for optimal placement of multiple DG units in distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 609–617. [Google Scholar] [CrossRef]
- Shaaban, M.F.; Atwa, Y.M.; El-Saadany, E.F. DG allocation for benefit maximization in distribution networks. IEEE Trans. Power Syst. 2013, 28, 639–649. [Google Scholar] [CrossRef]
- Ganguly, S.; Samajpati, D. Distributed generation allocation on radial distribution networks under uncertainties of load and generation using genetic algorithm. IEEE Trans. Sustain. Energy 2015, 6, 688–697. [Google Scholar] [CrossRef]
- Ganguly, S.; Samajpati, D. Distributed generation allocation with on-load tap changer on radial distribution networks using adaptive genetic algorithm. Appl. Soft Comput. 2017, 59, 45–67. [Google Scholar] [CrossRef]
- El-Zonkoly, A.M. Optimal placement of multi-distributed generation units including different load models using particle swarm optimization. Swarm Evol. Comput. 2011, 1, 50–59. [Google Scholar] [CrossRef]
- Kansal, S.; Kumar, V.; Tyagi, B. Optimal placement of different type of DG sources in distribution networks. Int. J. Electr. Power Energy Syst. 2013, 53, 752–760. [Google Scholar] [CrossRef]
- HassanzadehFard, H.; Jalilian, A. Optimal sizing and location of renewable energy based DG units in distribution systems considering load growth. Int. J. Electr. Power Energy Syst. 2018, 101, 356–370. [Google Scholar] [CrossRef]
- Abu-Mouti, F.S.; El-Hawary, M.E. Optimal distributed generation allocation and sizing in distribution systems via artificial bee colony algorithm. IEEE Trans. Power Deliv. 2011, 26, 2090–2101. [Google Scholar] [CrossRef]
- Niknam, T.; Taheri, S.I.; Aghaei, J.; Tabatabaei, S.; Nayeripour, M. A modified honey bee mating optimization algorithm for multiobjective placement of renewable energy resources. Appl. Energy 2011, 88, 4817–4830. [Google Scholar] [CrossRef]
- Abdul Kadir, A.F.; Mohamed, A.; Shareef, H.; Ibrahim, A.A.; Khatib, T.; Elmenreich, W. An improved gravitational search algorithm for optimal placement and sizing of renewable distributed generation units in a distribution system for power quality enhancement. J. Renew. Sustain. Energy 2014, 6, 033112. [Google Scholar] [CrossRef]
- Das, B.; Mukherjee, V.; Das, D. DG placement in radial distribution network by symbiotic organisms search algorithm for real power loss minimization. Appl. Soft Comput. 2016, 49, 920–936. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M. A combination of genetic algorithm and particle swarm optimization for optimal DG location and sizing in distribution systems. Int. J. Electr. Power Energy Syst. 2012, 34, 66–74. [Google Scholar] [CrossRef]
- Nowdeh, S.A.; Davoudkhani, I.F.; Moghaddam, M.J.H.; Najmi, E.S.; Abdelaziz, A.Y.; Ahmadi, A.; Razavi, S.E.; Gandoman, F.H. Fuzzy multi-objective placement of renewable energy sources in distribution system with objective of loss reduction and reliability improvement using a novel hybrid method. Appl. Soft Comput. 2019, 77, 761–779. [Google Scholar] [CrossRef]
- Kumar, S.; Mandal, K.K.; Chakraborty, N. Optimal DG placement by multi-objective opposition based chaotic differential evolution for techno-economic analysis. Appl. Soft Comput. 2019, 78, 70–83. [Google Scholar] [CrossRef]
- Kayalvizhi, S.; Vinod Kumar, D.M. Optimal planning of active distribution networks with hybrid distributed energy resources using grid-based multi-objective harmony search algorithm. Appl. Soft Comput. 2018, 67, 387–398. [Google Scholar]
- Sharma, S.; Bhattacharjee, S.; Bhattacharya, A. Quasi-oppositional swine influenza model based optimization with quarantine for optimal allocation of DG in radial distribution network. Int. J. Electr. Power Energy Syst. 2016, 74, 348–373. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Multi-objective quasi-oppositional teaching learning based optimization for optimal location of distributed generator in radial distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 534–545. [Google Scholar] [CrossRef]
- Injeti, S.K.; Kumar, N.P. A novel approach to identify optimal access point and capacity of multiple DGs in a small, medium and large scale radial distribution systems. Int. J. Electr. Power Energy Syst. 2013, 45, 142–151. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Krill herd algorithm for optimal location of distributed generator in radial distribution system. Appl. Soft Comput. 2016, 40, 391–404. [Google Scholar] [CrossRef]
- Nguyen, T.P.; Vo, D.N. A novel stochastic fractal search algorithm for optimal allocation of distributed generators in radial distribution systems. Appl. Soft Comput. 2018, 70, 773–796. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution – A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Tizhoosh, H.R. Opposition-based learning: A new scheme for machine intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; pp. 1–7. [Google Scholar]
- Simon, D.; Ergezer, M.; Du, D. Oppositional Biogeography-Based Optimization. Available online: http://embeddedlab.csuohio.edu/BBO/ (accessed on 3 June 2019).
- Surjanovic, S.; Bingham, D. Virtual Library of Simulation Experiments: Test Functions and Datasets. Available online: https://www.sfu.ca/~ssurjano/index.html (accessed on 1 June 2019).
- Reddy, V.U.; Manohar, T.G. A two stage approach: Capacitor placement for loss reduction in radial distribution system. In Proceedings of the 2012 11th International Conference on Environment and Electrical Engineering, Venice, Italy, 18–25 May 2012; pp. 555–558. [Google Scholar]
- Hung, D.Q.; Mithulananthan, N. Multiple distributed generator placement in primary distribution networks for loss reduction. IEEE Trans. Ind. Electron. 2013, 60, 1700–1708. [Google Scholar] [CrossRef]
- Zulpo, R.S.; Leborgne, R.C.; Bretas, A.S. Optimal siting and sizing of distributed generation through power losses and voltage deviation. In Proceedings of the 2014 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014; pp. 871–875. [Google Scholar]
- El-Fergany, A.A.; Abdelaziz, A.Y. Capacitor allocations in radial distribution networks using cuckoo search algorithm. IET Gener. Transm. Distrib. 2014, 8, 223–232. [Google Scholar] [CrossRef]




| Function | Formula | Input Domain | No. of Parameters |
|---|---|---|---|
| [−32.768,32.768] | 20 | ||
| [−600,600] | 20 | ||
| [−5.12,5.12] | 5 | ||
| [−10,10] | 20 | ||
| [−d,d] | 5 | ||
| [−10,10] | 30 | ||
| [−65.54,65.54] | 20 | ||
| [0,d] | 4 | ||
| [−5,10] | 4 | ||
| [−10,10] | 10 |
| Function | Value | GA | PSO | DE | FA | ABC | SCA | QODELFA |
|---|---|---|---|---|---|---|---|---|
| Min. | 0.001500000 | 7.9936E-15 | 5.5078E-05 | 3.5994E-05 | 0.001499 | 3.3672E-05 | 3.2346E-06 | |
| Max. | 1.501800000 | 1.5099E-14 | 9.1151E-05 | 5.0207E-05 | 0.005632 | 0.00136427 | 1.8930E-05 | |
| Mean | 0.494010000 | 1.1546E-14 | 7.7296E-05 | 4.3945E-05 | 0.003136 | 0.00052707 | 7.6498E-06 | |
| SD | 0.650915210 | 3.7449E-15 | 1.3982E-05 | 4.1056E-06 | 0.001235 | 0.00039639 | 4.6941E-06 | |
| Min. | 1.67057E-07 | 1.85E-13 | 1.89310E-06 | 4.48524E-08 | 0.023929 | 3.53044E-05 | 3.01981E-14 | |
| Max. | 0.007396679 | 0.058921 | 6.47944E-05 | 0.009864731 | 0.305490 | 0.260080741 | 0.022126734 | |
| Mean | 0.000740400 | 0.026802 | 1.42411E-05 | 0.002465738 | 0.088867 | 0.079647319 | 0.007140086 | |
| SD | 0.002338778 | 0.019734 | 1.85757E-05 | 0.004026563 | 0.085039 | 0.105481599 | 0.008401261 | |
| Min. | 0.994959 | 0 | 2.01E-11 | 0.994959 | 0.200500 | 0 | 0 | |
| Max. | 5.969749 | 1.989918 | 1.15E-09 | 5.969754 | 1.657200 | 9.32E-11 | 3.34E-13 | |
| Mean | 2.984877 | 0.596975 | 3.80E-10 | 3.283365 | 0.768219 | 9.40E-12 | 1.19E-13 | |
| SD | 1.483196 | 0.839023 | 3.53E-10 | 1.410988 | 0.537652 | 2.94E-11 | 1.23E-13 | |
| Min. | 3.02E-09 | 3.28E-19 | 6.41E-10 | 9.21E-11 | 0.000138 | 1.056931 | 1.80E-12 | |
| Max. | 0.998176 | 3.91E-18 | 2.03E-09 | 1.33E-10 | 0.001058 | 1.279176 | 4.79E-10 | |
| Mean | 0.172109 | 2.65E-18 | 1.14E-09 | 1.19E-10 | 0.000406 | 1.180877 | 9.38E-11 | |
| SD | 0.335319 | 1.52E-18 | 4.79E-10 | 1.27E-11 | 0.000265 | 0.085863 | 1.45E-10 | |
| Min. | 0.000224 | 3.50E-05 | 0.003839 | 8.36E-09 | 0.001526 | 0.204203 | 8.50E-11 | |
| Max. | 0.051547 | 0.000233 | 0.105156 | 0.031277 | 0.025481 | 1.154009 | 1.91E-09 | |
| Mean | 0.017779 | 0.000159 | 0.031891 | 0.005996 | 0.014717 | 0.523433 | 7.76E-10 | |
| SD | 0.018239 | 7.25E-05 | 0.030668 | 0.009571 | 0.008200 | 0.299470 | 5.70E-10 | |
| Min. | 1.50E-05 | 5.76E-13 | 6.34E-05 | 7.05E-09 | 0.119930 | 0.001221 | 4.21E-06 | |
| Max. | 0.000791 | 3.05E-11 | 0.000117 | 1.08E-08 | 0.221020 | 2.772696 | 9.49E-05 | |
| Mean | 0.000243 | 8.88E-12 | 9.21E-05 | 9.15E-09 | 0.169986 | 0.887205 | 3.10E-05 | |
| SD | 0.000294 | 9.99E-12 | 1.57E-05 | 1.02E-09 | 0.032625 | 1.029825 | 2.83E-05 | |
| Min. | 2.91E-08 | 2.22E-17 | 1.13E-07 | 7.16E-08 | 6.58E-05 | 1.14E-06 | 1.19E-09 | |
| Max. | 0.002864 | 5.91E-15 | 2.52E-07 | 1.09E-07 | 0.000191 | 0.001364 | 6.48E-08 | |
| Mean | 0.000306 | 1.21E-15 | 1.84E-07 | 9.21E-08 | 0.000109 | 0.000251 | 1.87E-08 | |
| SD | 0.000900 | 1.93E-15 | 3.93E-08 | 1.36E-08 | 3.71E-05 | 0.000455 | 2.12E-08 | |
| Min. | 0.000104 | 3.97E-09 | 0.001110 | 6.21E-08 | 0.002016 | 0.068476 | 1.36E-11 | |
| Max. | 0.067100 | 0.000751 | 0.035307 | 0.000303 | 0.024256 | 1.294515 | 4.61E-07 | |
| Mean | 0.012986 | 0.000230 | 0.016135 | 0.09E-07 | 0.009848 | 0.832464 | 8.88E-08 | |
| SD | 0.021051 | 0.000288 | 0.012371 | 0.000102 | 0.007333 | 0.404648 | 1.34E-07 | |
| Min. | 0.044047 | 0.002463 | 0.003089 | 1.01E-11 | 0.004665 | 0.389459 | 0 | |
| Max. | 3.750229 | 0.007062 | 0.068908 | 8.66E-11 | 0.146660 | 1.238042 | 3.72E-29 | |
| Mean | 1.217668 | 0.004882 | 0.023161 | 4.15E-11 | 0.052185 | 0.694527 | 5.08E-30 | |
| SD | 1.364193 | 0.001598 | 0.022713 | 2.45E-11 | 0.041106 | 0.247694 | 1.16E-29 | |
| Min. | 0.666667 | 1.84E-12 | 1.19E-11 | 0.666667 | 0.592410 | 0.666668 | 0.028088 | |
| Max. | 0.666747 | 0.666667 | 0.743694 | 0.666667 | 0.667160 | 0.666776 | 0.097842 | |
| Mean | 0.666675 | 0.600000 | 0.572044 | 0.666667 | 0.659358 | 0.666689 | 0.058687 | |
| SD | 2.54E-05 | 0.210819 | 0.302020 | 3.24E-11 | 0.023524 | 3.59E-05 | 0.026335 |
| Technique | Optimal Locations | Optimal Sizes (MW/MVAr) | APL (kW) | VD (p.u.) | VSI−1 (p.u.) | VSI (p.u.) | LR% | SD |
|---|---|---|---|---|---|---|---|---|
| Case 1.1: DGs with unity power factor (PF = 1) | ||||||||
| SIMBO-Q [28] | 14 | 0.7638/0.0 | 73.40 | 0.0151 | 1.1444 | 0.8738 | 65.21 | - |
| 24 | 1.0415/0.0 | |||||||
| 29 | 1.1352/0.0 | |||||||
| QOSIMBO-Q [28] | 14 | 0.7708/0.0 | 72.80 | 0.0151 | 1.1358 | 0.8804 | 65.50 | - |
| 24 | 1.0965/0.0 | |||||||
| 30 | 1.0655/0.0 | |||||||
| MINLP [13] | 13 | 0.8000/0.0 | 72.79 | - | - | - | 65.34 | - |
| 24 | 1.0900/0.0 | |||||||
| 30 | 1.0500/0.0 | |||||||
| SFSA [32] | 13 | 0.8020/0.0 | 72.785 | 0.01509 | 1.1357 | 0.8805 | 65.50 | 5.91E-09 |
| 24 | 1.0920/0.0 | |||||||
| 30 | 1.0537/0.0 | |||||||
| QODELFA | 13 | 0.8018/0.0 | 72.785 | 0.01509 | 1.1358 | 0.8804 | 65.50 | 4.84E-08 |
| 24 | 1.0913/0.0 | |||||||
| 30 | 1.0536/0.0 | |||||||
| Case 1.2: DGs with lagging power factor (PF = 0.95) | ||||||||
| SIMBO-Q [28] | 13 | 0.8875/0.2917 | 29.00 | 0.00098 | 1.0367 | 0.9646 | 86.26 | - |
| 24 | 1.0853/0.3567 | |||||||
| 30 | 1.3092/0.4303 | |||||||
| QOSIMBO-Q [28] | 13 | 0.8303/0.2729 | 28.500 | 0.00210 | 1.0493 | 0.9530 | 86.49 | - |
| 24 | 1.1239/0.3694 | |||||||
| 30 | 1.2398/0.4075 | |||||||
| SFSA [32] | 13 | 0.8306/0.2730 | 28.533 | 0.00207 | 1.0493 | 0.9530 | 86.48 | 5.24E-08 |
| 24 | 1.1256/0.3700 | |||||||
| 30 | 1.2396/0.4074 | |||||||
| QODELFA | 13 | 0.8302/0.2728 | 28.533 | 0.00207 | 1.0493 | 0.9530 | 86.48 | 4.95E-07 |
| 24 | 1.1247/0.3697 | |||||||
| 30 | 1.2396/0.4074 | |||||||
| Case 1.3: DGs with lagging power factor (PF = 0.866) | ||||||||
| KHA [31] | 13 | 0.8530/0.4925 | 19.578 | - | 1.0769 | 0.9286 | 90.72 | - |
| 24 | 0.9000/0.5196 | |||||||
| 30 | 0.8999/0.5196 | |||||||
| QODELFA | 13 | 0.7582/0.4378 | 15.347 | 0.00065 | 1.0317 | 0.9692 | 92.73 | 5.82E-07 |
| 24 | 1.0273/0.5930 | |||||||
| 30 | 1.2139/0.7009 | |||||||
| Technique | Optimal Locations | Optimal Sizes (MW/MVAr) | APL (kW) | VD (p.u.) | VSI−1 (p.u.) | VSI (p.u.) | LR% | SD |
|---|---|---|---|---|---|---|---|---|
| Case 2.1: DGs with unity power factor (PF = 1) | ||||||||
| SIMBO-Q [28] | 14 | 0.9029/0.0 | 92.50 | 0.0022 | - | - | 56.16 | - |
| 26 | 1.4491/0.0 | |||||||
| 31 | 0.9137/0.0 | |||||||
| QOSIMBO-Q [28] | 12 | 1.3232/0.0 | 88.90 | 0.0022 | - | - | 57.87 | - |
| 24 | 1.0223/0.0 | |||||||
| 30 | 1.3735/0.0 | |||||||
| QODELFA | 13 | 1.0204/0.0 | 78.308 | 0.0055 | 1.0900 | 0.9175 | 62.88 | 3.45E-10 |
| 24 | 1.1504/0.0 | |||||||
| 30 | 1.2702/0.0 | |||||||
| Case 2.2: DGs with lagging power factor (PF = 0.95) | ||||||||
| SIMBO-Q [28] | 13 | 0.8813/0.2897 | 32.20 | 0.0003 | - | - | 84.74 | - |
| 24 | 1.3048/0.4289 | |||||||
| 30 | 1.5000/0.4930 | |||||||
| QOSIMBO-Q [28] | 13 | 0.8303/0.2729 | 31.10 | 0.0003 | - | - | 85.26 | - |
| 24 | 1.1239/0.3694 | |||||||
| 30 | 1.2398/0.4075 | |||||||
| QODELFA | 13 | 0.9001/0.2958 | 29.231 | 0.0007 | 1.0331 | 0.9679 | 86.48 | 4.13E-08 |
| 24 | 1.1438/0.3759 | |||||||
| 30 | 1.3214/0.4343 | |||||||
| Case 2.3: DGs with lagging power factor (PF = 0.866) | ||||||||
| QODELFA | 13 | 0.7582/0.4378 | 15.502 | 0.0003 | 1.0243 | 0.9763 | 92.65 | 3.71E-08 |
| 24 | 1.0273/0.5930 | |||||||
| 30 | 1.2139/0.7009 | |||||||
| Technique | Optimal Locations | Optimal Sizes (MW/MVAr) | APL (kW) | VD (p.u.) | VSI−1 (p.u.) | VSI (p.u.) | LR% | SD |
|---|---|---|---|---|---|---|---|---|
| Case 3.1: DGs with unity power factor (PF = 1) | ||||||||
| SIMBO-Q [28] | 12 | 1.3482/0.0 | 98.20 | 0.00081 | 1.0370 | 0.9643 | 53.46 | - |
| 24 | 1.3805/0.0 | |||||||
| 30 | 1.5000/0.0 | |||||||
| QOSIMBO-Q [28] | 12 | 1.3465/0.0 | 97.10 | 0.00088 | 1.0383 | 0.9631 | 53.98 | - |
| 24 | 1.3043/0.0 | |||||||
| 30 | 1.5000/0.0 | |||||||
| SFSA [32] | 13 | 0.9647/0.0 | 77.410 | 0.00623 | 1.0891 | 0.9182 | 63.31 | 2.73E-07 |
| 24 | 1.1337/0.0 | |||||||
| 30 | 1.3018/0.0 | |||||||
| QODELFA | 13 | 0.9647/0.0 | 77.408 | 0.00621 | 1.0891 | 0.9182 | 63.31 | 2.62E-10 |
| 24 | 1.1334/0.0 | |||||||
| 30 | 1.3017/0.0 | |||||||
| Case 3.2: DGs with lagging power factor (PF = 0.95) | ||||||||
| SIMBO-Q [28] | 13 | 0.9429/0.3099 | 32.40 | 0.0003 | 1.0234 | 0.9771 | 84.74 | - |
| 24 | 1.3271/0.4362 | |||||||
| 30 | 1.4429/0.4742 | |||||||
| QOSIMBO-Q [28] | 13 | 0.8980/0.2952 | 31.70 | 0.0003 | 1.0235 | 0.9770 | 85.26 | - |
| 24 | 1.3928/0.4578 | |||||||
| 30 | 1.4193/0.4665 | |||||||
| SFSA [32] | 13 | 0.9174/0.3015 | 29.383 | 0.0007 | 1.0312 | 0.9697 | 86.07 | 1.47E-07 |
| 24 | 1.1463/0.3768 | |||||||
| 30 | 1.3157/0.4324 | |||||||
| QODELFA | 13 | 0.9169/0.3013 | 29.386 | 0.0007 | 1.0311 | 0.9698 | 86.07 | 1.97E-09 |
| 24 | 1.1466/0.3768 | |||||||
| 30 | 1.3167/0.4327 | |||||||
| Case 3.3: DGs with lagging power factor (PF = 0.866) | ||||||||
| QODELFA | 13 | 0.7911/0.4567 | 15.498 | 0.0003 | 1.0242 | 0.9764 | 92.65 | 3.52E-08 |
| 24 | 1.0411/0.5991 | |||||||
| 30 | 1.2431/0.7178 | |||||||
| Technique | Optimal Locations | Optimal Sizes (MW/MVAr) | APL (kW) | VD (p.u.) | VSI−1 (p.u.) | VSI (p.u.) | LR% | SD |
|---|---|---|---|---|---|---|---|---|
| Case 1.1: DGs with unity power factor (PF = 1) | ||||||||
| QOSIMBO-Q [28] | 9 | 0.8336/0.0 | 71.000 | 0.0071 | 1.1131 | 0.8984 | 68.44 | - |
| 18 | 0.4511/0.0 | |||||||
| 61 | 1.5000/0.0 | |||||||
| MINLP [13] | 11 | 0.5300/0.0 | 69.590 | - | - | - | 69.07 | - |
| 17 | 0.3800/0.0 | |||||||
| 61 | 1.7200/0.0 | |||||||
| KHA [31] | 12 | 0.4962/0.0 | 69.563 | - | 1.0887 | 0.9185 | 69.08 | - |
| 22 | 0.3113/0.0 | |||||||
| 61 | 1.7354/0.0 | |||||||
| SFSA [32] | 11 | 0.5273/0.0 | 69.428 | 0.00518 | 1.0886 | 0.9186 | 69.14 | 5.24E-08 |
| 18 | 0.3805/0.0 | |||||||
| 61 | 1.7198/0.0 | |||||||
| QODELFA | 11 | 0.5267/0.0 | 69.426 | 0.00519 | 1.0887 | 0.9185 | 69.15 | 3.16E-10 |
| 18 | 0.3806/0.0 | |||||||
| 61 | 1.7189/0.0 | |||||||
| Case 1.2: DGs with lagging power factor (PF = 0.95) | ||||||||
| SIMBO-Q [28] | 19 | 0.5656/0.1859 | 23.100 | 0.00075 | 1.0281 | 0.9727 | 89.73 | - |
| 61 | 1.5000/0.4930 | |||||||
| 64 | 0.4220/0.1387 | |||||||
| QOSIMBO-Q [28] | 17 | 0.5828/0.1916 | 22.800 | 0.00069 | 1.0266 | 0.9741 | 89.87 | - |
| 61 | 1.5000/0.4930 | |||||||
| 64 | 0.4272/0.1404 | |||||||
| SFSA [32] | 11 | 0.5435/0.1786 | 20.727 | 0.00033 | 1.0234 | 0.9772 | 90.79 | 6.51E-06 |
| 17 | 0.4132/0.1358 | |||||||
| 61 | 1.8728/0.6156 | |||||||
| QODELFA | 11 | 0.5597/0.1839 | 20.716 | 0.00027 | 1.0235 | 0.9770 | 90.79 | 4.33E-08 |
| 18 | 0.4172/0.1371 | |||||||
| 61 | 1.8775/0.6171 | |||||||
| Case 1.3: DGs with lagging power factor (PF = 0.82) | ||||||||
| IA [39] | 17 | 0.5100/0.3560 | 4.950 | - | - | - | 97.74 | - |
| 50 | 0.6798/0.4745 | |||||||
| 61 | 1.6999/1.1865 | |||||||
| QODELFA | 11 | 0.4986/0.3480 | 4.286 | 0.00012 | 1.0234 | 0.9771 | 98.09 | 1.84E-05 |
| 18 | 0.3762/0.2559 | |||||||
| 61 | 1.6869/1.1774 | |||||||
| Technique | Optimal Locations | Optimal Sizes (MW/MVAr) | APL (kW) | VD (p.u.) | VSI−1 (p.u.) | VSI (p.u.) | LR% | SD |
|---|---|---|---|---|---|---|---|---|
| Case 2.1: DGs with unity power factor (PF = 1) | ||||||||
| SIMBO-Q [28] | 16 | 0.7693/0.0 | 78.100 | 0.00100 | - | - | 65.29 | - |
| 59 | 0.7233/0.0 | |||||||
| 61 | 1.4597/0.0 | |||||||
| QOSIMBO-Q [28] | 18 | 0.6987/0.0 | 77.400 | 0.00100 | - | - | 65.6 | - |
| 59 | 0.7037/0.0 | |||||||
| 61 | 1.5000/0.0 | |||||||
| QODELFA | 11 | 0.6616/0.0 | 72.154 | 0.00150 | 1.0535 | 0.9492 | 67.93 | 4.17E-05 |
| 20 | 0.4554/0.0 | |||||||
| 61 | 1.9201/0.0 | |||||||
| Case 2.2: DGs with lagging power factor (PF = 0.95) | ||||||||
| SIMBO-Q [28] | 14 | 0.7976/0.2622 | 25.900 | 0.00020 | - | - | 88.48 | - |
| 61 | 0.6549/0.2153 | |||||||
| 62 | 1.3615/0.4475 | |||||||
| QOSIMBO-Q [28] | 14 | 0.8167/0.2685 | 24.600 | 0.00020 | - | - | 89.06 | - |
| 61 | 1.5000/0.4930 | |||||||
| 64 | 0.4615/0.1517 | |||||||
| QODELFA | 11 | 0.5859/0.1926 | 20.806 | 0.00014 | 1.0235 | 0.9770 | 90.75 | 3.21E-04 |
| 18 | 0.4359/0.1433 | |||||||
| 61 | 1.9080/0.6272 | |||||||
| Case 2.3: DGs with lagging power factor (PF = 0.82) | ||||||||
| QODELFA | 11 | 0.5077/0.3544 | 4.302 | 0.00010 | 1.0234 | 0.9771 | 98.08 | 2.96E-04 |
| 18 | 0.3875/0.2593 | |||||||
| 61 | 1.6959/1.1837 | |||||||
| Technique | Optimal Locations | Optimal Sizes (MW/MVAr) | APL (kW) | VD (p.u.) | VSI−1 (p.u.) | VSI (p.u.) | LR% | SD |
|---|---|---|---|---|---|---|---|---|
| Case 3.1: DGs with unity power factor (PF = 1) | ||||||||
| SIMBO-Q [28] | 15 | 0.7722/0.0 | 80.000 | 0.00070 | 1.0235 | 0.9770 | 64.44 | - |
| 61 | 1.3526/0.0 | |||||||
| 62 | 0.8232/0.0 | |||||||
| QOSIMBO-Q [28] | 15 | 0.7754/0.0 | 79.700 | 0.00070 | 1.0237 | 0.9770 | 64.58 | - |
| 61 | 1.4385/0.0 | |||||||
| 63 | 0.7235/0.0 | |||||||
| SFSA [32] | 11 | 0.5703/0.0 | 72.445 | 0.00143 | 1.0485 | 0.9537 | 67.80 | 3.80E-05 |
| 19 | 0.4661/0.0 | |||||||
| 61 | 1.9674/0.0 | |||||||
| QODELFA | 11 | 0.6294/0.0 | 72.295 | 0.00150 | 1.0499 | 0.9525 | 67.87 | 2.12E-05 |
| 20 | 0.4386/0.0 | |||||||
| 61 | 1.9537/0.0 | |||||||
| Case 3.2: DGs with lagging power factor (PF = 0.95) | ||||||||
| SIMBO-Q [28] | 15 | 0.5380/0.1768 | 30.900 | 0.00020 | 1.0233 | 0.9772 | 86.27 | - |
| 56 | 1.2817/0.4213 | |||||||
| 62 | 1.5000/0.4930 | |||||||
| QOSIMBO-Q [28] | 14 | 0.8276/0.2720 | 25.700 | 0.00020 | 1.0234 | 0.9771 | 88.58 | - |
| 60 | 0.5339/0.1755 | |||||||
| 61 | 1.5000/0.4930 | |||||||
| SFSA [32] | 11 | 0.5804/0.1908 | 20.774 | 0.00016 | 1.0234 | 0.9772 | 90.77 | 1.10E-04 |
| 18 | 0.4344/0.1428 | |||||||
| 61 | 1.8992/0.6242 | |||||||
| QODELFA | 11 | 0.5797/0.1905 | 20.774 | 0.00015 | 1.0235 | 0.9770 | 90.77 | 1.24E-04 |
| 18 | 0.4340/0.1426 | |||||||
| 61 | 1.9013/0.6249 | |||||||
| Case 3.3: DGs with lagging power factor (PF = 0.82) | ||||||||
| QODELFA | 11 | 0.5058/0.3531 | 4.297 | 0.00010 | 1.0234 | 0.9771 | 98.09 | 2.27E-04 |
| 18 | 0.3859/0.2589 | |||||||
| 61 | 1.6939/1.1823 | |||||||
| Technique | Optimal Locations | Optimal Sizes (MW/MVAr) | APL (kW) | VD (p.u.) | VSI−1 (p.u.) | VSI (p.u.) | LR% | SD |
|---|---|---|---|---|---|---|---|---|
| Case 1.1: DGs with unity power factor (PF = 1) | ||||||||
| QOTLBO [29] | 24 | 1.2463/0.0 | 576.182 | 0.0629 | 1.2093 | 0.8269 | 55.61 | - |
| 42 | 0.7322/0.0 | |||||||
| 47 | 3.5392/0.0 | |||||||
| 74 | 2.6792/0.0 | |||||||
| 78 | 1.2483/0.0 | |||||||
| 94 | 1.0865/0.0 | |||||||
| 108 | 3.2432/0.0 | |||||||
| KHA [31] | 48 | 1.7242/0.0 | 574.710 | - | 1.2433 | 0.8043 | 55.73 | - |
| 53 | 1.3356/0.0 | |||||||
| 74 | 1.8623/0.0 | |||||||
| 80 | 1.8653/0.0 | |||||||
| 96 | 1.6631/0.0 | |||||||
| 109 | 1.9473/0.0 | |||||||
| 112 | 1.1848/0.0 | |||||||
| SFSA [32] | 21 | 1.3757/0.0 | 525.277 | 0.0612 | 1.2090 | 0.8271 | 59.53 | 6.40E-03 |
| 42 | 1.1997/0.0 | |||||||
| 50 | 2.7418/0.0 | |||||||
| 71 | 2.8915/0.0 | |||||||
| 81 | 1.7025/0.0 | |||||||
| 97 | 1.3321/0.0 | |||||||
| 110 | 2.6674/0.0 | |||||||
| QODELFA | 20 | 1.7908/0.0 | 518.653 | 0.0578 | 1.2129 | 0.8245 | 60.04 | 7.50E-03 |
| 39 | 2.7341/0.0 | |||||||
| 47 | 1.8329/0.0 | |||||||
| 73 | 2.4034/0.0 | |||||||
| 80 | 1.7505/0.0 | |||||||
| 90 | 2.2945/0.0 | |||||||
| 110 | 2.7998/0.0 | |||||||
| Case 1.2: DGs with lagging power factor (PF = 0.866) | ||||||||
| KHA [31] | 43 | 1.9726/1.1389 | 312.661 | - | 1.1393 | 0.8777 | 75.91 | - |
| 51 | 1.9849/1.1460 | |||||||
| 69 | 1.7929/1.0351 | |||||||
| 73 | 1.8551/1.0710 | |||||||
| 88 | 1.8975/1.0955 | |||||||
| 108 | 1.9905/1.1492 | |||||||
| 109 | 1.9951/1.1519 | |||||||
| SFSA [32] | 21 | 1.9351/1.1174 | 155.159 | 0.00861 | 1.1015 | 0.9078 | 88.05 | 1.10E-02 |
| 40 | 2.0810/1.2016 | |||||||
| 50 | 3.1301/1.8074 | |||||||
| 71 | 2.8920/1.6699 | |||||||
| 80 | 2.0541/1.1861 | |||||||
| 96 | 1.3859/0.8003 | |||||||
| 110 | 3.2306/1.8654 | |||||||
| QODELFA | 20 | 1.8771/1.0839 | 148.931 | 0.00860 | 1.1024 | 0.9071 | 88.53 | 2.17E-02 |
| 39 | 3.0909/1.7847 | |||||||
| 46 | 2.1775/1.2573 | |||||||
| 74 | 2.3591/1.3621 | |||||||
| 85 | 1.7023/0.9829 | |||||||
| 90 | 2.4516/1.4156 | |||||||
| 110 | 3.1123/1.7971 | |||||||
| Case 1.3: DGs with lagging power factor (PF = 0.82) | ||||||||
| QODELFA | 20 | 1.7850/1.2459 | 132.787 | 0.00790 | 1.1033 | 0.9064 | 89.77 | 3.42E-03 |
| 39 | 2.9683/2.0719 | |||||||
| 46 | 2.0693/1.4443 | |||||||
| 74 | 2.2927/1.4828 | |||||||
| 85 | 1.7000/1.0798 | |||||||
| 91 | 2.1408/1.4943 | |||||||
| 110 | 2.9738/2.0758 | |||||||
| Technique | Optimal Locations | Optimal Sizes (MW/MVAr) | APL (kW) | VD (p.u.) | VSI−1 (p.u.) | VSI (p.u.) | LR% | SD |
|---|---|---|---|---|---|---|---|---|
| Case 2.1: DGs with unity power factor (PF = 1) | ||||||||
| QODELFA | 20 | 2.0856/0.0 | 536.134 | 0.0365 | 1.1641 | 0.8590 | 58.69 | 6.74E-03 |
| 39 | 3.3381/0.0 | |||||||
| 47 | 2.1249/0.0 | |||||||
| 73 | 2.7940/0.0 | |||||||
| 80 | 2.0369/0.0 | |||||||
| 90 | 2.6069/0.0 | |||||||
| 110 | 3.1877/0.0 | |||||||
| Case 2.2: DGs with lagging power factor (PF = 0.866) | ||||||||
| QODELFA | 20 | 2.0187/1.1656 | 149.215 | 0.0067 | 1.1044 | 0.9055 | 88.50 | 5.39E-03 |
| 39 | 3.2905/1.9000 | |||||||
| 47 | 2.0615/1.1903 | |||||||
| 74 | 2.4092/1.3911 | |||||||
| 85 | 1.7437/1.0069 | |||||||
| 90 | 2.5473/1.4709 | |||||||
| 110 | 3.1775/1.8348 | |||||||
| Case 2.3: DGs with lagging power factor (PF = 0.82) | ||||||||
| QODELFA | 20 | 1.8988/1.3254 | 134.049 | 0.0064 | 1.1045 | 0.9054 | 89.67 | 3.68E-03 |
| 39 | 3.1073/2.1689 | |||||||
| 46 | 2.2465/1.5680 | |||||||
| 74 | 2.3442/1.5137 | |||||||
| 85 | 1.7033/1.1081 | |||||||
| 91 | 2.2008/1.5361 | |||||||
| 110 | 3.0356/2.1189 | |||||||
| Technique | Optimal Locations | Optimal Sizes (MW/MVAr) | APL (kW) | VD (p.u.) | VSI−1 (p.u.) | VSI (p.u.) | LR% | SD |
|---|---|---|---|---|---|---|---|---|
| Case 3.1: DGs with unity power factor (PF = 1) | ||||||||
| QOTLBO [29] | 43 | 1.5880/0.0 | 677.588 | 0.02330 | 1.1372 | 0.8794 | 47.80 | - |
| 49 | 3.8459/0.0 | |||||||
| 54 | 0.9852/0.0 | |||||||
| 74 | 3.1904/0.0 | |||||||
| 80 | 3.1632/0.0 | |||||||
| 94 | 1.9527/0.0 | |||||||
| 111 | 3.6013/0.0 | |||||||
| SFSA [32] | 19 | 2.0313/0.0 | 564.104 | 0.03085 | 1.1420 | 0.8757 | 56.54 | 6.20E-03 |
| 41 | 1.9135/0.0 | |||||||
| 49 | 4.0113/0.0 | |||||||
| 73 | 2.7996/0.0 | |||||||
| 79 | 3.0734/0.0 | |||||||
| 96 | 2.0861/0.0 | |||||||
| 108 | 3.8194/0.0 | |||||||
| SOS [32] | 18 | 3.1920/0.0 | 561.000 | 0.0675 | 1.2032 | 0.8311 | 56.78 | - |
| 39 | 2.7580/0.0 | |||||||
| 48 | 1.2360/0.0 | |||||||
| 66 | 1.4450/0.0 | |||||||
| 74 | 2.0650/0.0 | |||||||
| 80 | 1.9480/0.0 | |||||||
| 110 | 2.6780/0.0 | |||||||
| QODELFA | 20 | 2.1256/0.0 | 554.682 | 0.0297 | 1.1250 | 0.8889 | 57.26 | 6.74E-03 |
| 39 | 3.8797/0.0 | |||||||
| 47 | 2.3173/0.0 | |||||||
| 73 | 2.8518/0.0 | |||||||
| 80 | 2.0957/0.0 | |||||||
| 91 | 2.4212/0.0 | |||||||
| 110 | 3.2376/0.0 | |||||||
| Case 3.2: DGs with lagging power factor (PF = 0.866) | ||||||||
| SFSA [32] | 19 | 1.8454/1.0656 | 176.969 | 0.00852 | 1.0978 | 0.9109 | 86.37 | 1.30E-02 |
| 39 | 2.2060/1.2738 | |||||||
| 50 | 3.6561/2.1111 | |||||||
| 74 | 2.2638/1.3071 | |||||||
| 80 | 2.4474/1.4132 | |||||||
| 90 | 2.0355/1.1753 | |||||||
| 108 | 3.4768/2.0076 | |||||||
| QODELFA | 18 | 2.4594/1.4201 | 156.142 | 0.00670 | 1.1024 | 0.9071 | 87.97 | 2.21E-02 |
| 39 | 3.3315/1.9237 | |||||||
| 47 | 2.1185/1.2233 | |||||||
| 73 | 2.4898/1.4377 | |||||||
| 80 | 1.8385/1.0616 | |||||||
| 91 | 2.3071/1.3322 | |||||||
| 110 | 3.1879/1.8407 | |||||||
| Case 3.3: DGs with lagging power factor (PF = 0.82) | ||||||||
| QODELFA | 20 | 1.9294/1.3467 | 134.978 | 0.00600 | 1.1009 | 0.9083 | 89.60 | 1.84E-02 |
| 39 | 3.1467/2.1964 | |||||||
| 46 | 2.3361/1.6306 | |||||||
| 74 | 2.3503/1.5174 | |||||||
| 85 | 1.7077/1.1109 | |||||||
| 91 | 2.2096/1.5423 | |||||||
| 110 | 3.0441/2.1248 | |||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamil Mahfoud, R.; Sun, Y.; Faisal Alkayem, N.; Haes Alhelou, H.; Siano, P.; Shafie-khah, M. A Novel Combined Evolutionary Algorithm for Optimal Planning of Distributed Generators in Radial Distribution Systems. Appl. Sci. 2019, 9, 3394. https://doi.org/10.3390/app9163394
Jamil Mahfoud R, Sun Y, Faisal Alkayem N, Haes Alhelou H, Siano P, Shafie-khah M. A Novel Combined Evolutionary Algorithm for Optimal Planning of Distributed Generators in Radial Distribution Systems. Applied Sciences. 2019; 9(16):3394. https://doi.org/10.3390/app9163394
Chicago/Turabian StyleJamil Mahfoud, Rabea, Yonghui Sun, Nizar Faisal Alkayem, Hassan Haes Alhelou, Pierluigi Siano, and Miadreza Shafie-khah. 2019. "A Novel Combined Evolutionary Algorithm for Optimal Planning of Distributed Generators in Radial Distribution Systems" Applied Sciences 9, no. 16: 3394. https://doi.org/10.3390/app9163394
APA StyleJamil Mahfoud, R., Sun, Y., Faisal Alkayem, N., Haes Alhelou, H., Siano, P., & Shafie-khah, M. (2019). A Novel Combined Evolutionary Algorithm for Optimal Planning of Distributed Generators in Radial Distribution Systems. Applied Sciences, 9(16), 3394. https://doi.org/10.3390/app9163394









