A Review of Low-Frequency Active Vibration Control of Seat Suspension Systems
Abstract
1. Introduction
2. Seating Systems with Active Suspension
2.1. Experiments with Prototypes
2.1.1. Pneumatic Actuator
2.1.2. Hydraulic Actuator
2.1.3. Electromagnetic Actuator
2.2. Simulation
3. ANN Control
4. Biodynamic Modeling
5. Our Contributions
Identified Research Gaps, Research Questions, and New Directions
- What kind of ANN algorithm can be used to improve the PID control algorithm for active vibration control seating systems?
- How can an unsupervised deeper learning algorithm be used to improve the performance of vibration cancellation in active seating systems?
- How can an ANN algorithm be used to improve the robustness of a control system?
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Krajnak, K. Health effects associated with occupational exposure to hand-arm or whole body vibration. J. Toxicol. Environ. Health Part B 2018, 21, 320–334. [Google Scholar] [CrossRef] [PubMed]
- Coyte, J.L.; Stirling, D.; Du, H.; Ros, M. Seated Whole-Body Vibration Analysis, Technologies, and Modeling: A Survey. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 725–739. [Google Scholar] [CrossRef]
- Tiemessen, I.J.; Hulshof, C.T.; Frings-Dresen, M.H. An overview of strategies to reduce whole-body vibration exposure on drivers: A systematic review. Int. J. Ind. Ergon. 2007, 37, 245–256. [Google Scholar] [CrossRef]
- Slota, G.P.; Granata, K.P.; Madigan, M.L. Effects of seated whole-body vibration on postural control of the trunk during unstable seated balance. Clin. Biomech. 2008, 23, 381–386. [Google Scholar] [CrossRef] [PubMed]
- Burdorf, A.; Swuste, P. The effect of seat suspension on exposure to whole-body vibration of professional drivers. Ann. Occup. Hyg. 1993, 37, 45–55. [Google Scholar] [PubMed]
- Johanning, E. Diagnosis of whole-body vibration related health problems in occupational medicine. J. Low Freq. Noise Vib. Act. Control 2011, 30, 207–220. [Google Scholar] [CrossRef]
- Paddan, G.; Griffin, M.; Griffin, M. Effect of seating on exposures to whole-body vibration in vehicles. J. Sound Vib. 2002, 253, 215–241. [Google Scholar] [CrossRef]
- Toward, M.G.; Griffin, M.J. The transmission of vertical vibration through seats: Influence of the characteristics of the human body. J. Sound Vib. 2011, 330, 6526–6543. [Google Scholar] [CrossRef]
- Wu, X.; Rakheja, S.; Boileau, P.-É. Study of Human-Seat Interactions for Dynamic Seating Comfort Analysis; SAE Technical Paper; SAE International in United States: Warrendale, PA, USA, 1999. [Google Scholar]
- Mozaffarin, A.; Pankoke, S.; Wölfel, H.-P. MEMOSIK V—An active dummy for determining three-directional transfer functions of vehicle seats and vibration exposure ratings for the seated occupant. Int. J. Ind. Ergon. 2008, 38, 471–482. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. Experimental investigation of a vibration isolation system using negative stiffness structure. Int. J. Mech. Sci. 2013, 70, 99–112. [Google Scholar] [CrossRef]
- Maciejewski, I.; Meyer, L.; Krzyzynski, T. Modelling and multi-criteria optimization of passive seat suspension Vibro-isolating properties. J. Sound Vib. 2009, 324, 520–538. [Google Scholar] [CrossRef]
- McManus, S.; Clair, K.S.; Boileau, P.; Boutin, J.; Rakheja, S. Evaluation of vibration and shock attenuation performance of a suspension seat with a semiactive magnetorheological fluid damper. J. Sound Vib. 2002, 253, 313–327. [Google Scholar] [CrossRef]
- Bai, X.-X.; Jiang, P.; Qian, L.-J. Integrated semiactive seat suspension for both longitudinal and vertical vibration isolation. J. Intell. Mater. Syst. Struct. 2017, 28, 1036–1049. [Google Scholar] [CrossRef]
- Li, W.; Zhang, X.; Du, H. Development and simulation evaluation of a magnetorheological elastomer isolator for seat vibration control. J. Intell. Mater. Syst. Struct. 2012, 23, 1041–1048. [Google Scholar] [CrossRef]
- Sireteanu, T.; Stancioiu, D.; Stammers, C.W. Use of magnetorheological fluid dampers in semi-active driver seat vibration control. In Proceedings of the ACTIVE 2002, Southampton, UK, 15–17 July 2002. [Google Scholar]
- Choi, S.-B.; Han, Y.-M. Vibration control of electrorheological seat suspension with a human-body model using sliding mode control. J. Sound Vib. 2007, 303, 391–404. [Google Scholar] [CrossRef]
- Lee, C.-M.; Bogatchenkov, A.; Goverdovskiy, V.; Shynkarenko, Y.; Temnikov, A. Position control of seat suspension with minimum stiffness. J. Sound Vib. 2006, 292, 435–442. [Google Scholar] [CrossRef]
- Kim, J.H.; Marin, L.S.; Dennerlein, J.T. Evaluation of commercially available seat suspensions to reduce whole body vibration exposures in mining heavy equipment vehicle operators. Appl. Ergon. 2018, 71, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Ning, D.; Sun, S.; Yu, J.; Zheng, M.; Du, H.; Zhang, N.; Li, W. A rotary variable admittance device and its application in vehicle seat suspension vibration control. J. Frankl. Inst. 2019. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Du, H.; Li, W.; Zhang, N. Vibration control of an energy regenerative seat suspension with variable external resistance. Mech. Syst. Signal Process. 2018, 106, 94–113. [Google Scholar] [CrossRef]
- Choi, S.-B.; Lee, B.; Nam, M.H.; Cheong, C. Vibration control of an MR seat damper for commercial vehicles. J. Intell. Mater. Syst. Struct. 2000, 11, 936–944. [Google Scholar] [CrossRef]
- Han, Y.M.; Nam, M.H.; Han, S.S.; Lee, H.G.; Choi, S.B.; Choi, S. Vibration Control Evaluation of a Commercial Vehicle Featuring MR Seat Damper. J. Intell. Mater. Syst. Struct. 2002, 13, 575–579. [Google Scholar] [CrossRef]
- Song, X.; Ahmadian, M. Study of Semiactive Adaptive Control Algorithms with Magneto-Rheological Seat Suspension; SAE Technical Paper; SAE International in United States: Warrendale, PA, USA, 2004. [Google Scholar]
- Jung, J.Y.; Choi, S.B.; Wereley, N.M.; Han, Y.M.; Choi, Y.T. Ride quality investigation of an electrorheological seat suspension to minimize human body vibrations. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2006, 220, 139–150. [Google Scholar]
- Zhao, Y.; Zhao, L.; Gao, H. Vibration Control of Seat Suspension using H∞ Reliable Control. J. Vib. Control 2010, 16, 1859–1879. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, W.; Gao, H. Robust control synthesis for seat suspension systems with actuator saturation and time-varying input delay. J. Sound Vib. 2010, 329, 4335–4353. [Google Scholar] [CrossRef]
- Choi, S.-B.; Lee, Y.-S.; Han, M.-S.; Phu, D.X. Vibration control of a vehicle’s seat suspension featuring a magnetorheological damper based on a new adaptive fuzzy sliding-mode controller. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2015, 230, 437–458. [Google Scholar]
- Gao, H.; Zhao, Y.; Sun, W. Input-Delayed Control of Uncertain Seat Suspension Systems with Human-Body Model. IEEE Trans. Control Syst. Technol. 2010, 18, 591–601. [Google Scholar] [CrossRef]
- Yao, H.J.; Fu, J.; Yu, M.; Peng, Y.X. Semi-active control of seat suspension with MR damper. J. Phys. Conf. Ser. 2013, 412, 012054. [Google Scholar] [CrossRef]
- Ning, D.; Du, H.; Sun, S.; Li, W.; Zhang, N.; Dong, M. A novel electrical variable stiffness device for vehicle seat suspension control with mismatched disturbance compensation. IEEE/ASME Trans. Mechatron. 2019. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Du, H.; Li, W.; Zhang, N.; Zheng, M.; Luo, L. An electromagnetic variable inertance device for seat suspension vibration control. Mech. Syst. Signal Process. 2019, 133, 106259. [Google Scholar] [CrossRef]
- Wu, X.; Griffin, M. A semi-active control policy to reduce the occurrence and severity of end-stop impacts in a suspension seat with an electrorheological fluid damper. J. Sound Vib. 1997, 203, 781–793. [Google Scholar] [CrossRef]
- Sathishkumar, P.; Jancirani, J.; John, D. Reducing the seat vibration of vehicle by semi active force control technique. J. Mech. Sci. Technol. 2014, 28, 473–479. [Google Scholar] [CrossRef]
- Metered, H.; Šika, Z. Vibration control of a semi-active seat suspension system using magnetorheological damper. In Proceedings of the 2014 IEEE/ASME 10th International Conference on Mechatronic and Embedded Systems and Applications (MESA), Senigallia, Italy, 10–12 September 2014; pp. 1–7. [Google Scholar]
- Huseinbegovic, S.; Tanovic, O. Adjusting stiffness of air spring and damping of oil damper using a fuzzy controller for vehicle seat vibration isolation. In Proceedings of the 2009 International Siberian Conference on Control and Communications, Tomsk, Russia, 27–28 March 2009; pp. 83–92. [Google Scholar]
- Kawana, M.; Shimogo, T. Active Suspension of Truck Seat. Shock Vib. 1998, 5, 35–41. [Google Scholar] [CrossRef]
- Choi, Y.-T.; Wereley, N.M. Mitigation of biodynamic response to vibratory and blast-induced shock loads using magnetorheological seat suspensions. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2005, 219, 741–753. [Google Scholar] [CrossRef]
- Sun, S.S.; Ning, D.H.; Yang, J.; Du, H.; Zhang, S.W.; Li, W.H. A seat suspension with a rotary magnetorheological damper for heavy duty vehicles. Smart Mater. Struct. 2016, 25, 105032. [Google Scholar] [CrossRef]
- Park, C.; Jeon, D. Semiactive vibration control of a smart seat with an mr fluid damper considering its time delay. J. Intell. Mater. Syst. Struct. 2002, 13, 521–524. [Google Scholar] [CrossRef]
- Qiang, Z.; Yaxun, Y. Improved single neuron PID control for heavy-duty vehicle magnetorheological seat suspension. In Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; pp. 1–3. [Google Scholar]
- Liu, P.; Xia, X.; Zhang, N.; Ning, D.; Zheng, M. Torque response characteristics of a controllable electromagnetic damper for seat suspension vibration control. Mech. Syst. Signal Process. 2019, 133, 106238. [Google Scholar] [CrossRef]
- Phu, D.X.; Shin, D.K.; Choi, S.-B. Design of a new adaptive fuzzy controller and its application to vibration control of a vehicle seat installed with an MR damper. Smart Mater. Struct. 2015, 24, 85012. [Google Scholar] [CrossRef]
- Phu, D.X.; An, J.-H.; Choi, S.-B. A Novel Adaptive PID Controller with Application to Vibration Control of a Semi-Active Vehicle Seat Suspension. Appl. Sci. 2017, 7, 1055. [Google Scholar] [CrossRef]
- Phu, D.X.; Choi, S.-M.; Choi, S.-B. A new adaptive hybrid controller for vibration control of a vehicle seat suspension featuring MR damper. J. Vib. Control 2017, 23, 3392–3413. [Google Scholar] [CrossRef]
- Nguyen, S.D.; Nguyen, Q.H.; Choi, S.-B. A hybrid clustering based fuzzy structure for vibration control—Part 2: An application to semi-active vehicle seat-suspension system. Mech. Syst. Signal Process. 2015, 56, 288–301. [Google Scholar] [CrossRef]
- Phu, D.X.; Hung, N.Q.; Choi, S.-B. A novel adaptive controller featuring inversely fuzzified values with application to vibration control of magneto-rheological seat suspension system. J. Vib. Control 2017, 24, 5000–5018. [Google Scholar] [CrossRef]
- Guclu, R. Fuzzy Logic Control of Seat Vibrations of a Non-Linear Full Vehicle Model. Nonlinear Dyn. 2005, 40, 21–34. [Google Scholar] [CrossRef]
- Bouazara, M.; Richard, M.; Rakheja, S. Safety and comfort analysis of a 3-D vehicle model with optimal non-linear active seat suspension. J. Terramech. 2006, 43, 97–118. [Google Scholar] [CrossRef]
- Stein, G.J. A Driver’s Seat with Active Suspension of Electro-pneumatic Type. J. Vib. Acoust. 1997, 119, 230–235. [Google Scholar] [CrossRef]
- Stein, G.J. Vibration control system with a proportionally controlled pneumatic actuator. In Proceedings of the 1997 European Control Conference (ECC), Brussels, Belgium, 1–7 July 1997; pp. 1814–1818. [Google Scholar]
- Maciejewski, I.; Meyer, L.; Krzyżyński, T. The vibration damping effectiveness of an active seat suspension system and its robustness to varying mass loading. J. Sound Vib. 2010, 329, 3898–3914. [Google Scholar] [CrossRef]
- Maciejewski, I. Control system design of active seat suspensions. J. Sound Vib. 2012, 331, 1291–1309. [Google Scholar] [CrossRef]
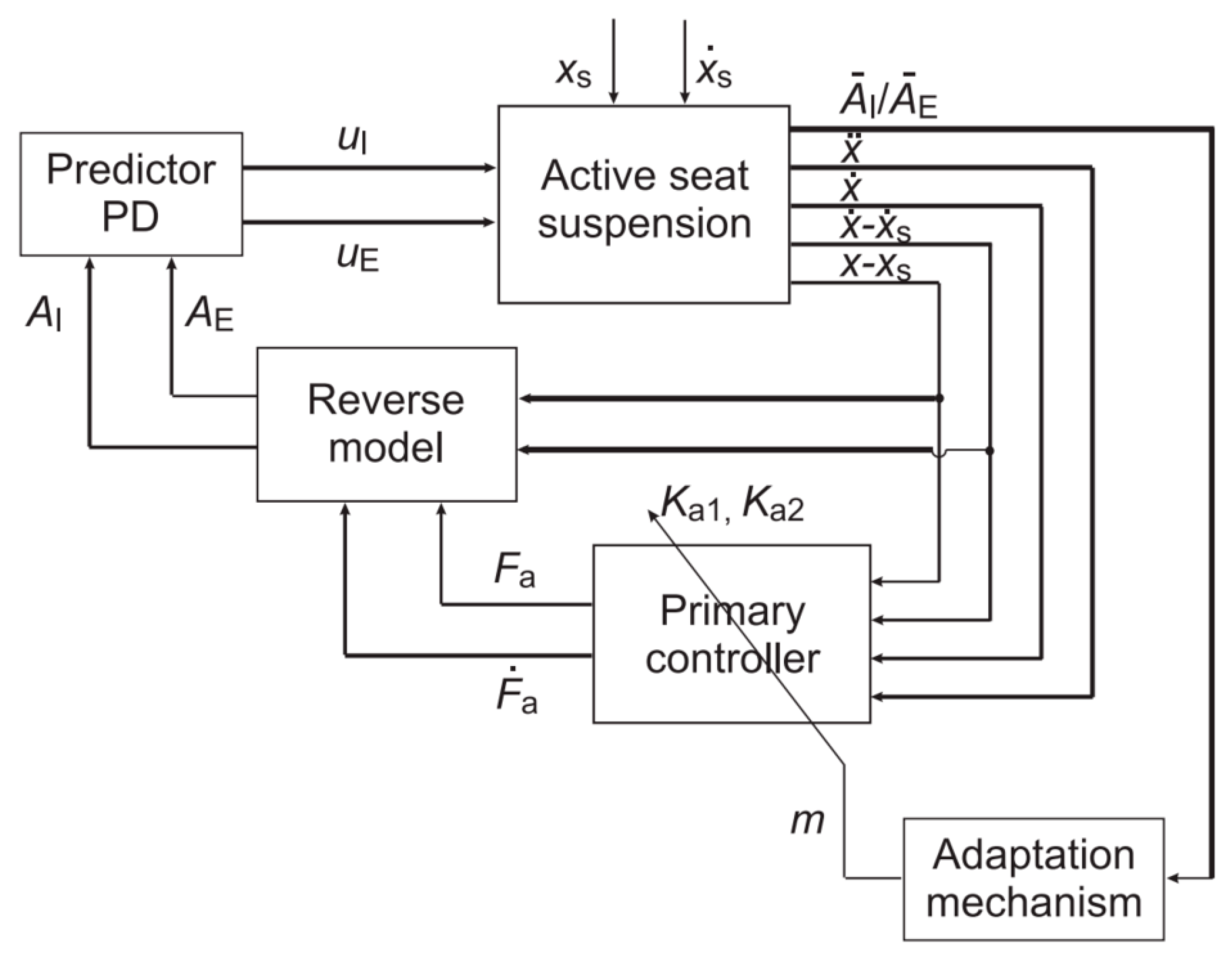
- Maciejewski, I.; Glowinski, S.; Krzyżyński, T. Active control of a seat suspension with the system adaptation to varying load mass. Mechatronics 2014, 24, 1242–1253. [Google Scholar] [CrossRef]
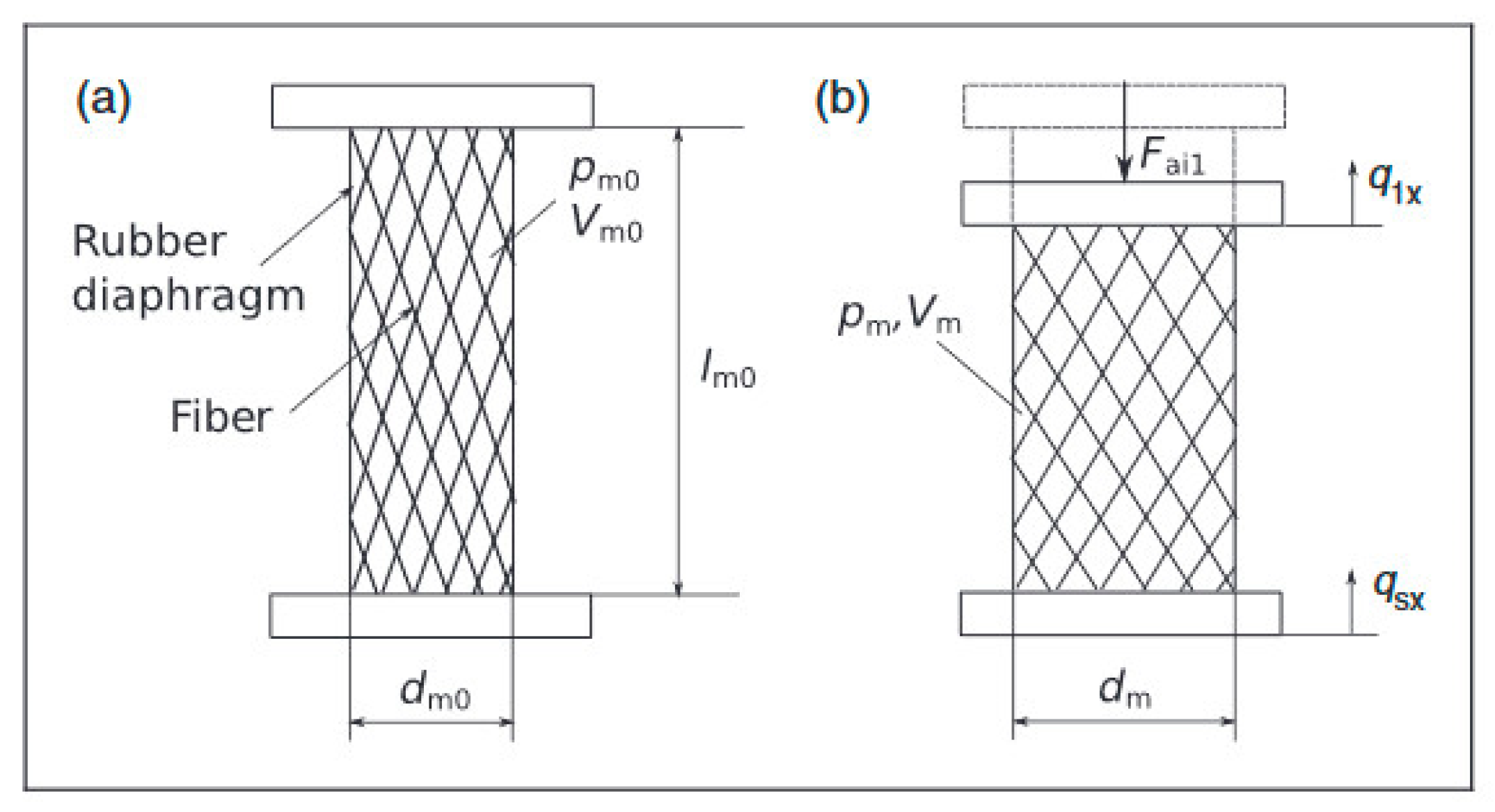
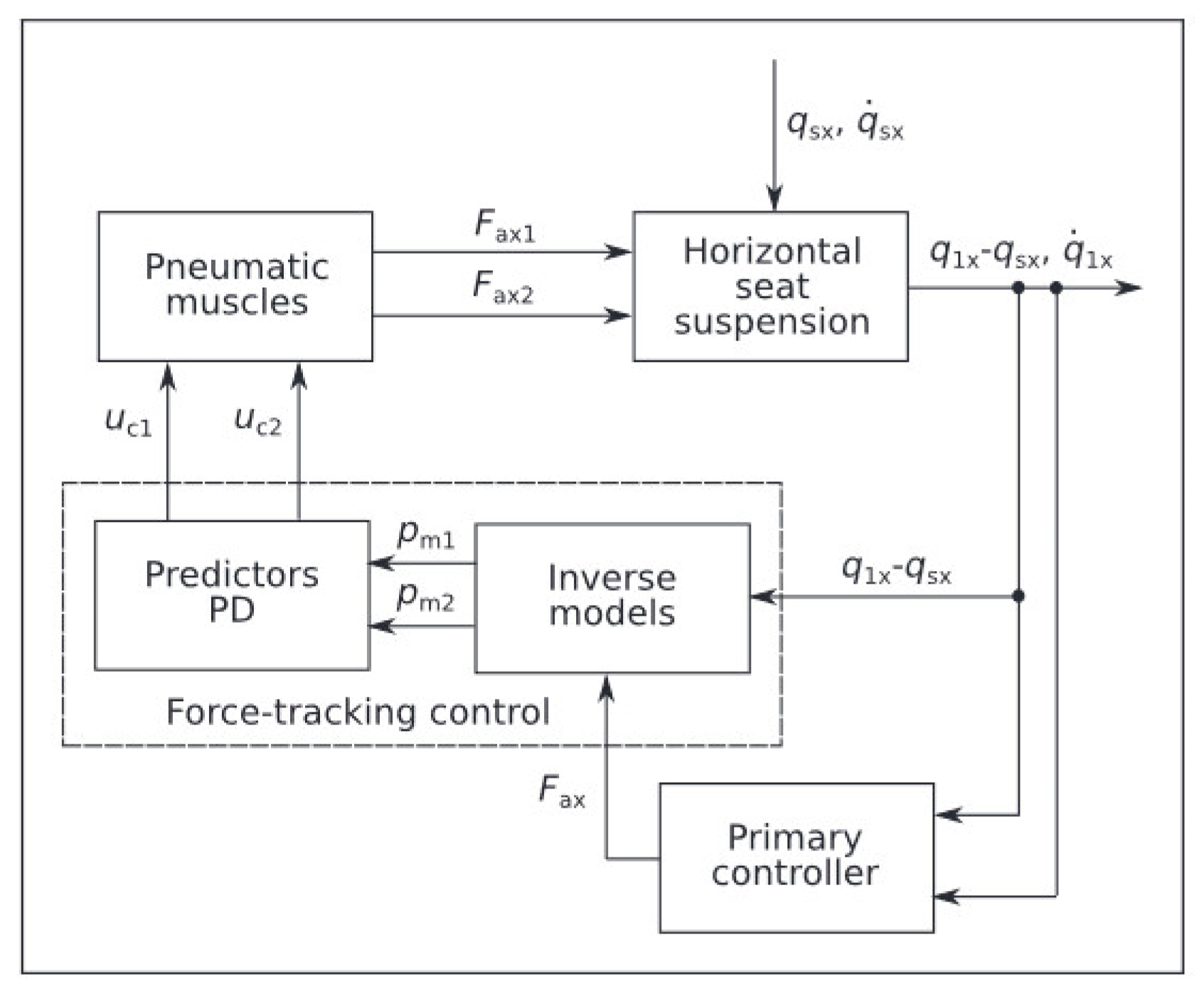
- Maciejewski, I.; Krzyżyński, T.; Meyer, H. Modeling and vibration control of an active horizontal seat suspension with pneumatic muscles. J. Vib. Control 2018, 24, 5938–5950. [Google Scholar] [CrossRef]
- Stein, G.J.; Ballo, I. Active Vibration Control System for the Driver’s Seat for Off-Road Vehicles. Veh. Syst. Dyn. 1991, 20, 57–78. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Zhang, J.; Du, H.; Li, W.; Wang, X. An active seat suspension design for vibration control of heavy-duty vehicles. J. Low Freq. Noise Vib. Act. Control 2016, 35, 264–278. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Li, H.; Du, H.; Li, W. Active control of an innovative seat suspension system with acceleration measurement based friction estimation. J. Sound Vib. 2016, 384, 28–44. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Wei, L.; Zhang, B.; Du, H.; Li, W. Vibration reduction of seat suspension using observer based terminal sliding mode control with acceleration data fusion. Mechatronics 2017, 44, 71–83. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Zhang, F.; Du, H.; Li, W.; Zhang, B. Disturbance observer based Takagi-Sugeno fuzzy control for an active seat suspension. Mech. Syst. Signal Process. 2017, 93, 515–530. [Google Scholar] [CrossRef]
- Ning, D.; Sun, S.; Du, H.; Li, W.; Li, W. Control of a multiple-DOF vehicle seat suspension with a roll and vertical vibration. J. Sound Vib. 2018, 435, 170–191. [Google Scholar] [CrossRef]
- Ning, D.; Du, H.; Sun, S.; Li, W.; Zhang, B. An Innovative Two-Layer Multiple-DOF Seat Suspension for Vehicle Whole Body Vibration Control. IEEE/ASME Trans. Mechatron. 2018, 23, 1787–1799. [Google Scholar] [CrossRef]
- Gan, Z.; Hillis, A.J.; Darling, J. Adaptive control of an active seat for occupant vibration reduction. J. Sound Vib. 2015, 349, 39–55. [Google Scholar] [CrossRef]
- Frechin, M.M.; Ariño, S.B.; Fontaine, J. ACTISEAT: Active vehicle seat for acceleration compensation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2004, 218, 925–933. [Google Scholar] [CrossRef]
- Du, H.; Li, W.; Zhang, N. Vibration Control of Vehicle Seat Integrating with Chassis Suspension and Driver Body Model. Adv. Struct. Eng. 2013, 16, 1–9. [Google Scholar] [CrossRef]
- Wang, L.; Kazmierski, T. VHDL-AMS modeling of an automotive vibration isolation seating system. In Proceedings of the IASTED International Conference on Circuits, Signals, and Systems (CSS 2005), Marina Del Rey, CA, USA, 24–26 October 2005. [Google Scholar]
- Al-Junaid, H.; Kazmierski, T.; Wang, L. SystemC-A Modeling of an Automotive Seating Vibration Isolation System. In Proceedings of the Forum on Specification and Design Languages (FDL 2006), Darmstadt, Germany, 19–22 September 2006. [Google Scholar]
- Wang, X.; Bi, F.; Du, H. Reduction of low-frequency vibration of a truck driver and seating system through system parameter identification, sensitivity analysis, and active control. Mech. Syst. Signal Process. 2018, 105, 16–35. [Google Scholar] [CrossRef]
- Ali, S.A.; Metered, H.; Bassiuny, A.M.; Abdel-Ghany, A. Vibration Control of an Active Seat Suspension System Integrated Pregnant Woman Body Model; SAE Technical Paper; SAE International in United States: Warrendale, PA, USA, 2019. [Google Scholar]
- Wu, J.-D.; Chen, R.-J. Application of an active controller for reducing small-amplitude vertical vibration in a vehicle seat. J. Sound Vib. 2004, 274, 939–951. [Google Scholar] [CrossRef]
- Sun, W.; Li, J.; Zhao, Y.; Gao, H. Vibration control for active seat suspension systems via dynamic output feedback with limited frequency characteristic. Mechatronics 2011, 21, 250–260. [Google Scholar] [CrossRef]
- Du, H.; Li, W.; Zhang, N. Integrated Seat and Suspension Control for a Quarter Car With Driver Model. IEEE Trans. Veh. Technol. 2012, 61, 3893–3908. [Google Scholar]
- Guclu, R.; Gulez, K. Neural network control of seat vibrations of a non-linear full vehicle model using PMSM. Math. Comput. Model. 2008, 47, 1356–1371. [Google Scholar] [CrossRef]
- Tahmasebi, M.; Gohari, M. Active Off-Road Seat Suspension System Using Intelligent Active Force Control. J. Low Freq. Noise Vib. Act. Control 2015, 34, 475–489. [Google Scholar]

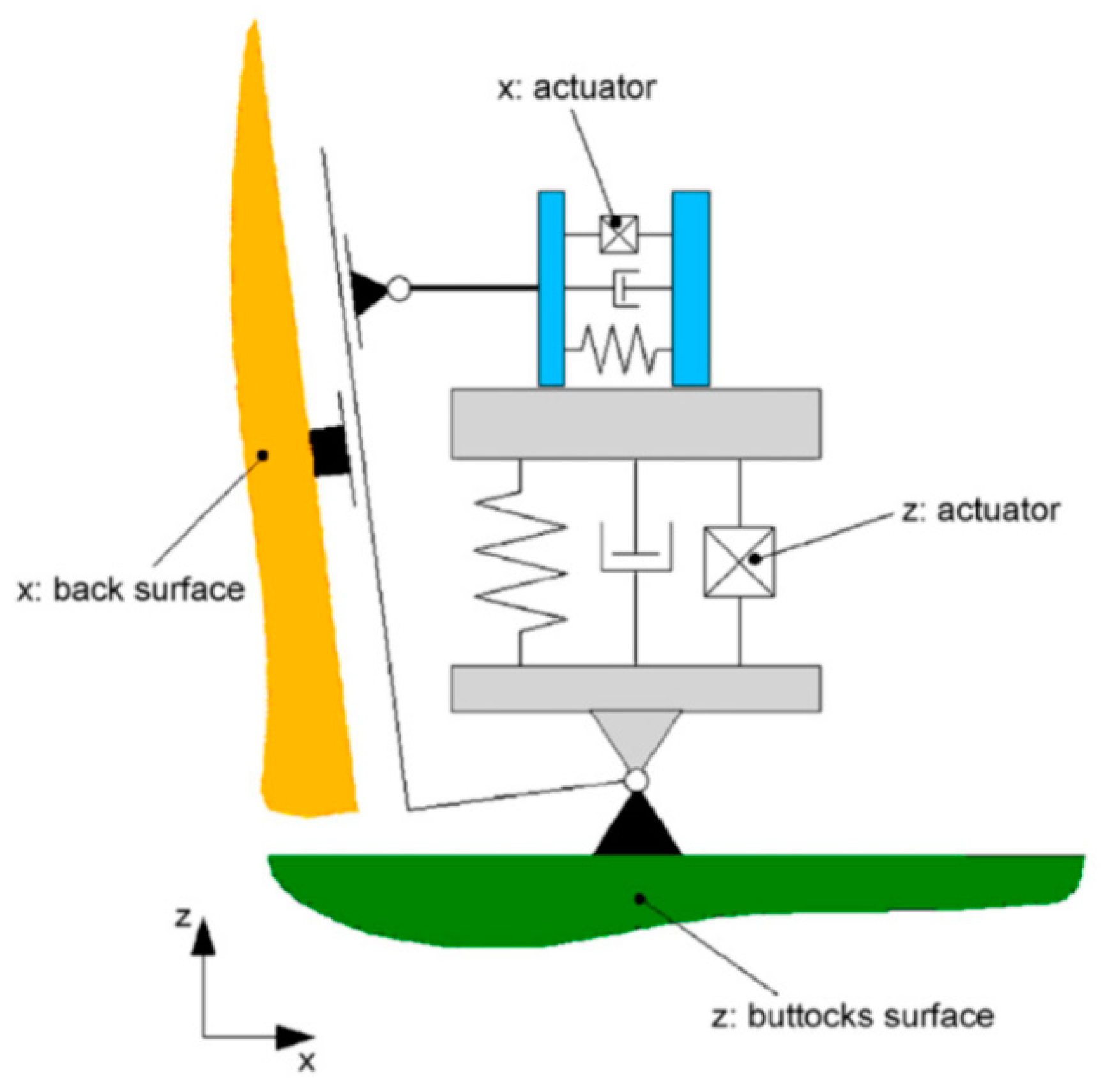
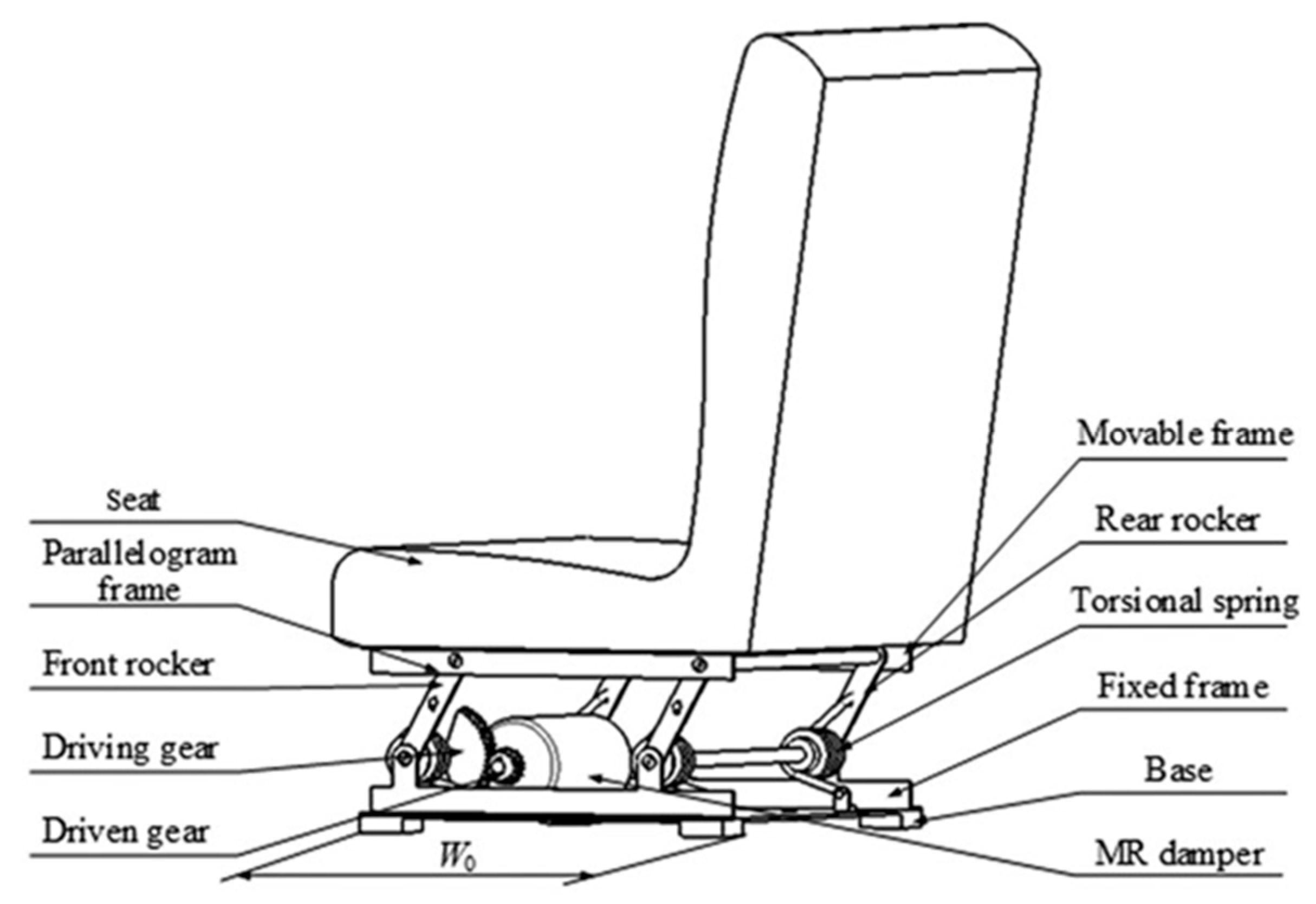
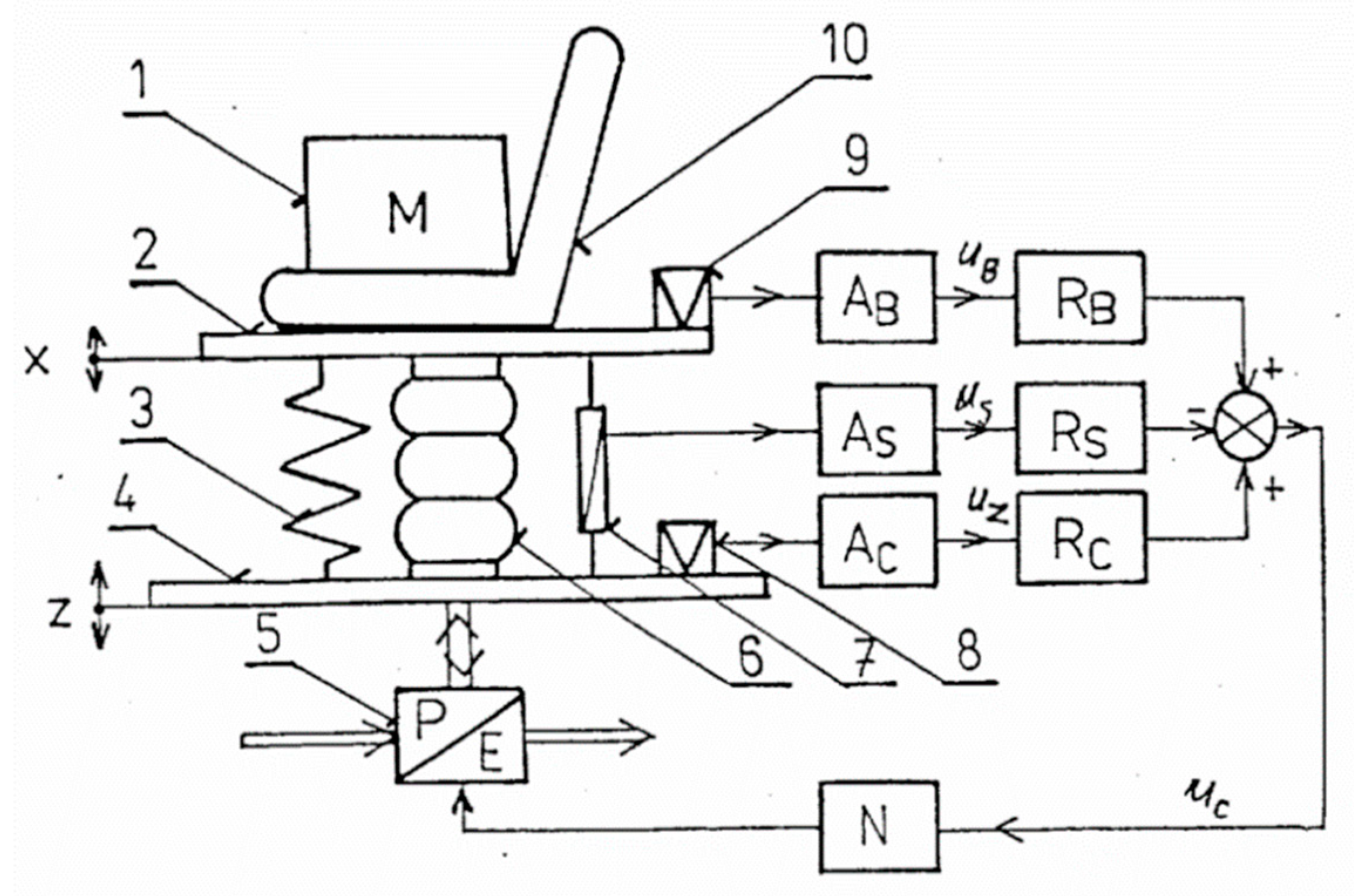
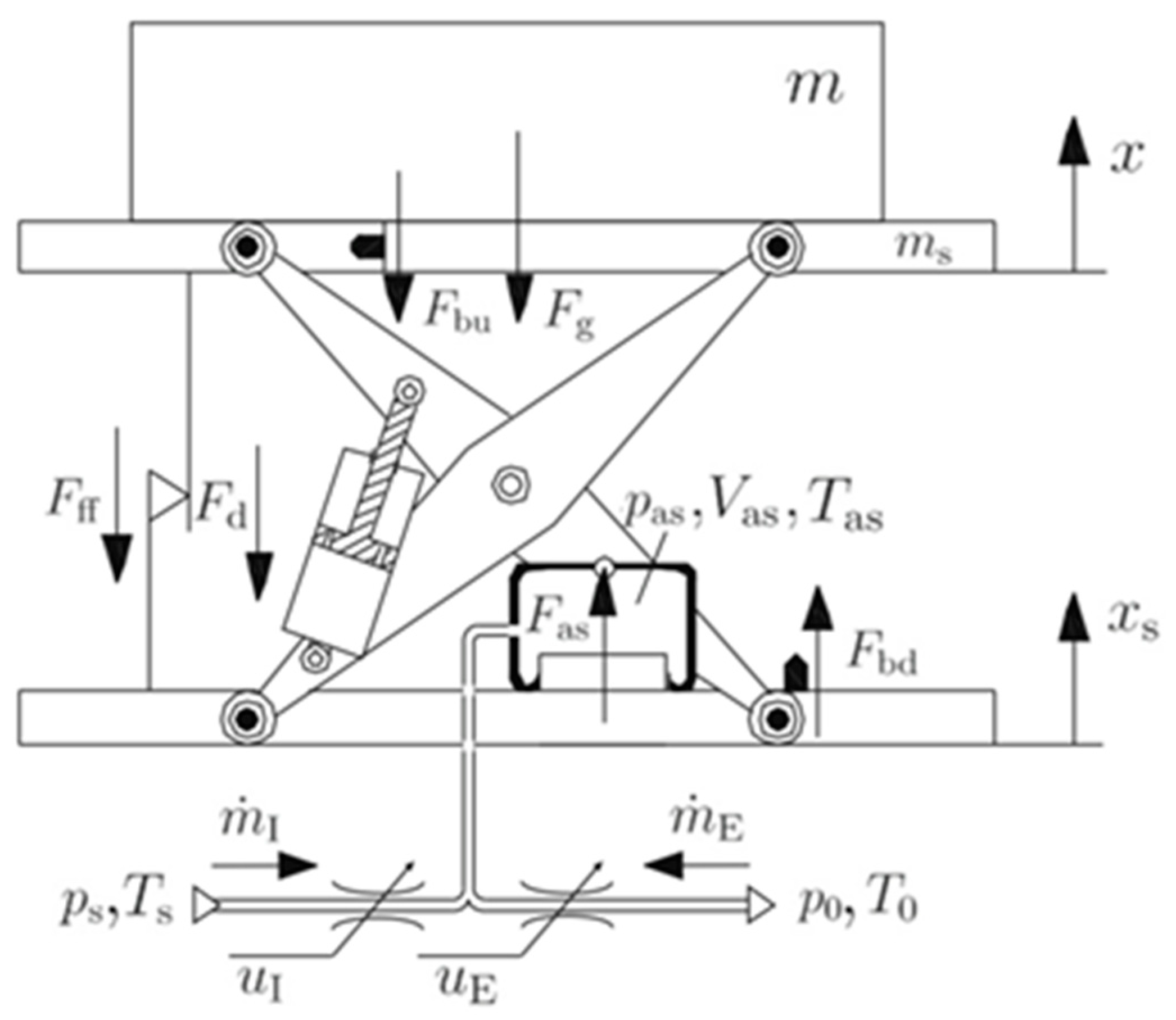
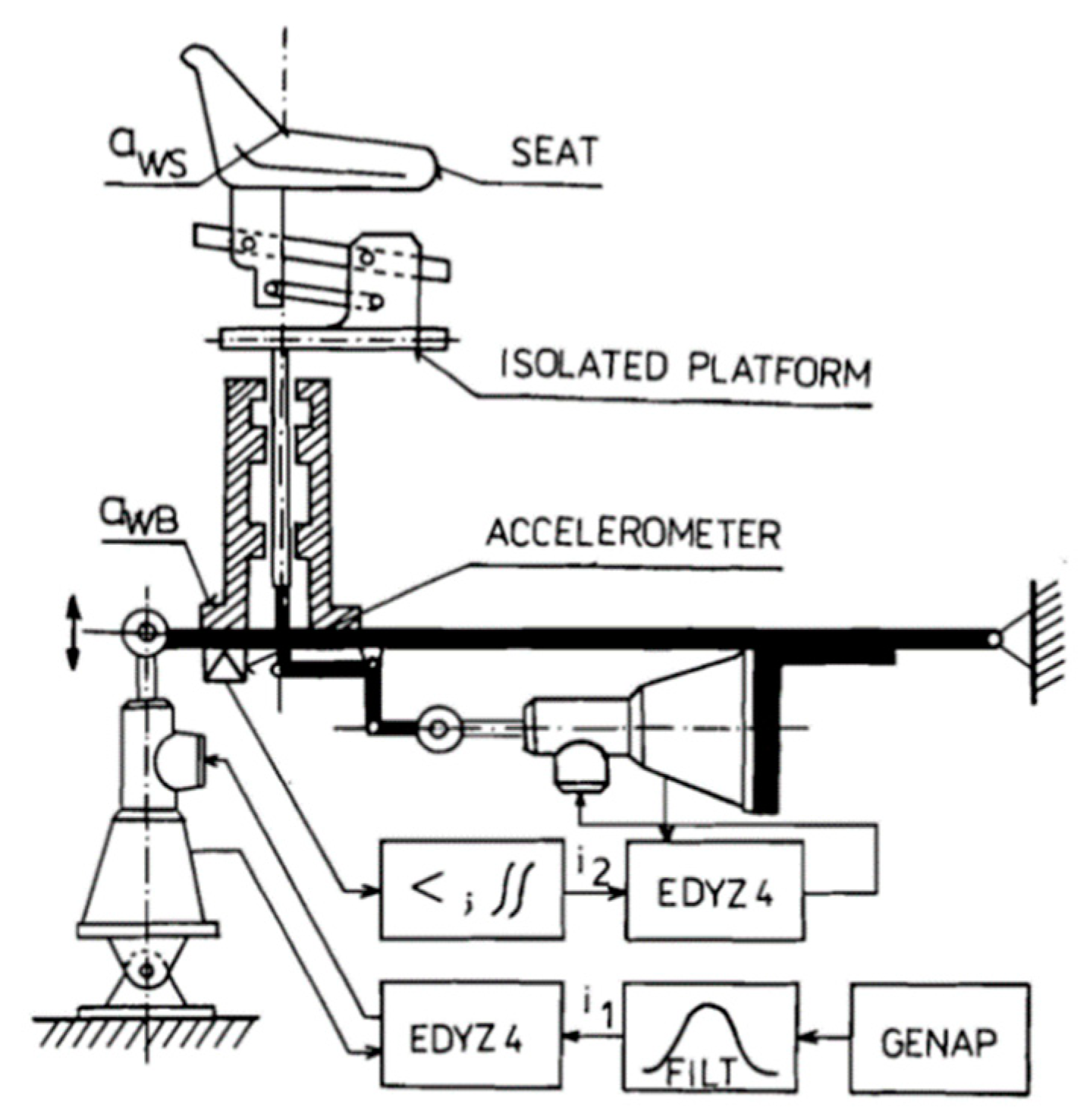
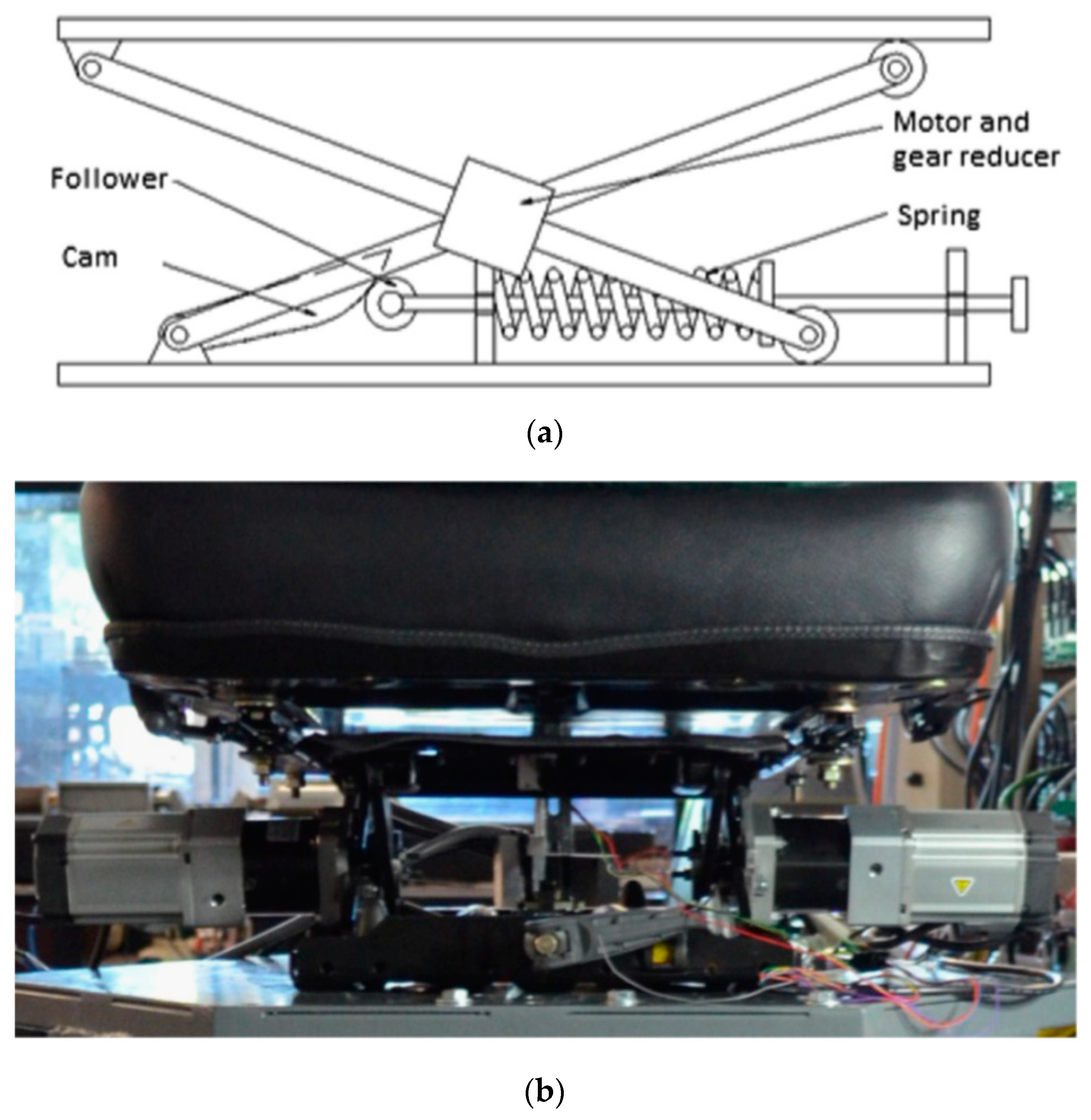
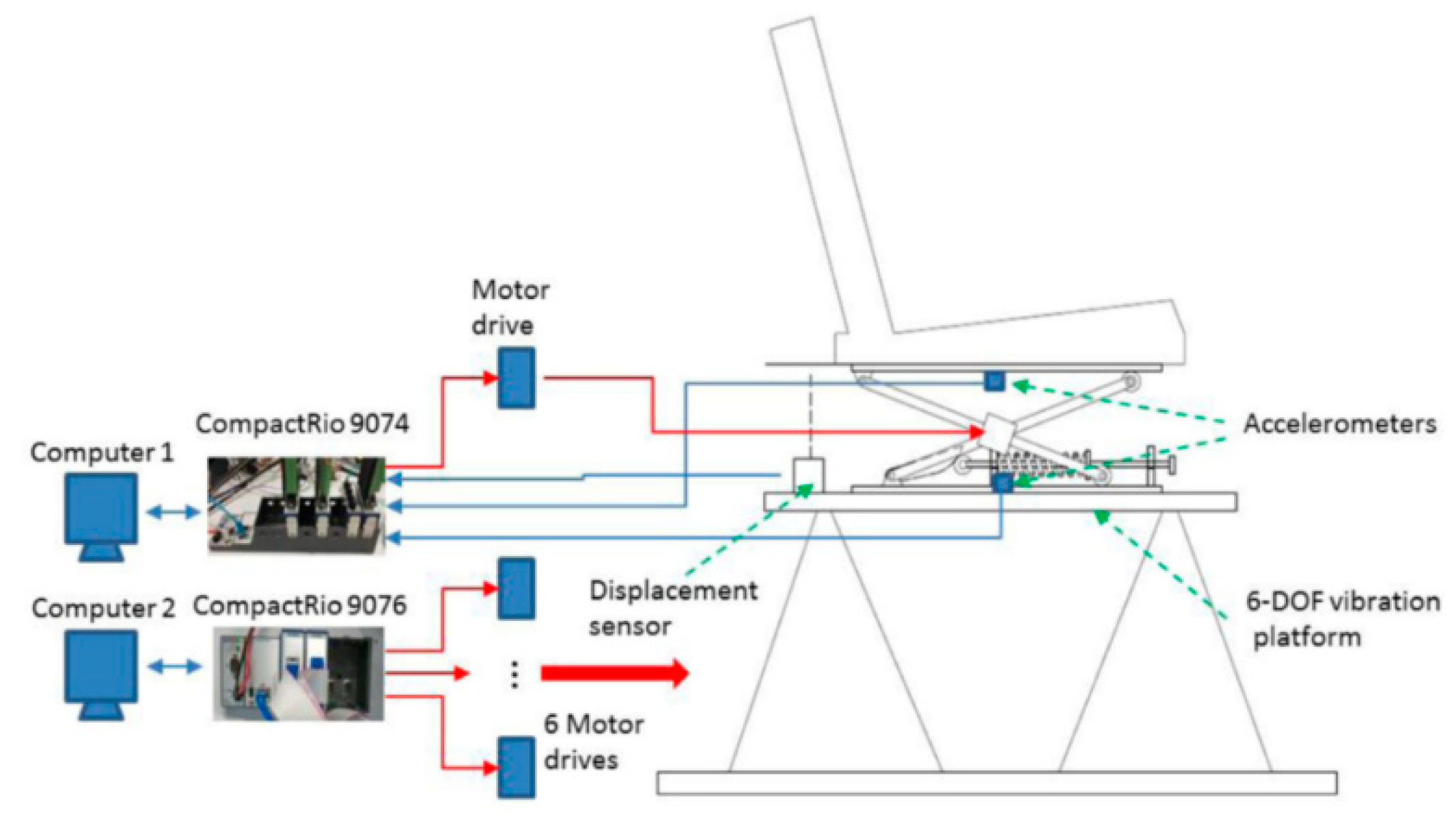
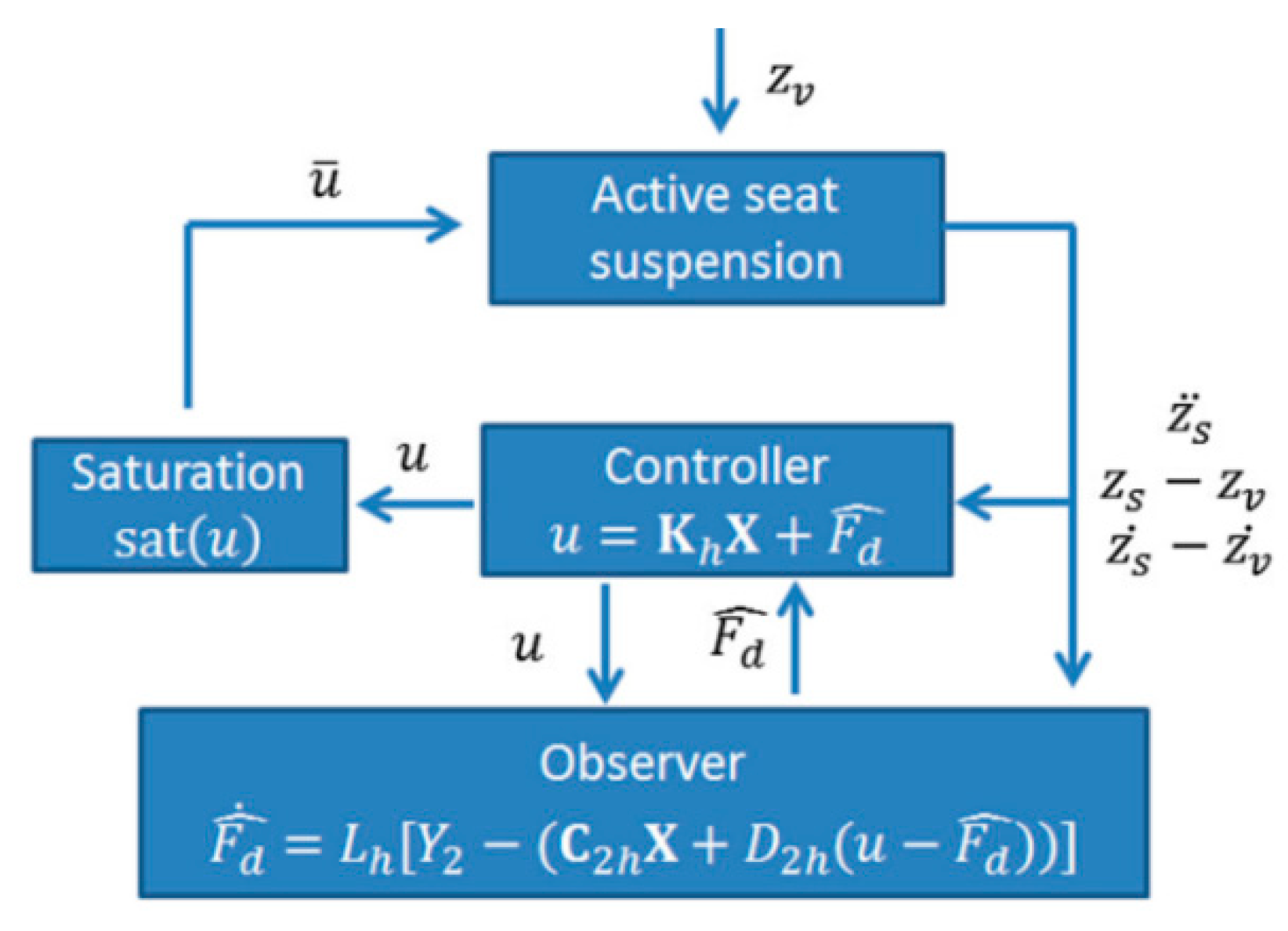

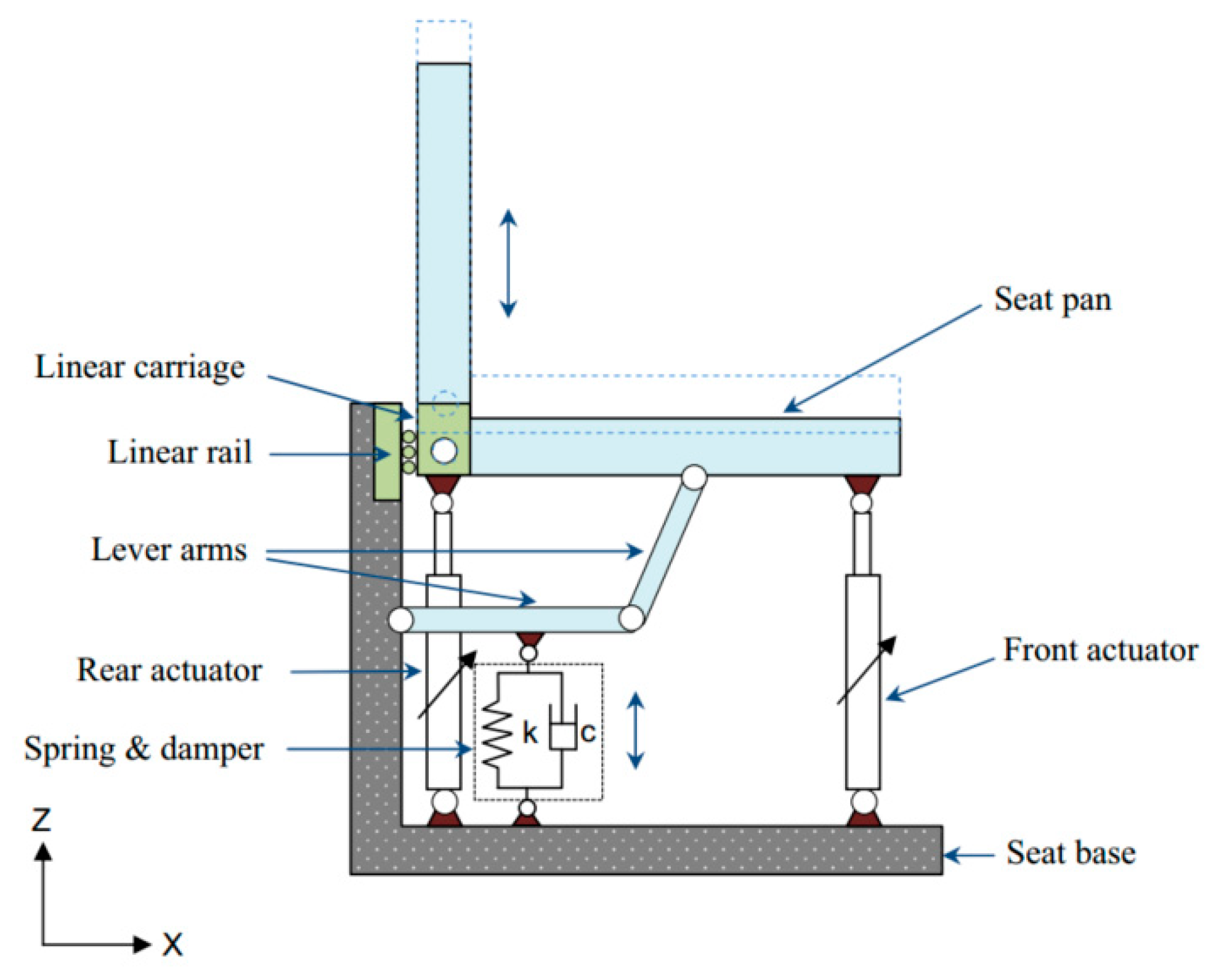
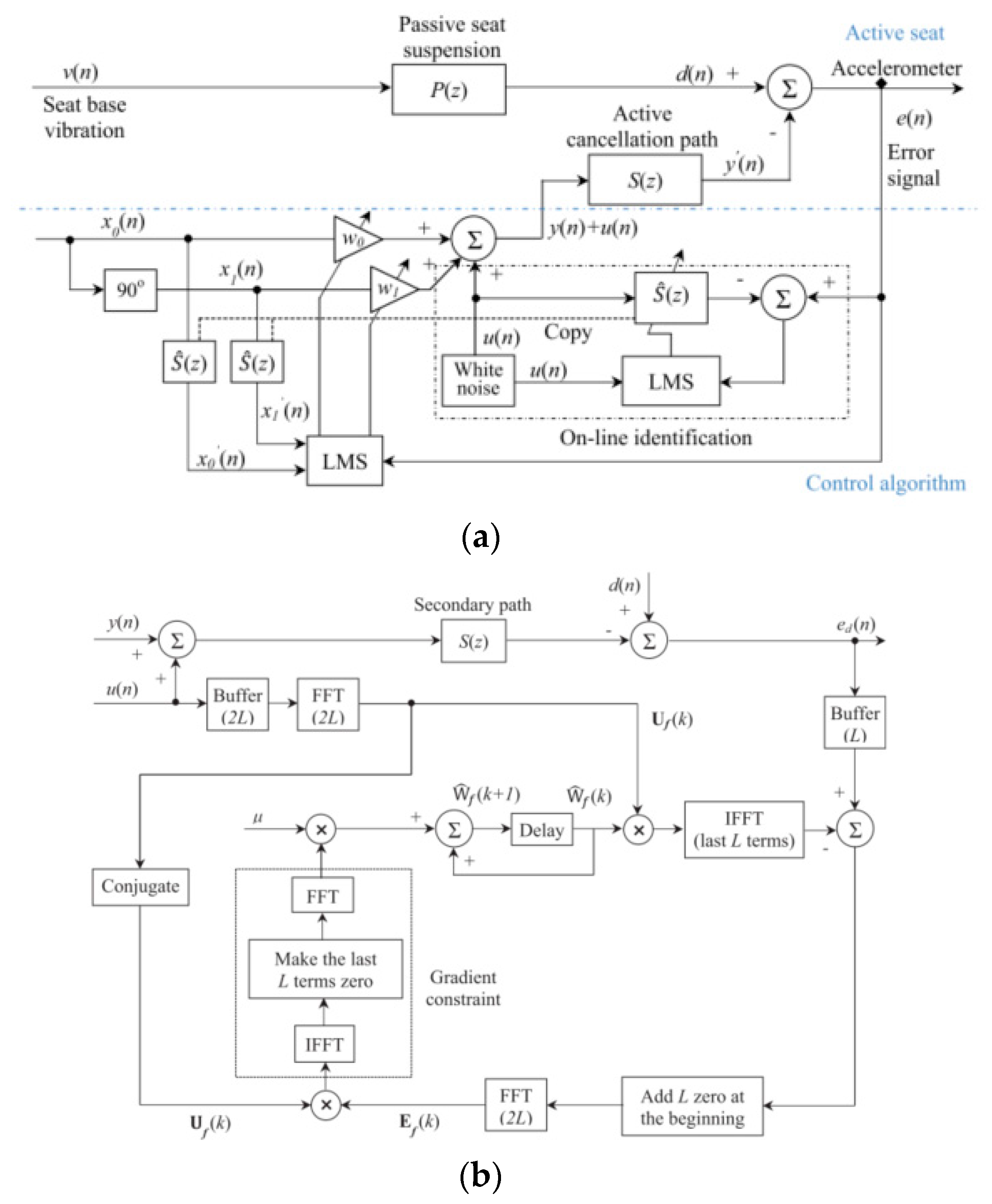
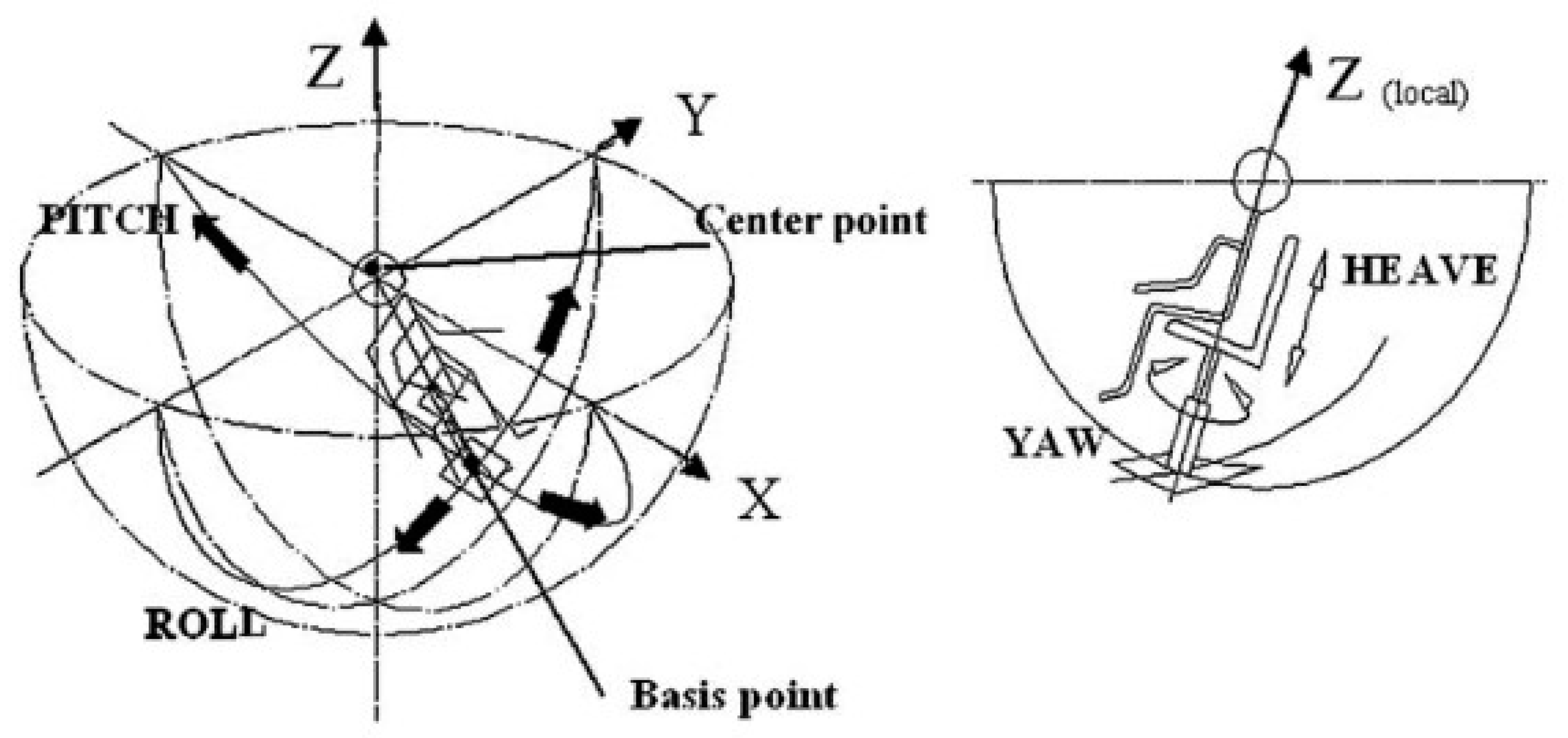
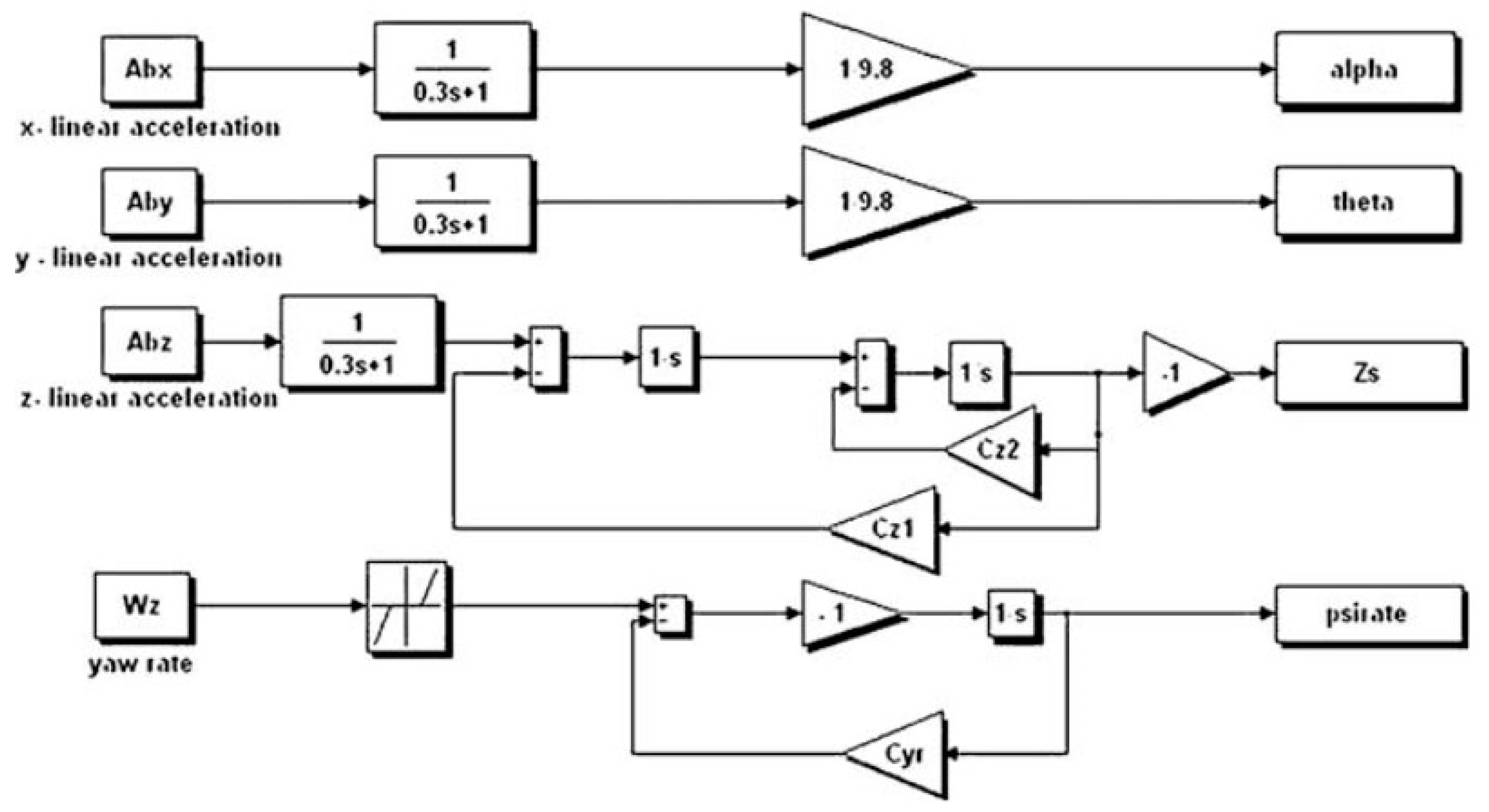
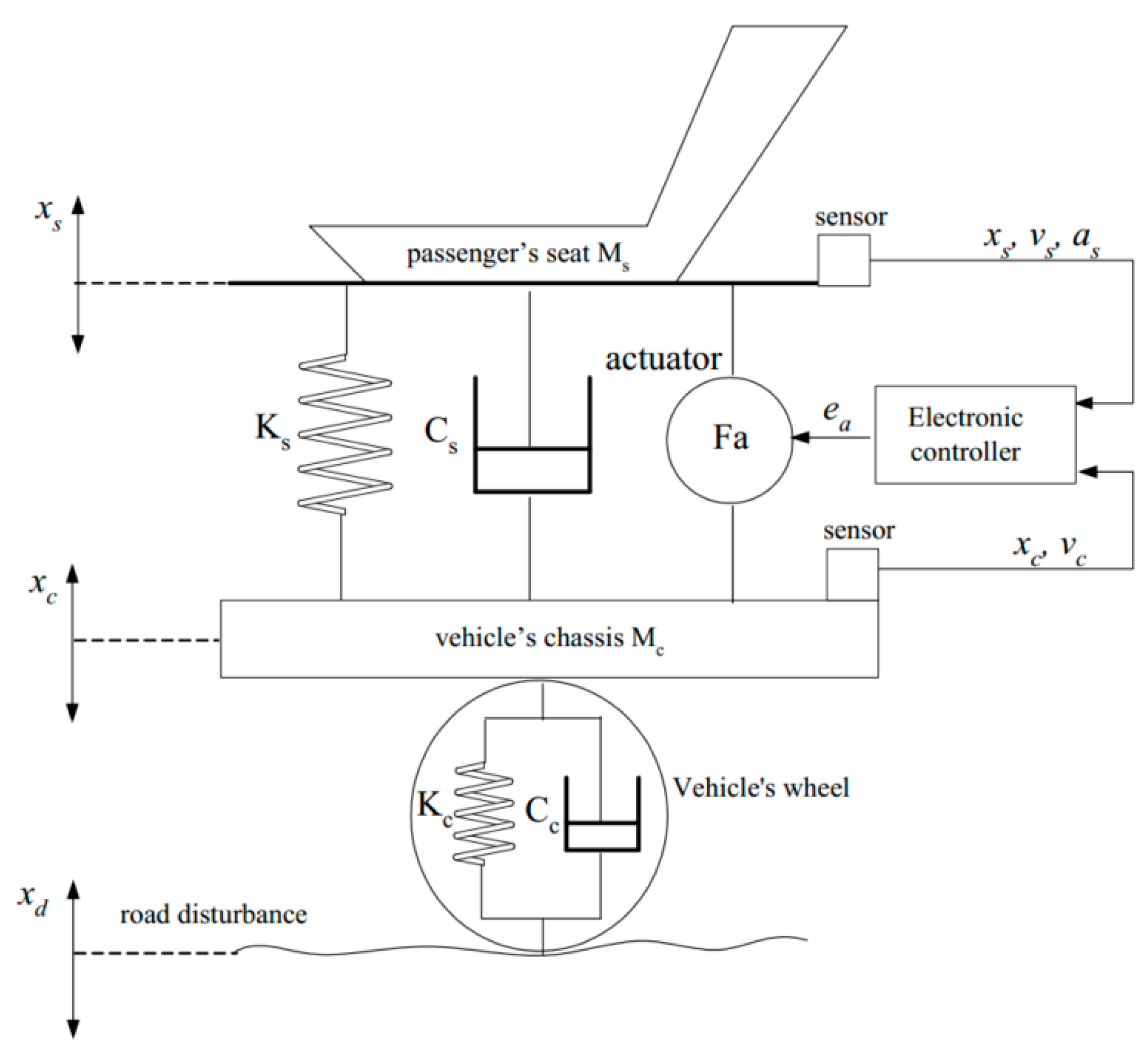
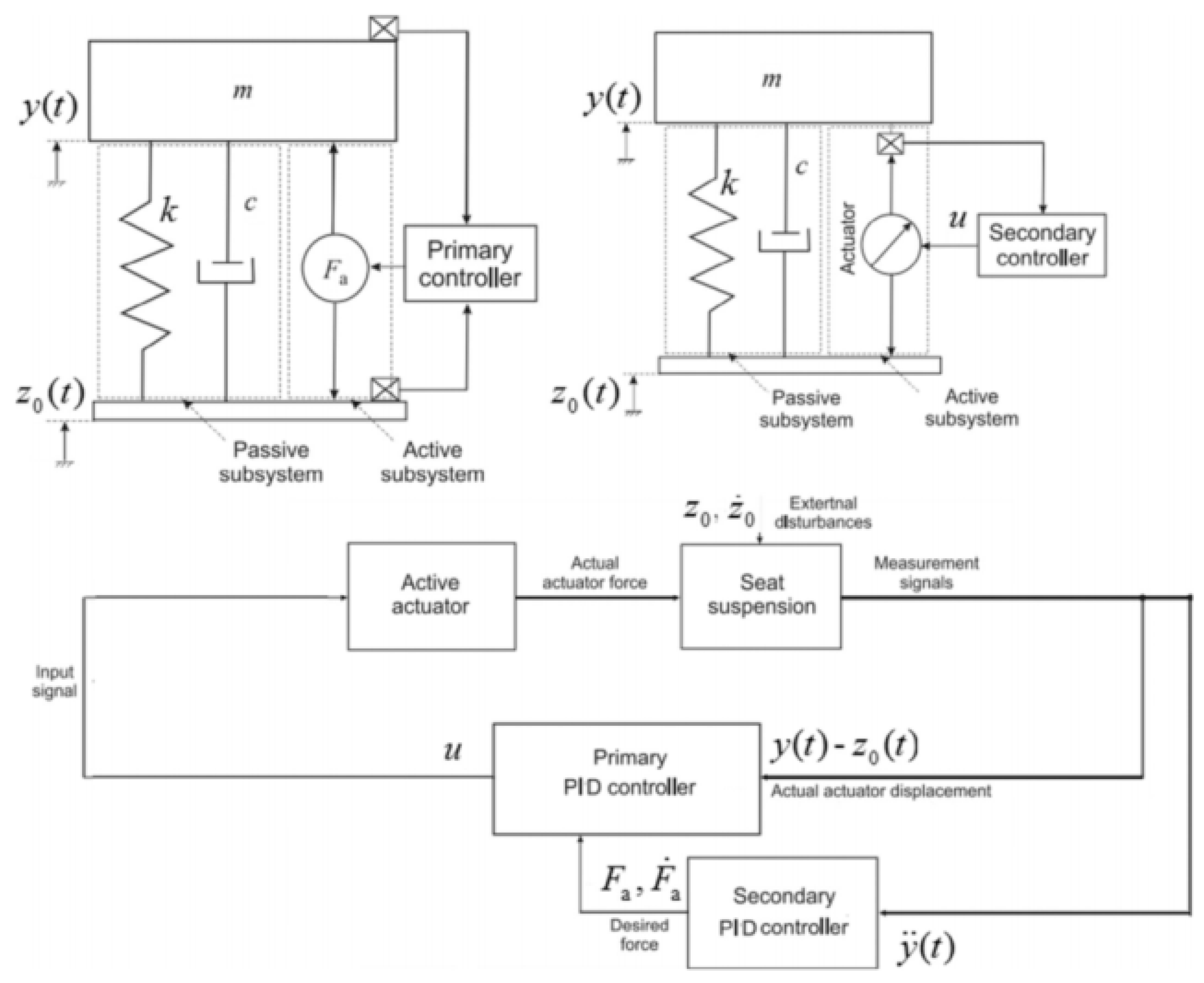
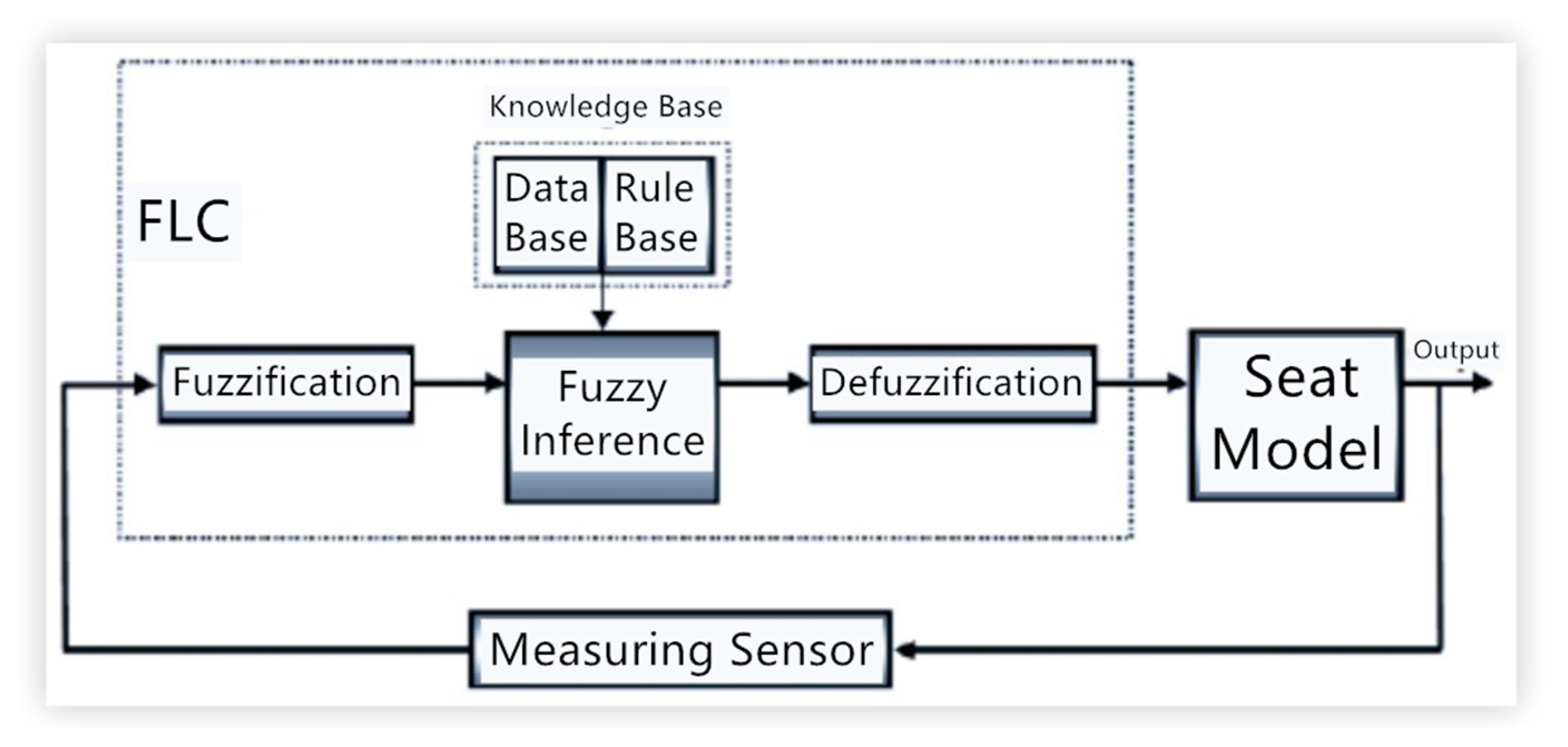
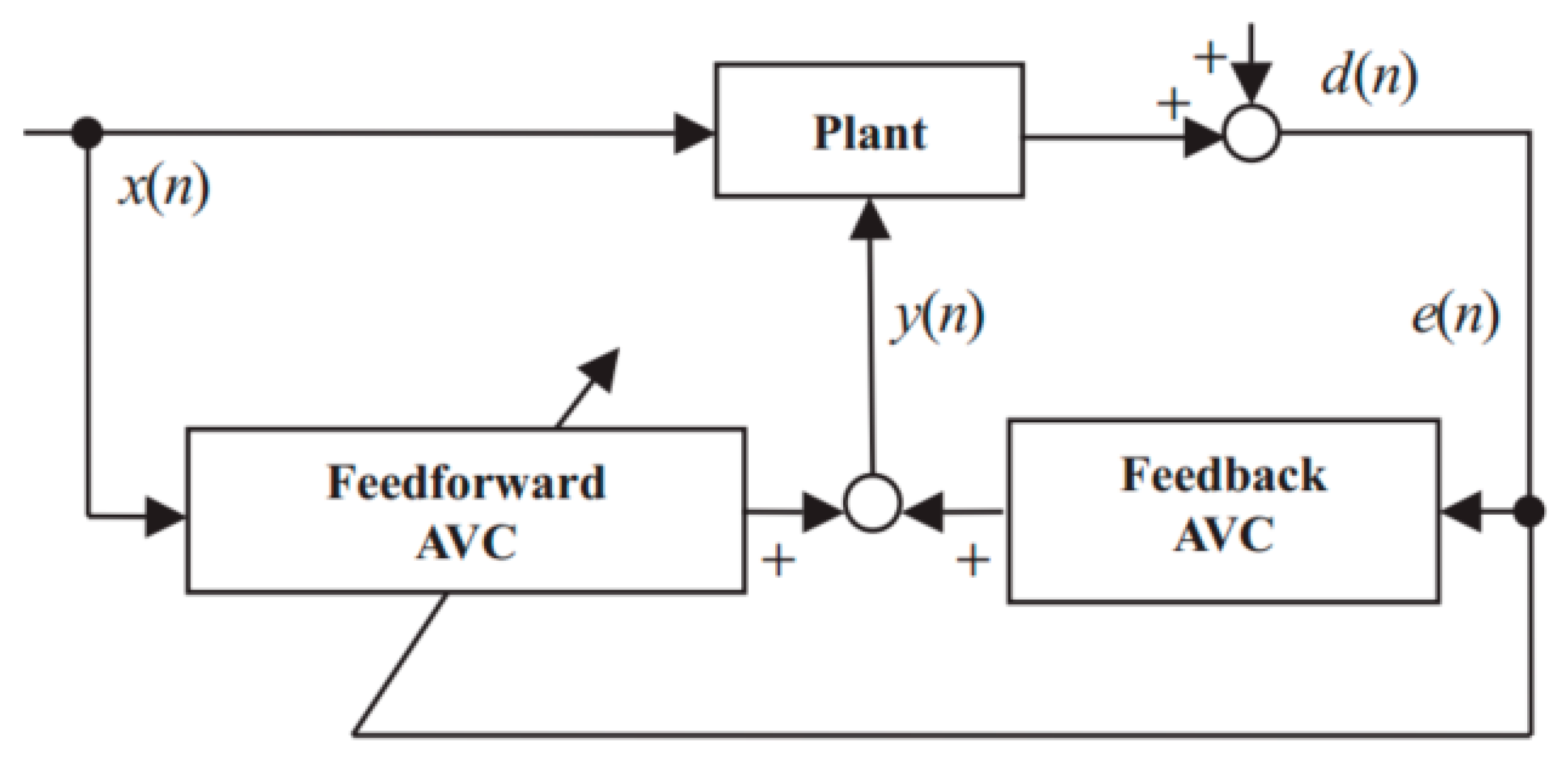
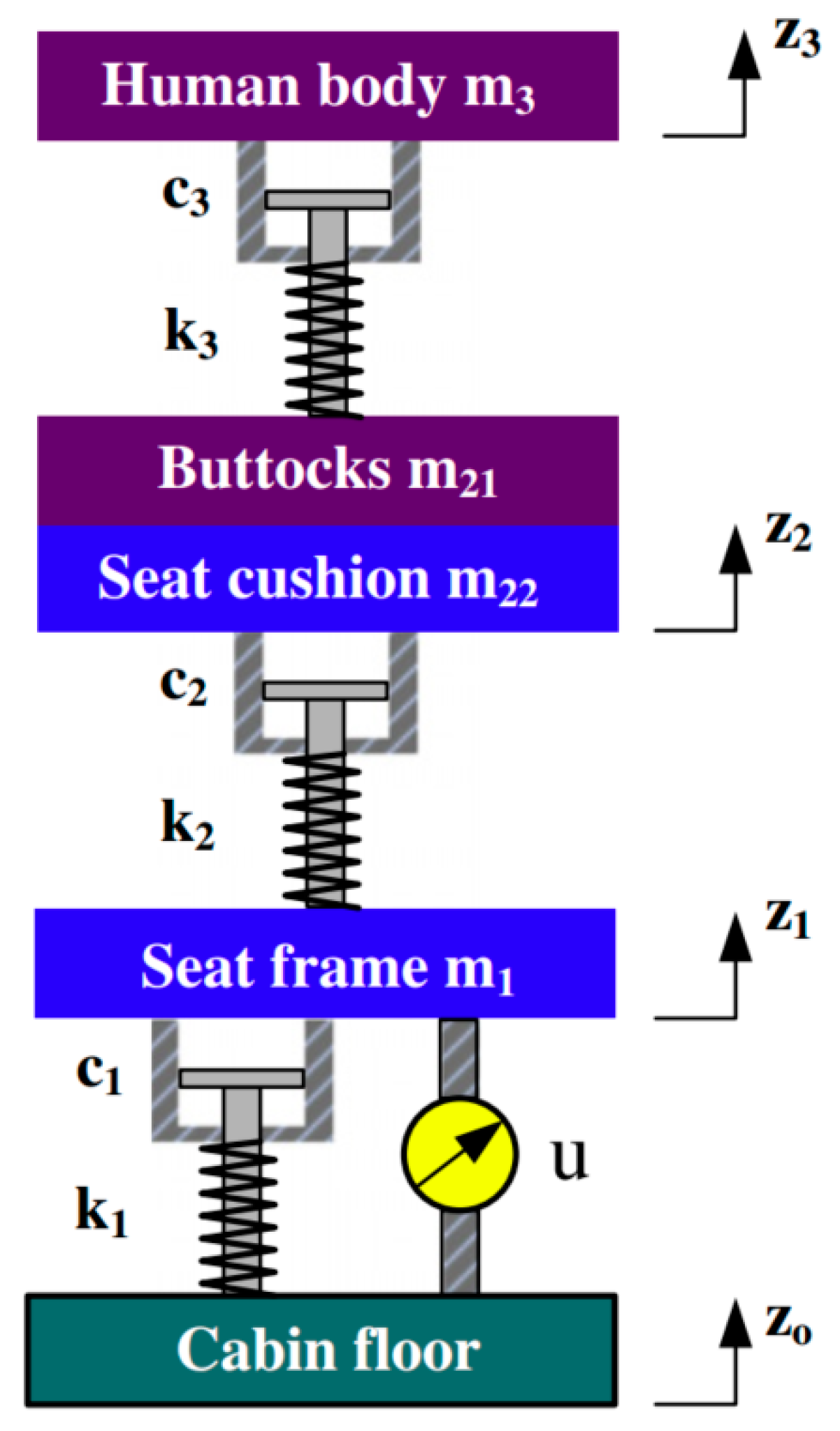
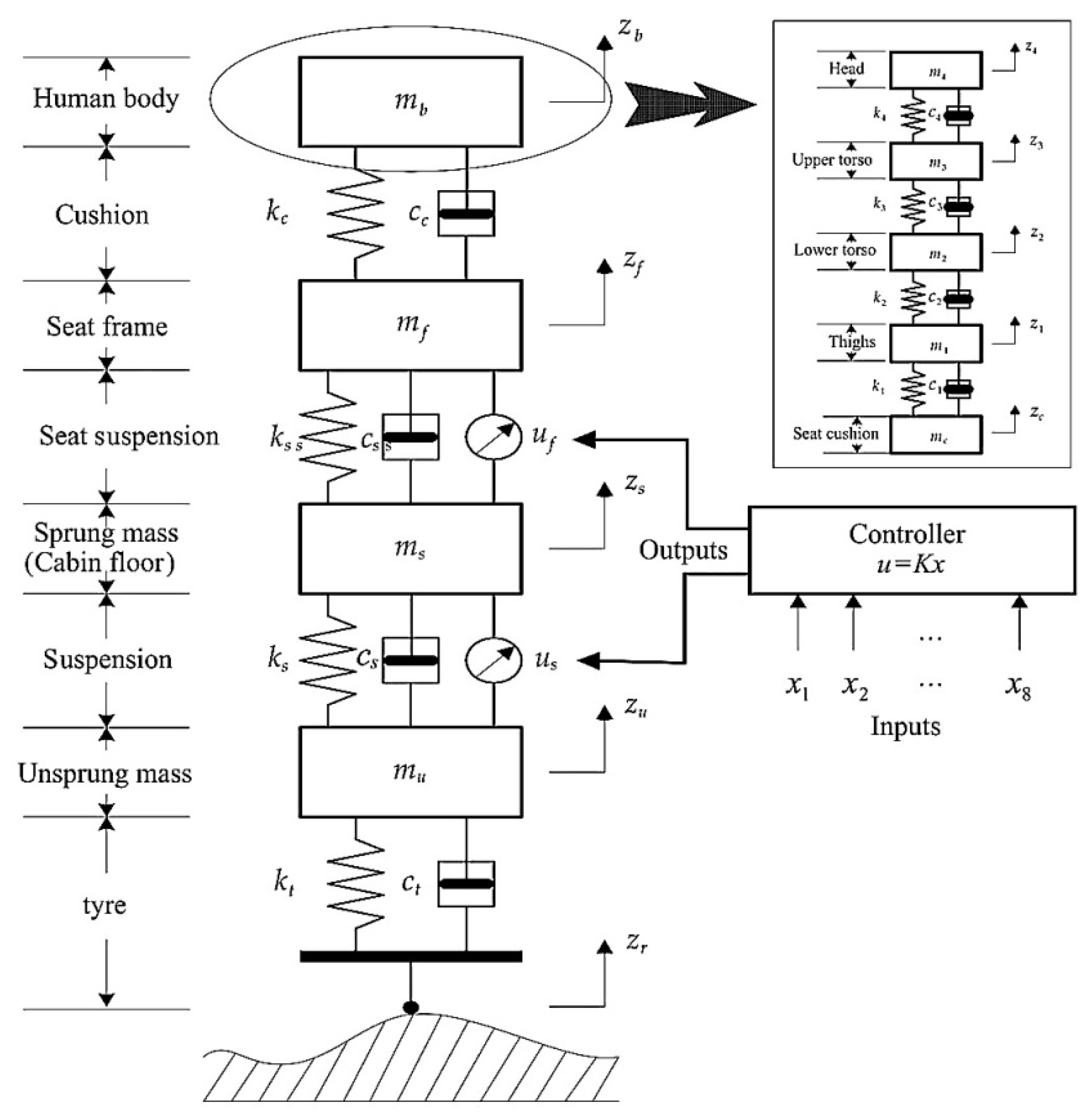
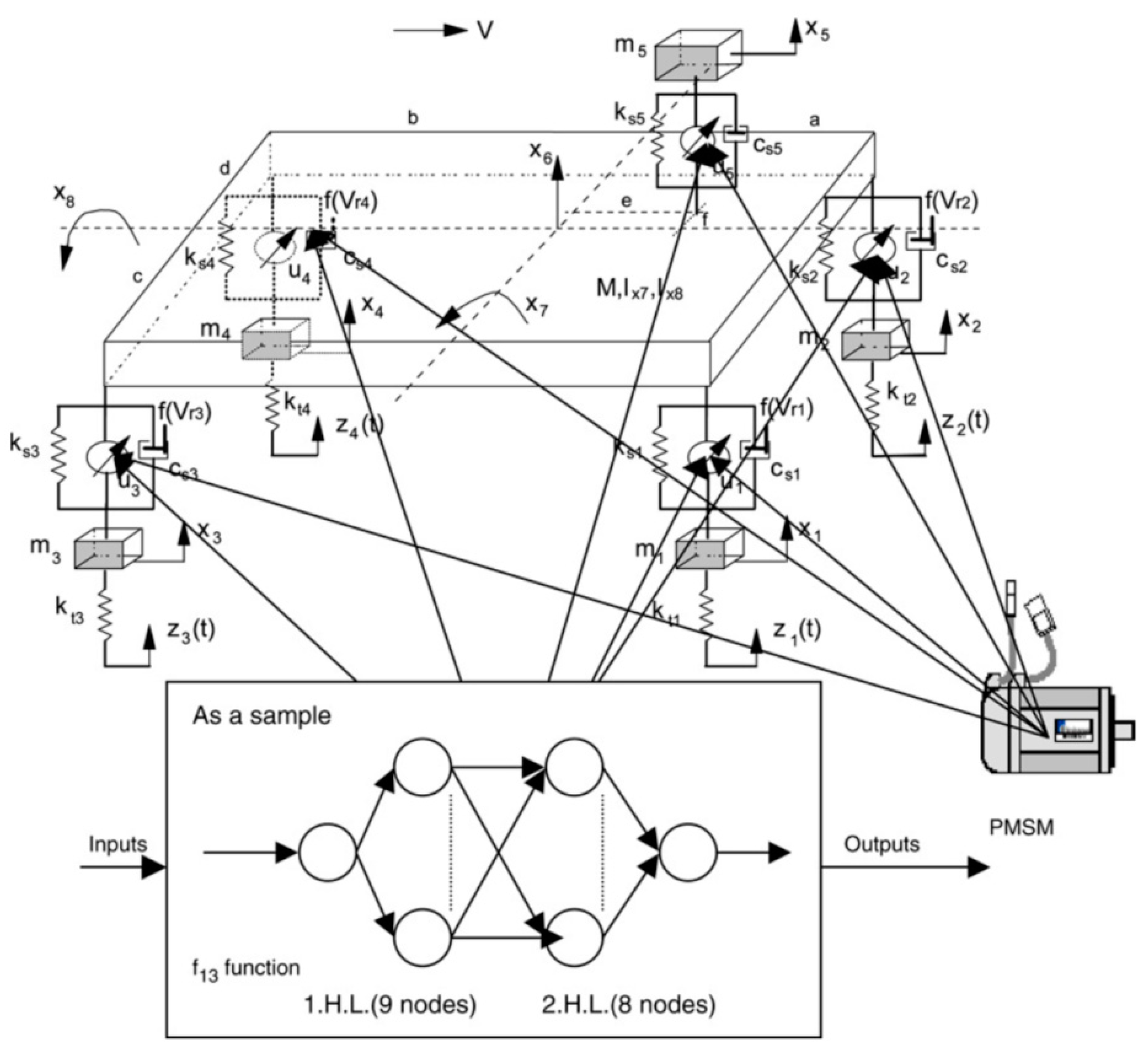
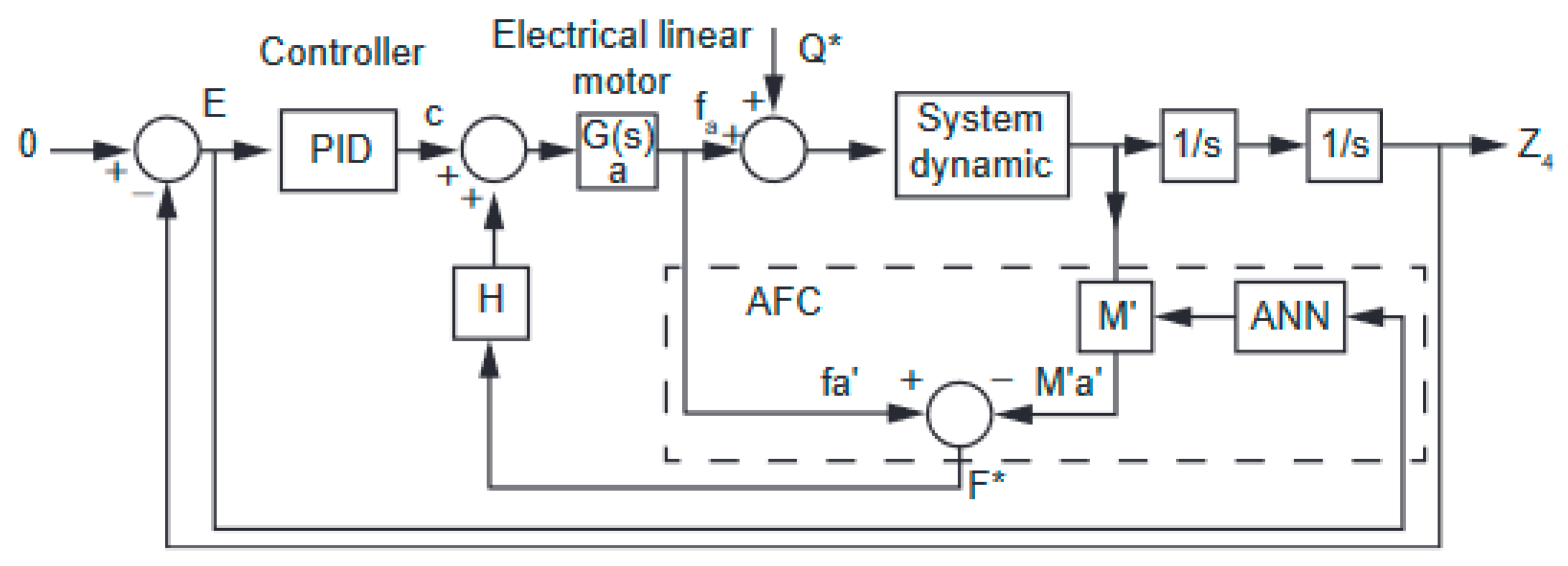
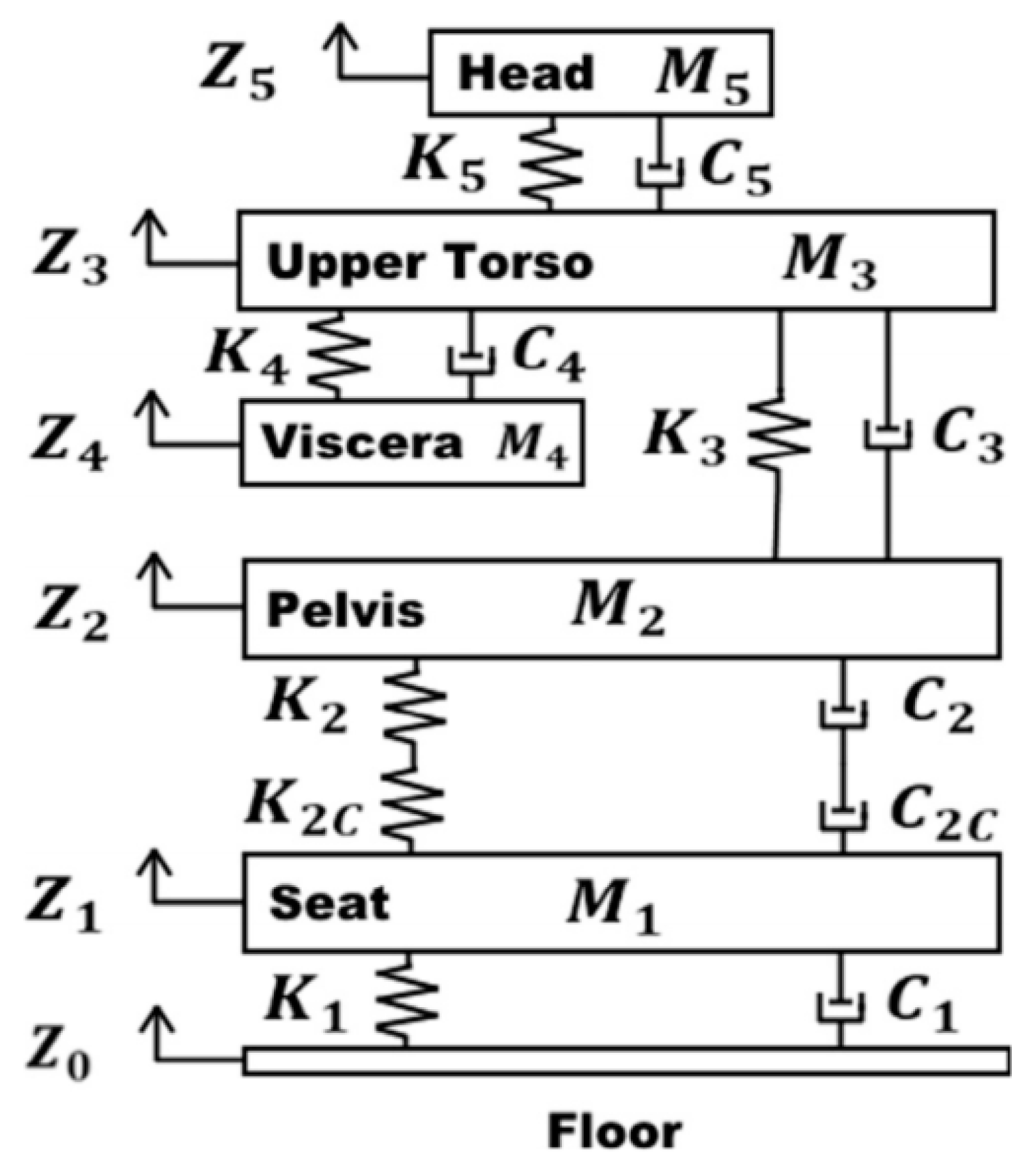
| Author | Actuator and Driver | Degree-of-Freedom (DOF) Control | Max Output | Work Load | Pros and Cons |
|---|---|---|---|---|---|
| Stein (1997) | Pneumatic spring Proportional electropneumatic transducer | Vertical 1-DOF | Pros Simple structure The characteristics of the pneumatic spring itself help to reduce vibration Cons The pneumatic structure responds slowly Low control accuracy | ||
| Maciejewski et al. (2014) | Pneumatic spring | Vertical 1-DOF | 55 kg 98 kg | Pros Common structure Traditional shock absorbers reduce energy consumption Cons Slow dynamic response Need pipeline and compressor | |
| Maciejewski et al. (2010) | Pneumatic spring | Vertical 1-DOF | 50 kg 80 kg 120 kg | Pros Common structure Traditional shock absorbers reduce energy consumption Cons Slow dynamic response Need pipeline and compressor | |
| Maciejewski (2012) | Pneumatic spring | Vertical 1-DOF | Force = 400 N | 51 kg 102 kg | Pros Common structure Traditional shock absorbers reduce energy consumption Cons Slow dynamic response Need pipeline and compressor |
| Ning et al. (2016) | 400 W Panasonic servo motors 2 (MSMJ042G1U)2 | Vertical 1-DOF | Torque = 104 Nm | 80 kg | Pros Simple structure Responsive Easy to control Con Bulky |
| Ning et al. (2017) | 400 W Panasonic servo motors servo motor drivers (MBDKT2510CA1) | Vertical 1-DOF | Torque = 26 Nm | 55 kg 70 kg | Pros Simple structure Responsive Easy to control Con Bulky |
| Ning et al. (2017) | 400 W Panasonic servo motors servo motor drivers (MBDKT2510CA1) | Vertical 1-DOF | Pros Simple structure Responsive Easy to control Con Bulky | ||
| Ning et al. (2016) | 400 W Panasonic servo motors servo motor drivers (MBDKT2510CA1) | Vertical 1-DOF | Torque = 52 Nm | 55 kg | Pros Simple structure Responsive Easy to control Con Bulky |
| Ning et al. (2018) | 400 W Panasonic servo motors 4 servo motor drivers (MBDKT2510CA1) 4 | Vertical and roll 2-DOF | Torque = 52 Nm Force = 350 N | 80 kg | Pros Simple structure Responsive Easy to control Con Bulky |
| Stein and Ballo (1991) | Electrohydraulic | Vertical 1-DOF | 75 kg | Pros High output power High control precision ConBulky | |
| Gan et al. (2015) | Electromagnetic linear actuator (XTA-3086) 2 | Vertical 1-DOF | Force = 1116 N | 55 kg | Pros Simple structure Responsive Easy to control Con High power consumption |
| Author | Method | Target Frequency | Vibration Control Performance Criterion | Model | Performance | Pros and Cons |
|---|---|---|---|---|---|---|
| Wang et al. (2018) | PID control | 7.51 Hz | Displacement (m) | 5-DOF | The peaks of vibration amplitude are reduced to around | Pros Simple Practical Con Poor robustness |
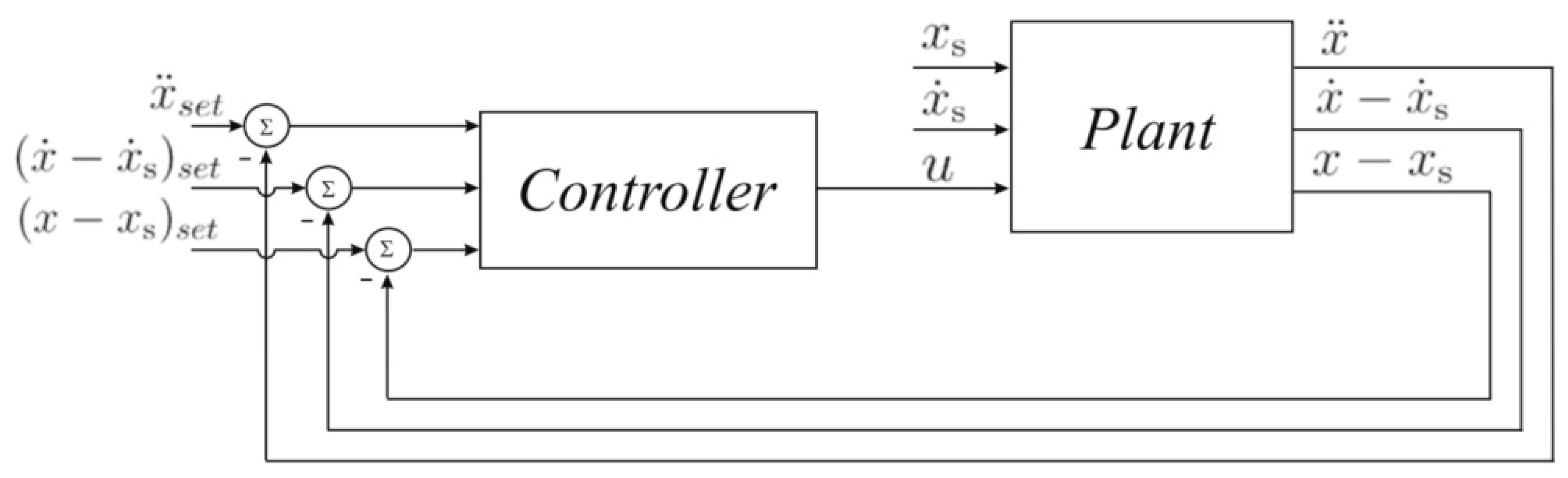
| Maciejewski et al. (2014) | Adaptive control Reverse model Proportional-Derivative (PD) control | 0.5–4 Hz | Seat Effective Amplitude Transmissibility (SEAT) (dimensionless) Transmissibility (Dimensionless) Acceleration (m/s2) | 1-DOF | The vibrations at about 1.3 Hz are reduced by about 50% | Pros Adaptable Large range of load Con Signal delay |
| Maciejewski et al. (2010) | Robust control Triple feedback control | 0.5–4 Hz | SEAT (Dimensionless) Transmissibility (Dimensionless) | The amplitude at resonance is reduced by about 50% | Pro Can work with a different mass load Con May cause chattering | |
| Wu and Chen (2004) | FXLMS control H-infinity control | 10, 20, and 30 Hz | Accelerations in dB ref 1 m/s2 | The active seating system achieves 11 dB vibration attenuation at 10 Hz | Pro Good robustness Con May cause chattering | |
| Ning et al. (2016) | H-infinity control with friction compensation | 1–4.5 Hz | Root-mean-square (RMS) acceleration (m/s2) Frequency-weighted RMS (FW-RMS) acceleration (m/s2) Vibration Dose Value (VDV) () SEAT (dimensionless) VDV ratio (dimensionless) | 1-DOF | Compared with a passive seating system, the RMS is reduced by 57%, the FW-RMS is reduced by 35.5%, the VDV value is reduced by 34.6%, the SEAT value is reduced 35.6%, and the VDV ratio is reduced by 34.6%. | Pro Good robustness Con Highly reliant on the accuracy of the model |
| Sun et al. (2011) | H-infinity control in the finite frequency domain | 4–8 Hz | Power Spectral Density (PSD) (m2/s3) Acceleration (m/s2) | 3-DOF | Pro Good robustness Con Highly reliant on the accuracy of the model | |
| Gan et al. (2015) | FXLMS control FBLMS control | 4–12 Hz | dB ref m/s2 | For single-frequency cancellation, a 26 dB cancellation is achieved on the seat pan at the frequency of 6 Hz. For the multiple harmonic cancellation, the average level of vibration reduction is around 20 dB at 4, 6, 8, and 12 Hz. | Pro Adaptable Con Can be affected by noise or disturbance | |
| Ning et al. (2016) | H-infinity control | 2–6 Hz | RMS acceleration (m/s2) FW-RMS acceleration (m/s2) VDV () SEAT (Dimensionless) VDV ratio (Dimensionless) | 2-DOF | Compared with a passive seating system, the RMS is reduced by 31.96%, the FW-RMS is reduced by 43.42%, the VDV value is reduced by 42.96%, the SEAT value is reduced 43.41%, and the VDV ratio is reduced by 42.68%. | Pro Good robustness Con Highly reliant on the accuracy of the model |
| Ning et al. (2018) | Sliding mode control H-infinity control | RMS (m/s2) FW-RMS (m/s2) VDV () | 2-DOF | Compared with a passive seating system, for vertical acceleration, the RMS is reduced by 41.9%, the FW-RMS is reduced by 32.1%, and the VDV is reduced by 32.8%. For lateral acceleration cancellation, the RMS is reduced by 55.4%, the FW-RMS is reduced by 49.4%, and the VDV is reduced by 52.2%. | Pros Adaptable High robustness Con Highly reliant on the accuracy of the model | |
| Ning et al. (2017) | Disturbance observer Takagi–Sugeno fuzzy control | 2–4 Hz | Acceleration (m/s2) Transmissibility (Dimensionless) | 2-DOF | Compared with a well-tuned passive seating system, the active seating system can reduce the RMS by 45.5% and 49.5% with a mass load of 55 and 70 kg, respectively. | Pro Effectively reduce the workload |
| Du et al. (2012) | H-infinity state feedback control | Head acceleration (m/s2) | 8-DOF | Pro Good robustness Con Highly reliant on the accuracy of the model | ||
| Ning et al. (2017) | Sliding mode control | 1.5 Hz | RMS acceleration (m/s2) FW-RMS acceleration (m/s2) VDV () SEAT (Dimensionless) VDV ratio (Dimensionless) | 2-DOF | Compared with a passive seating system, the RMS is reduced by 54.6%, the FW-RMS is reduced by 34.1%, the VDV value is reduced by 32.6%, the SEAT value is reduced 34.1%, and the VDV ratio is reduced by 32.6%. | Pros Adaptable High robustness Con Highly reliant on the accuracy of the model |
| Author | Number of Hidden Layers | Number of Nodes | Training Method | Pros and Cons | |
|---|---|---|---|---|---|
| Guclu and Gulez (2008) | 2 | First layer: 9 Second layer:10 | Back Propagation | Compared with an uncontrolled system, the maximum displacement of the passenger seat with NN control is reduced from to . | Pro Good on multi-input and multioutput control Con Low robustness |
| Gohari and Tahmasebi (2015) | 1 | 10 | Back Propagation | Pro Good on nonlinear problems Con Need large ideal training data |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Wang, X. A Review of Low-Frequency Active Vibration Control of Seat Suspension Systems. Appl. Sci. 2019, 9, 3326. https://doi.org/10.3390/app9163326
Zhao Y, Wang X. A Review of Low-Frequency Active Vibration Control of Seat Suspension Systems. Applied Sciences. 2019; 9(16):3326. https://doi.org/10.3390/app9163326
Chicago/Turabian StyleZhao, Yuli, and Xu Wang. 2019. "A Review of Low-Frequency Active Vibration Control of Seat Suspension Systems" Applied Sciences 9, no. 16: 3326. https://doi.org/10.3390/app9163326
APA StyleZhao, Y., & Wang, X. (2019). A Review of Low-Frequency Active Vibration Control of Seat Suspension Systems. Applied Sciences, 9(16), 3326. https://doi.org/10.3390/app9163326






