1. Introduction
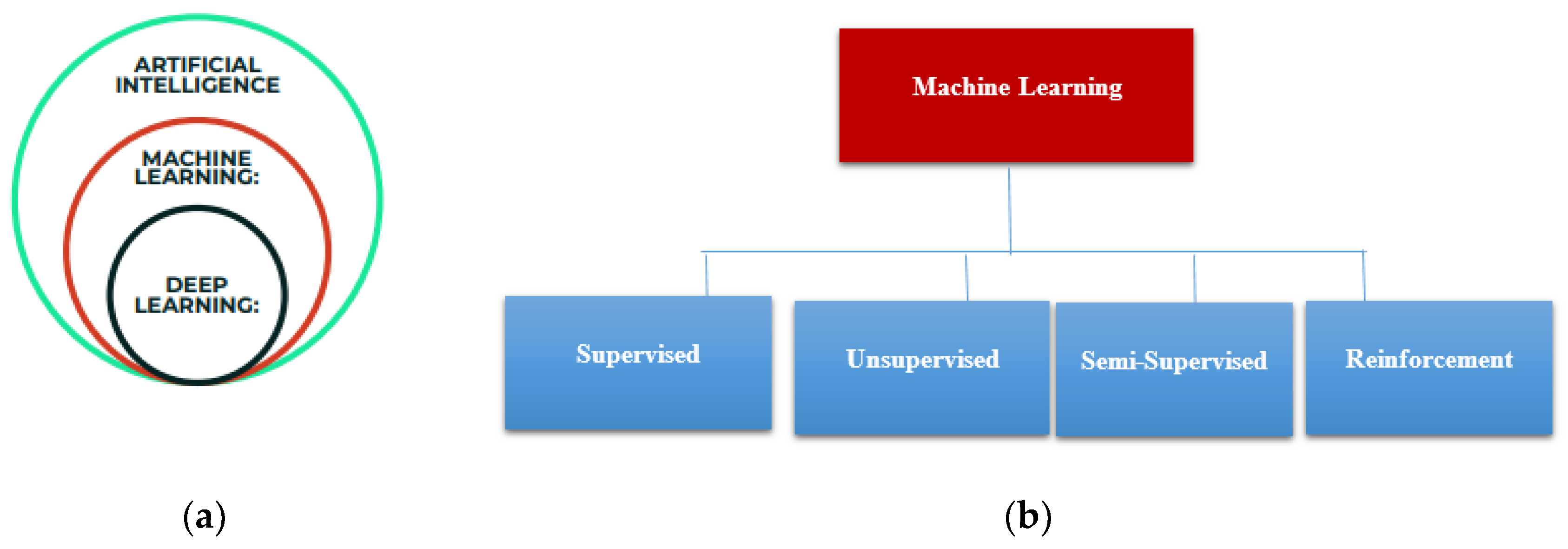
Machine learning is a subfield of Artificial Intelligence as shown in
Figure 1a, that allows a computer system to learn from the environment, through re-iterative processes and improve itself from experience. Machine learning algorithms organize the data, learn from it, gather insights and make predictions based on the information it analyzed without the need for additional explicit programming. Training a model with data and after that using the model to predict any new data is the concern of machine learning. Machine learning algorithms are widely composed of supervised, unsupervised, semi-supervised, and reinforcement learning as shown in
Figure 1b. In this current work, we focused on supervised learning, where there is a part of the training data which behaves as an instructor to the algorithm to determine the model.
The development of machine learning has proven to better describe data as a result of providing both engineering solutions and an important benchmark. According to Vinitha et al. [
1], as a result of big data development in biomedical and healthcare communities, precise study of medical data benefits early disease recognition, patient care and community services.
Machine learning algorithms were developed with numerous features such as effective performance on healthcare related data that includes text, images, X-rays, blood samples etc. [
2]. The choice of the algorithm to be used depends on the type of dataset, be it large or small. Sometimes the noise in a dataset can be a drawback to some machine learning algorithms [
2]. Sometimes, after viewing a dataset, interpreting the pattern and extracting meaningful information becomes difficult, hence the need of machine learning [
3,
4]. At a regularization point where a model quality is highest, variance and bias problems are compromised, and that is where Random Forest (RF) model is used. Random Forest has the capability of building numerous numbers of decision trees using random samples with a replacement to overcome the shortcomings of the Decision tree algorithm.
Support Vector Machines (SVM) is a pattern classification technique which, when trained, has the capability to learn classification and regression rules from observation data [
2,
5]. Support Vector Machine theory is based on statistics which have a fundamental principle of estimating the optimal linear hyperplane in a feature space that maximally separates the two-mark groups or classes. Support Vector Machine algorithm shows the feasibility and superiority to extract higher-order statistics [
6].
Artificial Neural Networks (ANNs) are computational models based on the neural structure of the brain. ANN has the capability of searching for patterns among patients’ healthcare and personal records to retrieve and identify meaningful information [
2,
7]. Application of machine learning algorithms in the medical field for disease diagnosis and prediction can help experts in disease identification depending on the symptoms at an early stage [
8].
When it comes to diagnosing and predicting diseases using machine learning algorithms, especially on biomedical text datasets, several researchers have done significant work to predict other diseases such as diabetes [
9], heart diseases [
10,
11,
12,
13,
14,
15], breast cancer disease [
7,
16,
17], and even in the prediction of medical costs of Spinal Fusion [
18], etc. However, to the best of our knowledge, much has not been explored in predicting kyphosis disease. Kyphosis is a dangerous disease and equally needs attention as the aforementioned diseases.
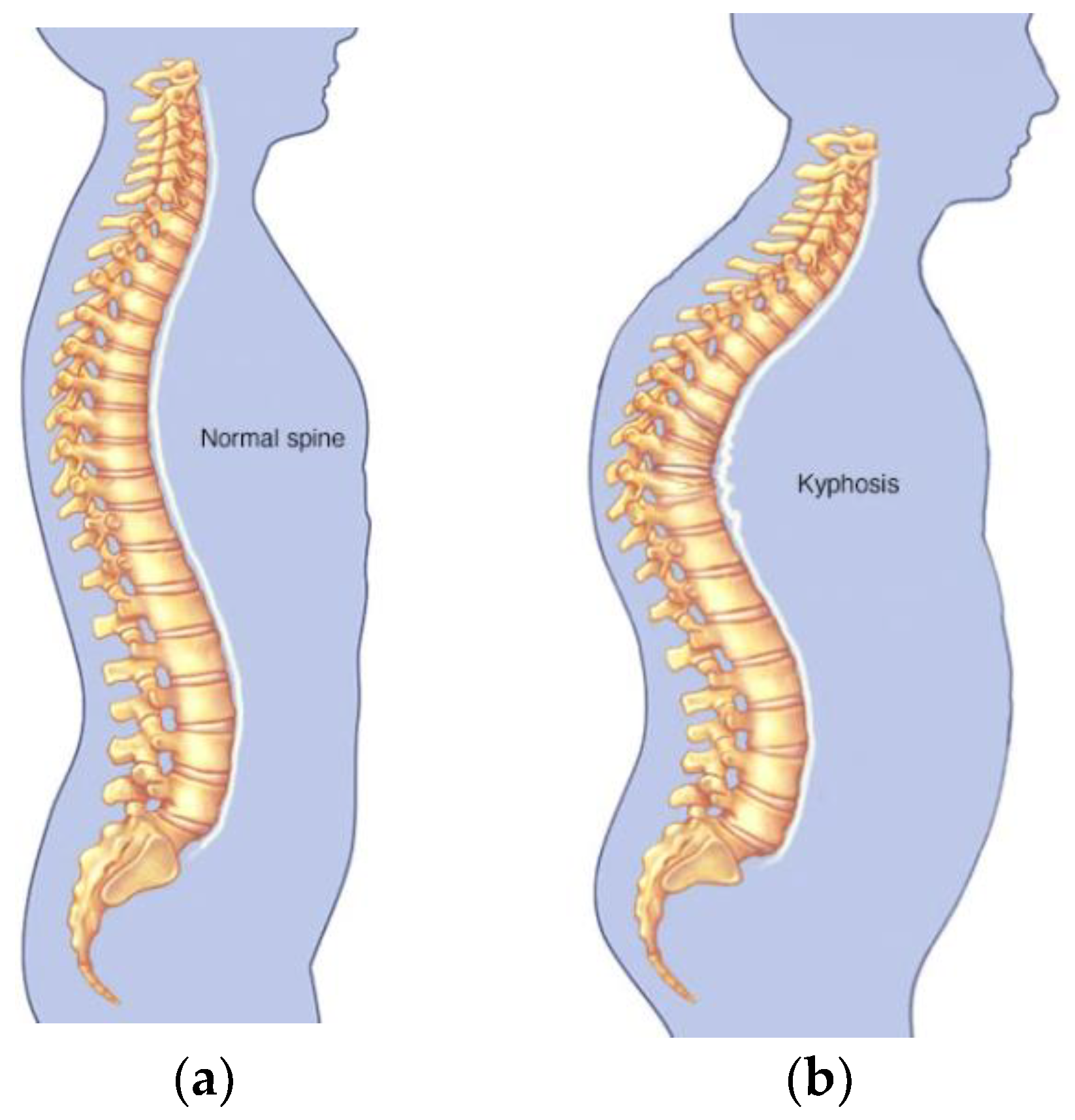
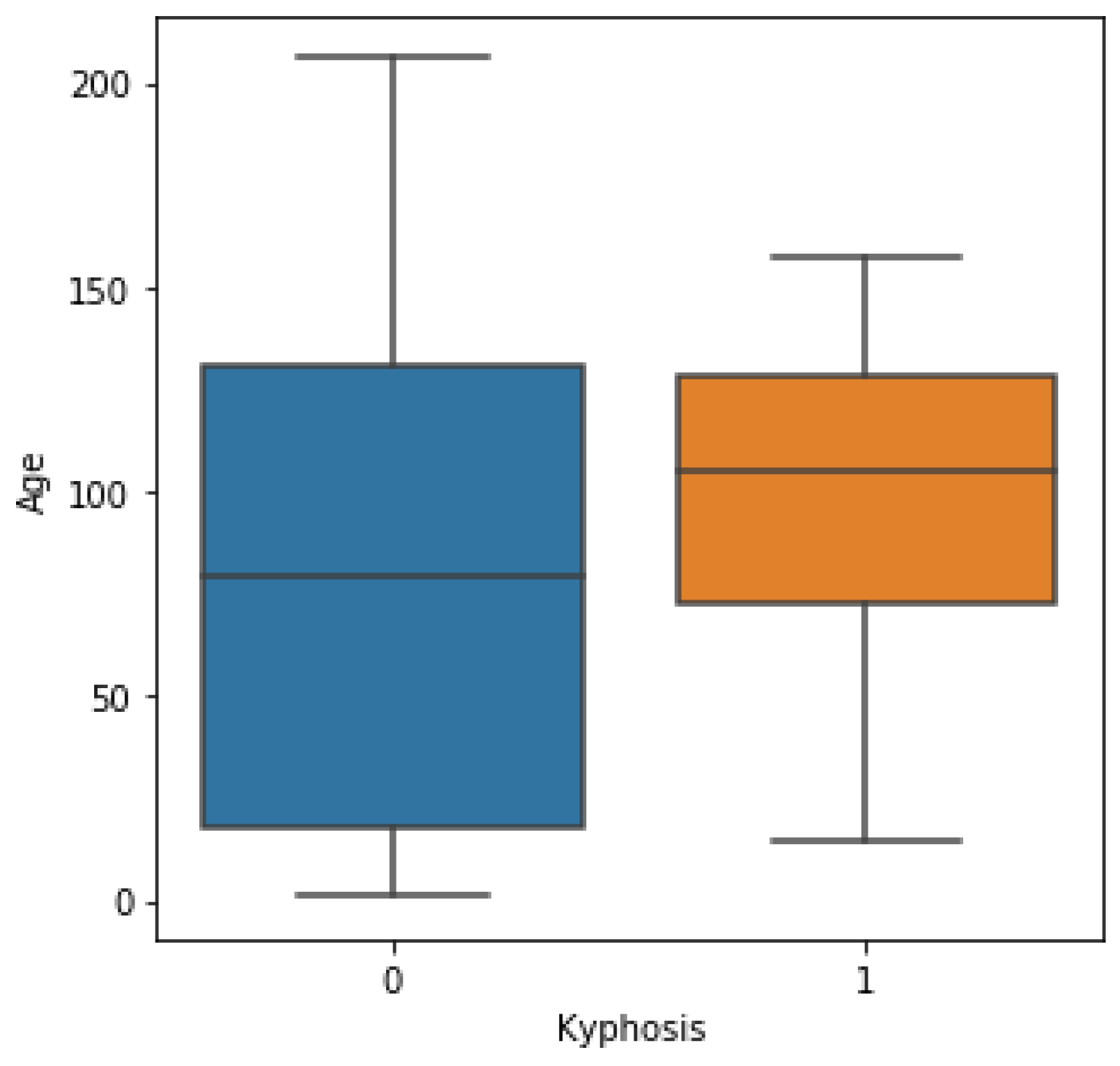
Kyphosis is an exaggerated, forward rounding of the back and which can occur at any age as shown in
Figure 2b. Kyphosis can appear in infants or teenagers as a result to malformation of the spine of the spinal bones over time. Severe kyphosis can cause pain and disfiguring. Sometimes, the patient may experience back pain and stiffness in addition to an abnormally curved spine. Abnormal vertebrae can be caused by fractures (broken or crushed vertebrae), osteoporosis (bone-thinning disorder), disk degeneration (soft, circular disks act as cushions between spinal vertebrae), birth defects (spinal bones that don’t develop properly) etc. For further reading on kyphosis, refer to (
https://www.mayoclinic.org/diseases-conditions/kyphosis/symptoms-causes/syc-20374205). More importantly, detecting kyphosis disease at the early stage in children will prevent abnormal spinal vertebrae problems.
Therefore, in this current research, based on a biomedical dataset, we apply Random Forest (RF), Support Vector Machines (SVM), and Artificial Neural Network (ANN) algorithms to build models to predict the absence or presence of a kyphosis disease based on a historical healthcare and personal records of a kyphosis disease patients after they have gone through surgery. The results of the models were then evaluated and compared.
The importance of this current research is to present to the biomedical community how machine learning algorithms have been applied to classify and predict kyphosis disease based on a biomedical data.
2. Materials and Methods
This section presents the dataset used, the preprocessing of the data and the machine learning algorithms, namely, Random Forest (RF), Support Vector Machines, and the Artificial Neural Network. The preprocessing of the data and the implementations of the models were achieved by using the Python environment. We used Python 3 as the version in writing the codes, which was achieved through the Jupyter Notebook by installing the Anaconda software (version 3.6, manufactured by the Anaconda Inc., Austin, TX, USA) (
https://www.anaconda.com/).
2.1. Data and Preprocessing
We obtained the kyphosis [
19] dataset from (
https://www.kaggle.com/abbasit/kyphosis-dataset). The data has 81 rows and 4 columns which represents records on patients who have had corrective spinal surgery. The dataset is in a comma separate value (csv) format. Due to the small sample size of the data, we used all the data representing 100% for the training.
The features of the data represent 3 inputs and 1 output, where:
Output
Kyphosis: a factor with levels absent or present indicating if a kyphosis (a type of deformation) was present after the operation or surgery.
In order to model the data, we processed the data in a format where the models can be trained.
We achieved the preprocessing of the data by using the Scikit-Learn library (
https://scikit-learn.org/stable/index.html). Scikit-Learn helps to implement machine learning algorithms in Python, which provides simple and efficient tools for data mining and data analysis.
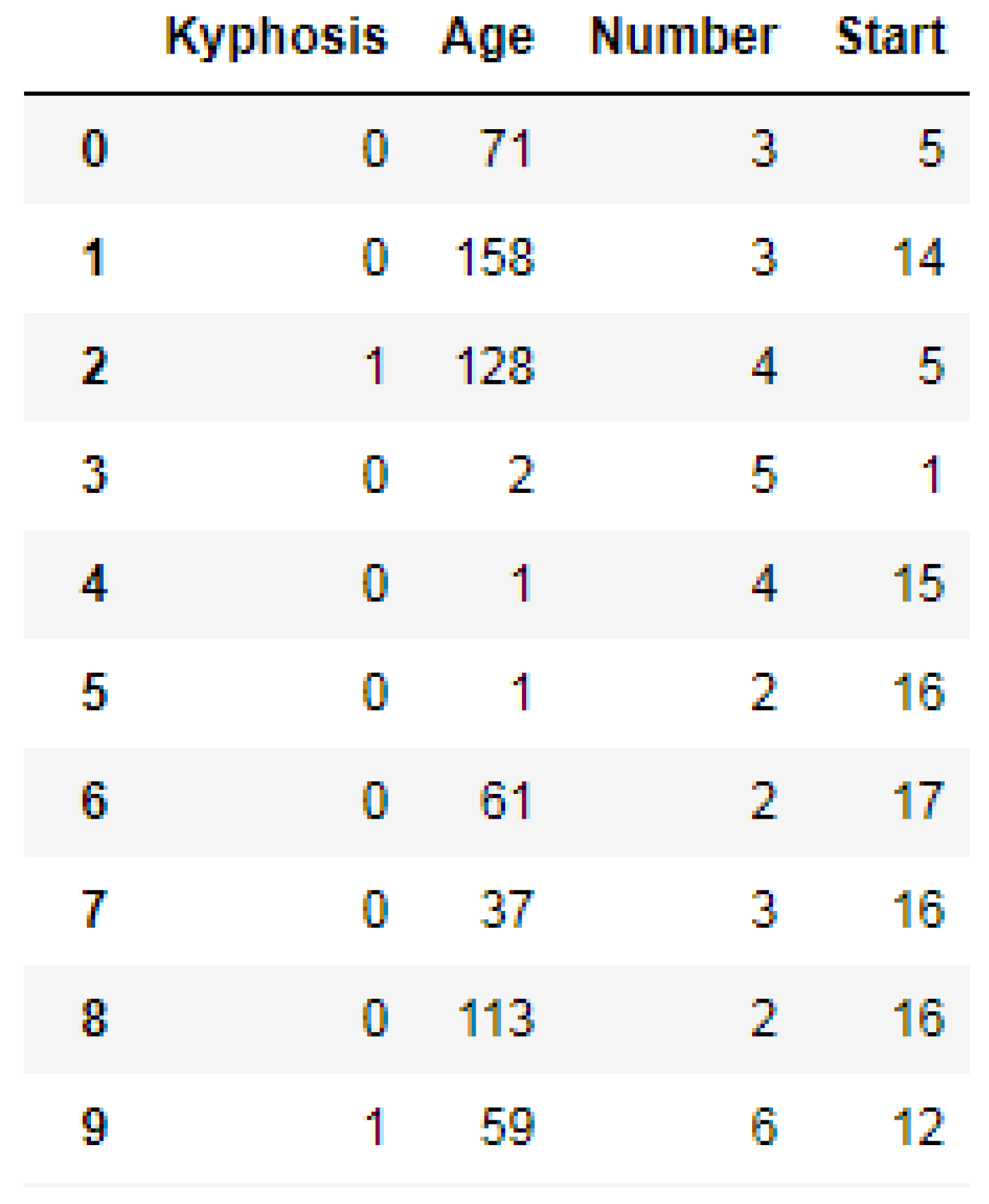
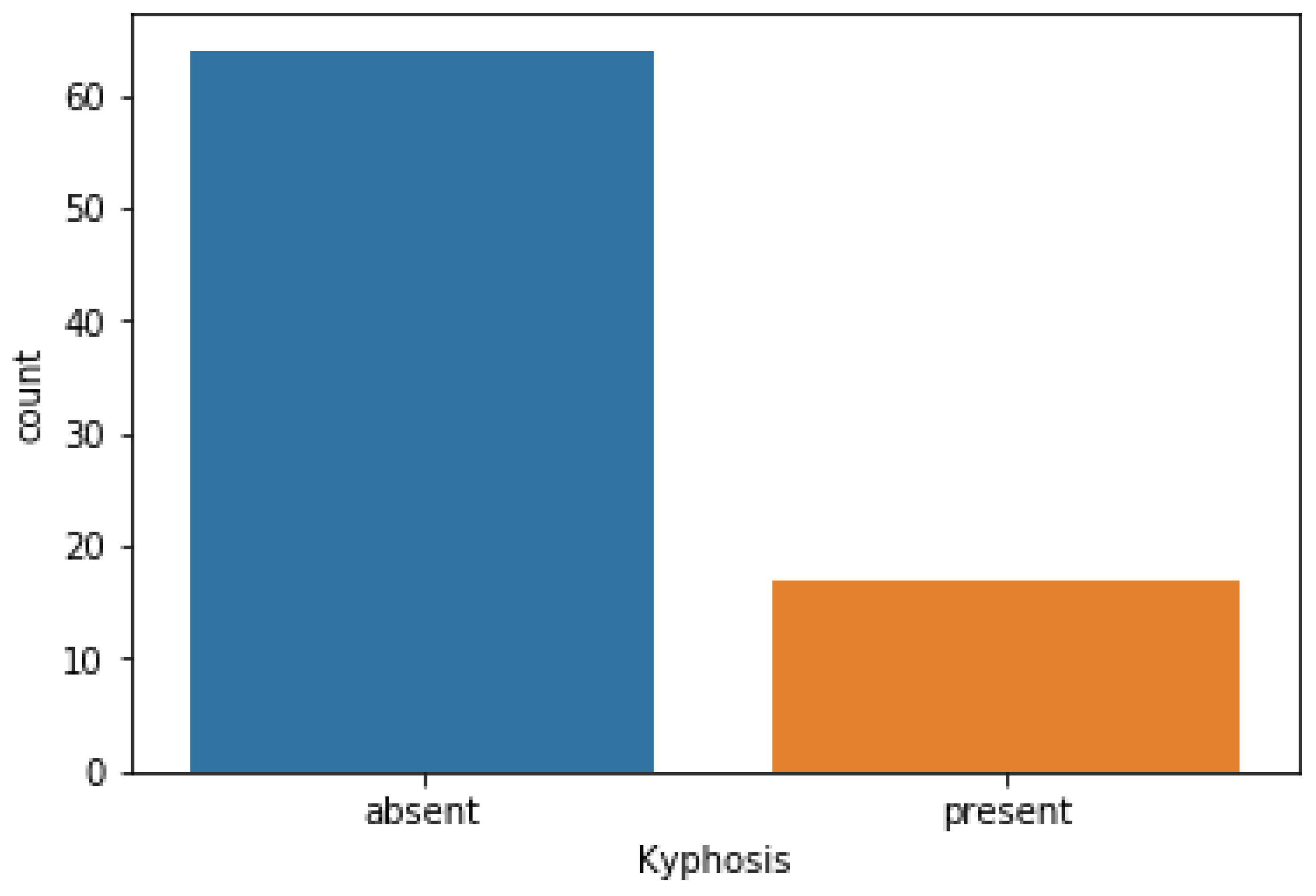
We used the Label Encoder function imported from the sklearn library to transform the Kyphosis column into zeros (0′s) and ones (1′s) as shown in
Figure 3, where (1) represents presence of the disease and (0) represents absence of the disease. In order to obtain good performances by the models, we then standardized the data using the Standard Scaler function as a preprocessing tool which was imported from the sklearn library.
2.2. Logistic Regression
Logistic Regression (LR) is one of the fundamental and famous algorithms to solve classification problems. LR is used to obtain odds ratio in the presence of more than one independent variable [
20]. LR deals with outliers by using sigmoid function. Therefore, Logistic function is a sigmoid function, which takes any real value between 0 and 1 [
21]. It is mathematically expressed as:
Considering
t as a linear function in a univariate regression model:
Therefore, the Logistic Regression is represented as:
2.3. Random Forest
Random Forest was proposed by Breiman [
22] as an ensemble classifier or regression tree based on many decision trees. Each of the trees is based on a bootstrap sample from the original training dataset using a tree classification procedure. Bootstrapping is a metric or test that depends on random sampling with replacement. A random selection of the whole variable set is used as variables for splitting the tree nodes. After formation of the forest, a new object which needs to be classified is noted for classification by each of the trees in the forest. A vote is cast by each of the trees to indicate the tree’s decision about the group or class of the object. The group or class with the majority of the votes is chosen by the forest.
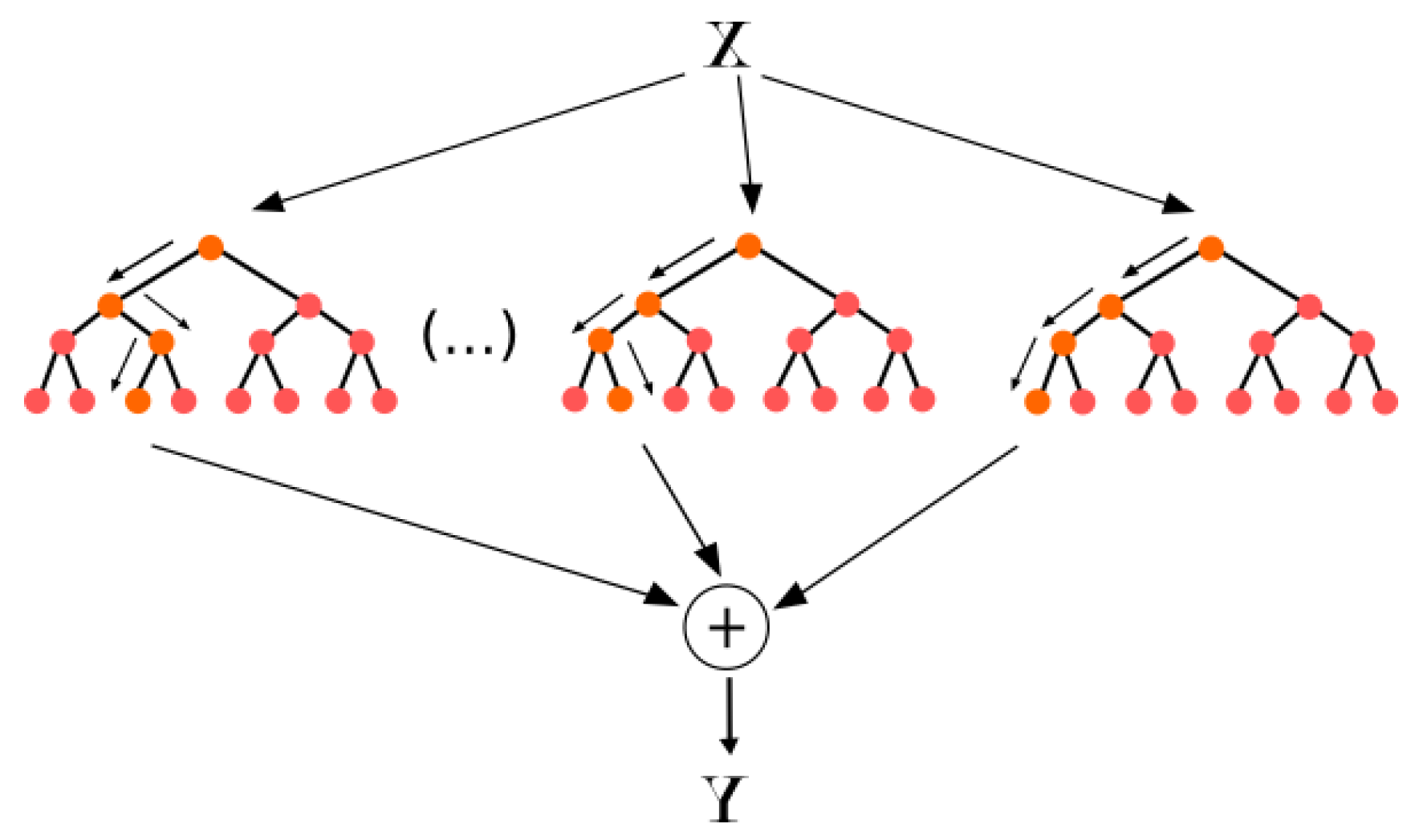
According to Neural Designer [
23], Random Forest is one of the most famous algorithms used by data scientists. In Random Forest, each tree is influenced by the values of a random vector sampled independently as shown in
Figure 4.
Random Forest algorithm follows as:
Select number of trees to grow (ntree)
- ➢
For i = 1 to ntree
Randomly sample with replacement, same size as original dataset (bootstrap).
Grow a tree.
For every split of tree.
Randomly select mtry predictors.
Grow trees till stopping criteria is reached.
Each tree then casts a vote for the most famous class, and the class with most votes wins.
- ➢
end
The formal definition of the random forest in our case is given as:
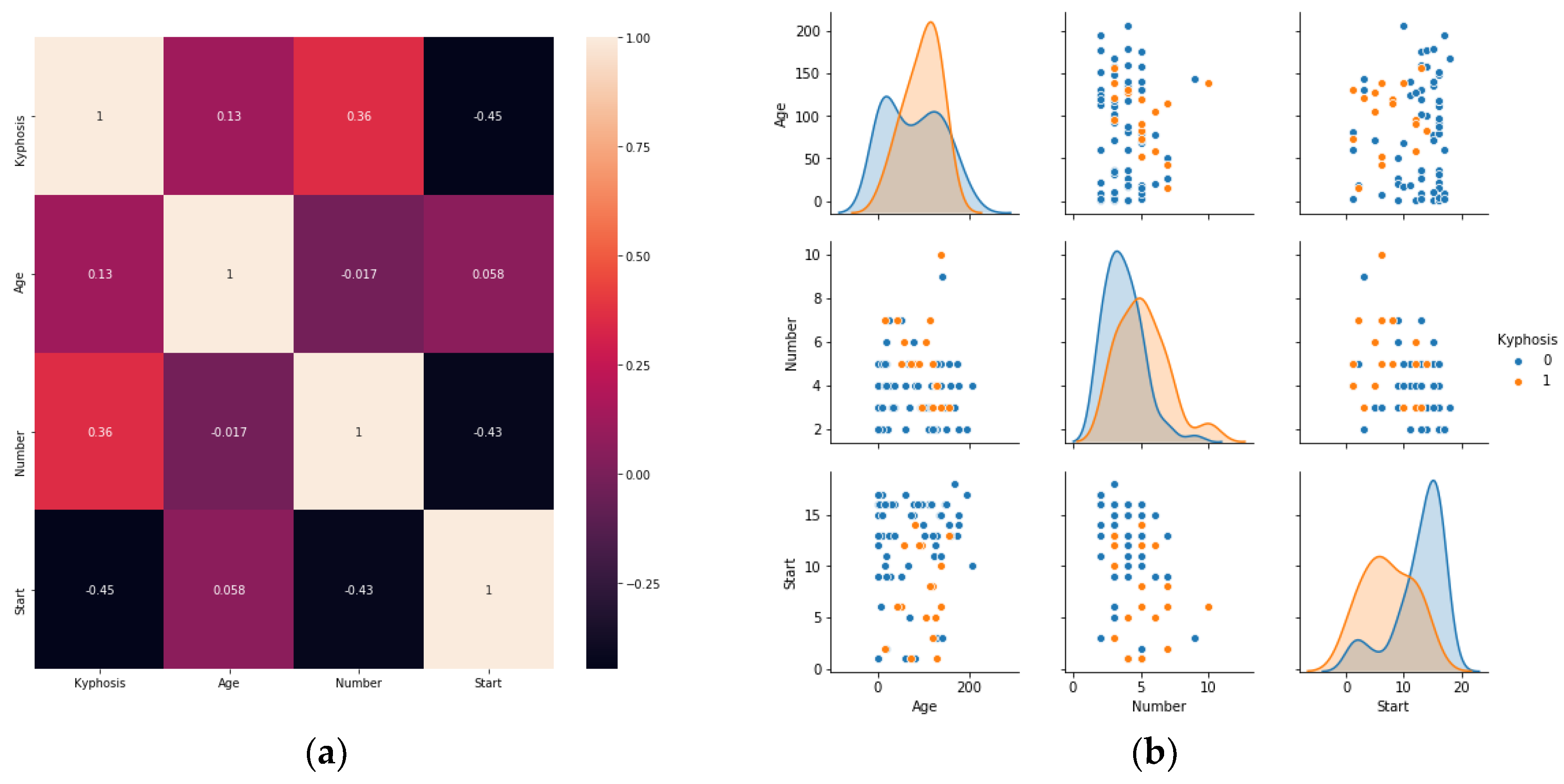
Assume training set (Kyphosis) of microarrays
, where D is the full dataset, is drawn from a random probability distribution . The goal is to build a classifier which predicts y (target: kyphosis disease) from X (input features: Age, Number, Start) based on the dataset D.
Therefore, given ensemble of classifiers , if each is a decision tree, then the ensemble is a random forest. We, therefore, define the parameters of the decision tree for classifier to be . The relationships between the classifiers and the parameters are sometimes given as . That is, decision tree k leads to a classifier . The appearance of the features which are selected in the nodes of the occur at random, according to parameters , that are randomly chosen from a model variable .
The final classification combines the classifiers , each tree then casts a vote for the most famous class at input X, and the class with the most votes wins.
The RF model was achieved by importing the RF algorithm from the sklearn library. We further performed a grid search to help automate the selection of the best parameters to produce a model with the highest performance. The selected parameters for the grid search are as follows:
n_estimators (100, 150, 200, 250, 300): this correspond to the number of trees in the forest.
Criterion (gini, entropy): The criterion is the function used to measure the quality of the split. By default, gini is selected for the Gini impurity and entropy is for the information gain. They are in a string format.
Bootstrap (true, false): The bootstrap is the random sampling with replacement. The bootstrap samples are used by default (bootstrap = True) whereas the default strategy for extra-trees is to use the whole dataset (bootstrap = False)
2.4. Support Vector Machine
Support Vector Machine theory is based on statistics which have a fundamental principle of estimating the optimal linear hyperplane in a feature space that maximally separates the two-mark groups or classes. SVM modeling geometrically finds an optimal hyperplane with the maximal interval to separate two groups or classes. The procedure for solving such a constraint problem is as follows [
24,
25,
26,
27]:
Subject to:
, x = the feature vectors or the input pattern, w = the direction of the optimal hyperplane, b = bias
To make rooms for errors, the optimization problem currently becomes:
Subject to:
The Lagrange multiplier method assists us to obtain the two formulas, that is expressed in terms of the variable
αi:
Subject to:
For all i = 1, 2, 3…., n
The linear classifier based on a linear discriminant function is then given as:
A non-linear classifier sometimes assists in providing better accuracy in many applications. A fragile way of making a non-linear classifier out of linear classifier is by mapping out data from the input space X to a feature space F based on a non-linear function
. Using kernel function, in the space F, the optimization assumes the following:
Subject to:
For all i = 1, 2, 3…., n
The classifier
is given as a SVM-Polynomial, where, if d is large, the kernel still requires n multiplications to compute. So, given
The RBF classifier is given as
In this current research paper, we implemented (7), (9) and (10) as the SVM kernels which represent Linear, Polynomial and Radial Basis Function (RBF) respectively. The cost function (C) presents the measure of how wrong a model is in terms of its ability to estimate the relationship between x and y as seen from (11). The cost parameter was optimized by grid search in the training dataset. Given a Hypothesis -> H0 (x) = β0 + β1x, then the cost function (C) is represented as:
where
N is the number of observations.
In developing the SVM classifiers, the values of the cost function used were (0.1, 1, 10, 100).
2.5. Artificial Neural Network
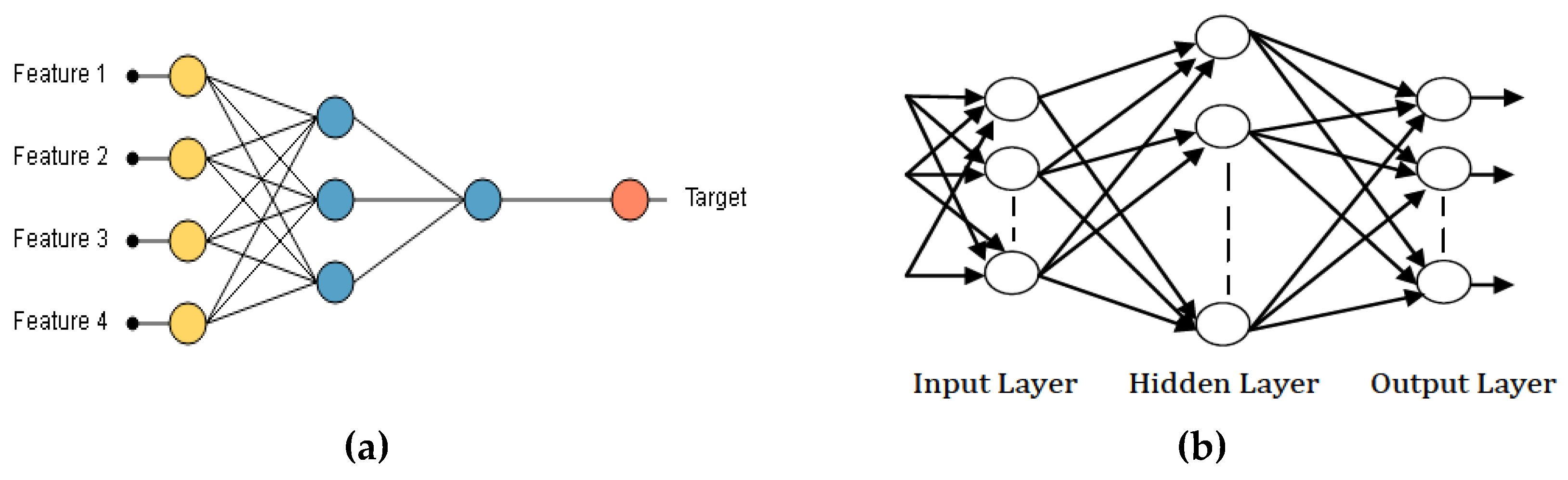
Artificial Neural Network is a computational model which depends on the neural structure of the brain. The outcome from the neural network is dependent on the features or inputs (
Figure 5a) provided to it and the various parameters in the neural network. From
Figure 5a, Feature 1, Feature 2, Feature 3, and Feature 4 represent the input samples while the target represents the output sample. In this current work, we designed a three-layered ANN [
17], which includes input layer, Hidden Layer, and Output Layer as shown in
Figure 5b.
In order to build neural networks, the following properties must be taken into consideration [
28]:
A set of inputs (1, …., n) (i).
A set of outputs (1, …, m).
Number of Hidden Layers.
Number of neurons in each Hidden Layer.
Bias for each neuron in the Hidden Layer (s) and Output Layer .
Weights of the bias in the Hidden Layer (s) and Output Layer .
Weights connecting neurons (w).
Therefore, the mathematical relation between these properties is given as:
The implementation of the ANN model was achieved by using Keras (
https://keras.io/). Keras is high-level neural networks Application Programming Interface (API) which was written in Python. It was built with a focus on enabling fast experimentation. The steps that were followed in developing the ANN model in this study, as summarized in
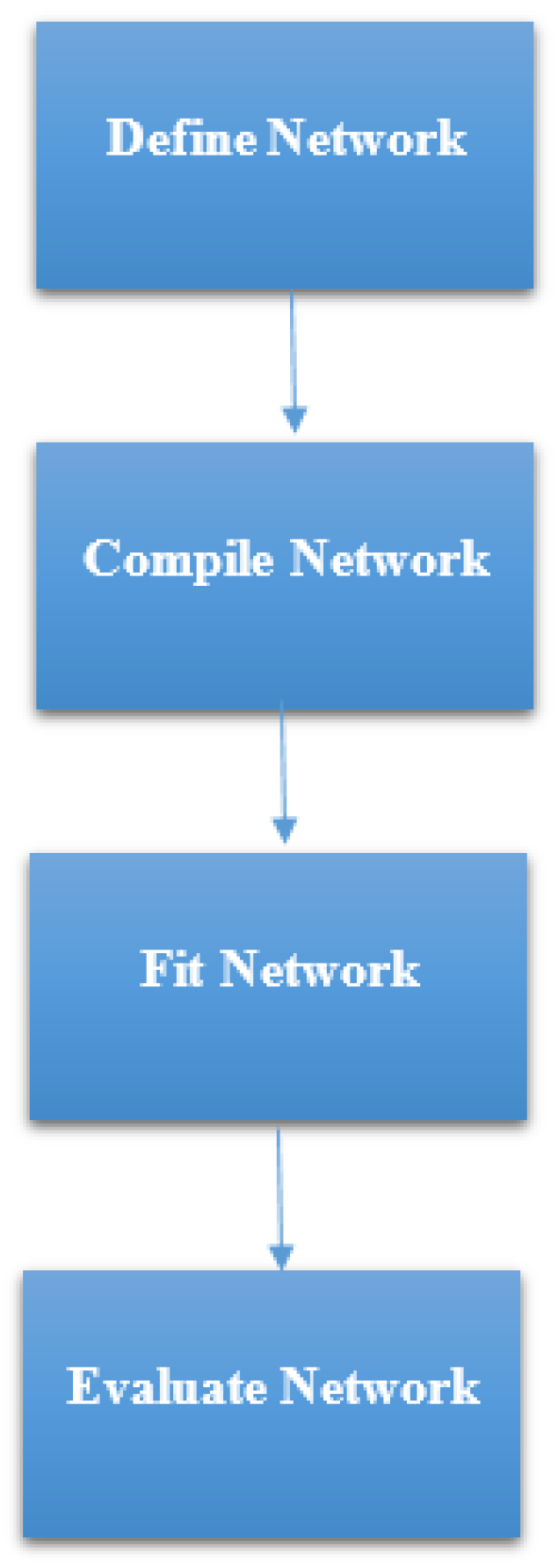
Figure 6 were:
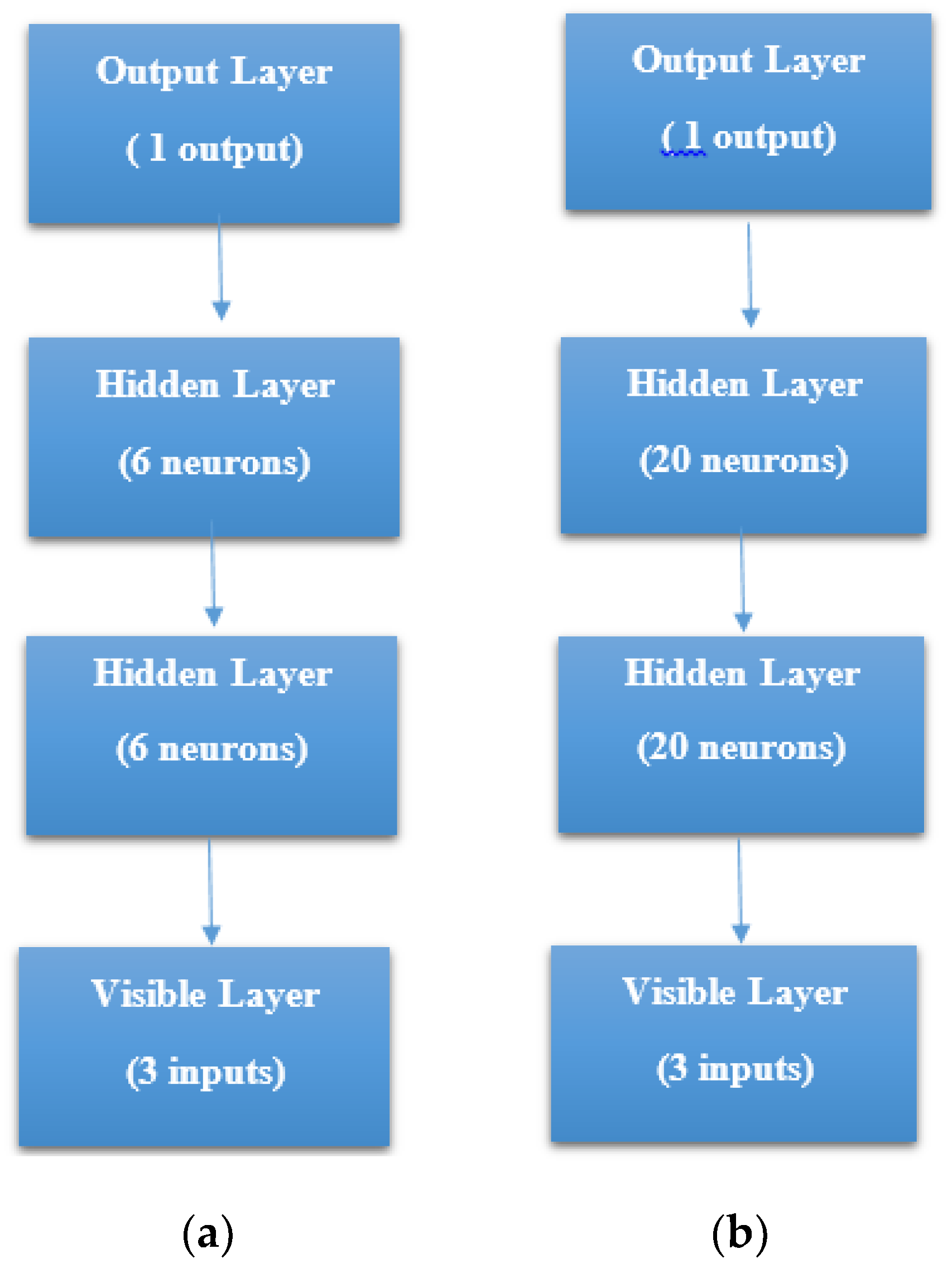
STEP 1: Defining the network—We defined the model as a sequence of layers by using the sequential class in Keras. The sequential class serves as the container for the subsequent layers. In this current work, we built two architectures, which were, 3-6-6-1 network and 3-20-20-1 network as shown in
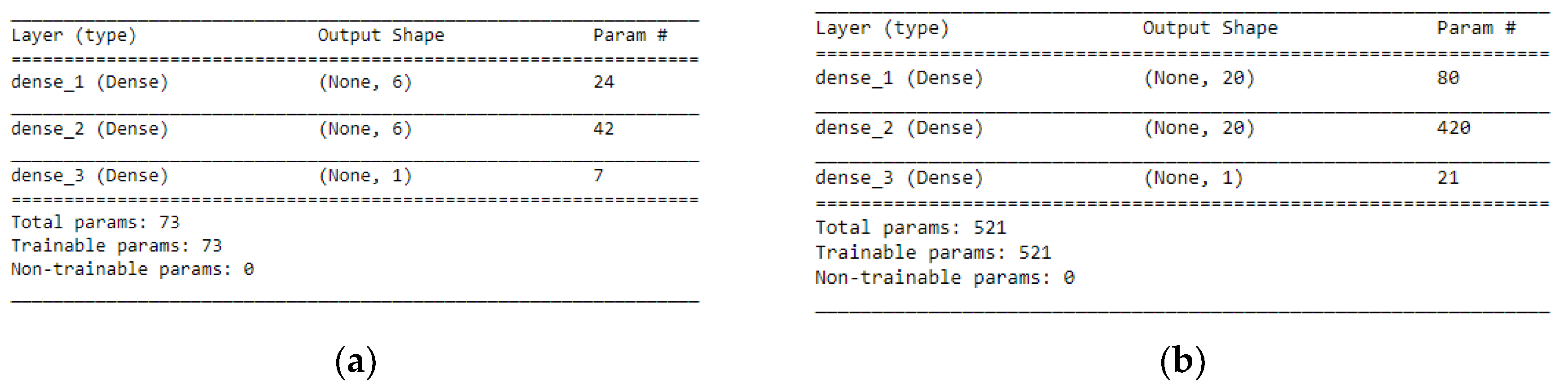
Figure 7a, b respectively. Both the Hidden Layers were activated using the Rectified Linear Unit function (ReLu). The Output Layer was activated by using the sigmoid function, which is better when dealing with binary classification. The activation functions transform a summed signal from each neuron in a layer by extracting and adding to the sequential as a layer-like object. This was achieved by using the Activation class in Keras. In total, we observed a trainable parameter of 73 for the 3-6-6-1 network as shown in
Figure 8a, and in the 3-20-20-1 network, we observed trainable parameters of 521 as shown in
Figure 8b.
STEP 2: Compile the network—After defining the network, we then compiled it. This step is efficient since it transforms the simple sequence of layers that we have defined into highly efficient series of matrix in a format intended to be executed on the CPU. In this work, we achieved the compiling of our network by using the compile class in Keras which has optimization algorithm, loss function, and metrics as parameters. We compared both Adam [
29] and RMSprop (Root Mean Square probability) as the optimization algorithms and binary_crossentropy as the loss function.
STEP 3: Fit the Network—The compiled model is then fit, means adapting the model weights in response to the training dataset. In this step, we specified the training dataset with matrix of input patterns, X, and array of the matching output patterns, y. Here, we compared a batch size of 25 and 32. We also compared epochs of 100 and 500.
STEP 4: Evaluate the Network—In this current work, the ANN model was evaluated using K-Fold Cross-Validation, by which much detailed is given in
Section 2.6.
2.6. Evaluation of the Models
According to k-Fold Cross-Validating Neural Networks [
30], it can be useful to benefit from K-Fold cross-validation when dealing with a small sample size, in order to maximize the ability to evaluate the performance of the model. In addition, as stated by Cross-Validation: Evaluating Estimator Performance [
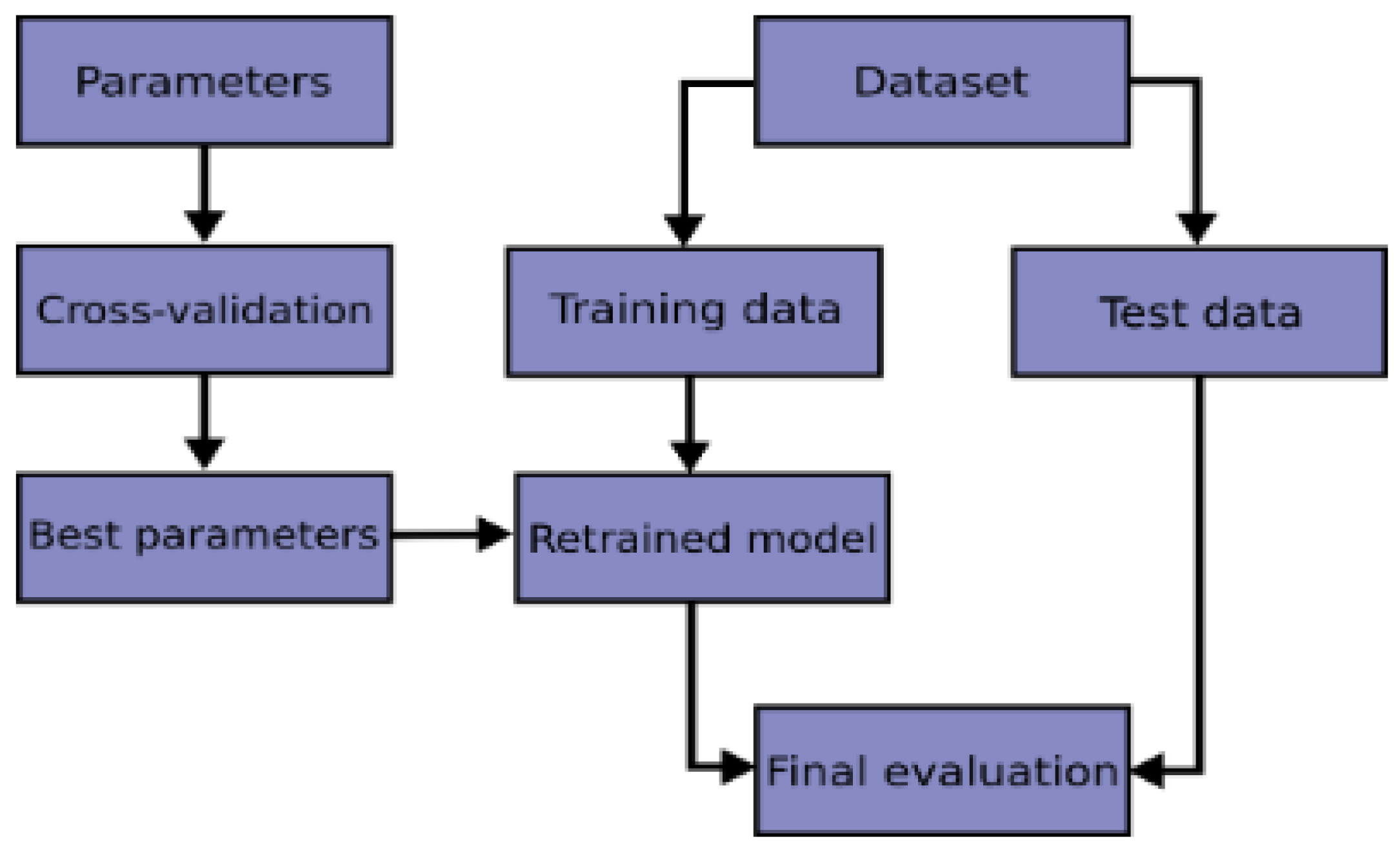
31], it would be a methodological mistake to learn the parameters of a prediction function and then test it on the same data. They further stated that the best parameters can be achieved by using grid search method.
Therefore, in this current work, we performed K-Fold cross-validation to evaluate our models and then used grid search technique to choose the best parameters that helped to produce high performance. The flowchart of a typical cross-validation workflow can be seen from
Figure 9.
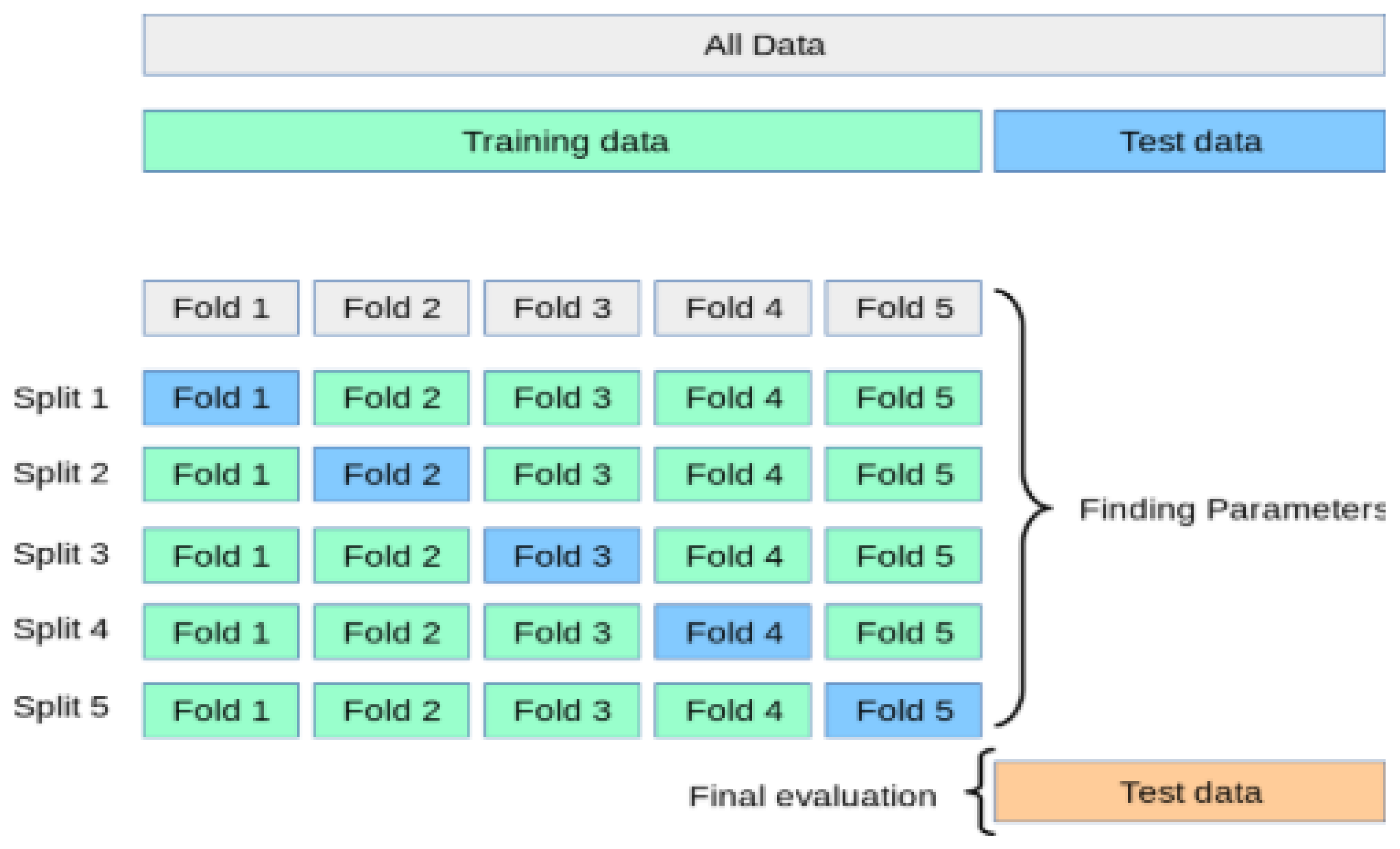
The process of the K-Fold cross-validation is explained as:
Divide the data into K folds.
Out of the K folds, K-1 sets are used for training whereas the remaining set is used for testing.
The model is then trained and tested K times, each time a new set is used as testing whereas the remaining sets are used for training.
Lastly, the result of the K-Fold cross-validation is the average of the results obtained on each set.
The process of the K-Fold cross-validation can be illustrated as shown in
Figure 10.
The only problem was how to use the K-Fold cross-validation from the Sci-Kit Learn library on the ANN models. The problem was that the ANN algorithm is not part of the Sci-Kit Learn learning algorithm, which produced error. We then solved this problem by wrapping the neural networks with the KerasClassifier class [
30], which helped us to use the Sci-Kit Learn. This method rendered the neural networks to behave as any other Sci-Kit Learn learning algorithm (Random forest, SVM). In this current work, we performed both 5- and 10-Fold Cross-Validation based on empirical evidence that 5- or 10-Fold Cross Validation should be preferred [
31].
4. Discussion
In previous works, other practitioners have compared and applied several machine learning algorithms to diagnose and predict diseases [
7,
9,
10,
11,
12,
13,
14,
15,
16,
17,
32]. When it comes to a literature review on using machine learning algorithms in predicting other diseases, the work of Animesh et al. [
12] has done a good job. In the work of Kavitha et al. [
13], they modeled an ANN to detect heart disease using 13 inputs, 2 hidden nodes and 1 output. Also, the work of Noura [
14] used ANN to predict heart disease, which achieved 88% accuracy. It was further stated that ANN is broadly used in medical diagnosis and healthcare systems as result to the predictive power it possesses as a model as confirmed by Animesh et al. [
12]. The work of Mrudula et al. [
15] compared SVM and ANN to predict heart disease, they stated that, ANN outperformed the SVM model to predict the disease.
Furthermore, the work of Tahmooresi et al. [
2] compared several machine learning algorithms such as SVM, ANN, KNN, DT for breast cancer detection. They have performed an in-depth literature review on various machine learning algorithms for further reading. They concluded that SVM outperformed all the other models, which achieved an accuracy of 99.8% to detect the breast cancer disease. Also, the work of Ayeldeen et al. [
16] compared several machine learning algorithms on a case-based retrieval approach of clinical breast cancer patients. They concluded that the RF model showed the maximum accuracy of 99%. The work of Kuo et al. [
18] compared the performance of naïve-Bayesian, SVM, logistic regression, C4.5 decision tree, and random forest methods in predicting the medical costs of spinal fusion. They concluded that the random forest algorithm had the best predictive performance in comparison to the other techniques, achieving an accuracy of 84.30%, a sensitivity of 71.4%, a specificity of 92.2%, and an AUC of 0.904. ly. This predictive power of RF model can be noticed in this current research work in terms of accuracy as shown in
Table 15 and
Table 16.
And lastly, in the work of Abdullah et al. [
8], they used machine learning techniques to predict spinal abnormalities based on KNN and RF models. They concluded that the KNN model which achieved an accuracy of 85.32% outperformed the RF model which had an accuracy of 79.57%.
Therefore, the purpose of this current research was to compare the performances of three most used and famous machine learning algorithms such as the RF, SVM, and ANN in the classification and prediction of kyphosis disease based on a biomedical dataset.
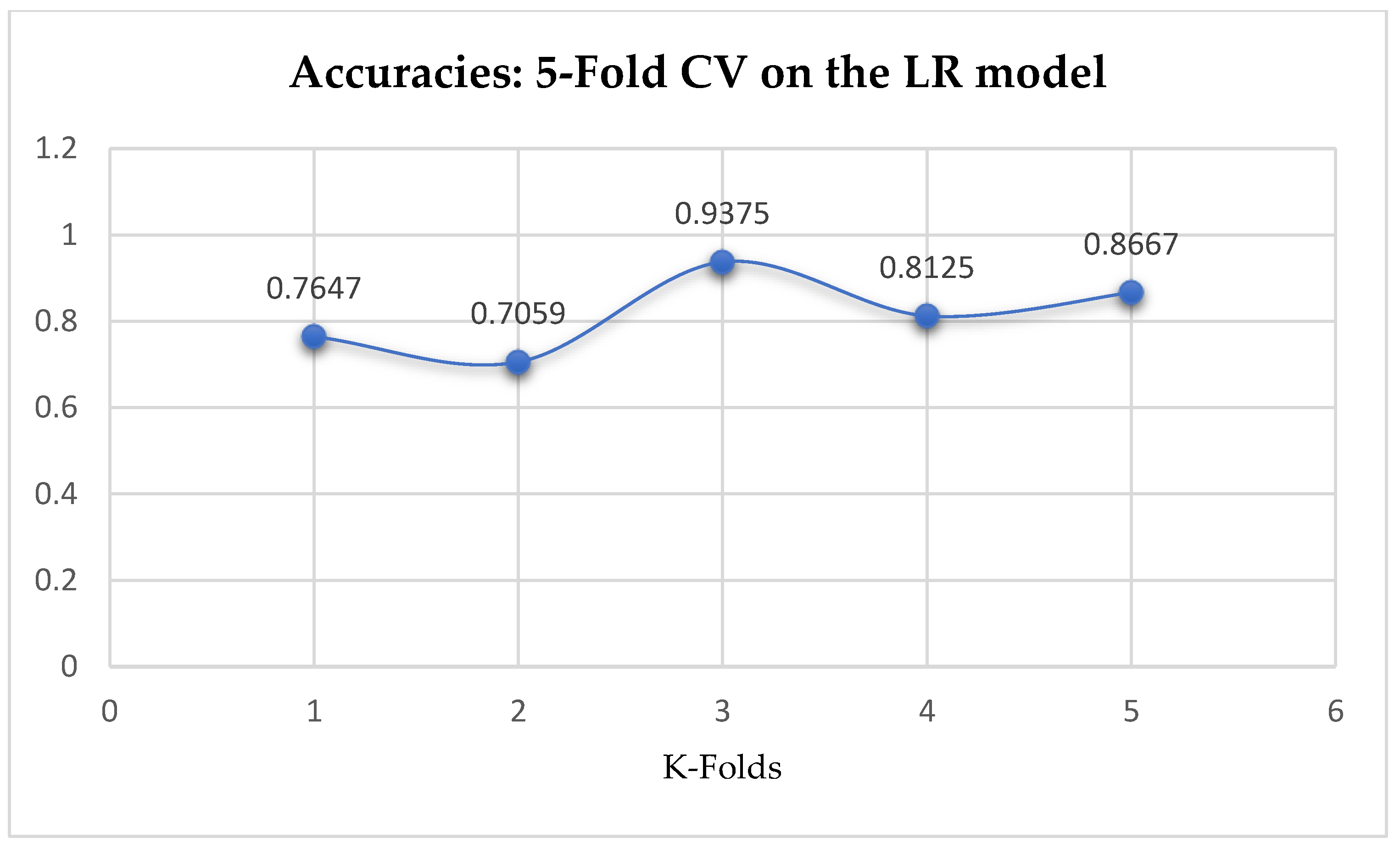
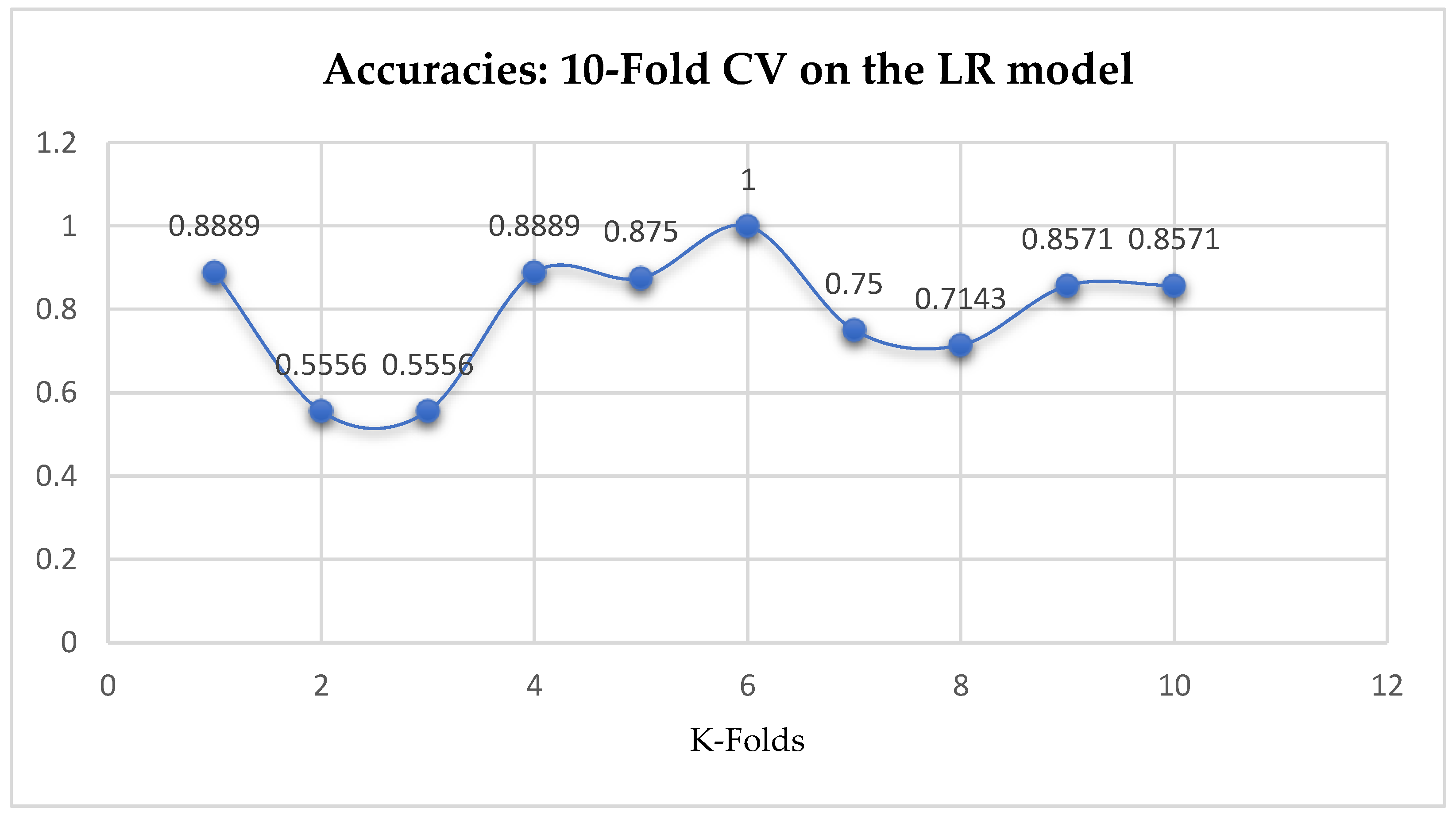
At first, we performed 5-Fold and 10-Fold Cross-Validations using Logistic Regression as a baseline model to compare with our ML models in terms of K-Fold CV without performing grid searching. The idea was based on the assumption concluded in the work of Christodoulou et al. [
33] that they found no evidence of superior performance of machine learning over Logistic Regression when performing clinical prediction modeling. We observed a mean accuracy of 81.75% as seen from
Figure 15, based on the 5-Fold Cross-Validation after evaluating the LR model. After performing 10-Fold Cross-Validation, the LR model achieved a mean accuracy of 79.42% as seen from
Figure 15.
Based on the ML models, we performed two categories of experiments, (1) K-Fold Cross-Validation without Grid Search, and (2) Grid Search with K-Fold Cross-Validation. In each of the experiments, we performed both 5-Fold and 10-Fold Cross-Validation. When dealing with K-Fold Cross-Validation, 5 or 10 Fold is mostly preferred [
30].
In terms of the 5-Fold Cross-Validation, without Grid Searching, the RF model achieved a mean accuracy of 79.01%. By evaluating the RF model based on the K-Fold Cross-Validation, without grid searching, the baseline model, LR outperformed the RF model as seen from
Table 17.
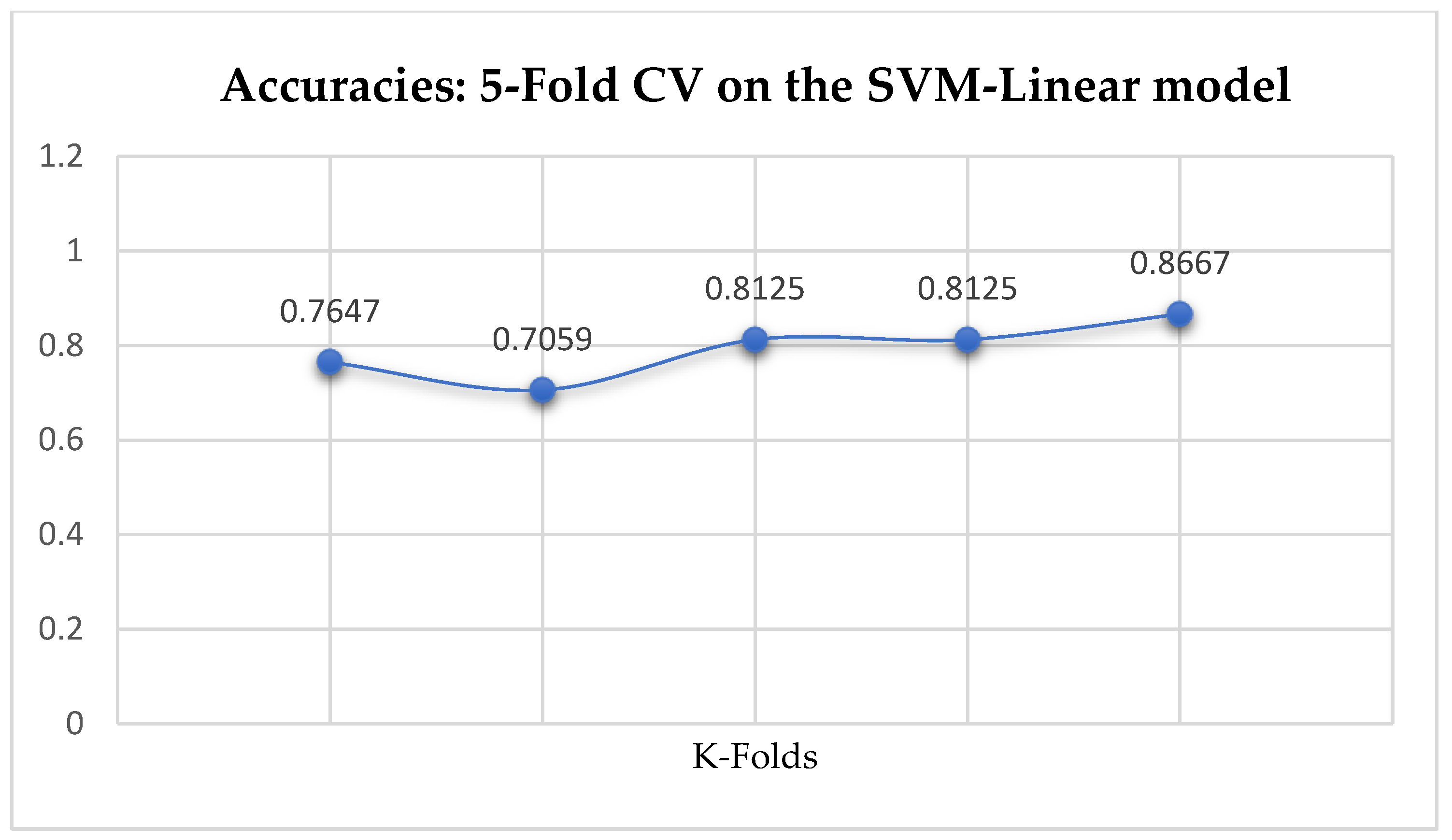
Among the SVM classifiers, The SVM-Linear achieved a mean accuracy of 79.25% based on the 5-Fold Cross-Validation as shown in
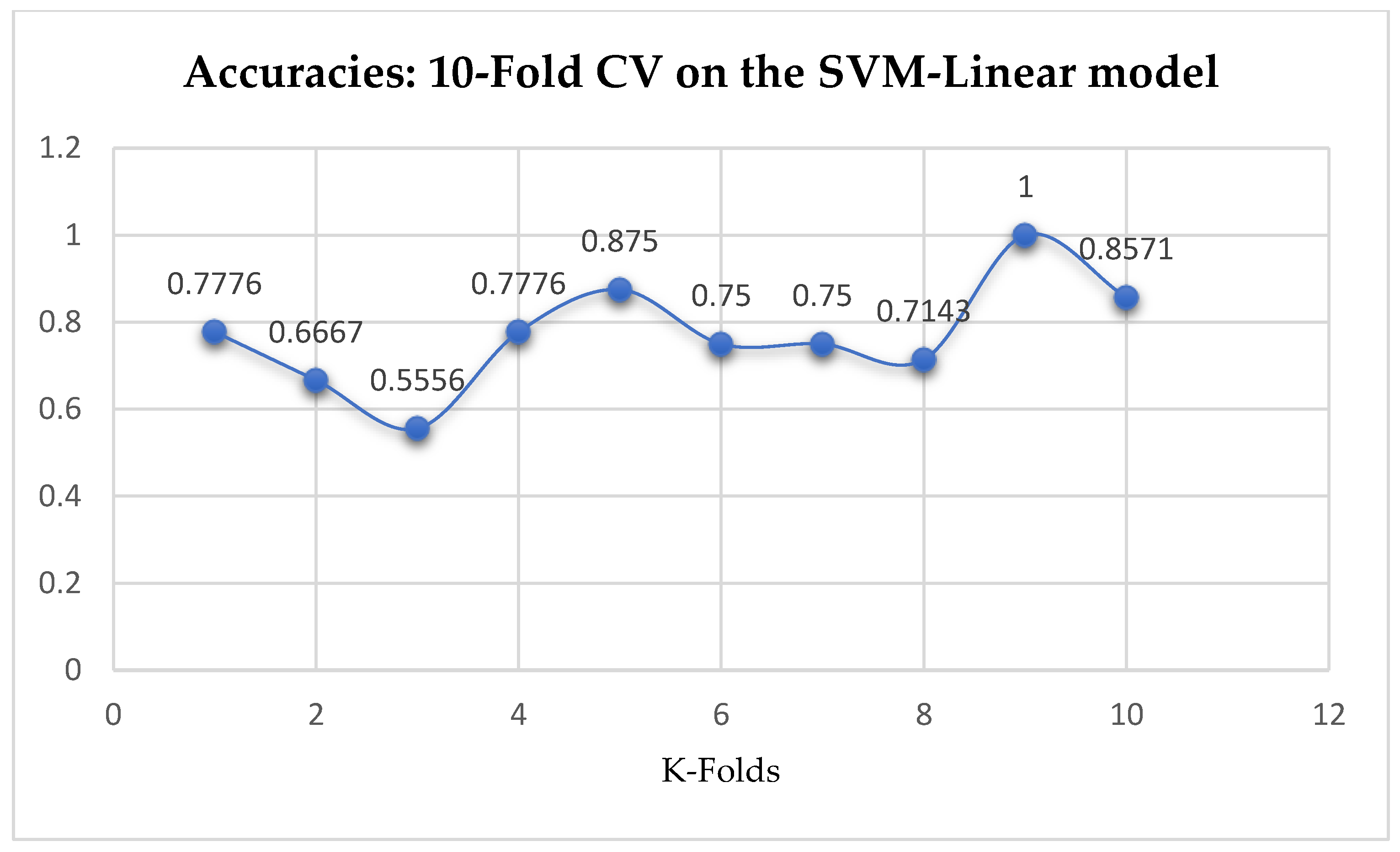
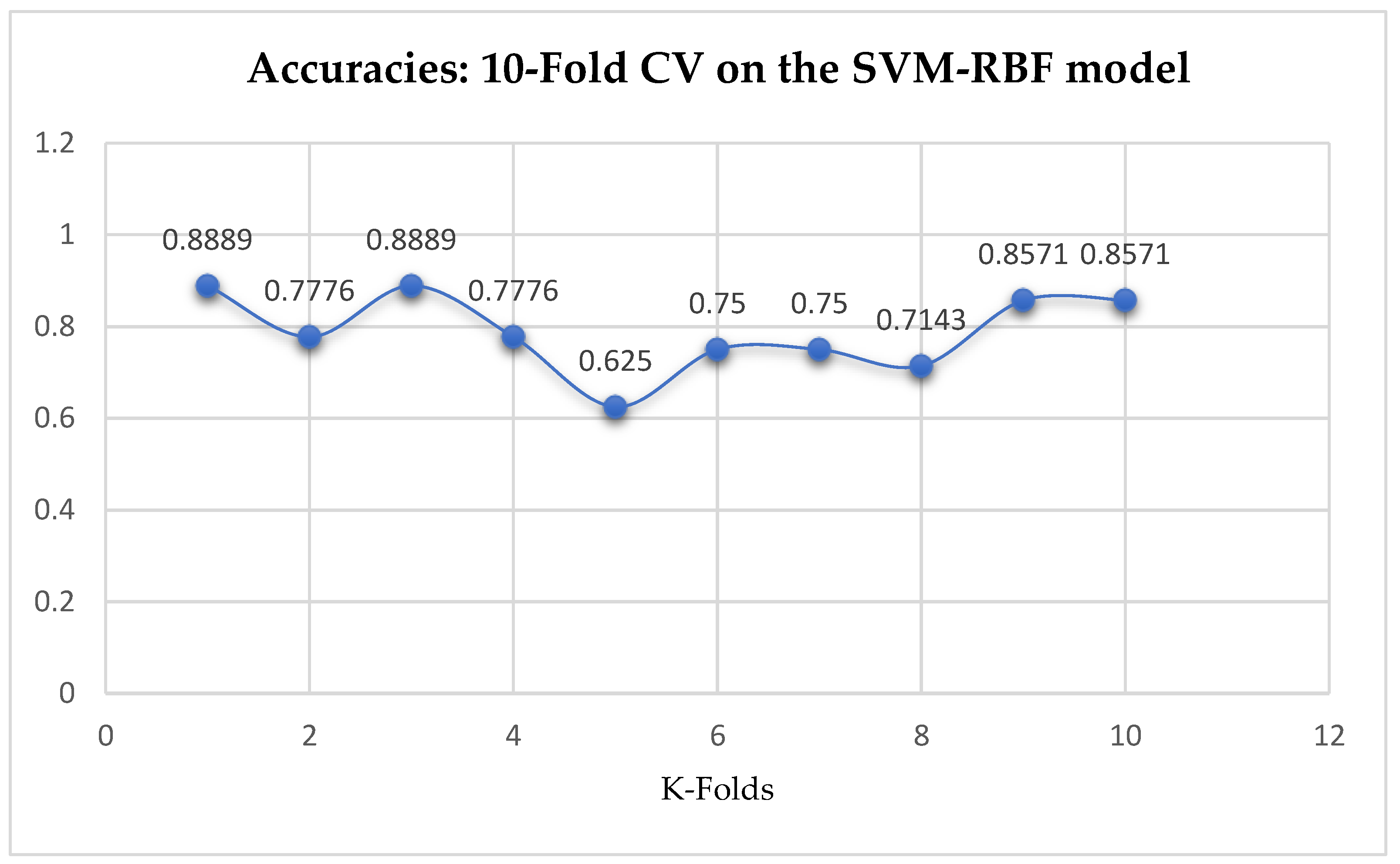
Table 17. We can observe a decrease in accuracy from 79.25% to 77.24% after the 10-Fold CV as seen from
Table 17. Also, based on the K-Fold Cross-Validation, without Grid Searching, the baseline model, LR outperformed the SVM-Linear model as seen from
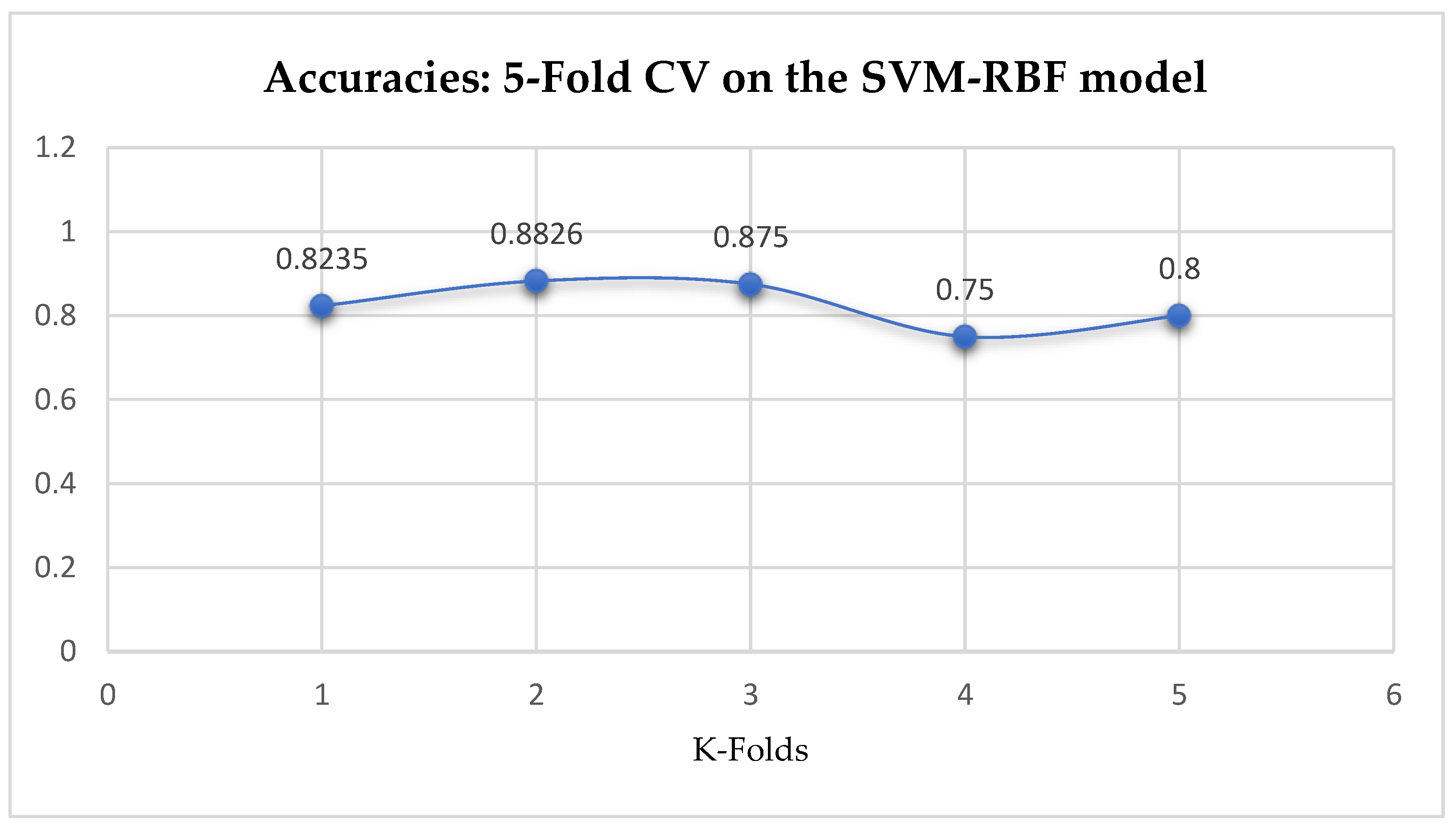
Table 17. The SVM-RBF classifier achieved a mean accuracy of 82.62% based on the 5-Fold Cross-Validation as seen from
Table 17. With the 10-Fold Cross-Validation, the SVM-RBF classifier achieved a mean accuracy of 78.87% as seen from
Table 17. We can observe a decrease in accuracy from 82.62% to 78.87% after the 10-Fold CV by the SVM-RBF classifier as shown in
Table 17. By comparing the SVM-RBF with the LR model, based on the 5-Fold Cross-Validation, the SVM-RBF model outperformed the LR model. Whereas, based on the 10-Fold Cross-Validation, the LR model slightly outperformed the SVM-RBF model as seen from
Table 17. Finally, the SVM-Poly classifier achieved a mean accuracy of 76.42% based on the 5-Fold Cross-Validation as seen from
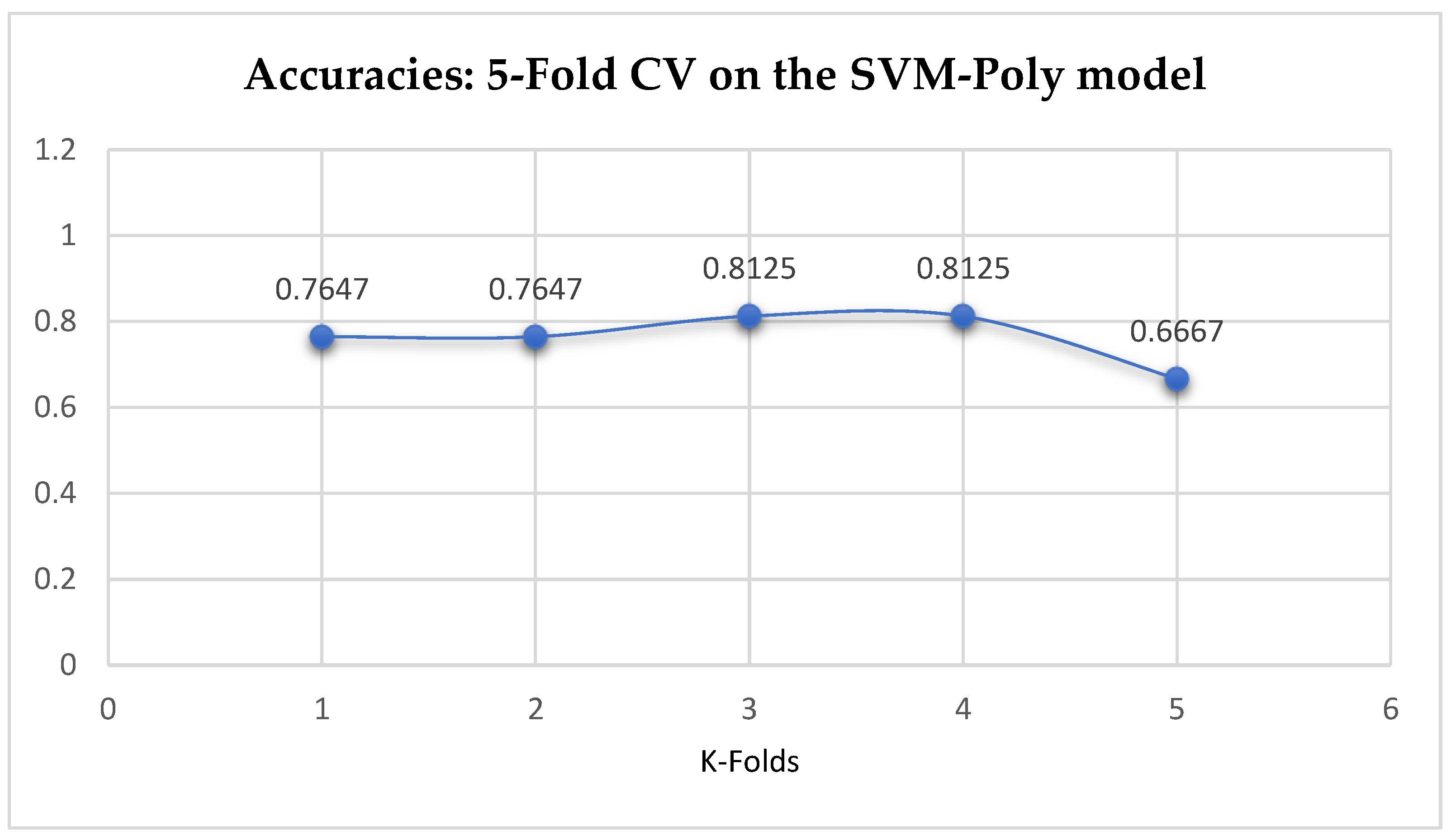
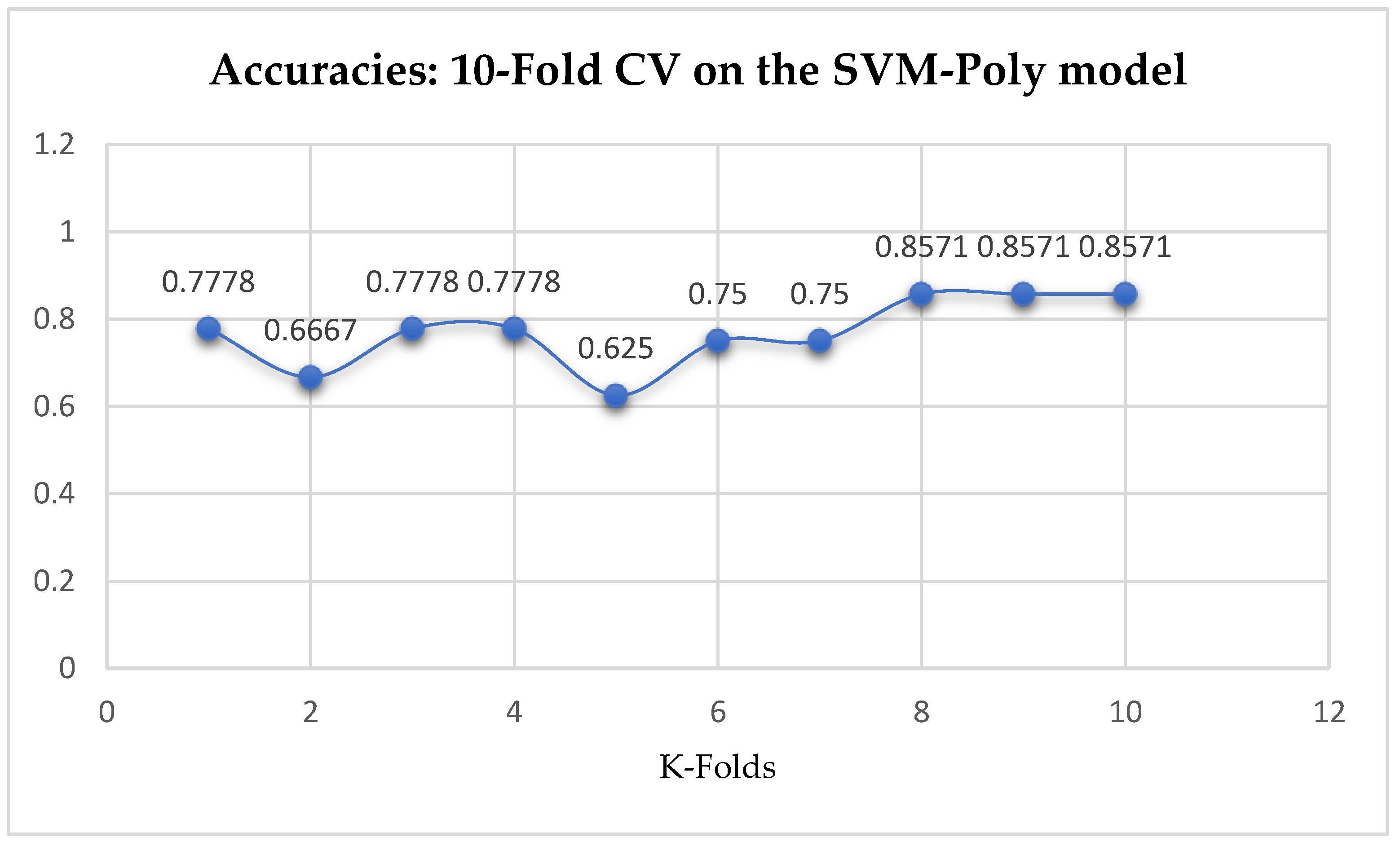
Table 17. With the 10-Fold Cross-Validation, the SVM-Poly classifier achieved a mean accuracy of 76.96%. We can observe an increase in accuracy from 76.42% to 76.96% after the 10-Fold CV by the SVM-Poly classifier as seen from
Table 17. By comparing the SVM-Poly model with the LR model, based on the K-Fold Cross-Validation, without grid search, the LR model outperformed the SVM-Poly model.
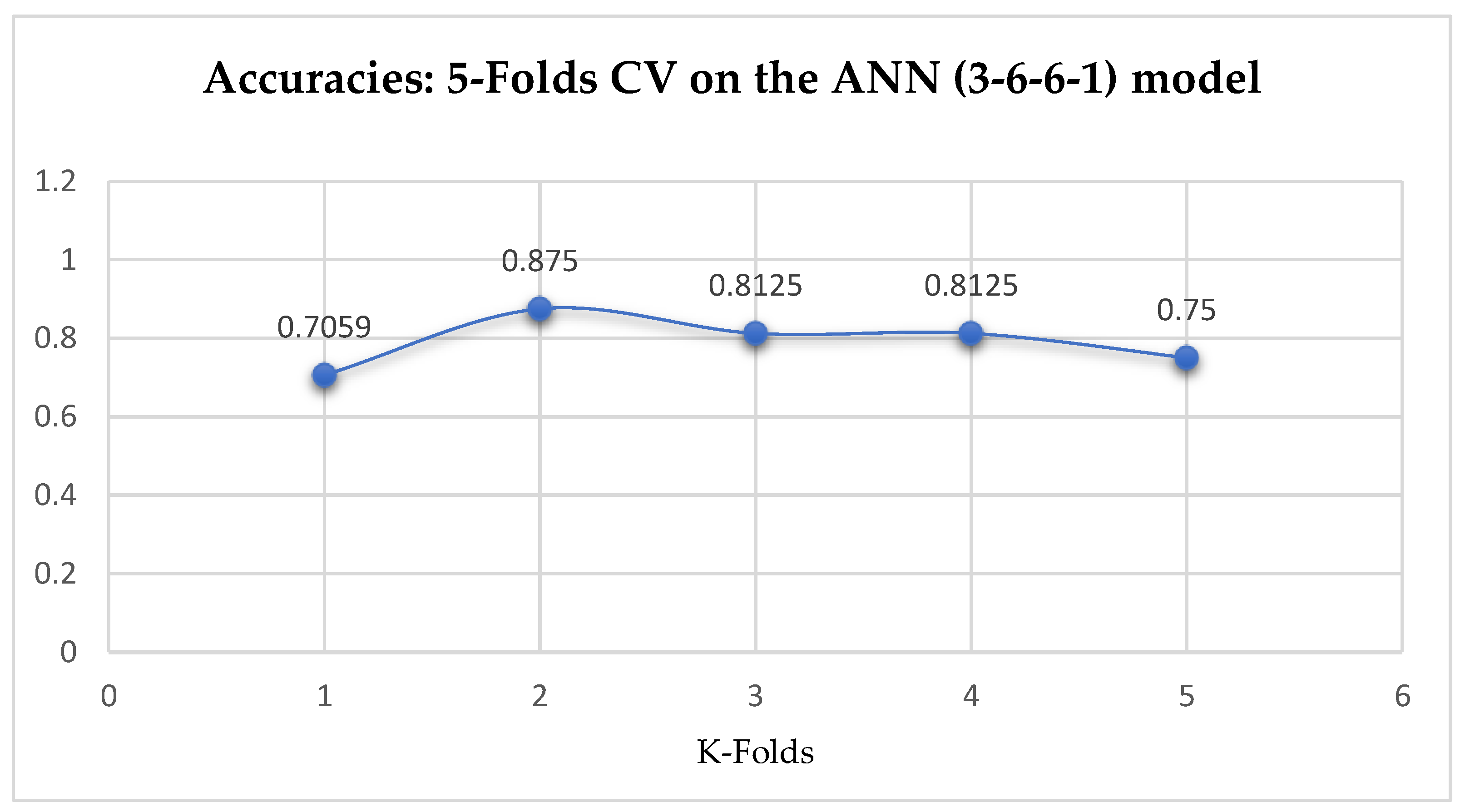
Lastly, based on the K-Fold Cross-Validation, without Grid Searching, the ANN (3-6-6-1) model achieved a mean accuracy of 79.12% based on the 5-Fold Cross-Validation as seen from
Table 17. With the 10-Fold Cross-Validation, the ANN (3-6-6-1) model achieved a mean accuracy of 79.03% as seen from
Table 17. We can observe a decrease in accuracy from 79.12% to 79.03% after the 10-Fold CV by the ANN (3-6-6-1) model as shown in
Table 17. Also, the ANN (3-20-20-1) model achieved a mean accuracy of 79.12% based on the 5-Fold Cross-Validation as seen from
Table 17. With the 10-Fold Cross-Validation, the ANN (3-20-20-1) model achieved a mean accuracy of 79.03%. We can observe a decrease in accuracy from 79.12% to 79.03% after the 10-Fold CV by the ANN (3-6-6-1) model as shown in
Table 17. By comparing the ANN models with the LR model, based on the K-Fold Cross-Validation, without grid search, the LR model outperformed both the ANN models as seen from
Table 17.
With the analysis in this current work, based on performing 5- and 10-Fold Cross-Validation without grid searching (as summarized in
Table 17), we then state that the assumption concluded in the work of Christodoulou et al. [
33] that they found no evidence of superior performance of machine learning over Logistic Regression when performing clinical prediction modeling is somehow quite true.
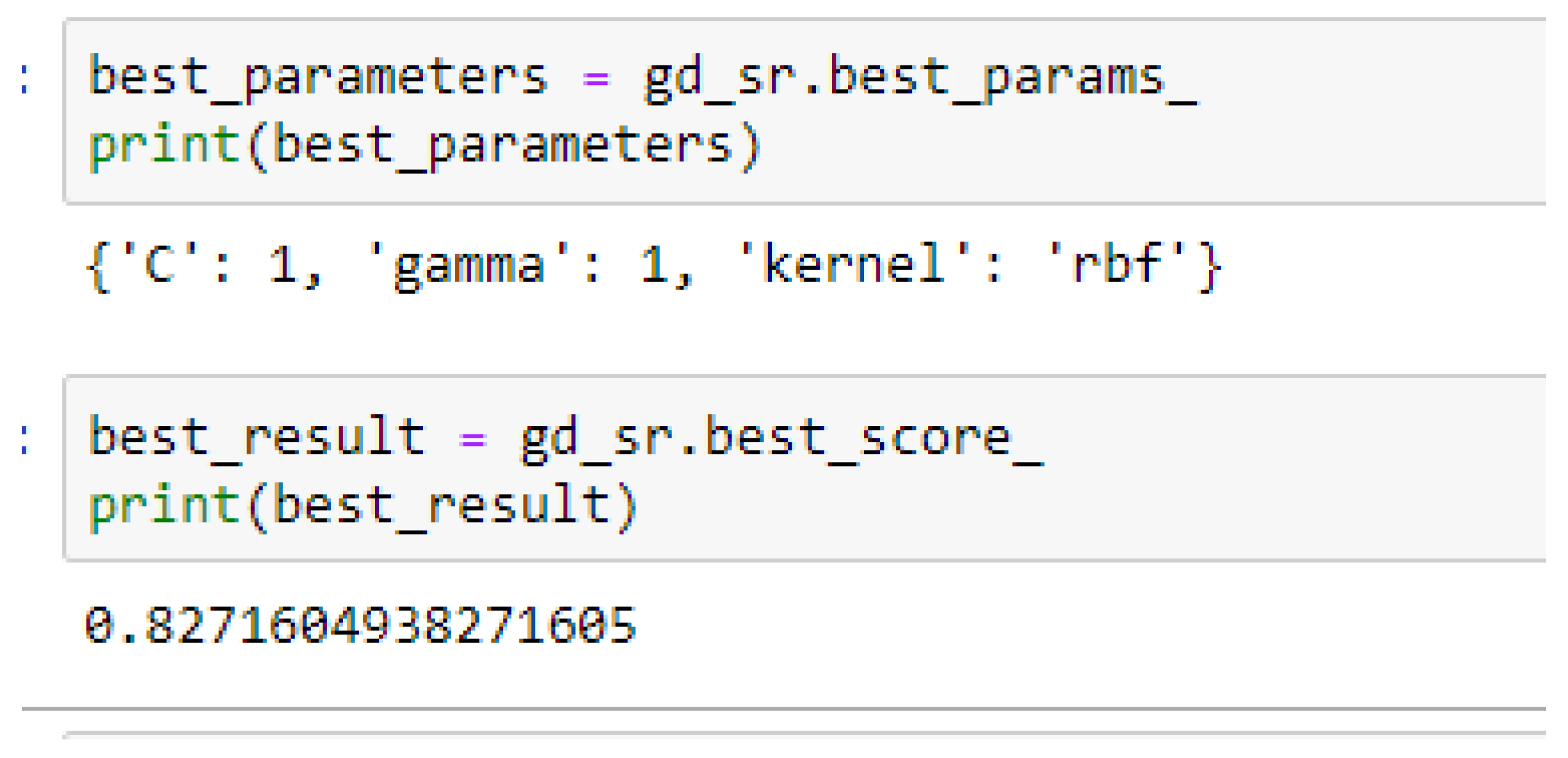
We observed that, among the ML algorithms, the SVM-RBF outperformed all the other ML models, which achieved an accuracy of 82.62% based on the 5-Fold Cross-Validation with grid searching as shown in
Table 17. Whereas, based on the 10-Fold Cross-Validation without grid searching, the ANN models outperformed the other ML models, by which both the ANN models achieved an accuracy of 79.03% as shown in
Table 17.
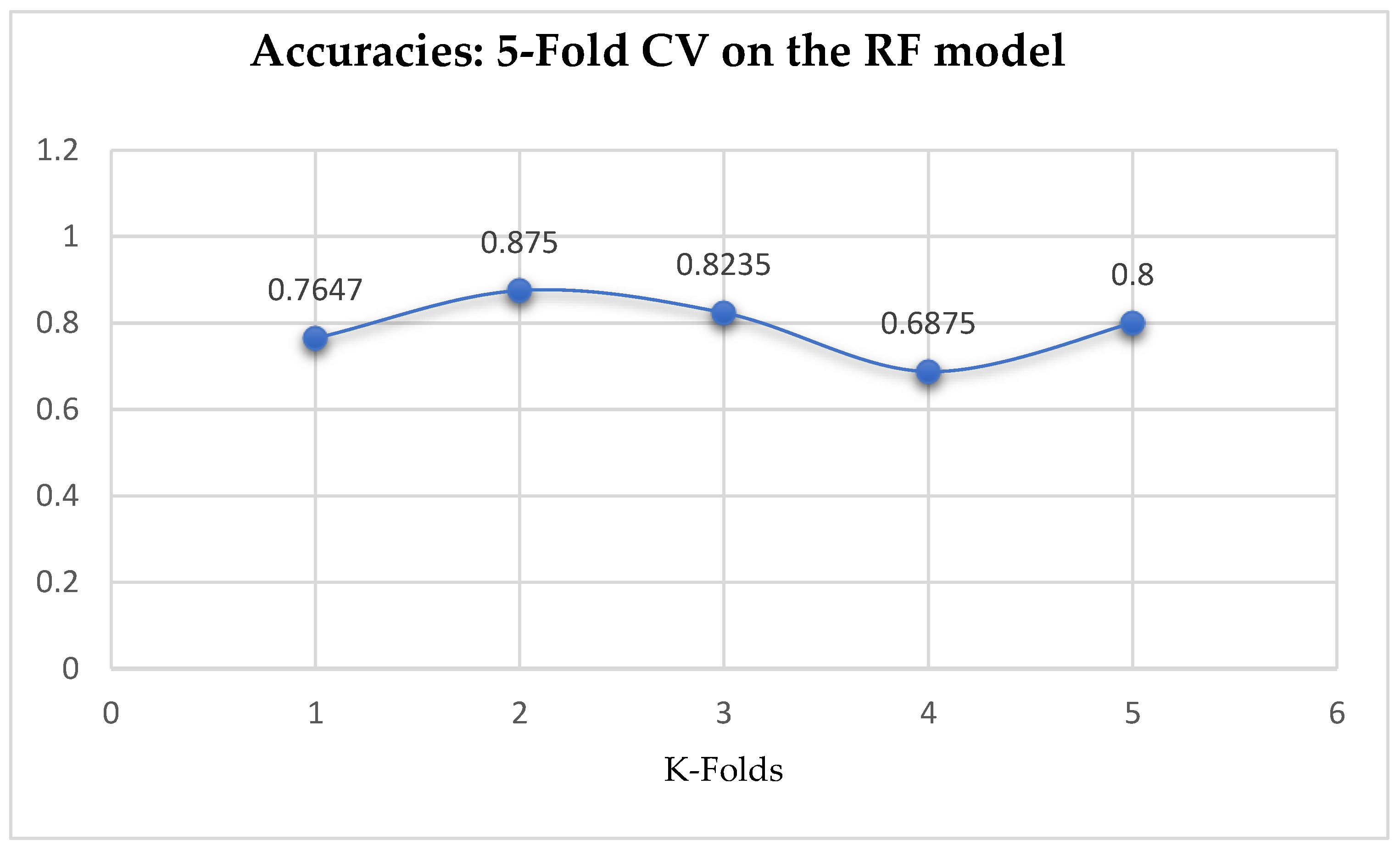
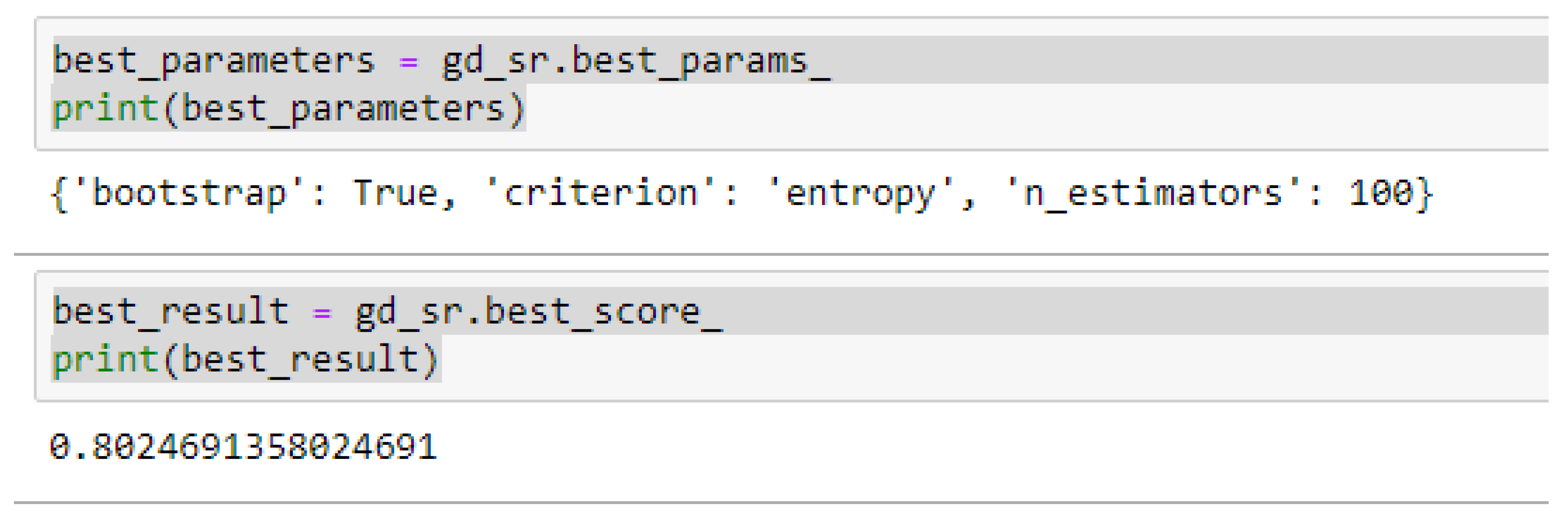
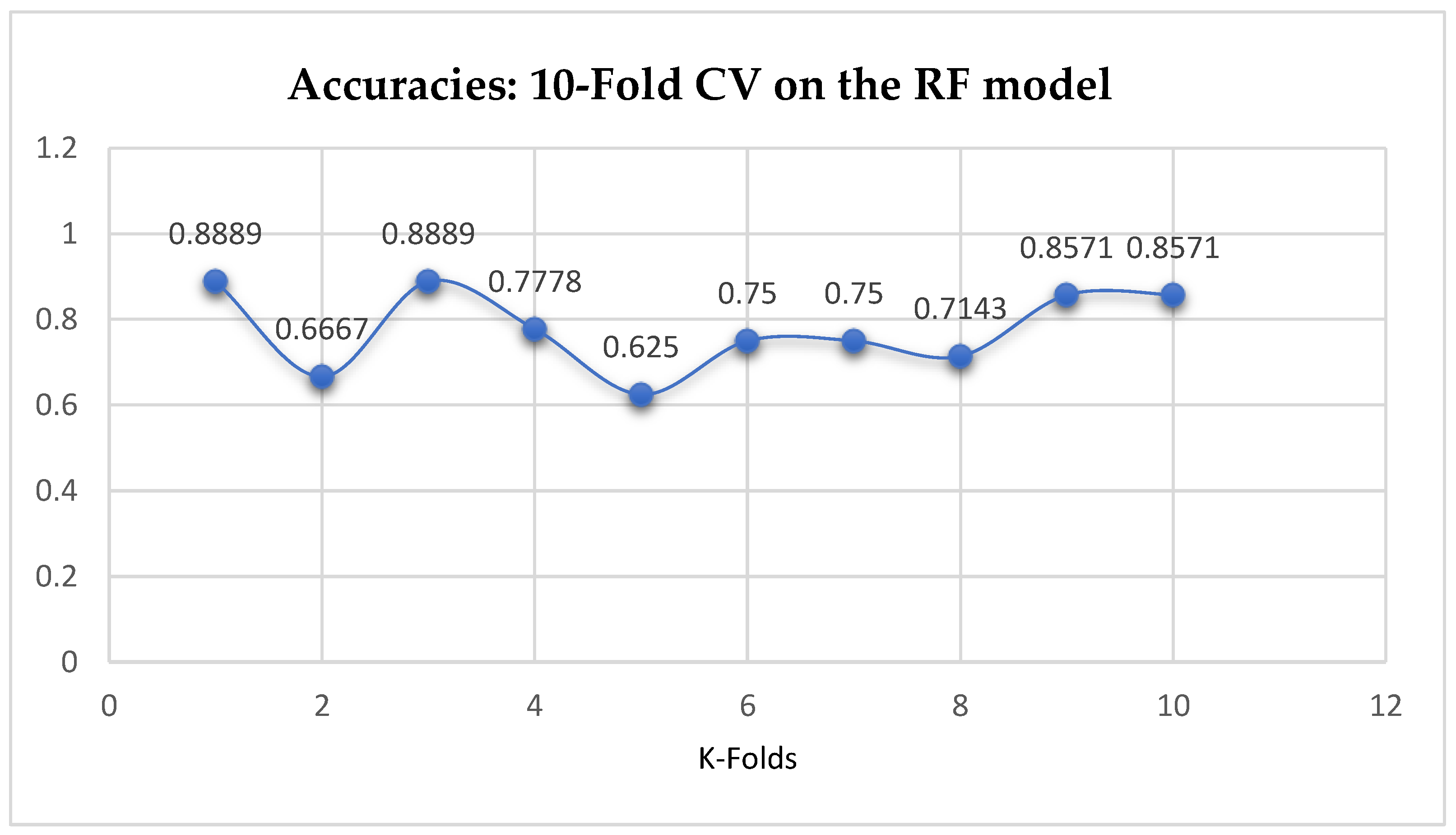
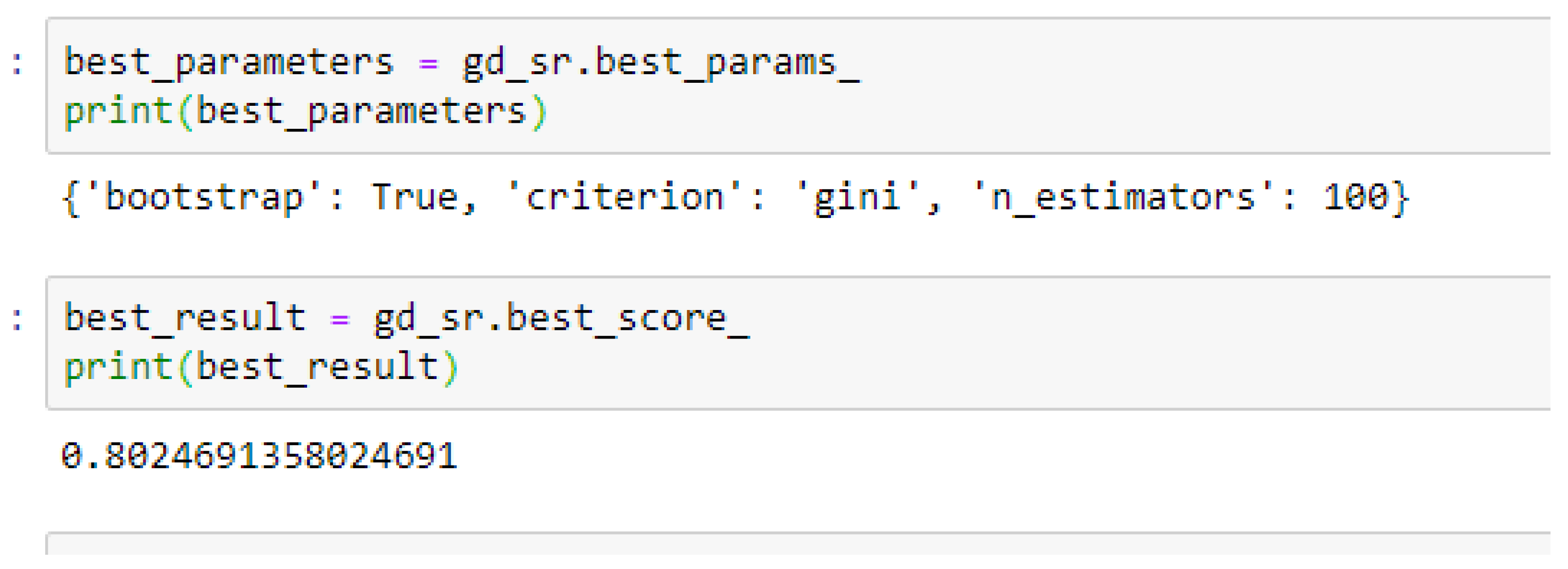
The second category of our experiment was to improve on the performances of the ML models, and then find the best parameters with the highest accuracies. We achieved these by performing grid search with 5- and 10-Fold Cross-Validation. After running the grid search algorithms, the performance of the RF model improved from 79.01%, and 77.76% to 80.25% based on both the 5- and 10-Fold Cross-Validation as seen from
Table 15 and
Table 16 respectively. We observed that, based on 10-Fold CV with grid search, the RF model outperformed the LR model as seen from
Table 15 and
Table 16 respectively.
Among the SVM classifiers, we also observed that, the accuracies of the SVM-Linear did not improve significantly after performing the grid search with the K-Fold CV (as shown in
Table 15 and
Table 16) to that of the K-Fold CV without grid search as shown in
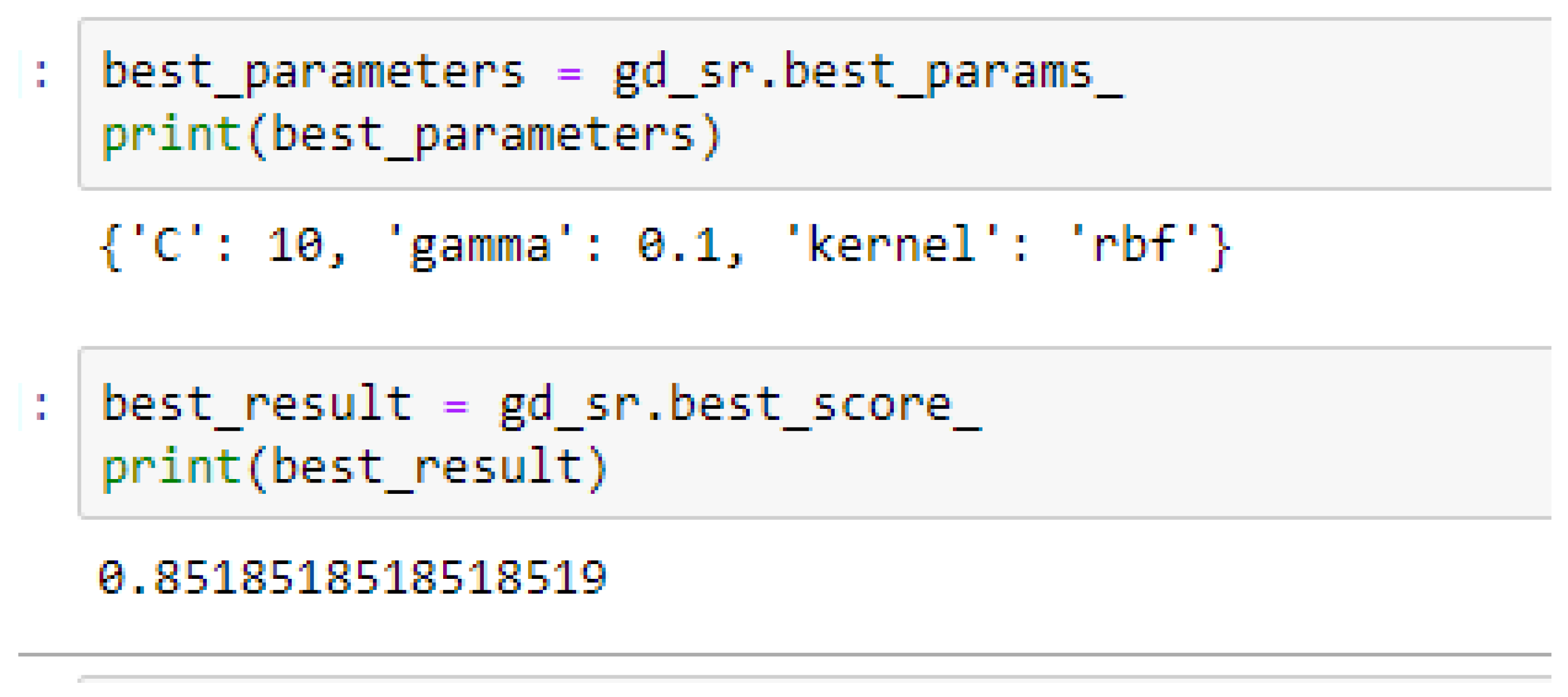
Table 17. Again, the LR model outperformed the SVM-Linear model. We observed an improvement of the SVM-RBF model from 82.62%, and 78.87% to 82.72, and 85.19% based on the 5- and 10-Fold Cross-Validation as seen from
Table 15 and
Table 16 respectively. By comparing the SVM-RBF model with the LR model, after performing grid search with K-Fold CV, the SVM-RBF model then outperformed the LR model as seen from (
Table 15 and
Table 16) and
Table 17 respectively.
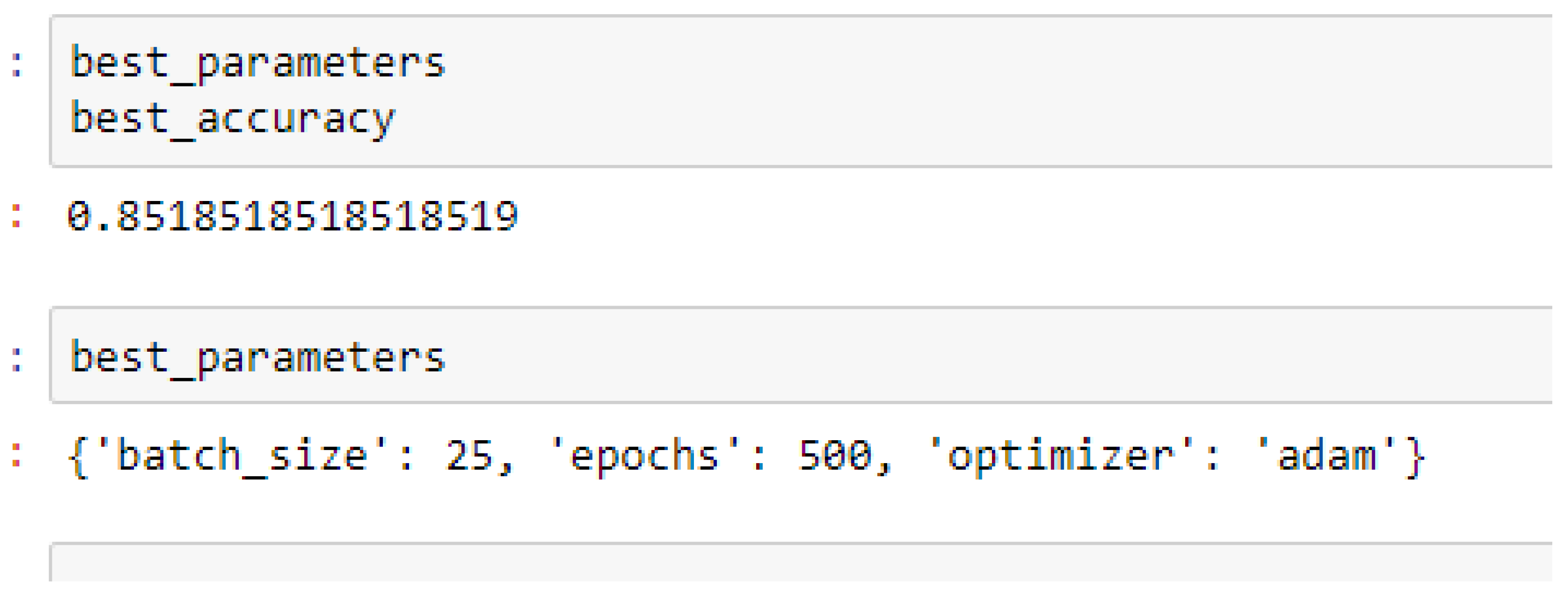
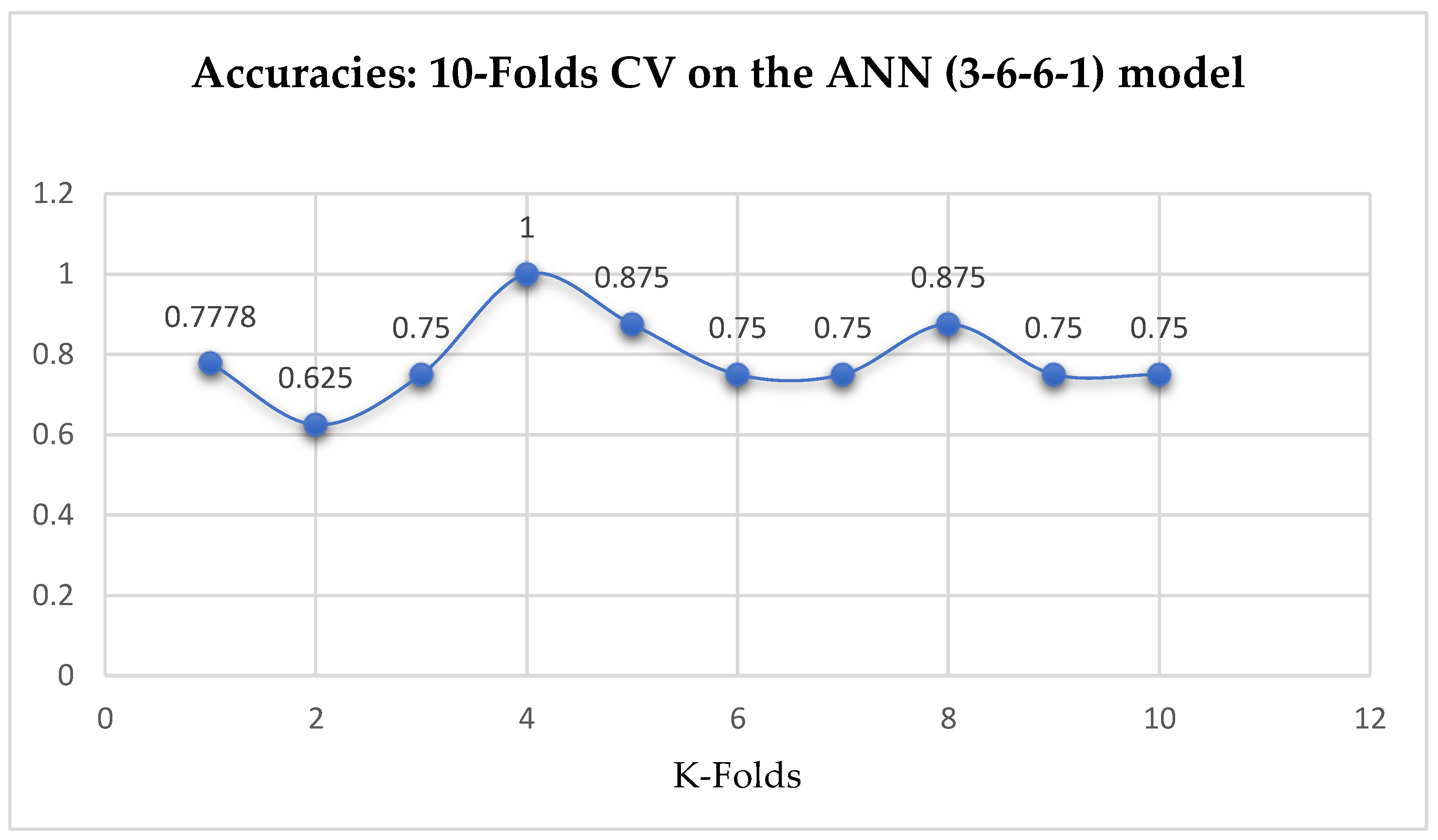
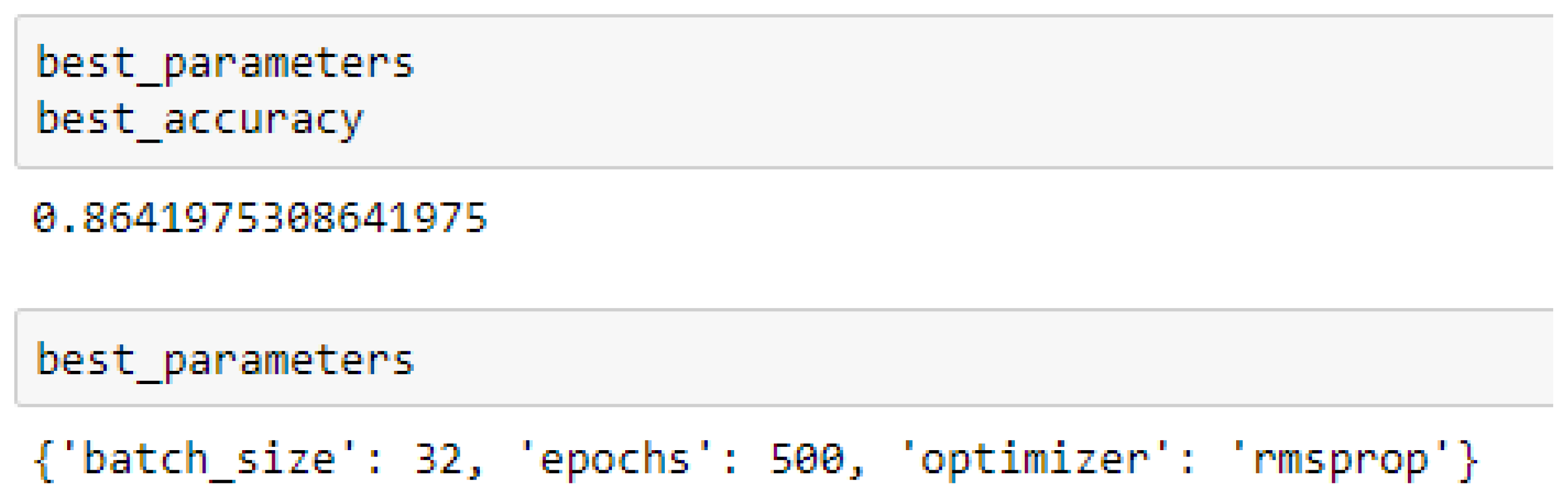
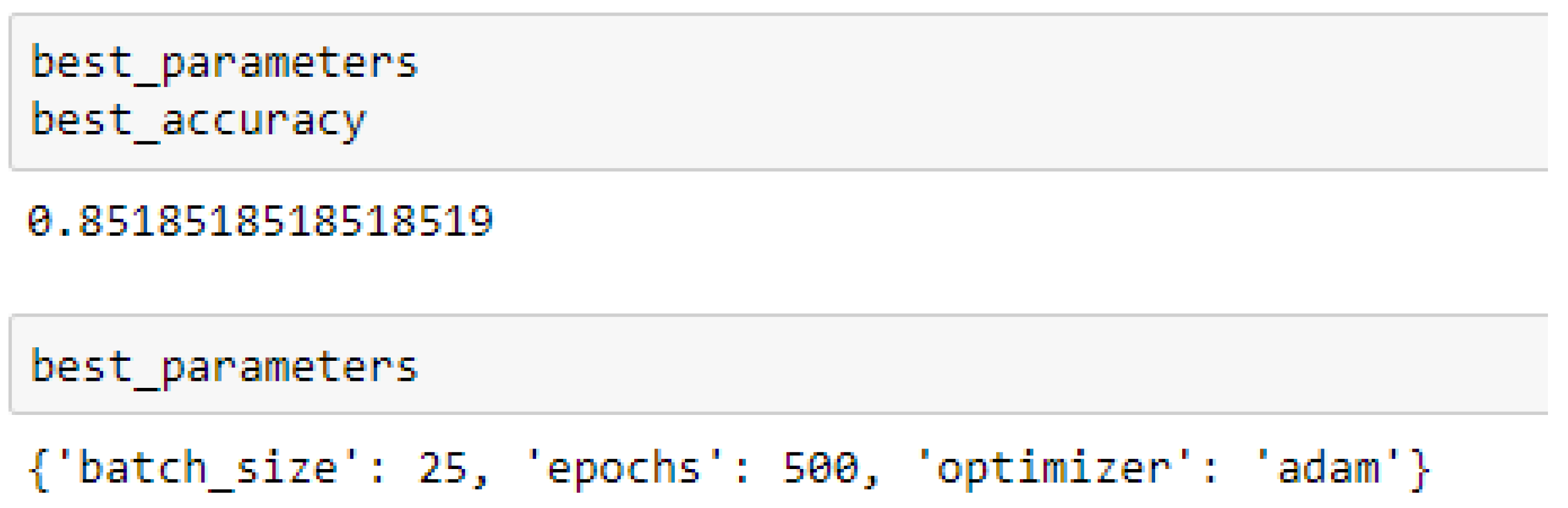
Finally, among the ANN models, the accuracies of the ANN (3-6-6-1) improved from 79.12%, and 79.03% to 85.19%, and 86.42% based on the 5- and 10-Fold Cross-Validation as seen from
Table 15 and
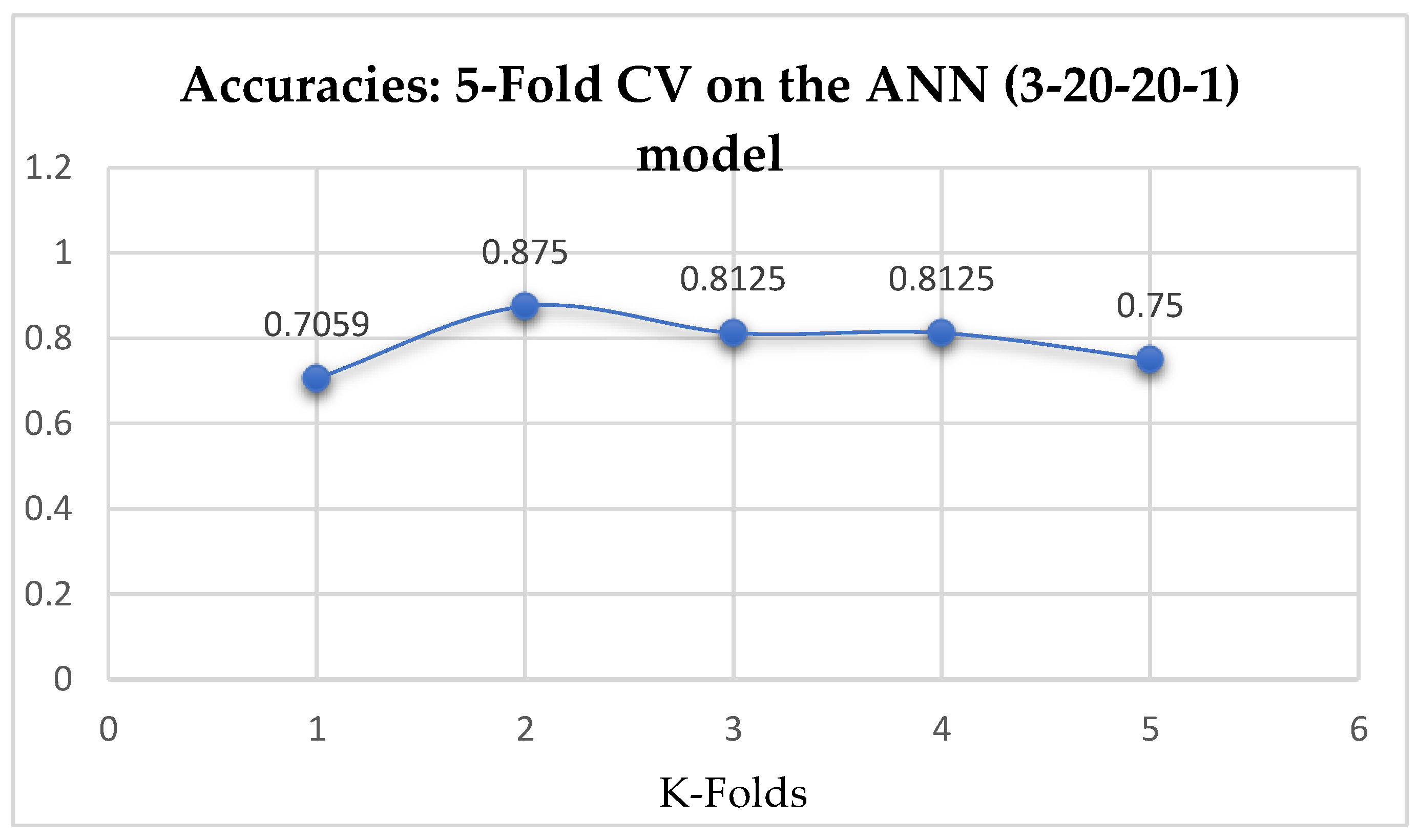
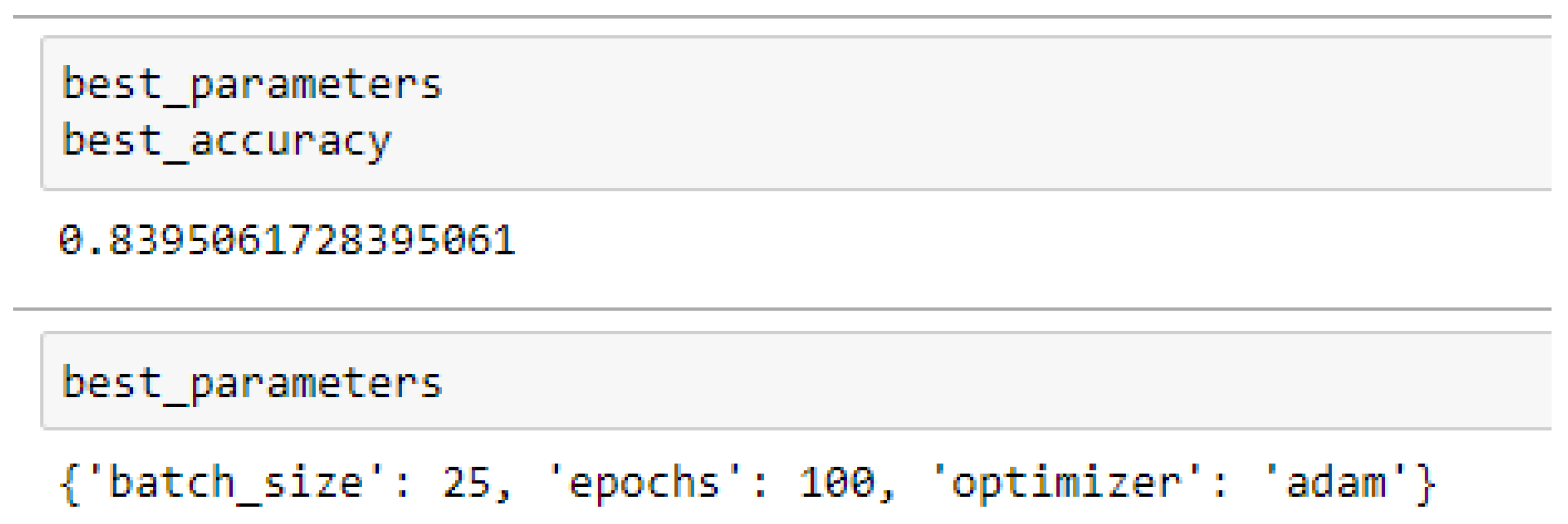
Table 16 respectively. Also, the accuracies of the ANN (3-20-20-1) improved from 79.12%, and 79.03% to 83.95%, and 85.19% based on the 5- and 10- Fold Cross-Validation as seen from
Table 15 and
Table 16 respectively.
By comparing the ML models as seen from
Table 15 and
Table 16, we observed that, by performing 5- or 10-Fold Cross-Validation based on the RF model, the best parameters did not change much, setting bootstrap to true, criterion to either entropy or gini, and the number of trees to 100, really improved the RF model in both cases as seen from
Figure 16 and
Figure 17 respectively.
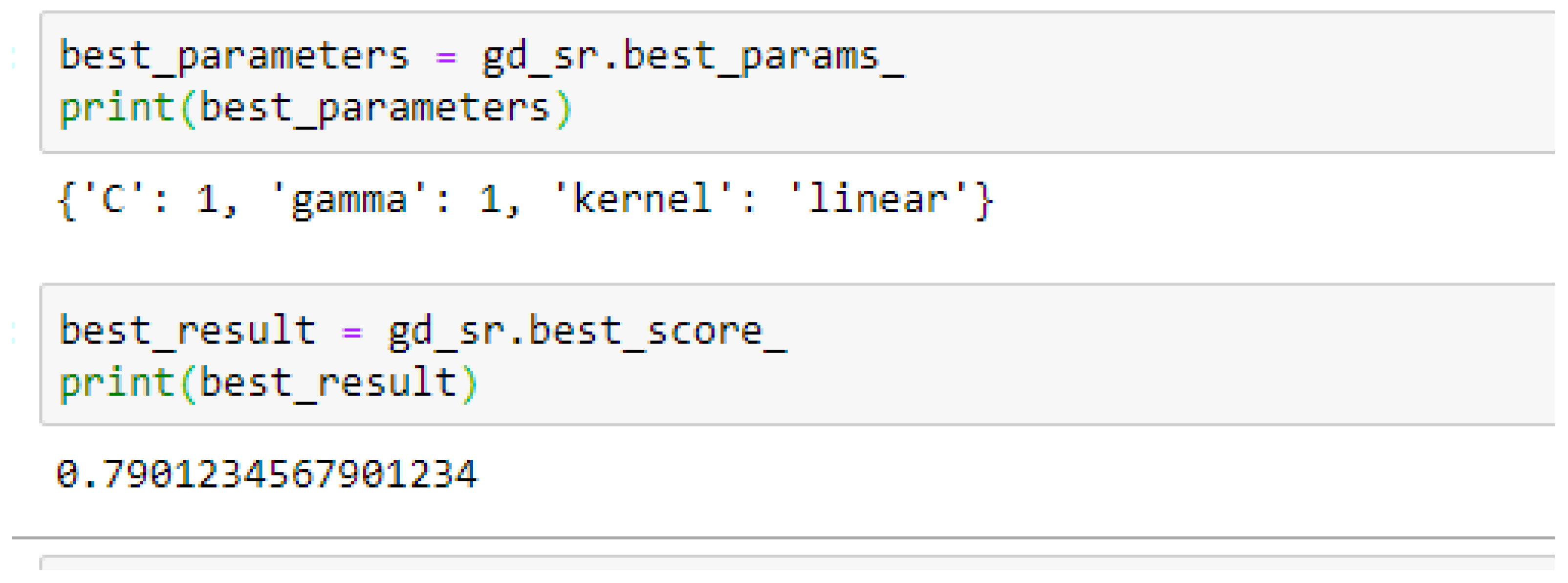
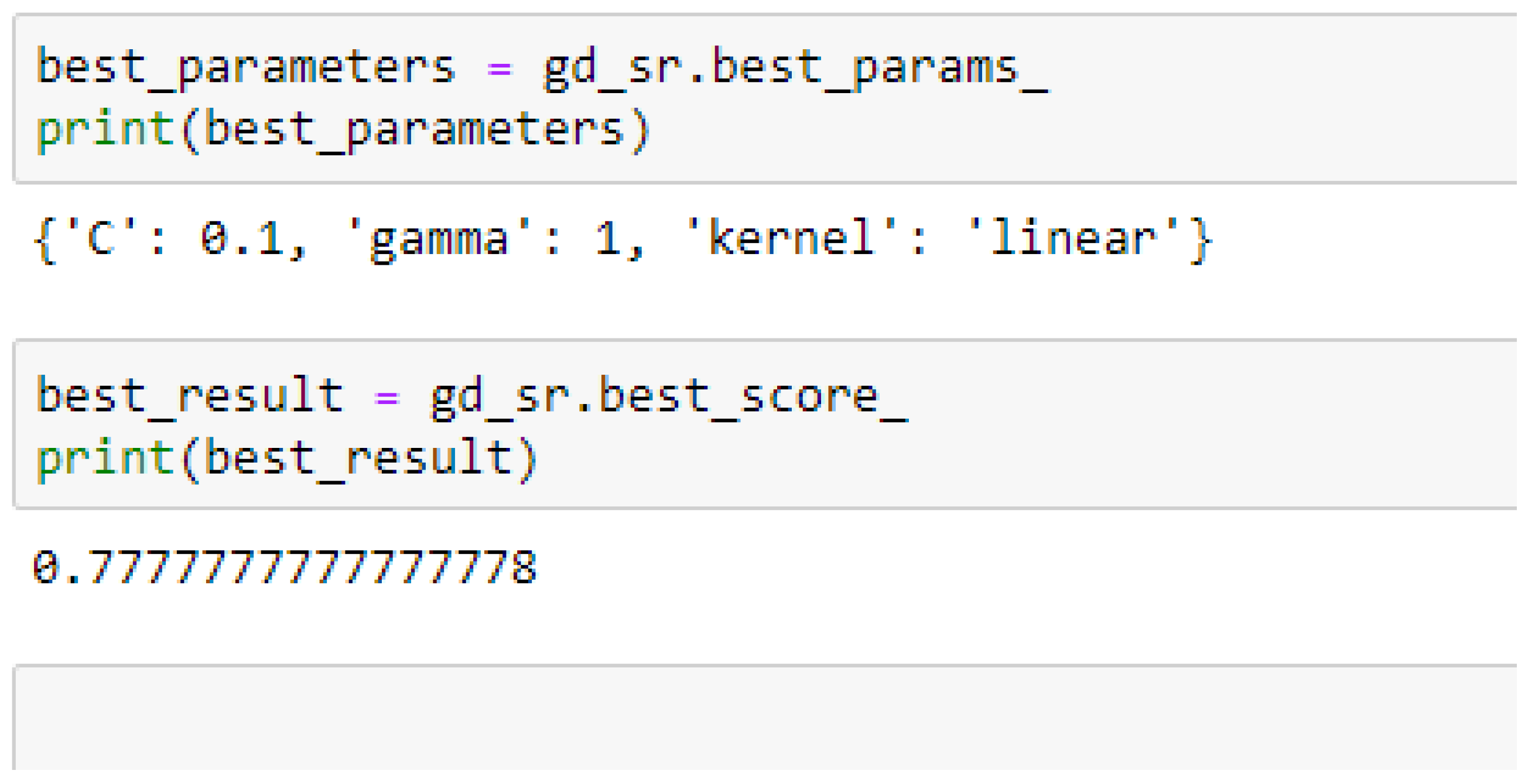
Among the SVM classifiers, the SVM-Linear model performed better when both the cost function and gamma had the same value of 1, based on the 5-Fold Cross-Validation, as compared with the 10-Fold Cross-Validation when the value of the cost function was 0.1 and gamma was 1, as shown in
Table 15 and
Table 16 respectively. The SVM-RBF model performed better based on the 10-Fold Cross-Validation when the values of the cost function and the gamma were 10 and 0.1 respectively, as compared with the 5-Fold Cross-Validation when both the cost function and the gamma had the same value of 1, as seen from
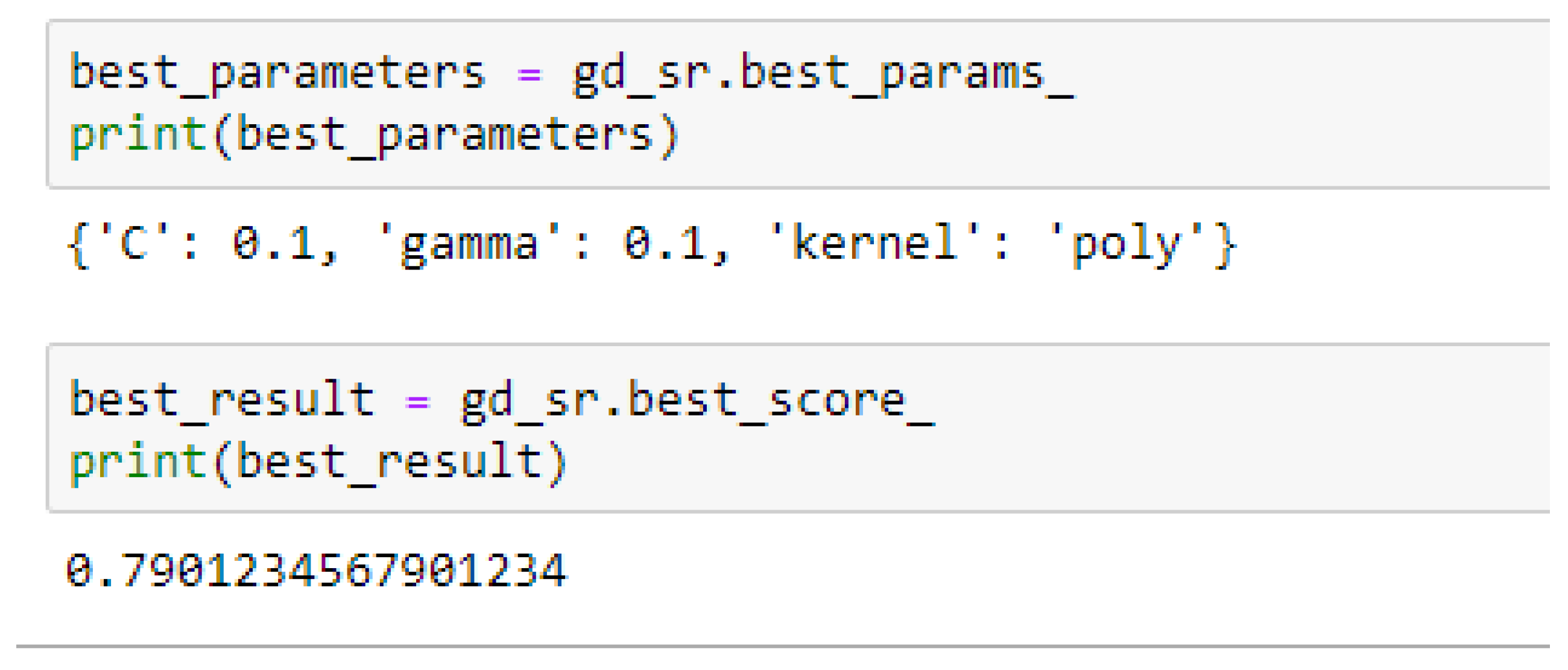
Table 15. For the SVM-Poly model, the model gave the same accuracy in both cases, based on the 5- and 10- Fold Cross-validation when the values of the cost function and the gamma were 0.1 and 0.1 respectively.
The ANN (3-6-6-1) model performed better based on the 10-Fold Cross-Validation when the values of the batch size, epochs were 32 and 500 respectively, and the optimizer was the rmsprop (root mean square) as compared with the 5-Fold Cross-Validation when the values of the batch size, epochs were 25 and 500 respectively, and the optimizer was Adam, as seen from
Table 15 and
Table 16 respectively. And also, the ANN (3-20-20-1) model performed better based on the 10-Fold Cross-Validation when the values of the batch size, epochs were 25 and 500 respectively, and the optimizer was Adam, as compared with the 5-Fold Cross-Validation when the values of the batch size, epochs were 25 and 100 respectively, and the optimizer was the Adam, as seen from
Table 15 and
Table 16 respectively.
Based on the 5- and 10- Fold Cross-Validation after grid searching the RF, SVM-RBF and ANN models achieved more than 80% as seen from
Table 15 and
Table 16 respectively. The RF, SVM-RBF and ANN models outperformed the baseline model based on the 10-Fold Cross-Validation with grid search. Overall, in terms of accuracies, the ANN (3-6-6-1) model outperformed all the other models, achieving 85.19% and 86.42% based on the 5- and 10-Fold Cross-Validation respectively, after running grid search algorithms.
Based on the findings of the ML algorithms, we have achieved the objective of this work to predict kyphosis disease. We compared the results of our ML models with the LR model, we found out that, LR is also capable in making clinical predictions, and for that matter, must not be overlooked, as can be verified from
Table 17. Based on the small sample size used in this work, we took advantage of K-Fold Cross-Validation to evaluate the models, and also took advantage of grid search to obtained the best parameters for the models.
For the ML Algorithms in making clinical predictions (kyphosis), the following are the implications based on our findings:
In using RF model to making clinical predictions, it is better to set bootstrap to true, both gini or entropy can be tried as the criterion, and the value of 100 can be tried as the starting point for the number of trees.
In SVM-Linear model, given the value of gamma equals 1, the values of (0.1 or 1) can be tried as the cost function when making clinical predictions.
In SVM-RBF model, the highest value for the cost function can be 10, while the lowest value can be 1, and the highest value for the gamma can be 1 while the lowest value can be 0.1, when making clinical predictions to obtain high accuracies.
In using the SVM-Poly to making clinical predictions, the value of 0.1 can be tried for both the cost function and the gamma.
In making clinical predictions based on ANN model, the values of the batch size and the epochs can be tried with 32 and 500 respectively, and the optimizer can either be rmsprop or Adam. However, most preferably, the rmsprop optimizer can firstly be experimented with.
The highest accuracies achieved by the ANN models, as seen from
Table 15 and
Table 16, imply that the number of the neurons may have increased the size of the data, since ML algorithms demand big sample size to be trained. Finally, the findings of our results show that, by performing 10-Fold Cross-Validation with grid search, will actually bring out the best model with the highest accuracy, as seen from
Figure 17.
Our current work serves as an opportunity for other researchers to improve upon the accuracies, and also research on how to obtain big data on kyphosis disease in order to explore the predictive power of the proposed ML algorithms. The findings of our work would also trigger further research into the comparison between the Logistic regression and ML algorithms in clinical prediction problems.
In future works, the ML models can be extended to make other clinical predictions with big data, so as to further observe and compare the performances of the ML models as confined in this current work.