A New Maximum Likelihood Estimator Formulated in Pole-Residue Modal Model
Abstract
:1. Introduction
2. Structure of the Combined LSCF-MLE-PMM
2.1. Modal Identification with the LSCF and LSFD Estimators (1st Step)
2.1.1. The LSCF Estimator
2.1.2. The LSFD Estimator
2.2. The MLE-PMM (2rd Step)
- Solve the normal equations
- Compute an update of the previous solution
2.2.1. Fast Estimation of the Perturbations on Modal Parameters
2.2.2. Estimation of the Covariance of the Measured FRFs
- the noise on the measured FRFs is circular complex normally distributed;
- the noise on the measured FRFs is zero-mean valued;
- the noise on the measured FRFs is uncorrelated over the frequencies; and
- the noise on the measured FRFs is uncorrelated over the outputs.
2.2.3. Convergence of the ML Algorithm
2.2.4. Estimation of the Uncertainty Bounds
2.2.5. Logarithmic MLE-PMM
3. Simulated Data Analysis
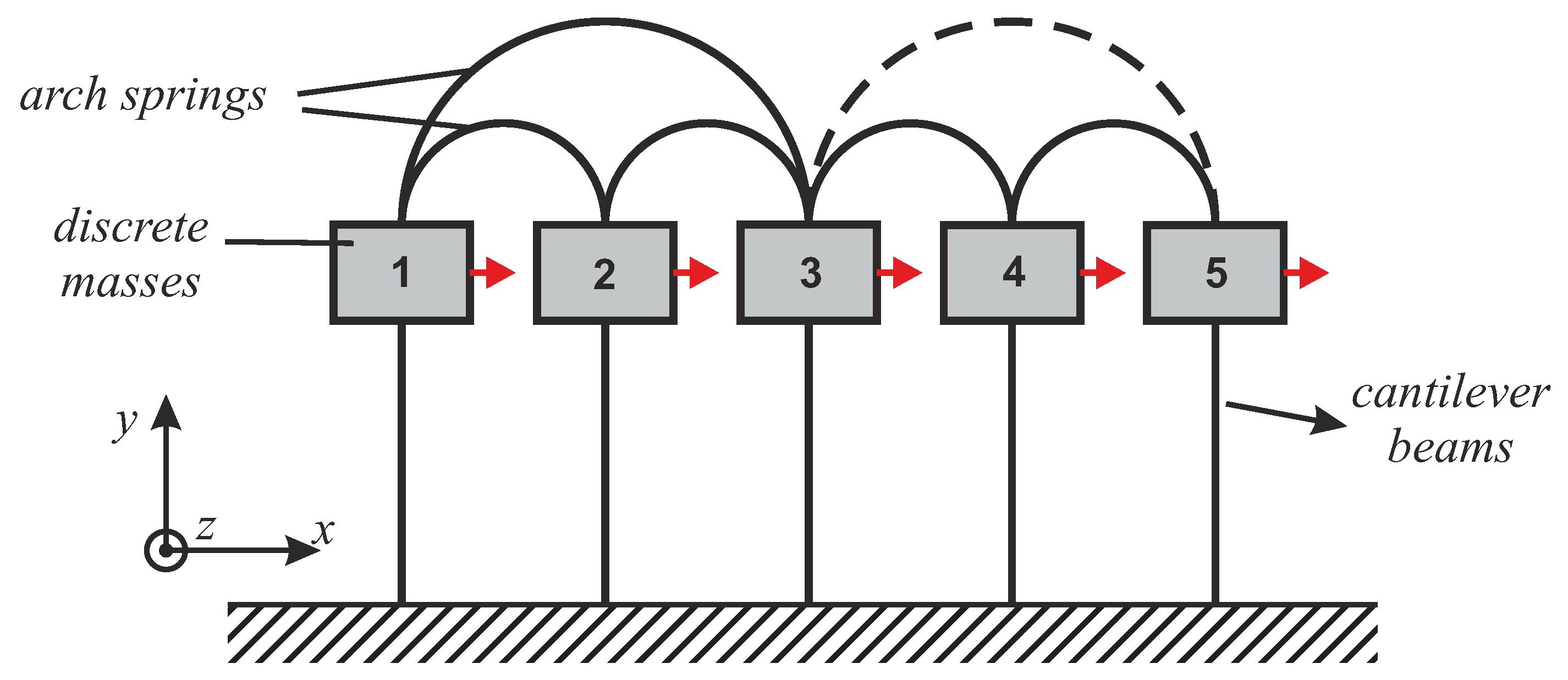
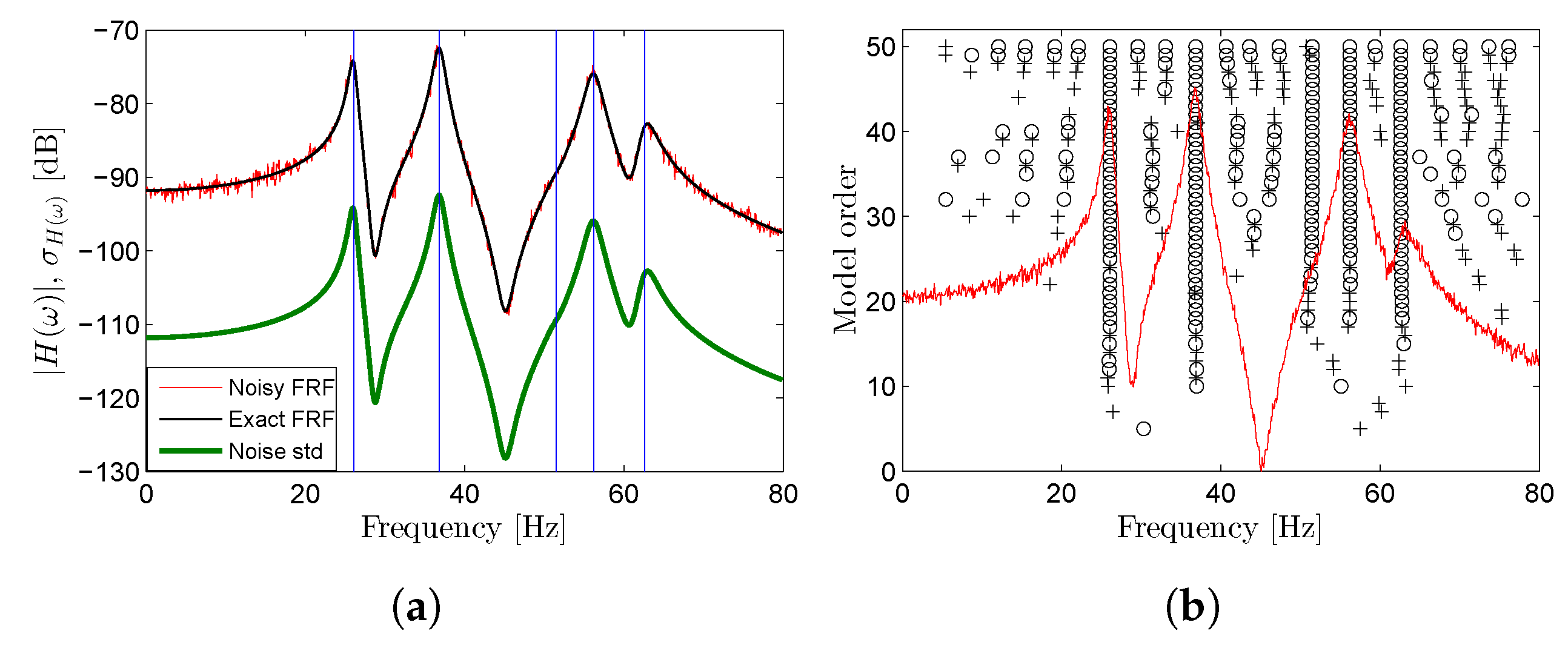
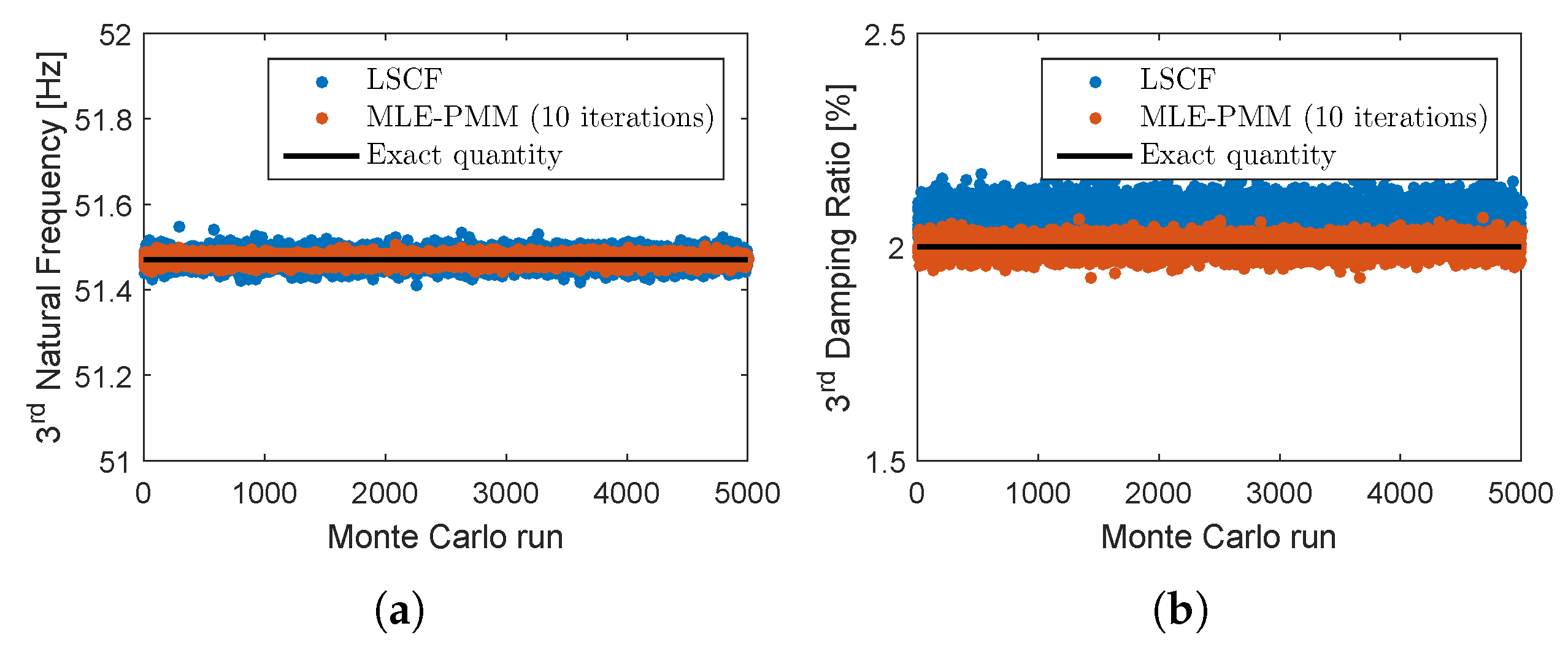
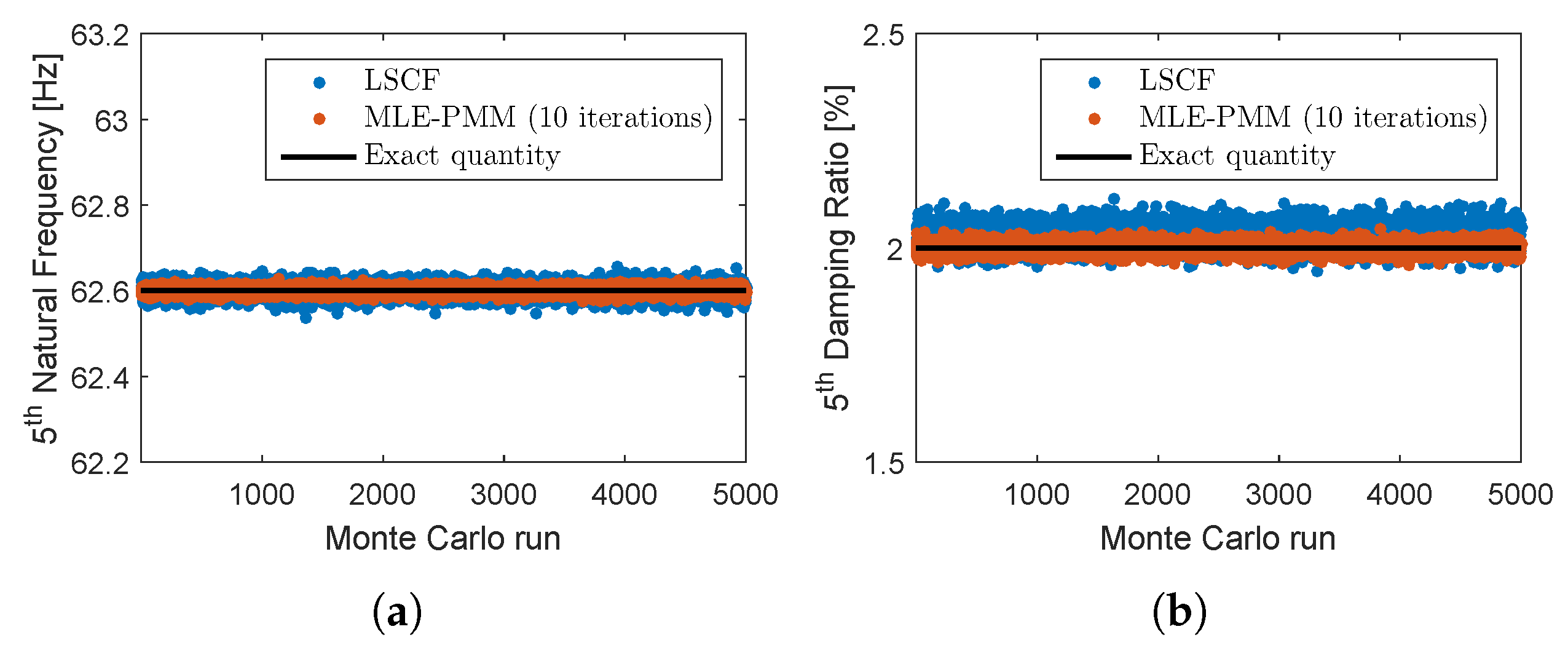
3.1. Five-DOF System
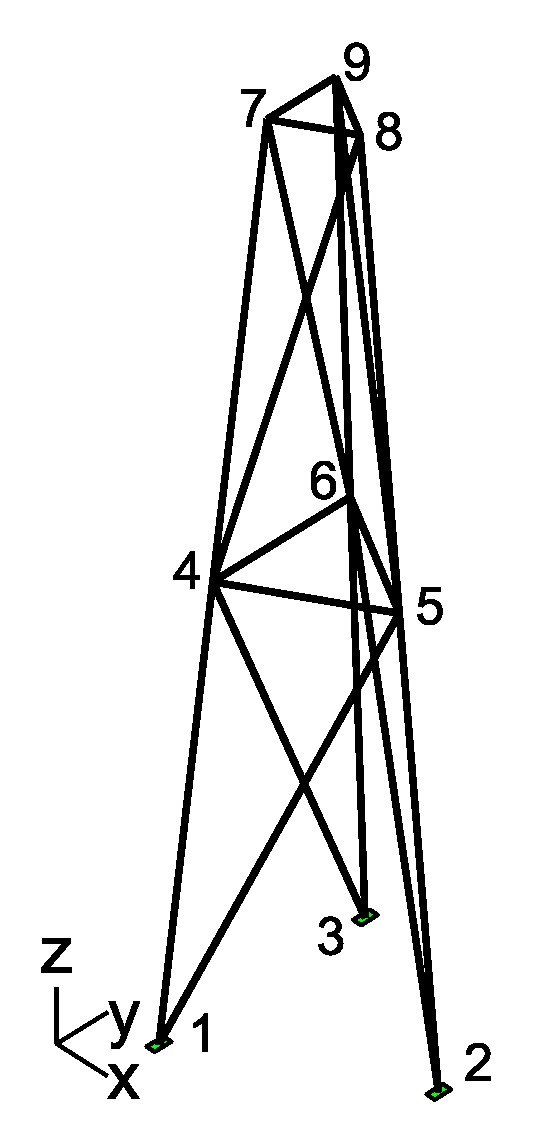
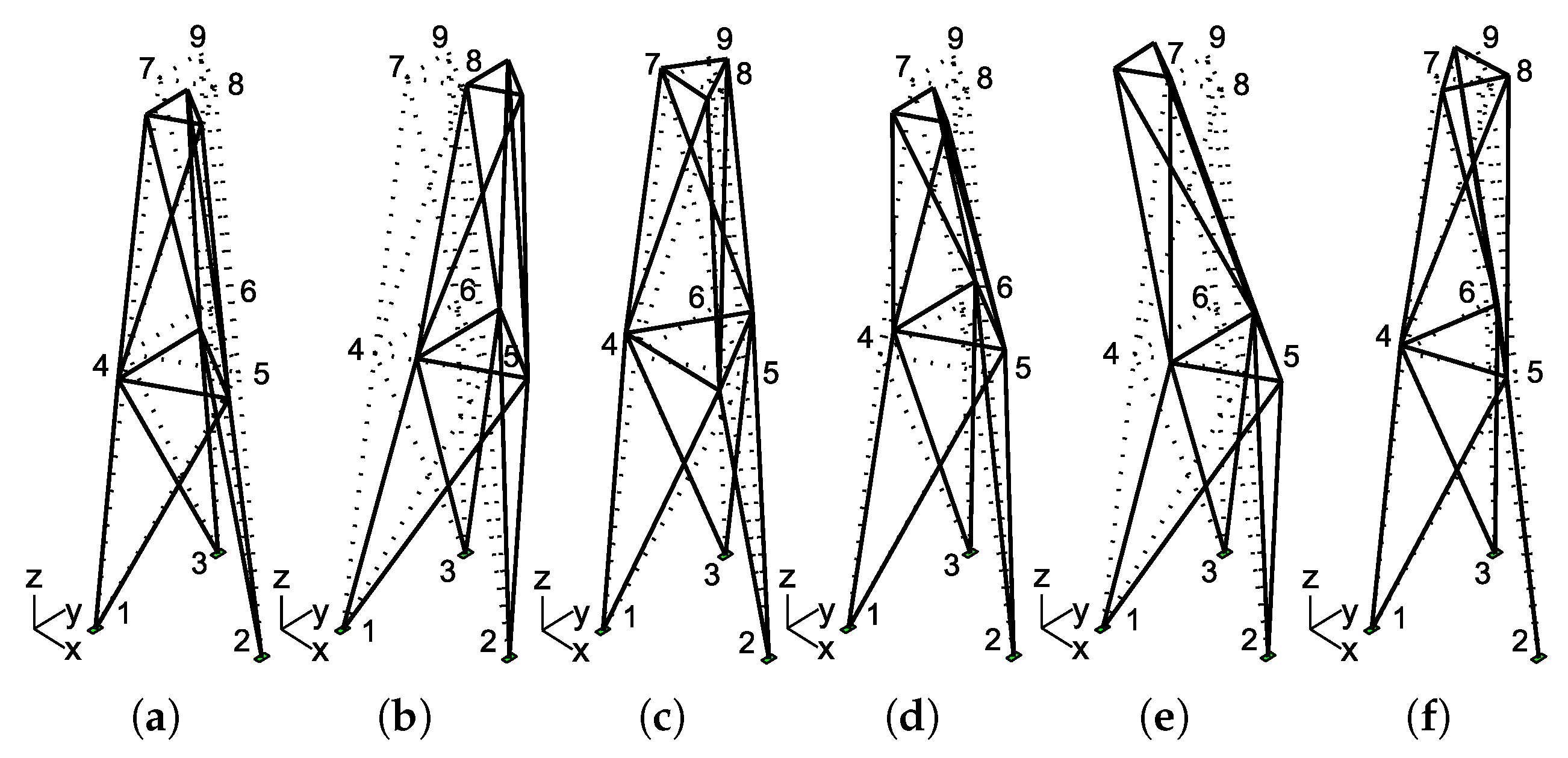
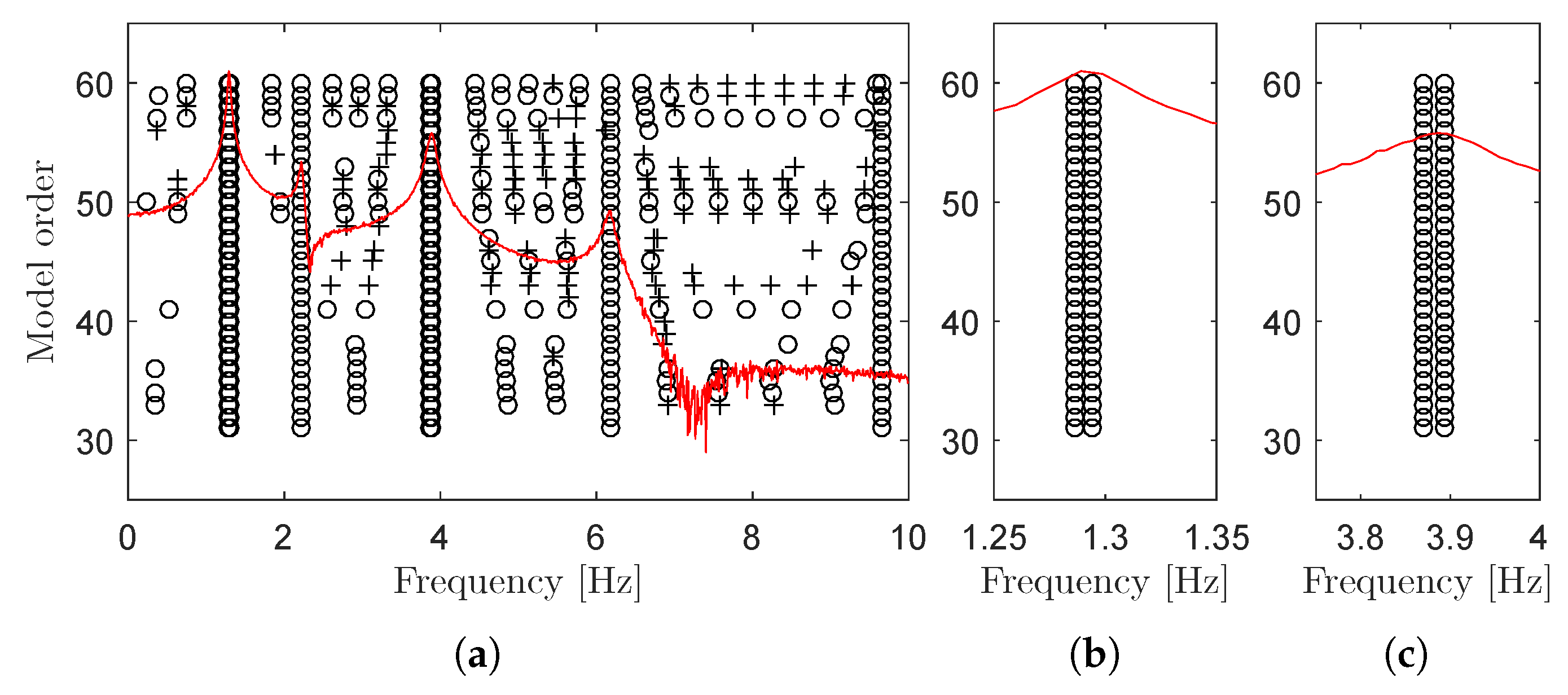
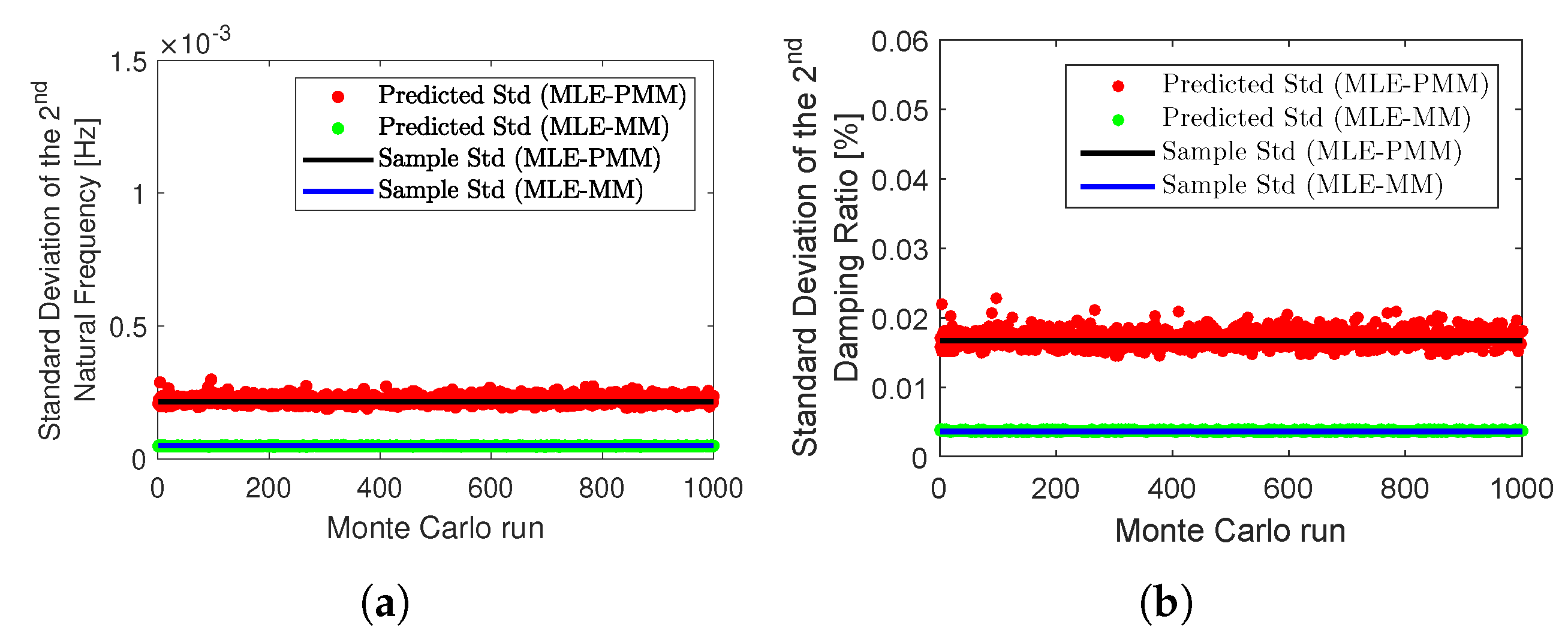
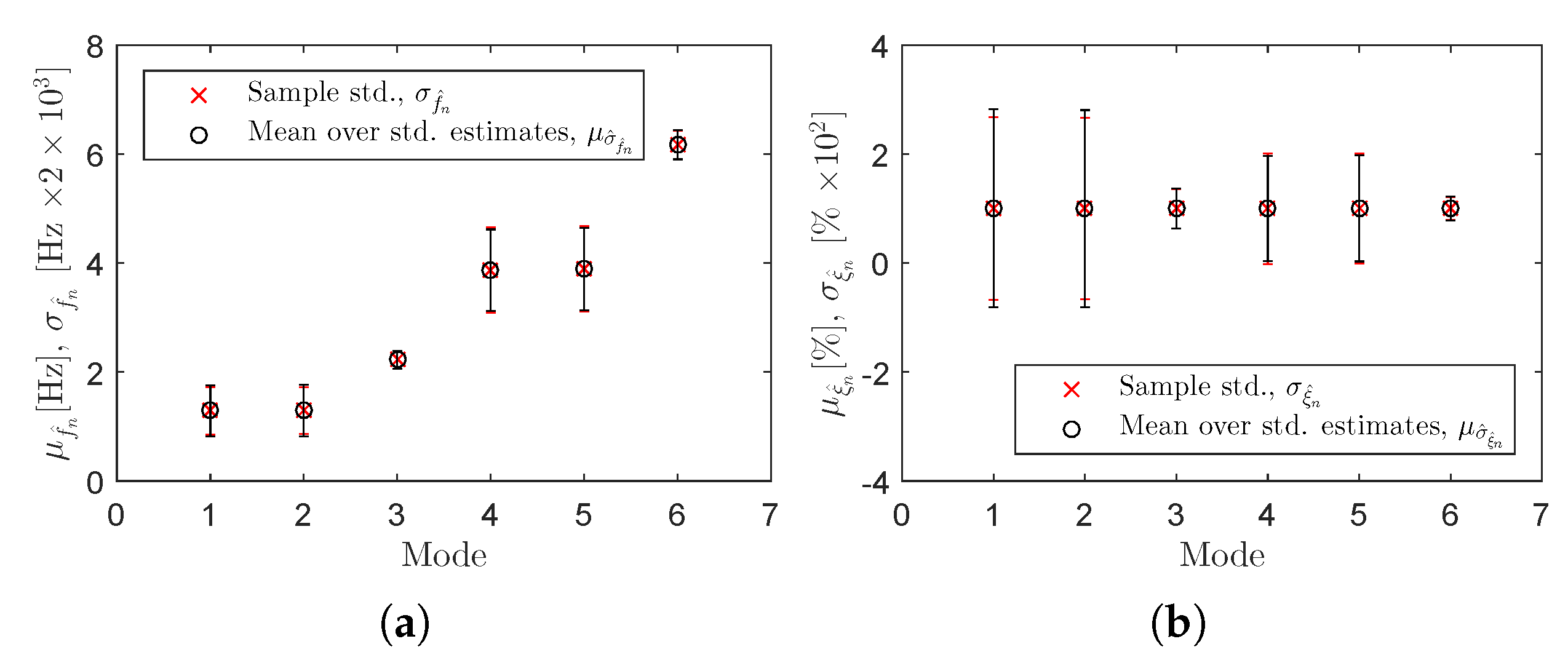
3.2. Lattice Tower Example
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Identification of Modal Residues and Upper and Lower Residuals with the LSFD Technique
Appendix B. Derivation of the Reduced Normal Equations
Appendix C. Partial Derivatives of the Classical ML-PMM
Appendix D. Partial Derivatives of the Log-Like ML-PMM
References
- Guillaume, P.; Verboven, P.; Vanlanduit, S.; Van-der-Auweraer, H.; Peeters, B. A Poly-reference Implementation of the Least-squares Complex Frequency-domain Estimator. In Proceedings of the 21st International Modal Analysis Conference (IMACXXI), Kissimmee, FL, USA, 3–6 February 2003. [Google Scholar]
- Peeters, B.; Van-der-Auweraera, H.; Guillaume, P.; Leuridana, J. The PolyMAX frequency-domain method: A new standard for modal parameter estimation? Shock Vib. 2004, 1, 395–409. [Google Scholar] [CrossRef]
- Peeters, B. System Identification and Damage Detection in Civil Engineering. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2000. [Google Scholar]
- Peeters, B.; Van-der-Auweraer, H.; Vanhollebeke, F.; Guillaume, P. Operational modal analysis for estimating the dynamic properties of a stadium structure during a football game. Shock Vib. 2007, 14, 283–303. [Google Scholar] [CrossRef]
- Maia, N.; He, L.; Lin, S.; To, U. Theoretical and Experimental Modal Analysis; Research Studies Press Ltd.: London, UK, 1998. [Google Scholar]
- De-Troyer, T.; Guillaume, P.; Pintelon, R.; Vanlanduit, S. Fast calculation of confidence intervals on parameter estimates of least-squares frequency-domain estimators. Mech. Syst. Signal Process. 2009, 23, 261–273. [Google Scholar] [CrossRef]
- De-Troyer, T.; Guillaume, P.; Steenackers, G. Fast variance calculation of polyreference least-squares frequency-domain estimates. Mech. Syst. Signal Process. 2009, 23, 1423–1433. [Google Scholar] [CrossRef]
- Reynders, E.; Pintelon, R.; De-Roeck, G. Uncertainty bounds on modal parameters obtained from stochastic subspace identification. Mech. Syst. Signal Process. 2008, 22, 948–969. [Google Scholar] [CrossRef]
- Döhler, M.; Lam, X.-B.; Mevel, L. Uncertainty quantification for modal parameters from stochastic subspace identification on multi-setup measurements. Mech. Syst. Signal Process. 2013, 36, 562–581. [Google Scholar] [CrossRef]
- Reynders, E.; Maes, K.; De-Roeck, G. Uncertainty quantification in operational modal analysis with stochastic subspace identification: Validation and applications. Mech. Syst. Signal Process. 2016, 66–67, 13–30. [Google Scholar] [CrossRef]
- El-Kafafy, M.; Guillaume, P.; De-Troyer, T.; Peeters, B. A Frequency—Domain Maximum Likelihood Implementation using the modal model formulation. In Proceedings of the 16th IFAC Symposium on System Identification the International Federation of Automatic Control, Brussels, Belgium, 11–13 July 2012. [Google Scholar]
- El-Kafafy, M. Design and Validation of Improved Modal Parameter Estimators. Ph.D. Thesis, Department of Mechanical Engineering, Vrije Universiteit Brussel, Brussels, Belgium, 2013. [Google Scholar]
- Peeters, B.; El-Kafafy, M.; Guillaume, P. The new PolyMAX Plus method: Confident modal parameter estimation even in very noisy cases. In Proceedings of the 2012 Conference on Noise and Vibration Engineering (ISMA), Leuven, Belgium, 17–19 September 2012. [Google Scholar]
- El-Kafafy, M.; De-Troyer, T.; Peeters, B.; Guillaume, P. Fast maximum-likelihood identification of modal parameters with uncertainty intervals: A modal model–based formulation. Mech. Syst. Signal Process. 2013, 37, 422–439. [Google Scholar] [CrossRef]
- El-Kafafy, M.; De-Troyer, T.; Guillaume, P. Fast maximum-likelihood identification of modal parameters with uncertainty intervals: A modal model formulation with enhanced residual term. Mech. Syst. Signal Process. 2014, 48, 49–66. [Google Scholar] [CrossRef]
- Diord, S.; Magalhães, F.; Cunha, A.; Caetano, E. High spatial resolution modal identification of a stadium suspension roof: Assessment of the estimates uncertainty and of modal contributions. Eng. Struct. 2017, 135, 117–135. [Google Scholar] [CrossRef]
- El-kafafy, M.; Guillaume, P.; Peeters, B.; Marra, F.; Coppotelli, G. Advanced frequency-domain modal analysis for dealing with measurement noise and parameter uncertainty. In Proceedings of the 19th International Modal Analysis Conference (IMACXXX), Jacksonville, FL, USA, 30 January–2 February 2012. [Google Scholar]
- El-Kafafy, M.; Peeters, B.; Guillaume, P.; De-Troyer, T. Constrained maximum likelihood modal parameter identification applied to structural dynamics. Mech. Syst. Signal Process. 2016, 72–73, 567–589. [Google Scholar] [CrossRef]
- Balmès, E. Frequency domain identification of structural dynamics using the pole-residue parametrization. In Proceedings of the 1996 International Modal Analysis Conference (IMAC), Orlando, FL, USA, 12–15 February 1996. [Google Scholar]
- Heylen, W.; Lammens, S.; Sas, P. Modal Analysis Theory and Testing, 2nd ed.; Mechanical Engineering, Katholieke Universiteit Leuven: Leuven, Belgium, 1998; Volume 1. [Google Scholar]
- Guillaume, P.; Verboven, P.; Vanlanduit, S. The new PolyMAX Plus method: Confident modal parameter estimation even in very noisy cases. In Proceedings of the 23rd International Seminar on Modal Analysis, Leuven, Belgium, 16–18 September 1998. [Google Scholar]
- Cauberghe, B. Applied Frequency-Domain System Identification in the Field of Experimental and Operational Modal Analysis. Ph.D. Thesis, Department of Mechanical Engineering, Vrije Universiteit, Brussel, Belgium, 2004. [Google Scholar]
- Pintelon, R.; Schoukens, J. System Identification: A Frequency Domain Approach, 1st ed.; IEEE Press: Piscataway, NJ, USA, 2001; Volume 1. [Google Scholar]
- Schoukens, J.; Pintelon, R. System Identification: A Frequency Domain Approach, 1st ed.; Pergamon Press: London, UK, 1991; Volume 1. [Google Scholar]
- Kailath, T. Linear Systems, 1st ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1998; Volume 1. [Google Scholar]
- Pintelon, R.; Guillaume, P.; Schoukens, J. Uncertainty calculation in (operational) modal analysis. Mech. Syst. Signal Process. 2007, 21, 2359–2373. [Google Scholar] [CrossRef]
- Verboven, P. Frequency-Domain System Identification for Modal Analysis. Ph.D. Thesis, Department of Mechanical Engineering, Vrije Universiteit Brussel, Brussels, Belgium, 2002. [Google Scholar]
- Böswald, M.; Göge, D.; Füllekrug, U.; Govers, Y. A review of experimental modal analysis methods with respect to their applicability to test data of large aircraft. In Proceedings of the International Conference on Noise and Vibration Engineering, Leuven, Belgium, 18–20 September 2006. [Google Scholar]
- Diord, S.; Magalhães, F.; Cunha, A.; Caetano, E.; Martins, N. Automated modal tracking in a football stadium suspension roof for detection of structural changes. Struct. Control Health Monit. 2017, 24, e2006. [Google Scholar] [CrossRef]
- Amador, S.D.R. Uncertainty Quantification in Operational Modal Analysis and Continuous Monitoring of Special Structures. Ph.D. Thesis, Department of Civil Engineering, Faculty of Engineering of University of Porto, Porto, Portugal, 2015. [Google Scholar]







| Output Quantity | FRFs | Full Spectra | Half Spectra | |||
|---|---|---|---|---|---|---|
| Displacement | 1 | 1 | ||||
| Velocity | ||||||
| Acceleration | 1 | 1 | ||||
| Mode | [Hz] | [%] | [Kg] |
|---|---|---|---|
| 1 | 26.06 | 2 | 2.52 |
| 2 | 36.84 | 2 | 2.97 |
| 3 | 51.47 | 2 | 0.90 |
| 4 | 56.21 | 2 | 1.09 |
| 5 | 62.60 | 2 | 1.05 |
| DOF/Mode | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 0.7147 | 1.0000 | −0.0911 | −0.9230 | −0.6083 |
| 2 | 0.7166 | 0.9999 | −0.1493 | 1.0000 | −0.1937 |
| 3 | 0.7981 | 0.2257 | 0.1554 | −0.1518 | 1.0000 |
| 4 | 0.8518 | −0.5166 | 1.0000 | 0.1231 | −0.3936 |
| 5 | 1.0000 | −0.8590 | −0.5860 | 0.0196 | −0.2041 |
| Mode | LSCF Estimates | MLE-PMM Estimates (10 Iterations) | ||||||
|---|---|---|---|---|---|---|---|---|
| Rel.Bias | Rel.Bias | Rel.Bias | Rel.Bias | |||||
| (Hz) | (% ) | (%) | (% ) | (Hz) | (% ) | (%) | (% ) | |
| 1 | 26.0603 | 1.129 | 2.0449 | 2.246 | 26.0600 | 0.152 | 1.9998 | 0.011 |
| 2 | 36.8404 | 1.131 | 2.0317 | 1.585 | 36.8398 | 0.425 | 1.9999 | 0.004 |
| 3 | 51.4715 | 2.927 | 2.0685 | 3.423 | 51.4702 | 0.337 | 2.0005 | 0.025 |
| 4 | 56.2125 | 4.378 | 2.0274 | 1.370 | 56.2100 | 0.042 | 1.9999 | 0.004 |
| 5 | 62.6006 | 0.934 | 2.0275 | 1.373 | 62.6001 | 0.216 | 2.0000 | 0.002 |
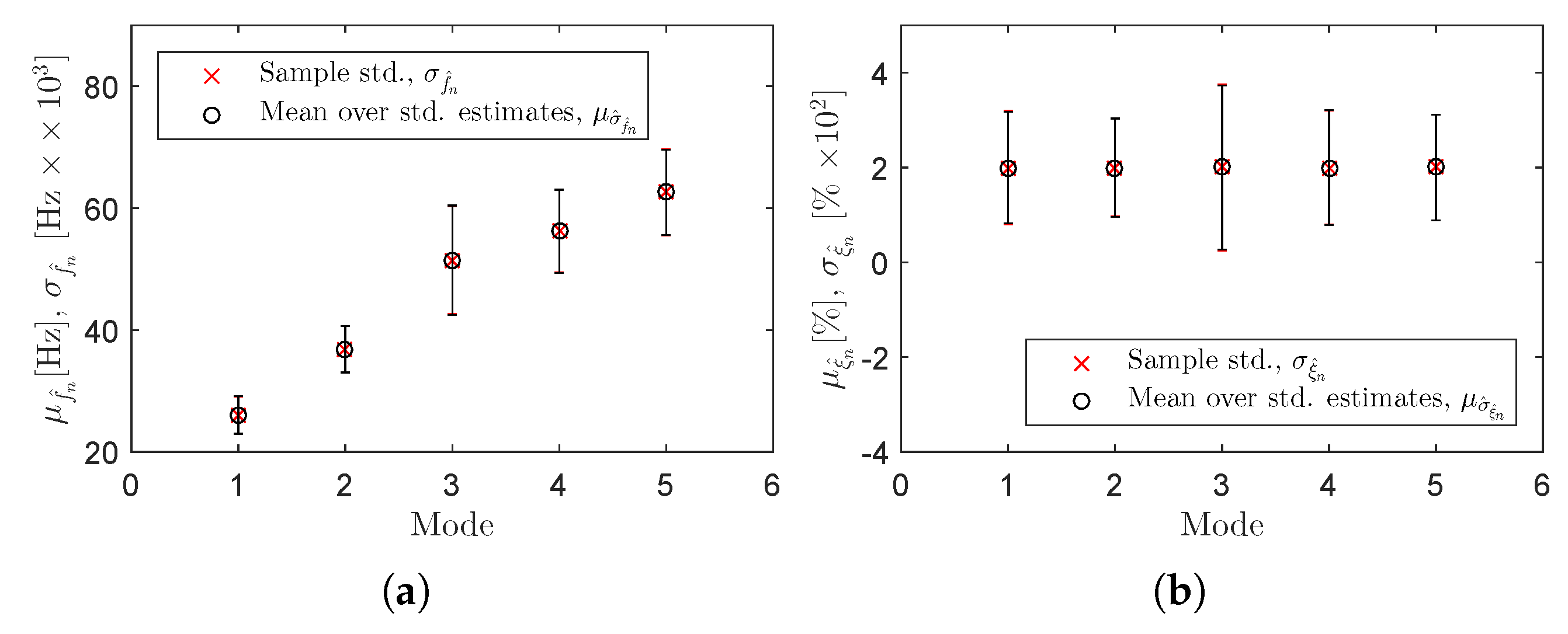
| Estimator | Mode | Sample Std. | Mean Over the Std. Estimates | Rel. Difference () | |||
|---|---|---|---|---|---|---|---|
(Hz × 103) | (% × 102) | (Hz × 103) | (% × 102) | (%) | (%) | ||
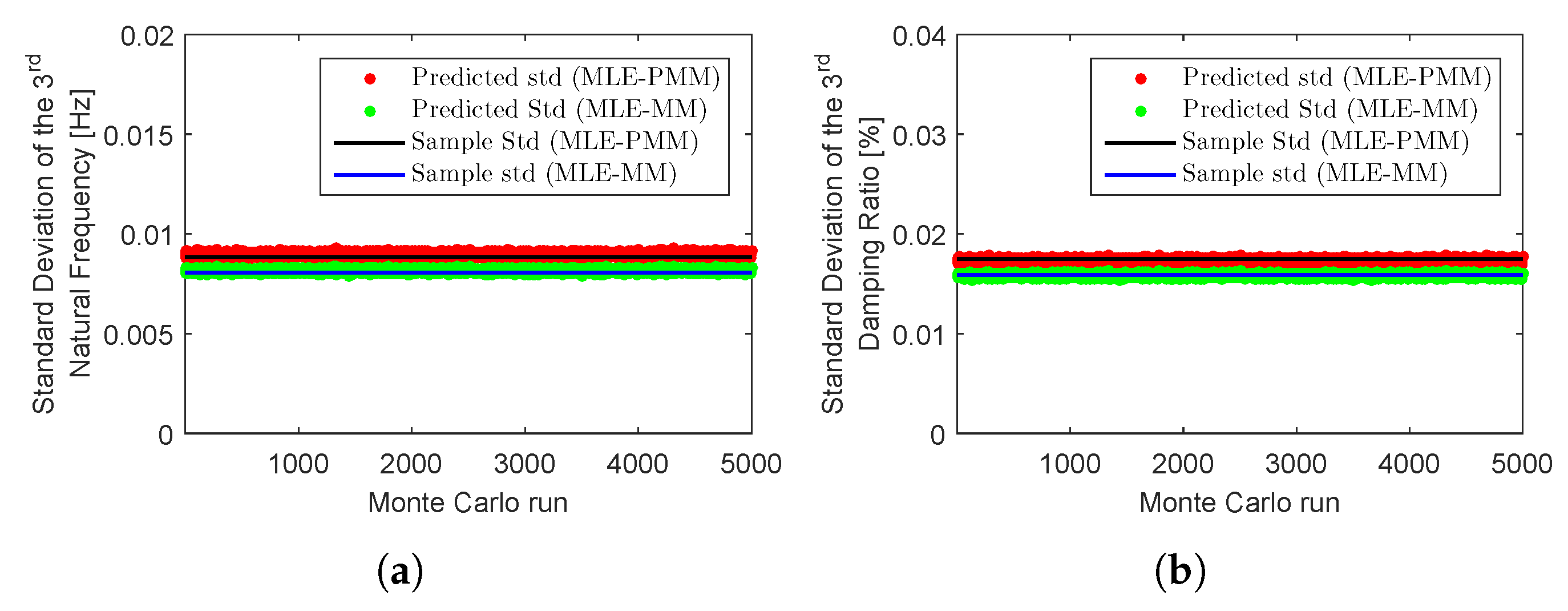
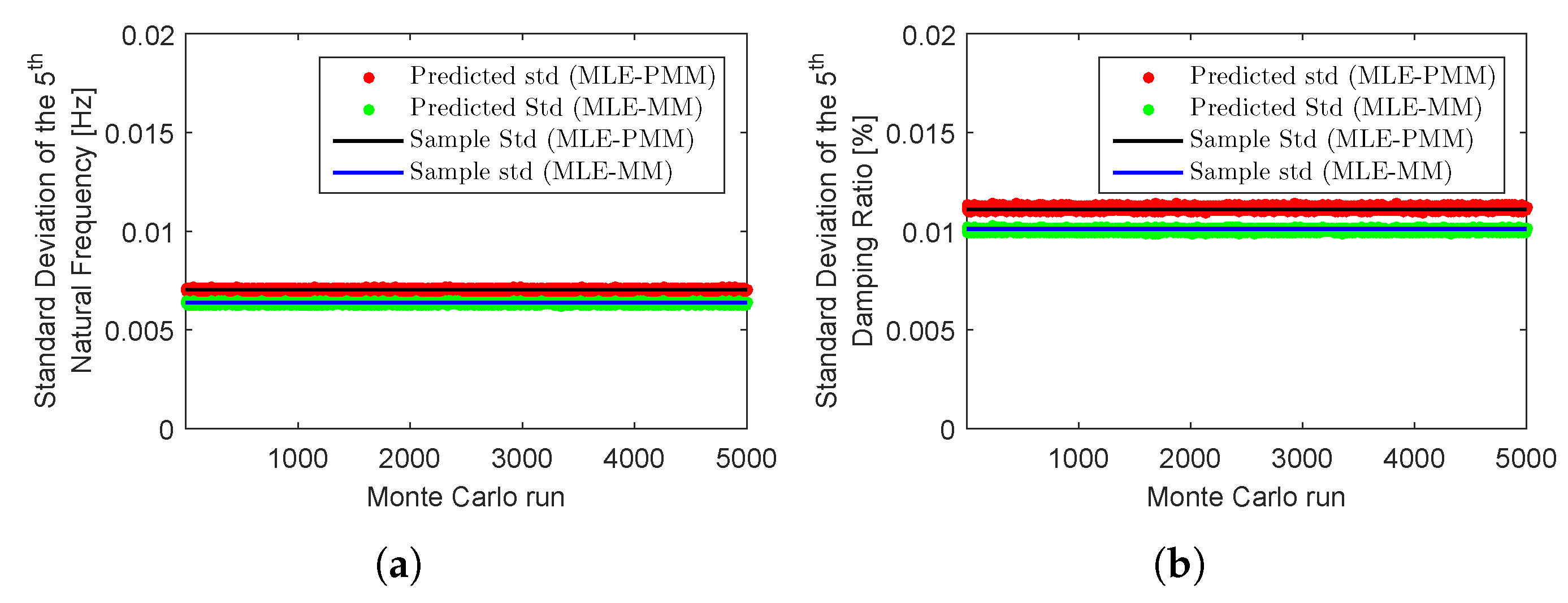
| MLE-PMM | 1 | 3.04 | 1.20 | 3.10 | 1.18 | 1.74 | 2.23 |
| 2 | 3.80 | 1.03 | 3.80 | 1.04 | 0.05 | 0.38 | |
| 3 | 8.83 | 1.75 | 8.97 | 1.73 | 1.60 | 1.05 | |
| 4 | 6.74 | 1.20 | 6.81 | 1.21 | 1.12 | 1.20 | |
| 5 | 7.04 | 1.11 | 7.02 | 1.12 | 0.29 | 0.51 | |
| MLE-MM | 1 | 3.01 | 1.19 | 3.06 | 1.16 | 1.53 | 2.15 |
| 2 | 3.70 | 1.01 | 3.70 | 1.01 | 0.20 | 0.33 | |
| 3 | 8.07 | 1.59 | 8.15 | 1.58 | 1.01 | 0.49 | |
| 4 | 5.34 | 0.98 | 5.47 | 0.97 | 2.39 | 0.35 | |
| 5 | 6.37 | 1.01 | 6.35 | 1.00 | 0.36 | 0.68 | |
| DOF/Mode | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 0.4468 | −0.6874 | 0.3127 | 0.3392 | 0.6939 | 0.1024 |
| 2 | −0.6972 | −0.4527 | −0.1825 | −0.6996 | 0.3094 | −0.0583 |
| 3 | −0.1535 | 0.0972 | 0.6919 | 0.1836 | 0.1287 | −0.0468 |
| 4 | 0.4489 | −0.6965 | 0.0014 | 0.3186 | 0.6843 | 0.0022 |
| 5 | −0.7059 | −0.4370 | 0.3573 | −0.7115 | 0.3235 | 0.1151 |
| 6 | 0.1269 | 0.1106 | 0.6946 | −0.1849 | 0.0980 | −0.0492 |
| Mode | Type | [Hz] | [%] | [Kg] |
|---|---|---|---|---|
| 1 | bending mode in Y direction (BY1) | 1.2869 | 1.0 | 2608.8271 |
| 2 | bending mode in X direction (BX1) | 1.2937 | 1.0 | 2592.8286 |
| 3 | torsional mode (T1) | 2.2251 | 1.0 | 281.0965 |
| 4 | bending mode in Y direction (BY2) | 3.8713 | 1.0 | 1431.1279 |
| 5 | bending mode in X direction (BX2) | 3.8932 | 1.0 | 1410.8619 |
| 6 | torsional mode (T2) | 6.1745 | 1.0 | 54.2551 |
| Mode | LSCF Estimates | MLE-PMM Estimates (20 Iterations) | ||||||
|---|---|---|---|---|---|---|---|---|
| Rel.Bias | Rel.Bias | Rel.Bias | Rel.Bias | |||||
| (Hz) | (% ) | (%) | (% ) | (Hz) | (% ) | (%) | (% ) | |
| 1 | 1.2869 | 0.294 | 1.0000 | 0.003 | 1.2869 | 0.050 | 1.0003 | 2.816 |
| 2 | 1.2937 | 0.839 | 1.0020 | 20.201 | 1.2937 | 0.272 | 1.0000 | 0.334 |
| 3 | 2.2251 | 0.107 | 1.0001 | 0.723 | 2.2251 | 0.001 | 0.9999 | 1.282 |
| 4 | 3.8712 | 0.154 | 1.0007 | 6.951 | 3.8713 | 0.209 | 1.0002 | 2.035 |
| 5 | 3.8932 | 0.805 | 1.0000 | 0.014 | 3.8932 | 0.002 | 0.9998 | 1.957 |
| 6 | 6.1745 | 0.119 | 1.0004 | 3.687 | 6.1745 | 0.059 | 1.0000 | 0.001 |
| Estimator | Mode | Sample Std. | Mean Over the Std. Estimates | Rel. Difference () | |||
|---|---|---|---|---|---|---|---|
(Hz × 103) | (% × 102) | (Hz × 103) | (% × 102) | (%) | (%) | ||
| MLE-PMM | 1 | 0.22 | 1.68 | 0.22 | 1.70 | 2.00 | 1.52 |
| 2 | 0.21 | 1.67 | 0.22 | 1.70 | 3.35 | 2.08 | |
| 3 | 0.08 | 0.36 | 0.08 | 0.37 | 0.26 | 1.30 | |
| 4 | 0.39 | 1.01 | 0.37 | 0.97 | 4.54 | 4.45 | |
| 5 | 0.39 | 1.01 | 0.38 | 0.97 | 3.33 | 3.97 | |
| 6 | 0.13 | 0.21 | 0.13 | 0.22 | 3.05 | 3.27 | |
| MLE-MM | 1 | 0.05 | 0.38 | 0.05 | 0.37 | 1.54 | 1.56 |
| 2 | 0.05 | 0.36 | 0.05 | 0.37 | 2.86 | 2.88 | |
| 3 | 0.08 | 0.33 | 0.08 | 0.34 | 0.86 | 1.44 | |
| 4 | 0.11 | 0.27 | 0.11 | 0.28 | 2.07 | 3.21 | |
| 5 | 0.11 | 0.28 | 0.11 | 0.28 | 2.10 | 0.64 | |
| 6 | 0.13 | 0.20 | 0.13 | 0.21 | 1.66 | 3.46 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amador, S.; El-Kafafy, M.; Cunha, Á.; Brincker, R. A New Maximum Likelihood Estimator Formulated in Pole-Residue Modal Model. Appl. Sci. 2019, 9, 3120. https://doi.org/10.3390/app9153120
Amador S, El-Kafafy M, Cunha Á, Brincker R. A New Maximum Likelihood Estimator Formulated in Pole-Residue Modal Model. Applied Sciences. 2019; 9(15):3120. https://doi.org/10.3390/app9153120
Chicago/Turabian StyleAmador, Sandro, Mahmoud El-Kafafy, Álvaro Cunha, and Rune Brincker. 2019. "A New Maximum Likelihood Estimator Formulated in Pole-Residue Modal Model" Applied Sciences 9, no. 15: 3120. https://doi.org/10.3390/app9153120
APA StyleAmador, S., El-Kafafy, M., Cunha, Á., & Brincker, R. (2019). A New Maximum Likelihood Estimator Formulated in Pole-Residue Modal Model. Applied Sciences, 9(15), 3120. https://doi.org/10.3390/app9153120







