Enhanced NOMA System Using Adaptive Coding and Modulation Based on LSTM Neural Network Channel Estimation
Abstract
1. Introduction
2. NOMA System Model
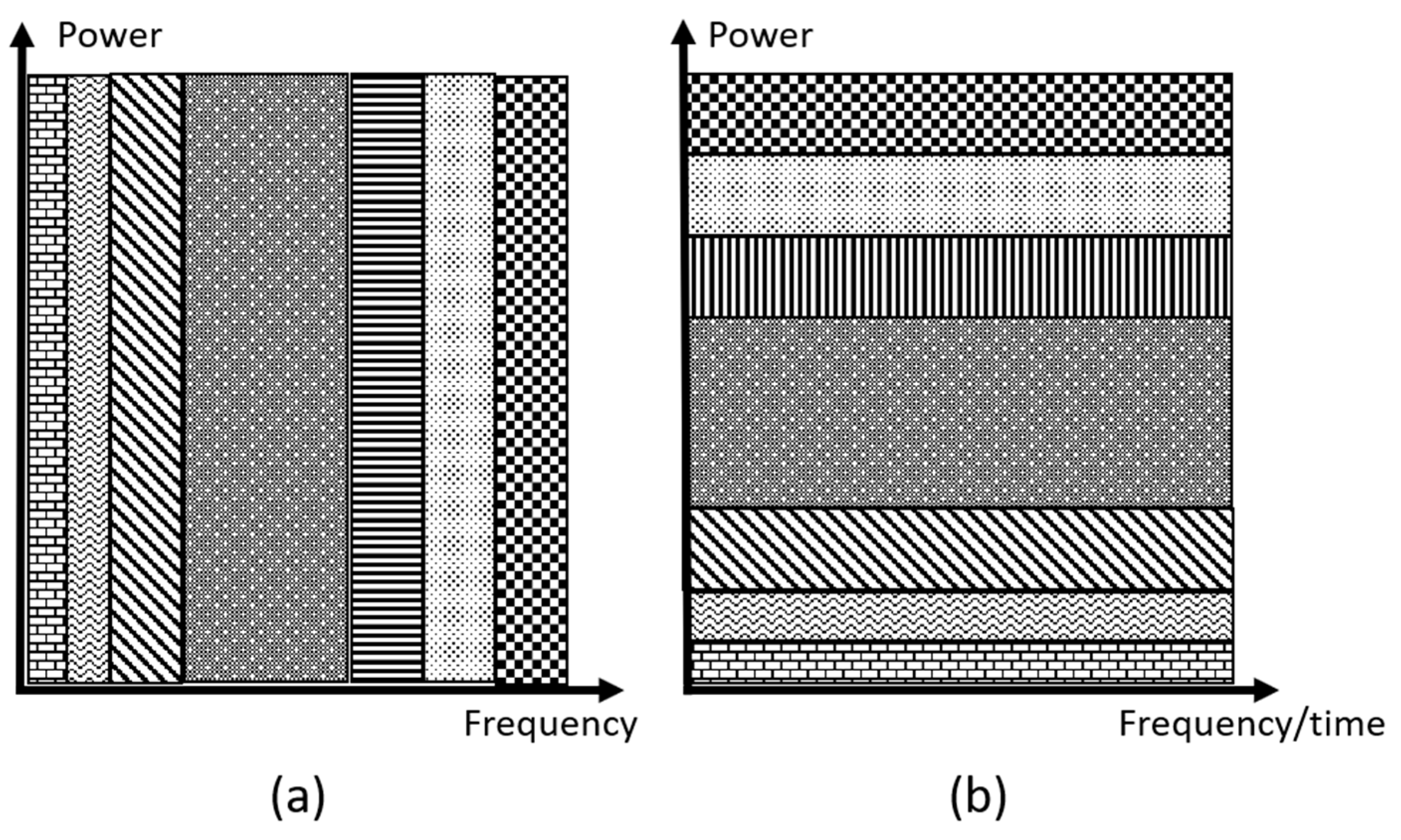
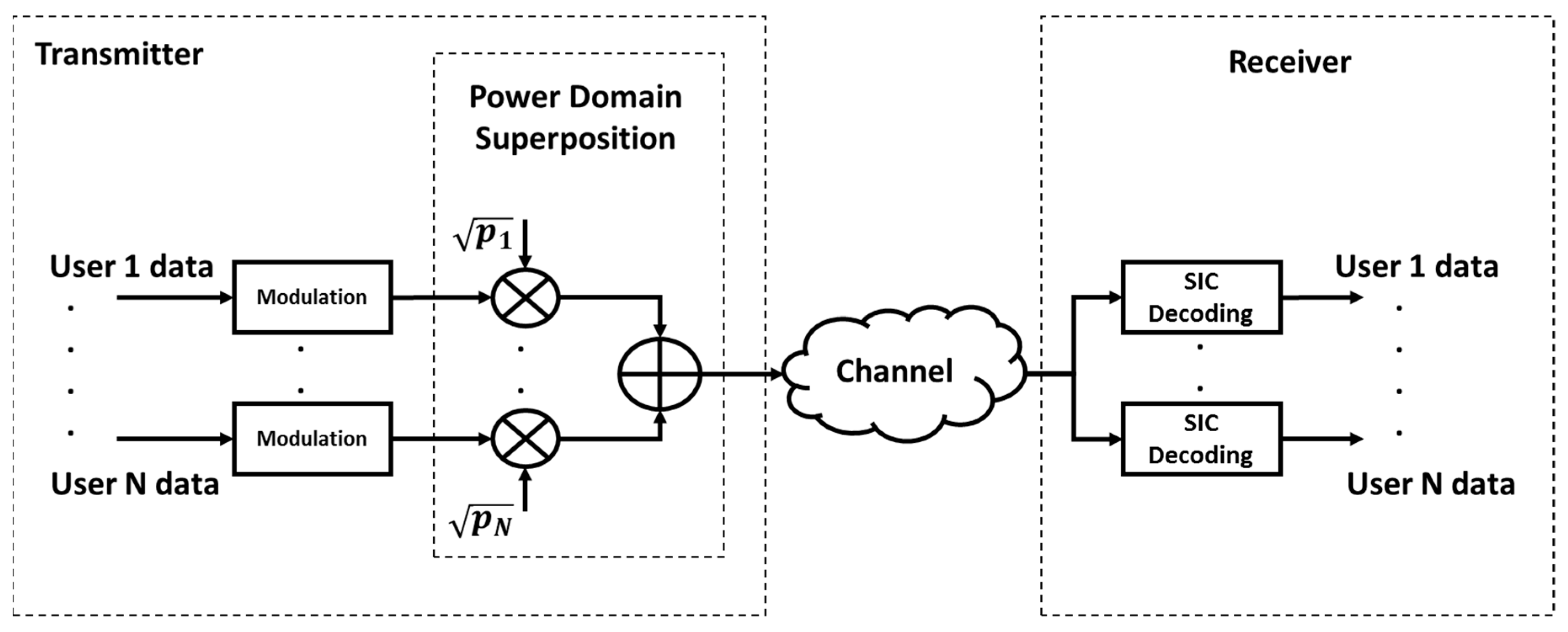
2.1. Superposition Coding (SC)
| Algorithm 1 SNR comparison and Power Re-Allocation for UEs |
| Inputs: Channel Matrices () for each UE from the stage of channel estimation (CE) |
| 1: Loop I = 1: N 2: (3) |
| 3: End loop |
| 4: Sort SNR values in ascending order |
| 5: Assign the power coefficients according to the SNR values subject to given by Equation (2). |
| 6: Sort the power coefficients, , in descending order. |
| 7: Update and retransmit the super-positioned sequences with the new power coefficients. |
| Outputs: Power coefficients re-assigned for each user’s transmitted message |
2.2. Data Transmission
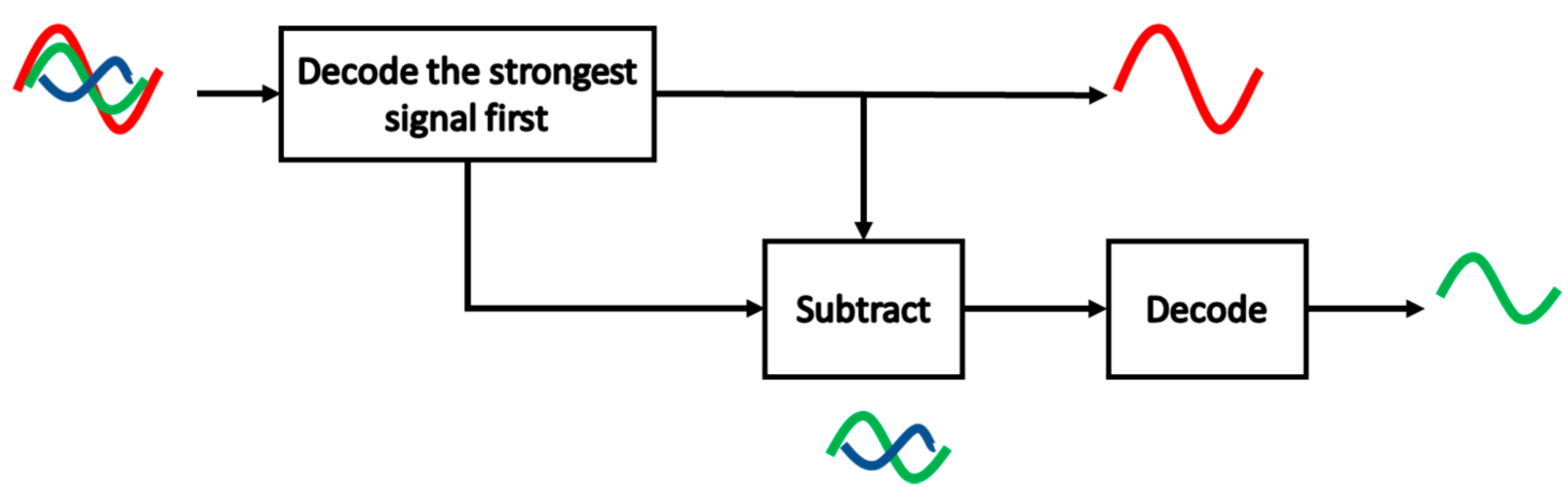
2.3. Successive Interference Cancellation (SIC)
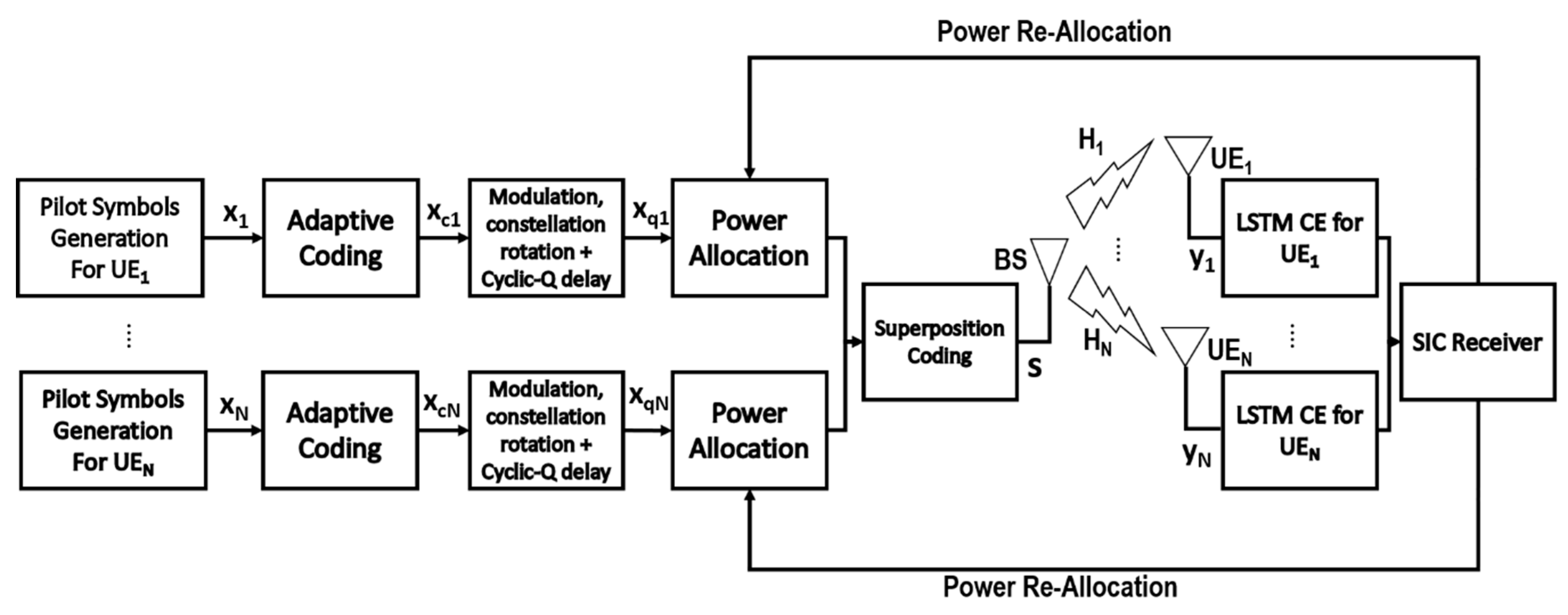
3. Proposed System Model
3.1. Adaptive BCH Codes
3.2. Modulation, Constellation Rotation, and Cyclic-Q Delay
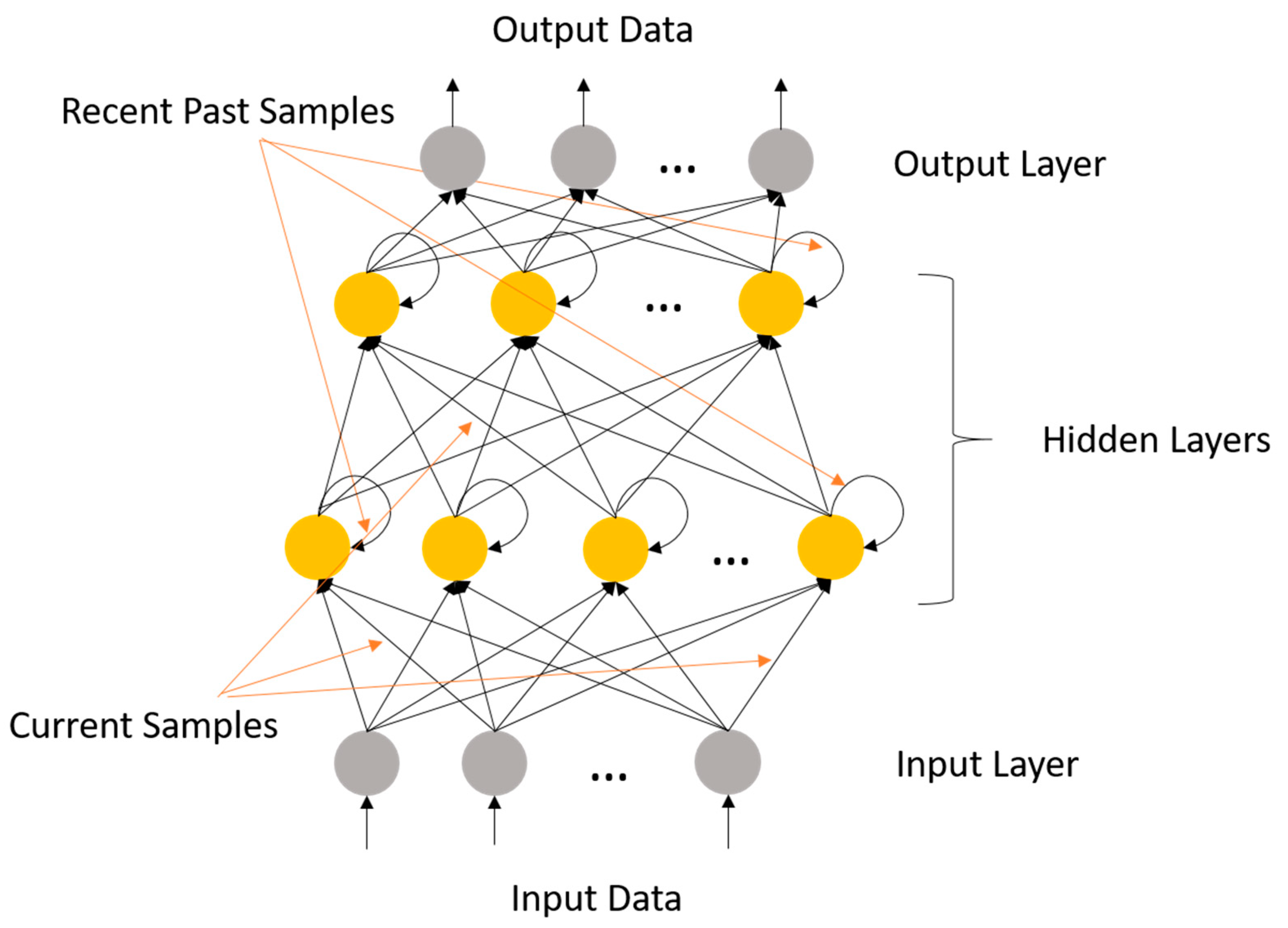
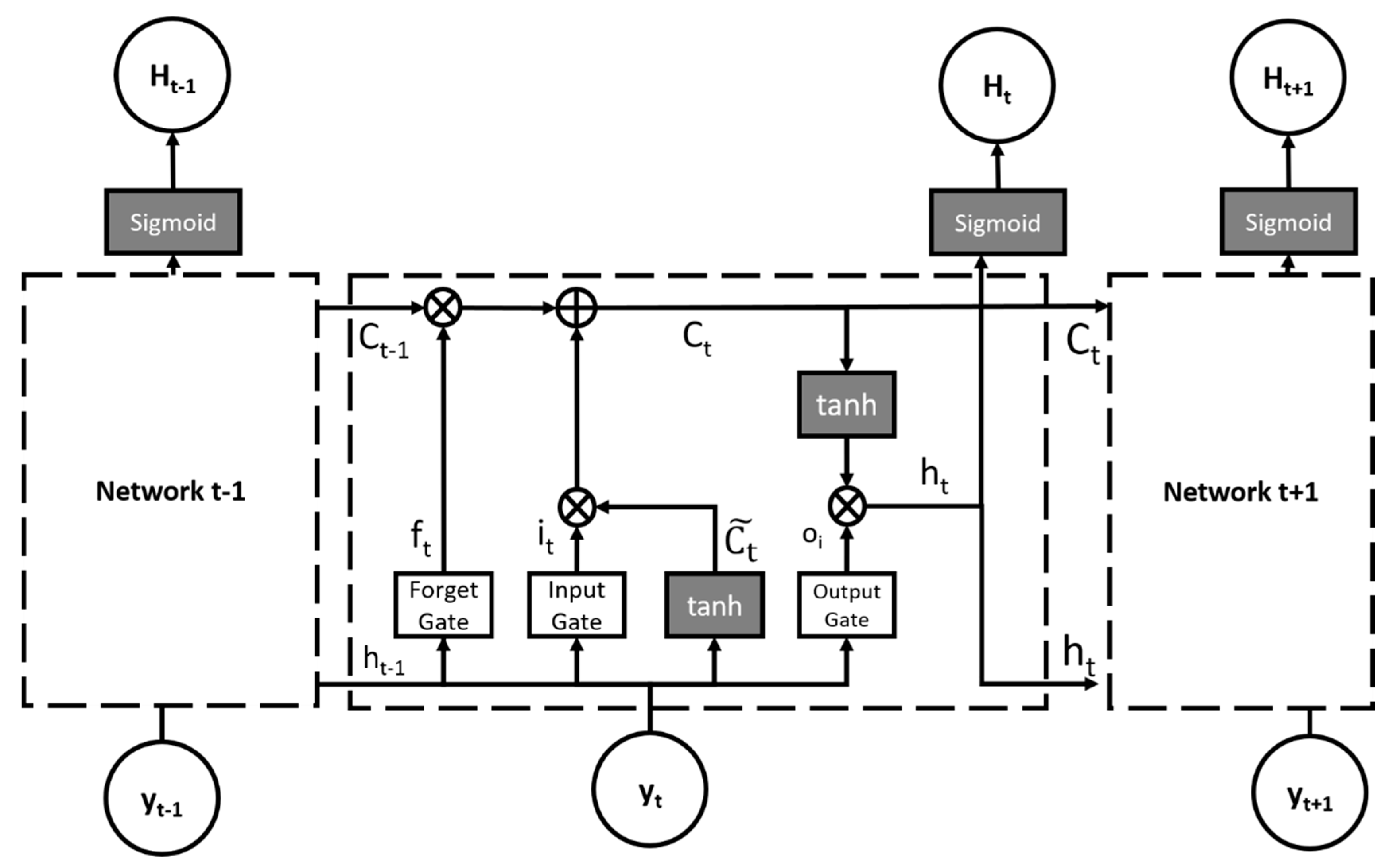
3.3. LSTM Channel Estimation
| Algorithm 2 LSTM Channel Estimation scheme |
| Inputs: Transmitted pilot data, xi, for users, target channel matrices, Hi. |
| 1: Randomly initialize the weights (W’s) and bias (b’s) values |
| 2: The forget gate: |
| 3: The input gate: |
| 4: The candidate value: |
| 5: Update the old cell state, , into the new cell state, , by |
| 6: Update the output of the LSTM by: |
| The output gate: |
| The estimated channel matrix: |
| Outputs: Estimated channel matrices, Ht, and the equivalent SNR values. |
3.4. Assignment of Power Coefficients
| Algorithm 3 Power Coefficient Allocation |
| Inputs: Required number of users, N. |
| 1: loop i = 1: N |
| 2: |
| 3: end loop |
| 4: Sum = |
| 5: loop I = 1: N |
| 6: p 7: end loop |
| 8: loop I = 1: N/2 |
| 9: p(i) = p(i) × (4/5) |
| 10: end loop |
| 11: loop I = (N/2) + 1: N |
| 12: p(i) = p(i) × (1/5) |
| 13: end loop |
| Outputs: Power coefficient, pi, for each user. |
4. Proposed System Evaluation
4.1. Outage Probability Calculation
4.2. Sum Rate Calculation
5. Simulations and Discussion
5.1. Simulation Settings
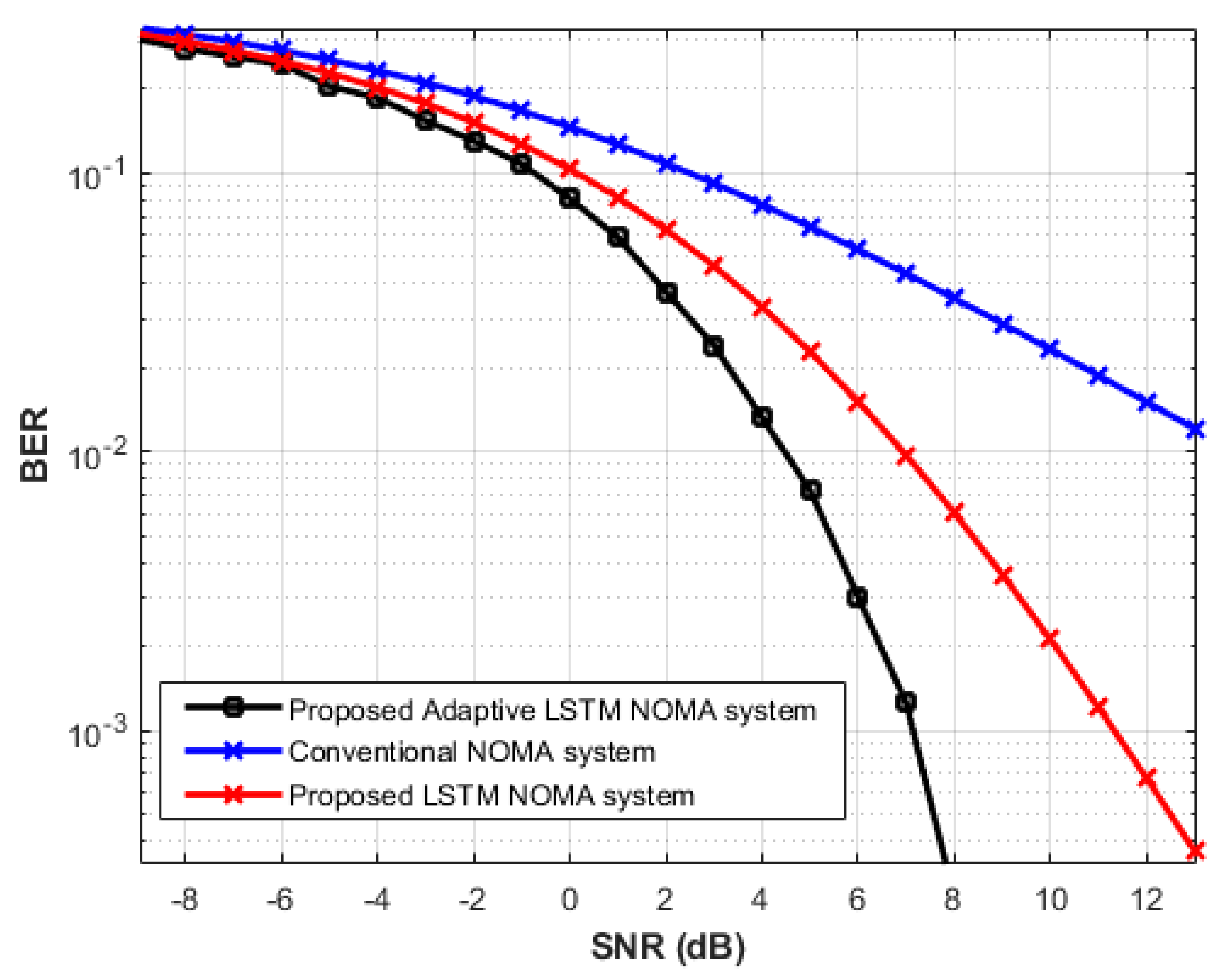
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fadlullah, Z.M.; Tang, F.; Mao, B.; Kato, N.; Akashi, O.; Inoue, T.; Mizutani, K. State-of-the-Art Deep Learning: Evolving Machine Intelligence Toward Tomorrow’s Intelligent Network Traffic Control Systems. IEEE Commun. Surv. Tutor. 2017, 19, 2432–2455. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Elkashlan, M.; Ding, Z.; Nallanathan, A.; Hanzo, L. Nonorthogonal Multiple Access for 5G and Beyond. Proc. IEEE 2017, 105, 2347–2381. [Google Scholar] [CrossRef]
- Xia, B.; Wang, J.; Xiao, K.; Gao, Y.; Yao, Y.; Ma, S. Outage Performance Analysis for the Advanced SIC Receiver in Wireless NOMA Systems. IEEE Trans. Veh. Technol. 2018, 67, 6711–6715. [Google Scholar] [CrossRef]
- Ding, Z.; Lei, X.; Karagiannidis, G.K.; Schober, R.; Yuan, J.; Bhargava, V.K. A Survey on Non-Orthogonal Multiple Access for 5G Networks: Research Challenges and Future Trends. IEEE J. Sel. Areas Commun. 2017, 35, 2181–2195. [Google Scholar] [CrossRef]
- Liu, Q.; Hui, B.; Chang, K. A Survey on Non-orthogonal Multiple Access Schemes. In Proceedings of the KICS Winter Conference, YongPyong, Korea, 15–17 December 2014; pp. 98–101. [Google Scholar]
- Islam, S.M.R.; Avazov, N.; Dobre, O.A.; Kwak, K. Power-Domain Non-Orthogonal Multiple Access (NOMA) in 5G Systems: Potentials and Challenges. IEEE Commun. Surv. Tutor. 2017, 19, 721–742. [Google Scholar] [CrossRef]
- Sedtheetorn, P.; Chulajata, T. Accurate spectral efficiency analysis for non orthogonal multiple access. In Proceedings of the 19th International Conference on Advanced Communication Technology (ICACT), PyeongChang, Korea, 19–22 February 2017; pp. 844–850. [Google Scholar]
- Kizilirmak, R.C. Non-Orthogonal Multiple Access (NOMA) for 5G Networks. In Towards 5G Wireless Networks—A Physical Layer Perspective; Bizaki, H.K., Ed.; Intechopen Limited: London, UK, 2016; ISBN 978-953-51-2833-5. [Google Scholar]
- Xiong, X.; Xiang, W.; Zheng, K.; Shen, H.; Wei, X. An open source SDR-based NOMA system for 5G networks. IEEE Wirel. Commun. 2015, 22, 24–32. [Google Scholar] [CrossRef]
- Benjebbour, A.; Saito, K.; Li, A.; Kishiyama, Y.; Nakamura, T. Non-orthogonal multiple access (NOMA): Concept, performance evaluation and experimental trials. In Proceedings of the International Conference on Wireless Networks and Mobile Communications (WINCOM), Marrakech, Morocco, 20–23 October 2015; pp. 1–6. [Google Scholar]
- Zhang, R.; Hanzo, L. A Unified Treatment of Superposition Coding Aided Communications: Theory and Practice. IEEE Commun. Surv. Tutor. 2011, 13, 503–520. [Google Scholar] [CrossRef]
- Ding, Z.; Fan, P.; Poor, H.V. Impact of User Pairing on 5G Nonorthogonal Multiple-Access Downlink Transmissions. IEEE Trans. Veh. Technol. 2016, 65, 6010–6023. [Google Scholar] [CrossRef]
- Shieh, S.-L.; Lin, C.-H.; Huang, Y.-C.; Wang, C.-L. On Gray Labeling for Downlink Non-Orthogonal Multiple Access without SIC. IEEE Commun. Lett. 2016, 20, 1721–1724. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, J.; Serpedin, E. Performance Analysis of a 5G Energy-Constrained Downlink Relaying Network with Non-Orthogonal Multiple Access. IEEE Trans. Wirel. Commun. 2017, 16, 8333–8346. [Google Scholar] [CrossRef]
- Shi, S.; Yang, L.; Zhu, H. Outage Balancing in Downlink Nonorthogonal Multiple Access with Statistical Channel State Information. IEEE Trans. Wirel. Commun. 2016, 15, 4718–4731. [Google Scholar]
- Ding, Z.; Yang, Z.; Fan, P.; Poor, H.V. On the Performance of Non-Orthogonal Multiple Access in 5G Systems with Randomly Deployed Users. IEEE Signal Process. Lett. 2014, 21, 1501–1505. [Google Scholar] [CrossRef]
- Yang, Z.; Ding, Z.; Fan, P.; Karagiannidis, G.K. On the Performance of Non-orthogonal Multiple Access Systems with Partial Channel Information. IEEE Trans. Commun. 2016, 64, 654–667. [Google Scholar] [CrossRef]
- Tabassum, H.; Ali, M.S.; Hossain, E.; Hossain, M.J.; Kim, D.I. Non-Orthogonal Multiple Access (NOMA) in Cellular Uplink and Downlink: Challenges and Enabling Techniques. Available online: https://arxiv.org/pdf/1608.05783.pdf (accessed on 16 July 2019).
- Yang, Z.; Xu, W.; Li, Y. Fair Non-Orthogonal Multiple Access for Visible Light Communication Downlinks. IEEE Wirel. Commun. Lett. 2017, 6, 66–69. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, W.; Pan, C.; Pan, Y.; Chen, M. On the Optimality of Power Allocation for NOMA Downlinks with Individual QoS Constraints. IEEE Commun. Lett. 2017, 21, 1649–1652. [Google Scholar] [CrossRef]
- Ye, N.; Han, H.; Zhao, L.; Wang, A. Uplink Nonorthogonal Multiple Access Technologies Toward 5G: A Survey. Wirel. Commun. Mob. Comput. 2018, 1–26. [Google Scholar] [CrossRef]
- Basharat, M.; Ejaz, W.; Naeem, M.; Khattak, A.M.; Anpalagan, A. A survey and taxonomy on nonorthogonal multiple-access schemes for 5G networks. Trans. Emerg. Telecommun. Technol. 2018, 29, e3202. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Ding, Z.; Wang, Z.; Chen, S.; Hanzo, L. A Survey of Non-Orthogonal Multiple Access for 5G. IEEE Commun. Surv. Tutor. 2018, 20, 2294–2323. [Google Scholar] [CrossRef]
- Ribeiro, F.C.; Guerreiro, J.; Dinis, R.; Cercas, F.; Jayakody, D.N.K. Multi-user detection for the downlink of NOMA systems with multi-antenna schemes and power-efficient amplifiers. Phys. Commun. 2019, 33, 199–205. [Google Scholar] [CrossRef]
- Khan, R.; Jayakody, D.N.K.; Pervaiz, H.; Tafazolli, R. Modulation Based Non-Orthogonal Multiple Access for 5G Resilient Networks. In Proceedings of the IEEE Globecom Workshops (GC Wkshps), Abu Dhabi, UAE, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Gui, G.; Huang, H.; Song, Y.; Sari, H. Deep Learning for An Effective Non-Orthogonal Multiple Access Scheme. IEEE Trans. Veh. Technol. 2018, 67, 8440–8450. [Google Scholar] [CrossRef]
- Kato, N.; Fadlullah, Z.M.; Mao, B.; Tang, F.; Akashi, O.; Inoue, T.; Mizutani, K. The Deep Learning Vision for Heterogeneous Network Traffic Control: Proposal, Challenges, and Future Perspective. IEEE Wirel. Commun. 2017, 24, 146–153. [Google Scholar] [CrossRef]
- Nour, C.A.; Douillard, C. Rotated QAM Constellations to Improve BICM Performance for DVB-T2. In Proceedings of the 10th IEEE International Symposium on Spread Spectrum Techniques and Applications 2008, Bologna, Italy, 25–28 August 2008; pp. 354–359. [Google Scholar]
- Awan, D.A.; Cavalcante, R.L.G.; Yukawa, M.; Stanczak, S. Detection for 5G-NOMA: An Online Adaptive Machine Learning Approach. In Proceedings of the International IEEE Conference on Communications (ICC), Kansas City, MO, USA, 20 May 2018; pp. 1–6. [Google Scholar]
- Yang, L.; Chen, J.; Ni, Q.; Shi, J.; Xue, X. NOMA-Enabled Cooperative Unicast–Multicast: Design and Outage Analysis. IEEE Trans. Wirel. Commun. 2017, 16, 7870–7889. [Google Scholar] [CrossRef]
- Lee, E.-H.; Kim, J.-J.; Song, H.-K. Adaptive Channel Coding Based on Channel Condition in Cooperative Communication System. Wirel. Pers. Commun. 2016, 88, 701–710. [Google Scholar] [CrossRef]
- Grönroos, S.; Nybom, K.; Björkqvist, J. Implementation and Performance Analysis of DVB-T2 Rotated Constellation Demappers on a GPU. Analog Integr. Circuits Signal Process. 2014, 78, 589–598. [Google Scholar] [CrossRef]
- Fahmy, H.A.; Shehata, K.A.; Gasser, S. Design an optimized hardware implementation of DVB-T2 modules on an FPGA. In Proceedings of the 6th International Conference on Digital Information Processing and Communications (ICDIPC), Beirut, Lebanon, 20–22 April 2016; pp. 125–128. [Google Scholar]
- Koliopanos, C.; Chronopoulos, S.; Tzechilidou, A.M.; Angelis, C.T. Simulation, modeling, and performance analysis of IEEE 802.16e OFDMA Systems for Urban and Rural Environments. In Proceedings of the 2nd International Conference on Signals, Circuits and Systems, Nabeul, Tunisia, 7–9 November 2008; pp. 1–4. [Google Scholar]
- Aldababsa, M.; Toka, M.; Gökçeli, S.; Kurt, G.K.; Kucur, O. A Tutorial on Nonorthogonal Multiple Access for 5G and Beyond. Wirel. Commun. Mob. Comput. 2018. [Google Scholar] [CrossRef]
- Higuchi, K.; Benjebbour, A. Non-orthogonal Multiple Access (NOMA) with Successive Interference Cancellation for Future Radio Access. IEICE Trans. Commun. 2015, 98, 403–414. [Google Scholar] [CrossRef]
- Yathiraj, H.U. Implementation of BCH Code (n, k) Encoder and Decoder for Multiple Error Correction Control. Int. J. Comput. Sci. Mob. Appl. 2014, 2, 45–54. [Google Scholar]
- Bergmans, P. Random coding theorem for broadcast channels with degraded components. IEEE Trans. Inf. Theory 1973, 19, 197–207. [Google Scholar] [CrossRef]
- Böcherer, G.; Steiner, F.; Schulte, P. Bandwidth efficient and rate-matched low-density parity-check coded modulation. IEEE Trans. Commun. 2015, 63, 4651–4665. [Google Scholar] [CrossRef]
- Hojeij, M.; Farah, J.; Nour, C.A.; Douillard, C. Resource Allocation in Downlink Non-Orthogonal Multiple Access (NOMA) for Future Radio Access. In Proceedings of the 81st IEEE Vehicular Technology Conference (VTC Spring), Glasgow, Scotland, 11–14 May 2015; pp. 1–6. [Google Scholar]
- Xu, P.; Cumanan, K. Optimal Power Allocation Scheme for Non-Orthogonal Multiple Access With α-Fairness. IEEE J. Select. Areas Commun. 2017, 35, 2357–2369. [Google Scholar] [CrossRef]
- Dawadi, R.; Parsaeefard, S.; Derakhshani, M.; Le-Ngoc, T. Power-Efficient Resource Allocation in NOMA Virtualized Wireless Networks. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Lei, M.; Zhang, X.; Zhang, T.; Lei, L.; He, Q.; Yuan, D. Successive Interference Cancellation for Throughput Maximization in Wireless Powered Communication Networks. In Proceedings of the 84th IEEE Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 18–21 September 2016; pp. 1–6. [Google Scholar]
- Ez-zazi, I.; Arioua, M.; el Oualkadi, A.; el Assari, Y. Performance analysis of efficient coding schemes for wireless sensor networks. In Proceedings of the 3rd International Workshop on RFID And Adaptive Wireless Sensor Networks (RAWSN), Agadir, Morocco, 13–15 May 2015; pp. 42–47. [Google Scholar]
- Clark, G.C., Jr.; Cain, J.B. Error-Correction Coding for Digital Communications; Springer Science & Business Media: New York, NY, USA, 2013; ISBN 9781489921741. [Google Scholar]
- Zhang, M.; Li, Z.; Xing, L.; Tang, N. Construction of Some New Quantum BCH Codes. IEEE Access 2018, 6, 36122–36131. [Google Scholar] [CrossRef]
- Chaari, L.; Fourati, M.; Masmoudi, N.; Kamoun, L. Adaptive BCH coding Performance analysis. In Proceedings of the WSEAS International Conference for Mathematics and Computers in Science and Engineering, World Scientific and Engineering Academy and Society, Wisconsin, WI, USA, 6 April 2008; pp. 9–11. [Google Scholar]
- Regis, C.D.M.; Mota, M.F.; Lopes, R.F.; de Alencar, M.S. Performance Analysis of a 64-QAM Rotated Constellation Subject to Rice Fading. In Proceedings of the 3rd Brazilian Telecommunications Symposium, Fortaleza, Brazil, 13–16 September 2012; pp. 4–6. [Google Scholar]
- Polak, L.; Kratochvil, T. Performance of the Rotated Constellation in DVB-T2. In Proceedings of the 7th International Conference on Digital Telecommunications (ICDT 2012), Blanc, France, 29 April 2012; pp. 84–87. [Google Scholar]
- Prasad, S.C.; Prasad, P. Deep Recurrent Neural Networks for Time—Series Prediction. Available online: https://arxiv.org/ftp/arxiv/papers/1407/1407.5949.pdf (accessed on 16 July 2019).
- Salehinejad, H.; Sankar, S.; Barfett, J.; Colak, E.; Valaee, S. Recent Advances in Recurrent Neural Networks. Available online: https://arxiv.org/pdf/1801.01078.pdf (accessed on 16 July 2019).
- Zhang, J.; Man, K.F. Time series prediction using RNN in multi-dimension embedding phase space. In Proceedings of the International Conference on Systems, Man, and Cybernetics (SMC’98), San Diego, CA, USA, 14 October 1998; pp. 1868–1873. [Google Scholar]
- Mago, V. Cross-Disciplinary Applications of Artificial Intelligence and Pattern Recognition: Advancing Technologies; Mago, V.K., Bhatia, N., Eds.; Advances in Computational Intelligence and Robotics; IGI Global: Chocolate Ave, Hershey, PA, USA, 2012; ISBN 978-1-61350-429-1. [Google Scholar]
- Sarma, K.K.; Mitra, A. Estimation of MIMO channels using complex time delay fully Recurrent Neural Network. In Proceedings of the 2nd National Conference on Emerging Trends and Applications in Computer Science, Shillong, India, 21–22 December 2011; pp. 1–5. [Google Scholar]
- Cain, G.D.; Gryka, J.; Kale, I. Complex IIR filter design through balanced model reduction of FIR prototypes. Electron. Lett. 1995, 31, 1332–1334. [Google Scholar]
- Rudko, M.; Cain, G.D.; Kale, I.; Beliczynski, B. A note on the Approximation of FIR by IIR digital filters: An algorithm based on balanced model reduction. IEEE Trans. Signal Process. 1995, 43, 314–317. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Edwards, A.W.F. Pascal’s Arithmetical Triangle: The Story of a Mathematical Idea; JHU Press: Charles St, Baltimore, MD, USA, 2002; ISBN 978-0-8018-6946-4. [Google Scholar]
- Qin, Q.; Lai, X.; Zou, J. Direct Multistep Wind Speed Forecasting Using LSTM Neural Network Combining EEMD and Fuzzy Entropy. Appl. Sci. 2019, 9, 126. [Google Scholar] [CrossRef]
- Donges, N. Recurrent Neural Networks and LSTM. Towards Data Sci. 2018, 18. Available online: https://arxiv.org/pdf/1801.01078.pdf (accessed on 16 July 2019).
- El Hihi, S.; Bengio, Y. Hierarchical recurrent neural networks for long-term dependencies. In Proceedings of the 8th International Conference on Neural Information Processing Systems, Denver, CO, USA, 27 November–2 December 1995. [Google Scholar]
- Recommendation, I.R. Guidelines for Evaluation of Radio Transmission Technologies for IMT-2000; ITU-R M 1225: Geneva, Switzerland, 1997. [Google Scholar]




| Parameter | Value |
|---|---|
| Carrier frequency | 2 GHz |
| Base station (BS) power | 46 dBm |
| System bandwidth (BW) | 5–10 MHz |
| Number of users per cell (N) | 10–20 |
| Bandwidth per user | 5.4 MHz |
| Number of data subcarriers | 1200 |
| Number of pilot subcarriers () | 4 |
| Number of guard-band subcarriers | 76 |
| Channel matrices () | Rayleigh or Rician fading |
| Subcarrier spacing | 15 kHz |
| Bose–Chaudhuri–Hocquenghem (BCH) code length | [7,4] up to [31,26] |
| Symbol length | Data: 66.67 msec + cyclic prefix: 4.69 msec |
| Modulation | QPSK and 64QAM |
| Constellation rotation angles | 0.506 rad for QPSK 0.150 rad for 64QAM |
| AWGN (w) | −10 to 30 dBm |
| Power allocation coefficients (p) | 2/3 and 1/3 3/4 and 1/4 4/5 and 1/5 |
| Parameter | Value |
|---|---|
| Number of layers | 4 |
| Number of neurons/layer (Input layer) | 1000 |
| Number of neurons/layer (LSTM) | 200 |
| Number of neurons/layer (fully connected layer) | 6 |
| Learning rates | 0.005, 0.0001 |
| Length of training data | 1333 × 1 |
| Length of testing data | 666 × 1 |
| Size of data | 2000 × 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
AbdelMoniem, M.; Gasser, S.M.; El-Mahallawy, M.S.; Fakhr, M.W.; Soliman, A. Enhanced NOMA System Using Adaptive Coding and Modulation Based on LSTM Neural Network Channel Estimation. Appl. Sci. 2019, 9, 3022. https://doi.org/10.3390/app9153022
AbdelMoniem M, Gasser SM, El-Mahallawy MS, Fakhr MW, Soliman A. Enhanced NOMA System Using Adaptive Coding and Modulation Based on LSTM Neural Network Channel Estimation. Applied Sciences. 2019; 9(15):3022. https://doi.org/10.3390/app9153022
Chicago/Turabian StyleAbdelMoniem, Mai, Safa M. Gasser, Mohamed S. El-Mahallawy, Mohamed Waleed Fakhr, and Abdelhamid Soliman. 2019. "Enhanced NOMA System Using Adaptive Coding and Modulation Based on LSTM Neural Network Channel Estimation" Applied Sciences 9, no. 15: 3022. https://doi.org/10.3390/app9153022
APA StyleAbdelMoniem, M., Gasser, S. M., El-Mahallawy, M. S., Fakhr, M. W., & Soliman, A. (2019). Enhanced NOMA System Using Adaptive Coding and Modulation Based on LSTM Neural Network Channel Estimation. Applied Sciences, 9(15), 3022. https://doi.org/10.3390/app9153022






