Facing Missing Observations in Data—A New Approach for Estimating Strength of Earthquakes on the Pacific Coast of Southern Mexico Using Random Censoring
Abstract
:1. Introduction
2. Materials and Methods
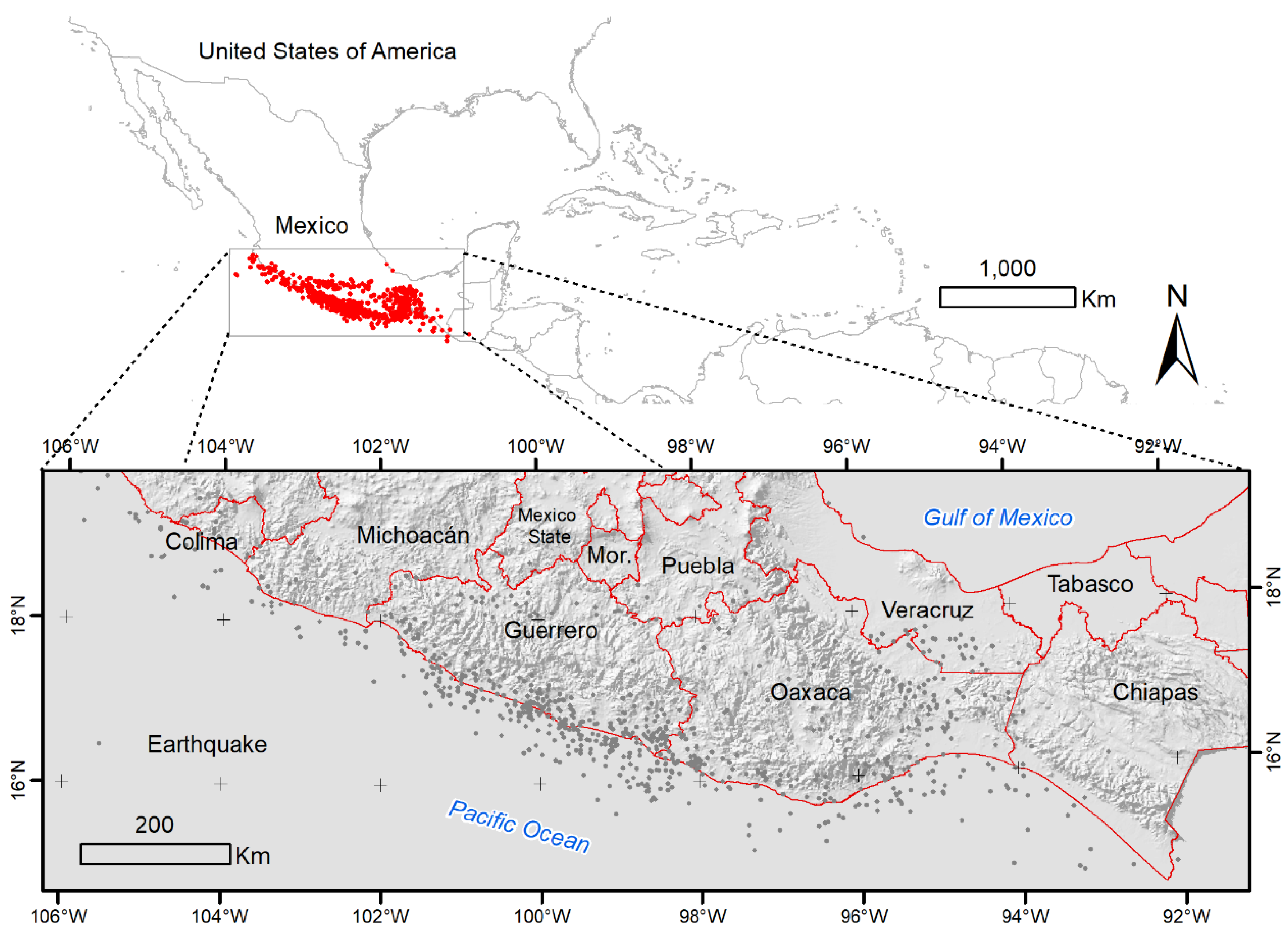
2.1. Study Area
2.2. Methodology
2.2.1. The GEV Distribution
2.2.2. Estimation of the Parameters of the GEV under Random Censoring
2.2.3. Bayesian Implementation
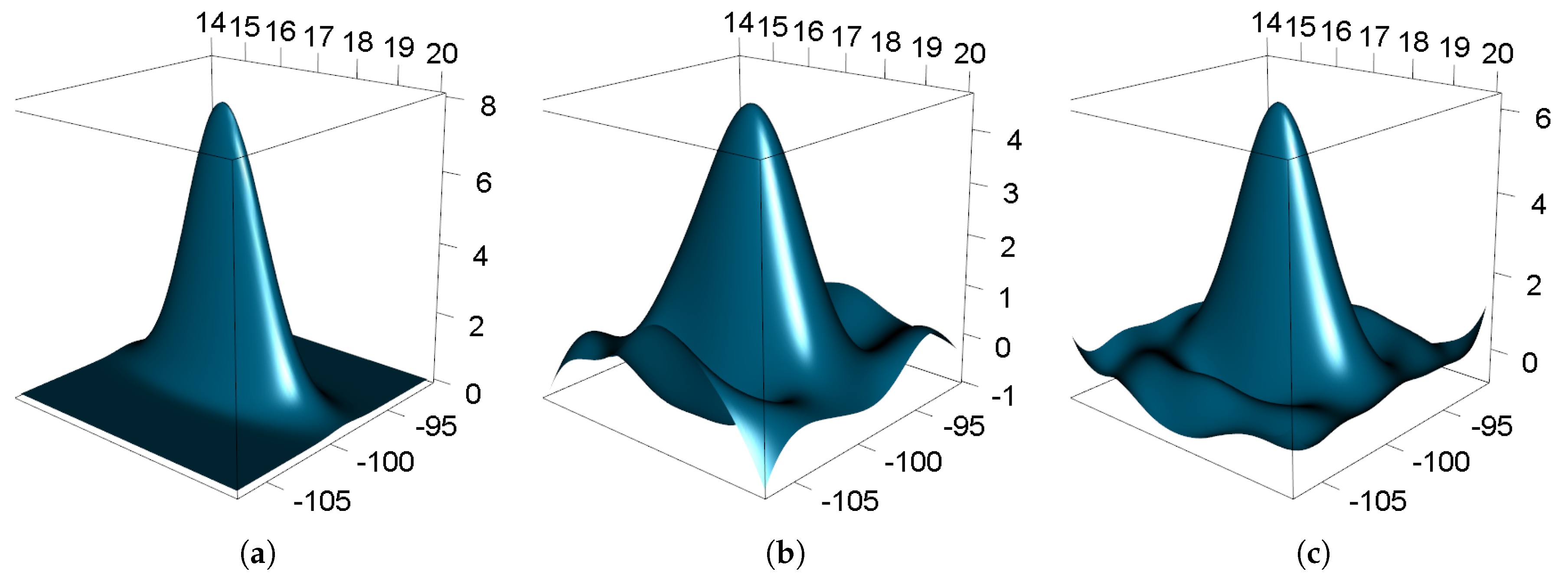
2.2.4. Simulation Study
2.3. Data Collection
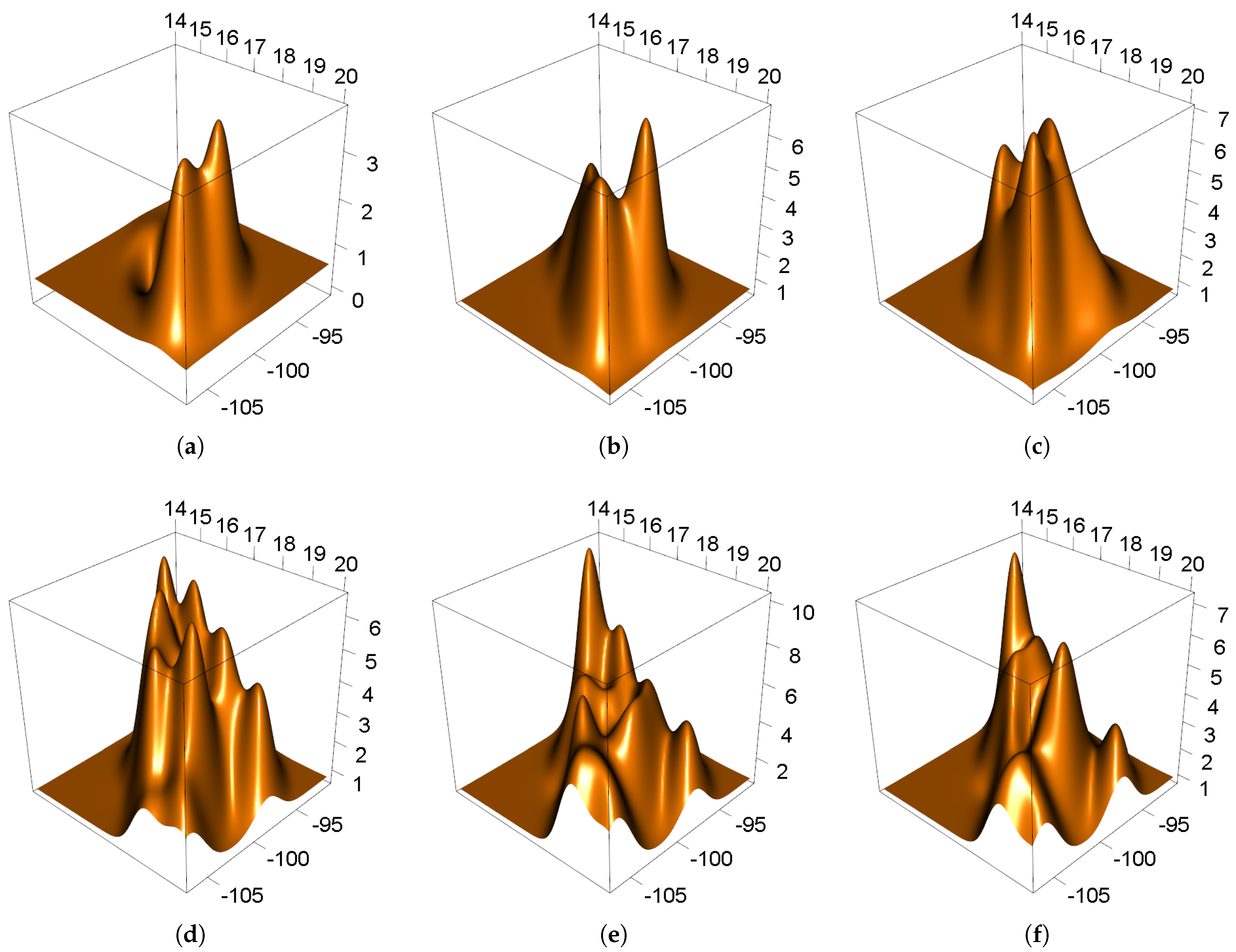
2.4. Data Analysis
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| EVT | Extreme Value Theory |
| MCMC | Markov Chain Monte-Carlo |
| SASMEX | Sistema de Alerta Sísmica de Mexico |
| SAS | Sistema de Alerta Sísmica de la Ciudad de Mexico |
| SASO | Sistema de Alerta Sísmica de Oaxaca |
| CIRES | Centro de Instrumentación y Registro Sísmico |
References
- Rundle, J.B.; Turcotte, D.L.; Shcherbakov, R.; Klein, W.; Sammis, C. Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef] [Green Version]
- Karaboga, T.; Canyilmaz, M.; Ozcan, O. Investigation of the relationship between ionospheric foF2 and earthquakes. Adv. Space Res. 2018, 61, 2022–2030. [Google Scholar] [CrossRef]
- Holliday, J.R.; Rundle, J.B.; Turcotte, D.L. Earthquake forecasting and verification. In Encyclopedia of Complexity and Systems Science; Springer: London, UK, 2009; pp. 2438–2449. [Google Scholar]
- Uyeda, S.; Kamogawa, M.; Nagao, T. Earthquakes, Electromagnetic Signals of. In Encyclopedia of Complexity and Systems Science; Springer: London, UK, 2009; pp. 2621–2635. [Google Scholar]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Phenomena preceding major earthquakes interconnected through a physical model. Ann. Geophys. 2019, 37, 315–324. [Google Scholar] [CrossRef] [Green Version]
- Sarlis, N. Statistical Significance of Earthś Electric and Magnetic Field Variations Preceding Earthquakes in Greece and Japan Revisited. Entropy 2018, 20, 561. [Google Scholar] [CrossRef]
- Uyeda, S.; Nagao, T.; Kamogawa, M. Short-term earthquake prediction: Current status of seismo-electromagnetics. Tectonophysics 2009, 470, 205–213. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R.; Wood, E.F. Estimation of the Generalized Extreme-Value Distribution by the Method of Probability-Weighted Moments. Technometrics 1985, 27, 251–261. [Google Scholar] [CrossRef]
- Bocci, C.; Caporali, E.; Petrucci, A. Geoadditive modeling for extreme rainfall data. AStA Adv. Stat. Anal. 2013, 97, 181–193. [Google Scholar] [CrossRef]
- Dupuis, D.; Field, C. Large wind speeds: Modeling and outlier detection. J. Agric. Biol. Environ. Stat. 2004, 9, 105. [Google Scholar] [CrossRef]
- Reich, B.; Shaby, B.; Cooley, D. A Hierarchical Model for Serially-Dependent Extremes: A Study of Heat Waves in the Western US. J. Agric. Biol. Environ. Stat. 2014, 19, 119–135. [Google Scholar] [CrossRef]
- Nordquist, J.M. Theory of largest values applied to earthquake magnitudes. Eos Trans. Am. Geophys. Union 1945, 26, 29–31. [Google Scholar] [CrossRef]
- Makjanić, B. On the frequency distribution of earthquake magnitude and intensity. Bull. Seismol. Soc. Am. 1980, 70, 2253–2260. [Google Scholar]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; Volume 208. [Google Scholar]
- Leese, M.N. Use of censored data in the estimation of Gumbel distribution parameters for annual maximum flood series. Water Resour. Res. 1973, 9, 1534–1542. [Google Scholar] [CrossRef]
- Kalbfleisch, J.D. The Statistical Analysis of Failure Time Data; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Einmahl, J.H.; Fils-Villetard, A.; Guillou, A. Statistics of extremes under random censoring. Bernoulli 2008, 14, 207–227. [Google Scholar] [CrossRef]
- Gomes, M.I.; Neves, M.M. Estimation of the extreme value index for randomly censored data. Biom. Lett. 2011, 48, 1–22. [Google Scholar]
- Bhattarai, K.P. Partial L-moments for the analysis of censored flood samples/Utilisation des L-moments partiels pour lánalyse d’échantillons tronqués de crues. Hydrol. Sci. J. 2004, 49. [Google Scholar] [CrossRef]
- Danish, M.Y.; Aslam, M. Bayesian inference for the randomly censored Weibull distribution. J. Stat. Comput. Simul. 2014, 84, 215–230. [Google Scholar] [CrossRef]
- Abbas, K.; Tang, Y. Estimation of Parameters for Fréchet Distribution Based on Type-II Censored Samples. Casp. J. Appl. Sci. Res. 2013, 2, 36–43. [Google Scholar]
- Hakamipour, N.; Rezaei, S. Optimizing the simple step stress accelerated life test with type I censored Fréchet data. REVSTAT–Stat. J. 2017, 15, 1–23. [Google Scholar]
- Prescott, P.; Walden, A. Maximum likeiihood estimation of the parameters of the three-parameter generalized extreme-value distribution from censored samples. J. Stat. Comput. Simul. 1983, 16, 241–250. [Google Scholar] [CrossRef]
- Phien, H.N.; Fang, T.S.E. Maximum likelihood estimation of the parameters and quantiles of the general extreme-value distribution from censored samples. J. Hydrol. 1989, 105, 139–155. [Google Scholar] [CrossRef]
- Wang, Q. Using partial probability weighted moments to fit the extreme value distributions to censored samples. Water Resour. Res. 1996, 32, 1767–1771. [Google Scholar] [CrossRef]
- Hosking, J.R. L-moments: analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. Ser. B (Methodol.) 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Hosking, J.R.M. The use of L-moments in the analysis of censored data. In Recent Advances in Life-Testing and Reliability; Chapter 29; Balakrishnan, N., Ed.; CRC Press: Boca Raton, FL, USA, 1995; pp. 546–564. [Google Scholar]
- Pardo, M.; Suarez, G. Shape of the subducted Rivera and Cocos plates in southern Mexico: Seismic and tectonic implications. J. Geophys. Res. Solid Earth 1995, 100, 12357–12373. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Clayton, R.; Jackson, J. Geometry and seismic properties of the subducting Cocos plate in central Mexico. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 1955, 81, 158–171. [Google Scholar] [CrossRef]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Proc. Camb. Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Espinosa-Aranda, J.; Cuellar, A.; Garcia, A.; Ibarrola, G.; Islas, R.; Maldonado, S.; Rodriguez, F. Evolution of the Mexican seismic alert system (SASMEX). Seismol. Res. Lett. 2009, 80, 694–706. [Google Scholar] [CrossRef]
- Gumbel, E. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958. [Google Scholar]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A.; Ramírez-Rojas, A.; Flores-Márquez, E.L. Natural time analysis: On the deadly Mexico M8. 2 earthquake on 7 September 2017. Phys. A Stat. Mech. Its Appl. 2018, 506, 625–634. [Google Scholar] [CrossRef]
- Stănică, D.; Stănică, D. ULF Pre-Seismic Geomagnetic Anomalous Signal Related to Mw8. 1 Offshore Chiapas Earthquake, Mexico on 8 September 2017. Entropy 2019, 21, 29. [Google Scholar] [CrossRef]
- Fawcett, L.; Green, A.C. Bayesian posterior predictive return levels for environmental extremes. In Stochastic Environmental Research and Risk Assessment; Springer: London, UK, 2018; pp. 1–20. [Google Scholar]
- Cameletti, M.; De Rubeis, V.; Ferrari, C.; Sbarra, P.; Tosi, P. An ordered probit model for seismic intensity data. Stoch. Environ. Res. Risk Assess. 2017, 31, 1593–1602. [Google Scholar] [CrossRef]
- Scitovski, S. A density-based clustering algorithm for earthquake zoning. Comput. Geosci. 2018, 110, 90–95. [Google Scholar] [CrossRef]
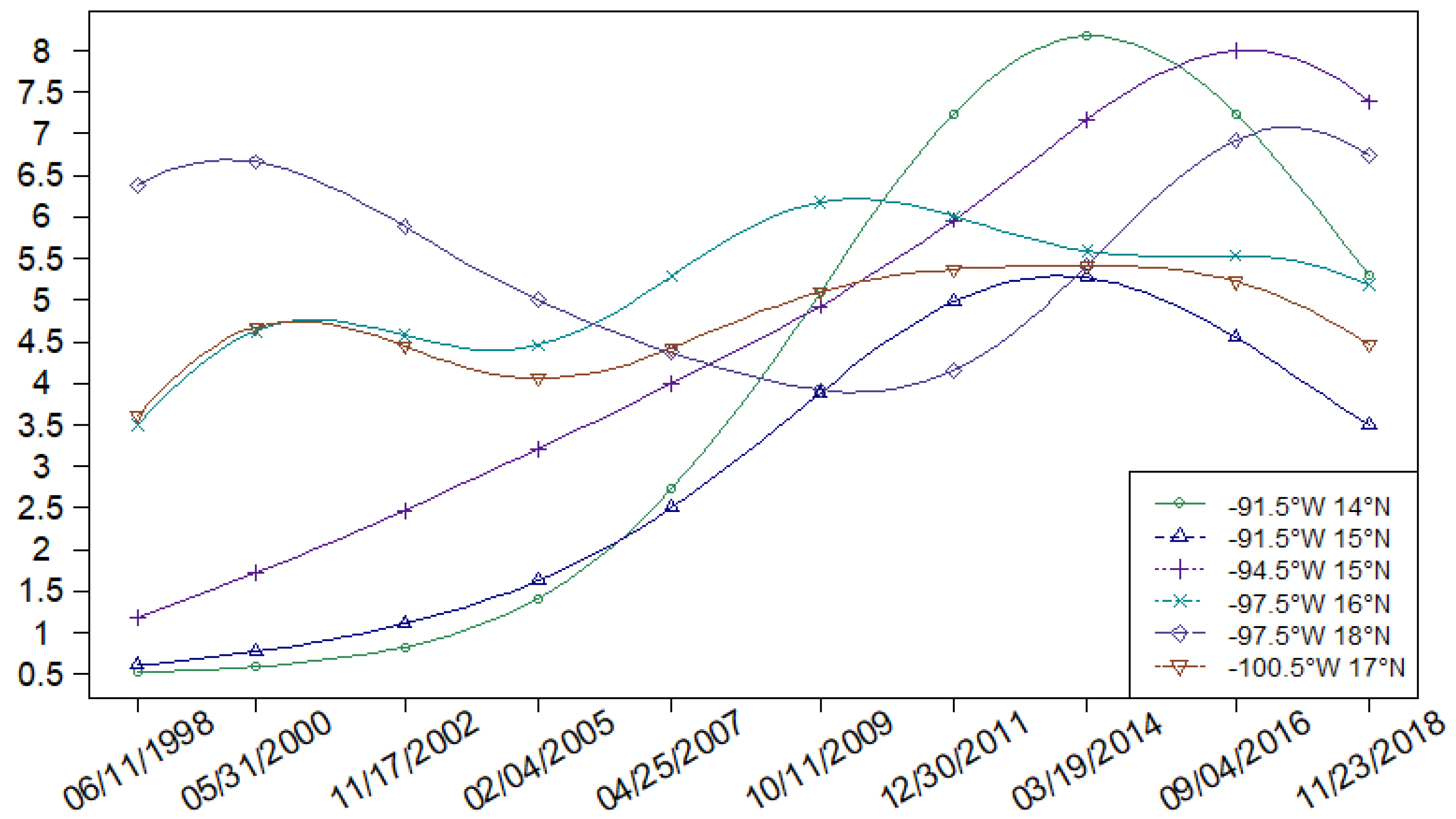
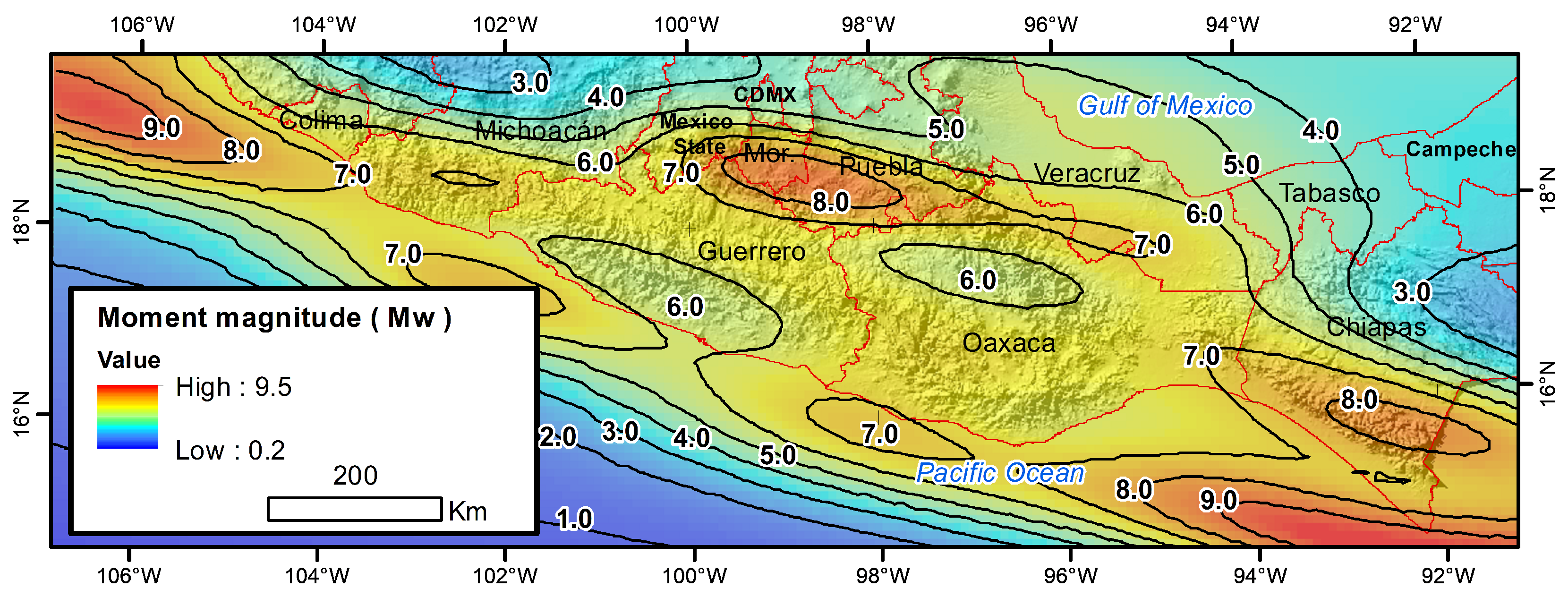
| Block ID | Long | Lat | Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|---|---|---|
| 1 | −91.5 | 14 | 6.1 | 6.2 | 6.8 | 6.7 | 7.3 | 7.3 |
| 2 | −91.5 | 15 | 6.9 | 6.9 | 7 | 7 | 7 | 7 |
| 3 | −91.5 | 16 | 4.7 | 4.9 | 5.1 | 5.1 | 5.2 | 5.4 |
| 4 | −94.5 | 15 | 4.2 | 5 | 5.3 | 5.5 | 5.8 | 8.2 |
| 5 | −94.5 | 16 | 3 | 4.1 | 4.3 | 4.4 | 4.7 | 6.6 |
| 6 | −94.5 | 17 | 3.8 | 4.2 | 4.4 | 4.5 | 4.7 | 6.7 |
| 7 | −94.5 | 18 | 4 | 4.4 | 4.6 | 4.8 | 4.9 | 6.4 |
| 8 | −94.5 | 19 | 5.5 | 5.5 | 5.5 | 5.5 | 5.5 | 5.5 |
| 9 | −97.5 | 15 | 4.1 | 4.2 | 4.6 | 4.6 | 5 | 5.1 |
| 10 | −97.5 | 16 | 2.9 | 3.9 | 4 | 4.2 | 4.3 | 7.4 |
| 11 | −97.5 | 17 | 2.2 | 3.8 | 4 | 4.1 | 4.2 | 5.8 |
| 12 | −97.5 | 18 | 3.8 | 4.1 | 4.4 | 4.7 | 5.3 | 7.1 |
| 13 | −97.5 | 19 | 4.8 | 4.8 | 4.8 | 4.8 | 4.8 | 4.8 |
| 14 | −100.5 | 16 | 3.6 | 4 | 4.3 | 4.3 | 4.6 | 5.2 |
| 15 | −100.5 | 17 | 3.1 | 3.9 | 4.1 | 4.2 | 4.4 | 7.2 |
| 16 | −100.5 | 18 | 3.5 | 4 | 4.1 | 4.4 | 4.4 | 6.5 |
| 17 | −100.5 | 19 | 4.2 | 4.3 | 4.4 | 4.3 | 4.4 | 4.4 |
| 18 | −103.5 | 17 | 5.1 | 5.1 | 5.1 | 5.1 | 5.1 | 5.1 |
| 19 | −103.5 | 18 | 3.7 | 4 | 4.3 | 4.5 | 4.7 | 6.5 |
| 20 | −103.5 | 19 | 3.7 | 4 | 4.1 | 4.3 | 4.4 | 5.9 |
| 21 | −106.5 | 19 | 4.1 | 4.2 | 4.2 | 4.8 | 5.3 | 6.3 |
| 22 | −106.5 | 20 | 3.8 | 4 | 4.1 | 4.2 | 4.3 | 4.6 |
| Coef. | Mode | Mean | 95% CI |
|---|---|---|---|
| 0.8136 | 0.7004 | (0.4677, 0.8079) | |
| 0.5710 | 1.1110 | (1.0855, 1.1697) | |
| −0.5900 | −0.5930 | (−0.6014, −0.5900) | |
| 26.1363 | 83.3487 | (26.2751, 810.0938) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguirre-Salado, A.I.; Vaquera-Huerta, H.; Aguirre-Salado, C.A.; Jiménez-Hernández, J.d.C.; Barragán, F.; Guzmán-Martínez, M. Facing Missing Observations in Data—A New Approach for Estimating Strength of Earthquakes on the Pacific Coast of Southern Mexico Using Random Censoring. Appl. Sci. 2019, 9, 2863. https://doi.org/10.3390/app9142863
Aguirre-Salado AI, Vaquera-Huerta H, Aguirre-Salado CA, Jiménez-Hernández JdC, Barragán F, Guzmán-Martínez M. Facing Missing Observations in Data—A New Approach for Estimating Strength of Earthquakes on the Pacific Coast of Southern Mexico Using Random Censoring. Applied Sciences. 2019; 9(14):2863. https://doi.org/10.3390/app9142863
Chicago/Turabian StyleAguirre-Salado, Alejandro Ivan, Humberto Vaquera-Huerta, Carlos Arturo Aguirre-Salado, José del Carmen Jiménez-Hernández, Franco Barragán, and María Guzmán-Martínez. 2019. "Facing Missing Observations in Data—A New Approach for Estimating Strength of Earthquakes on the Pacific Coast of Southern Mexico Using Random Censoring" Applied Sciences 9, no. 14: 2863. https://doi.org/10.3390/app9142863
APA StyleAguirre-Salado, A. I., Vaquera-Huerta, H., Aguirre-Salado, C. A., Jiménez-Hernández, J. d. C., Barragán, F., & Guzmán-Martínez, M. (2019). Facing Missing Observations in Data—A New Approach for Estimating Strength of Earthquakes on the Pacific Coast of Southern Mexico Using Random Censoring. Applied Sciences, 9(14), 2863. https://doi.org/10.3390/app9142863





