Determination of the Material Parameters in the Holzapfel-Gasser-Ogden Constitutive Model for Simulation of Age-Dependent Material Nonlinear Behavior for Aortic Wall Tissue under Uniaxial Tension
Abstract
1. Introduction
2. Constitutive Model
2.1. Strain-Based Formula
2.2. Invariant-Based Formula
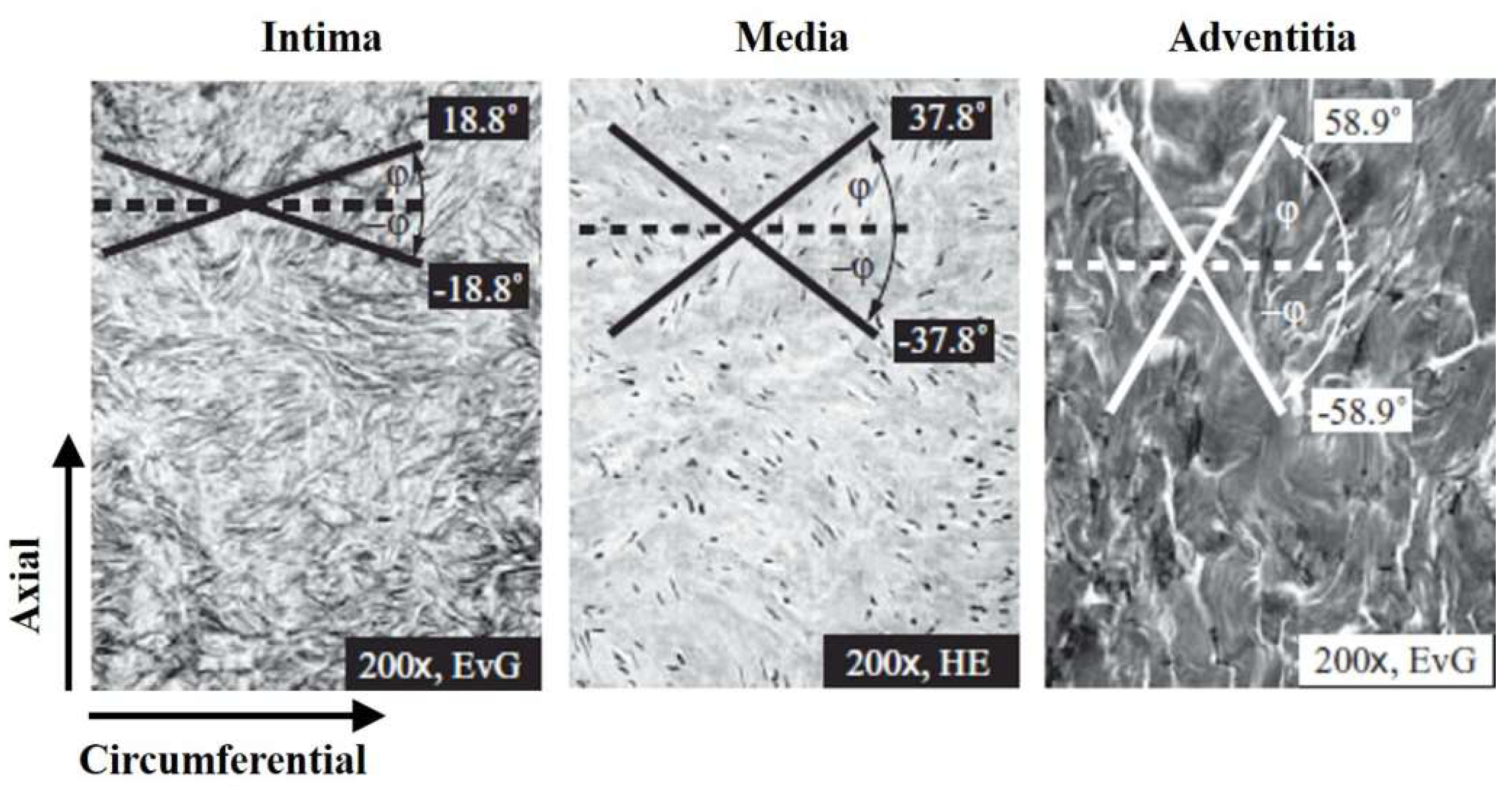
2.3. Anisotropic Hyper-Elastic Materials
3. Experiments and Simulations
3.1. Experiment Details for the Material Test
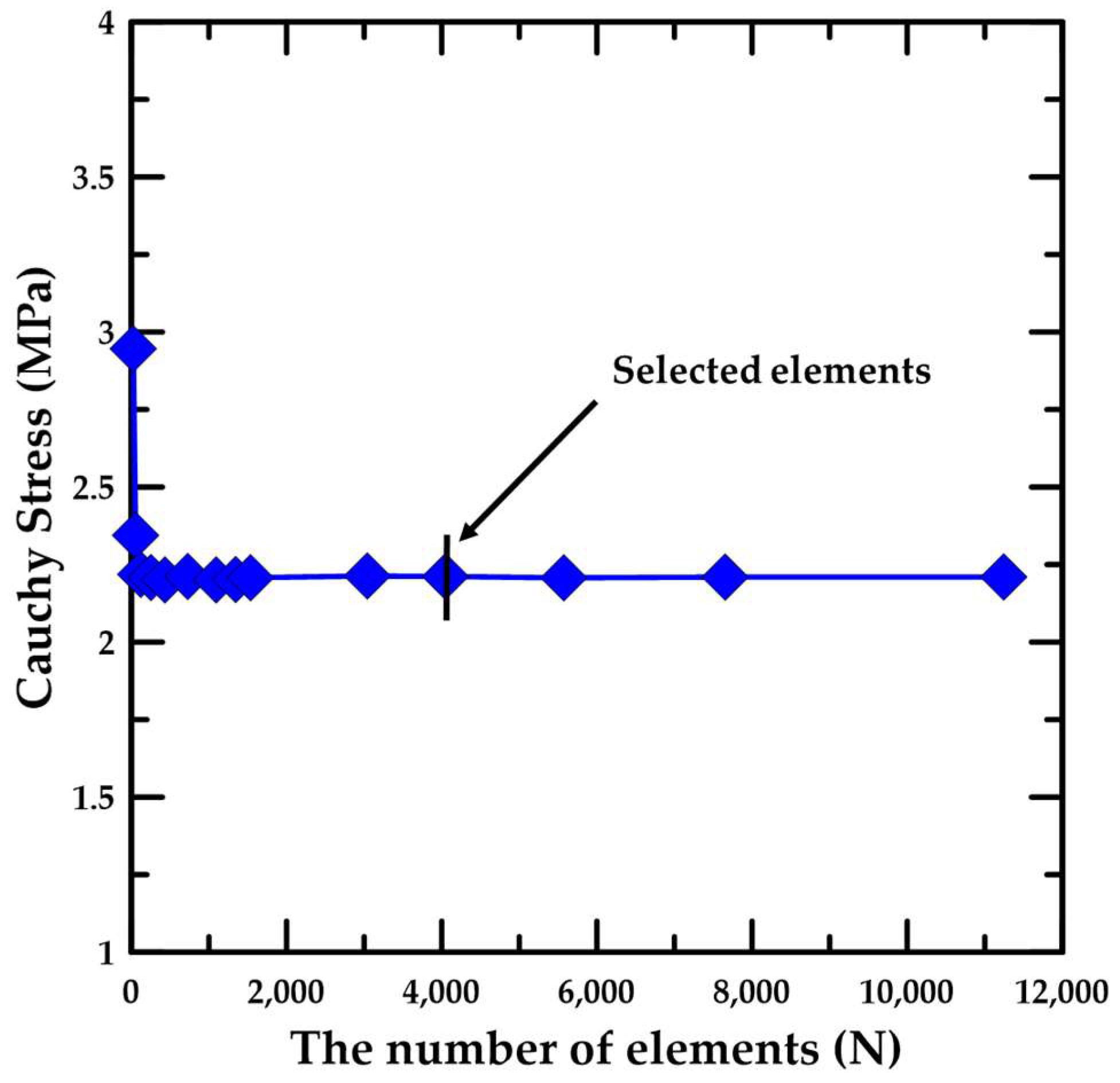
3.2. Simulation Details for the Material Test
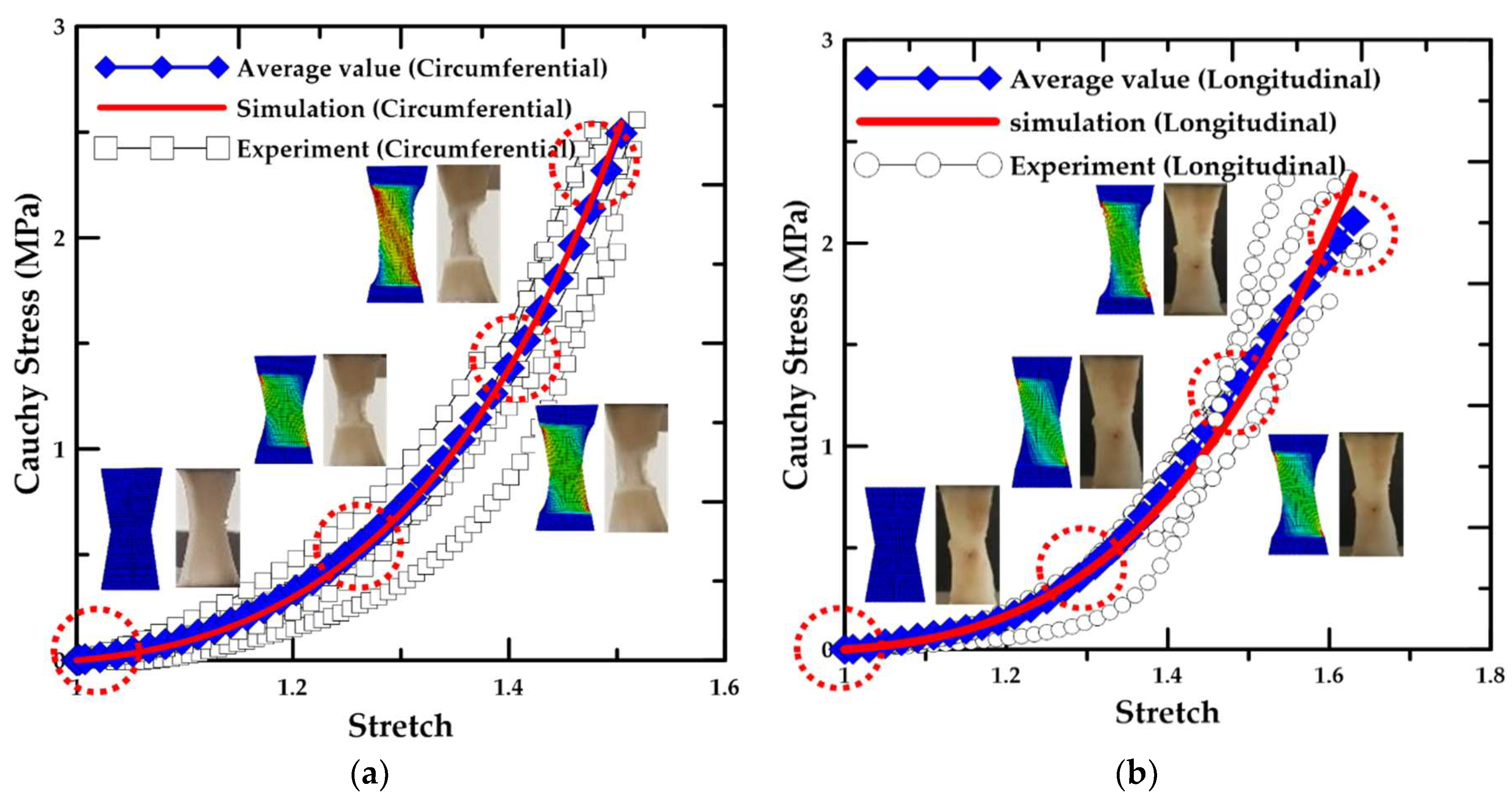
3.3. Results for the Material Test
4. Results
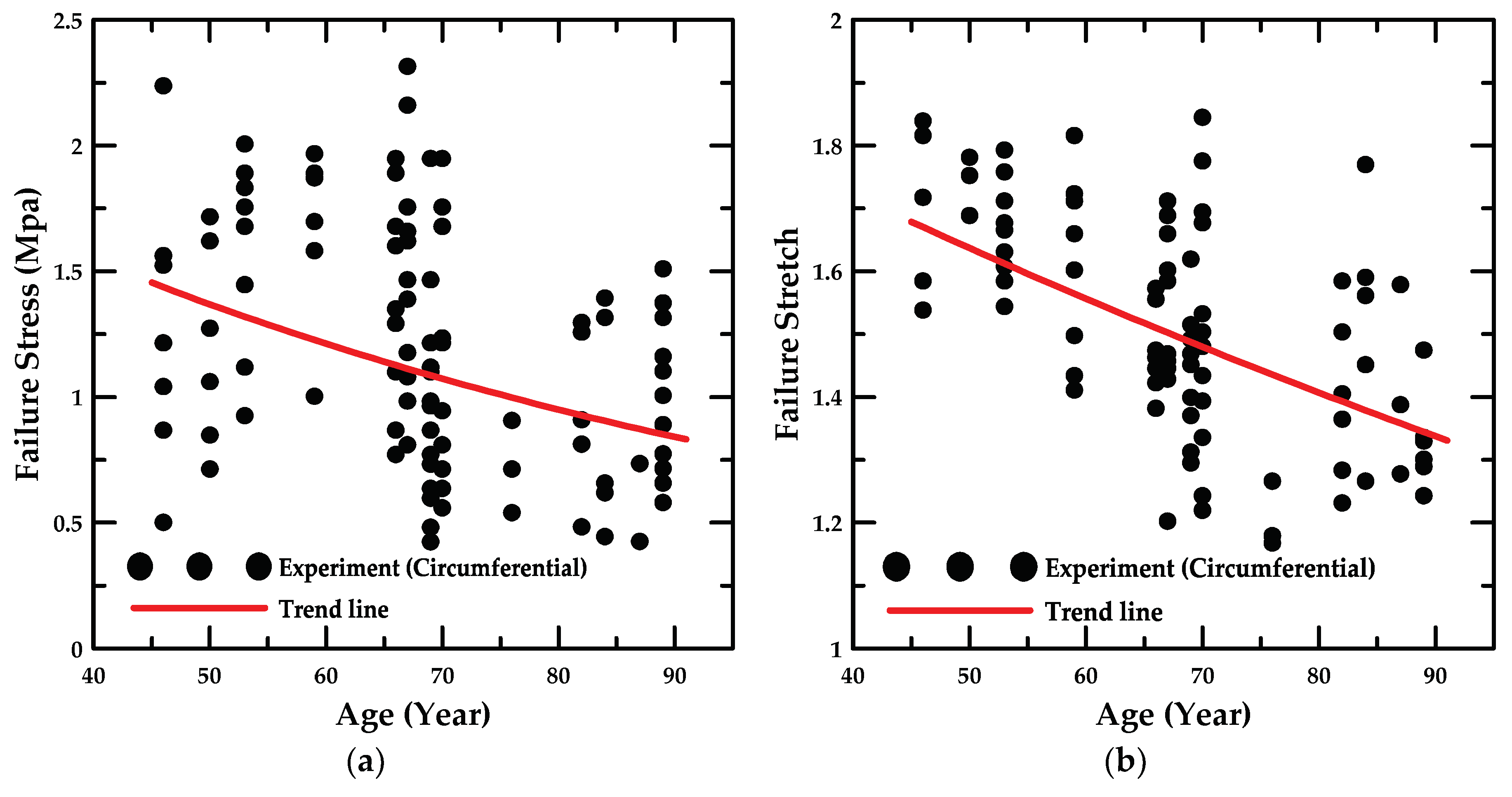
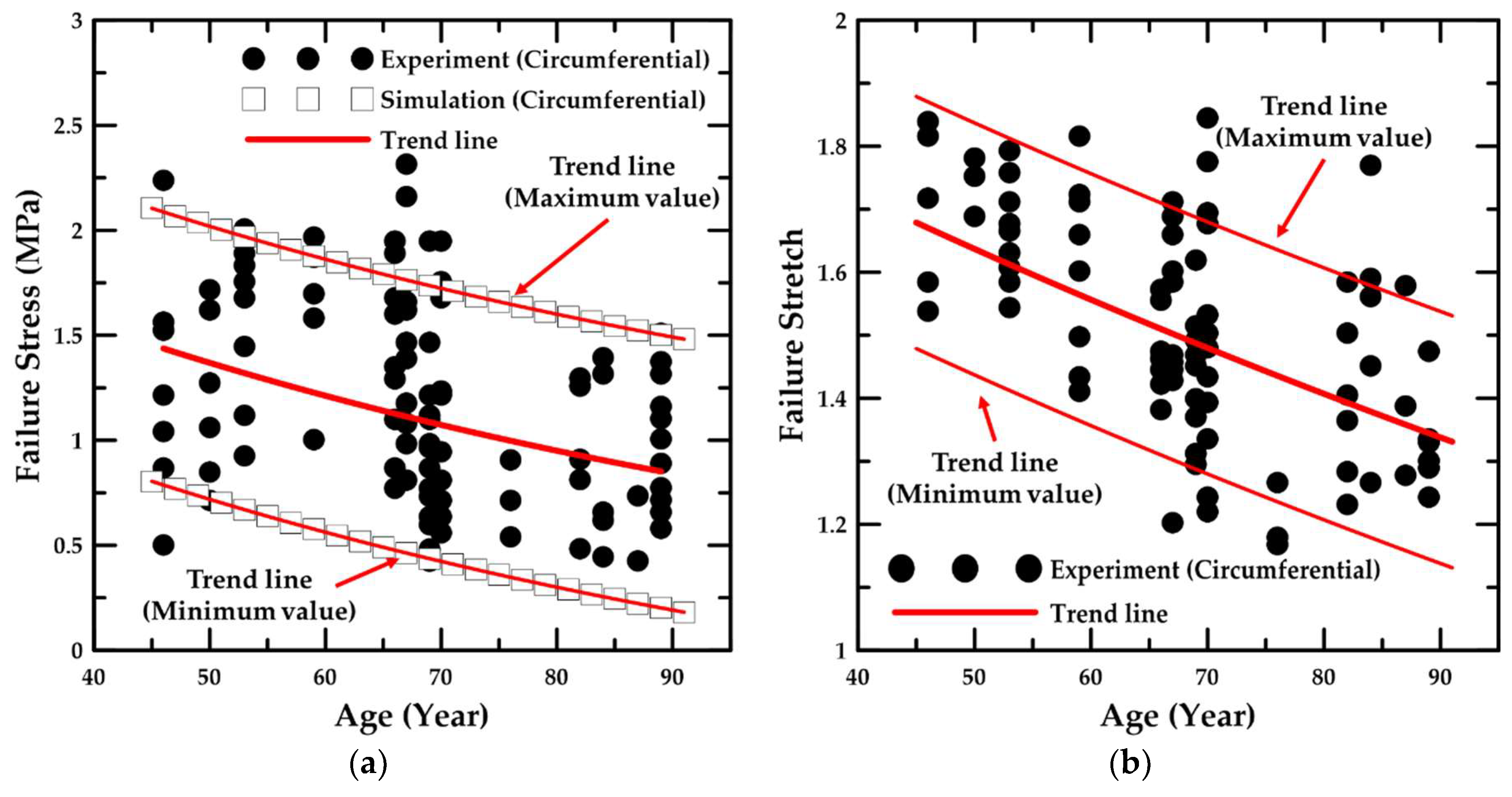
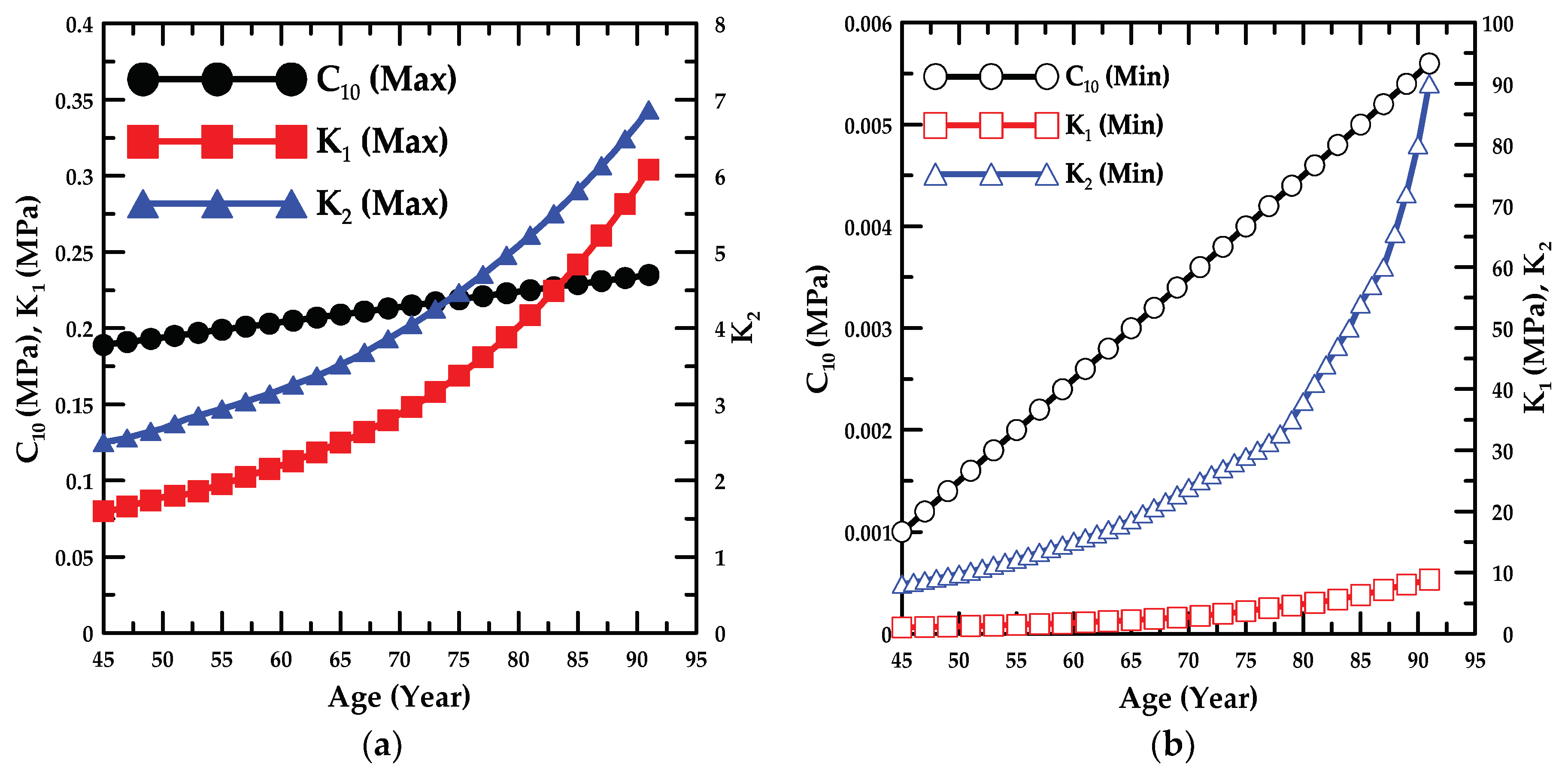
4.1. Experiment Details and Trend Lines
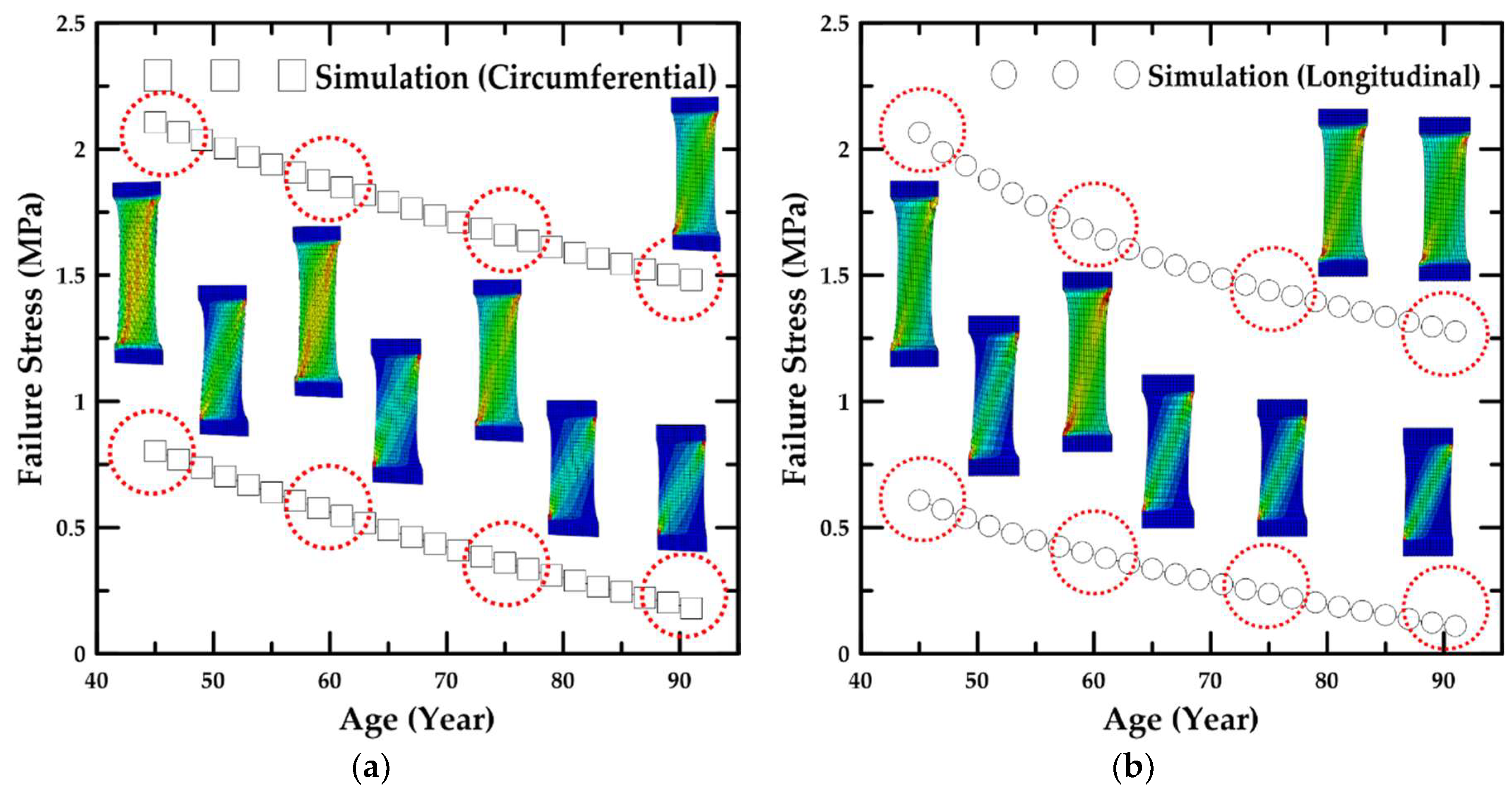
4.2. Simulation Results Based on Age
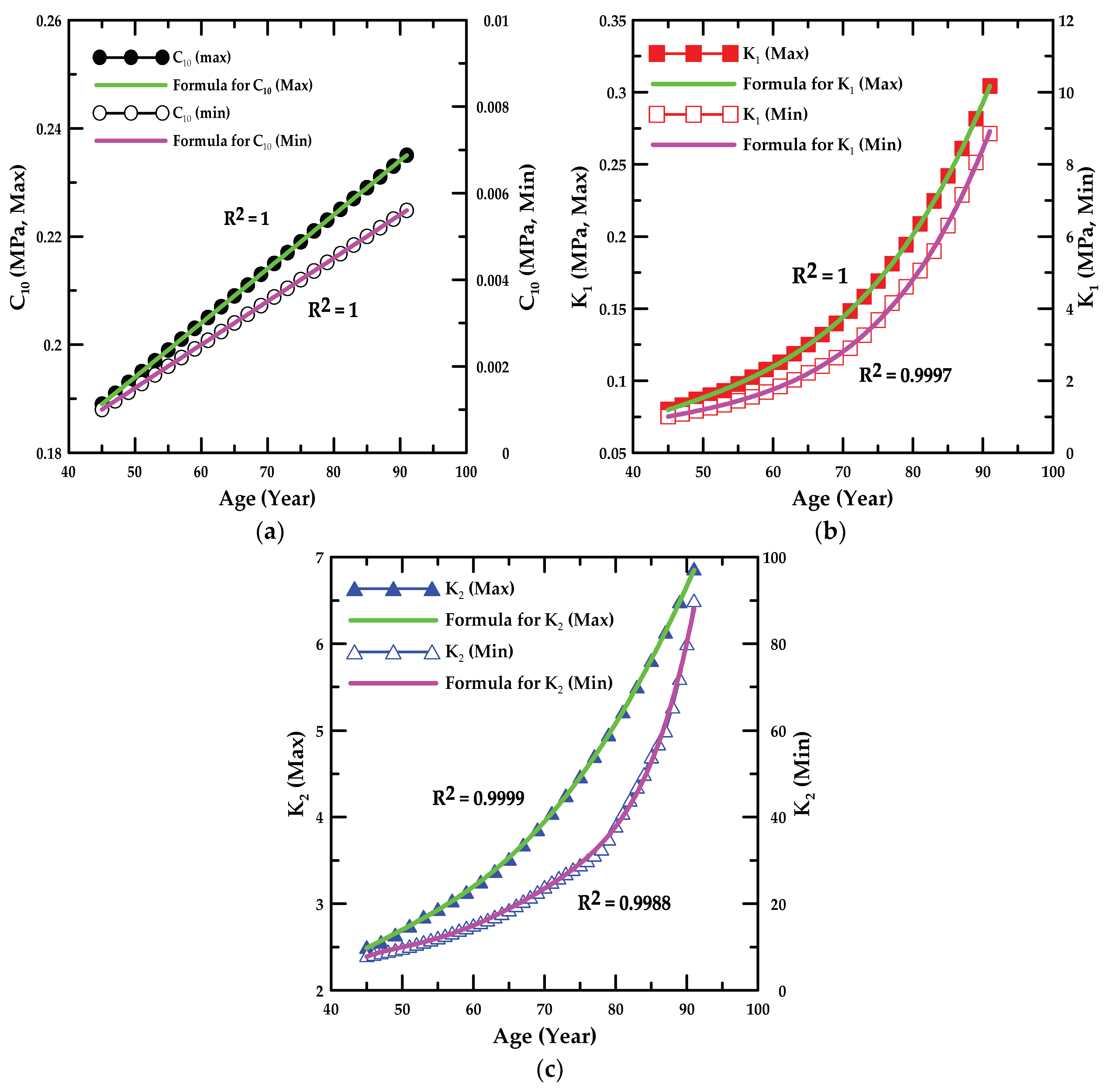
4.3. Parametric Study for the Material Constants of the HGO Model
5. Discussion
6. Concluding Remarks
- According to the uniaxial tensile test results with respect to the loading direction, the circumferentially-oriented strip samples exhibited a maximum tensile strength value of 2.49 MPa, which was 18.3% higher than that for the longitudinally-oriented strip samples, based on the average value of the experimental results. Therefore, the uniaxial tensile stress and stretch in the arterial tissue were identified to be dependent on the fiber orientation.
- In addition, the failure stress and stretch were investigated as a function of age, and the material constants for age were calculated based on the maximum and minimum trend lines. The HGO model was applied to the numerical model for anisotropic hyper-elastic materials during the numerical simulations.
- In the parametric study, the formulae associated with the value of the material constant for the ages of 46–89 years were proposed, and the proportion variance in the dependent variable that was predictable from the independent variable was examined.
Author Contributions
Funding
Conflicts of Interest
References
- Tortora, G.J. Principles of Human Anatomy; HarperCollins College: New York, NY, USA, 1995. [Google Scholar]
- Tortora, G.J.; Grabowski, S.R. Principles of Anatomy and Physiology; HarperCollins College: New York, NY, USA, 1996. [Google Scholar]
- Hole, J.W.; Koos, K.A. Human Anatomy; William C. Brown: Dubuque, Iowa, 1994. [Google Scholar]
- Van De Graaff, K.M. Human Anatomy; WCB/McGraw-Hill: Boston, MA, USA, 1998. [Google Scholar]
- Sobotta, J. Atlas van de Menselijke Anatomie; Bohn Stafleu van Loghum: Houten, Netherlands, 2006. [Google Scholar]
- Tsamis, A.; Krawiec, J.T.; Vorp, D.A. Elastin and collagen fibre microstructure of the human aorta in ageing and disease: A review. J. R. Soc. Interface 2013, 10, 20121004. [Google Scholar] [CrossRef] [PubMed]
- Saphirstein, R.J.; Gao, Y.Z.; Jensen, M.H.; Gallant, C.M.; Vetterkind, S.; Moore, J.R.; Morgan, K.G. The focal adhesion: A regulated component of aortic stiffness. PLoS ONE 2013, 8, e62461. [Google Scholar] [CrossRef]
- Gao, Y.Z.; Saphirstein, R.J.; Yamin, R.; Suki, B.; Morgan, K.G. Aging impairs smooth muscle-mediated regulation of aortic stiffness: A defect in shock absorption function? Am. J. Physiol. Heart Circ. Physiol. 2014, 307, H1252–H1261. [Google Scholar] [CrossRef] [PubMed]
- Hong, Z.; Reeves, K.J.; Sun, Z.; Li, Z.; Brown, N.J.; Meininger, G.A. Vascular smooth muscle cell stiffness and adhesion to collagen I modified by vasoactive agonists. PLoS ONE 2015, 10, e0119533. [Google Scholar] [CrossRef]
- Leloup, A.J.; Van Hove, C.E.; Heykers, A.; Schrijvers, D.M.; De Meyer, G.R.; Fransen, P. Elastic and muscular arteries differ in structure, basal NO production and voltage-gated Ca2+-channels. Front. Physiol. 2015, 6, 375. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, M.L.; Webster, M.W.; Vorp, D.A. Ex vivo biomechanical behavior of abdominal aortic aneurysm: Assessment using a new mathematical model. Ann. Biomed. Eng. 1996, 24, 573–582. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.H.; Makaroun, M.; Webster, M.W.; Vorp, D.A. Mechanical properties and microstructure of intraluminal thrombus from abdominal aortic aneurysm. J. Biomech. Eng. 2001, 123, 536–539. [Google Scholar] [PubMed]
- Tong, J.; Cohnert, T.; Holzapfel, G. Diameter-related variations of geometrical, mechanical, and mass fraction data in the anterior portion of abdominal aortic aneurysms. Eur. J. Vasc. Endovasc. Surg. 2015, 49, 262–270. [Google Scholar] [CrossRef]
- Shahmansouri, N.; Alreshidan, M.; Emmott, A.; Lachapelle, K.; El-Hamamsy, I.; Cartier, R.; Leask, R.; Mongrain, R. Investigation on the regional loss factor and its anisotropy for aortic aneurysms. Materials 2016, 9, 867. [Google Scholar] [CrossRef]
- Yang, T.; Chui, C.K.; Yu, R.Q.; Qin, J.; Chang, S.K. Quasi-linear viscoelastic modeling of arterial wall for surgical simulation. Int. J. Comput. Assist. Radiol. Surg. 2011, 6, 829–838. [Google Scholar] [CrossRef]
- Horny, L.; Adamek, T.; Gultova, E.; Zitny, R.; Vesely, J.; Chlup, H.; Konvickova, S. Correlations between age, prestrain, diameter and atherosclerosis in the male abdominal aorta. J. Mech. Behav. Biomed. Mater. 2011, 4, 2128–2132. [Google Scholar] [CrossRef] [PubMed]
- Ninomiya, O.H.; Monteiro, J.A.T.; de Lourdes Higuchi, M.; Puech-Leão, P.; de Luccia, N.; Raghavan, M.L.; da Silva, E.S. Biomechanical properties and microstructural analysis of the human nonaneurysmal aorta as a function of age, gender and location: An autopsy study. J. Vasc. Res. 2015, 52, 257–264. [Google Scholar] [CrossRef] [PubMed]
- Courtial, E.-J.; Fanton, L.; Orkisz, M.; Douek, P.; Huet, L.; Fulchiron, R. Hyper-viscoelastic behavior of healthy abdominal aorta. IRBM 2016, 37, 158–164. [Google Scholar] [CrossRef]
- Laksari, K.; Shahmirzadi, D.; Acosta, C.J.; Konofagou, E. Energy-based constitutive modelling of local material properties of canine aortas. R. Soc. Open Sci. 2016, 3, 160365. [Google Scholar] [CrossRef] [PubMed]
- Fung, Y.; Fronek, K.; Patitucci, P. Pseudoelasticity of arteries and the choice of its mathematical expression. Am. J. Physiol. Heart Circ. Physiol. 1979, 237, H620–H631. [Google Scholar] [CrossRef]
- Humphrey, J.D. Mechanics of the arterial wall: Review and directions. Crit. Rev. Biomed. Eng. 1995, 23, 1–162. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. Phys. Sci. Solids 2000, 61, 1–48. [Google Scholar]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 2005, 3, 15–35. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Ogden, R.W. Constitutive modelling of arteries. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2010, 446, 1551–1597. [Google Scholar] [CrossRef]
- ABAQUS. ABAQUS/Standard User’s Manual; ABAQUS: Waltham, MA, USA, 2014. [Google Scholar]
- Holzapfel, G. Arterial tissue in health and disease: Experimental data, collagen-based modeling and simulation, including aortic dissection. In Biomechanical Modelling at the Molecular, Cellular and Tissue Levels; Springer: Berlin/Heidelberg, Germany, 2009; pp. 259–344. [Google Scholar]
- Spencer, A.J.M. Constitutive theory for strongly anisotropic solids. In Continuum Theory of the Mechanics of Fibre-Reinforced Composites; Springer: Berlin/Heidelberg, Germany, 1984; pp. 1–32. [Google Scholar]
- Holzapfel, A.G. Nonlinear Solid Mechanics II; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Forsell, C.; Swedenborg, J.; Roy, J.; Gasser, T.C. The quasi-static failure properties of the abdominal aortic aneurysm wall estimated by a mixed experimental-numerical approach. Ann. Biomed. Eng. 2013, 41, 1554–1566. [Google Scholar] [CrossRef]
- Pierce, D.M.; Maier, F.; Weisbecker, H.; Viertler, C.; Verbrugghe, P.; Famaey, N.; Fourneau, I.; Herijgers, P.; Holzapfel, G.A. Human thoracic and abdominal aortic aneurysmal tissues: Damage experiments, statistical analysis and constitutive modeling. J. Mech. Behav. Biomed. Mater. 2015, 41, 92–107. [Google Scholar] [CrossRef] [PubMed]
- Zulliger, M.A.; Stergiopulos, N. Structural strain energy function applied to the ageing of the human aorta. J. Biomech. 2007, 40, 3061–3069. [Google Scholar] [CrossRef] [PubMed]
- Spronck, B.; Heusinkveld, M.H.; Donders, W.P.; de Lepper, A.G.; Op’t Roodt, J.; Kroon, A.A.; Delhaas, T.; Reesink, K.D. A constitutive modeling interpretation of the relationship among carotid artery stiffness, blood pressure, and age in hypertensive subjects. Am. J. Physiol. Heart Circ. Physiol. 2014, 308, H568–H582. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A. Determination of material models for arterial walls from uniaxial extension tests and histological structure. J. Theor. Biol. 2006, 238, 290–302. [Google Scholar] [CrossRef] [PubMed]
- Peyraut, F.; Feng, Z.-Q.; Labed, N.; Renaud, C. A closed form solution for the uniaxial tension test of biological soft tissues. Int. J. Non-Linear Mech. 2010, 45, 535–541. [Google Scholar] [CrossRef]
- Skacel, P.; Bursa, J. Comparison of constitutive models of arterial layers with distributed collagen fibre orientations. Acta Bioeng. Biomech. 2014, 16, 47–58. [Google Scholar] [PubMed]
- Hajhashemkhani, M.; Hematiyan, M.R. Determination of material parameters of isotropic and anisotropic hyper-elastic materials using boundary measured data. J. Theor. Appl. Mech. 2015, 53, 895–910. [Google Scholar] [CrossRef]
- Karimi, A.; Navidbakhsh, M.; Shojaei, A. A combination of histological analyses and uniaxial tensile tests to determine the material coefficients of the healthy and atherosclerotic human coronary arteries. Tissue Cell 2015, 47, 152–158. [Google Scholar] [CrossRef]
- Shazly, T.; Rachev, A.; Lessner, S.; Argraves, W.S.; Ferdous, J.; Zhou, B.; Moreira, A.M.; Sutton, M. On the uniaxial ring test of tissue engineered constructs. Exp. Mech. 2015, 55, 41–51. [Google Scholar] [CrossRef]
- Latorre, M.; Romero, X.; Montans, F.J. The relevance of transverse deformation effects in modeling soft biological tissues. Int. J. Solids Struct. 2016, 99, 57–70. [Google Scholar] [CrossRef]
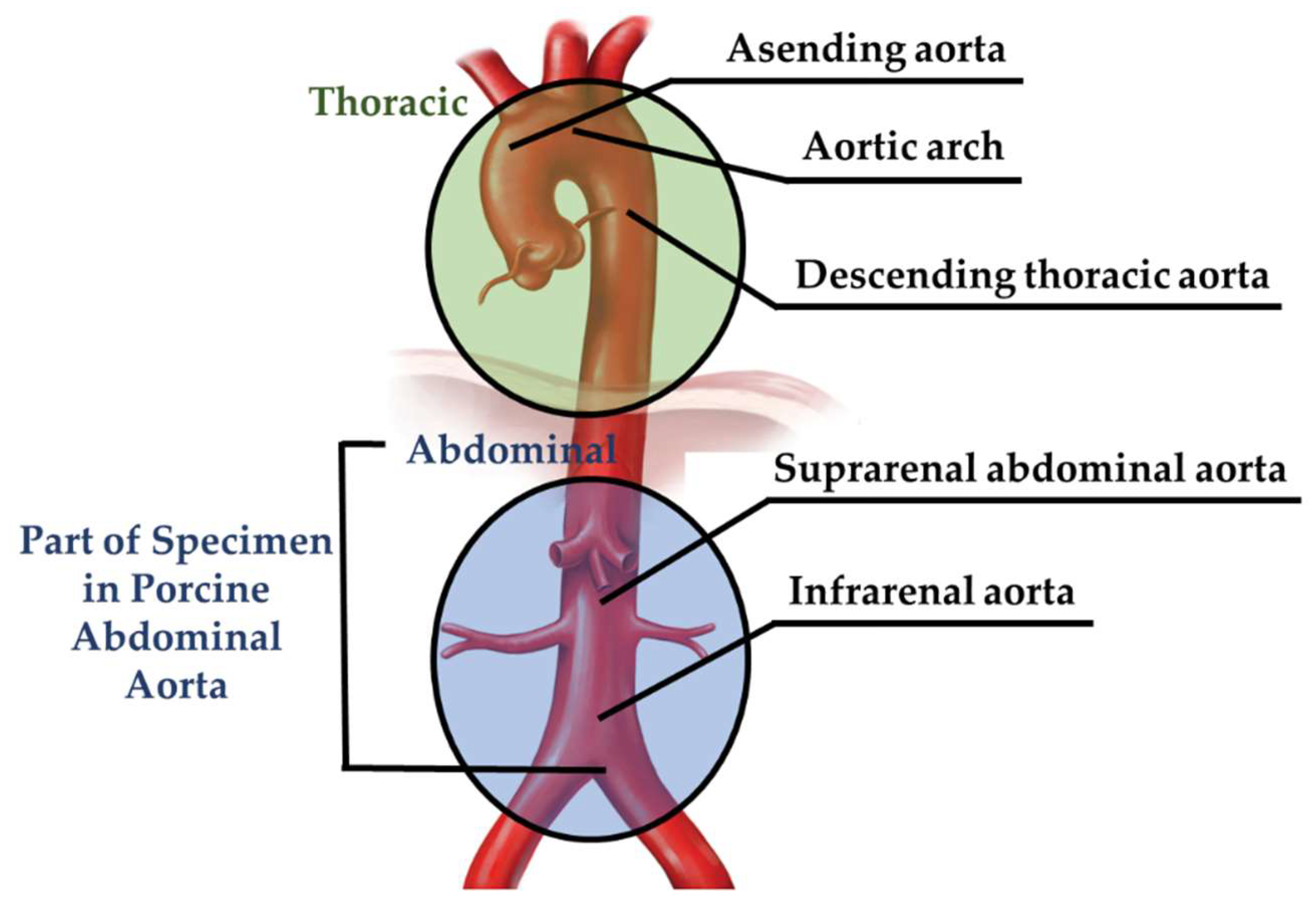
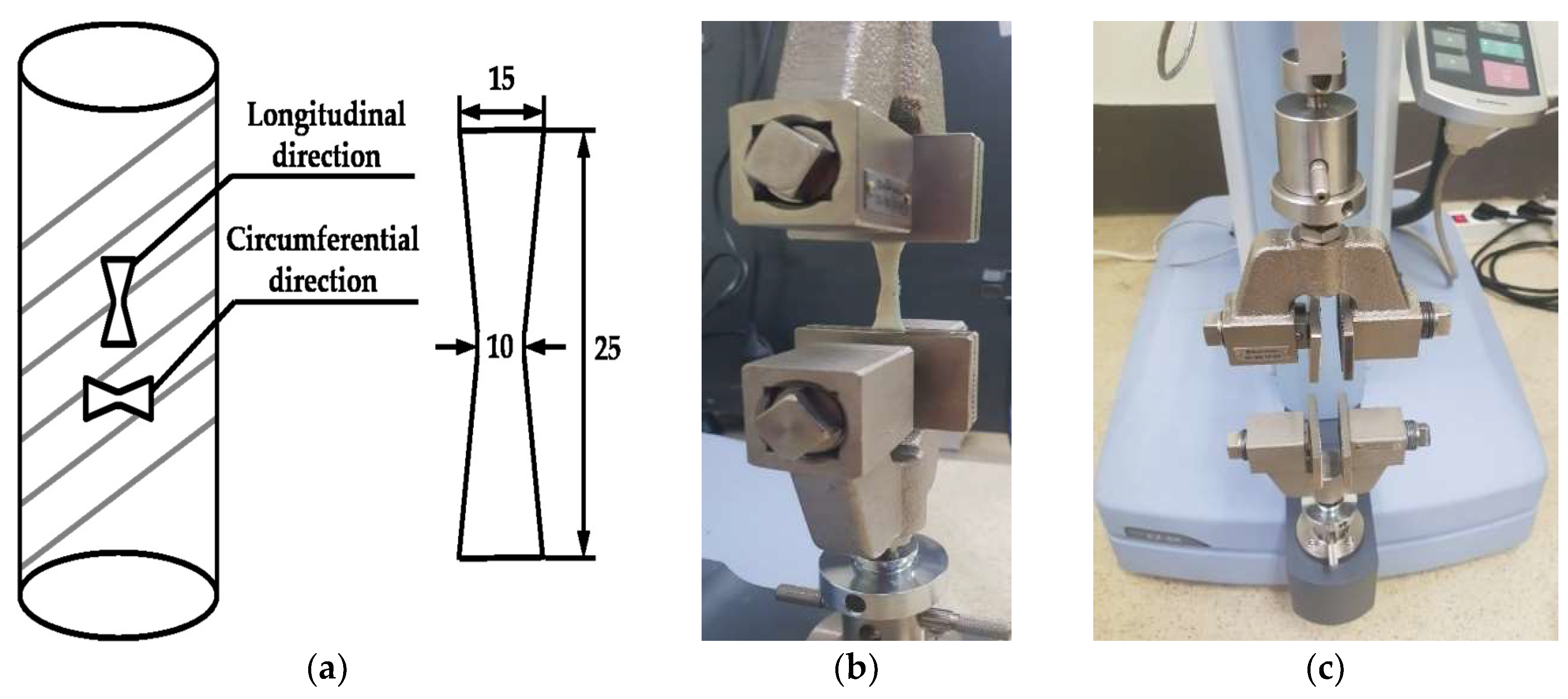

| Specimen | Sample Dimension (in mm) | Tensile Load Direction Relative to Oriented Strip | |||
|---|---|---|---|---|---|
| Width (Top) | Width (Middle) | Length | Thickness | ||
| AC1 | 14.96 | 9.98 | 24.97 | 1.98 | Circumferentially |
| AC2 | 15.10 | 10.04 | 25.05 | 2.01 | Circumferentially |
| AC3 | 14.98 | 10.01 | 25.03 | 2.01 | Circumferentially |
| AC4 | 15.05 | 10.01 | 25.01 | 1.99 | Circumferentially |
| AC5 | 15.01 | 9.99 | 25.00 | 2.03 | Circumferentially |
| AL1 | 15.02 | 10.02 | 24.98 | 2.01 | Longitudinally |
| AL2 | 15.04 | 10.02 | 24.99 | 2.02 | Longitudinally |
| AL3 | 14.97 | 10.03 | 25.01 | 1.97 | Longitudinally |
| AL4 | 14.99 | 9.98 | 24.98 | 2.01 | Longitudinally |
| AL5 | 15.04 | 9.97 | 25.03 | 2.01 | Longitudinally |
| Material Constant | α1 | α2 | R2 | |||
| C10,max | 0.001 | 0.144 | 1.0 | |||
| C10,min | 0.0001 | 0.0035 | 1.0 | |||
| Material Constant | β1, γ1 | β2, γ2 | β3, γ3 | β4, γ4 | β5, γ5, γ6 | R2 |
| k1,max | 8.26 × 10−9 | −5.11 × 10−7 | −2.30 × 10−5 | 0.0038 | −0.0315 | 1.0 |
| k1,min | 8.58 × 10−7 | −0.0001 | 0.0099 | −0.2863 | 3.6079 | 0.9997 |
| k2,max | −2.59 × 10−7 | 8.92 × 10−5 | −0.0092 | 0.4205 | −4.9386 | 0.9999 |
| k2,min | 1.97 × 10−6 | −0.0006 | 0.0742 | −4.4980 | 135.35, −1611.33 | 0.9988 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huh, U.; Lee, C.-W.; You, J.-H.; Song, C.-H.; Lee, C.-S.; Ryu, D.-M. Determination of the Material Parameters in the Holzapfel-Gasser-Ogden Constitutive Model for Simulation of Age-Dependent Material Nonlinear Behavior for Aortic Wall Tissue under Uniaxial Tension. Appl. Sci. 2019, 9, 2851. https://doi.org/10.3390/app9142851
Huh U, Lee C-W, You J-H, Song C-H, Lee C-S, Ryu D-M. Determination of the Material Parameters in the Holzapfel-Gasser-Ogden Constitutive Model for Simulation of Age-Dependent Material Nonlinear Behavior for Aortic Wall Tissue under Uniaxial Tension. Applied Sciences. 2019; 9(14):2851. https://doi.org/10.3390/app9142851
Chicago/Turabian StyleHuh, Up, Chung-Won Lee, Ji-Hun You, Chan-Hee Song, Chi-Seung Lee, and Dong-Man Ryu. 2019. "Determination of the Material Parameters in the Holzapfel-Gasser-Ogden Constitutive Model for Simulation of Age-Dependent Material Nonlinear Behavior for Aortic Wall Tissue under Uniaxial Tension" Applied Sciences 9, no. 14: 2851. https://doi.org/10.3390/app9142851
APA StyleHuh, U., Lee, C.-W., You, J.-H., Song, C.-H., Lee, C.-S., & Ryu, D.-M. (2019). Determination of the Material Parameters in the Holzapfel-Gasser-Ogden Constitutive Model for Simulation of Age-Dependent Material Nonlinear Behavior for Aortic Wall Tissue under Uniaxial Tension. Applied Sciences, 9(14), 2851. https://doi.org/10.3390/app9142851





