Estimating Road Segments Using Kernelized Averaging of GPS Trajectories
Abstract
1. Introduction
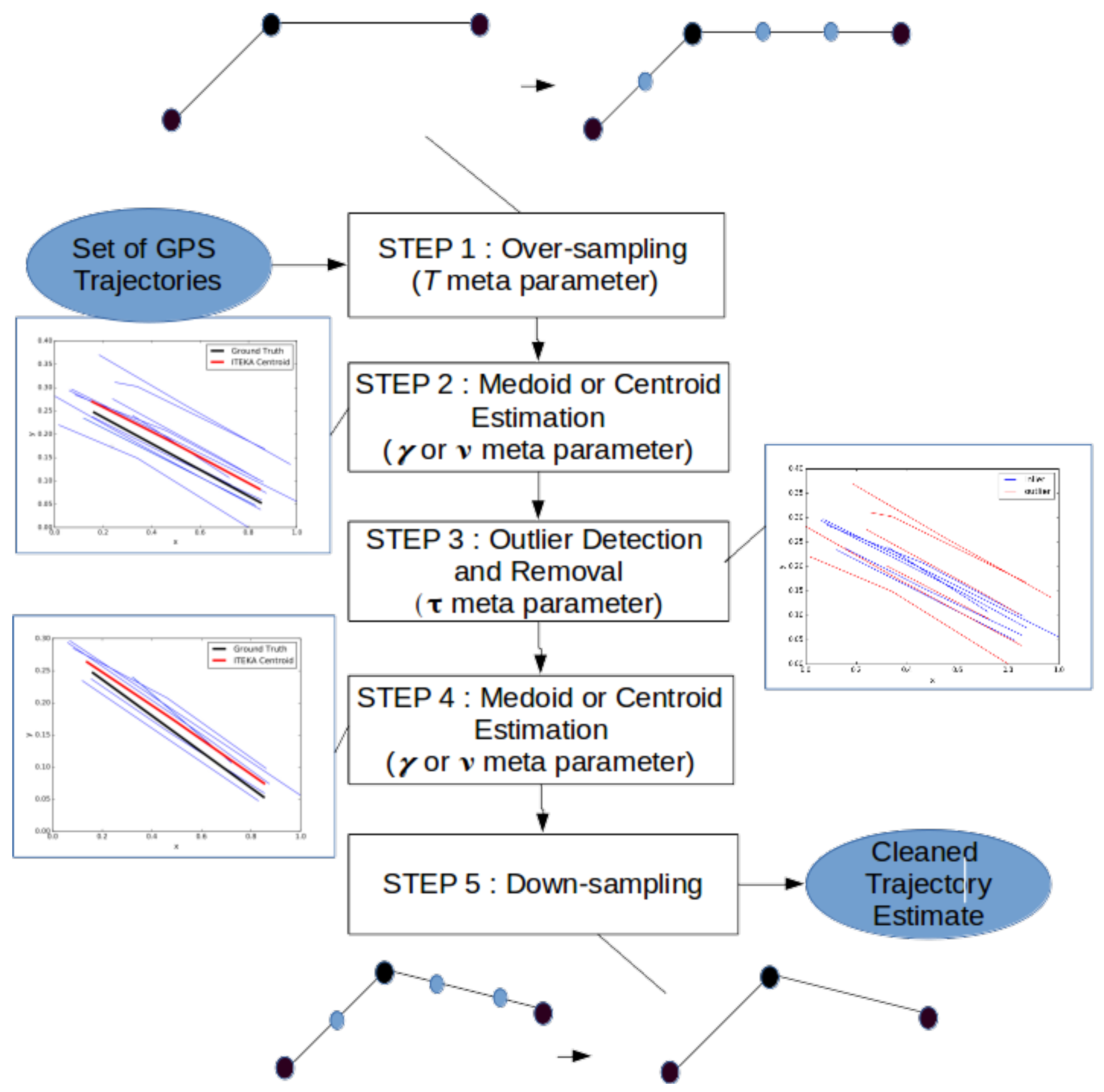
- an over-sampling of the trajectories such that they all share a higher sampling rate, namely they are described with the same higher number of samples (Section 3.1);
- a first extraction/estimation of a medoid/centroid for a subset of GPS trajectories (Section 2.4 and Section 3.2);
- anomaly (outlier) detection and removal (Section 3.2);
- a second extraction/estimation of a medoid/centroid for a subset of GPS trajectories (Section 2.4 and Section 3.2); and
- a final down-sampling to reduce the sampling precision of the trajectories down to the average sampling precision of the initial set of trajectories (Section 3.3).
2. From Dynamic Time Warping to Time Elastic Kernels Averaging
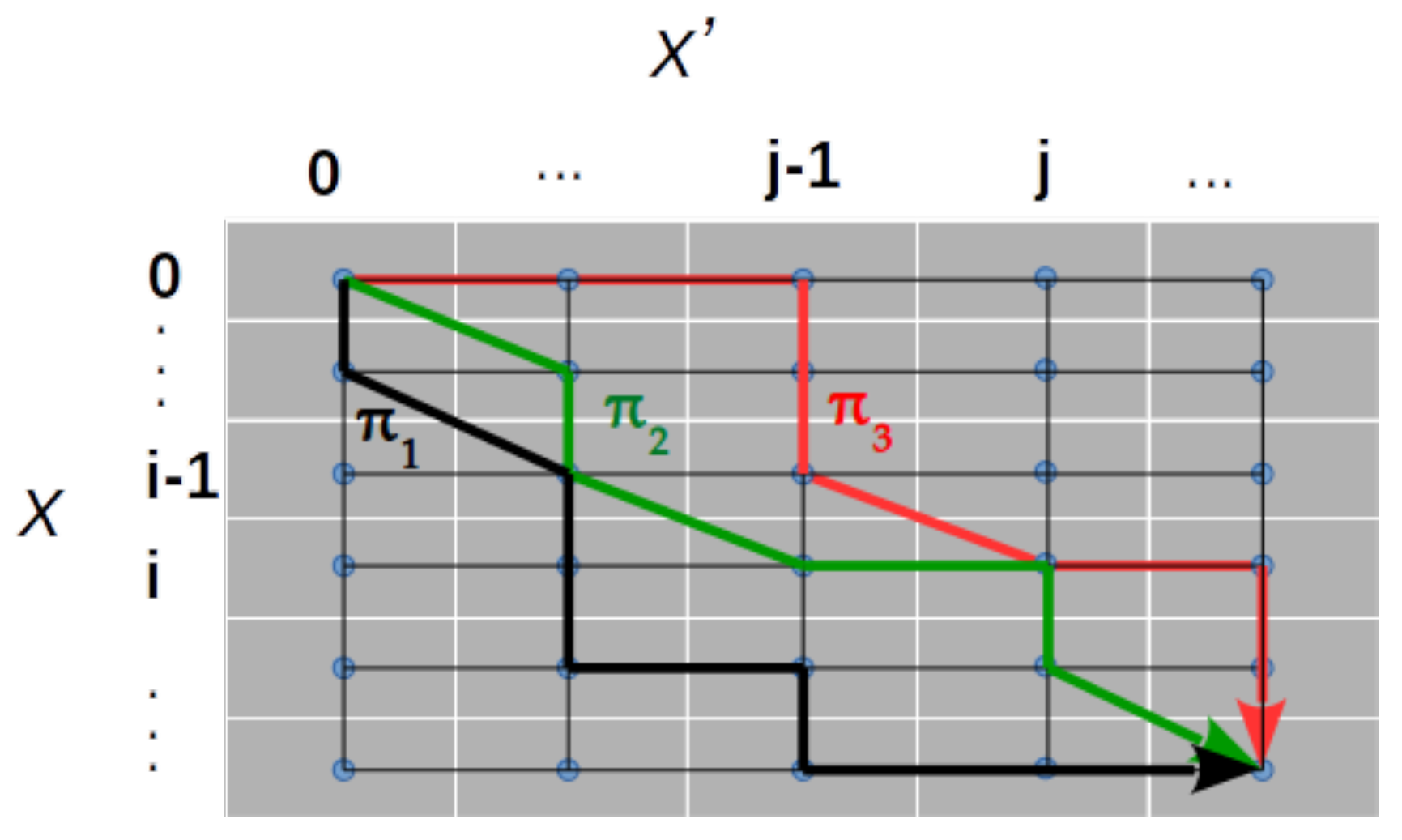
2.1. Dynamic Time Warping
2.2. Time Elastic Kernels
2.3. Time Elastic Averaging of a Set of Time Series
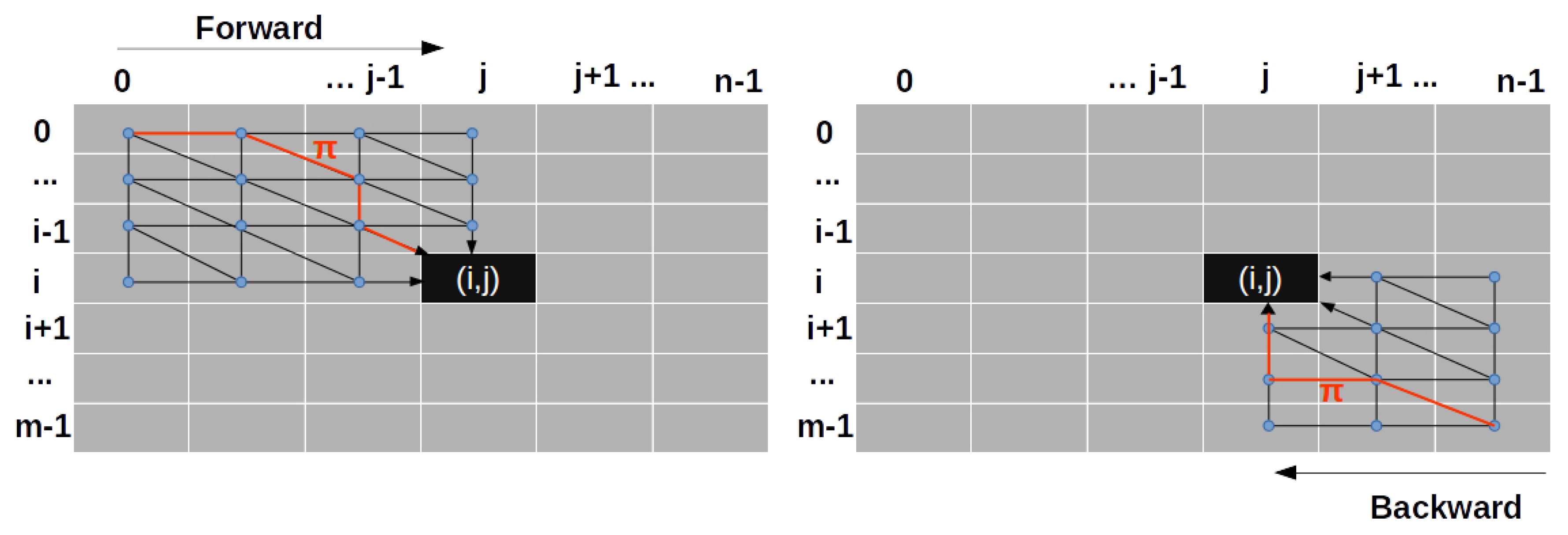
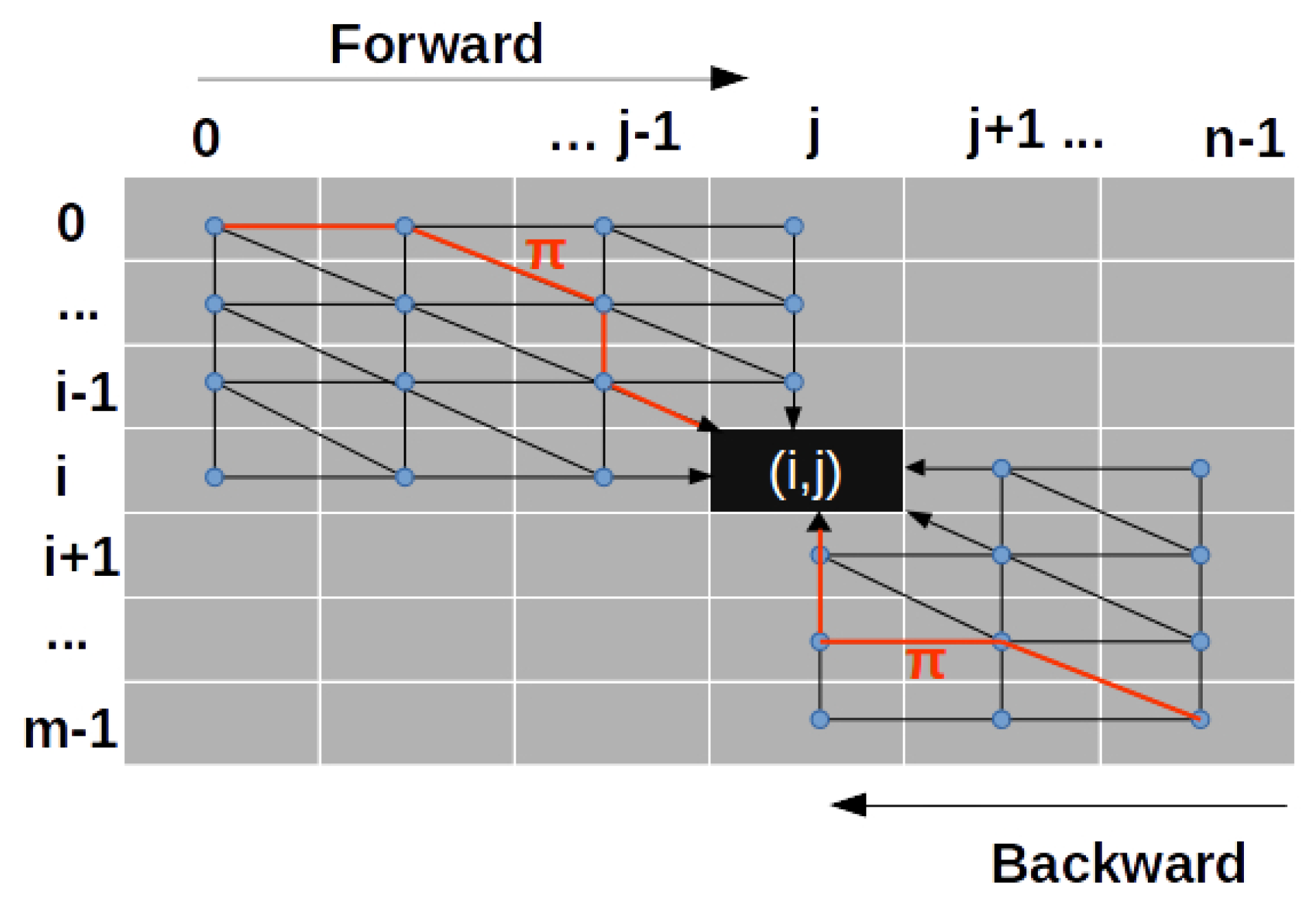
2.4. Kernelized Time Elastic Averaging of a Set of Time Series
| Algorithm 1 Iterative Time Elastic Kernel Averaging (iTEKA) of a set of time series. |
|
3. Averaging a Set of GPS Time Series
3.1. Preprocessing the GPS Trajectories
- The street segment is not necessarily traveled in a single direction.
- The trajectories are traveled with variable speed, hence the trajectories are possibly not sampled with the same level of detail or uniformly.
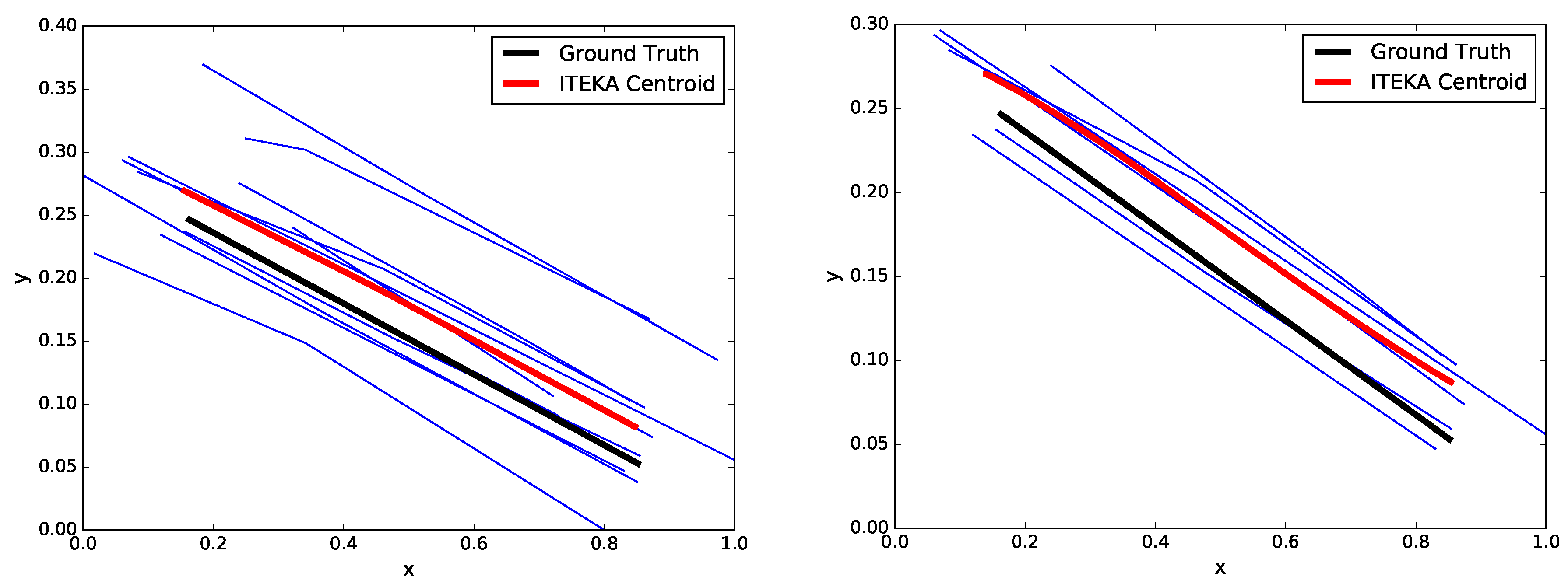
3.2. Averaging and Outliers Removal
3.3. Post-Processing of the Centroid Estimate
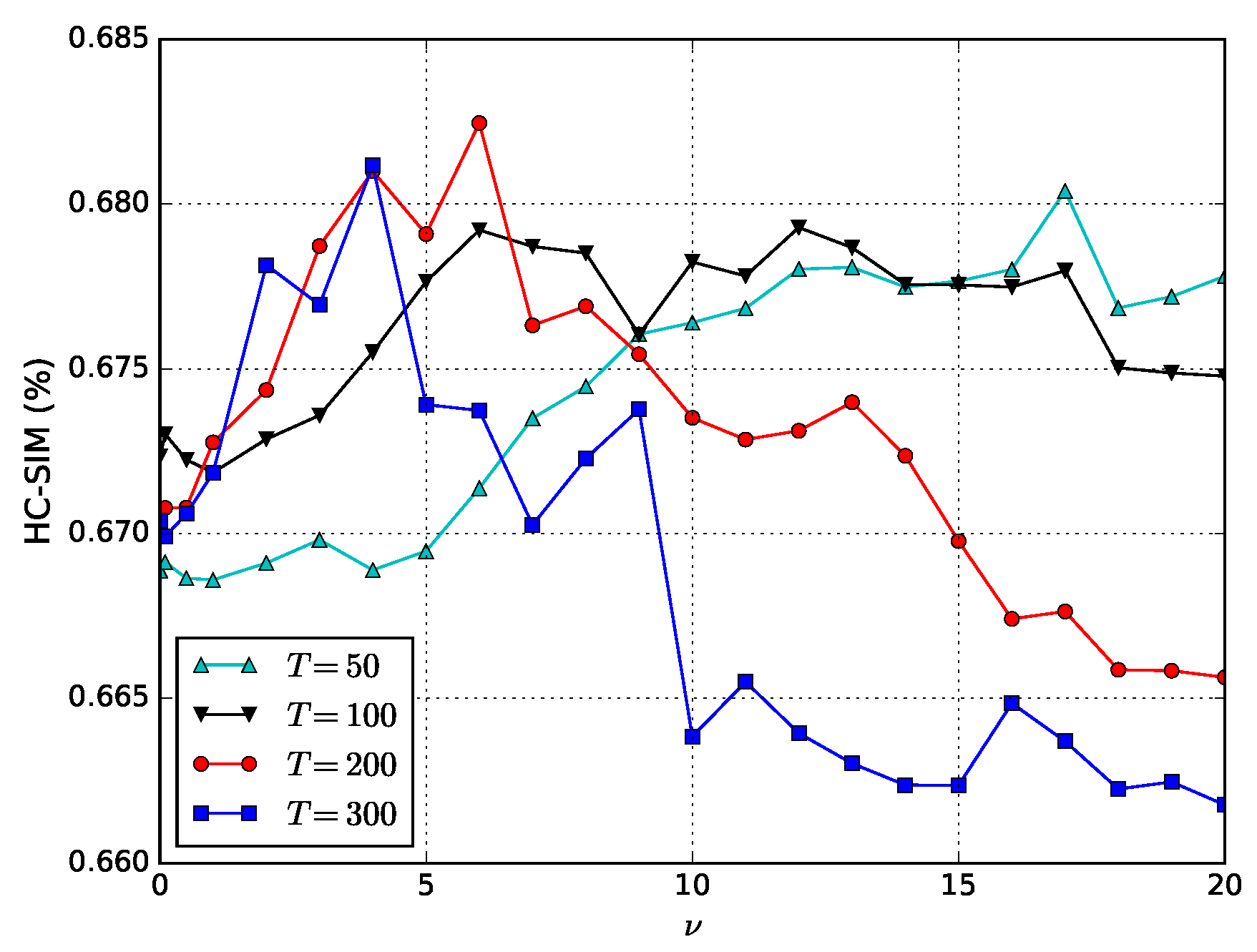
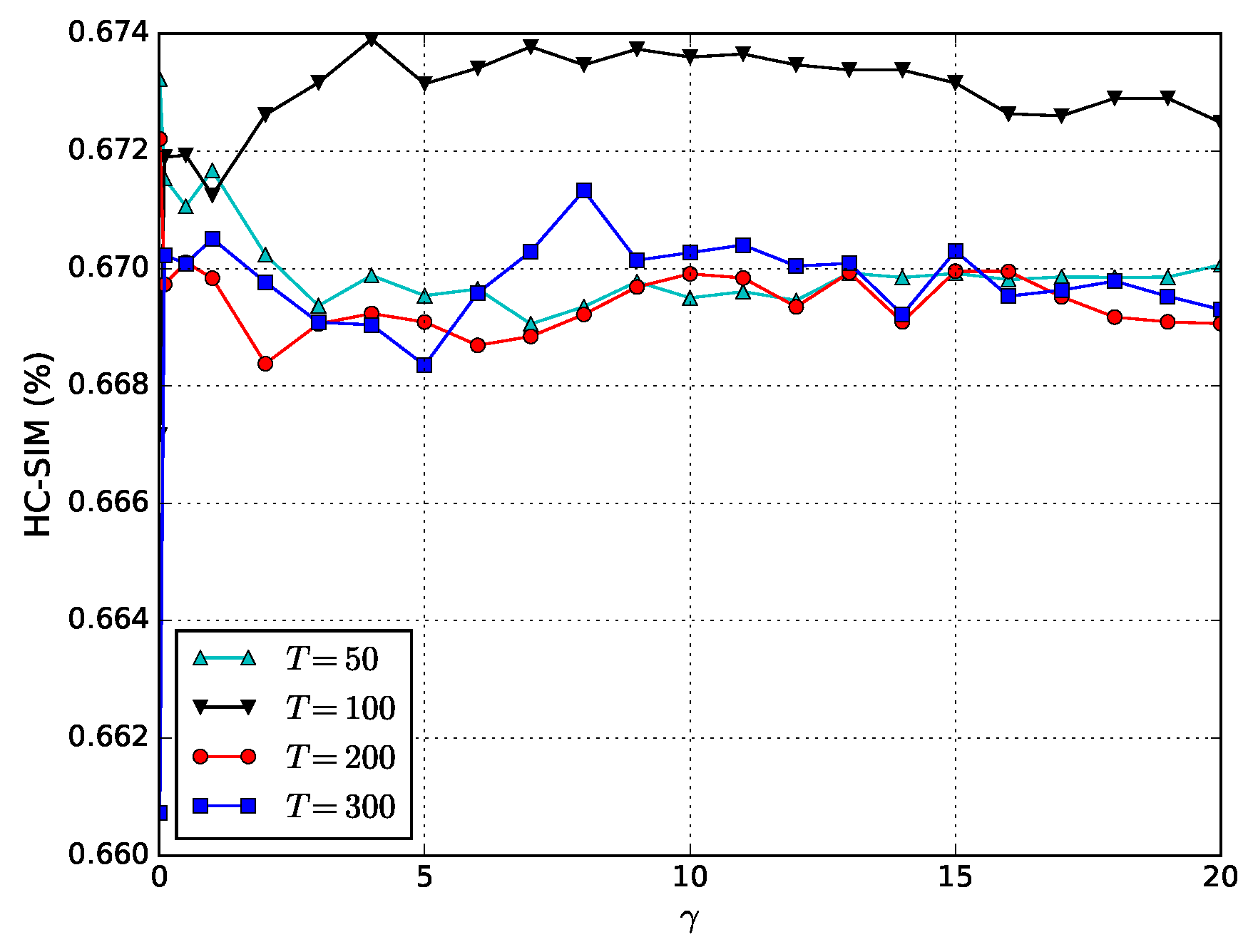
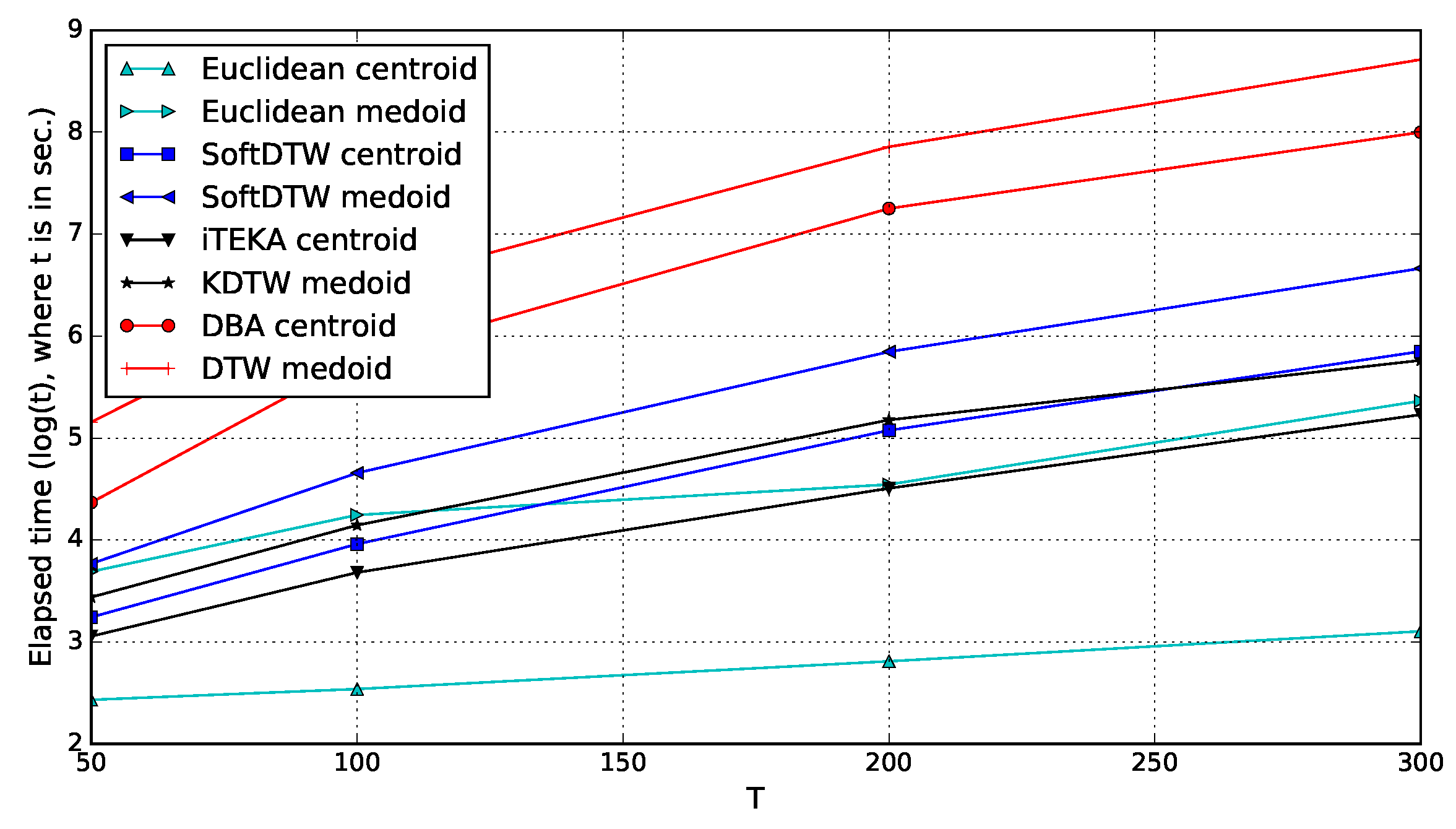
4. Experimentation
5. Conclusions
Funding
Conflicts of Interest
References
- Shi, W.; Shen, S.; Liu, Y. Automatic generation of road network map from massive GPS, vehicle trajectories. In Proceedings of the 2009 12th International IEEE Conference on Intelligent Transportation Systems, St. Louis, MO, USA, 4–7 October 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Mariescu-Istodor, R.; Fränti, P. Grid-Based Method for GPS Route Analysis for Retrieval. ACM Trans. Spat. Algorithms Syst. 2017, 3, 8:1–8:28. [Google Scholar] [CrossRef]
- Mariescu-Istodor, R.; Fränti, P. CellNet: Inferring Road Networks from GPS Trajectories. ACM Trans. Spat. Algorithms Syst. 2018, 4, 8:1–8:22. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; University of North Carolina at Chapel Hill: Chapel Hill, NC, USA, 1995. [Google Scholar]
- Evensen, G.; van Leeuwen, P.J. An Ensemble Kalman Smoother for Nonlinear Dynamics. Mon. Weather Rev. 2000, 128, 1852–1867. [Google Scholar] [CrossRef]
- Panangadan, A.V.; Talukder, A. A variant of particle filtering using historic datasets for tracking complex geospatial phenomena. In Proceedings of the 18th ACM SIGSPATIAL International Symposium on Advances in Geographic Information Systems, ACM-GIS, San Jose, CA, USA, 3–5 November 2010; pp. 232–239. [Google Scholar] [CrossRef]
- Velichko, V.M.; Zagoruyko, N.G. Automatic Recognition of 200 Words. Int. J. Man-Mach. Stud. 1970, 2, 223–234. [Google Scholar] [CrossRef]
- Sakoe, H.; Chiba, S. A dynamic programming approach to continuous speech recognition. In Proceedings of the 7th International Congress of Acoustic, Budapest, Hungary, 18–26 August 1971; pp. 65–68. [Google Scholar]
- Cuturi, M.; Blondel, M. Soft-DTW: A Differentiable Loss Function for Time-Series. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Precup, D., Teh, Y.W., Eds.; International Convention Centre: Sydney, Australia, 2017; Volume 70, pp. 894–903. [Google Scholar]
- Marteau, P.F.; Gibet, S. On Recursive Edit Distance Kernels with Application to Time Series Classification. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 1121–1133. [Google Scholar] [CrossRef] [PubMed]
- Hausner, M. A Vector Space Approach to Geometry; Dover Publications Inc.: Mineola, NY, USA, first edition 1965, second edition 1998.
- Petitjean, F.; Forestier, G.; Webb, G.; Nicholson, A.; Chen, Y.; Keogh, E. Dynamic Time Warping Averaging of Time Series Allows Faster and More Accurate Classification. In Proceedings of the 14th IEEE International Conference on Data Mining, Shenzhen, China, 14–17 December 2014; pp. 470–479. [Google Scholar]
- Marteau, P.F. Times series averaging and denoising from a probabilistic perspective on time-elastic kernels. Int. J. Appl. Math. Comput. Sci. 2019, 29, 375–392. [Google Scholar]
- Fränti, P.; Mariescu-Istodor, R. Averaging GPS segments challenge 2019. unpublished work. 2019. [Google Scholar]
- Bahlmann, C.; Haasdonk, B.; Burkhardt, H. On-Line Handwriting Recognition with Support Vector Machines A Kernel Approach. In Proceedings of the Eighth International Workshop on Frontiers in Handwriting Recognition (IWFHR’02), Niagara on the Lake, ON, Canada, 6–8 August 2002; IEEE Computer Society: Washington, DC, USA, 2002; p. 49. [Google Scholar]
- Shimodaira, H.; Noma, K.i.; Nakai, M.; Sagayama, S. Dynamic Time-alignment Kernel in Support Vector Machine. In Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic, Vancouver, BC, Canada, 3–8 December 2001; MIT Press: Cambridge, MA, USA, 2001; pp. 921–928. [Google Scholar]
- Cuturi, M.; Vert, J.P.; Birkenes, O.; Matsui, T. A Kernel for Time Series Based on Global Alignments. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech and Signal Processing–ICASSP ’07, Honolulu, HI, USA, 15–20 April 2007; pp. 413–416. [Google Scholar] [CrossRef]
- Fasman, K.H.; L., S.S. An introduction to biological sequence analysis. In Computational Methods in Molecular Biology; Salzberg, S.L., Searls, D.B., Kasif, S., Eds.; Elsevier: Amsterdam, The Netherlands, 1998; pp. 21–42. [Google Scholar]
- Wang, L.; Jiang, T. On the Complexity of Multiple Sequence Alignment. J. Comput. Biol. 1994, 1, 337–348. [Google Scholar] [CrossRef] [PubMed]
- Just, W.; Just, W. Computational Complexity Of Multiple Sequence Alignment With Sp-Score. J. Comput. Biol. 1999, 8, 615–623. [Google Scholar] [CrossRef] [PubMed]
- Hautamaki, V.; Nykanen, P.; Franti, P. Time-series clustering by approximate prototypes. In Proceedings of the 2008 19th International Conference on Pattern Recognition, Tampa, FL, USA, 8–11 December 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Petitjean, F.; Ketterlin, A.; Gançarski, P. A Global Averaging Method for Dynamic Time Warping, with Applications to Clustering. Pattern Recogn. 2011, 44, 678–693. [Google Scholar] [CrossRef]
- Marteau, P. Times series averaging from a probabilistic interpretation of time-elastic kernel. arXiv 2015, arXiv:1505.06897. [Google Scholar]
- Marteau, P.; Ménier, G. Speeding up simplification of polygonal curves using nested approximations. Pattern Anal. Appl. 2009, 12, 367–375. [Google Scholar] [CrossRef]
- Newling, J.; Fleuret, F. A Sub-Quadratic Exact Medoid Algorithm. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 185–193. [Google Scholar]
- Annam, J.R.; Mittapalli, S.S.; Bapi, R.S. Time series Clustering and Analysis of ECG heart-beats using Dynamic Time Warping. In Proceedings of the 2011 Annual IEEE India Conference, Hyderabad, India, 16–18 December 2011; pp. 1–3. [Google Scholar] [CrossRef]
- Liberti, L.; Lavor, C.; Maculan, N.; Mucherino, A. Euclidean Distance Geometry and Applications. SIAM Rev. 2014, 56, 3–69. [Google Scholar] [CrossRef]
- Petitjean, F.; Gançarski, P. Summarizing a set of time series by averaging: From Steiner sequence to compact multiple alignment. J. Theor. Comput. Sci. 2012, 414, 76–91. [Google Scholar] [CrossRef]
| Method | Without Outlier Removal | With Proposed Outlier Removal |
|---|---|---|
| Euclidean Medoid [25] | 60.90 | 60.49 |
| DTW Medoid [26] | 63.16 | 63.16 |
| Medoid [23] | 61.20 | 61.20 |
| soft-DTW Medoid [9] | 61.29 | 61.29 |
| Euclidean Centroid [27] | 67.28 | 67.54 |
| DBA Centroid [28] | 66.40 | 66.40 |
| soft-DTW Centroid [9] | 67.47 | 67.39 |
| iTEKA Centroid [13] | 68.21 | 68.28 |
| Rank | Train | Test | Length | Points | Time |
|---|---|---|---|---|---|
| A | 68.5% | 62.2% | 99% | 9882% | 30 min |
| B | 67.1% | 62.0% | 99% | 89% | seconds |
| C | 70.4% | 61.8% | 101% | 83% | seconds |
| D | 68.0% | 61.8% | 99% | 83% | seconds |
| E | 68.3% | 61.7% | 99% | 145% | 30 min |
| F | 66.6% | 61.5% | 100% | 70% | seconds |
| G | 67.4% | 61.2% | 100% | 107% | 10 min |
| H | 66.6% | 61.2% | 102% | 205% | seconds |
| I | 68.1% | 60.9% | 99% | 67% | seconds |
| DTW Medoid | 57.3% | 55.3% | 98% | 169% | 1 h |
| CellNet | 64.7% | 61.2% | 96.3% | 144% | seconds |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marteau, P.-F. Estimating Road Segments Using Kernelized Averaging of GPS Trajectories. Appl. Sci. 2019, 9, 2736. https://doi.org/10.3390/app9132736
Marteau P-F. Estimating Road Segments Using Kernelized Averaging of GPS Trajectories. Applied Sciences. 2019; 9(13):2736. https://doi.org/10.3390/app9132736
Chicago/Turabian StyleMarteau, Pierre-François. 2019. "Estimating Road Segments Using Kernelized Averaging of GPS Trajectories" Applied Sciences 9, no. 13: 2736. https://doi.org/10.3390/app9132736
APA StyleMarteau, P.-F. (2019). Estimating Road Segments Using Kernelized Averaging of GPS Trajectories. Applied Sciences, 9(13), 2736. https://doi.org/10.3390/app9132736





