Robust Visual-Aided Autonomous Takeoff, Tracking, and Landing of a Small UAV on a Moving Landing Platform for Life-Long Operation
Abstract
:Featured Application
Abstract
1. Introduction
2. Related Work
3. Proposed Approach
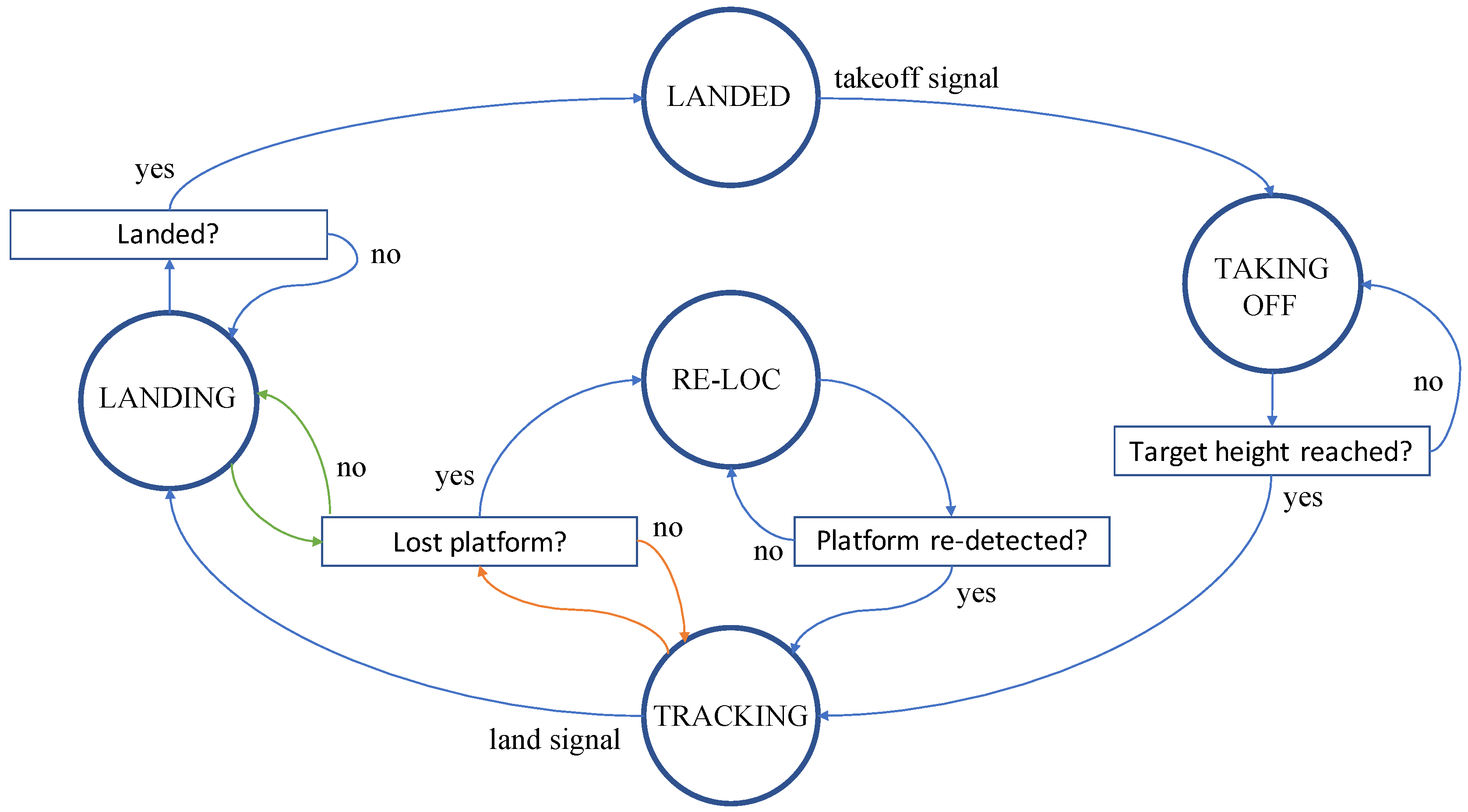
3.1. State Machine
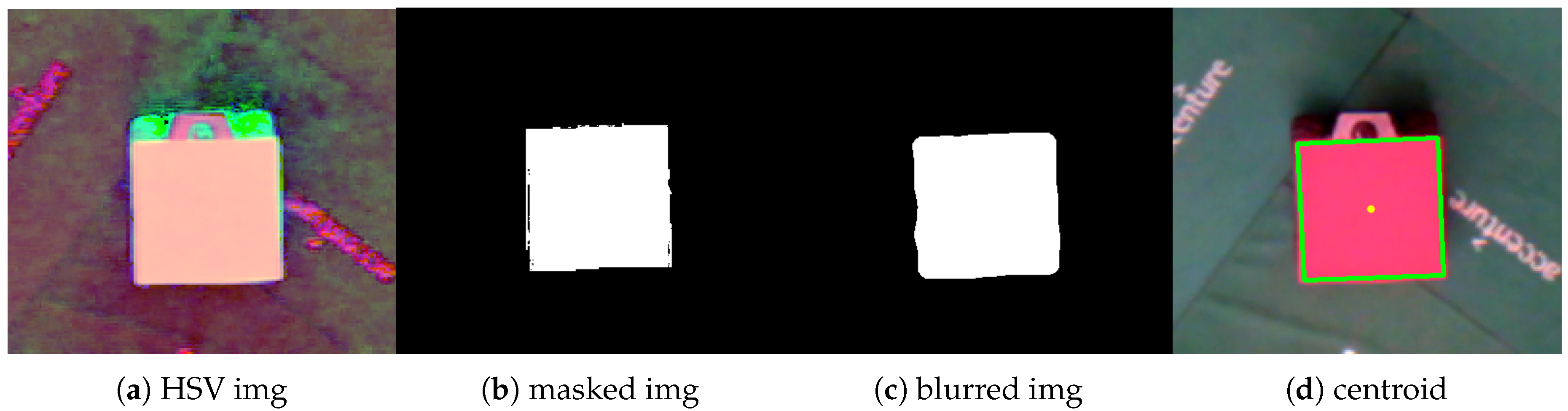
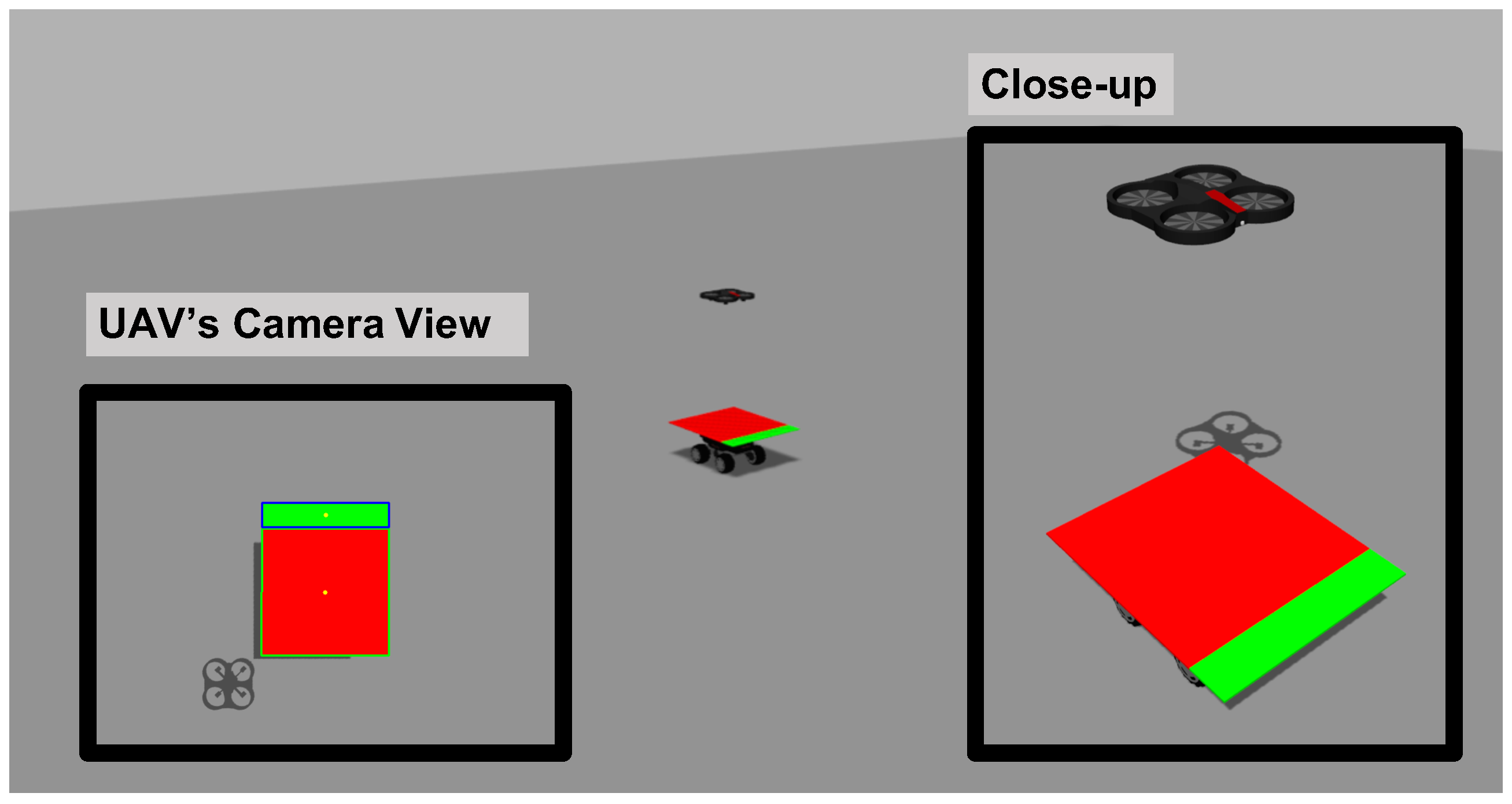
3.2. Detection and Localization of the Mobile Platform
| Algorithm 1 Detection algorithm. |
| Input: |
| Output: |
|
3.3. Tracking the Mobile Platform
3.3.1. Height-Adaptive, Non-Predictive PID Controller
3.3.2. Height-Adaptive, Predictive PID Controller
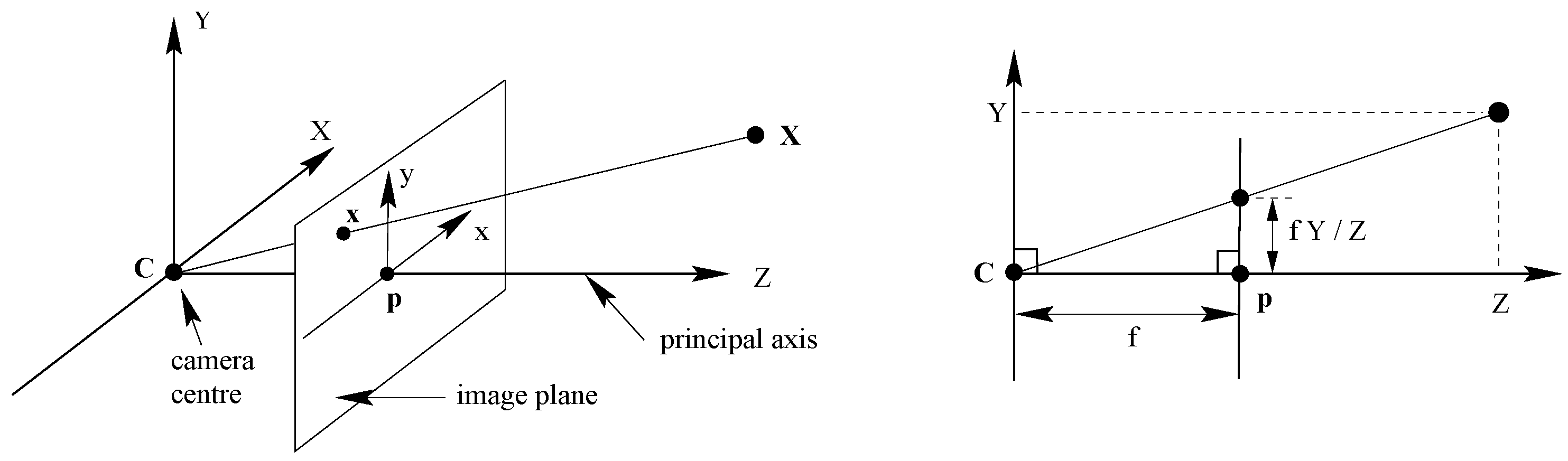
- The detection-localization algorithm (Section 3.2) outputs the centroid of the landing platform in the UAV’s camera frame. The prediction algorithm requires as input a 3D point relative to an inertial reference system. Therefore, we must transform the centroid of the landing platform from the drone’s camera frame into the the world’s frame:
- The new position is then sent to the prediction algorithm (Kalman filter), which returns a vector of future positions of the centroid of the landing platform relative to the world frame . The first element in this vector (with index zero) corresponds to the current position of the landing platform. The next element (index one) corresponds to the next predicted position after a user-defined time step. Correspondingly, the element with index two corresponds to a prediction carried out with twice the defined time step. In general, the number of steps in this path of predicted positions is computed as the ratio between a user-provided path time and the time step.
- Subsequently, the predicted future position of the landing platform is transformed from the world’s frame into the UAV’s body frame:
- Finally, the x and y coordinates of are used to calculate the controller’s error, i.e., the distance in the xy-plane between the UAV and the predicted position of the landing platform. Using this error we can now calculate the speed commands in x and y, i.e., in (4), that make this error converge to zero.
4. Results
4.1. Design of the Testing Environments
4.2. Experiments in the Simulated Environment
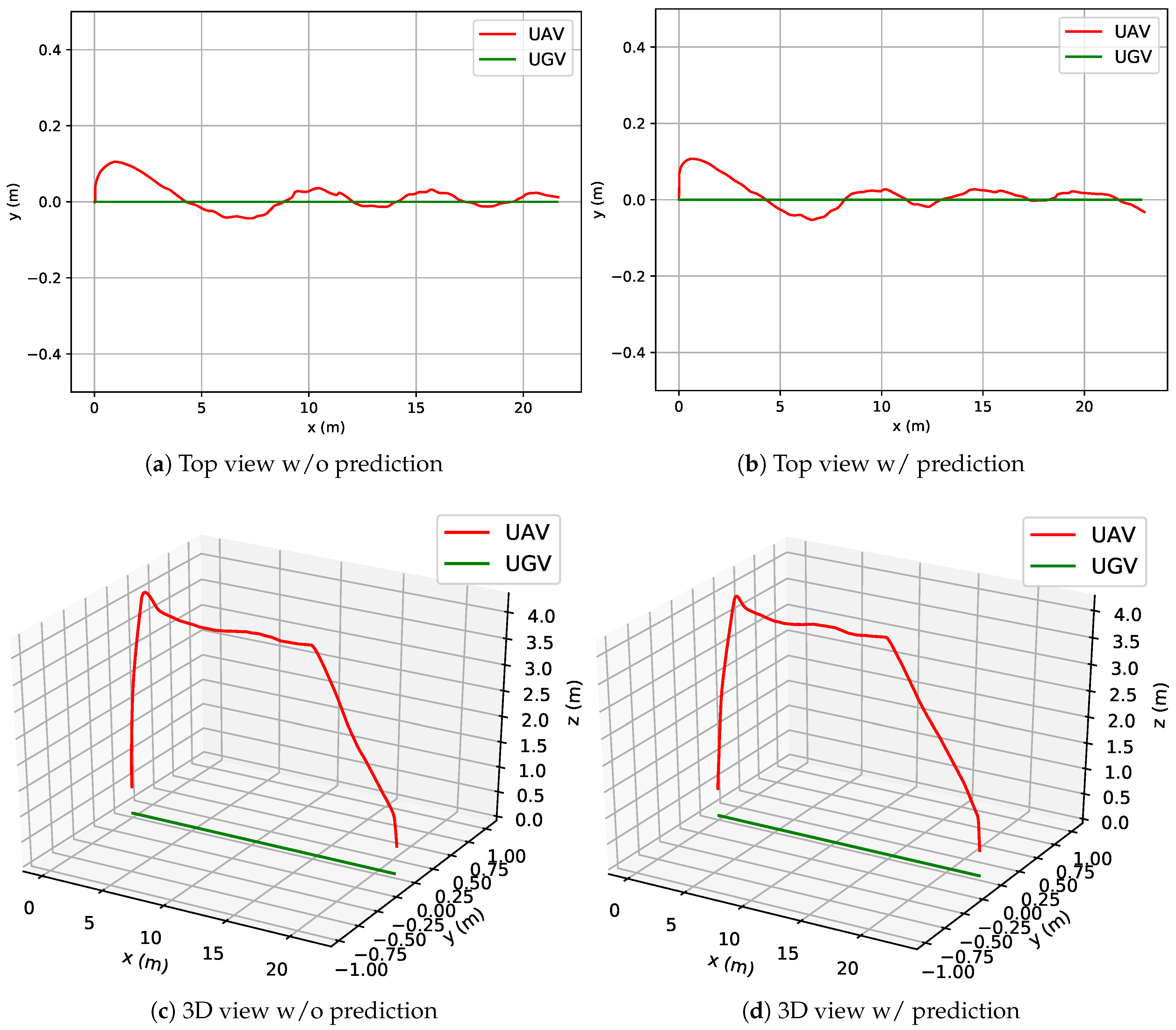
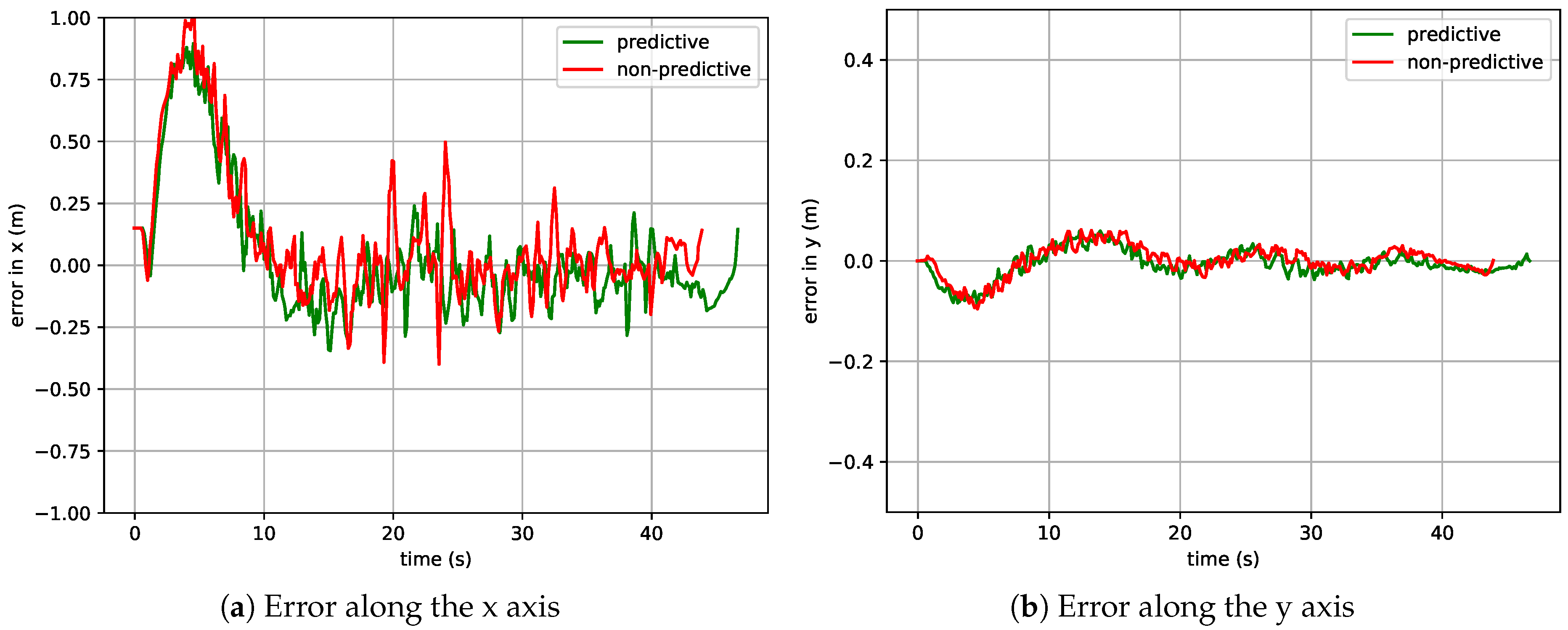
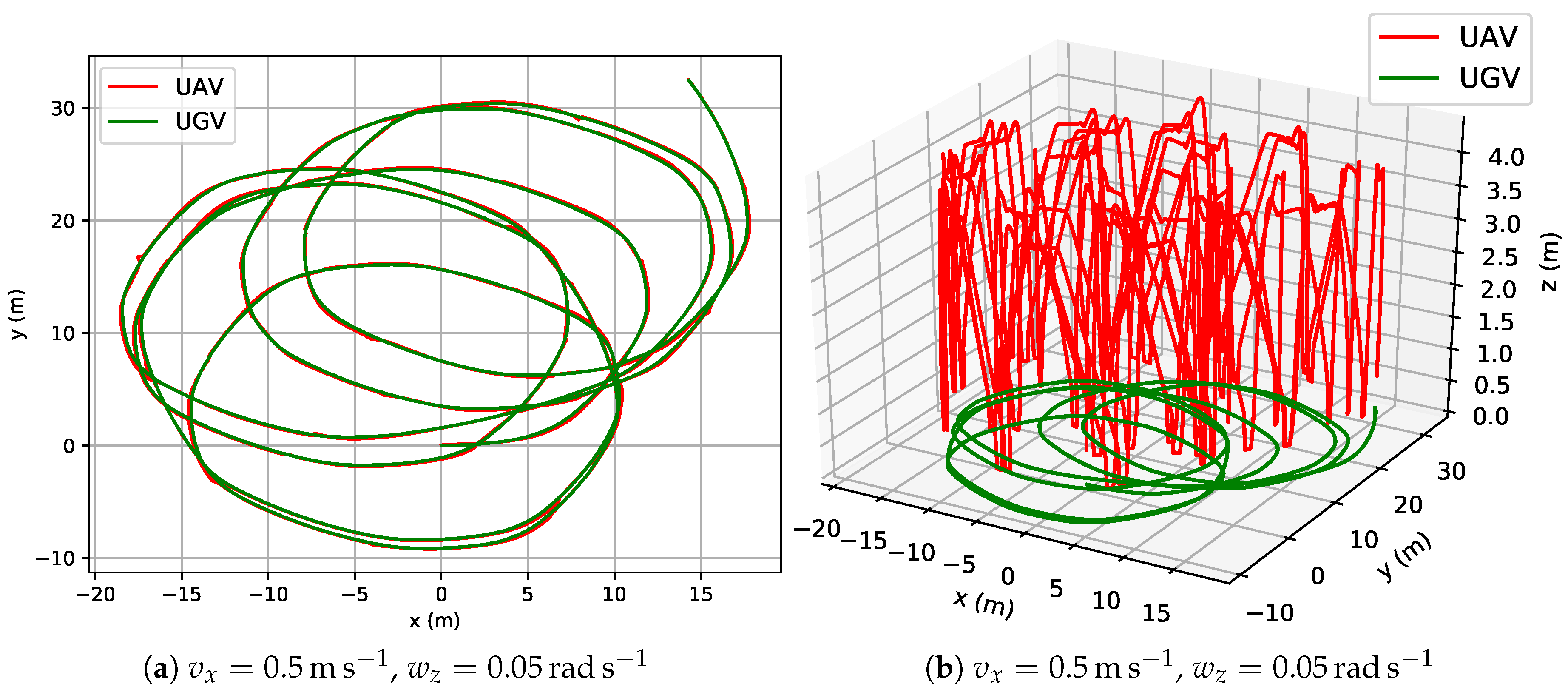
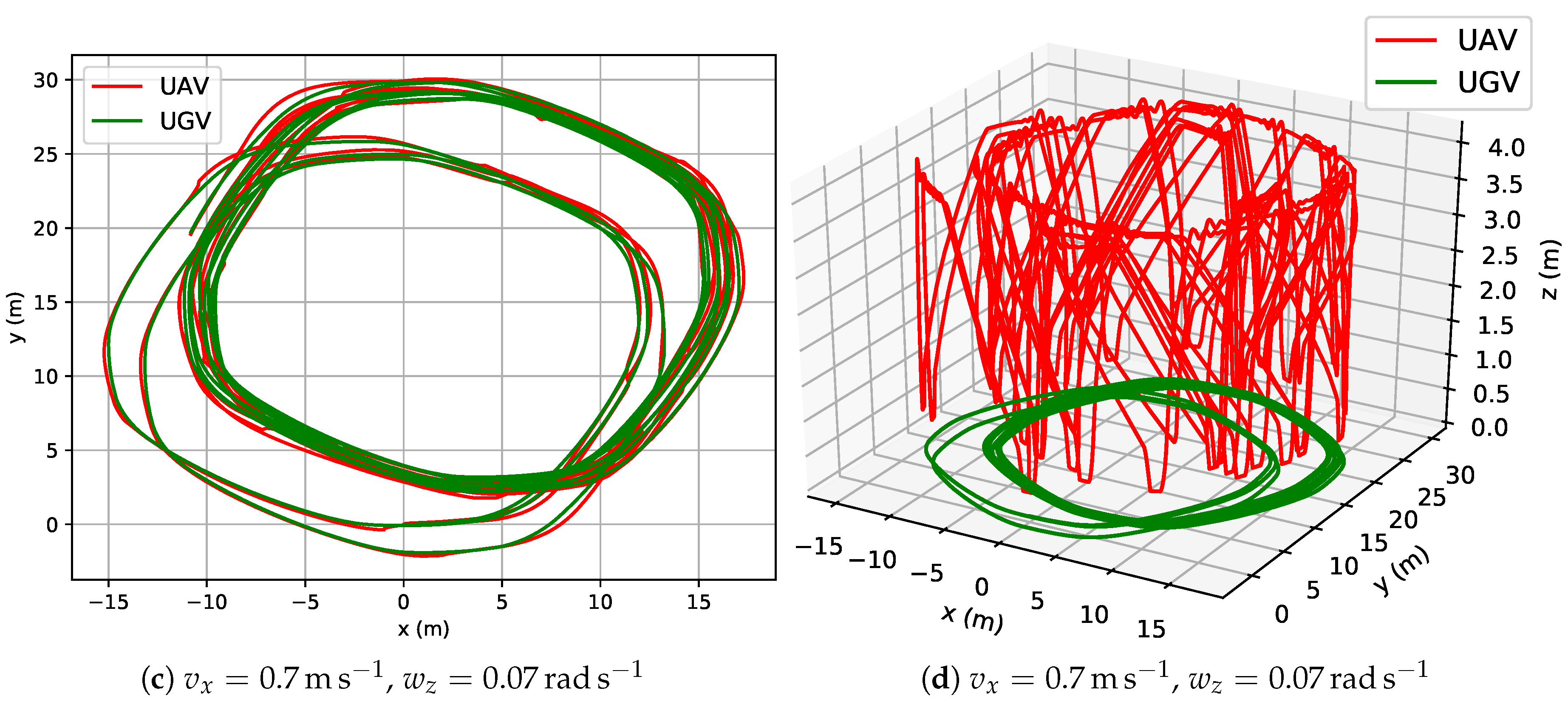
4.2.1. Experiments under the Same Initial Conditions
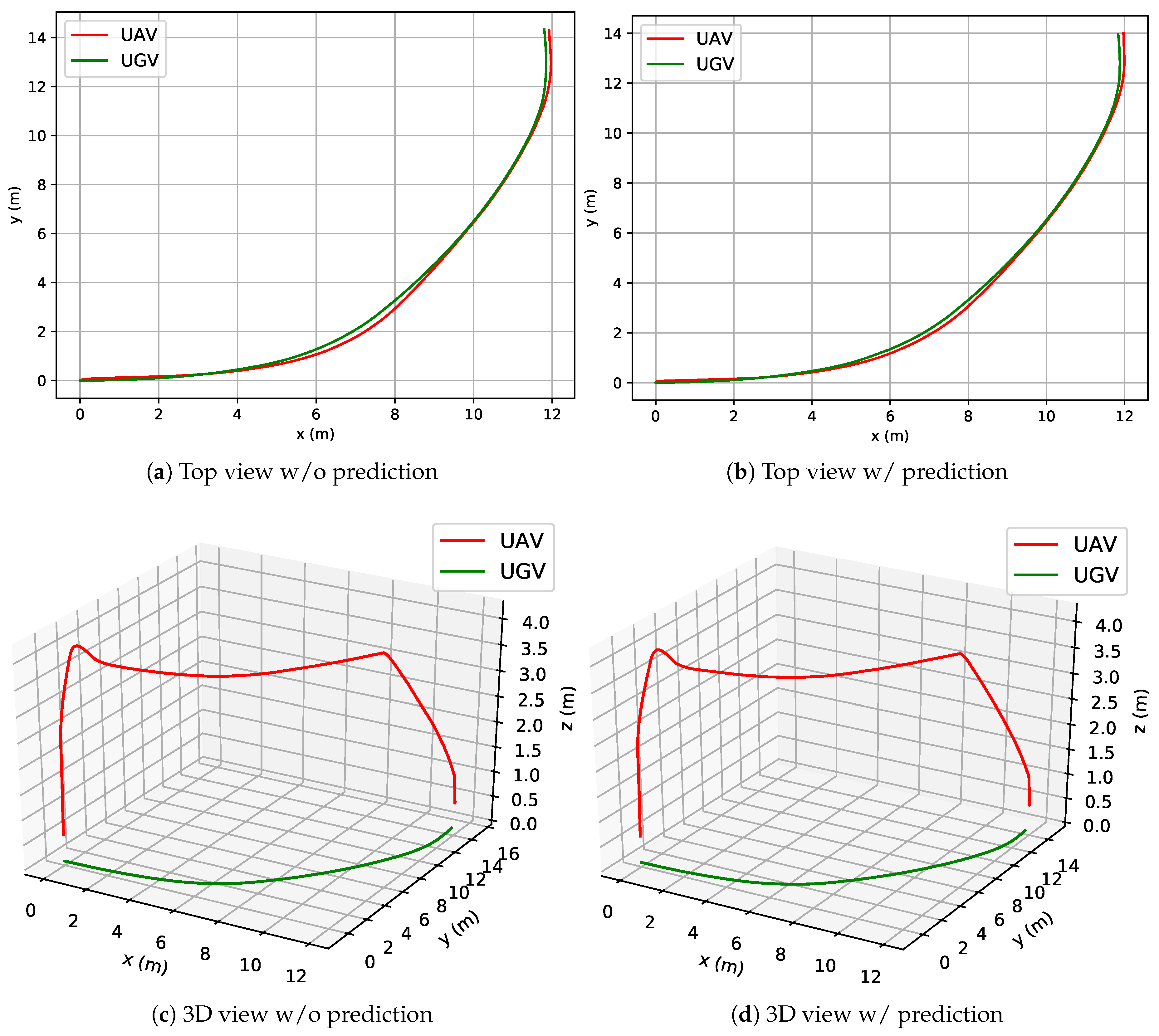
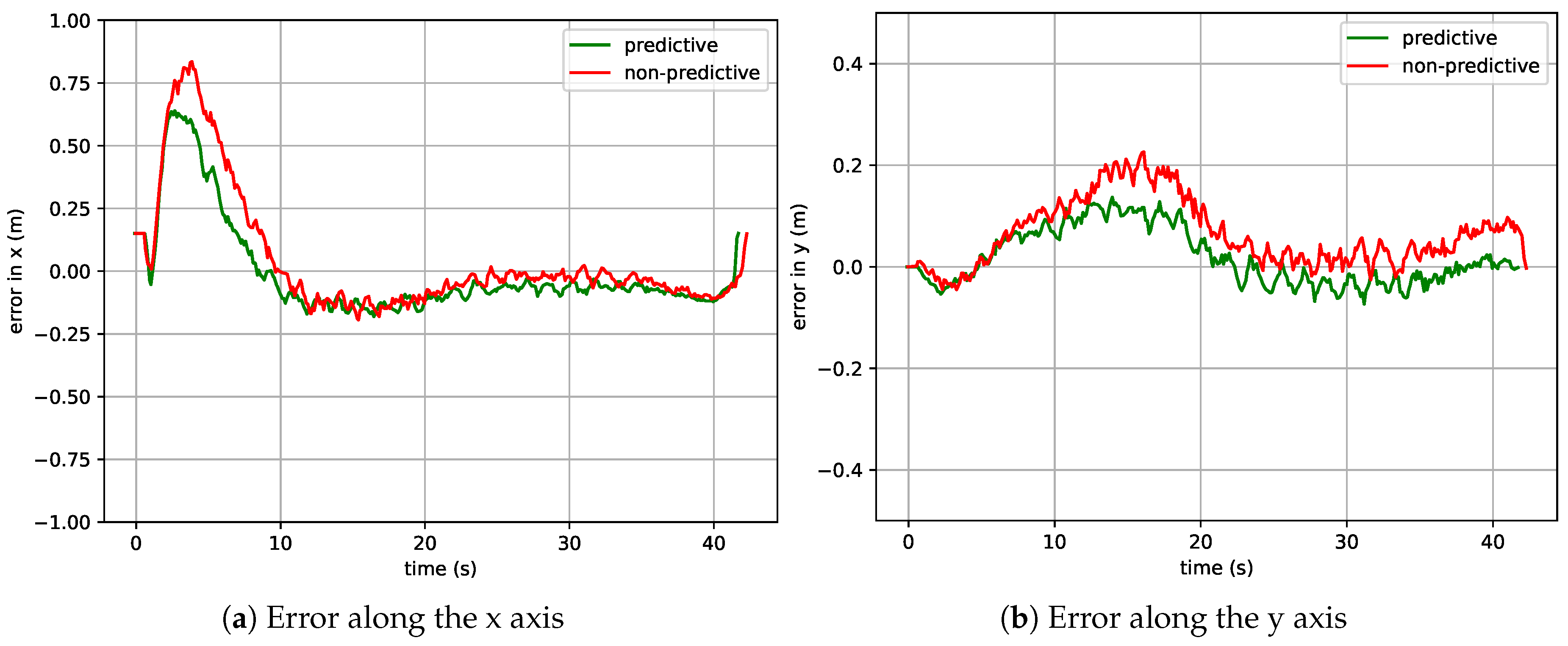
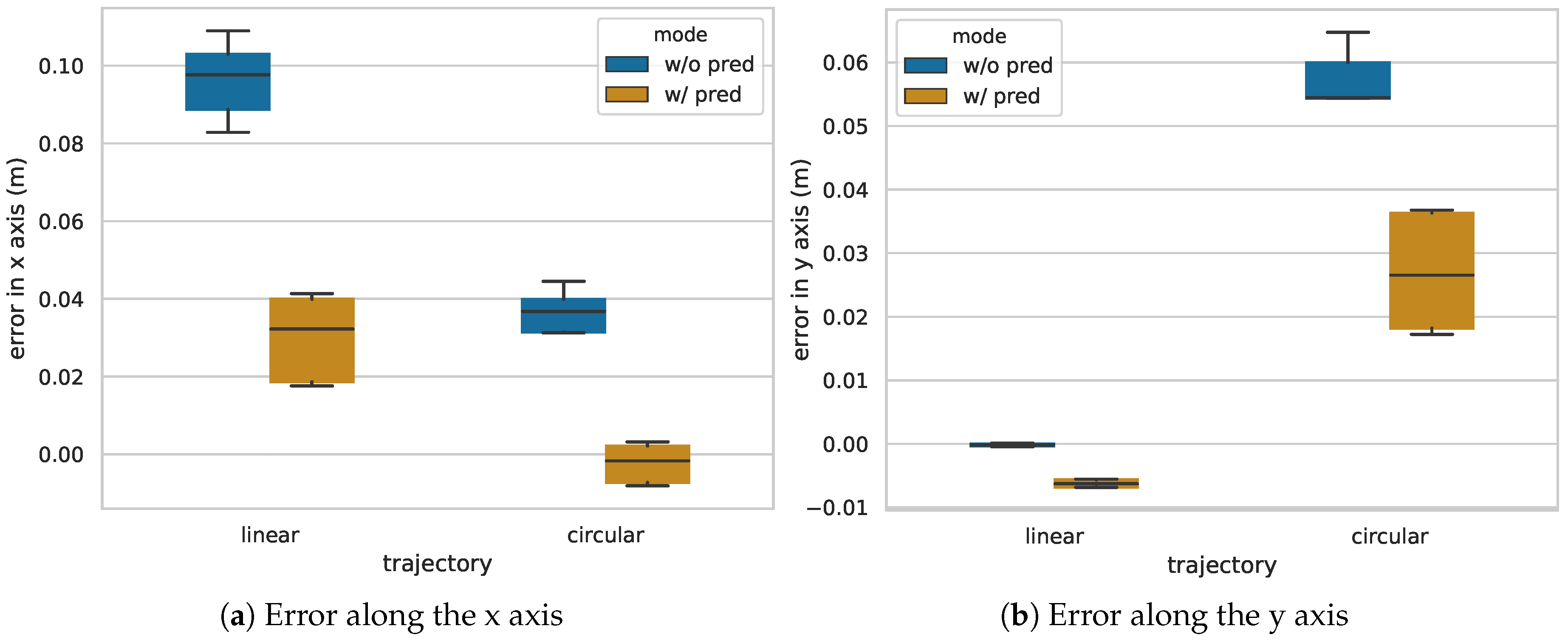
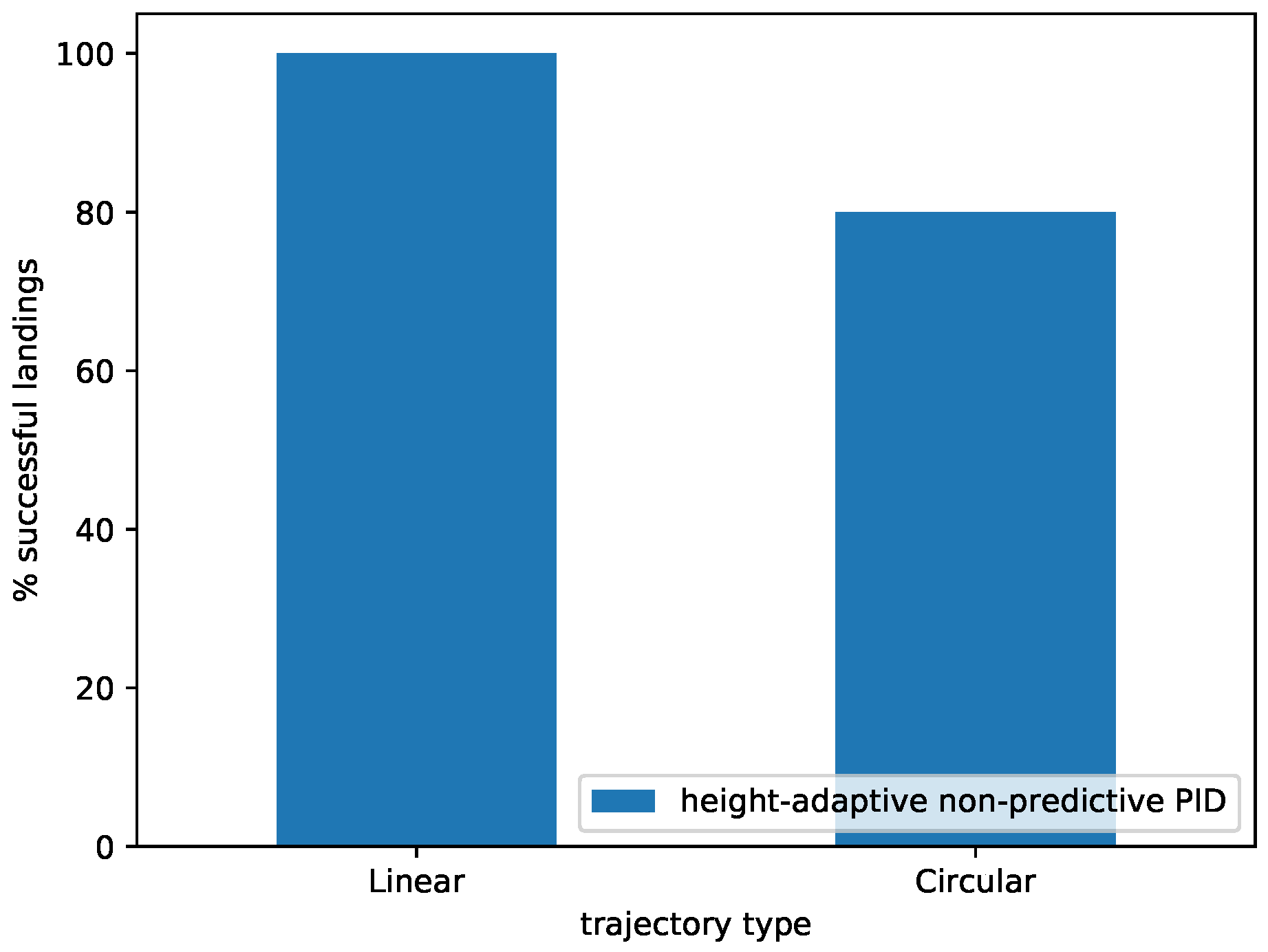
4.2.2. Overall Results in the Simulated Environment for a Linear and Circular Trajectory
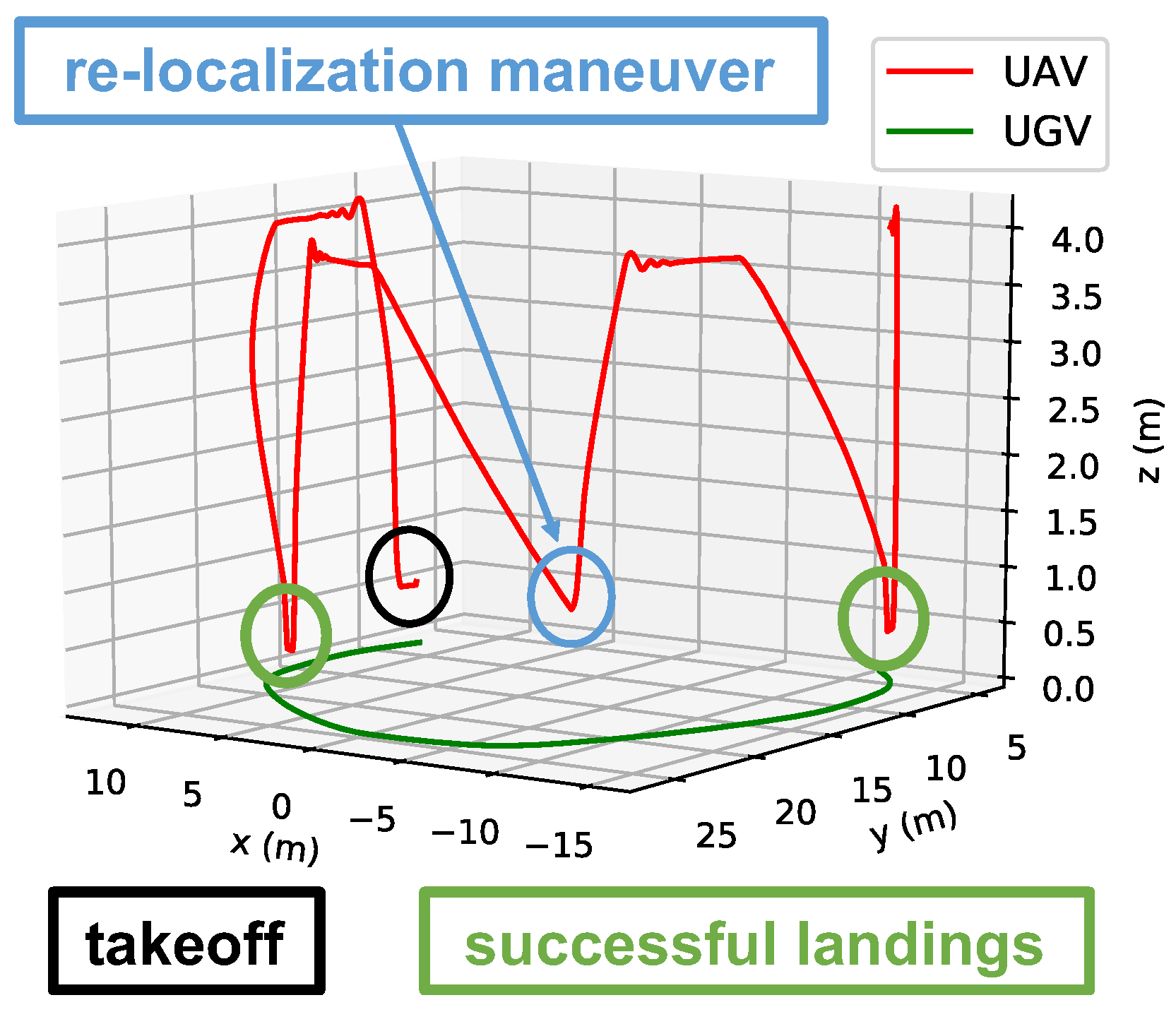
4.2.3. Experiments to Test the Life-Long Operation Capabilities of the System
4.3. Experiments in the Real Environment
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| UGV | Unmanned Ground Vehicle |
| PID | Proportional-Integral-Derivative |
| 3D | Three-Dimensional |
| IBVS | Image-Based Visual Servoing |
| ROS | Robot Operating System |
| MPC | Model Predictive Control |
| VTOL | Vertical Take-Off and Landing |
| HSV | Hue, Saturation, Value |
| IMU | Inertial Measurement Unit |
| MAE | Mean Absolute Error |
| CSV | Comma-Separated Values |
References
- Liu, Y.; Nejat, G. Robotic Urban Search and Rescue: A Survey from the Control Perspective. J. Intell. Robot. Syst. 2013, 72, 147–165. [Google Scholar] [CrossRef]
- Cardona, G.A.; Calderon, J.M. Robot Swarm Navigation and Victim Detection Using Rendezvous Consensus in Search and Rescue Operations. Appl. Sci. 2019, 9, 1702. [Google Scholar] [CrossRef]
- Garzón, M.; Valente, J.; Zapata, D.; Barrientos, A. An aerial-ground robotic system for navigation and obstacle mapping in large outdoor areas. Sensors 2013, 13, 1247–1267. [Google Scholar] [CrossRef] [PubMed]
- Polvara, R.; Sharma, S.; Wan, J.; Manning, A.; Sutton, R. Vision-Based Autonomous Landing of a Quadrotor on the Perturbed Deck of an Unmanned Surface Vehicle. Drones 2018, 2, 15. [Google Scholar] [CrossRef]
- Roldán, J.; Garcia-Aunon, P.; Garzón, M.; de León, J.; del Cerro, J.; Barrientos, A. Heterogeneous multi-robot system for mapping environmental variables of greenhouses. Sensors 2016, 16, 1018. [Google Scholar] [CrossRef]
- Reardon, C.; Fink, J. Air-ground robot team surveillance of complex 3D environments. In Proceedings of the 2016 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Lausanne, Switzerland, 23–27 October 2016; pp. 320–327. [Google Scholar]
- Borreguero, D.; Velasco, O.; Valente, J. Experimental Design of a Mobile Landing Platform to Assist Aerial Surveys in Fluvial Environments. Appl. Sci. 2018, 9, 38. [Google Scholar] [CrossRef]
- Koenig, N.; Howard, A. Design and use paradigms for gazebo, an open-source multi-robot simulator. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No. 04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2149–2154. [Google Scholar]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 17 May 2009; Volume 3, p. 5. [Google Scholar]
- Kong, W.; Zhou, D.; Zhang, D.; Zhang, J. Vision-based autonomous landing system for unmanned aerial vehicle: A survey. In Proceedings of the 2014 International Conference on Multisensor Fusion and Information Integration For Intelligent Systems (MFI), Beijing, China, 28–29 September 2014; pp. 1–8. [Google Scholar]
- Ling, K. Precision Landing of a Quadrotor UAV on a Moving Target Using Low-Cost Sensors. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2014. [Google Scholar]
- Lee, D.; Ryan, T.; Kim, H.J. Autonomous landing of a VTOL UAV on a moving platform using image-based visual servoing. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 971–976. [Google Scholar]
- Saripalli, S.; Sukhatme, G.S. Landing on a moving target using an autonomous helicopter. In Field and Service Robotics; Springer: Mt Fuji, Japan, 2006; pp. 277–286. [Google Scholar]
- Hu, M.K. Visual pattern recognition by moment invariants. IRE Trans. Inf. Theory 1962, 8, 179–187. [Google Scholar]
- Macés-Hernández, J.A.; Defaÿ, F.; Chauffaut, C. Autonomous landing of an UAV on a moving platform using Model Predictive Control. In Proceedings of the 2017 11th Asian Control Conference (ASCC), Gold Coast, QLD, Australia, 17–20 December 2017; pp. 2298–2303. [Google Scholar]
- Feng, Y.; Zhang, C.; Baek, S.; Rawashdeh, S.; Mohammadi, A. Autonomous Landing of a UAV on a Moving Platform Using Model Predictive Control. Drones 2018, 2, 34. [Google Scholar] [CrossRef]
- Almeshal, A.; Alenezi, M. A Vision-Based Neural Network Controller for the Autonomous Landing of a Quadrotor on Moving Targets. Robotics 2018, 7, 71. [Google Scholar] [CrossRef]
- Yang, T.; Ren, Q.; Zhang, F.; Xie, B.; Ren, H.; Li, J.; Zhang, Y. Hybrid Camera Array-Based UAV Auto-Landing on Moving UGV in GPS-Denied Environment. Remote Sens. 2018, 10, 1829. [Google Scholar] [CrossRef]
- German Aerospace Center. Autonomous Landing at Full Speed. Available online: https://www.dlr.de/dlr/en/desktopdefault.aspx/tabid-10080/150_read-16413/#/gallery/21679 (accessed on 29 May 2019).
- Bradski, G. The OpenCV Library. 2000. Available online: http://www.drdobbs.com/open-source/the-opencv-library/184404319 (accessed on 29 May 2019).
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Garzón, M.; Garzón-Ramos, D.; Barrientos, A.; Cerro, J.D. Pedestrian Trajectory Prediction in Large Infrastructures. In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics, Lisbon, Portugal, 29–31 July 2016; pp. 381–389. [Google Scholar]

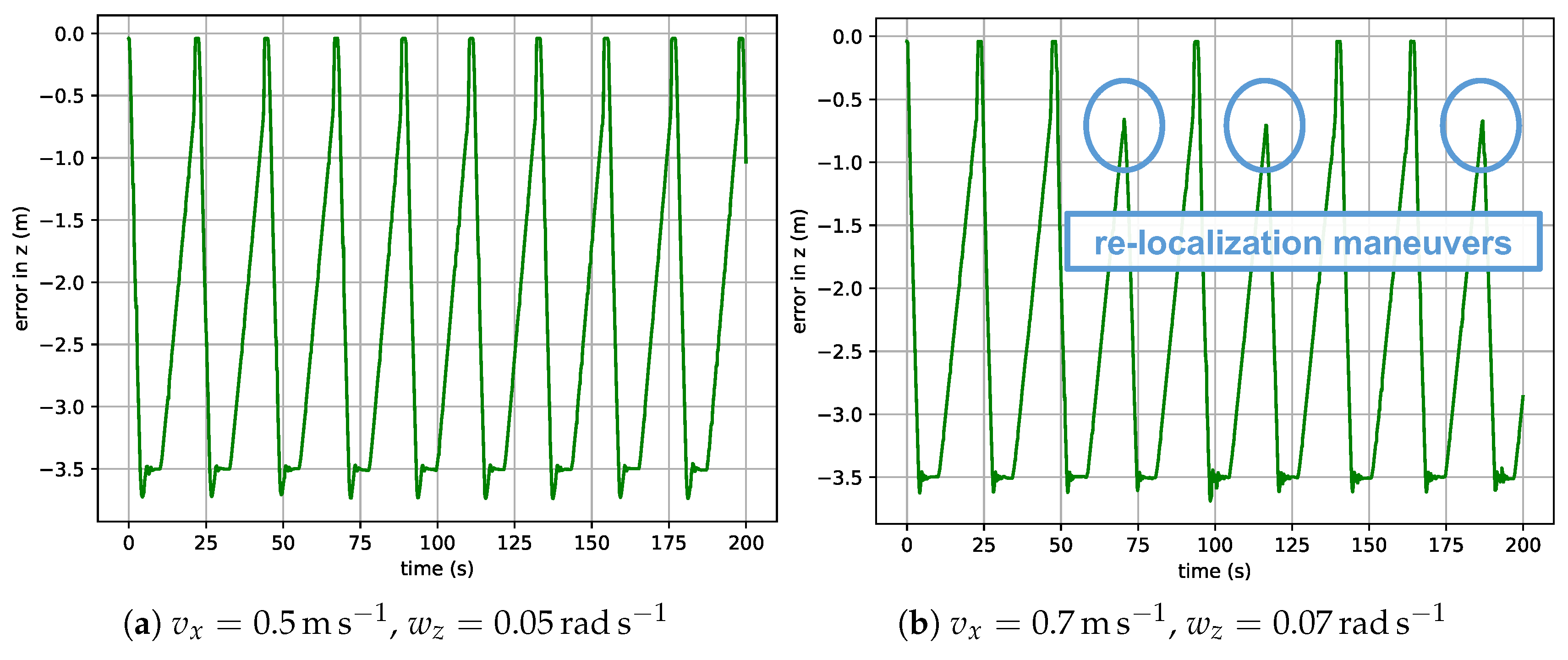


| PID Gains | Altitude Range | |
|---|---|---|
| 4 m | 2 m | |
| 0.694 | 0.697 | |
| 0.198 | 0.199 | |
| Study Variables | Landing Platform Velocities | |
|---|---|---|
| Total test time | ||
| Successful landings (num) | 50/50 | 34/50 |
| Successful landings (%) | 100% | 68% |
| Re-localization maneuvers | 0 | 16 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palafox, P.R.; Garzón, M.; Valente, J.; Roldán, J.J.; Barrientos, A. Robust Visual-Aided Autonomous Takeoff, Tracking, and Landing of a Small UAV on a Moving Landing Platform for Life-Long Operation. Appl. Sci. 2019, 9, 2661. https://doi.org/10.3390/app9132661
Palafox PR, Garzón M, Valente J, Roldán JJ, Barrientos A. Robust Visual-Aided Autonomous Takeoff, Tracking, and Landing of a Small UAV on a Moving Landing Platform for Life-Long Operation. Applied Sciences. 2019; 9(13):2661. https://doi.org/10.3390/app9132661
Chicago/Turabian StylePalafox, Pablo R., Mario Garzón, João Valente, Juan Jesús Roldán, and Antonio Barrientos. 2019. "Robust Visual-Aided Autonomous Takeoff, Tracking, and Landing of a Small UAV on a Moving Landing Platform for Life-Long Operation" Applied Sciences 9, no. 13: 2661. https://doi.org/10.3390/app9132661
APA StylePalafox, P. R., Garzón, M., Valente, J., Roldán, J. J., & Barrientos, A. (2019). Robust Visual-Aided Autonomous Takeoff, Tracking, and Landing of a Small UAV on a Moving Landing Platform for Life-Long Operation. Applied Sciences, 9(13), 2661. https://doi.org/10.3390/app9132661







