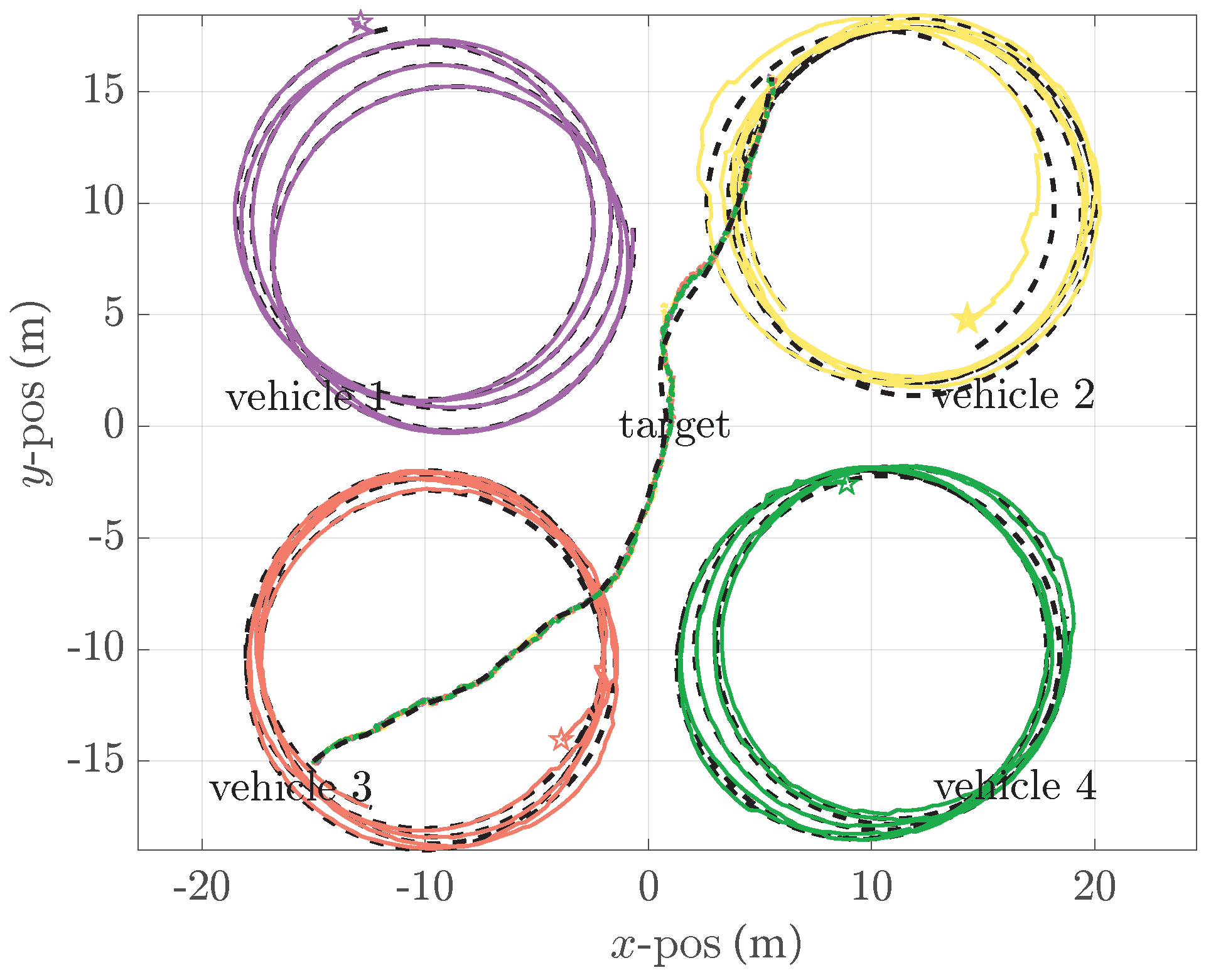1. Introduction
Multi-robot systems (MRSs) have garnered tremendous research interest in recent years [
1]. Compared with a single robot, an MRS usually has greater efficiency and operational capability in accomplishing complex tasks, such as transportation [
2], search and rescue [
3], and mapping [
4]. Among these MRS applications are the fundamental tasks of obtaining reliable localization information for the local robot and the uncooperative target using various measurements; these two processes are often referred to as collaborative self-localization (CL) [
5,
6,
7,
8,
9] and distributed target tracking (DT) [
10,
11,
12,
13], respectively. In the CL process, each robot measures the relative quantities with regard to neighboring cooperative robots. By cooperating with other robots, each robot is able to refine its own positioning information. In the DT process, each robot performs a measurement function on the uncooperative targets to be tracked. Then, the states of the target can be estimated cooperatively through interactions with other robots. Although the problems of CL and DT are usually solved by two separate techniques, such as in [
5,
6,
7,
8,
9,
10,
11,
13,
14,
15,
16,
17], they are correlated in most practical scenarios. In the DT process, the target tracking accuracy is dependent on the localization information of the corresponding robots, as well as the relative measurements between the robot and target. The target tracking results obtained by each local robot, in turn, can be implemented to improve the localization performance of the robots. To realize MRS self-localization and target tracking simultaneously, a combined collaborative self-localization and distributed target tracking (CLAT) framework is studied in this paper.
The problem of multi-robot collaborative localization has drawn significant attention in recent years. In [
18], the state of the art in collaborative localization is surveyed, and the theoretical limits, algorithms, and practical challenges are discussed. As one of the fundamental challenges in CL, the application of a proper data fusion strategy to deal with the correlations between robots was studied in [
5,
6,
7,
8,
9,
14,
15]. A direct approach involves the local robot treating the states of neighboring robots as fully confident variables that will lead to zero correlations between robots [
5]. However, this impractical assumption of neighboring positions can lead to overconfident estimates. A more practical method to fuse the relative measurements when the correlation is unknown is the implementation of conservative correlation approximation methods, such as covariance intersection (CI) [
6] or split covariance intersection (SCI) [
7]. A CL approach using CI was proposed in [
14]. This method is provably consistent and can handle asynchronous communication and measurement. The SCI-based approach, as studied in [
7,
8], further separates the covariance into correlated and uncorrelated parts, and the latter is fused using the CI method. Despite the ability of CI-based methods to preserve the consistency of the estimates, they often have overly conservative results. Making a trade-off between estimation accuracy and the corresponding cost during the CI-based collaborative localization process was investigated using the optimal scheduling problem in [
19]. Another popular method to deal with the CL problem is based on factor graphs, which are formulated on the basis of entire trajectories, such as in [
15]. The correlation can be explicitly tracked in the factor-graph-based method. However, storing all of the measurements resulting from this method requires significantly more storage space than the recursive method. To address the above drawbacks, a recursive extended Kalman filter (EKF)-based CL method was proposed in [
20], in which the correlation was accurately tracked in a decentralized manner. In [
21], the processing and storage costs were further reduced by introducing a server that broadcasts an update message when an inter-robot relative measurement is taken. However, in this method, when a relative measurement is taken between two robots, communication involves all robots rather than just the two in the relative measurement, and this significantly increases the communication burden. Another recursive EKF-based CL method was proposed in [
9]. This method efficiently approximates the correlation and only stores the current measurement. When the relative measurement is taken, only the communication between the two robots is required.
The distributed tracking problem has also been extensively studied [
22]. Early-stage algorithms that have been proposed to solve this problem can be roughly split into two categories: consensus-based algorithms [
16] and diffusion-based algorithms [
10]. The former category, in general, requires multiple communication iterations during each sampling time interval and hence could lead to a heavy communication burden. To reduce the communication bandwidth, a distributed Kalman filter with event-triggered communication was proposed in [
23], and the stability is guaranteed. The latter category does not have such drawbacks, but it may require local joint detectabilities at every single agent, and such a requirement might not be satisfied in a general multi-robot target tracking scenario. A more practical DT approach called distributed hybrid information fusion (DHIF) [
11] is able to guarantee stability and is asymptotically unbiased with very mild sufficient conditions. To further solve the distributed tracking problem with a nonlinear process and sensing models, an EKF-based paradigm was proposed in [
24], and the stability was analyzed in [
25]. Also, the unscented transformation-based approach, which has been regarded as a superior alternative to the EKF when the systems are highly nonlinear, was integrated with the DT process in [
26]. However, both the EKF and unscented Kalman filter (UKF) mentioned above are consensus-based and hence may generally result in a heavy communication burden. Recently, the aforementioned DHIF was extended to a nonlinear scenario using the DT approach in [
12], and the stochastic stability was analytically studied. Besides the methodology research and theoretical analyses above, the performance of different fusion strategies in terms of their communication rate, information type, and memory size were compared in [
27].
The CLAT framework has gained attention in recent years. There are two main kinds of methods: batch and recursive methods. The batch method estimates the entire state trajectory on the basis of all measurements and motion information up to the present, and the recursive method uses only the current measurement and control information. The batch-based method is supposed to outperform the recursive method but at the cost of significantly larger computation and storage requirements and, if in a distributed fashion, communication requirements. One batch-based method was proposed in [
28]. By introducing a factor graph that contained robot and target nodes and relative measurements, the problem was formulated as a least-square minimization problem and was solved with sparse optimization methods. Another batch-based method was presented in [
29], where the CLAT problem was formulated as a maximum a posteriori estimation problem, and the unscented transformation (UT) technique was implemented to better characterize the nonlinear process. Furthermore, the observability condition was extensively studied. For an MRS with limited computation and storage capacity, the recursive method is often preferred. A recursive-filter-based CLAT was studied in [
30], and the error bounds are theoretically provided. Nevertheless, the results in [
30] are based on a specially designed measurement graph so that the correlation can be tracked properly. A recursive Bayesian method was proposed in [
31] to perform the CLAT in a distributed sequential fashion; however, this method needs synchronous communication at each time instance and will therefore add a significant communication burden. Further, an error propagation analysis was carried out, and the convergence conditions are given in [
32], which showed that the localization and tracking accuracy only depends on the expectation of the measurement precision.
In this paper, the multi-robot localization and target tracking problem with a general nonlinear process and various measurement models is studied, and a UT-based CLAT scheme is proposed with consideration of the communication and memory limitations. The main contributions of this paper are summarized as follows: First, the proposed UT-based CLAT is recursive, and it does not store measurements; each robot only keeps the latest estimates of its own and the target, so the storage requirement is significantly reduced. Furthermore, communication is limited to the two robots to obtain a cooperative relative measurement, and no communication with other robots is needed. Meanwhile, to guarantee estimation consistency, inter-robot correlations are approximated in a distributed fashion on the basis of the covariance split method, and the robot–target correlation is discarded using the conservative CI method. Finally, the overall system is modeled on the basis of general nonlinear models and is characterized on the basis of the UT approach rather than the EKF method. Thus, the computation of a Jacobian is avoided. Simulations were carried out, and they indicate that the proposed UT-CLAT method is able to realize stable state estimates of both local robots and targets. More importantly, a hardware platform containing three quadrotors was implemented to verify the effectiveness of the proposed UT-CLAT method. Specifically, three types of measurements (absolute measurement, relative cooperative, and uncooperative measurement) from, respectively, the navigation system, ultra-wide bandwidth (UWB) transmitters, and onboard cameras were utilized to effectively estimate the states of the local robots and targets.
The rest of this paper is organized as follows:
Section 2 formulates the CLAT problem, and
Section 3 describes the proposed CLAT method.
Section 4 and
Section 5, respectively, provide the simulation results, which are based on synthetic data, and experimental results, which are based on hardware platforms.
Section 6 concludes the paper.
3. UT-Based CLAT
In this section, the proposed UT-CLAT is described. The states of local robots and targets are estimated using a recursive UT-based Kalman filter, with the aforementioned three types of measurements updated in an asynchronous fashion. For each robot
i, the local states, covariance, and the correlation between it and other robots
are tracked. Specifically, the correlation term is approximately tracked in a distributed fashion, similar to [
9]. As a matter of fact, the target may be detected by different robots at different times. It is difficult to track the robot–target correlation in a local robot when there are inter-robot correlations. To realize consistent state estimation under unknown robot–target correlations, a conservative CI method is introduced to safely remove the robot–target correlation terms and the correlation between target estimates from different robots. The above algorithm consists of state propagation (
Section 3.1) and three types of measurement update processes (
Section 3.2). In particular, the communication link is supposed to be established only during the cooperative relative measurement update process and the data from different robots are fused.
Suppose that at time
k, each robot
i has a posterior estimated state and its error covariance at a previous time instance, denoted as
and
, respectively. If a relative measurement between robots
i and
j is taken before time instance
k, then the correlated term
is arbitrarily decomposed as
and respectively stored in robots
i and
j. Robot
i also holds an estimation of the target
t locally, denoted as
and
.
3.1. Propagation
The propagation process involves the local robots as well as the target. According to the dynamics of Equations (1) and (2), each robot propagates its own state estimates and the local estimate of the target.
Let the augmented state vector and the corresponding augmented covariance matrix for each robot’s local state at time
be denoted respectively as
and
, where
,
A set of
sigma points, denoted as
, is selected as follows:
Here,
is a scaling parameter, with
and
as tuning parameters to control the spread of the sigma points. The weights for propagating the mean and covariances, denoted respectively as
and
, are computed as
where
is used to incorporate extra higher-order effects. Note that the definition of the sigma points directly implies that
or equivalently,
where
and
collect the components of
corresponding to, respectively,
and
.
The above unscented transform is summarized below:
By defining the augmented state vector and the covariance with regard to the local estimates of the target
t within robot
i similar to Equation (7), the UT of the target
t can be summarized as
Then, the prior local estimates and corresponding error covariance of the current state and target are computed respectively as
and
where
and
and
are the sigma points corresponding to
and
, and
The propagation of the correlation term
involves the pose and control inputs of both
i and
j, and therefore cannot be propagated locally by robot
i. To avoid communication, the local correlation term
is instead propagated as
where
is the inferred Jacobian matrix with regard to the dynamic function in Equation (1) and, according to [
33], is defined as
where
.
3.2. Update
In the update stage, three types of measurement (Equations (3)–(5)) are considered. When a private measurement or a target measurement is taken by robot i, the information is updated locally to avoid communication. When two robots i and j are within the relative range, a relative measurement is taken, and local beliefs of both robot and target and the inter-robot correlation term are exchanged to update the estimates of the local robots and target. For clarity, , and , are used respectively to denote the state estimate and covariance prior to and after a certain measurement update process.
3.2.1. Private Update
During each private update process, the local robot measures its local pose through, for example, a GPS receiver and magnetometer, to refine its local estimation. Only the local pose participates in the private update process.
First, the inferred Jacobian
corresponding to the measurement function in Equation (3) is obtained as
where
Then, the state and covariance can be updated as
where
The correlation term within local robot
i is updated as
3.2.2. Target Measurement Update
When a target is detected by robot
i, a relative measurement related to the pose of both robot
i and target
t, denoted as
, is obtained. The measurement update involves the estimates of the robot and the target, as well as their correlation term. As a matter of fact, the correlation term, denoted as
, is difficult to track in a distributed fashion owing to the existence of the inter-robot correlation term. Therefore, in this part, a conservative CI-based method [
34] is used to remove the robot–target correlations and guarantee consistency at the same time.
The weight
w is determined according to [
34]. Let
and
. The augmented state can be defined as
Then, the augmented sigma points are obtained as
The inferred measurement Jacobian is
where
The target measurement update process is finally summarized as Equations (19)–(22):
where the innovation covariance and gain are calculated as
Formally, the correlation between robots
i and
j should be updated as
On the basis of the decomposition in Equation (6), the correlation term
can be calculated as below without communication:
3.3. Neighbor Measurement Update and Target Information Fusion
When two robots
i and
j are within a given range, a relative measurement is taken, denoted as
, and a communication link between the two robots is established. The target update process is as follows. First, the covariance between two robots
is recovered according to Equation (6). Similar to the target measurement update process, we define the augmented state prior to the measurement update as
Then, the augmented sigma points are obtained as
The inferred measurement Jacobian is
where
Consequently, the update process for the relative measurement between robots
i and
j is as below:
where
After the relative measurement update, the correlation is decomposed again as two multiplicative parts and according to Equation (22). Then, and are stored in i and j, respectively.
The relative measurement update process also involves the correlation term
. Formally, the
should be updated as
The correlation term
is not available to robot
i. To reduce the overall communication and avoid communication with
l, the split term
in robot
i is instead updated in an approximate form, similar to the process in [
9], as below:
In addition to the measurement update, the target beliefs
and
are fused simultaneously. As a matter of fact, the correlation between the two estimates is unknown owing to the unknown target–robot correlation. Again, the conservative CI algorithm can be used as below:
The weight
can be determined according to [
11]. The fused results are then stored in both robots
i and
j.
4. Simulation
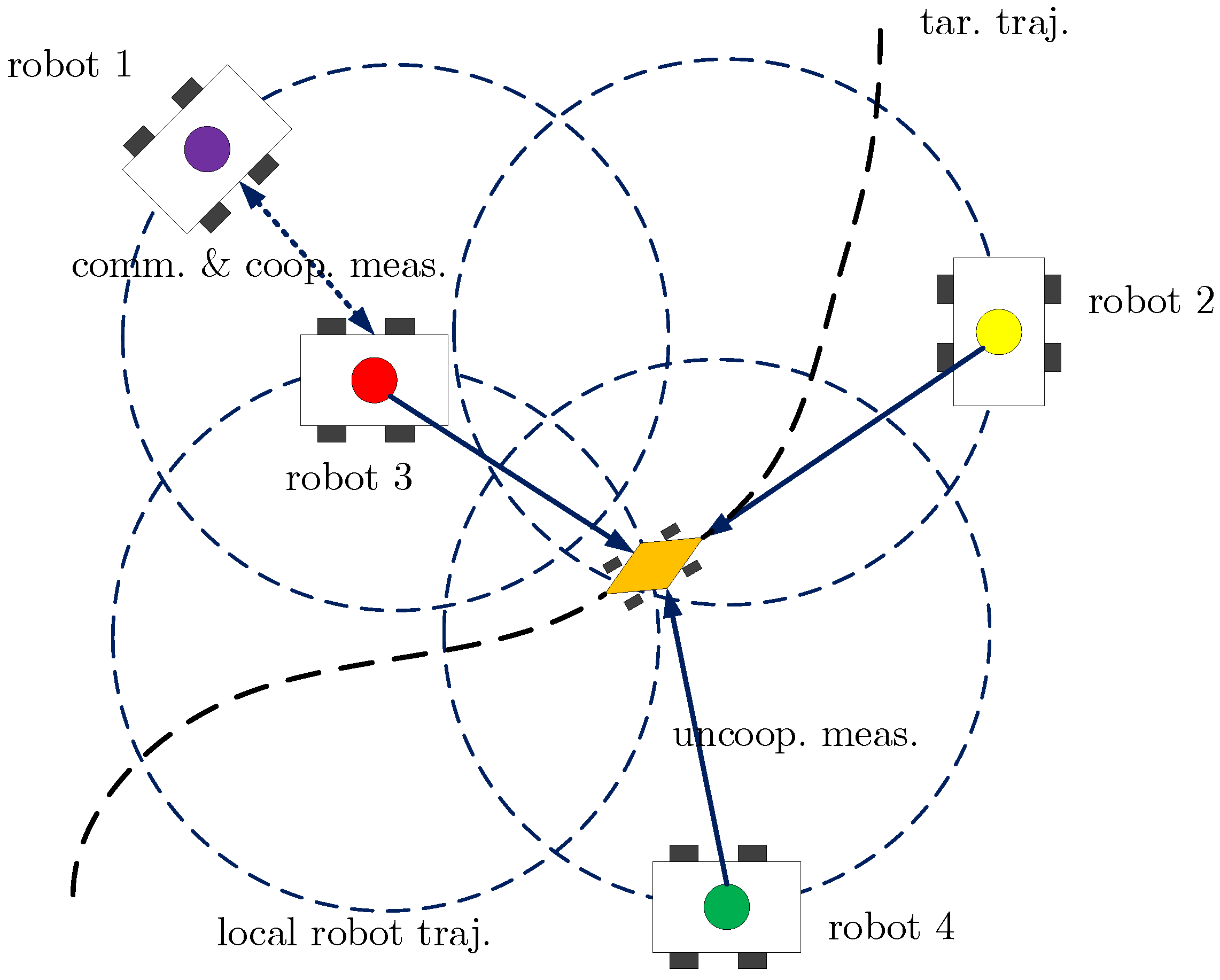
In this section, the proposed UT-CLAT method is validated using synthetic data. Without loss of generality, the scenario contains four cooperative robots, labeled 1–4, tracking an uncooperative target in 2D space (as shown in
Figure 1). The robots and the target are assumed to be subject to similar nonlinear unicycle models, as below:
A subscriber i or t is used to distinguish the robots or the target. The state vector to be estimated contains three entries—, , and —which represent the 2D position and the orientation of the robots and the target with respect to the global frame. It is assumed that at the initial time, the robots are randomly placed on different circles centered at . The same control command is applied to each robot to form four approximated circles with radii 8. The velocity and angular velocity noise are assumed to be subject to Gaussian distributions with the covariance . The target is initialized at in the global frame, and the control input is set as . Similarly, the target control is subject to zero-mean Gaussian noise with .
In the simulation, robot 1 is assumed to be accessible to the global position and orientation in the global frame with the following measurement model:
where
is the control noise.
Both the cooperative robots and uncooperative measurement are subject to a relative range measurement model as follows:
is the operator that calculates the relative range between two robots or a robot and the target. The sensing range for the target is set as
, and the sensing range for cooperative robots, as well as the communication range, is set as
. The measurement noises are
and
, respectively.
4.1. Scenario 1
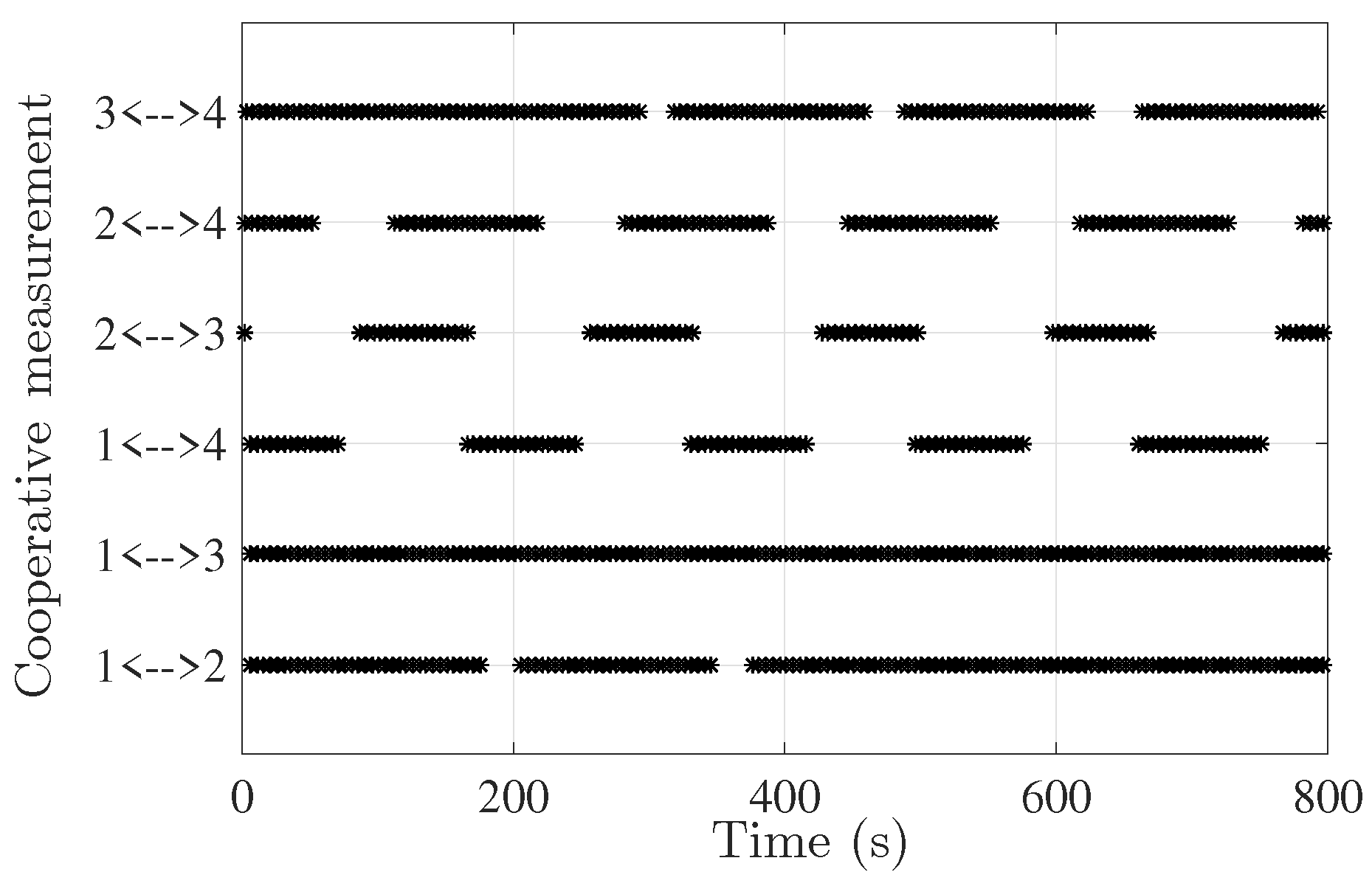
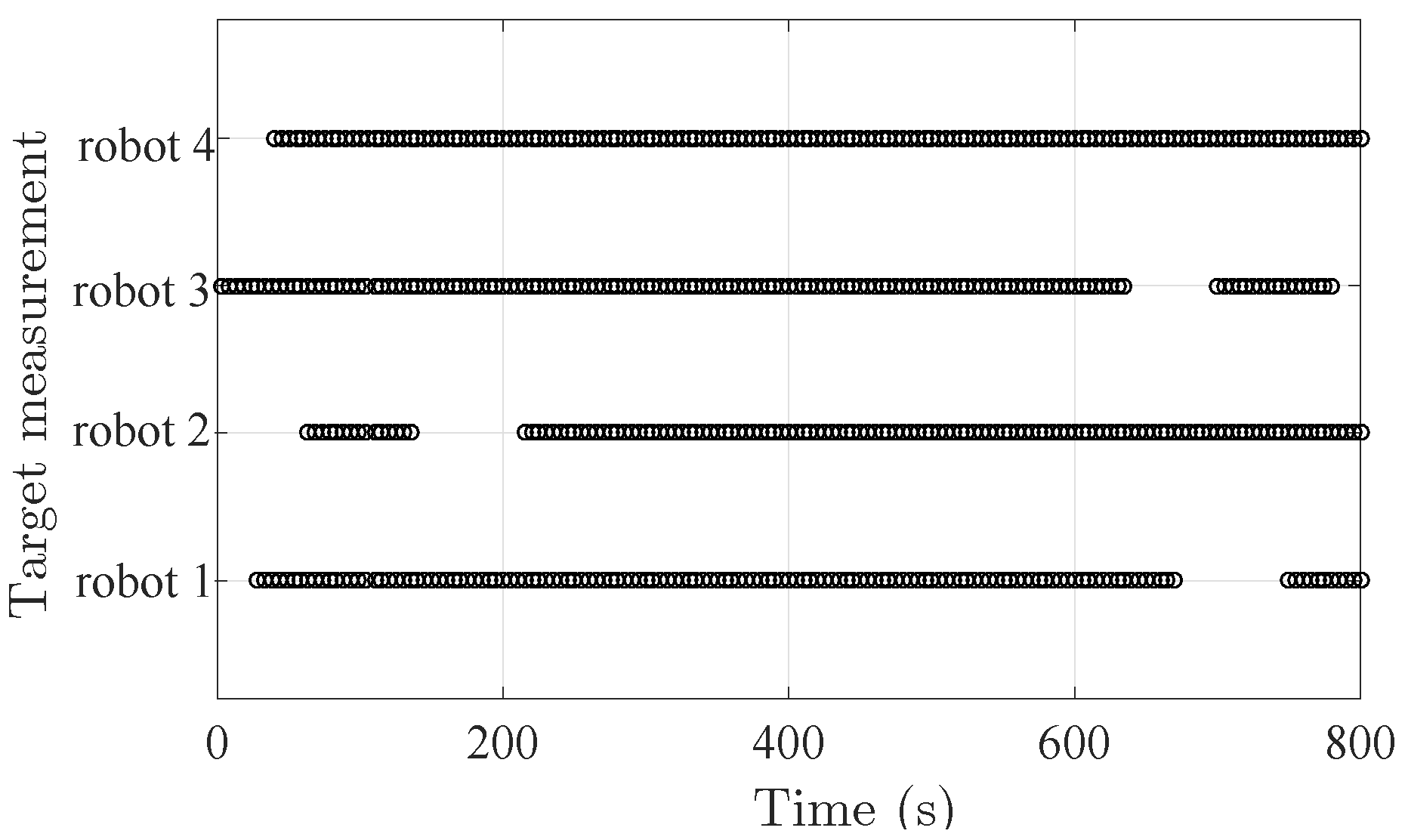
One trial of the simulation described above was carried out. In this scenario, the target is jointly observed by the four robots intermittently. The observation measurement availability for both cooperative measurement and target measurement is based on the sensing ranges
and
, respectively, and is shown in
Figure 2 and
Figure 3.
Although, for each robot, the observability of the local state and the target’s state cannot be guaranteed owing to the discontinuous range-only measurement, the joint observability for the entire system over a period of time can still be guaranteed through communication with neighbors according to [
35].
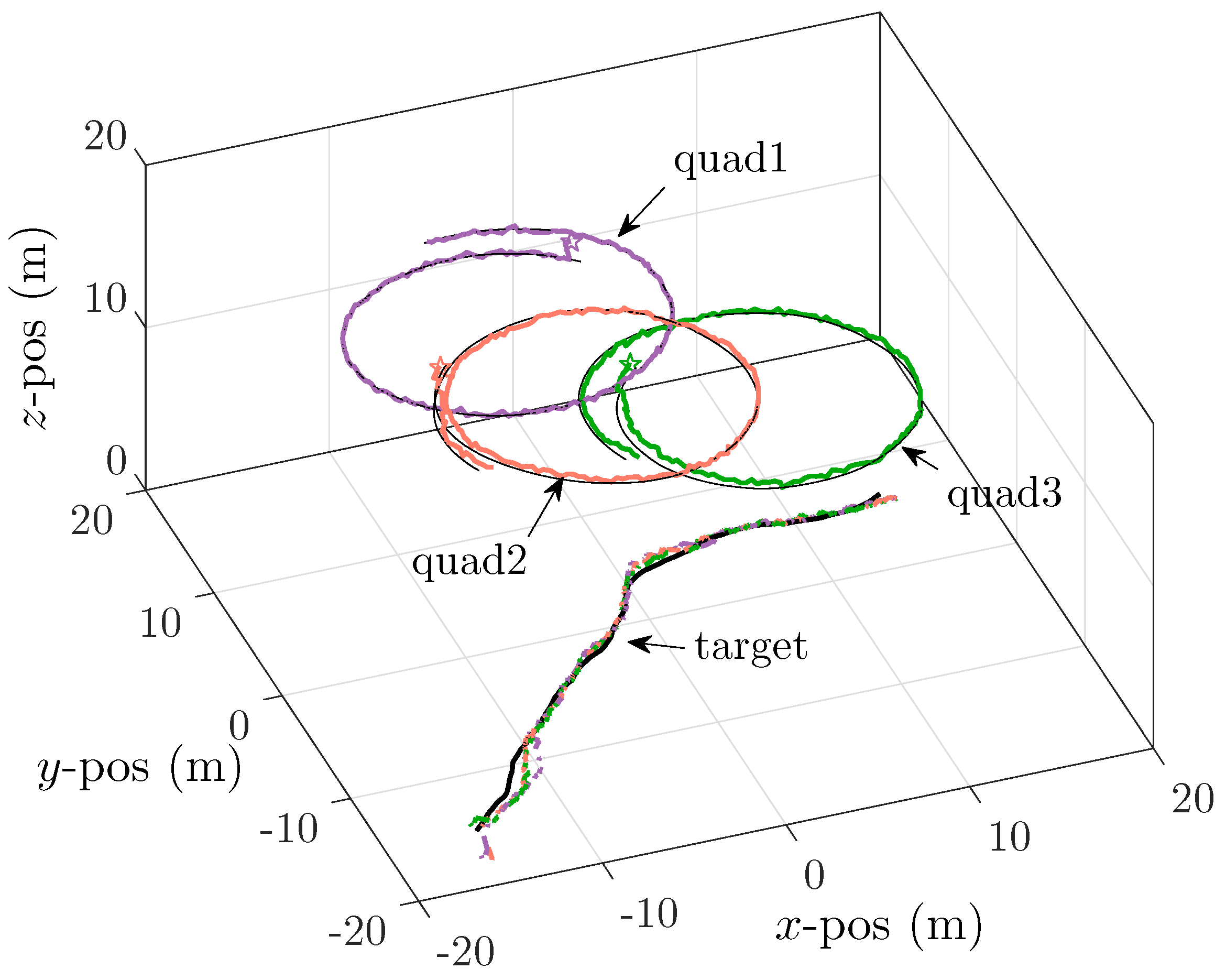
The estimated trajectories of both robots and the target are plotted in
Figure 4 in different colors. Each robot’s self-localization result and local target tracking result are drawn with solid lines of the same color. As observed in
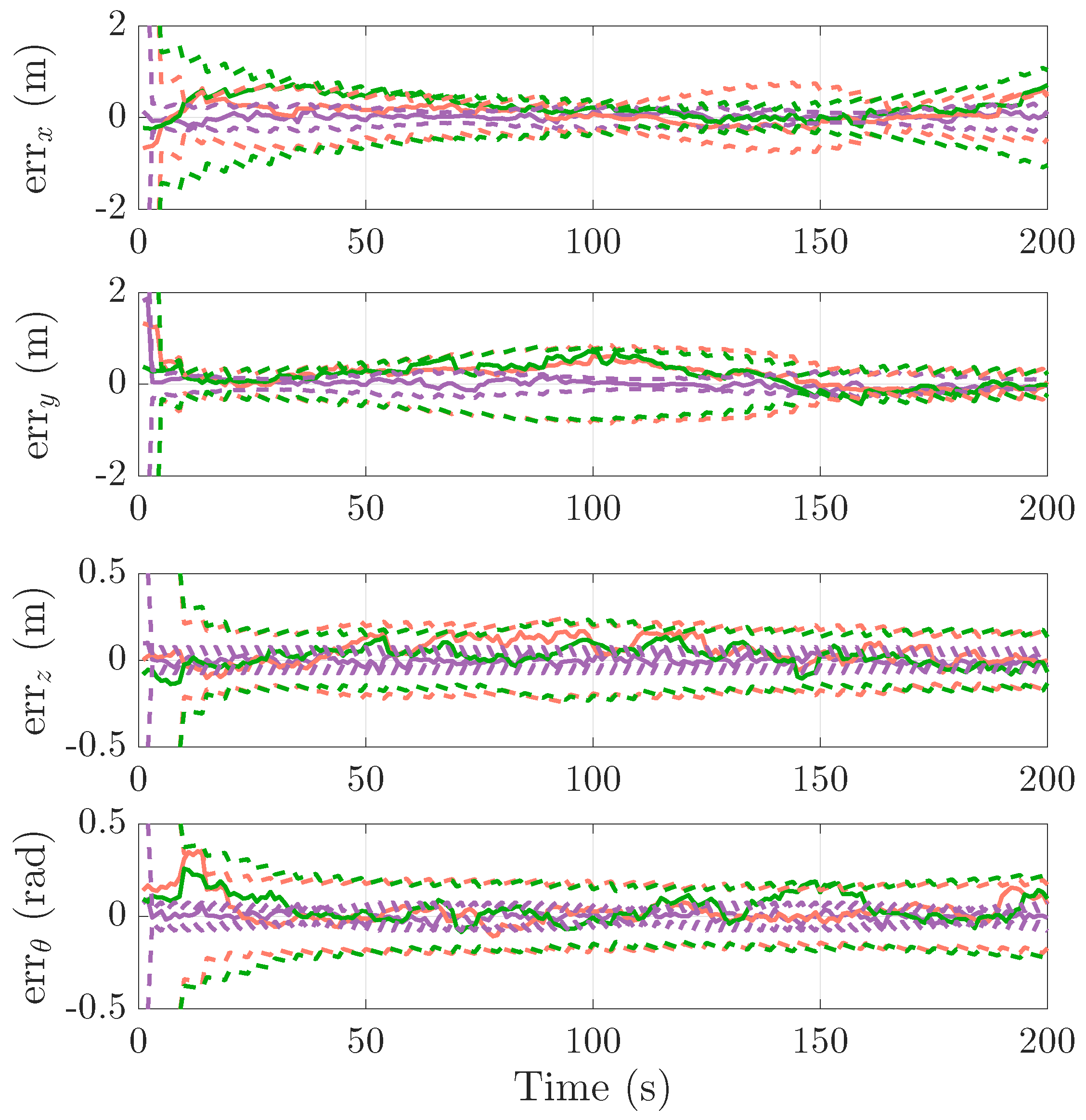
Figure 4, the estimated trajectories indicate that each robot is able to localize its true pose and track the true trajectory of the target. The four robots’ self-localization errors and covariances (
bounds) are plotted in
Figure 5, with solid lines in color and dashed lines in the same color, respectively. It shows that the self-localization errors by each robot are bounded by the
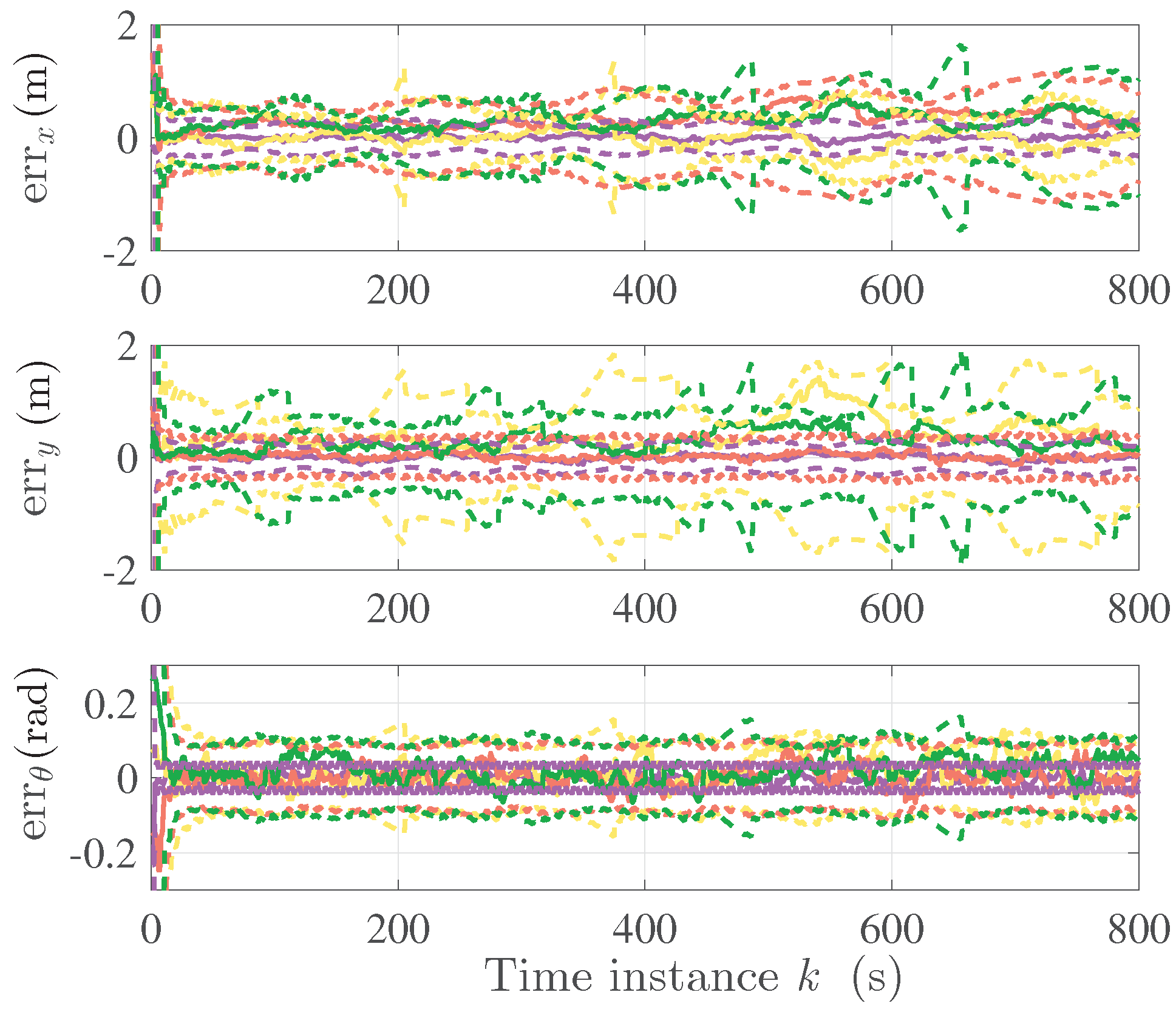
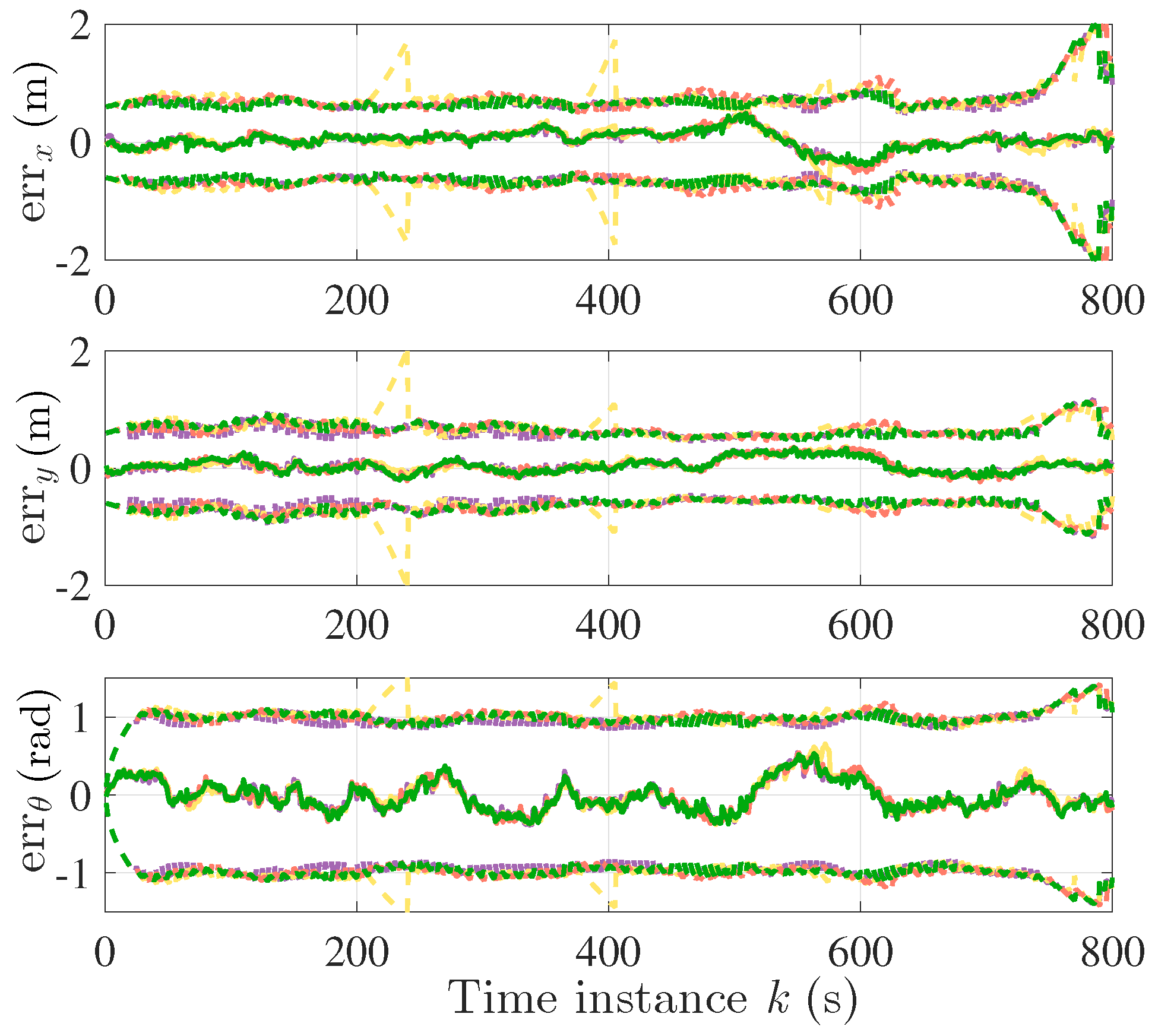
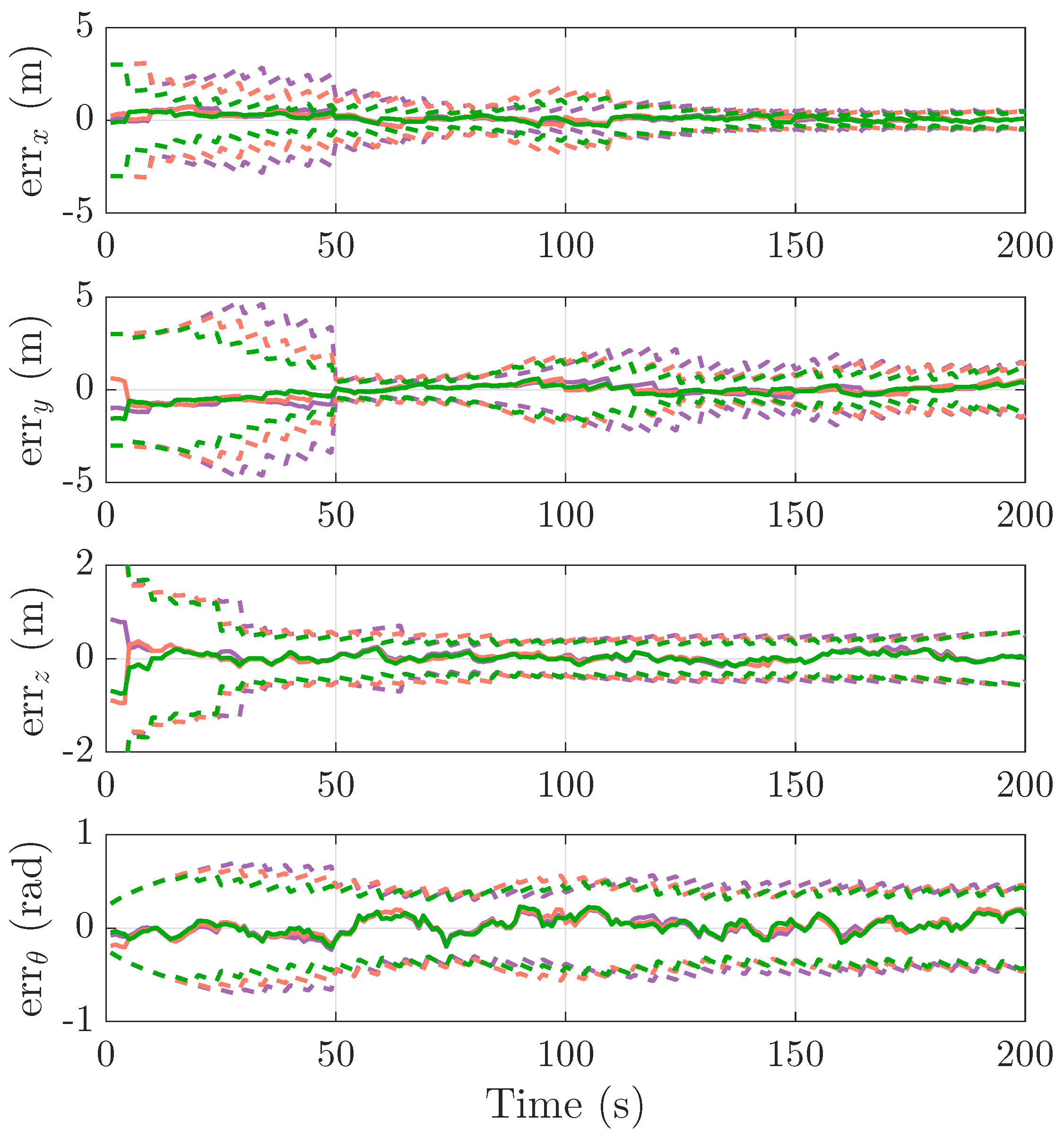
envelopes in the steady state. Robot 1 has the lowest tracking error as it can access its own absolute measurement. The target tracking results from the four robots are plotted in
Figure 6, where, for each robot, the target tracking errors (solid line in colors) are bounded by the corresponding
envelopes (dashed line in the same colors) in the steady state. On the basis of
Figure 5 and
Figure 6, the min/max self-localization and target tracking errors for time instance
are listed in
Table 1.
4.2. Scenario 2
In this part, the performance results of the proposed UT-CLAT method are presented on the basis of 1000 Monte Carlo simulations. Specifically, the simulation in Scenario 1 was repeated 1000 times with
. For each robot, the position root-mean-square errors (PRMSEs) of the local posterior estimates and target posterior estimates were computed for all trails. Moreover, to demonstrate the effectiveness in a nonlinear scenario, the proposed UT-CLAT method is compared to the EKF-CLAT method by extending the CL algorithm in [
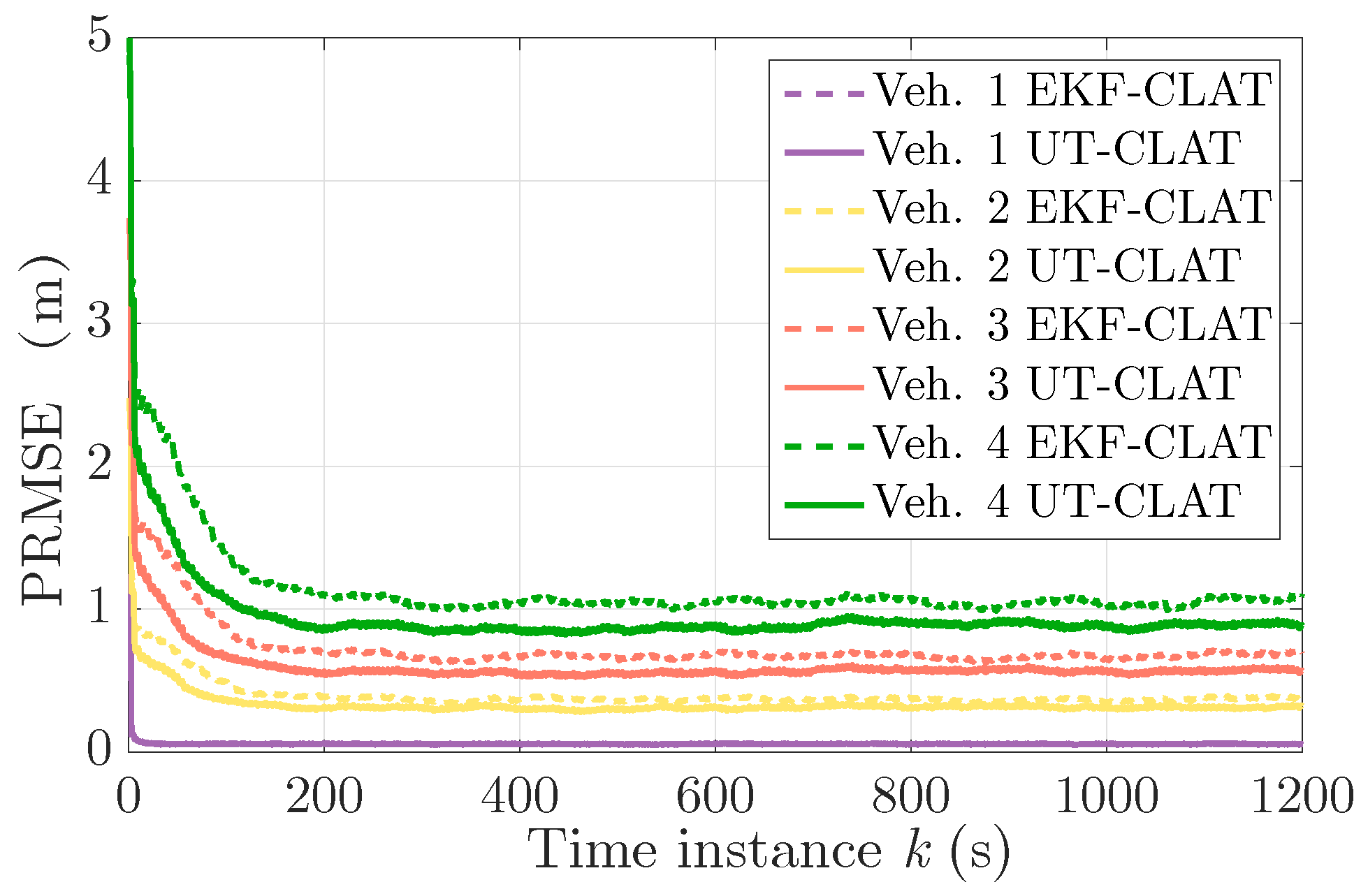
9] to the CLAT scenario. In
Figure 7, the averaged PRMSEs of the collaborative localization results of 1000 Monte Carlo simulations are plotted using both the UT-CLAT and EKF-CLAT methods.
As observed in
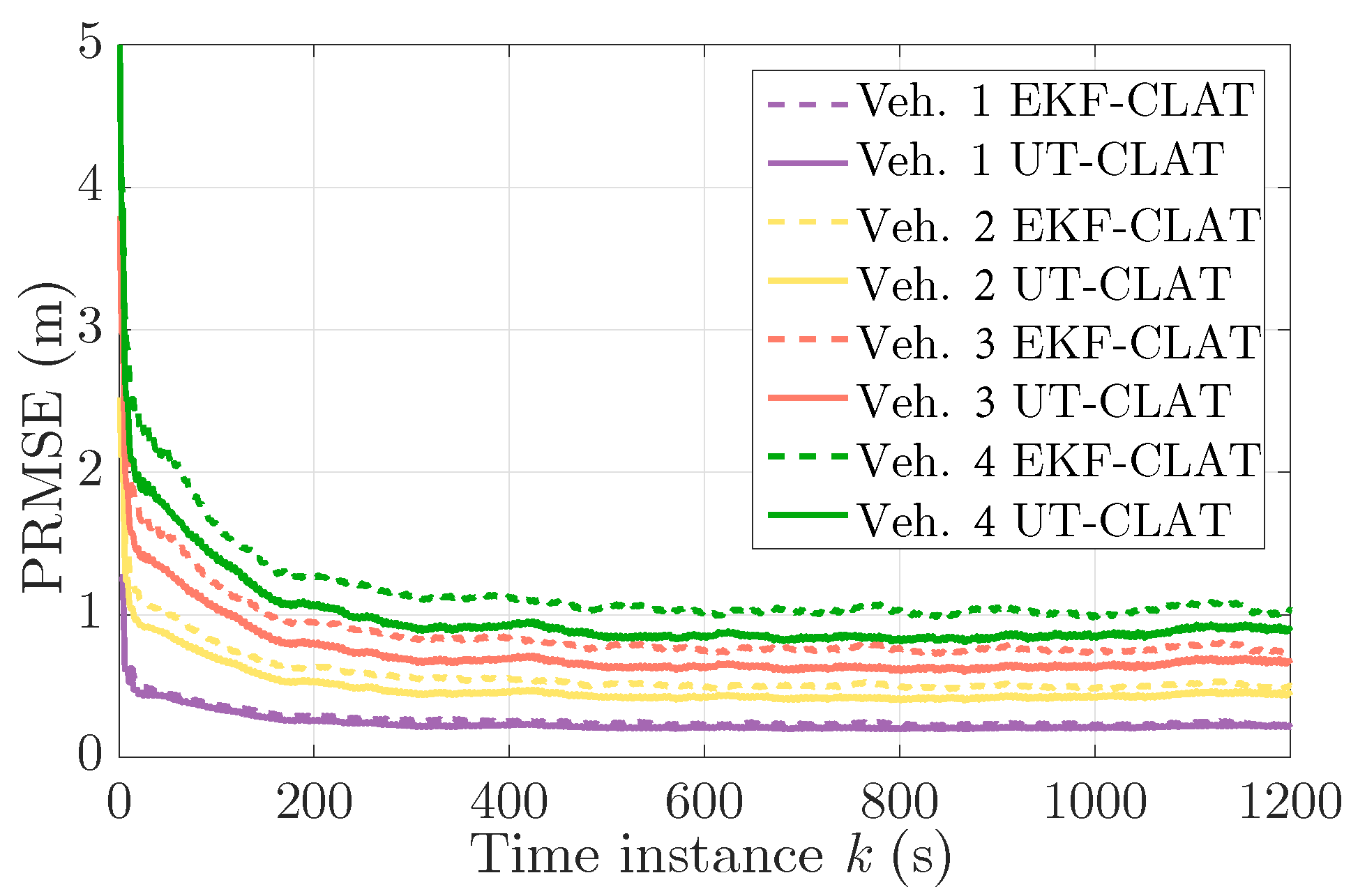
Figure 7, both methods can realize stable self-localization in around 200 time instances. In general, the UT-CLAT method is able to achieve more accurate self-localization results. In
Figure 8, the averaged PRMSEs of the target tracking results of different robots are plotted. Similar to the CL result in
Figure 7, the UT-CLAT is able to realize stable target tracking, and it outperforms the EKF-CLAT method for each robot.