Diagnosing Various Severity Levels of Congestive Heart Failure Based on Long-Term HRV Signal
Abstract
1. Introduction
2. Materials
2.1. Data Collection
2.2. Data Preprocessing
3. Methods
3.1. Feature Extraction
3.1.1. Linear Feature
3.1.2. Non-Linear HRV Features
3.2. Feature Selection
3.3. Classification
4. Results
4.1. The Setting of Feature Parameters
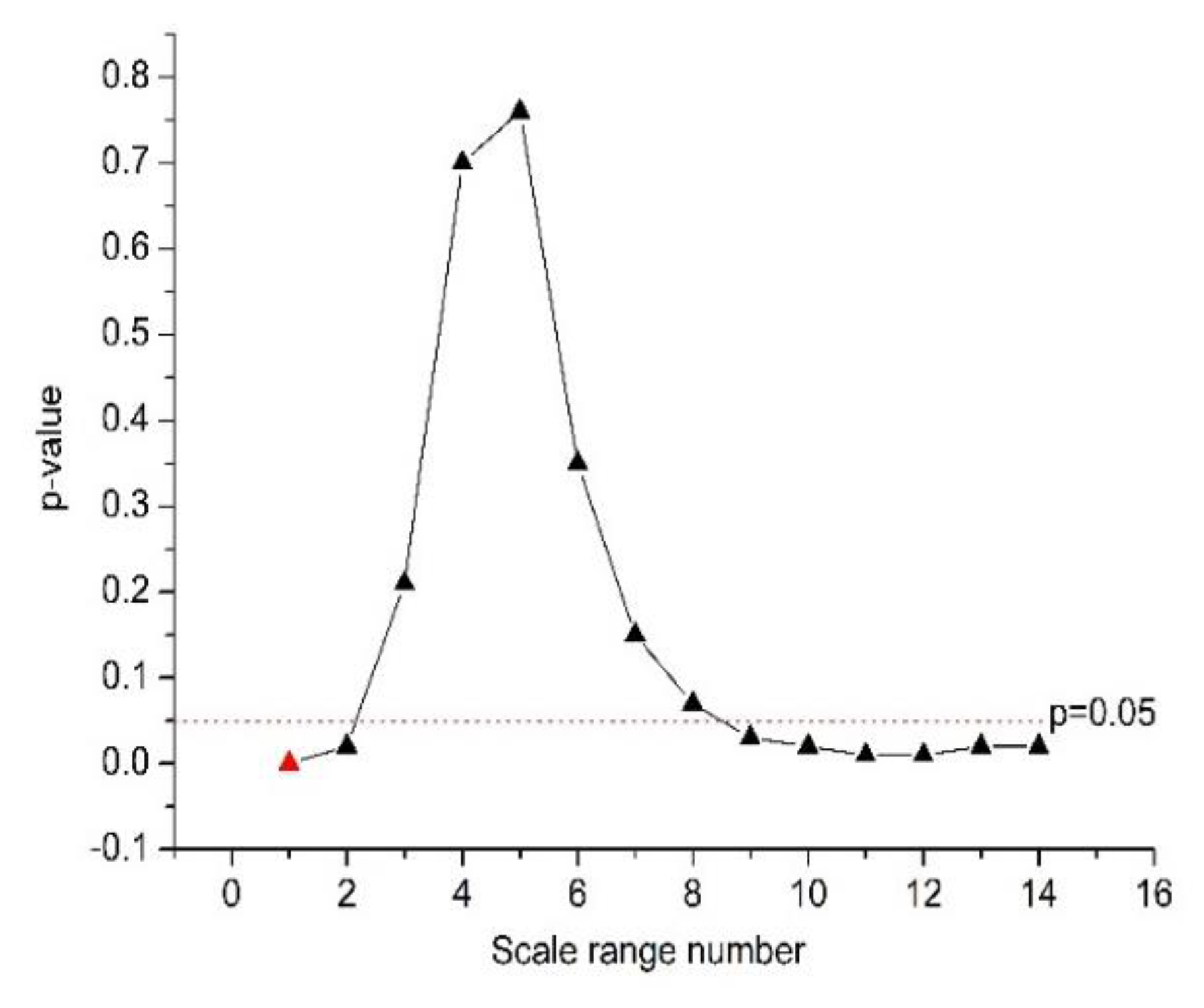
- The nonlinear feature α1 was extracted based on the DFA algorithm, and the small scale n ranges were from four to 16. Different ranges of the large scale n () show very different quantification power for HRV signals. In order to find an optimal scale range for large scale n, we analyzed the statistical difference of the feature α2 between the normal and CHF groups. The span of the scale range is 48, and the length of the sliding step is four.
- 2.
- Different parameters (m and r) of sample entropy (SampEn) and fuzzy measure entropy (FuzzyMEn) also lead to different quantification power of HRV signals. In order to find the best combinations of parameters, the parameter m changed from one to three with a step of one, and r changed from 0.10 to 0.20 with a step of 0.05. For the normal and CHF groups, Table 6 gives the statistical Kolmogorov-Smirnov (KS) test results of SampEn and FuzzyMEn with a different combination of parameters. For CHF diseases with different severity levels, Table 7 gives the statistical F-test results of SampEn and FuzzyMEn with different combinations of parameters.
4.2. Validation
4.2.1. Model A
4.2.2. Model B
5. Discussion
5.1. Comparison of Similar Work
5.2. Limitations of This Study
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Flavell, C.; Stevenson, L.W. Take heart with heart failure. Circulation 2001, 104, 89–91. [Google Scholar] [CrossRef][Green Version]
- Floras, J.S. Sympathetic nervous system activation in human heart failure: clinical implications of an updated model. J. Am. Coll. Cardiol. 2009, 54, 375–385. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, P.J. Vagal stimulation for heart diseases: from animals to men. - An example of translational cardiology. Jpn. Circ. J. 2011, 75, 20–27. [Google Scholar] [CrossRef]
- Kishi, T. Heart failure as an autonomic nervous system dysfunction. J. Cardiol. 2012, 59, 117–122. [Google Scholar] [CrossRef] [PubMed]
- Melillo, P.; De, L.N.; Bracale, M.; Pecchia, L. Classification tree for risk assessment in patients suffering from congestive heart failure via long-term heart rate variability. IEEE J. Biomed. Health Inform. 2013, 17, 727–733. [Google Scholar] [CrossRef]
- Akselrod, S.; Gordon, D.; Madwed, J.B.; Snidman, N.C.; Shannon, D.C.; Cohen, R.J. Hemodynamic regulation: investigation by spectral analysis. Am. J. Physiol. 1985, 249, 867–875. [Google Scholar] [CrossRef] [PubMed]
- Malik, M.; Bigger, J.T.; Camm, A.J.; Kleiger, R.E.; Malliani, A.; Moss, A.J.; Schwartz, P.J. Heart rate variability Standards of measurement, physiological interpretation, and clinical use. Ann. Noninvas. Electrocardiol. 1996, 93, 1043–1065. [Google Scholar] [CrossRef]
- Montano, N.; Ruscone, T.G.; Porta, A.; Lombardi, F.; Pagani, M.; Malliani, A. Power spectrum analysis of heart rate variability to assess the changes in sympathovagal balance during graded orthostatic tilt. Circulation 1994, 90, 1826–1831. [Google Scholar] [CrossRef]
- Yang, F.; Liao, W. Modeling and decomposition of HRV signals with wavelet transforms. IEEE Eng. Med. Biol. Mag. 1997, 16, 17–22. [Google Scholar] [CrossRef]
- Ivanov, P.C.; Zhi, C.; Hu, K.; Stanley, H.E. Multiscale aspects of cardiac control. Physica A 2004, 344, 685–704. [Google Scholar] [CrossRef][Green Version]
- Ivanov, P.C.; Amaral, L.A.; Goldberger, A.L.; Havlin, S.; Rosenblum, M.G.; Struzik, Z.R.; Stanley, H.E. Multifractality in human heartbeat dynamics. Nature 1999, 399, 461–465. [Google Scholar] [CrossRef]
- Peng, C.K.; Havlin, S.; Hausdorff, J.M.; Mietus, J.E.; Stanley, H.E.; Goldberger, A.L. Fractal mechanisms and heart rate dynamics *: Long-range correlations and their breakdown with disease. J. Electrocardiol. 1995, 28, 59. [Google Scholar] [CrossRef]
- Huikuri, H.V.; Makikallio, T.H.; Peng, C.; Goldberger, A.L.; Hintze, U.; Moller, M. Fractal Correlation Properties of R-R Interval Dynamics and Mortality in Patients with Depressed Left Ventricular Function After an Acute Myocardial Infarction. Circulation 2000, 101, 47–53. [Google Scholar] [CrossRef]
- Lake, D.E.; Richman, J.S.; Griffin, M.P.; Moorman, J.R. Sample entropy analysis of neonatal heart rate variability. Am J. Physiol. Regul. Integr. Comp. Physiol. 2002, 283, R789. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, L. Using Fuzzy Measure Entropy to improve the stability of traditional entropy measures. In Proceedings of the Computing in Cardiology, Hangzhou, China, 18–21 September 2011; pp. 681–684. [Google Scholar]
- Zhao, L.; Wei, S.; Zhang, C.; Zhang, Y.; Liu, C. Determination of Sample Entropy and Fuzzy Measure Entropy Parameters for Distinguishing Congestive Heart Failure from Normal Sinus Rhythm Subjects. Entropy 2015, 17, 6270–6288. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, S.; Zhang, S.; Zhang, Y.; Zhao, L.; Liu, C.; Murray, A. Comparison of time-domain, frequency-domain and non-linear analysis for distinguishing congestive heart failure patients from normal sinus rhythm subjects. Biomed. Signal Process. Control 2018, 42, 30–36. [Google Scholar] [CrossRef]
- Rn, M.A.W.; Stevenson, W.G.; Moser, D.K.; Trelease, R.B.; Harper, R.M. Patterns of beat-to-beat heart rate variability in advanced heart failure. Am. Heart J. 1992, 123, 704. [Google Scholar]
- Marciano, F.; Migaux, M.L.; Acanfora, D.; Furgi, G.; Rengo, F. Quantification of Poincare’ maps for the evaluation of heart rate variability. In Proceedings of the Computers in Cardiology, Bethesda, MD, USA, 25–28 September 1994; pp. 577–580. [Google Scholar]
- Brennan, M.; Palaniswami, M.; Kamen, P. Do existing measures of Poincaré plot geometry reflect nonlinear features of heart rate variability? IEEE Trans. Biomed. Eng. 2001, 48, 1342–1347. [Google Scholar] [CrossRef]
- Asyali, M.H. Discrimination power of long-term heart rate variability measures. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society, Cancun, Mexico, 17–21 September 2003; pp. 200–203. [Google Scholar]
- İşler, Y.; Kuntalp, M. Combining classical HRV indices with wavelet entropy measures improves to performance in diagnosing congestive heart failure. Comput. Biol. Med. 2007, 37, 1502–1510. [Google Scholar] [CrossRef]
- Yu, S.N.; Lee, M.Y. Bispectral analysis and genetic algorithm for congestive heart failure recognition based on heart rate variability. Comput. Biol. Med. 2012, 42, 816–825. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Oh, S.L.; Muhammad, A.; Koh, J.E.W.; Tan, J.H.; Chua, C.K.; Chua, K.P.; Tan, R.S. Application of empirical mode decomposition (EMD) for automated identification of congestive heart failure using heart rate signals. Neural Comput. Appl. 2017, 28, 3073–3094. [Google Scholar] [CrossRef]
- Mahajan, R.; Viangteeravat, T.; Akbilgic, O. Improved detection of congestive heart failure via probabilistic symbolic pattern recognition and heart rate variability metrics. Int. J. Med. Inform. 2017, 108, 55–63. [Google Scholar] [CrossRef]
- Shahbazi, F.; Asl, B.M. Generalized discriminant analysis for congestive heart failure risk assessment based on long-term heart rate variability. Comput. Methods Programs Biomed. 2015, 122, 191–198. [Google Scholar] [CrossRef]
- Chen, W.; Zheng, L.; Li, K.; Wang, Q.; Liu, G.; Jiang, Q. A Novel and Effective Method for Congestive Heart Failure Detection and Quantification Using Dynamic Heart Rate Variability Measurement. PLoS ONE 2016, 11, e0165304. [Google Scholar] [CrossRef]
- Li, D.; Li, X.; Zhao, J.; Bai, X. Automatic staging model of heart failure based on deep learning. Biomed. Signal Process. Control 2019, 52, 77–83. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, 215–220. [Google Scholar] [CrossRef] [PubMed]
- Facc, D.S.B.; Facc, W.S.C.; Monrad, E.S.; Smith, H.S.; Wright, R.F.; Lanoue, A.; Gauthier, D.F.; Ransil, B.J.; Grossman, W.; Braunwald, E. Survival of patients with severe congestive heart failure treated with oral milrinone. J. Am. Coll. Cardiol. 1986, 7, 661–670. [Google Scholar]
- Tarvainen, M.P.; Rantaaho, P.O.; Karjalainen, P.A. An advanced detrending method with application to HRV analysis. IEEE Trans. Biomed. Eng. 2002, 49, 172–175. [Google Scholar] [CrossRef]
- Narin, A.; Isler, Y.; Ozer, M. Investigating the performance improvement of HRV Indices in CHF using feature selection methods based on backward elimination and statistical significance. Comput. Biol. Med. 2014, 45, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Laguna, P.; Moody, G.B.; Mark, R.G. Power spectral density of unevenly sampled data by least-square analysis: performance and application to heart rate signals. IEEE Trans. Biomed. Eng. 1998, 45, 698–715. [Google Scholar] [CrossRef]
- Clifford, G.D.; Lionel, T. Quantifying errors in spectral estimates of HRV due to beat replacement and resampling. IEEE Trans. Biomed. Eng. 2005, 52, 630–638. [Google Scholar] [CrossRef] [PubMed]
- Stanley, H.E.; Ahlers, G. Introduction to Phase Transitions and Critical Phenomena. Phys. Today 1973, 26, 71–72. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, Y.; Ye, P.; Zhang, J.; Zou, J. Detecting driving stress in physiological signals based on multimodal feature analysis and kernel classifiers. Expert Syst. Appl. 2017, 85, 279–291. [Google Scholar] [CrossRef]
- Biagetti, G.; Crippa, P.; Falaschetti, L.; Orcioni, S.; Turchetti, C. Multivariate Direction Scoring for Dimensionality Reduction in Classification Problems. In Intelligent Decision Technologies; Czarnowski, I., Caballero, A., Howlett, R., Jain, L., Eds.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Kudo, M.; Somol, P.; Pudil, P.; Shimbo, M.; Sklansky, J. Comparison of Classifier-Specific Feature Selection Algorithms. In Advances in Pattern Recognition; Ferri, F.J., Iñesta, J.M., Amin, A., Pudil, P., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1876, pp. 677–686. [Google Scholar]
- Schenk, J.; Kaiser, M.; Rigoll, G. Selecting Features in On-Line Handwritten Whiteboard Note Recognition: SFS or SFFS? In Proceedings of the International Conference on Document Analysis and Recognition, Barcelona, Spain, 26–29 July 2009; pp. 1251–1254. [Google Scholar]
- Pecchia, L.; Melillo, P.; Sansone, M.; Bracale, M. Discrimination Power of Short-Term Heart Rate Variability Measures for CHF Assessment. IEEE Trans. Inform. Technol. Biomed. 2011, 15, 40–46. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Song, D.; Zhang, P.; Zhang, Y.; Hou, Y.; Hu, B. Exploring EEG Features in Cross-Subject Emotion Recognition. Front. Neurosci. 2018, 12, 162. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Zhao, L.; Zhang, Y.; Liu, C.; Zhang, L.; Zhang, L.; Li, Z.; Wang, B.; Ng, E.Y.K. Combining Convolutional Neural Network and Distance Distribution Matrix for Identification of Congestive Heart Failure. IEEE Access 2018, 6, 39734–39744. [Google Scholar] [CrossRef]
- Guidi, G.; Pettenati, M.C.; Melillo, P.; Iadanza, E. A Machine Learning System to Improve Heart Failure Patient Assistance. IEEE J. Biomed. Health Inform. 2014, 18, 1750–1756. [Google Scholar] [CrossRef]
- Ali, A.; Shamsuddin, S.M.; Ralescu, A.L. Classification with class imbalance problem: a review. Int. J. Adv. Soft Comput. Appl. 2013, 5, 176–204. [Google Scholar]
- Zou, Q.; Xie, S.; Lin, Z.; Wu, M.; Ju, Y. Finding the Best Classification Threshold in Imbalanced Classification. Big Data Res. 2016, 5, 2–8. [Google Scholar] [CrossRef]

| Group | Database | DL | NR | Age |
|---|---|---|---|---|
| Normal | Nrsdb | Norm | 18 | 34 ± 8 |
| Nrs2db | Norm | 54 | 61 ± 11 | |
| CHF | Chfdb | NYHA III-IV | 15 | 56 ± 11 |
| Chf2db | NYHA I | 4 | 55 ± 11 | |
| NYHA II | 8 | |||
| NYHA III | 17 |
| Model | Level | Database | CL | NR | NS | Samples |
|---|---|---|---|---|---|---|
| Model A | 2-class | Nrsdb, Nrs2db | Norm | 72 | 72 × 1 | 113 |
| Chfdb, Chf2db | CHF | 41 | 41 × 1 | |||
| Model B | 4-class | Chf2db | CHF I | 4 | 4 × 1 | 41 |
| CHF II | 7 | 7 × 1 | ||||
| CHF III | 16 | 16 × 1 | ||||
| Chfdb | CHF IV | 14 | 14 × 1 |
| Variable | Unit | Description |
|---|---|---|
| PNN10 | % | Percentage of differences between adjacent NN intervals that are longer than 10 ms. |
| PNN20 | % | Percentage of differences between adjacent NN intervals that are longer than 20 ms. |
| PNN30 | % | Percentage of differences between adjacent NN intervals that are longer than 30 ms. |
| pNN50 | % | Percentage of differences between adjacent NN intervals that are longer than 50 ms. |
| Mean | ms | Mean of all NN intervals. |
| SDNN | ms | Standard deviation of all NN intervals. |
| RMSSD | ms | Square root of the mean of the sum of the square of differences between adjacent NN intervals. |
| Triangular Index | The number of all NN divided by the height of histogram of all NN Intervals. The interval of the histogram is set to 1/128 ms. | |
| TOTPWR | ms2 | The power between 0 and 0.4 Hz. |
| PVLF | ms2 | The power between 0 and 0.04 Hz, reflecting the activity of sympathetic. |
| PLF | ms2 | The power between 0.04 and 0.15 Hz, reflecting dual regulation of sympathetic and parasympathetic nerves. |
| PHF | ms2 | The power between 0.15 and 0.4 Hz, reflecting the activity of parasympathetic. |
| RATIO1 | PLF/PHF, reflecting the balance between sympathetic and parasympathetic nerves. | |
| RATIO2 | PHF/PLF, reflecting the balance between sympathetic and parasympathetic nerves. | |
| NPLF | Normalized power of LF, PLF/ (PLF + PHF). | |
| NPHF | Normalized power of HF, PHF/ (PLF + PHF). |
| Scales | 16–64 | 20–68 | 24–72 | 28–76 | 32–80 | 36–84 | 40–88 |
| Norm | 1.05 ± 0.14 | 1.03 ± 0.13 | 1.01 ± 0.13 | 1.00 ± 0.12 | 1.00 ± 0.12 | 1.00 ± 0.12 | 0.99 ± 0.12 |
| CHF | 0.89 ± 0.33 | 0.93 ± 0.32 | 0.96 ± 0.31 | 0.98 ± 0.30 | 1.00 ± 0.30 | 1.03 ± 0.29 | 1.04 ± 0.29 |
| p-value | 4 × 10−4 * | 0.02 * | 0.21 | 0.70 | 0.76 | 0.35 | 0.15 |
| Scales | 44–92 | 48–96 | 52–100 | 56–104 | 60–108 | 64–112 | 68–116 |
| Norm | 0.98 ± 0.12 | 0.98 ± 0.12 | 0.98 ± 0.12 | 0.98 ± 0.12 | 0.98 ± 0.12 | 0.98 ± 0.12 | 0.98 ± 0.12 |
| CHF | 1.05 ± 0.28 | 1.06 ± 0.28 | 1.07 ± 0.28 | 1.07 ± 0.27 | 1.07± 0.27 | 1.07± 0.27 | 1.06 ± 0.26 |
| p-value | 0.07 | 0.03 * | 0.02 * | 0.01 ** | 0.01 ** | 0.02 * | 0.02 * |
| Scales | 16–64 | 20–68 | 24–72 | 28–76 | 32–80 | 36–84 | 40–88 |
| CHF I | 1.03 ± 0.01 | 1.01 ± 0.01 | 1.00 ± 0.01 | 0.99 ± 0.01 | 0.98 ± 0.16 | 0.96 ± 0.02 | 0.94 ± 0.02 |
| CHF II | 0.93 ± 0.07 | 0.96 ± 0.06 | 1.00 ± 0.04 | 1.03 ± 0.03 | 1.05 ± 0.03 | 1.05 ± 0.03 | 1.08 ± 0.38 |
| CHF III | 0.97 ± 0.05 | 1.00 ± 0.05 | 1.02 ± 0.05 | 1.03 ± 0.06 | 1.04 ± 0.06 | 1.05 ± 0.07 | 1.05 ± 0.08 |
| CHF IV | 0.83 ± 0.08 | 0.89 ± 0.08 | 0.93 ± 0.08 | 0.97 ± 0.08 | 1.00 ± 0.09 | 1.02 ± 0.09 | 1.04 ± 0.09 |
| p-value | 0.34 | 0.55 | 0.73 | 0.87 | 0.91 | 0.92 | 0.85 |
| Scales | 44–92 | 48–96 | 52–100 | 56–104 | 60–108 | 64–112 | 68–116 |
| CHF I | 0.91 ± 0.02 | 0.92 ± 0.02 | 0.90 ± 0.02 | 0.88 ± 0.02 | 0.87 ± 0.03 | 0.96 ± 0.03 | 0.93 ± 0.06 |
| CHF II | 1.09 ± 0.04 | 1.10 ± 0.04 | 1.09 ± 0.05 | 1.08 ± 0.05 | 1.07 ± 0.05 | 1.05 ± 0.04 | 1.03 ± 0.04 |
| CHF III | 1.05 ± 0.08 | 1.05 ± 0.09 | 1.04 ± 0.93 | 1.03 ± 0.09 | 1.02 ± 0.09 | 1.01 ± 0.09 | 0.99 ± 0.09 |
| CHF IV | 1.07 ± 0.09 | 1.07 ± 0.09 | 1.08 ± 0.09 | 1.08 ± 0.08 | 1.08 ± 0.08 | 1.08 ± 0.09 | 1.07 ± 0.07 |
| p-value | 0.79 | 0.74 | 0.67 | 0.60 | 0.58 | 0.54 | 0.46 |
| Tolerance Threshold | Group | Embedding Dimension SampEn | Embedding Dimension FuzzyMEn | ||||
|---|---|---|---|---|---|---|---|
| m = 1 | m = 2 | m = 3 | m = 1 | m = 2 | m = 3 | ||
| r= 0.10 | Norm | 1.58 ± 0.44 | 1.43 ± 0.46 | 1.34 ± 0.46 | 1.03 ± 0.27 | 1.34 ± 0.46 | 0.92 ± 0.27 |
| CHF | 1.61 ± 0.42 | 1.43 ± 0.44 | 1.43 ± 0.44 | 1.28 ± 0.37 | 1.43 ± 0.44 | 0.97 ± 0.28 | |
| p-value | 0.95 | 1.00 | 1.00 | 6 × 10−5 ** | 0.12 | 0.37 | |
| r= 0.15 | Norm | 1.09 ± 0.33 | 0.96 ± 0.33 | 0.89 ± 0.33 | 0.71 ± 0.23 | 0.87 ± 0.27 | 0.67 ± 0.23 |
| CHF | 1.35 ± 0.40 | 1.18 ± 0.41 | 1.09 ± 0.41 | 0.99± 0.36 | 1.02 ± 0.34 | 0.74 ± 0.25 | |
| p-value | 1 × 10−3 ** | 3 × 10−3 ** | 0.02 * | 3.8 × 10−6 ** | 0.01 ** | 0.15 | |
| r= 0.20 | Norm | 0.88 ± 0.28 | 0.76 ± 0.30 | 0.70 ± 0.30 | 0.53 ± 0.20 | 0.67 ± 0.23 | 0.52 ± 0.20 |
| CHF | 1.06 ± 0.37 | 0.90 ± 0.37 | 0.82 ± 0.36 | 0.79 ± 0.34 | 0.83 ± 0.32 | 0.59 ± 0.22 | |
| p-value | 0.06 | 0.23 | 0.35 | 9 × 10−7 ** | 3 × 10−3 ** | 0.10 | |
| Tolerance Threshold | Group | Embedding Dimension SampEn | Embedding Dimension FuzzyMEn | ||||
|---|---|---|---|---|---|---|---|
| m = 1 | m = 2 | m = 3 | m = 1 | m = 2 | m = 3 | ||
| r= 0.10 | CHF I | 1.12 ± 0.11 | 0.96 ± 0.10 | 0.85 ± 0.08 | 0.81 ±0.04 | 0.96 ± 0.06 | 0.73 ± 0.05 |
| CHF II | 1.52 ± 0.08 | 1.37 ± 0.12 | 1.31 ± 0.13 | 1.26 ± 0.03 | 1.31 ± 0.06 | 0.99 ± 0.05 | |
| CHF III | 1.69 ± 0.10 | 1.55 ± 0.13 | 1.47 ± 0.14 | 1.27 ± 0.11 | 1.36 ± 0.11 | 1.04 ± 0.08 | |
| CHF IV | 1.94 ± 0.15 | 1.78 ± 0.16 | 1.68 ± 0.16 | 1.38 ± 0.20 | 1.48 ± 0.15 | 1.08 ± 0.07 | |
| p-value | 8 × 10−4 ** | 2 × 10−3 ** | 2 × 10−3 ** | 0.05 * | 0.12 | 0.13 | |
| r= 0.15 | CHF I | 0.96 ± 0.05 | 0.80 ± 0.05 | 0.70 ± 0.04 | 0.87 ± 0.02 | 0.67 ± 0.05 | 0.51 ± 0.03 |
| CHF II | 1.48 ± 0.06 | 1.33 ± 0.08 | 1.27 ± 0.10 | 1.02 ± 0.07 | 1.07 ± 0.04 | 0.82 ± 0.05 | |
| CHF III | 1.41 ± 0.19 | 1.27 ± 0.20 | 1.19 ± 0.18 | 0.99 ± 0.13 | 1.10 ± 0.14 | 0.81 ± 0.07 | |
| CHF IV | 1.59 ± 0.21 | 1.39 ± 0.25 | 1.30 ± 0.23 | 1.04 ± 0.18 | 1.15 ± 0.15 | 0.82 ± 0.06 | |
| p-value | 0.06 | 0.13 | 0.10 | 0.10 | 0.09 | 0.13 | |
| r= 0.20 | CHF I | 0.68 ± 0.04 | 0.56 ± 0.04 | 0.48 ± 0.03 | 0.38 ± 0.02 | 0.50 ± 0.03 | 0.38 ± 0.03 |
| CHF II | 1.19 ± 0.10 | 1.04 ± 0.10 | 0.98 ± 0.10 | 0.83 ± 0.08 | 0.93 ± 0.08 | 0.65 ± 0.03 | |
| CHF III | 1.18± 0.12 | 1.04 ± 0.11 | 0.97 ± 0.11 | 0.79 ± 0.12 | 0.91 ± 0.12 | 0.65 ± 0.06 | |
| CHF IV | 1.20 ± 0.23 | 1.07 ± 0.23 | 0.98 ± 0.21 | 0.82 ± 0.16 | 0.92 ± 0.13 | 0.66 ± 0.05 | |
| p-value | 0.11 | 0.13 | 0.11 | 0.14 | 0.13 | 0.15 | |
| Classifier | NF | Best Features | TN | FP | TP | FN | Prec (%) | Sens (%) | Spec (%) | Acc (%) | AUC |
|---|---|---|---|---|---|---|---|---|---|---|---|
| SVM | 5 | TOTPWR, PLF/PHF, SD1, α2, SampEn | 70 | 2 | 40 | 1 | 95.24 | 97.56 | 97.22 | 97.35 | 0.963 |
| LDA | 4 | PNN50, PLF/(PLF+PHF), ∆h, SD1/SD2 | 70 | 2 | 35 | 6 | 94.60 | 85.37 | 97.22 | 92.92 | 0.907 |
| DT | 7 | PNN30, RMSSD, Triangular Index, PHF, PLF/PHF, Mean of CD4, FuzzyMEn | 70 | 2 | 39 | 2 | 95.12 | 95.12 | 97.22 | 96.46 | 0.952 |
| NB | 5 | PNN50, SDNN, PLF/(PLF+PHF), Std of CD2, FuzzyMEn | 69 | 3 | 37 | 4 | 92.50 | 90.24 | 95.83 | 93.80 | 0.922 |
| 1-NN | 6 | PVLF, PHF/PLF, PLF/(PLF+PHF), SD2, SD1/SD2, α2 | 71 | 1 | 39 | 2 | 97.50 | 95.12 | 98.61 | 97.35 | 0.959 |
| 3-NN | 5 | TOTPWR, Mean of CD4, SD1/SD2, α2, SampEn | 71 | 1 | 38 | 3 | 97.44 | 92.68 | 98.61 | 96.46 | 0.948 |
| 5-NN | 4 | PVLF, PLF/(PLF+PHF), SD2, FuzzyMEn | 69 | 3 | 40 | 1 | 93.02 | 97.56 | 95.83 | 96.46 | 0.957 |
| 7-NN | 4 | Std of CA4, Mean of CD4, Std of CD2, SampEn | 69 | 3 | 37 | 4 | 92.50 | 90.24 | 95.83 | 93.80 | 0.922 |
| Classifier | NF | Best Features | Acc (%) |
|---|---|---|---|
| SVM | 4 | PNN50, Mean, RATIO1, SampEn | 78.05 |
| LDA | 3 | PNN20, PNN50, NPHF | 70.73 |
| DT | 3 | PNN50, FuzzyMEn, SD2 | 82.93 |
| NB | 4 | PNN20, SDNN, ∆h, SD1 | 70.73 |
| 1-NN | 4 | PNN20, PNN50, TOTPWR, FuzzyMEn | 87.80 |
| 3-NN | 4 | PNN50, SDNN, TOTPWR, SD1/SD2 | 73.17 |
| 5-NN | 3 | PNN20, RMSSD, PVLF | 78.05 |
| Group | Predicted Classes | Performance Evaluation | ||||||
|---|---|---|---|---|---|---|---|---|
| CHF I | CHF II | CHF III | CHF IV | Prec (%) | Sens (%) | Spec (%) | ||
| True Classes | CHF I | 3 | 0 | 1 | 0 | 75.00 | 75.00 | 97.30 |
| CHF II | 1 | 4 | 2 | 0 | 80.00 | 57.14 | 97.06 | |
| CHF III | 0 | 1 | 15 | 0 | 83.33 | 93.75 | 88.00 | |
| CHF IV | 0 | 0 | 0 | 14 | 100 | 100 | 100 | |
| Date | Study | CL | Dataset | FS | NF | Classifier | Acc (%) |
|---|---|---|---|---|---|---|---|
| 2003 [21] | Asyali | 2 | 74 × 1 × 24 h | -- | 9 | Bayesian | 93.24 |
| 2007 [22] | İşler | 2 | 83 × 1 × 5 min | GA | ≥8 | KNN | 96.39 |
| 2011 [40] | Leandro | 2 | 83 × 1 × 24 h | ESM | 6 | DT | 96.40 |
| 2012 [23] | Yu | 2 | 83 × 1 × 68 min | GA | 16 | SVM | 98.79 |
| 2013 [4] * | Melillo | 2 | 44 × 1 × 24 h | ESM | 7 | DT | 85.40 |
| 2014 [32] | Narin | 2 | 83 × 1 × 5 min | SBS | 27 | SVM | 91.56 |
| 2014 [43] * | Guidi | 3 | Non-uniform | -- | 5 | CART | 81.80% |
| 2015 [26] * | Shahbazi | 2 | 44 × 1 × 24 h | GDA | 1 | KNN | 100 |
| 2016 [24] | Acharya | 2 | Non-uniform | RM | 22 | SVM | 97.60 |
| 2016 [27] * | Chen | 4 | 116 × 1 × 24 h | SBS | 180 | DT-SVM | 96.61 |
| 2017 [25] | Mahajan | 2 | 107 × 1 × 24 h | RM | 10 | Ensemble | 98.10 |
| 2018 [42] | Li | 2 | Non-uniform | -- | 1 | CNN | 81.85 |
| 2019 [28] * | Li | 4 | Non-uniform | -- | 20 | CNN | 97.60 |
| Our work | 2 | 113 × 1 × 8 h | SFS | 5 | SVM | 97.35 | |
| Our work | 4 | 41 × 1 × 8 h | SFS | 4 | KNN | 87.80 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, Z.; Chen, C.; Zhang, R.; Liu, G.; Wen, W. Diagnosing Various Severity Levels of Congestive Heart Failure Based on Long-Term HRV Signal. Appl. Sci. 2019, 9, 2544. https://doi.org/10.3390/app9122544
Hua Z, Chen C, Zhang R, Liu G, Wen W. Diagnosing Various Severity Levels of Congestive Heart Failure Based on Long-Term HRV Signal. Applied Sciences. 2019; 9(12):2544. https://doi.org/10.3390/app9122544
Chicago/Turabian StyleHua, Zhengchun, Chen Chen, Ruiqi Zhang, Guangyuan Liu, and Wanhui Wen. 2019. "Diagnosing Various Severity Levels of Congestive Heart Failure Based on Long-Term HRV Signal" Applied Sciences 9, no. 12: 2544. https://doi.org/10.3390/app9122544
APA StyleHua, Z., Chen, C., Zhang, R., Liu, G., & Wen, W. (2019). Diagnosing Various Severity Levels of Congestive Heart Failure Based on Long-Term HRV Signal. Applied Sciences, 9(12), 2544. https://doi.org/10.3390/app9122544





