1. Introduction
Speech-related services are pervasively available on mobile devices such as smartphones or tablets. However, reverberant and noisy environments, where these devices are frequently used, often degrade speech signal quality and/or intelligibility [
1]. Many current devices include several microphones, so that multi-channel speech processing techniques can be applied to reduce the distortions, which improves the noise reduction performance compared to single-channel approaches. This is our research focus.
The most common multi-channel speech processing technique is beamforming [
2], which applies spatial filtering to the noisy speech signals captured by several microphones. One of these beamformers is the well-known Minimum Variance Distortionless Response (MVDR) beamformer [
3], which has the advantage of being able to reduce the noise power without introducing speech distortion. The performance of MVDR depends on an accurate estimation of the noise spatial characteristics and the acoustic transfer function (ATF) between the target speaker and the microphones. For the estimation of the noise spatial statistics, methods based on multi-channel speech presence probability (SPP) [
4,
5] are commonly used when there is no prior knowledge of the signal propagation or the spatial structure of the noise. These techniques update the noise information when speech absence is detected, which allows for the tracking of time-varying noise signals.
However, the estimation of ATFs is a more challenging task, as these depend on the speaker’s location, room acoustics and microphone responses. One possible solution is based on the estimation of the beamformer weights for a certain reference microphone. As a result, the problem becomes that of estimating a relative transfer function (RTF) between the reference microphone and the rest of microphones [
6]. The most common RTF estimators are based on sub-space search, using estimates of the noisy speech and the noise spatial correlations. This category includes techniques such as covariance subtraction [
7], covariance whitening [
8,
9] and eigenvalue decomposition [
10,
11]. A weighted least-squares RTF estimator was proposed in Reference [
12] but it is unfeasible for real-time applications. Other approaches based on online expectation-maximization [
13,
14] have been analyzed to jointly estimate the RTF and the clean speech and noise statistics under the assumption of a spatially-white noise field. Recently, we proposed an extended Kalman filter (eKF) framework for the estimation of the RTF between two microphones [
15] and evaluated its performance on a dual-microphone smartphone under different noisy and reverberant environments. We showed that this technique obtains better estimation accuracy than the sub-space-based estimators while allowing for the tracking of the RTF variability, especially in highly reverberant scenarios.
Despite beamforming algorithms are often used in multi-microphone devices, their performance is quite limited on dual-microphone smartphones mainly due to the reduced number of microphones, their particular placement on the device and the short separation between them [
16]. Therefore, alternatives to beamforming are necessary to obtain a good performance in these situations. One possible approach is the use of single-channel filters for the reference microphone using statistical information obtained from the dual-channel signal. For example, the power level difference (PLD) algorithm proposed in Reference [
17] exploits the clean speech power difference between microphones when the smartphone is used in close-talk (CT) conditions (i.e., when the loudspeaker of the smartphone is placed at the ear of the user). An estimate of the single-channel noise statistics is obtained for both microphones and a Wiener filter is calculated from them. In the case of smartphones used in far-talk (FT) conditions (i.e., when the user holds the device at a distance from her/his face), the algorithm proposed in Reference [
18] exploits the spatial properties of the noisy speech and noise signals. This spatial information is used along with a single-channel SPP detector to estimate the noise at the reference channel and the signal-to-noise ratio (SNR), which are needed for the filter design. This proposal was later extended to general multi-channel devices in Reference [
19].
While the techniques mentioned above apply a single-channel filtering at the reference microphone, better performance can be achieved when the filter is designed to operate at the beamformer output, what is known as postfiltering [
1]. Moreover, the multi-channel Wiener filter can be expressed as an MVDR beamformer followed by a single-channel Wiener filter [
6]. Several postfilters based on the Wiener filter have been proposed in the literature [
20,
21,
22], mainly differing in the assumptions made about the noise field. The authors of Reference [
23] also evaluate the use of non-linear postfilters, showing improvements with respect to the linear approaches. The work in Reference [
24] evaluates the performance of a generalized sidelobe canceler (GSC) beamformer along with an SPP estimator and a non-linear postfilter, showing that the SPP information is useful in the postfiltering design. The postfiltering approach has also been studied on dual-microphone scenarios [
25,
26]. For example, in Reference [
27] we extended our eKF-RTF framework with the use of postfilters along with MVDR beamforming and the SPP estimator of Reference [
4] in order to improve noise reduction. These postfilters exploit the SPP and the RTFs previously obtained to estimate the required single-channel statistics. Both linear and non-linear postfilters were evaluated, showing better performance than a standalone MVDR and other state-of-the-art enhancement algorithms intended to be used in smartphones.
In this work we analyze and further extend our dual-microphone speech enhancement eKF-RTF framework presented in References [
15,
27]. This extension is developed in a threefold way. First, we present a more detailed derivation of the eKF-RTF estimator where we improve the estimation of the
a priori RTF statistics without any simplification in the estimation of the covariance matrices. Second, we analyze the
a posteriori SPP estimation and the importance of the
a priori speech absence probability (SAP). Then, we propose a novel SAP estimator suitable for dual-microphone smartphones, which exploits the spatial structure of the noise and the power differences between microphones, showing improvements with respect to the estimator used in our previous work. Third, we take advantage of the better estimates of SPP, RTFs and single-channel statistics to redefine the postfilters described in Reference [
27] and propose new ones. As a result, we end up with a comprehensive dual-microphone speech enhancement system for smartphones that shows a great performance in terms of both speech quality and intelligibility when compared to other state-of-the-art approaches.
The rest of the paper is organized as follows: in
Section 2, an overview of our dual-microphone speech enhancement system is given, presenting the constituent elements of the algorithm. Next, in
Section 3, the eKF-RTF framework is detailed. The estimation of the noise statistics and the SPP along with the new proposals for SAP estimation on smarthphones are developed in
Section 4. In
Section 5, the different postfilters are described and the estimation of the required single-channel statistics is addressed. In
Section 6, the experimental framework and results are presented and discussed, while
Section 7 finally summarizes the conclusions.
2. System Overview
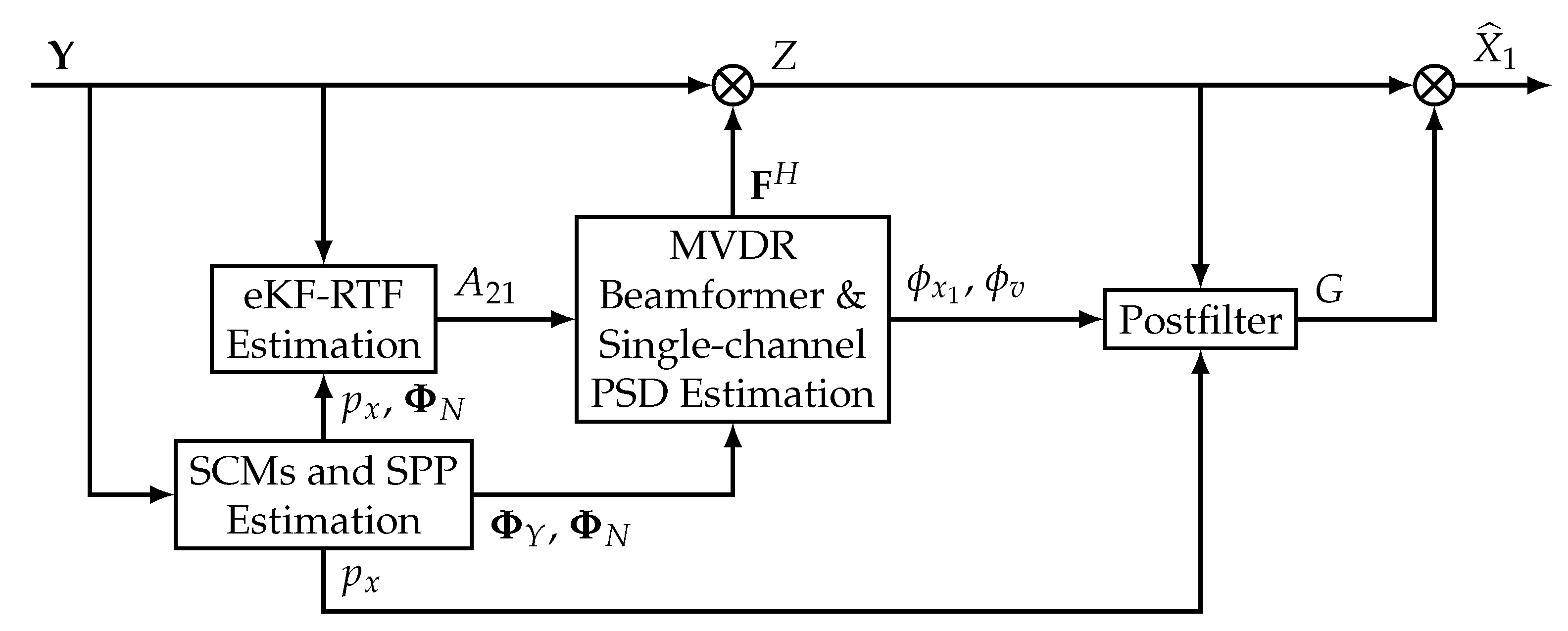
The proposed enhancement system for dual-microphone smartphones is depicted in
Figure 1. The microphones capture the noisy speech signals
, where
m indicates the microphone index (
). We assume an additive noise distortion model which in the short-time Fourier transform (STFT) domain can be expressed as
where
,
and
represent, respectively, noisy speech, clean speech and noise signal STFTs,
t is the frame index and
f the frequency bin. The two channel components can be stacked in a vector,
where
indicates matrix transposition. Similarly, we define vectors
and
. In the following, we will consider that each frequency component can be processed independently from the others, which is commonly referred to as narrowband approximation [
6].
As shown in
Figure 1, the beamforming block requires two previous procedures. First, a speech presence probability (SPP)-based algorithm is employed for the estimation of the noisy speech and noise spatial correlation matrices (SCM),
and
, respectively, and the SPP,
. Then, an extended Kalman filter (eKF)-based estimator obtains the relative transfer function (RTF) between the secondary microphone (
) and the reference microphone (
), defined as
Once the SCM matrices and RTF have been computed, the dual-channel noisy speech vector
is processed using a Minimum Variance Distortionless Response (MVDR) beamformer, which applies spatial filtering yielding an output signal
defined as
where
indicates a Hermitian transpose. The coefficients of the beamformer,
, are estimated as [
2],
where
is the steering vector normalized to the reference channel.
Finally, the speech signal at the beamformer output is enhanced by a single-channel postfilter for additional noise reduction. A spectral gain
is obtained using the power spectral density (PSD) of the speech at the reference microphone
, the PSD of the residual noise
and the SPP
. The above single-channel statistics (
and
) are estimated from the noisy speech and noise SCMs and the RTF. The gain function is further processed by a musical noise reduction algorithm [
28] and finally applied to the beamformer output, thus obtaining
where
is the estimate of the clean speech signal at the reference microphone. In the following sections, the description of the different parts of the system is addressed.
3. Extended Kalman Filter-Based Relative Transfer Function Estimation
The proposed system requires knowledge of the RTF between the two microphones, namely
. Among other approaches, the computation of this RTF can be addressed as the estimation of a variable that changes across frames in terms of a stochastic model. Given this dynamic model, the noise statistics and the noisy observations, we proposed in [
15] the tracking of the RTF using an extended Kalman filter (eKF), showing a better estimation performance in comparison with other state-of-the-art approaches. Next, we describe in detail the derivation of this eKF-based RTF estimation.
First, we formulate the narrowband approximation for a given frequency of the noisy speech signal at the secondary microphone in terms of the reference microphone as
where the frequency index
f has been omitted for the sake of simplicity. In addition, complex variables are expressed as stacked vectors of their real and imaginary parts. For example, given
with
, we can define
and, in a similar way,
Using these definitions for the model variables in terms of vectors, we propose the following dynamic and observation models needed by the Kalman filter:
Dynamic model for the RTF
: We assume that the state vector
is a random walk stochastic process which can be expressed as
where
is a zero-mean multivariate white Gaussian noise that models the variability of the RTF. A detailed discussion on this model is provided in
Section 3.2.
Observation model for the noisy speech at the secondary microphone,
: It is defined using the distortion model in (
8) as
where the noises are assumed to be zero-mean multivariate Gaussian variables,
where
is a noise covariance matrix whose estimation is addressed in
Section 4. Additionally, we assume that there is no correlation between
and
while
and
are correlated. The model
is non linear because of the product between the variables
and
. This model depends on the observation
, which acts as a model parameter.
Finally, the Kalman filter framework is applied to obtain a (recursive) minimum mean square error (MMSE) estimate of . This is a two-step procedure that is applied frame-by-frame for all frequencies:
The
prediction step, using the model (
12), is applied for every frame
,
where
are error covariance matrices. The Kalman filter is initialized using the overall mean and covariance of the RTF, that is,
and
. Further details about these parameters are provided in
Section 3.2.
The
updating step is applied to correct the previous estimation with the observations
and
(whose relationship is given by Equation (
14)),
where
is the Kalman gain, and
are necessary statistics, the estimation of which is developed in the next subsection. These equations correspond to the most general Kalman filter model as described in Reference [
29]. We define the equations in terms of
,
and
because the non-linearity of
in Equation (
14) makes their estimation non-trivial.
To deal with non-linear functions, two variants of the Kalman filter are widely used: the eKF and the unscented Kalman filter (uKF) [
29]. In the case of the model of (
14), it could be demonstrated that both eKF and uKF yield the same closed-form expressions for
,
and
. We choose the eKF approach because it gives a more stable computational solution and it is easier to implement than the uKF one. In the next subsection the eKF approach is presented.
3.1. Vector Taylor Series Approximation
The eKF is based on applying a linearization over the prediction and observation models using first-order vector Taylor series (VTS). In our case, the prediction model is linear, so the linearization is only applied to function
in the observation model. The first-order VTS approximates the model of Equation (
14) as
where
are the Jacobian matrices required for the VTS approach.
Finally, using (
26), the noisy speech statistics can be estimated as [
29]
3.2. A Priori RTF Statistics
The dynamic model for the RTF vector
presented in Equation (
12) accounts for the process variability across time in terms of a white noise
. This variability has a twofold meaning: first, the possible temporal variations of the acoustic channel due to environment changes, head or smartphone movements, etc., and, second, the inaccuracy of the narrowband approximation of Equation (
8) [
6]. This is due to the fact that, especially in reverberant environments where the analysis window of the STFT is shorter than the impulse response of the acoustic channel, the transfer function is not multiplicative but convolutive. This convolutive transfer function expands in both time and frequency dimensions. Thus, nearby frames and frequencies are correlated, which violates the narrowband approximation [
6]. In order to account for the variability associated to this effect, we will assume the statistical model proposed in (
12) so that, although the channel could be time-invariant, the RTF, as defined in Equation (
3), is time-variant.
The eKF-based RTF estimator requires the
a priori statistics of the RTF. These statistics are the overall mean vector and covariance matrix of the RTF, respectively,
and also the covariance of the RTF variability across frames,
Additionally, we can define the overall correlation matrix of the RTF as
The previous statistics can be estimated in advance using a training set of dual-channel clean speech utterances in different acoustic environments and device positions. In order to avoid outliers which might yield useless estimates, we select, on an utterance basis, time-frequency bins where the speech power at the reference channel is large enough (higher than the maximum power at that frequency in the utterance minus 3 dB). For those bins, we estimate the RTF using (
3), which yields a set of RTFs
for the
l-th utterance, that are later converted to RTF vectors
. For each utterance, a sample mean vector
and a sample correlation matrix
are estimated using those
vectors, while a sample covariance matrix
is computed from consecutive RTF vectors. Finally, the global sample statistics
,
and
are obtained by averaging the particular utterance-dependent statistics. The sample covariance
can then be estimated using
and
in (
35).
4. Speech Presence Probability-Based Noise Statistics Estimation
The eKF-RTF estimator and the beamforming algorithm also require knowledge of the noise spatial correlation matrix (SCM)
. In this work, we follow the multi-channel speech presence probability (SPP) approach described in Reference [
4]. This estimation method is based on the recursive updating of the noise SCM in those time-frequency bins where speech is absent. First, two hypotheses,
and
, are considered for speech presence and speech absence, respectively,
Assuming zero-mean random variables, the SCM of the noise will be updated by means of the following recursion,
where the forgetting factor is computed as
where
is an updating constant and
is the
a posteriori SPP. The estimation of this probability is detailed in
Section 4.1.
From now on, the time and frequency indices are omitted whenever possible. The noise statistics for the RTF estimator (required by (
30)) are directly derived from
. Assuming a zero-mean, symmetric circular complex Gaussian distribution for
[
30] and
with
, the following relations can be demonstrated,
where
is the 2-dimensional identity matrix.
4.1. A Posteriori SPP Estimation
The
a posteriori SPP
allows us to control the updating procedure of Equation (
38) for the computation of the noise statistics. Nevertheless,
is also exploited in two additional parts of our system:
The estimation of the RTF presented in the previous section is only accurate in time-frequency bins where speech is present. The a posteriori SPP indicates those bins where speech presence is more likely. Therefore, in our implementation we only update the eKF in those bins where , with being a predefined probability threshold. Otherwise, the previous values are preserved.
The postfiltering performance can be improved if additional information about SPP is provided, as shown later in
Section 5.
The estimation of the
a posteriori SPP can be addressed assuming complex multivariate Gaussian distributions for the noisy speech
[
4,
5], according to the two hypotheses previously formulated (see (
36) and (
37)). Using the Bayes’ rule, the
a posteriori SPP at each time-frequency bin can be calculated as
where
is the
a priori speech absence probability (SAP) and
are the likelihoods of observing the noisy speech signal under the different hypotheses, with
being the matrix determinant operator and
M the number of microphones. Equation (
46) can be redefined using these likelihoods, yielding the following expression for the SPP,
Then, the a posteriori SPP can be estimated at each frame for all frequencies according to the following two-iteration algorithm:
Initialization: Estimate the noisy SCM with a recursive updating,
where
is an updating constant as in (
39). Also, estimate the
a priori SAP
(see
Section 4.2).
1st iteration: Estimate
using
in (
49). Then, estimate
using
in (
38).
2nd iteration: Re-estimate
using now
in (
49). Finally, re-estimate
using
.
4.2. A Priori SAP Estimation
To obtain an accurate
a posteriori SPP that allows for robust tracking of the noise statistics, the
a priori SAP is a key parameter. Methods on single-channel noise tracking, as the fixed
a priori SNR algorithm of Reference [
31] or the minima controlled recursive averaging (MCRA) algorithm [
32], estimate this SAP in terms of the
a priori SNR. The MCRA framework was extended to multi-channel speech signals in Reference [
4]. This is the SPP estimator that we used in our previous works [
15,
27]. A major drawback of the MCRA scheme is the lack of robustness in case of a time-varying SNR, which makes noise changes to be detected as speech presence. More recently, the authors of [
5] proposed to use spatial information in the SAP estimation, specifically the coherent-to-diffuse ratio (CDR). Alternatively, the power level difference (PLD) between microphones is used in Reference [
17] to update the noise statistics, as it is a good indicator of speech presence in CT conditions. In this work, we propose a novel SAP estimator for dual-microphone smartphones that combines the CDR spatial information with the PLD between the reference and the secondary microphones.
First, an SCM
is estimated using a rectangular window of eight past frames as in Reference [
5]. Then, we calculate (1) the power spectral density (PSD) ratio between microphones as
where
is an estimate of
, and (2) the short-term complex coherence between microphones,
Both terms are needed by the SAP estimators.
The PLD-based
a priori SAP is based on the PLD noise estimator for CT conditions described in Reference [
17]. In that work, a normalized difference of the noisy speech PSDs was defined as
The noise statistics are updated by this parameter, as it gives information about speech presence. That is, assuming similar noise power at both microphones and that speech is more attenuated at the secondary microphone with respect to the primary one,
is close to one when speech is present and tends to zero otherwise. Thus, an
a priori SAP based on this indicator can be estimated as
where
is upper-bounded by 1. This estimator is valid for CT conditions, but it can also be useful in FT conditions for frequencies where speech at the secondary microphone is attenuated.
On the other hand, the CDR is another good indicator of speech presence [
33], which is defined as
where
is the clean speech short-term complex coherence (defined as in (
52)) and
is the diffuse noise field complex coherence, with
the sampling frequency,
K the number of frequency bins,
the distance between microphones and
the speed of sound. While higher values of the CDR indicate the presence of a strong coherent component, often a speech signal, lower values indicate that a diffuse component is dominant, which is more common for noise signals. In practice, the CDR is obtained using the estimator proposed in Reference [
33],
where
is the phase of
. Although the CDR is positive and real-valued, estimation errors yield complex-valued results, so the real-part
is taken in (
57). Additionally, a frequency-averaged CDR with a normalized Hamming window
is computed as
with
(the window width is
). Then, the local
a priori SAP estimate is obtained as in Reference [
5] using
,
where
and
define the minimum and maximum values of the function, respectively,
c is an offset parameter and
controls the steepness of the transition region. Similarly, the global
a priori SAP estimate
is computed using
in (
59). The CDR-based
a priori SAP is then obtained as in Reference [
5],
This estimator is the same as that proposed in Reference [
5], except for the term representing the frame
a priori SAP. This term was neglected as it did not increase the performance in our preliminary experiments.
Finally, the
a priori SAP estimates obtained by PLD and CDR are combined to achieve a more robust joint decision. Assuming statistical independence between both estimators, the final
a priori SAP estimate for dual-microphone smartphones is calculated as the joint probability of the speech absence decision by each estimator,
The above estimator can be used in both CT and FT conditions to obtain prior information about speech presence. Moreover, as it only allows for noise statistics updating when both estimates indicate speech absence, this estimator is expected to be more robust.
6. Experimental Evaluation
The performance of the different estimators and speech enhancement algorithms discussed along this paper is evaluated by means of objective speech quality and intelligibility metrics. Two different well-known objective metrics are used:
The Perceptual Evaluation Speech Quality (PESQ) [
37] metric is utilized to evaluate the speech quality of the enhanced speech signal. This metric gives a mean opinion score between one and five. The higher the PESQ values, the better the speech quality.
The Short-Time Objective Intelligibility (STOI) [
38] metric is intended to evaluate the speech intelligibility of the enhanced speech signal. The resulting score is a value between zero and one. The higher the STOI value, the better the speech intelligibility.
PESQ and STOI are both intrusive metrics, which means that they need a clean reference. As a reference, we use the clean speech signal at the reference microphone, .
Additionally, in order to evaluate the RTF estimation accuracy, we use the speech distortion (SD) index [
2]. This index measures the distortion level on the clean speech signal at the beamformer output, namely
(inverse STFT of
). The idea behind using this metric is that, because of the distortionless property of MVDR, more accurate RTF estimates should yield lower speech distortion. The SD index is measured segmentally across the speech signal, in such a way that the SD value at the
i-th segment is obtained as
where
T is the number of samples per segment. The segmental SD values are averaged to achieve the final SD index, which is a value between zero and one. The lower the SD value, the lower the speech distortion. As in Reference [
5], silence frames are excluded from this evaluation by means of calculating the median of the segment-wise signal power and removing those segments with a power 15 dB lower than that median.
We evaluate the proposed algorithms by using simulated dual-channel noisy speech recordings from a dual-microphone smartphone. Two different databases were developed for each device use mode: close-talk (CT) and far-talk (FT). To simulate the recordings, clean speech signals are filtered using dual-channel acoustic impulse responses and real dual-channel environmental noise is added at different signal-to-noise ratios (SNRs). We evaluate four different reverberation environments and eight different noises, which are matched as indicated in
Table 1, yielding eight different acoustic environments (including both reverberation and noise). Details about the methodology used to obtain the acoustic impulse responses and the noises can be found in References [
15,
39].
Clean speech signals are obtained from the TIMIT database [
40,
41] and downsampled to 16 kHz. In particular, a total of 850 clean speech utterances from different speakers are employed. All the utterances have a length of around seven seconds, which is achieved by same-speaker utterance concatenation. Two different sets are then defined, namely training and test. Speakers do not overlap across sets. Moreover, the number of utterances from female and male speakers is balanced. The distribution of utterances and the number of speakers in the training and test sets are indicated in
Table 2.
The training set consists of reverberated clean speech utterances and is only used to estimate the a priori statistics for the eKF-RTF estimator. Such utterances were obtained by filtering each clean speech utterance with a set of dual-channel acoustic impulse responses which model four reverberant environments, thereby yielding a total of 2800 training utterances. Sixteen different acoustic impulse responses were considered for each acoustic environment. For each utterance, the impulse response was randomly selected.
On the other hand, the test set consists of utterances contaminated according to the eight noisy environments defined in
Table 1. This set is intended to evaluate the different algorithms proposed in this work. Noises were added to the reverberated speech at six different SNRs from −5 dB to 20 dB, so a total of 7200 test utterances was obtained. In order to simulate reverberation, ten different acoustic impulse responses, in turn also different from those of the training set, were considered for each acoustic environment and, again, randomly applied.
For STFT computation, a 512-point DFT was applied using a 32 ms square-root Hann window with 50% overlap. This results in a total of 257 frequency bins for each time frame. The noisy speech and noise SCMs were estimated using an updating constant
. The parameters for CDR-based
a priori SAP calculation were set as [
5]:
cm,
,
,
and
. The SPP threshold for RTF updating was set as
. Finally, for the SPP-driven trade-off parameter of the parametric Wiener filter, the following parameter values were used [
5]:
,
,
and
.
The algorithm was implemented in Python and it is available at [
42]. The computational burden of the implementation was evaluated on a PC with an Intel Core i7-4790 CPU. The algorithm works on a frame-by-frame basis, so that the algorithmic delay is in this case the duration of a frame, that is, 32 ms. The average performance of the whole system (i.e., including SPP and RTF estimation, MVDR beamforming and postfiltering) on this machine achieved approximately 8x faster than real-time.
In the following, the performance of the different techniques is tested. In order to simplify the reading of the results tables, an acronym is provided (in parentheses) for each considered technique after its description.
6.1. Experimental Results: Performance of SAP Estimators
First, we compare the different
a priori SAP estimators when used along with our eKF-RTF estimator for MVDR beamforming (i.e., no postfilter is applied yet). This comparison is shown in
Table 3 in terms of PESQ and STOI. The techniques evaluated are the multi-channel version of MCRA (MCRA) [
4], CDR-based SAP estimation (CDR) [
5] and our proposed PLD-based SAP estimator (PLDn) and its combination with CDR-based estimation (P&C), both presented in
Section 4.2. Results for the noisy speech signal at the reference microphone (Noisy) are given as a baseline. In addition, we show the results achieved by the eKF-RTF estimator with an oracle estimation of the noise SCM (eKF-OracleN) as a performance upper-bound. This estimation was obtained using the true noise signals in a recursive procedure similar to Equation (
50). The speech presence probability obtained from clean speech was used in the eKF-RTF estimator to obtain these oracle results.
For CT conditions, the best results are obtained for the eKF-PLDn system. The speech power difference between microphones for CT conditions makes that the PLD-based SAP estimator can easily detect those bins where speech is absent. This power difference reduces the CDR ratio, defined in Equation (
57), of the multi-channel signal in the presence of speech, leading the CDR-based SAP method to underestimate the speech presence and decrease the performance of the noise tracking algorithm. Therefore, the combination of both approaches does not improve the single decision based on PLD between channels.
On the other hand, for FT conditions, speech power at both channels is more similar and CDR increases under the presence of speech. This is especially true at higher SNRs, where the CDR-based SAP detector outperforms the PLD-based one. However, the performance of the CDR-based detector degrades more severely at lower SNRs, while the PLD detector is more robust in these conditions. Finally, the combination of both detectors increases the performance in terms of both noise reduction and speech intelligibility, keeping a performance similar to the PLD one at lower SNRs and improving at higher SNRs.
To sum up, our proposals improve the tracking of the noise statistics in dual-microphone smartphones. The eKF-PLDn proposal is the best solution in CT conditions, with eKF-P&C having a similar performance. The joint decision proposed in eKF-P&C achieves the best results in FT conditions at higher SNRs, while eKF-PLDn performs slightly better at lower SNRs.
6.2. Experimental Results: Performance of RTF Estimators
In this subsection, we compare our eKF-RTF estimator with the well-known eigenvalue decomposition (EVD) [
11] and covariance whitening (CW) [
9] sub-space methods for RTF estimation. The results are shown in
Table 4. In addition, we show the results obtained with an oracle estimation of the RTF (OracleC) as a performance upper-bound. This oracle RTF was obtained from the clean speech signals using Equation (
3) for time-frequency bins where speech presence was detected (using the speech presence probability obtained from clean speech), while the RTF of the previous frame was reused for the remaining ones. The evaluation is carried out in terms of speech distortion (SD) and the speech intelligibility metric STOI. We evaluate SD instead of PESQ because here we are only interested in the distortion introduced over the reference clean speech due to RTF estimation errors when using a distortionless beamformer.
The comparison is performed using the best SAP estimator obtained for each device placement according to
Table 3 (eKF-PLDn for CT and eKF-P&C for FT). A similar improvement due to our proposed SAP estimators, as the one observed in
Table 3 for the eKF-RTF estimator, is expected for the other RTF estimators (due to the fact that these estimators would also take advantage of more accurate estimates of the noise SCM). We compare the RTF estimators using only one SAP estimator in order to narrow the number of possible system combinations. For a fair comparison, we use the same RTF initialization and the same updating scheme based on SPP for the different systems.
From
Table 4, we can see that our eKF proposal obtains slightly better results in terms of STOI and much lower speech distortion than the other approaches, particularly in FT conditions. As we previously analyzed in a former study [
15], the distortionless property of MVDR involves none or very low speech distortion if an accurate estimate of the RTF is available. Therefore, we can conclude that our estimator tracks better the RTF variability than the other approaches. This is more noticeable in FT conditions, where the reverberation level increases and the secondary microphone captures similar power to the reference one, thereby making the RTF more variable and its tracking more challenging.
Furthermore,
Table 5 shows the SD results for the different approaches grouped by reverberant environment (averaging by noise environment and SNR level). The oracle results for each reverberant environment are also shown, as they give an upper-bound reference of the performance of the different approaches. This can be useful when different reverberant environments are compared, as some of them include more challenging noise environments (e.g., cafe in low reverberation). It can be observed that the increase of the reverberation level makes the RTF estimation more difficult. The performance of the different algorithms degrades with the reverberation level, as the variations of the RTF are harder to track, although our proposal is more robust against reverberant environments than sub-space approaches.
6.3. Experimental Results: Performance of Single-Channel Clean Speech PSD Estimators
Next, we evaluate different clean speech PSD estimators when combined with Wiener postfiltering (Equation (
64)) applied to the MVDR beamformer output.
Table 6 shows a comparison between the estimator based on the power difference (WF-Ps) of Equation (
74), the one based on the distortionless constraint of MVDR (WF-Ms) of Equation (
75) and a standalone MVDR beamformer (i.e., with no postfiltering) as a reference, all of them with the best SAP configurations determined above. This comparison is done in terms of speech quality and intelligibility.
Results show that WF-Ms performs better than WF-Ps, obtaining slightly better results in CT conditions and clearly outperforming it in FT conditions. The WF-Ms estimation does not make any assumptions about the noise power similarity between microphones as the other approach does. This makes the WF-Ms estimation procedure, which also exploits the cross-correlation elements of the noisy speech and noise SCMs, more robust. Moreover, the power difference assumption is no longer valid in FT conditions, leading the WF-Ps approach to degrade the performance in this scenario, particularly at higher SNRs.
6.4. Experimental Results: Performance of Postfiltering Approaches
Finally, in
Table 7 we compare the pWF and OMLSA postfilters with a basic WF postfilter and two other related state-of-the-art dual-channel speech enhancement algorithms intended for smartphones: the PLD-based single-channel WF filter of Reference [
17] (PLDwf) and the SPP- and coherence-based single-channel WF filter of Reference [
18] (SPPCwf) for CT and FT conditions, respectively. The MVDR-based clean speech PSD estimator (Ms) is used for the different proposed postfilters (WF, pWF and OMLSA). The comparison is done in terms of PESQ and STOI metrics.
For CT conditions, both pWF and OMLSA outperform the WF and PLDwf approaches, with OMLSA achieving the best results in noise reduction performance and speech intelligibility. PLDwf achieves more noise reduction (better PESQ) than our WF due to the fact that the former introduces an overestimation of the noise. Such an overestimation also means more speech distortion, so the speech intelligibility is lower compared to our WF approach. The use of SPP information in our postfilters allows for larger noise reduction in frequency bins where speech is absent without additional speech distortion. The availability of accurate SPPs in CT conditions makes OMLSA the best approach in this case, as the LSA estimator performs better than the WF when bins where speech is present are clearly differentiated from those where speech is absent.
On the other hand, the SPPs obtained in FT conditions are less accurate for the postfiltering task, thereby degrading the performance of the OMLSA estimator. Nevertheless, this SPP information is still useful for the pWF, which, in general, outperforms the basic WF, especially at higher SNRs. Moreover, both WF and pWF outperform SPPCwf in terms of noise reduction and speech intelligibility. In summary, the availability of accurate RTF and SPP estimates, as those provided by our proposal, clearly helps to improve the performance of postfiltering in FT mode.