System for Evaluation and Compensation of Leg Length Discrepancy for Human Body Balancing
Abstract
1. Introduction
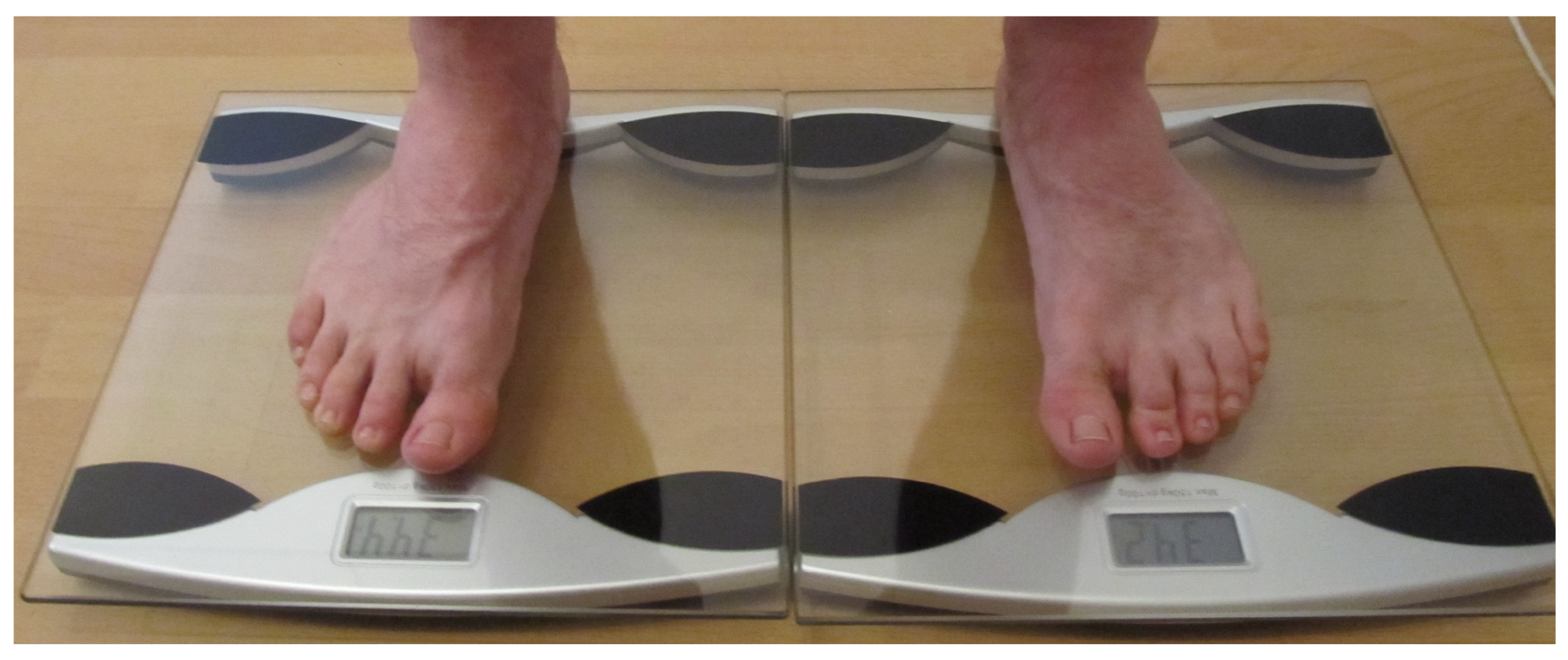
2. Problem Description
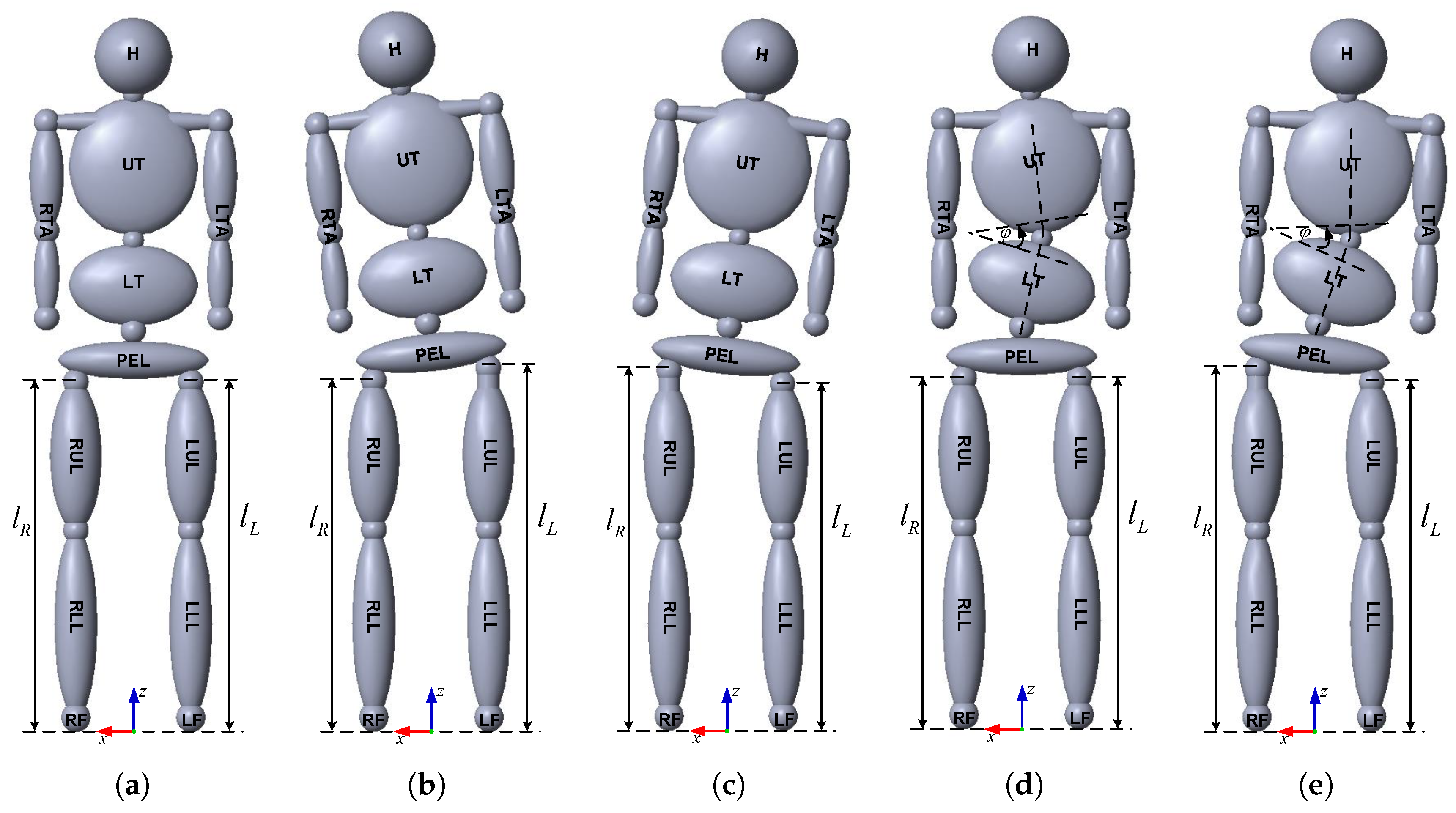
2.1. Anthropometric Human Body Model
2.2. Human Body Balancing
2.3. System Description
- a mechanical set of two 3-RPS parallel manipulators with mobile force plates;
- an electronic system for control, measuring and communication with the PC;
- a vision system with two cameras; and
- a PC application used for control and data collection.
3. Mathematical Model of the System
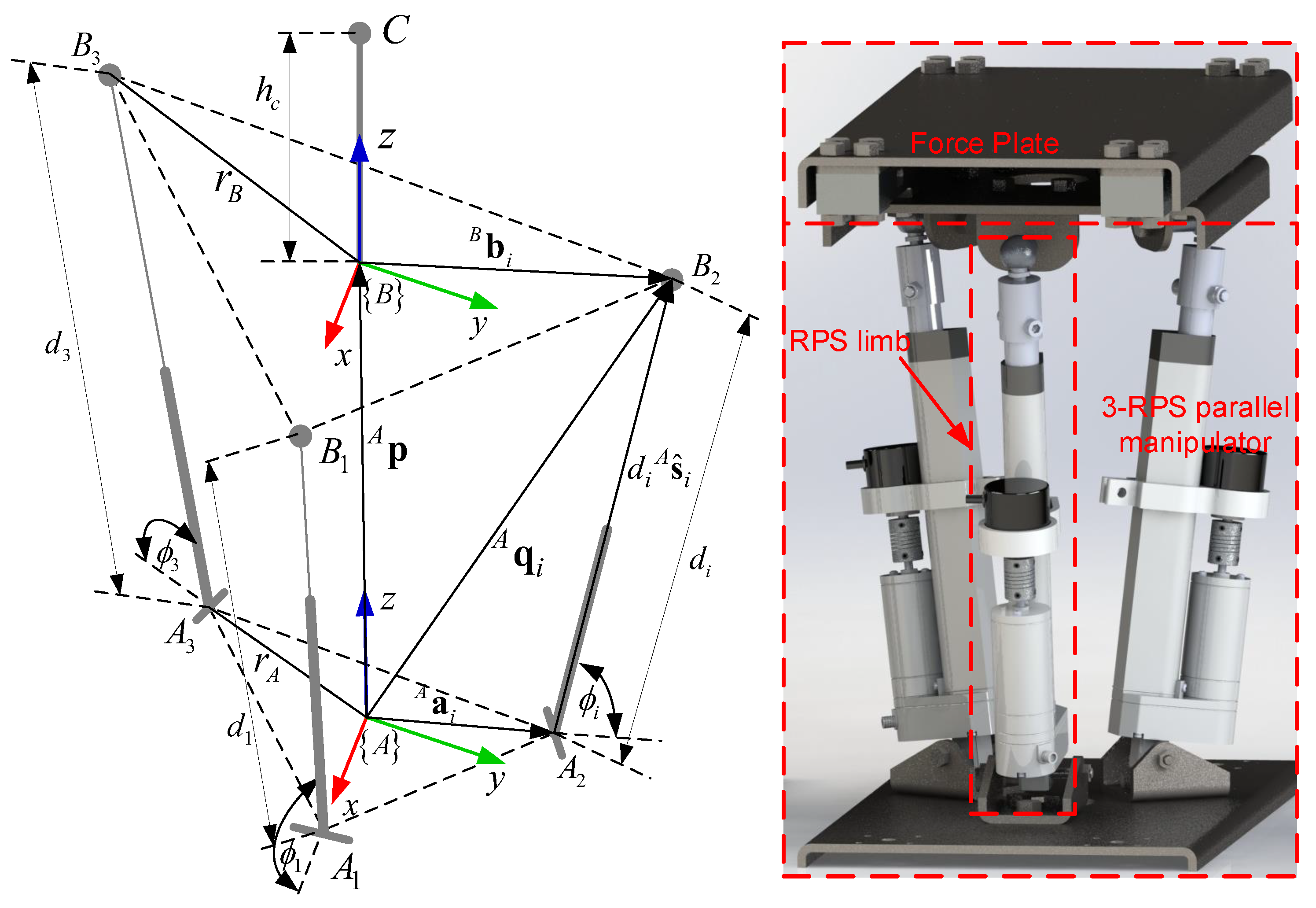
3.1. The Geometry of the 3-RPS Parallel Manipulator
3.2. Inverse Kinematic of the 3-RPS Parallel Manipulator
- is the unit vector of the prismatic joint;
- is the position vector of the moving platform center in the frame {A};
- is the rotation matrix of the moving frame {B} with respect to the frame {A};
- is the position vectors of spherical joints in the frame {B}; and
- is the position vectors of revolute joints in the frame {A}.
3.3. Forward Kinematics of the 3-RPS Parallel Manipulator
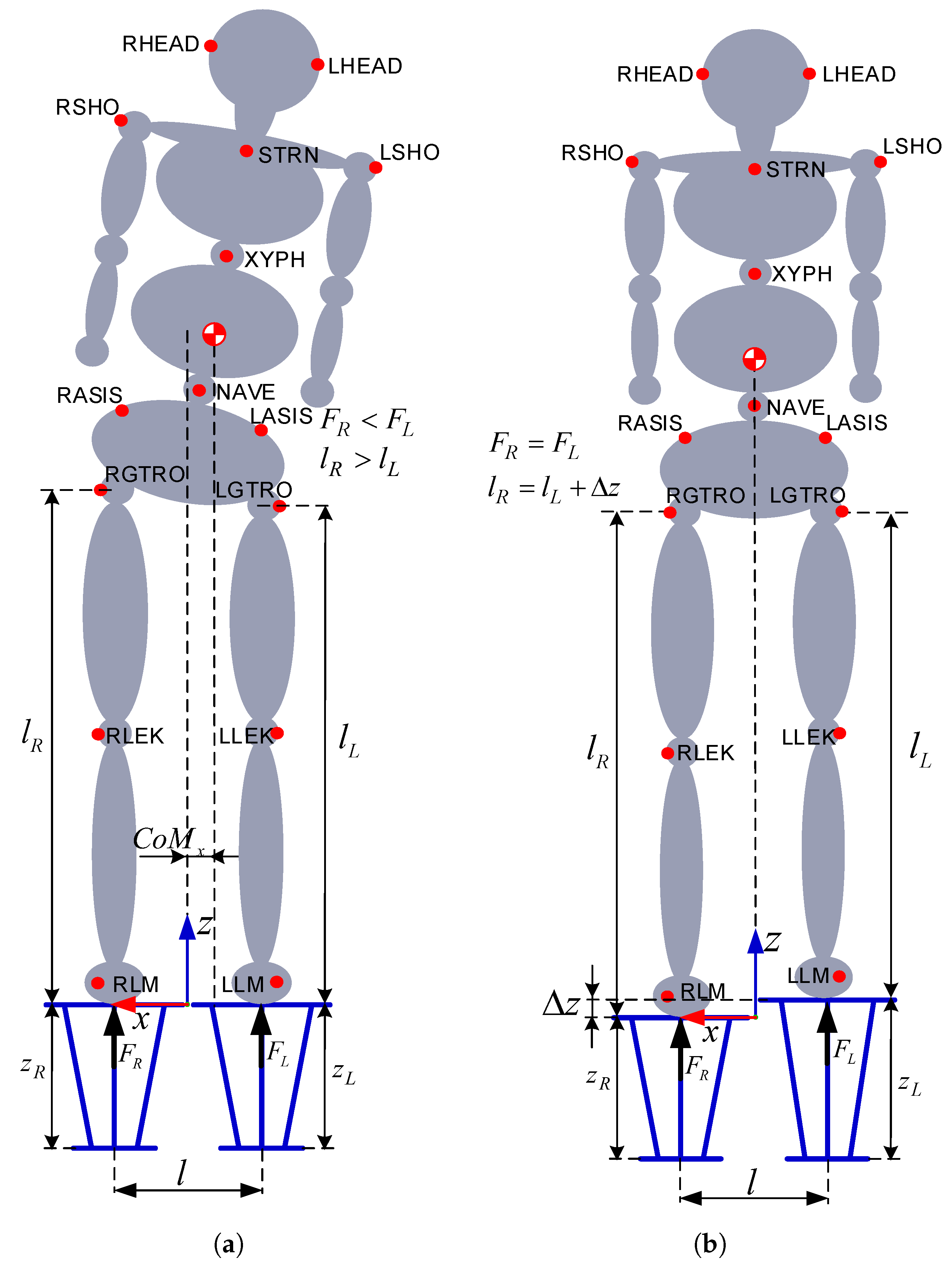
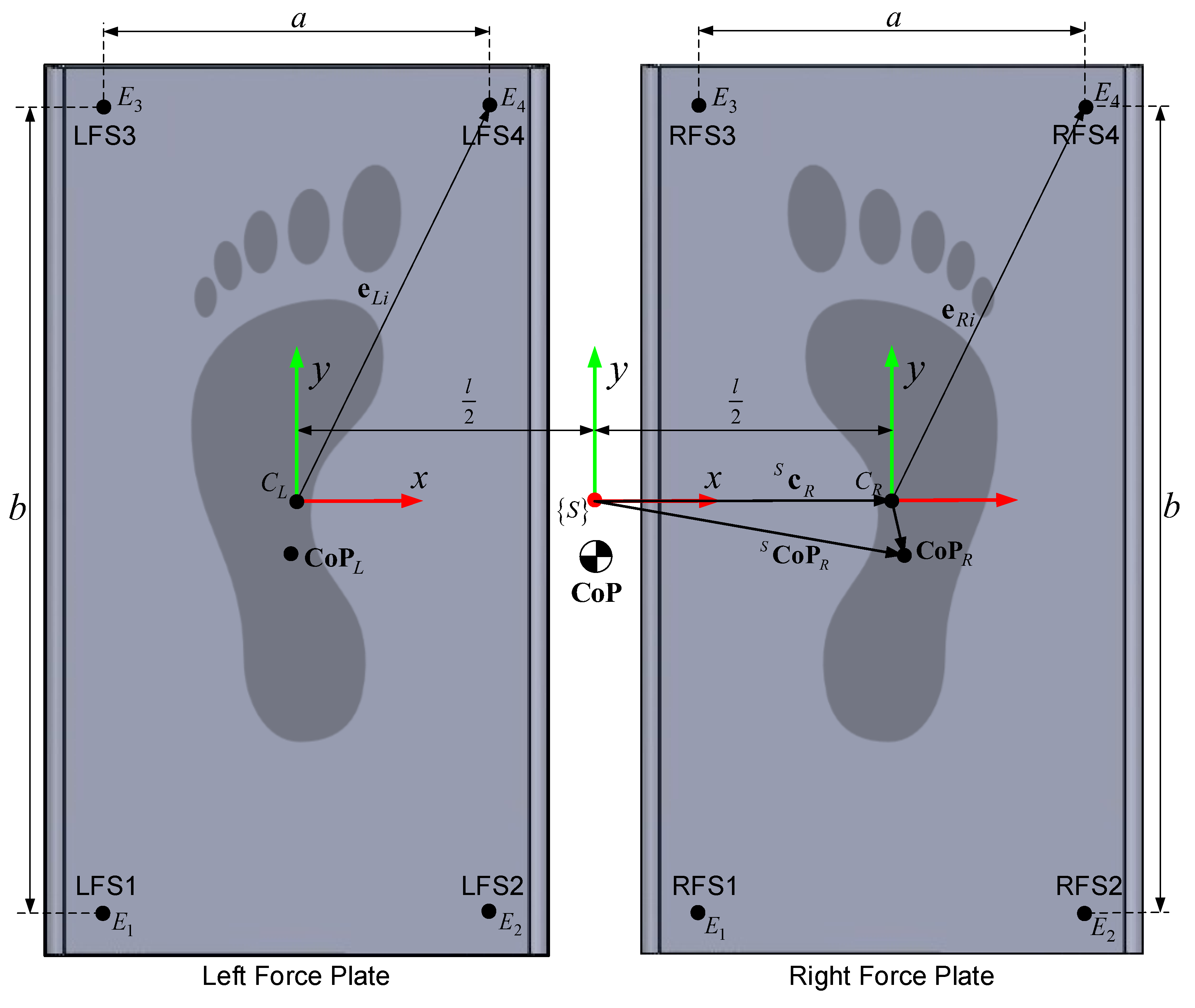
3.4. Force Plates
- a is the distance between the sensors along the x-axis;
- b is the distance between the sensors along the y-axis; and
- l is the distance between the origins of the left and right local force plate frame.
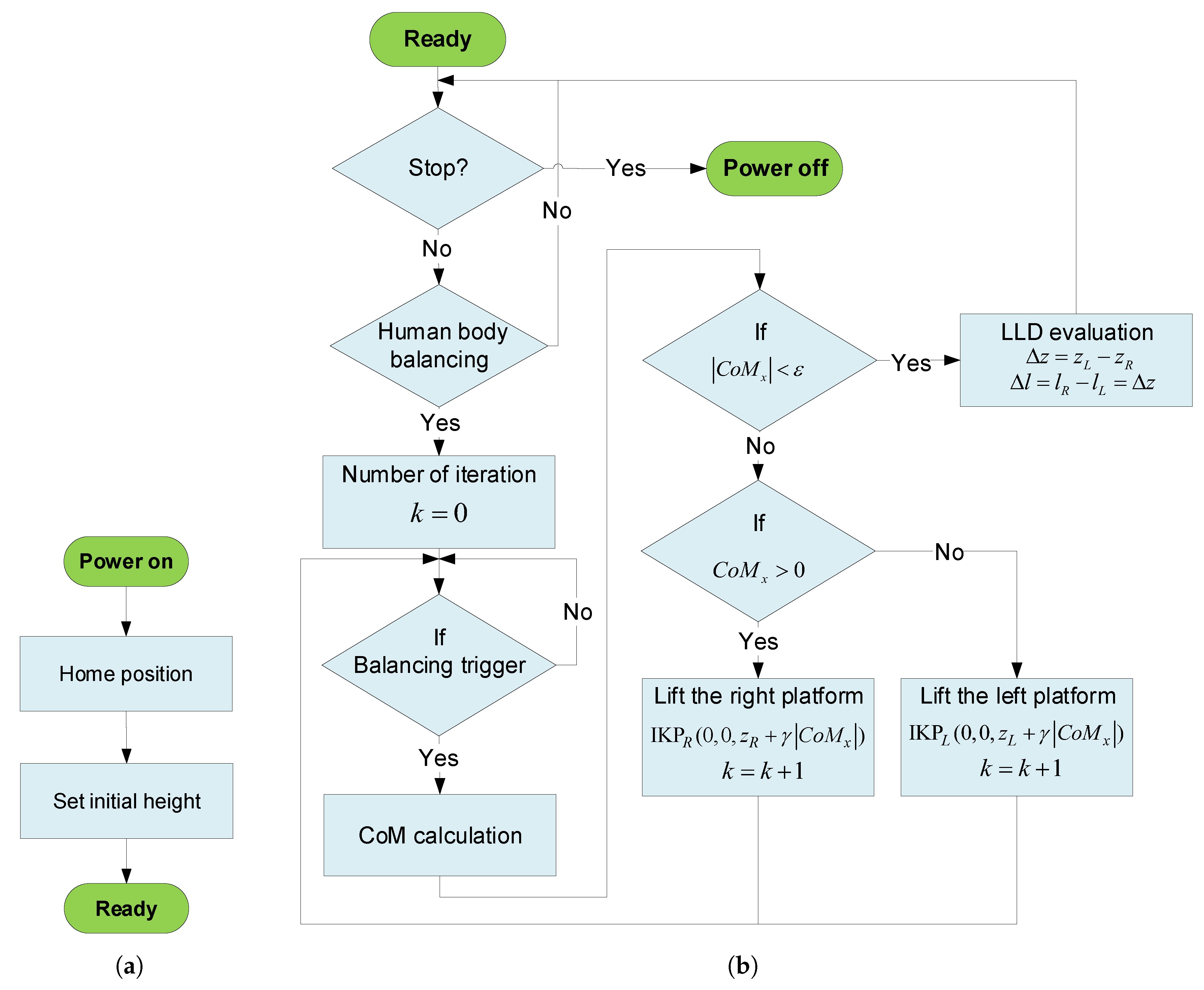
4. Human Body Balancing Algorithm
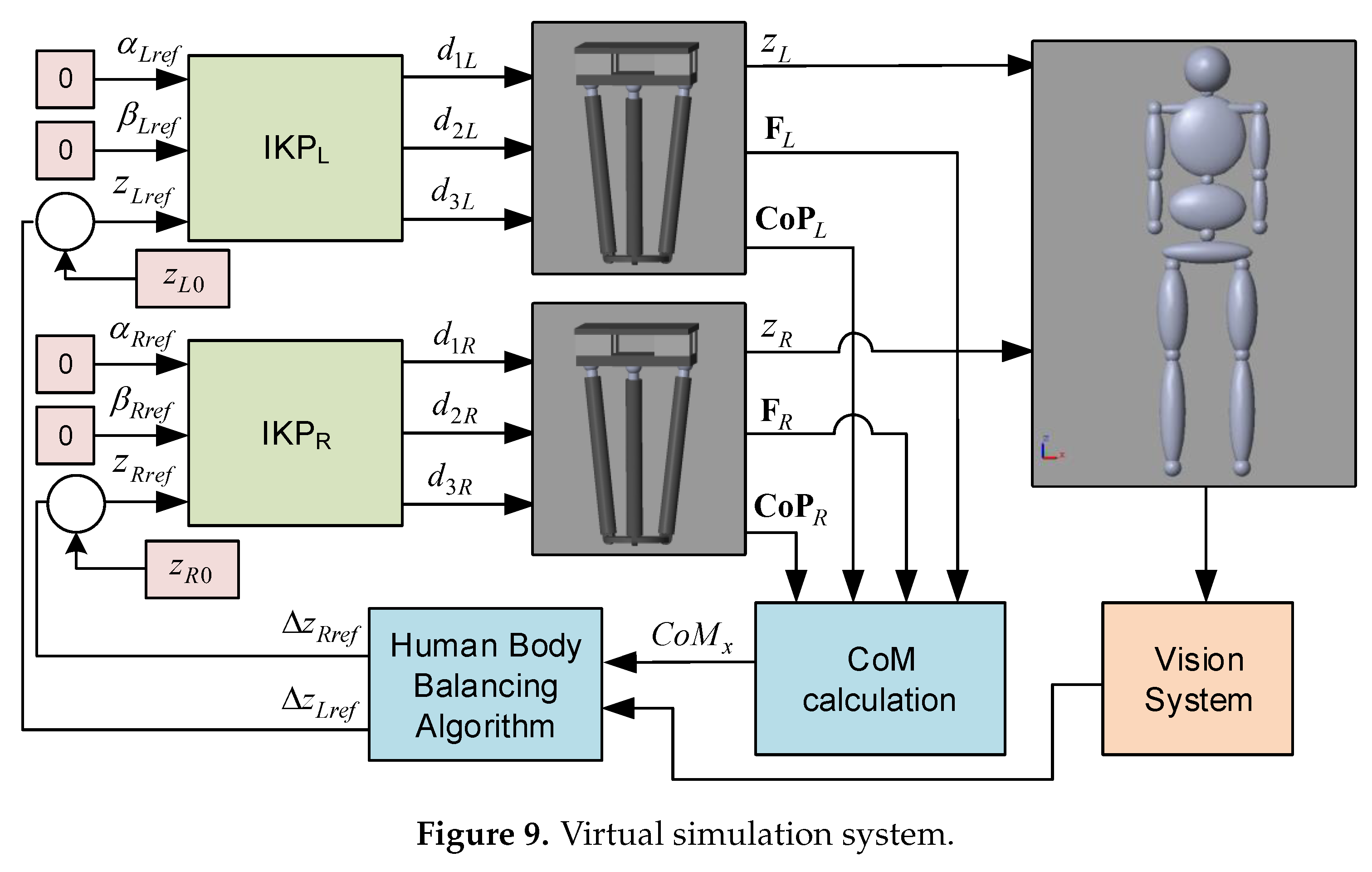
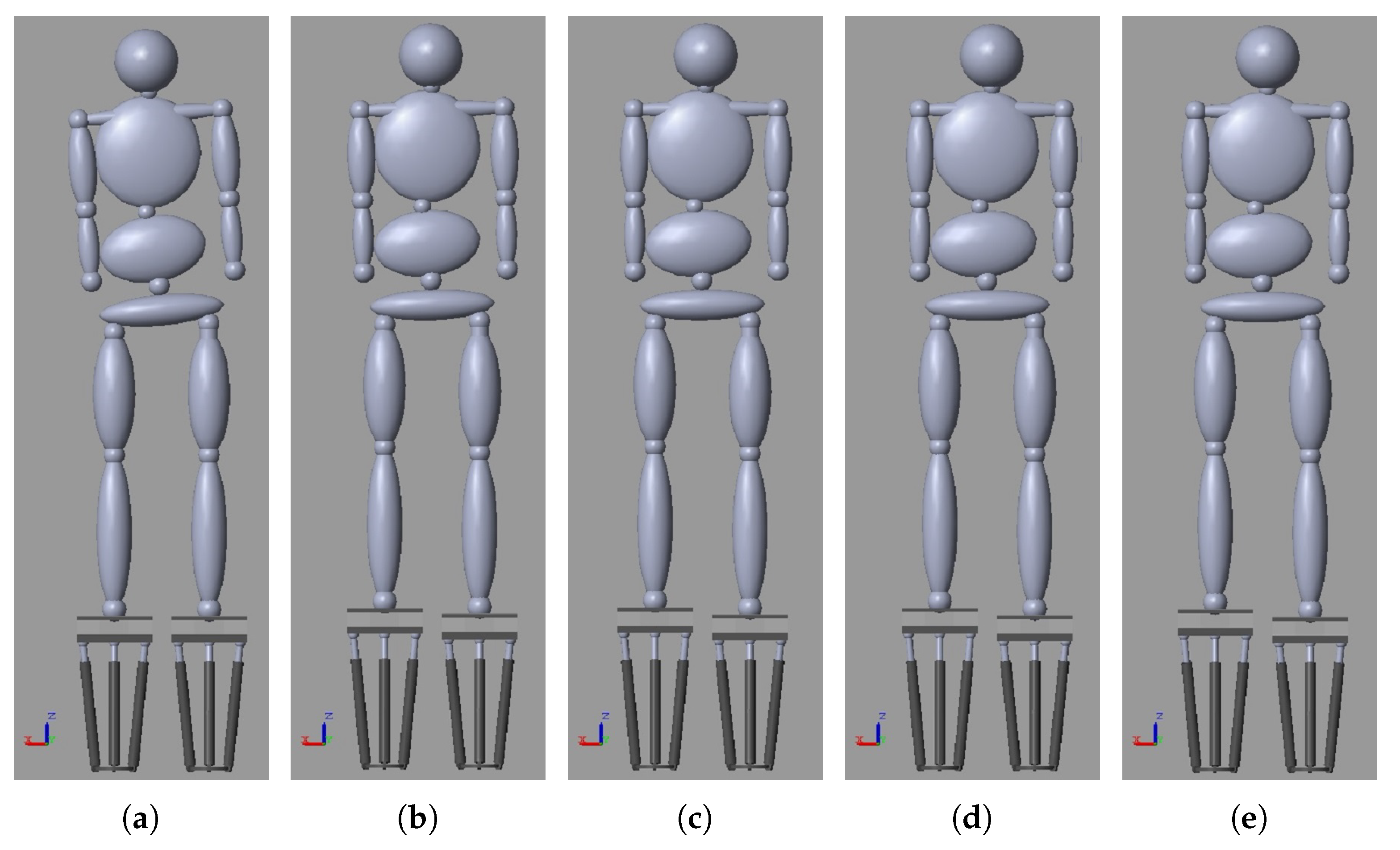
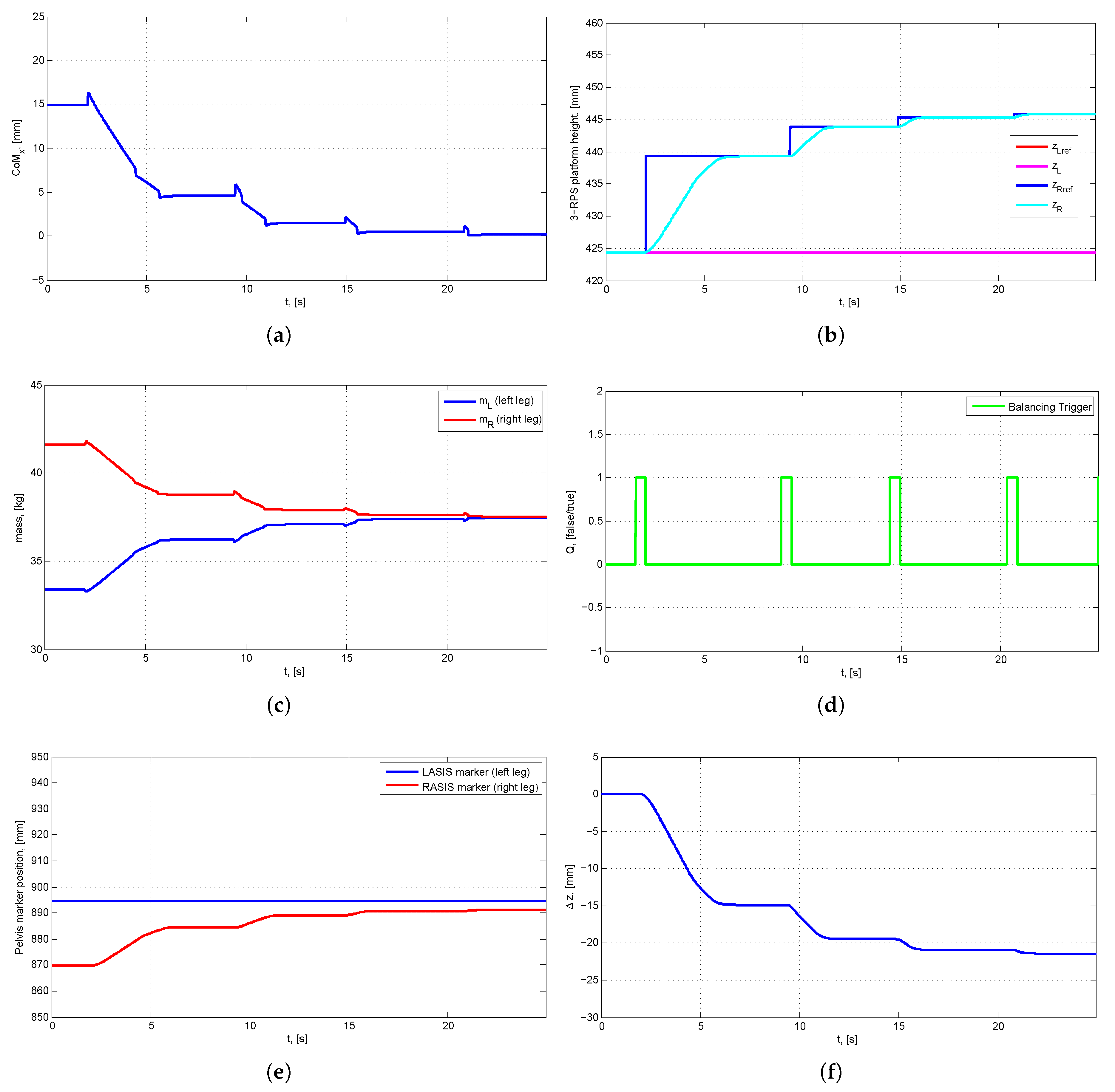
4.1. Simulation Results
4.1.1. Scenario 1: Human Body with LLD
4.1.2. Scenario 2: Human Body with LLD and Scoliosis
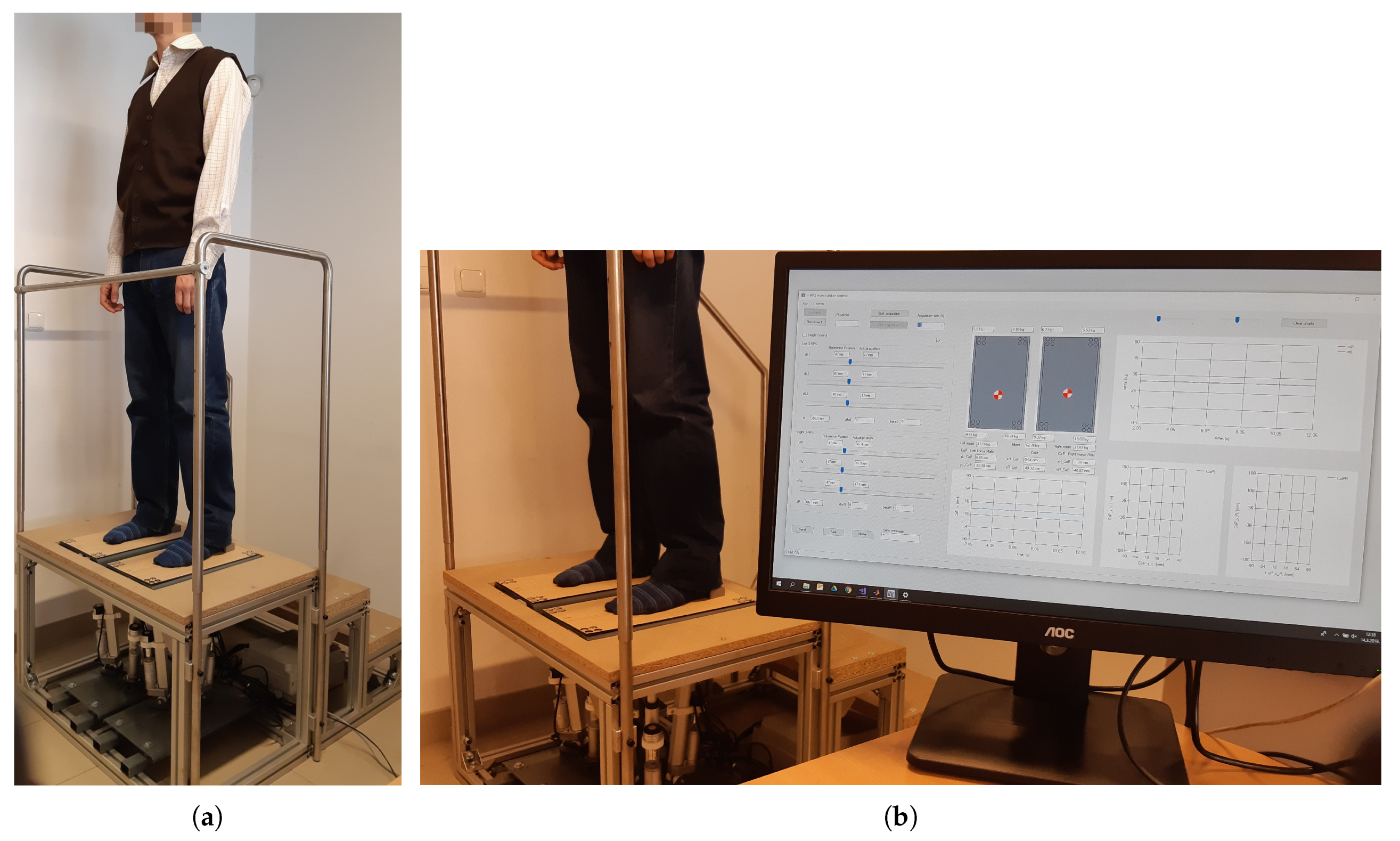
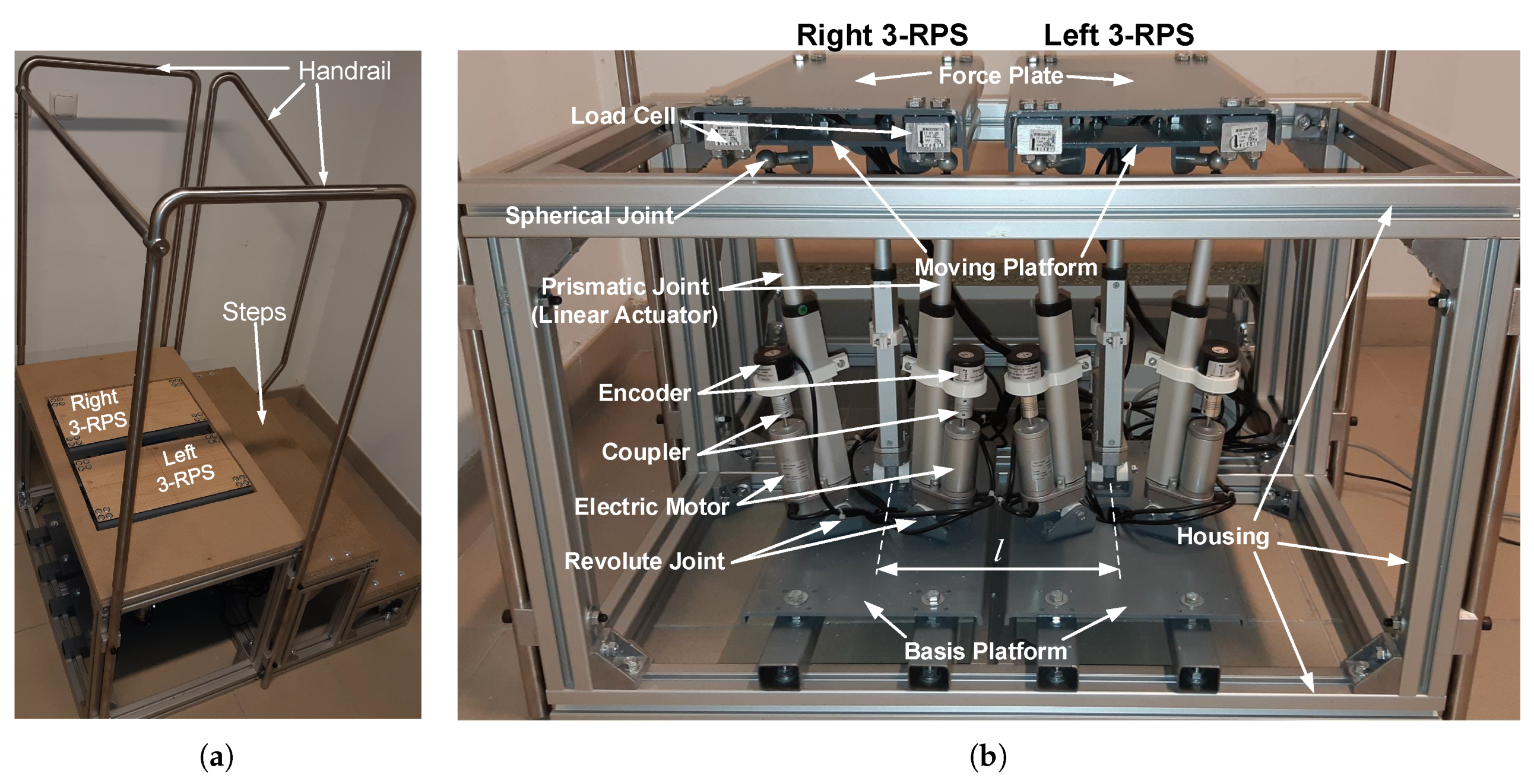
5. Mechatronic System Design
5.1. Mechanical Design
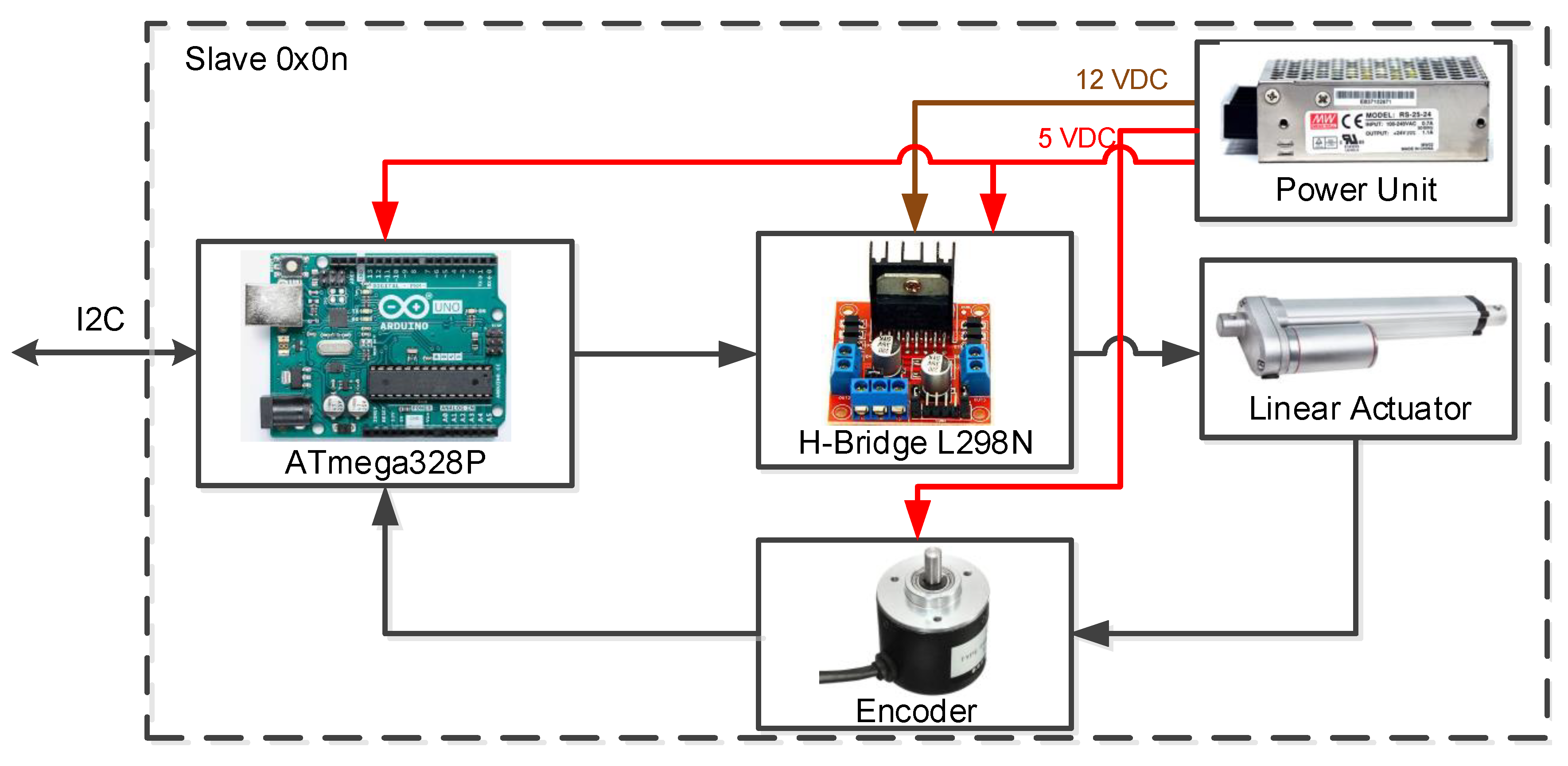
5.2. Electronic Design
5.2.1. Master Device
5.2.2. Slave Device
5.3. Software Design
5.3.1. Firmware for Microcontrollers
5.3.2. PC Application for Control and Data Collection
5.3.3. Vision System
5.4. Experimental Results
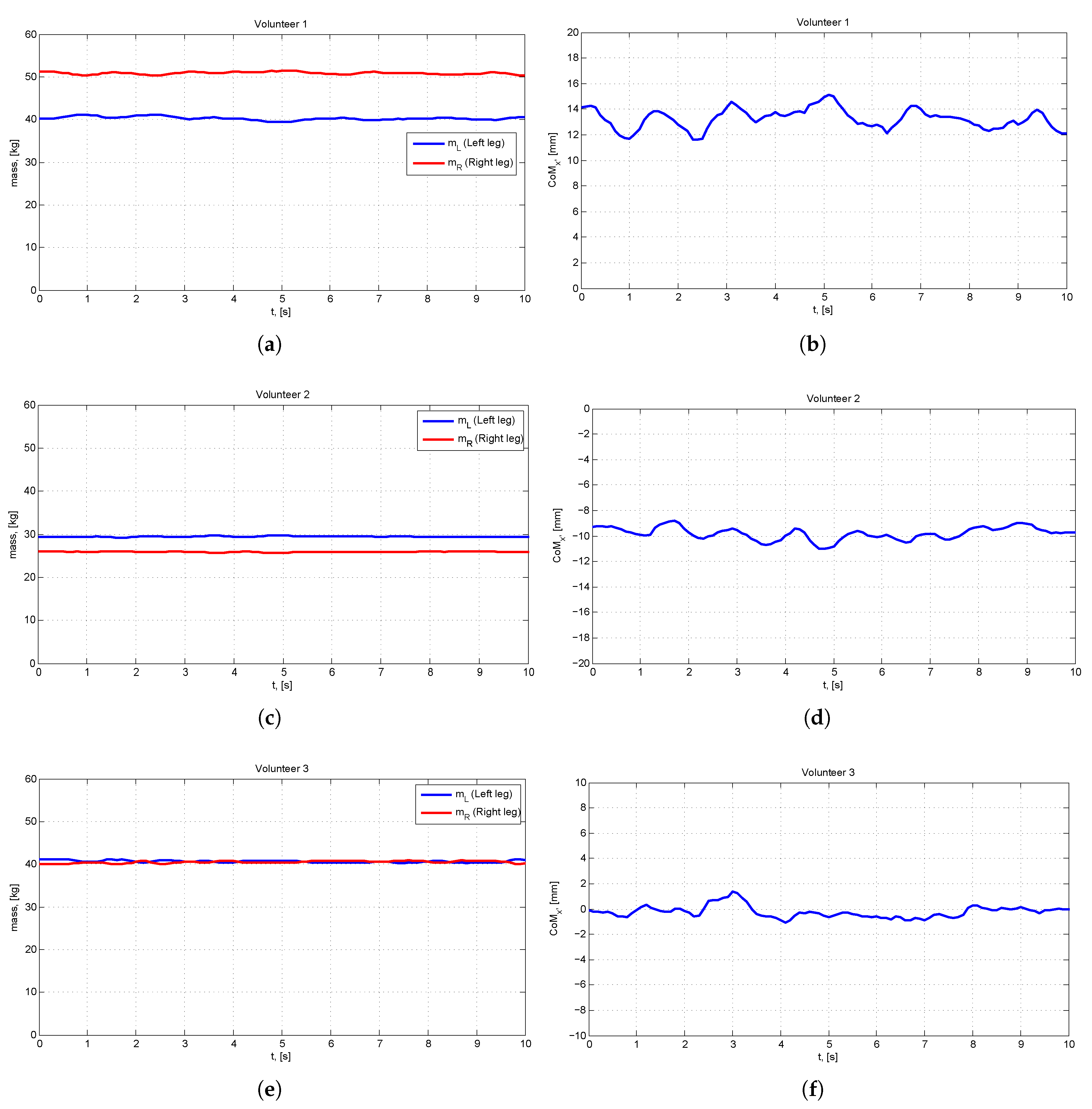
5.4.1. Experiment 1: Healthy Population—Left and Right Leg Load Distribution
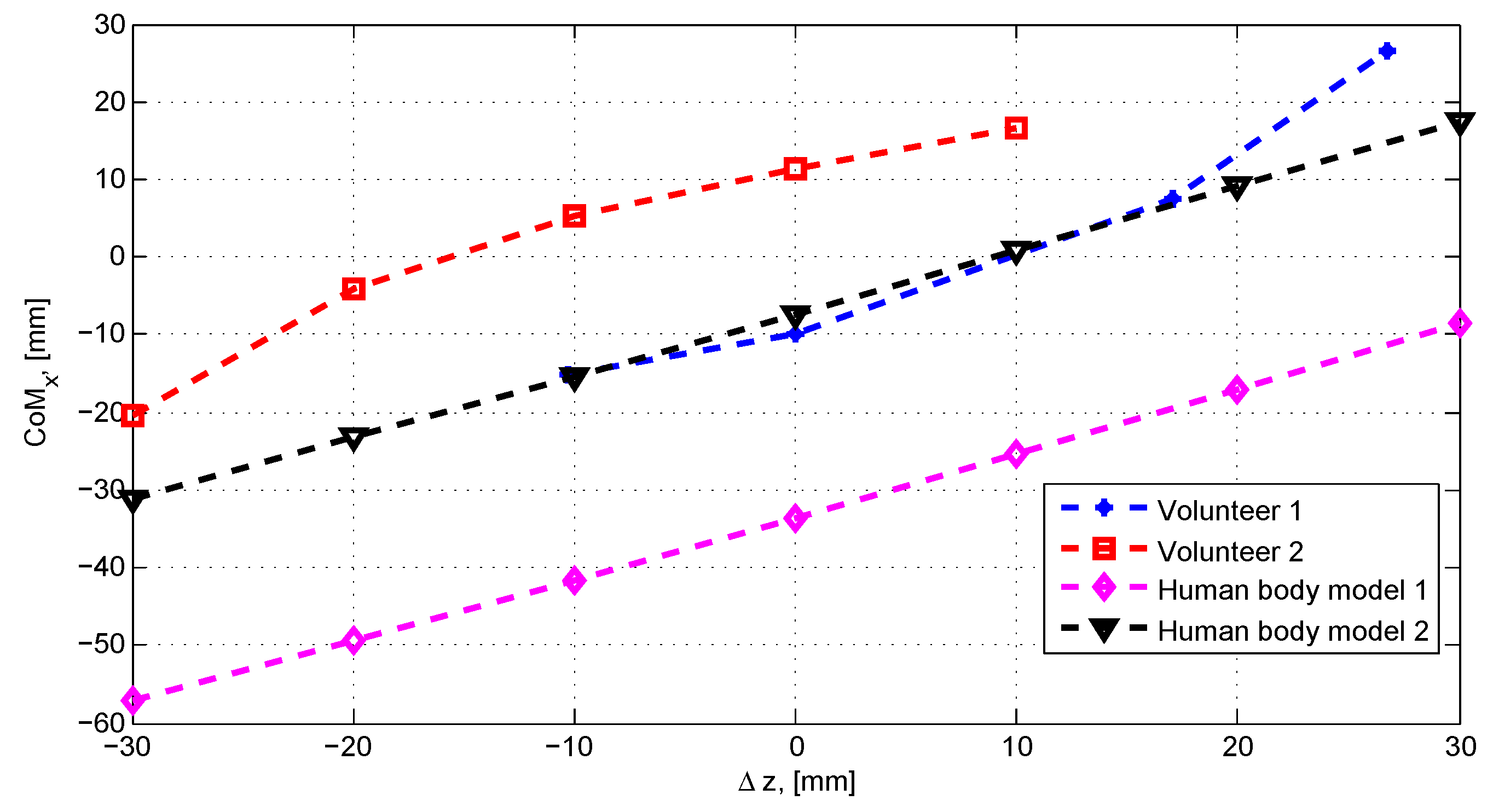
5.4.2. Experiment 2: Shift in the CoM Caused by a Force Plate Height Difference Shift
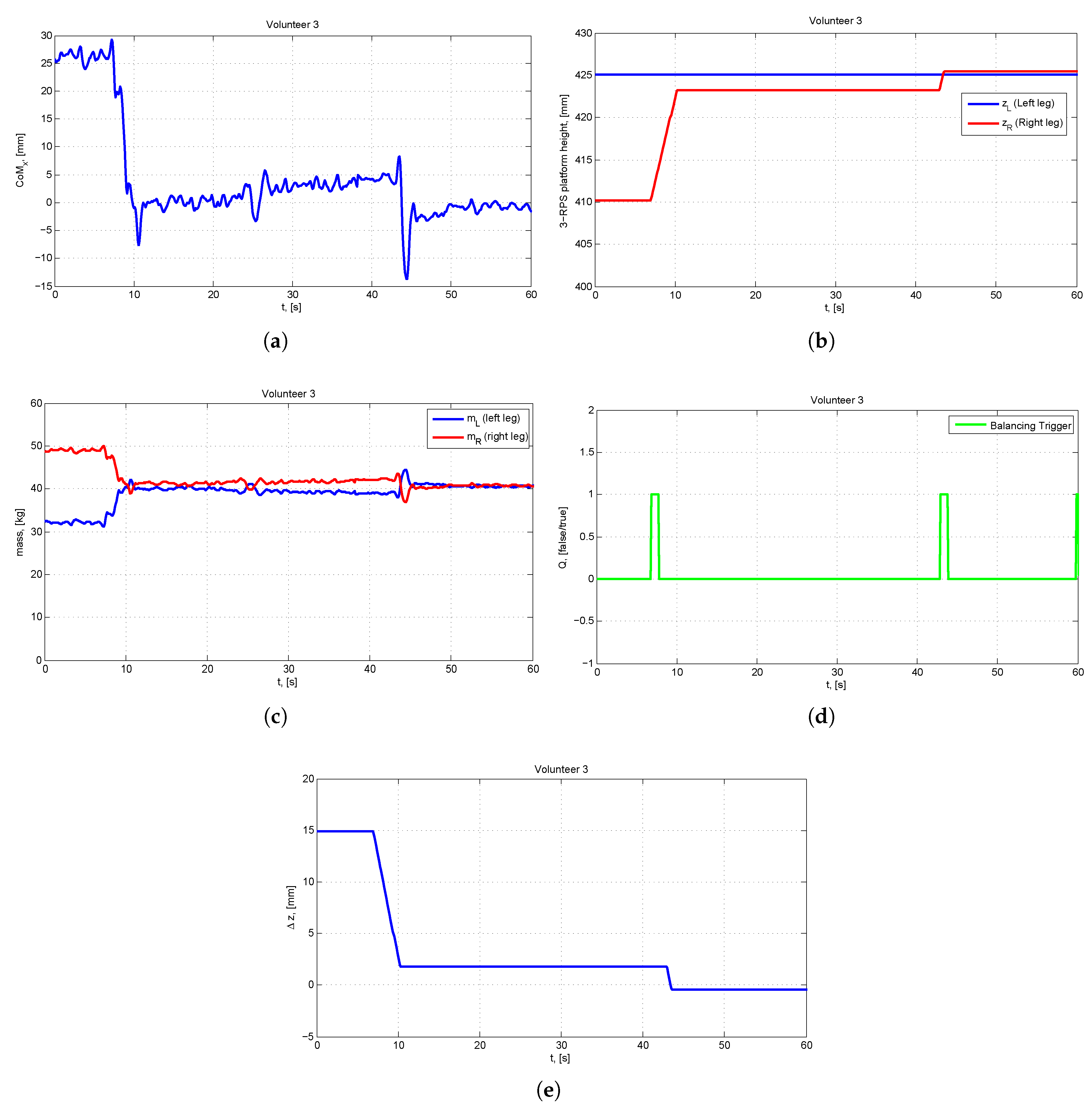
5.4.3. Experiment 3: A Healthy Volunteer with a Simulated LLD
6. Conclusions
Supplementary Files
Supplementary File 1Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LLD | Leg Length Discrepancy |
| CT | Computerized Tomography |
| MRI | Magnetic Resonance Imaging |
| ASIS | Anterior Inferior Iliac Spine |
| 3-RPS | 3-Revolute-Prismatic-Spherical |
| CoM | Center of Mass |
| CoP | Center of Pressure |
| 3-DOF | Three Degrees of Freedom |
| IKP | Inverse Kinematic Problem |
| FKP | Forward Kinematic Problem |
| IR | Infra-red |
| BMI | Body Mass Index |
References
- Eliks, M.; Ostiak-Tomaszewska, W.; Lisiński, P.; Koczewski, P. Does structural leg-length discrepancy affect postural control? Preliminary study. BMC Musculoskelet. Disord. 2017, 18, 346. [Google Scholar] [CrossRef] [PubMed]
- Azizan, N.A.; Basaruddin, K.S.; Salleh, A.F. The Effects of Leg Length Discrepancy on Stability and Kinematics-Kinetics Deviations: A Systematic Review. Appl. Bionics Biomech. 2018, 2018, 5156348. [Google Scholar] [CrossRef] [PubMed]
- Khamis, S.; Danino, B.; Springer, S.; Ovadia, D.; Carmeli, E. Detecting Anatomical Leg Length Discrepancy Using the Plug-in-Gait Model. Appl. Sci. 2017, 7, 926. [Google Scholar] [CrossRef]
- Khamis, S.; Danino, B.; Ovadia, D.; Carmeli, E. Correlation between Gait Asymmetry and Leg Length Discrepancy—What Is the Role of Clinical Abnormalities? Appl. Sci. 2018, 8, 1979. [Google Scholar] [CrossRef]
- Khamis, S.; Carmeli, E. The effect of simulated leg length discrepancy on lower limb biomechanics during gait. Gait Posture 2018, 61, 73–80. [Google Scholar] [CrossRef] [PubMed]
- Gurney, B. Leg length discrepancy. Gait Posture 2002, 15, 195–206. [Google Scholar] [CrossRef]
- Ali, A.; Walsh, M.; O’Brien, T.; Dimitrov, B.D. The importance of submalleolar deformity in determining leg length discrepancy. Surgeon 2014, 12, 20–205. [Google Scholar] [CrossRef][Green Version]
- Sabharwal, S.; Kumar, A. Methods for Assessing Leg Length Discrepancy. Clin. Orthop. Relat. Res. 2008, 466, 2910–2922. [Google Scholar] [CrossRef]
- Hanada, E.; Kirby, R.; Mitchell, M.; Swuste, J. Measuring leg-length discrepancy by the “iliac crest palpation and book correction” method: Reliability and validity. Arch. Phys. Med. Rehabil. 2001, 82, 938–942. [Google Scholar] [CrossRef]
- Khamis, S.; Springer, S.; Ovadia, D.; Krimus, S.; Carmeli, E. Measuring Dynamic Leg Length during Normal Gait. Sensors 2018, 18, 4191. [Google Scholar] [CrossRef]
- O’Brien, D.S.; Kernohan, G.; Fitzpatrick, C.; Hill, J.; Beverland, D. Perception of Imposed Leg Length Inequality in Normal Subjects. HIP Int. 2010, 20, 505–511. [Google Scholar] [CrossRef] [PubMed]
- Azizan, N.A.; Basaruddin, K.S.; Salleh, A.F.; Sakeran, H.; Sulaiman, A.R.; Cheng, E.M. The Effect of Structural Leg Length Discrepancy on Vertical Ground Reaction Force and Spatial—Temporal Gait Parameter: A Pilot Study. J. Telecommun. Electron. Comput. Eng. 2018, 10, 111–114. [Google Scholar]
- White, S.C.; Gilchrist, L.A.; Wilk, B.E. Asymmetric Limb Loading with True or Simulated Leg-Length Differences. Clin. Orthop. Relat. Res. 2004, 421, 287–292. [Google Scholar] [CrossRef] [PubMed]
- Swaminathan, V.; Cartwright-Terry, M.; Moorehead, J.; Bowey, A.; Scott, S. The effect of leg length discrepancy upon load distribution in the static phase (standing). Gait Posture 2014, 40, 561–563. [Google Scholar] [CrossRef] [PubMed]
- Abu-Faraj, Z.; MM, A.A.; RA, A.D. Leg Length Discrepancy: A Study on In-Shoe Plantar Pressure Distribution. In Proceedings of the 8th International Conference on Biomedical Engineering and Informatics (BMEI), Shenyang, China, 14–16 October 2015; pp. 381–385. [Google Scholar] [CrossRef]
- Vrhovski, Z.; Markov, M.; Pavlic, T.; Obrovac, K.; Mutka, A.; Nižetić, J. Design of a Mechanical Assembly for the Dynamic Evaluation of Human Body Posture. In Proceedings of the 16th International Scientific Conference on Production Engineering (CIM2017), Zadar, Croatia, 8–10 June 2017; pp. 237–242. [Google Scholar]
- Design of a Mechanical Assembly for the Dynamic Evaluation of Human Body Posture. Available online: https://youtu.be/C-4RpSqBi90 (accessed on 5 April 2019).
- Vrhovski, Z.; Obrovac, K.; Mutka, A.; Bogdan, S. Design, modeling and control of a system for dynamic measuring of leg length discrepancy. In Proceedings of the 21st International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 19–21 October 2017; pp. 693–698. [Google Scholar] [CrossRef]
- Vrhovski, Z.; Benkek, G.; Mutka, A.; Obrovac, K.; Bogdan, S. System for Compensating for Leg Length Discrepancy Based on the Estimation of the Centre of Mass of a Human Body. In Proceedings of the 26th Mediterranean Conference on Control and Automation (MED), Zadar, Croatia, 19–22 June 2018; pp. 637–642. [Google Scholar] [CrossRef]
- Lafond, D.; Duarte, M.; Prince, F. Comparison of three methods to estimate the center of mass during balance assessment. J. Biomech. 2004, 37, 1421–1426. [Google Scholar] [CrossRef]
- Robertson, D.; Caldwell, G.E.; Hamill, J.; Kamen, G.; Whittlesey, S.N. Research Methods in Biomechanics, 2nd ed.; Human Kinetics Publishers: Champaign, IL, USA, 2013. [Google Scholar]
- Ruiz-Hidalgo, N.C.; Blanco-Ortega, A.; Abúndez-Pliego, A.; Colín-Ocampo, J.; Arias-Montiel, M. Design and Control of a Novel 3-DOF Parallel Robot. In Proceedings of the International Conference on Mechatronics, Electronics and Automotive Engineering (ICMEAE), Cuernavaca, Mexico, 22–25 November 2016; pp. 66–71. [Google Scholar] [CrossRef]
- Garcia Gonzalez, L.; Campos, A. Maximal Singularity-Free Orientation Subregions Associated with Initial Parallel Manipulator Configuration. Robotics 2018, 7, 57. [Google Scholar] [CrossRef]
- Schadlbauer, J.; Walter, D.; Husty, M. The 3-RPS parallel manipulator from an algebraic viewpoint. Mech. Mach. Theory 2014, 75, 161–176. [Google Scholar] [CrossRef]
- Taghirad, H.D. Parallel Robots: Mechanics and Control; CRC Press: Boca Raton, FL, USA, 2013; pp. 77–95. [Google Scholar]
- Rad, C.; Manic, M.; Bälan, R.; Stan, S. Real time evaluation of inverse kinematics for a 3-RPS medical parallel robot usind dSpace platform. In Proceedings of the 3rd International Conference on Human System Interaction, Rzeszow, Poland, 13–15 May 2010; pp. 48–53. [Google Scholar] [CrossRef]
- Lukanin, V. Inverse kinematics, forward kinematics and working space determination of 3DOF parallel manipulator with S-P-R joint structure. Period. Polytech. Mech. Eng. 2005, 49, 39–61. [Google Scholar]
- Cotton, S.; Vanoncini, M.; Fraisse, P.; Ramdani, N.; Demircan, E.; Murray, A.; Keller, T. Estimation of the centre of mass from motion capture and force plate recordings: A study on the elderly. Appl. Bionics Biomech. 2011, 8, 67–84. [Google Scholar] [CrossRef]
- Eguchi, R.; Takahashi, M. Validity of the Nintendo Wii Balance Board for kinetic gait analysis. Appl. Sci. 2018, 8, 285. [Google Scholar] [CrossRef]
- Huang, C.W.; Sue, P.D.; Abbod, M.; Jiang, B.; Shieh, J.S. Measuring Center of Pressure Signals to Quantify Human Balance Using Multivariate Multiscale Entropy by Designing a Force Platform. Sensors 2013, 13, 10151–10166. [Google Scholar] [CrossRef] [PubMed]
- Vrhovski, Z.; Bogdan, S. Virtual Simulation Model for Evaluation and Compensation of Leg Length Discrepancy for Human Body Balancing. Available online: https://www.researchgate.net/publication/333668115_Virtual_Simulation_Model_for_Evaluation_and_Compensation_of_Leg_Length_Discrepancy_for_Human_Body_Balancing (accessed on 6 June 2019).
- Sheha, E.D.; Steinhaus, M.E.; Kim, H.J.; Cunningham, M.E.; Fragomen, A.T.; Rozbruch, S.R. Leg-Length Discrepancy, Functional Scoliosis, and Low Back Pain. JBJS Rev. 2018, 6, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y. Design and Validation of a Low-Cost Portable Device to Quantify Postural Stability. Sensors 2017, 17, 619. [Google Scholar] [CrossRef] [PubMed]

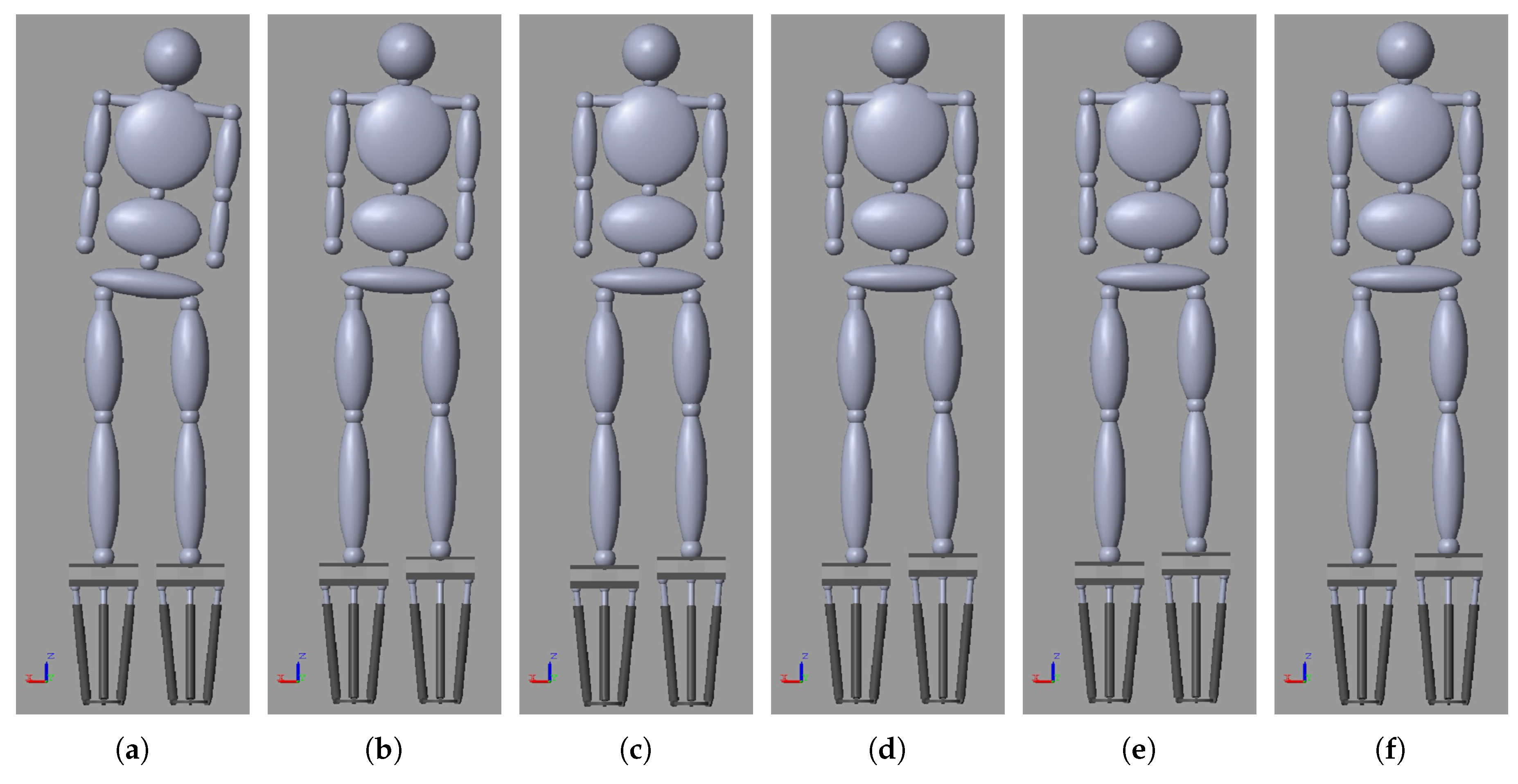
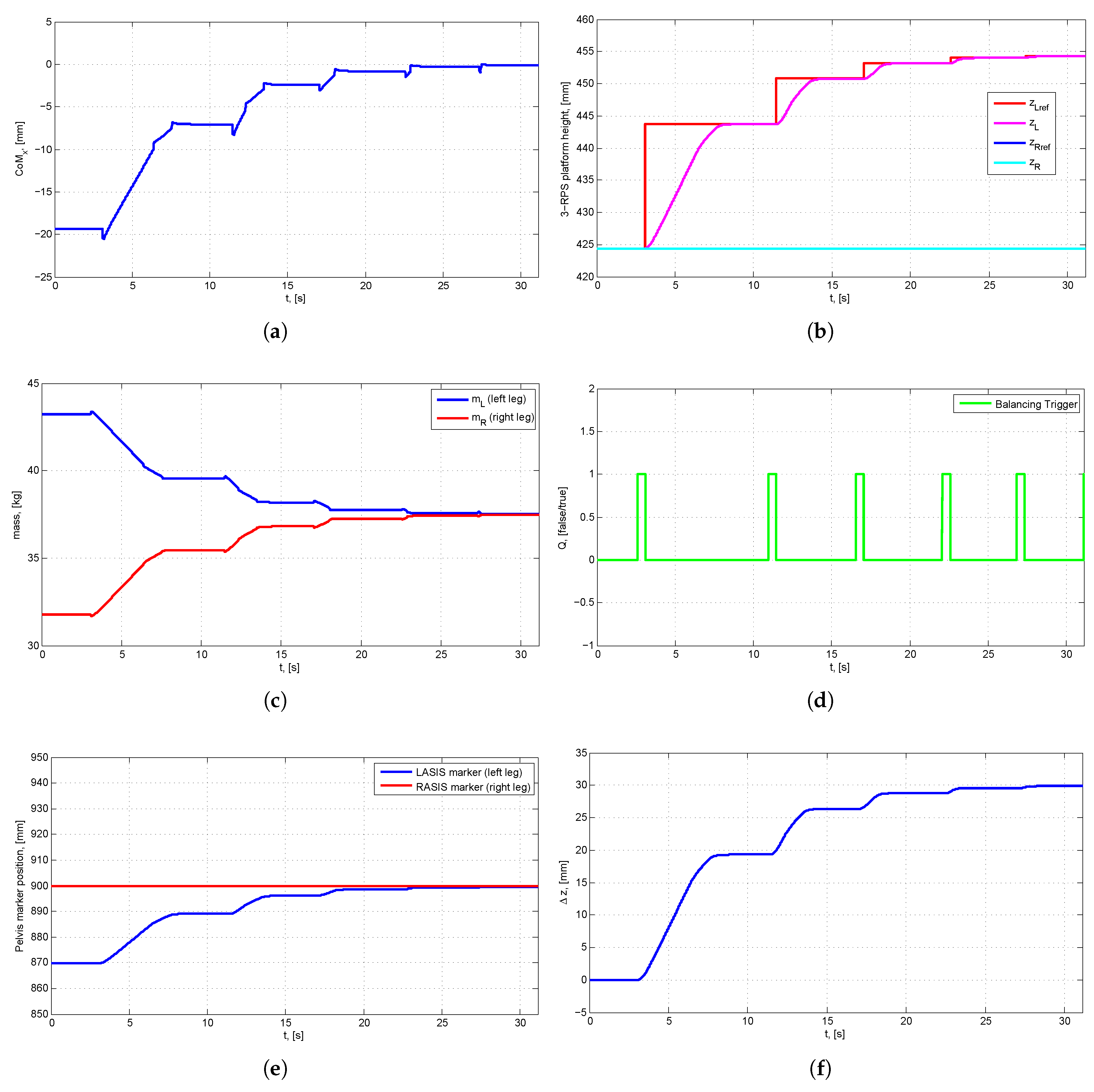



| Iteration | [mm] | [mm] | [mm] | [mm] | [kg] | [kg] | LASIS [mm] | RASIS [mm] |
|---|---|---|---|---|---|---|---|---|
| k = 0 | −19.35 | 424.40 | 424.40 | 0 | 43.22 | 31.78 | 869.8 | 899.8 |
| k = 1 | −7.06 | 443.75 | 424.40 | 19.35 | 39.53 | 35.47 | 889.1 | 899.8 |
| k = 2 | −2.42 | 450.81 | 424.40 | 26.41 | 38.19 | 36.81 | 896.1 | 899.8 |
| k = 3 | −0.81 | 453.23 | 424.40 | 28.83 | 37.73 | 37.27 | 898.5 | 899.8 |
| k = 4 | −0.27 | 454.04 | 424.40 | 29.64 | 37.58 | 37.42 | 899.4 | 899.8 |
| k = 5 | −0.09 | 454.31 | 424.40 | 29.91 | 37.53 | 37.47 | 899.7 | 899.8 |
| Iteration | [mm] | [mm] | [mm] | [mm] | [kg] | [kg] | LASIS [mm] | RASIS [mm] |
|---|---|---|---|---|---|---|---|---|
| k = 0 | 14.88 | 424.40 | 424.40 | 0 | 33.39 | 41.61 | 894.8 | 869.8 |
| k = 1 | 4.60 | 424.40 | 439.28 | −14.88 | 36.22 | 38.78 | 894.8 | 884.6 |
| k = 2 | 1.48 | 424.40 | 443.88 | −19.48 | 37.09 | 37.91 | 894.8 | 889.2 |
| k = 3 | 0.47 | 424.40 | 445.36 | −20.96 | 37.37 | 37.63 | 894.8 | 890.7 |
| k = 4 | 0.17 | 424.40 | 445.83 | −21.43 | 37.46 | 37.54 | 894.8 | 891.2 |
| Variable | Mass [kg] | [%] | [%] | Height [cm] | LASIS [cm] | RASIS [cm] | BMI [kg m] | |
|---|---|---|---|---|---|---|---|---|
| Mean | −2.99 | 75.26 | 51.12 | 48.88 | 174.9 | 101.2 | 101.2 | 24.45 |
| SD | 8.45 | 14.15 | 2.95 | 2.95 | 10.6 | 7.1 | 7.1 | 2.89 |
| Min | −27.08 | 53.68 | 44.90 | 41.94 | 155.0 | 88.0 | 88.0 | 18.72 |
| Max | 15.38 | 108.92 | 58.06 | 55.10 | 193.0 | 115.0 | 115.0 | 29.76 |
| Subject | Mass [kg] | [kg] | [kg] | Height [cm] | LASIS [cm] | RASIS [cm] | ||
|---|---|---|---|---|---|---|---|---|
| Mean [mm] | SD [mm] | |||||||
| Volunteer 1 | 13.25 | 0.798 | 91.15 | 40.29 | 50.86 | 178 | 104 | 104 |
| Volunteer 2 | −9.80 | 0.490 | 55.34 | 29.44 | 25.90 | 157 | 96 | 96 |
| Volunteer 3 | −0.21 | 0.861 | 81.14 | 40.65 | 40.49 | 179 | 106 | 106 |
| Iteration | [mm] | [mm] | [mm] | [mm] | [kg] | [kg] |
|---|---|---|---|---|---|---|
| k = 0 | 26.4 | 425.0 | 410.0 | 15.0 | 32.16 | 48.98 |
| k = 1 | 4.4 | 425.0 | 423.2 | 1.8 | 39.21 | 41.94 |
| k = 2 | −0.6 | 425.0 | 425.4 | −0.4 | 40.73 | 40.46 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrhovski, Z.; Obrovac, K.; Nižetić, J.; Mutka, A.; Klobučar, H.; Bogdan, S. System for Evaluation and Compensation of Leg Length Discrepancy for Human Body Balancing. Appl. Sci. 2019, 9, 2504. https://doi.org/10.3390/app9122504
Vrhovski Z, Obrovac K, Nižetić J, Mutka A, Klobučar H, Bogdan S. System for Evaluation and Compensation of Leg Length Discrepancy for Human Body Balancing. Applied Sciences. 2019; 9(12):2504. https://doi.org/10.3390/app9122504
Chicago/Turabian StyleVrhovski, Zoran, Karlo Obrovac, Josip Nižetić, Alan Mutka, Hrvoje Klobučar, and Stjepan Bogdan. 2019. "System for Evaluation and Compensation of Leg Length Discrepancy for Human Body Balancing" Applied Sciences 9, no. 12: 2504. https://doi.org/10.3390/app9122504
APA StyleVrhovski, Z., Obrovac, K., Nižetić, J., Mutka, A., Klobučar, H., & Bogdan, S. (2019). System for Evaluation and Compensation of Leg Length Discrepancy for Human Body Balancing. Applied Sciences, 9(12), 2504. https://doi.org/10.3390/app9122504







