Transferring of Continuous Variable Squeezed States in 20 km Fiber
Abstract
Featured Application
Abstract
1. Introduction
2. Theoretical Analysis
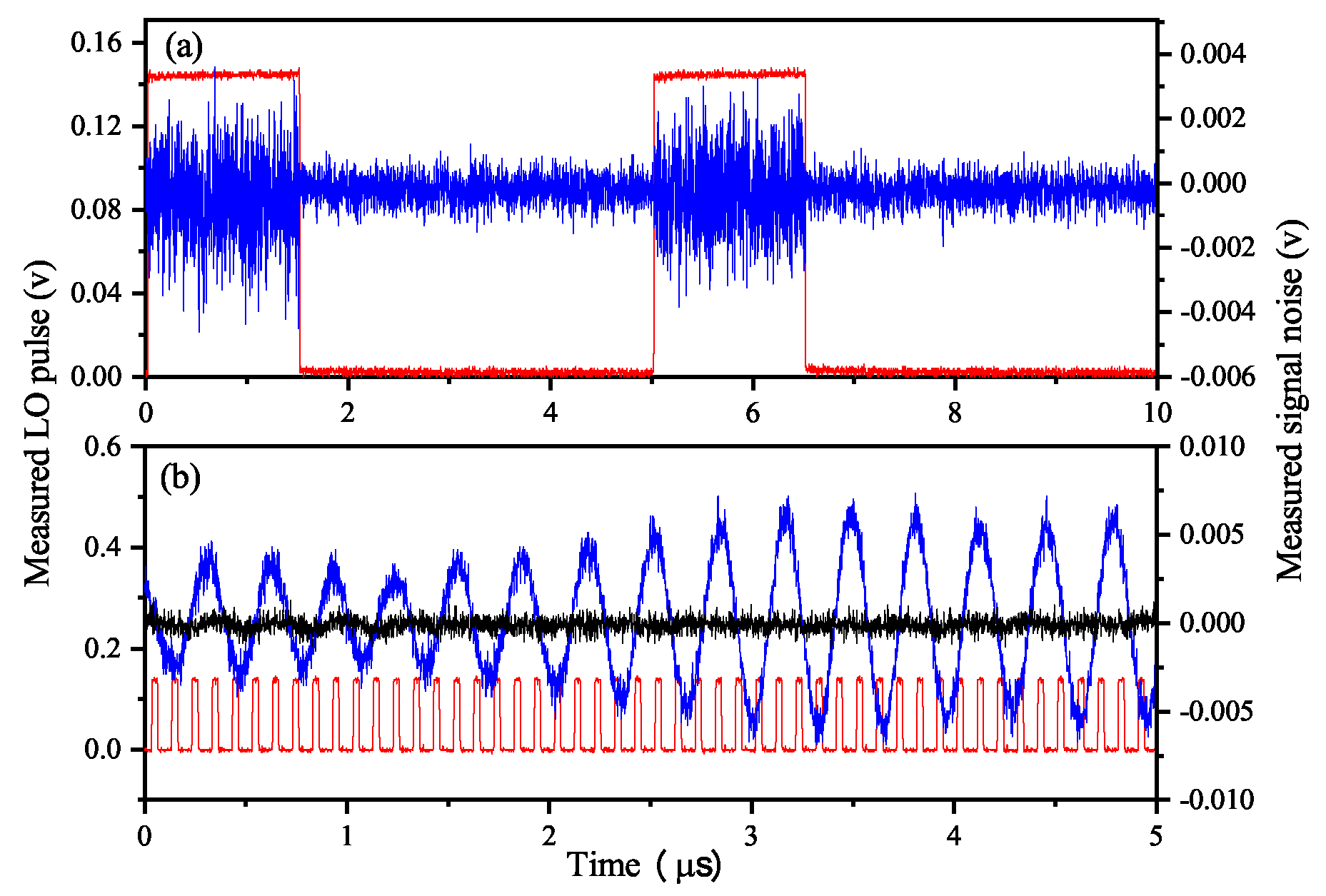
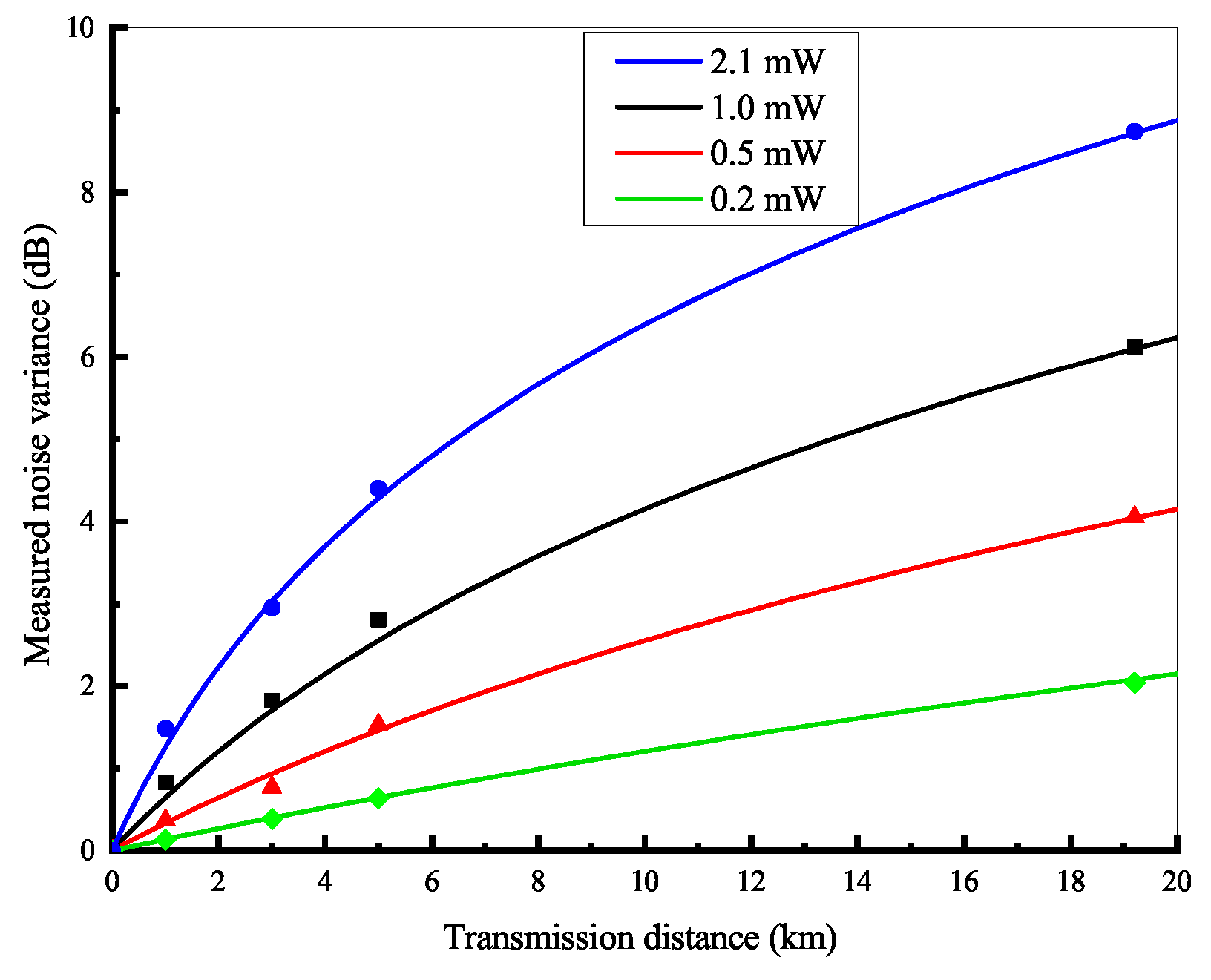
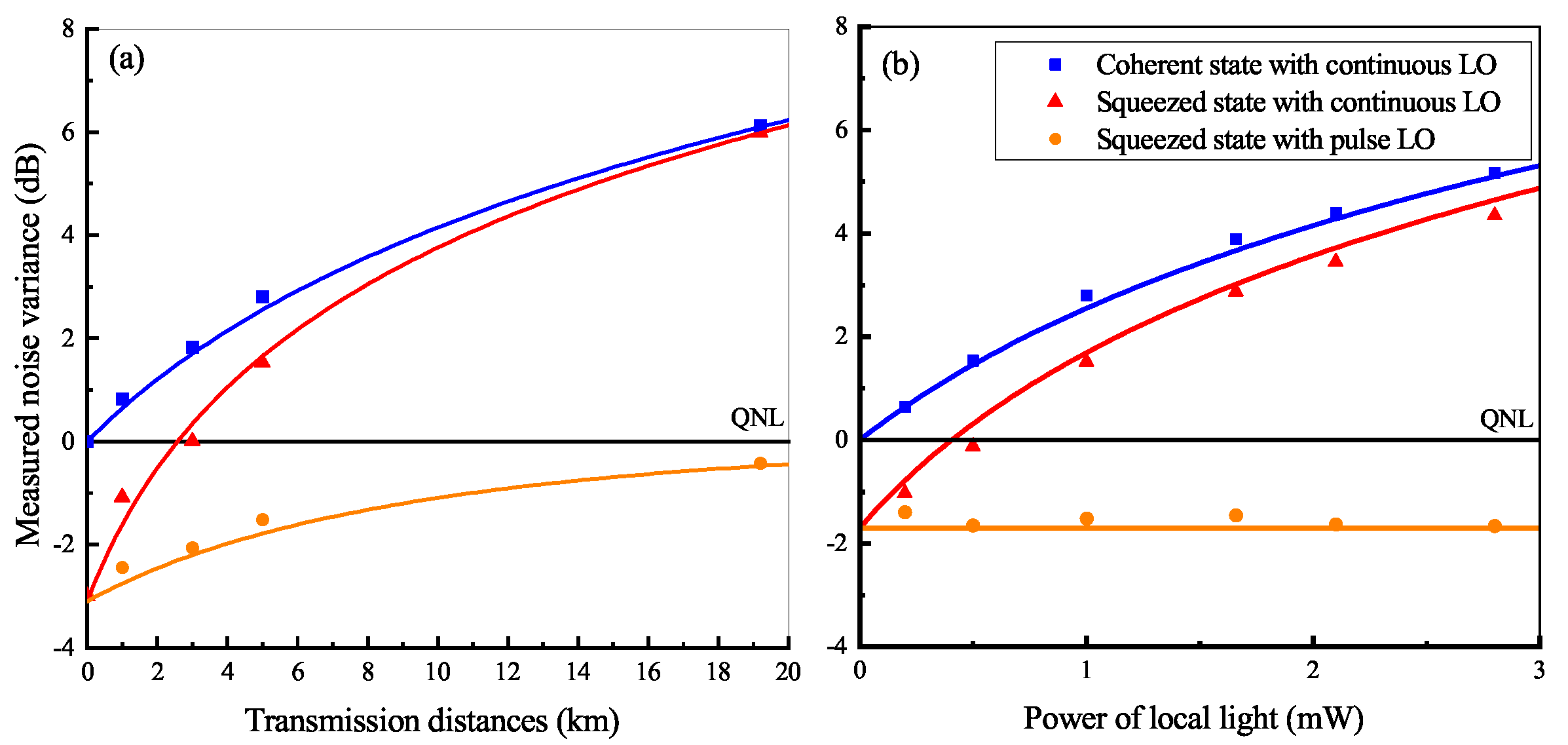
3. Experimental Setup and Results
4. Results
Author Contributions
Funding
Conflicts of Interest
References
- Braunstein, S.L.; van Loock, P. Quantum information theory with continuous variables. Rev. Mod. Phys. 2005, 77, 513. [Google Scholar] [CrossRef]
- Ou, Z.Y.; Pereira, S.F.; Kimble, H.J. Realization of the Einstein-Podolsky-Rosen paradox for continuous variables in nondegenerate parametric amplification. Appl. Phys. B 1992, 55, 265–278. [Google Scholar] [CrossRef]
- Huo, M.R.; Qin, J.L.; Yan, Z.H.; Jia, X.J.; Peng, K.C. Generation of two types of nonclassical optical states using an optical parametric oscillator with a PPKTP crystal. Appl. Phys. Lett. 2016, 109, 221101. [Google Scholar] [CrossRef]
- Vahlbruch, H.; Mehmet, M.; Danzmann, K.; Schnabel, R. Detection of 15 dB squeezed states of light and their application for the absolute calibration of photoelectric quantum efficiency. Phys. Rev. Lett. 2016, 117, 110801. [Google Scholar] [CrossRef]
- Wen, X.; Han, Y.S.; Liu, J.Y.; He, J.; Wang, J.M. Polarization squeezing at the audio frequency band for the Rubidium D1 line. Opt. Express 2017, 25, 20737–20748. [Google Scholar] [CrossRef] [PubMed]
- Furusawa, A.; Sorensen, J.L.; Braunstein, S.L.; Fuchs, C.A.; Kimble, H.J.; Polzik, E.S. Unconditional quantum teleportation. Science 1998, 282, 706–709. [Google Scholar] [CrossRef] [PubMed]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Cirac, J.I.; Ekert, A.K.; Huelga, S.F.; Macchiavello, C. Distributed quantum computation over noisy channels. Phys. Rev. A 1999, 59, 4249. [Google Scholar] [CrossRef]
- Goda, K.; Miyakawa, O.; Mikhailov, E.E.; Saraf, S.; Adhikari, R.; Mchenzie, K.; Ward, R.; Vass, S.; Weinstein, A.J.; Mavalvala, N. A quantum-enhanced prototype gravitational-wave detector. Nat. Phys. 2008, 4, 472–476. [Google Scholar] [CrossRef]
- Eberle, T.; Steinlechner, S.; Bauchrowitz, J.; Händchen, V.; Vahlbruch, H.; Mehmet, M.; Müller-Ebhardt, H.; Schnabel, R. Quantum enhancement of the zero-area sagnac interferometer topology for gravitational wave detection. Phys. Rev. Lett. 2010, 104, 251102. [Google Scholar] [CrossRef]
- Lunghi, T.; Brask, J.B.; Lim, C.C.W.; Lavigne, Q.; Bowles, J.; Martin, A.; Zbinden, H.; Brunner, N. Self-testing quantum random number generator. Phys. Rev. Lett. 2015, 114, 150501. [Google Scholar] [CrossRef] [PubMed]
- Aasi, J.; Abadie, J.; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. The LIGO scientific collaboration. Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light. Nat. Photonics 2013, 7, 613–619. [Google Scholar] [CrossRef]
- Nicolas, A.; Veissier, L.; Giner, L.; Giacobino, E.; Maxein, D.; Laurat, J. A quantum memory for orbital angular momentum photonic qubits. Nat. Photonics 2014, 8, 234–238. [Google Scholar] [CrossRef]
- Huo, M.R.; Qin, J.L.; Cheng, J.L.; Yan, Z.H.; Qin, Z.Z.; Su, X.L.; Jia, X.J.; Xie, C.D.; Peng, K.C. Deterministic quantum teleportation through fiber channels. Sci. Adv. 2018, 4, eaas9401. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Zhou, J.; Gong, X.; Guo, Y.; Zhang, Z.M.; He, G.Q. Continuous-variable measurement-device-independent multipartite quantum communication. Phys. Rev. A 2016, 93, 022325. [Google Scholar] [CrossRef]
- Hosseinidehaj, N.; Malaney, R. Quantum entanglement distribution in next-generation wireless communication systems. Phys. Rev. A 2015, 91, 022304. [Google Scholar] [CrossRef]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef]
- Ren, J.G.; Xu, P.; Yong, H.L.; Zhang, L.; Liao, S.K.; Yin, J.; Liu, W.Y.; Cai, W.Q.; Yang, M.; Li, L.; et al. Ground-to-satellite quantum teleportation. Nature 2017, 549, 70–73. [Google Scholar] [CrossRef]
- Pirandola, S.; Eisert, J.; Weedbrook, C.; Furusawa, A.; Braunstein, S.L. Advances in quantum teleportation. Nat. Photonics 2015, 9, 641–652. [Google Scholar] [CrossRef]
- Zhou, Y.Y.; Yu, J.; Yan, Z.H.; Jia, X.J.; Zhang, J.; Xie, C.D.; Peng, K.C. Quantum secret sharing among four players using multipartite bound entanglement of an optical field. Phys. Rev. Lett. 2018, 121, 150502. [Google Scholar] [CrossRef]
- Bowen, W.P.; Treps, N.; Buchler, B.C.; Schnabel, R.; Ralph, T.C.; Bachor, H.A.; Symul, T.; Lam, P.K. Experimental investigation of continuous variable quantum teleportation. Phys. Rev. A 2003, 67, 032302. [Google Scholar] [CrossRef]
- Takei, N.; Aoki, T.; Koike, S.; Yoshino, K.; Wakui, K.; Yonezawa, H.; Hiraoka, T.; Mizuno, J.; Takeoka, M.; Ban, M.; et al. Experimental demonstration of quantum teleportation of a squeezed state. Phys. Rev. A 2005, 72, 042304. [Google Scholar] [CrossRef]
- Heim, B.; Peuntinger, C.; Killoran, N.; Khan, I.; Wittmann, C.; Marquardt, C.; Leuchs, G. Atmospheric continuous-variable quantum communication. New J. Phys. 2014, 16, 113018. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Li, Z.; Yu, S.; Gu, W.; Peng, X.; Guo, H. Continuous-variable measurement-device-independent quantum key distribution using squeezed states. Phys. Rev. A 2014, 90, 052325. [Google Scholar] [CrossRef]
- Li, Y.M.; Wang, N.; Wang, X.Y.; Bai, Z.L. Influence of guided acoustic wave Brillouin scattering on excess noise in fiber-based continuous variable quantum key distribution. J. Opt. Soc. Am. B 2014, 31, 2379. [Google Scholar] [CrossRef]
- Peuntinger, C.; Heim, B.; Muller, C.R.; Gabriel, C.; Marquardt, C.; Leuchs, G. Distribution of squeezed states through an atmospheric channel. Phys. Rev. Lett. 2014, 113, 060502. [Google Scholar] [CrossRef]
- Grosshans, F.; Assche, G.V.; Wenger, J.; Brouri, R.; Cerf, N.J.; Grangier, P. Quantum key distribution using gaussian-modulated coherent states. Nature 2003, 421, 238–241. [Google Scholar] [CrossRef]
- Huang, D.; Lin, D.; Wang, C.; Liu, W.Q.; Fang, S.H.; Peng, J.Y.; Huang, P.; Zeng, G.H. Continuous-variable quantum key distribution with 1 Mbps secure key rate. Opt. Express 2015, 23, 17511–17519. [Google Scholar] [CrossRef]
- Valivarthi, R.; Puigibert, M.I.G.; Zhou, Q.; Aguilar, G.H.; Verma, V.B.; Marsili, F.; Shaw, M.D.; Nam, S.W.; Oblak, D.; Tittel, W. Biunitary constructions in quantum information. Nat. Photonics 2016, 10, 676–680. [Google Scholar] [CrossRef]
- Feng, J.X.; Wan, Z.J.; Li, Y.J.; Zhang, K.S. Distribution of continuous variable quantum entanglement at a telecommunication wavelength over 20 km of optical fiber. Opt. Lett. 2017, 42, 3399–3402. [Google Scholar] [CrossRef]
- Wang, N.; Du, S.N.; Liu, W.Y.; Wang, X.Y.; Li, Y.M.; Peng, K.C. Long-Distance Continuous-Variable Quantum Key Distribution with Entangled States. Phys. Rev. Appl. 2018, 10, 064028. [Google Scholar] [CrossRef]
- Xuan, Q.D.; Zhang, Z.S.; Voss, P.L. A 24 km fiber-based discretely signaled continuous variable quantum key distribution system. Opt. Express 2009, 17, 24244–24249. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.H.; Huo, N.; Li, J.M.; Li, X.Y. Long-distance distribution of the telecom band intensity difference squeezing generated in a fiber optical parametric amplifier. Opt. Lett. 2018, 43, 5559–5562. [Google Scholar] [CrossRef] [PubMed]
- Shelby, R.M.; Levenson, M.D.; Bayer, P.W. Guided acoustic-wave Brillouin scattering. Phys. Rev. B 1985, 31, 5244–5252. [Google Scholar] [CrossRef]
- Shelby, R.M.; Levenson, M.D.; Bayer, P.W. Resolved forward Brillouin scattering in optical fiber. Phys. Rev. Lett. 1985, 54, 939–942. [Google Scholar] [CrossRef] [PubMed]
- Jouguet, P.; Kunz-Jacques, S.; Leverrier, A.; Grangier, P.; Diamanti, E. Experimental demonstration of long-distance continuous-variable quantum key distribution. Nat. Photonics 2013, 7, 378–381. [Google Scholar] [CrossRef]
- Qi, B.; Huang, L.L.; Qian, L.; Lo, H.K. Experimental study on Gaussian-modulated coherent states quantum key distribution over standard telecom fiber. Phys. Rev. A 2007, 76, 052323. [Google Scholar] [CrossRef]
- Lodewyck, J.; Bloch, M.; Garcia-Patron, R.; Fossier, S.; Karpov, E.; Diamanti, E.; Debuisschert, T.; Cerf, N.J.; Tualle-Brouri, R.; McLaughlin, S.W.; et al. Quantum key distribution over 25 km with an all-fiber continuous-variable system. Phys. Rev. A 2007, 76, 042305. [Google Scholar] [CrossRef]
- Huo, M.R.; Qin, J.L.; Sun, Y.R.; Cheng, J.L.; Yan, Z.H.; Jia, X.J. Generation of Intensity Difference Squeezed State of Light at Optical Fiber Communication Wavelength. J. Quantum Opt. 2015, 24, 134–140. [Google Scholar]
- Yang, W.H.; Wang, Y.J.; Zheng, Y.H.; Lu, H.D. Comparative study of the frequency-doubling performance on ring and linear cavity at short wavelength region. Opt. Express 2015, 23, 243738. [Google Scholar] [CrossRef]
- Zhao, H.; Ma, H.Q.; Li, Y.L.; Wu, L.A. Polarization control for optical fiber quantum cryptography. J. Quantum Opt. 2015, 11, 74–78. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, J.; Cheng, J.; Liang, S.; Yan, Z.; Jia, X.; Peng, K. Transferring of Continuous Variable Squeezed States in 20 km Fiber. Appl. Sci. 2019, 9, 2397. https://doi.org/10.3390/app9122397
Qin J, Cheng J, Liang S, Yan Z, Jia X, Peng K. Transferring of Continuous Variable Squeezed States in 20 km Fiber. Applied Sciences. 2019; 9(12):2397. https://doi.org/10.3390/app9122397
Chicago/Turabian StyleQin, Jiliang, Jialin Cheng, Shaocong Liang, Zhihui Yan, Xiaojun Jia, and Kunchi Peng. 2019. "Transferring of Continuous Variable Squeezed States in 20 km Fiber" Applied Sciences 9, no. 12: 2397. https://doi.org/10.3390/app9122397
APA StyleQin, J., Cheng, J., Liang, S., Yan, Z., Jia, X., & Peng, K. (2019). Transferring of Continuous Variable Squeezed States in 20 km Fiber. Applied Sciences, 9(12), 2397. https://doi.org/10.3390/app9122397




