1. Introduction
The etiology of trauma-induced vocal fold (VF) lesions, such as nodules and polyps, has been long associated with detrimental vocal patterns and compensatory behaviors that result in increased VF collision pressures [
1,
2,
3,
4,
5]. Unfortunately, a direct in vivo quantification of VF collision pressure is not feasible in routine clinical examinations due to the invasive nature of the procedure, i.e., placing a pressure probe in the glottis constitutes a risk for the VF tissue [
6,
7,
8]. Therefore, current objective assessments of VF collision in clinical environments relies on indirect methods (e.g., aerodynamic [
4], acoustic [
9], ambulatory [
10], etc.) and does not take advantage of the most direct and common procedure to clinically assess VF function: Laryngeal endoscopy. At the same time, the recent development of laryngeal high-speed videoendoscopy (HSV), with frame rates above 4000 fps, has significantly improved the temporal resolution of this medical examination, thus allowing for an accurate visualization and quantification of vocal fold vibration patterns that are challenging to capture using standard stroboscopic imaging methods [
11,
12,
13,
14]. In spite of these benefits, the adoption of HSV into the clinical practice has been slow, in part because current analysis methods and tools to navigate the data are not yet sufficiently intuitive or useful to the clinician [
11,
12]. Thus, there is a clear need for enhanced analysis methods for laryngeal endoscopy, and given the high prevalence of nodules and polyps [
15], the estimation of VF collision pressure directly from endoscopic observations is poised to have a strong impact in the clinical practice.
In spite of the significant interest for directly assessing VF collision, only a few studies have been able to gather contact pressure data in human subjects by placing pressure probes at the glottis [
6,
7,
8]. Sensing contact pressure is a challenge in terms of probe size (flow and tissue interference), sensor bandwidth, risk to the VF tissue, and subject tolerance during the examination. Nevertheless, these pilot studies reported values for peak collision pressure of 0.5 to 3.0 kPa [
7] in normal participants and 1 to 4 kPa in subjects with organic pathologies, wherein the values were larger near the lesions [
6]. A stronger collision has been associated with an increased voice intensity [
8]. These results are consistent with intraglottal pressures reported from excised canine hemilarynges [
16,
17,
18], where it was observed that the impact produced sharp pressure pulses that were positively correlated with subglottal pressure and VF elongation.
In addition to clinical measures, numerical approaches have been used to investigate the role of collision pressures in the development of VF lesions. Using internal stress or ad hoc solutions for computing contact, finite element studies have shown that (1) the elastic forces within the VF tissue are responsible for the impact strength [
19]; (2) there is a relationship between the subglottal pressure and peak collision [
19,
20]; and (3) VF impact causes a transient in the tissue stress that can be related to fatigue damage [
20] and a reduction of hydration [
21]. More recently, models of collision have incorporated descriptions of fluid displacement in the VF cover [
22] and asymmetric conditions [
23] that better represent the underlying physics; these studies yielded VF contact pressures in the same range as the experimental data.
Silicone VF replicas have also been used to study VF collision [
24,
25]. In these studies, a digital image correlation (DIC) approach and a Hertzian impact model [
26,
27] were utilized to quantify surface strain distributions on the superior VF surface and to obtain collision pressures in silicone models of the VFs. The Hertzian contact model has also been used to quantify collision forces in numerically reduced order models of the vocal folds [
28,
29]. The Hertz contact theory provides a framework for quantifying non-adhesive elastic contact mechanics in terms of effective contact surface and material deformation by means of an apparent penetration. The general method has been validated against nonlinear finite element models, where it has been shown that it is a valid approach at small deformations [
30]. When studying VF contact with Hertz contact [
24,
25], the VF geometry has been assumed to conform to a spherical shape and the Hertz penetration depth was estimated from surface strain extrapolation for known synthetic materials. The resulting contact pressure yielded results comparable to prior experimental studies [
8,
16]. It is worth noting that DIC is currently not feasible in vivo, since there is no safe way to apply a speckle pattern to the VF tissue. In addition and up to this point, the Hertzian approach required a calibration stage for the laryngeal HSV to compute the exact contact surface and apparent penetration in physical units. Raw HSV recordings can only provide relative VF dimensions. For the in vivo experiments, this problem is solved by projecting an additional laser grid on the glottis that is used to determine the scale with offline processing. However, the projected grid can introduce problems in the lighting conditions, can affect the temporal resolution as the grid can be difficult to observe at high frame rates, and requires custom made hardware [
13,
14,
31,
32]. Note that Hertz contact pressure also requires knowledge (or estimation) of VF tissue properties that are difficult, if not impossible, to directly measure in vivo.
Despite the simplicity and apparent validity of the Hertzian approach for estimating VF contact pressure in vivo, there are limitations that need to be addressed: (1) A possible bias of VF collision pressure since the superior surface stress may yield larger deformations than that of the actual contacting tissue; (2) the use of a non-physiological VF contact geometry (i.e., contact between two spheres); (3) the requirement of calibrated laryngeal HSV to obtain physical dimensions; and (4) the need for VF tissue properties (Young’s modulus and Poisson’s ratio) that are difficult to measure in practice.
The aim of this work is to obtain in vivo estimations of the VF contact pressure directly from laryngeal HSV recordings using a modified version of Hertz contact that addresses the current limitations of the approach. We hypothesize that the apparent penetration and contact surface can be approximated solely from raw HSV videos, which will allow an estimation of the collision forces directly from the observed kinematics. We expect that these direct estimations are simple enough to be applied in a clinical setting. Specifically, we propose a Hertz contact geometry based on two contacting cylinders both to improve the physiological representation of VF contact and to remove the need for a calibrated HSV system. In this formulation, contact pressure is normalized by the tissue properties and a correction factor is introduced to remove the potential bias in estimating contact from employing only a superior view; this enables a focus on same-subject variations.
At the same time, we construct an underlying elastic model with an appropriate stiffness and damping to relate deformation and apparent Hertz tissue penetration and to account for prestress conditions. Finally, to interface the proposed elastic model with a non-colliding condition, a Kalman filter approach is proposed. The approach is contrasted against a separate numerical VF model, silicone VF model experiments, reported experimental data, and in vivo HSV videos to allow for comprehensive insights.
2. Contact Pressure Estimation from Laryngeal High-Speed Video
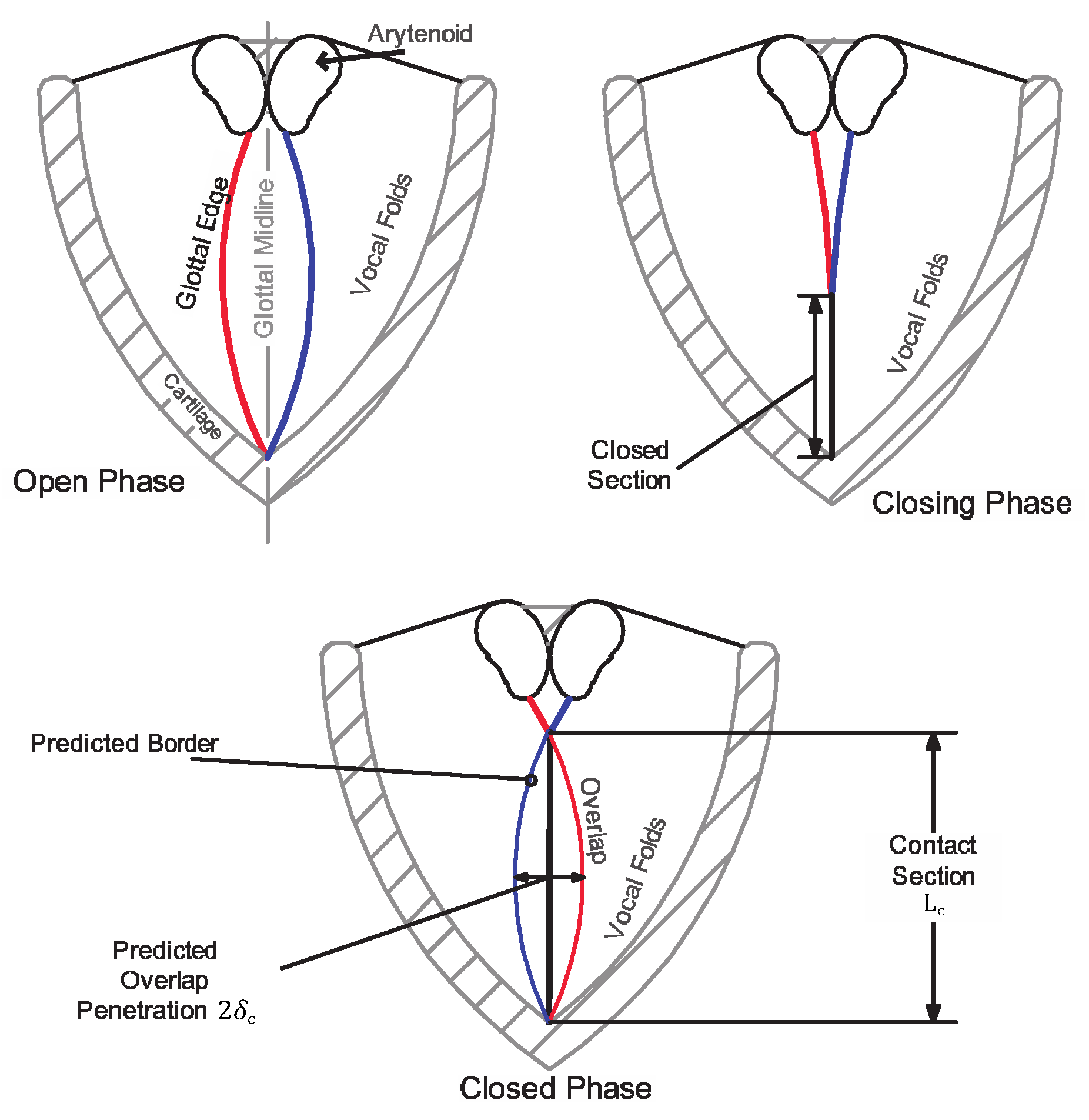
Herein, we propose a method for estimating the contact pressure experienced by colliding vocal folds based purely on kinematic and geometric information extracted from laryngeal a high-speed video. We refer to this method as Contact Pressure Analysis (CPA). Briefly, the motion of each observed VF edge is extracted from HSV during the open phase of the glottal cycle. The trajectories of the two folds are tracked until collision at which point a simple spring-mass-damper VF model is employed to predict the fictitious overlap of the colliding folds such that the trajectory of each edge matches the observations in the bookending opening phases. It is assumed that the rebounding force due to collision can be estimated using a Hertz contact model, wherein the fictitious overlap is related to the penetration depth for contact between elastic bodies. A schematic of the procedure is illustrated in
Figure 1, which shows the VF edges in the open phase and the fictitious penetration depth
and contact length
during collision.
Implementation of the procedure consists of five stages: (1) video pre-processing to remove camera motion effects and to create a uniform viewing orientation; (2) VF edge detection to locate the projected medial surface of each vocal fold; (3) VF curve fitting to convert the extracted edge location data into a polynomial function; (4) VF edge tracking during the open and collision phases; and (5) contact pressure estimation through an adapted Hertzian contact model. This section is devoted to expanding on the details of each step in the proposed CPA method.
2.1. Video Pre-Processing
Videoendoscopy recordings normally have an undesirable rotation and low frequency movements related to endoscope manipulation. A motion compensation algorithm is first applied to remove low-frequency components [
33]. Rotation compensation is achieved by identifying the end-points of the glottis, the line connecting which is used to compute the angle of the anatomical structure with respect to the camera. This measured angle is then used to rotate the image such that the glottis is vertical in the image plane.
A Region of Interest (ROI) centered on the glottis and encompassing the entire glottal length and excursion distance of the VFs is identified for further analysis. A mask is applied to remove information outside of the ROI for each frame in the HSV sequence. A Cartesian coordinate system is defined with x oriented horizontally in the image (medial-lateral direction) and y oriented vertically (anterior-posterior direction).
The anterior and posterior attachment points of each vocal fold, expressed as and , respectively, are identified and recorded for later use. The straight line connecting the attachment points for each VF is assumed to be the rest position of that fold.
2.2. Edge Detection
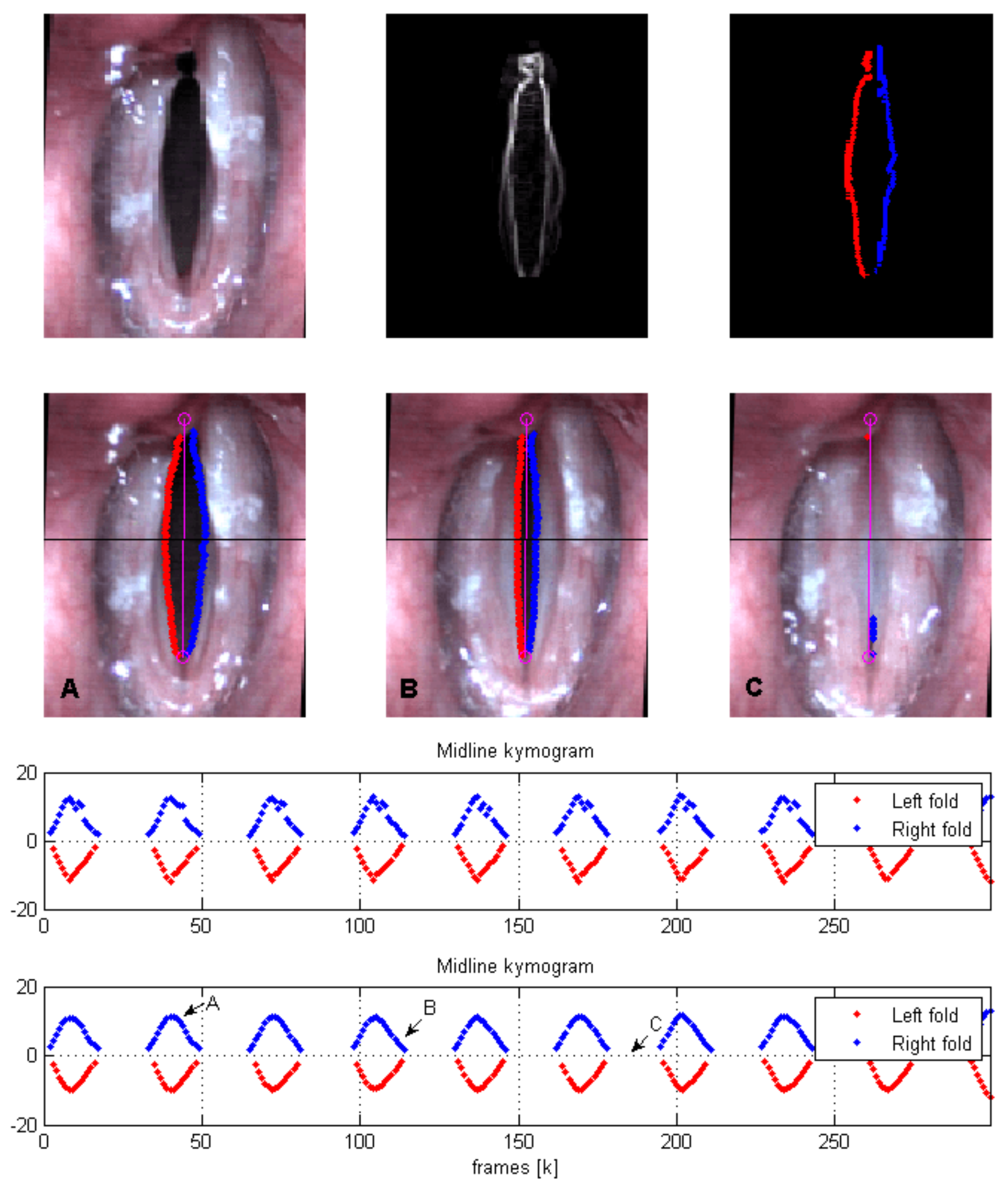
Each HSV frame is converted to a grayscale image and a morphological reconstruction operation (
imfill in MatLab) is applied to remove bright regions on the VF mucosa. A Prewitt gradient kernel with a user-defined threshold value is employed for edge detection, wherein the phase angle of the gradient vector is used to differentiate between the left and right vocal folds. Specifically, the location of the edge for a given vocal fold at a given
y location is determined from the weighted average of the magnitude of the gradient function
as
where
w is the width of the ROI in pixels. We note that data are only considered between
and
for a given fold.
Lastly, a temporal moving average with a 5 frame uniform kernel is applied to reduce detection errors and noise associated with lighting and/or quantization problems. The first two frames in
Figure 2 show the HSV ROI and the output of the edge detection algorithm, respectively.
2.3. Curve Fitting
In this step, a polynomial curve of order
p is fitted to the
points from the edge detection, defining the boundary of a given vocal fold with respect to the attachment line (the line defined by the attachment points
and
). A least squares (LS) estimator is used, taking into account the attachment points as root constraints for the solution. Letting
u and
v be the coordinates orthogonal to and aligned with the attachment line, respectively, the polynomial model
M can be defined as:
where
is the vector of unknown model parameters with superscript
indicating vector transposition and
,
, and
are the attachment point locations in the
coordinate system. Note that, assuming a rotation angle
of the attachment line with respect to the vertical axis, the relationship between the
and
coordinate systems is given by
Using an LS estimator solution, the polynomial parameters contained in
are computed as
where
where
,
, and
l is an integer ranging from 1 to
D, with
D representing the number of points defining the glottal edge detected in the previous stage. The velocity of the glottal edge is embedded in the rate of change of the coefficients
, which can be obtained via differentiating between frames as
where the subscript
k is the frame index and
is the time lapse between successive HSV frames.
The third frame in
Figure 2 shows the output of the edge detection scheme. The second row of the figure shows how the edges are tracked from an open phase to a closed phase. Midline kymograms of the VF trajectories during the open phases are plotted at the bottom of the figure for both VFs.
2.4. Edge Tracking
The tracking stage treats VF collision as a state estimation problem in the presence of noise and lost data. A Kalman Filter (KF) is implemented to predict the value and rate of change of the coefficients during the contact phase, wherein
and
are observations for the filter. A dynamical model is needed for the KF process for which we assume a spring-mass-damper representation for each VF connected to their respective attachment lines (defined in the pre-processing stage). The mass in this system is normalized for simplicity. Thus, the structural VF model is given by
where
is the state variable of a particular coefficient
in
at the instant
k,
are observations of the state (which we assume is available with
C as the identity matrix),
and
are the process and measurement noise (uncorrelated and Gaussian distributed with variances
and
, respectively),
K is the coefficient stiffness, and
b is the damping parameter of the model.
The spring-mass-damper model needs to operate at a particular resonance , for which we define stiffness K and damping b values as functions of the control parameters and as
Typical damping values associated with
are set between (0 to
). The resonance
is calculated automatically from the kinematic information
at the previous instant of impact (
), using these as initial conditions. Then, the known analytic solution for the initial conditions is used to coincide the rebounding position
at the end of contact (
) with its analytic value. Thus, the proposed scheme adapts the elastic contact properties (stiffness and damping) to match the fundamental frequency of the VFs, which allows for the capture of pre-stress conditions. Thus, we need to find a particular resonance frequency
that satisfies
where
. The
parameter controls the required stiffness of the model to mimic a damped harmonic oscillation during collision.
When the edges are visible, this contact model is not needed and, thus, is no longer used. To define when KF estimations are required, we calculate a “non-detected points ratio”
and an uncertainty factor
as
where
is the upper bound of all possible detected points at the edge,
is the actual detected points,
is a gain factor, and
is an uncertainty threshold.
When
is low, for example,
tends to be larger than the uncertainly threshold and
goes to one; that is, there are too many lost data points, the polynomial fit is poor, and thus, KF estimations are needed. The KF implementation considers the uncertainty factor
from Equation (
12) and follows
where the coefficient index
i has been dropped for simplicity. The estimated outputs are defined as
, which are a linear combination of the observations
, and KF estimated observations
that are related through
We note that controls the behavior of the filter; by selecting the best available curve coefficients, the evolution of each curve is completed smoothly throughout collision.
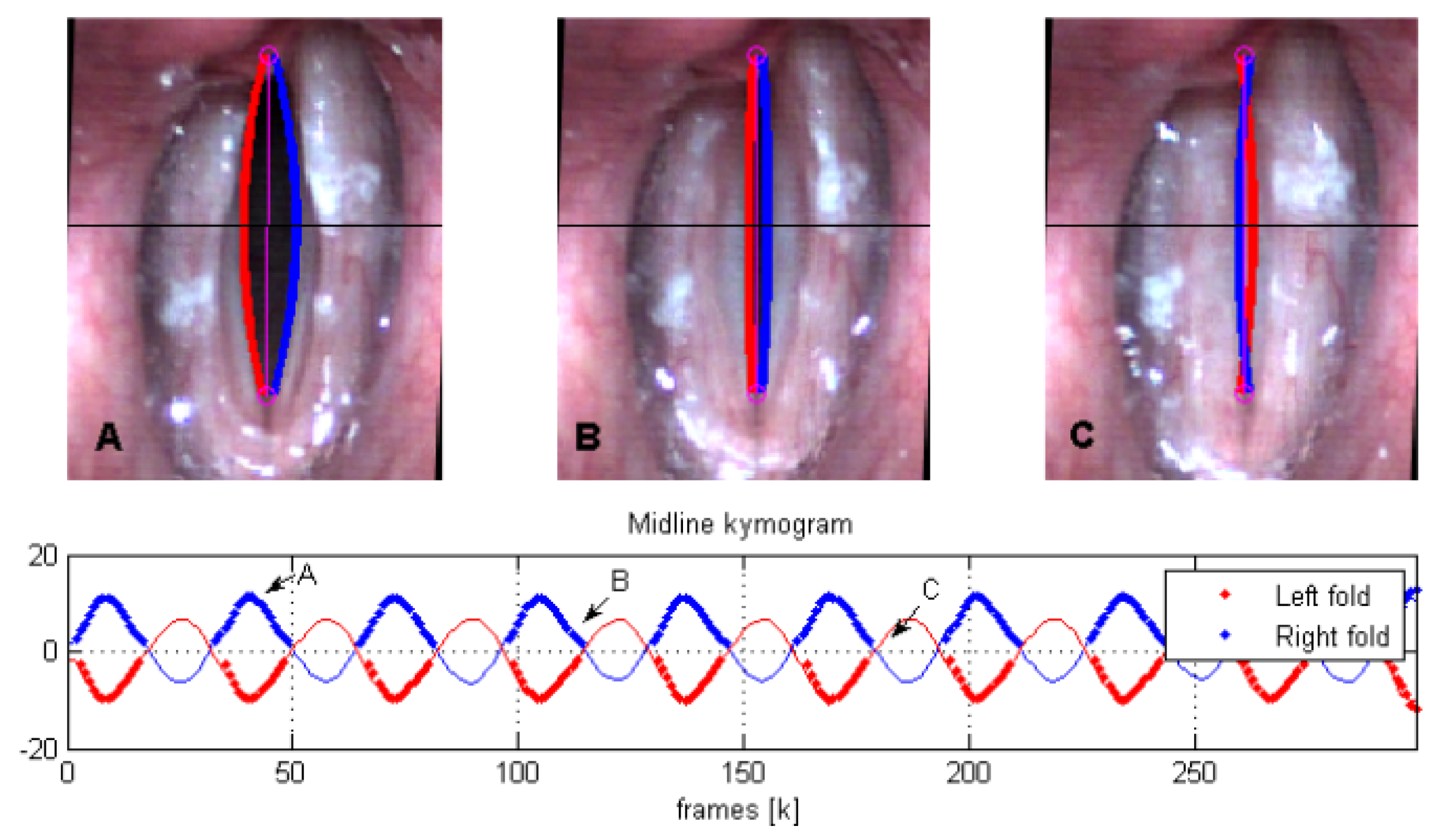
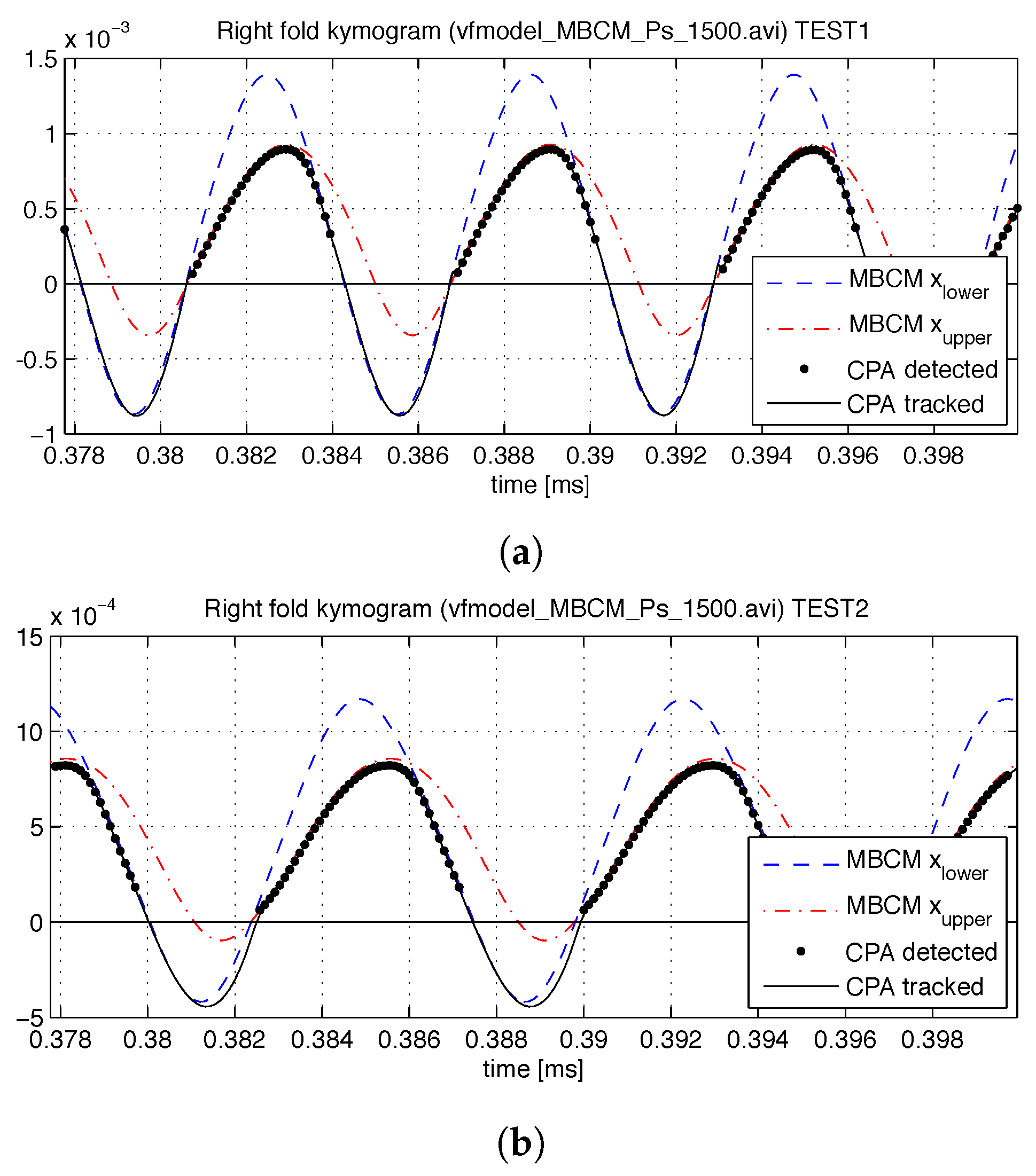
An example of polynomial fitting during open phases and KF during closure for vertically oriented attachment lines (that is,
) with
is shown in
Figure 3. In this case
and the plotted coefficients
are computed as
. The top row shows a plot of
and
, indicating when edge tracking is used (high
) versus when it should fail (low
) and thus requiring KF to complete the cycle. We note that the coefficients
are prone to producing poor fits during collision, since the LS estimation is not well-conditioned when
D decreases suddenly due to failure of the edge detection algorithm during closure. As such, during collision, we lose the VF location. As shown in
Figure 4, the KF handles the loss of detection points by switching to model predictions considering the last position and velocity. When collision ends, the uncertainty factor drops and the estimation returns to the detected edges from the previous stage.
2.5. Contact Pressure Estimation
Hertzian contact theory [
26,
27] describes the stresses occurring in elastic bodies in contact when the local deformation is small in comparison to the characteristic scale of the body. As such, the contact mechanics can be described in terms of the effective contact surface and apparent penetration, that is, the degree to which a body with the same geometry would “penetrate” the contacting body under the same displacement condition [
25]. As a first-order approximation, we herein assume that the contact area between opposing vocal folds begin as a line in the inferior-superior direction, with the contact area increasing as the folds progress through the collision event (refer back to
Figure 1 for the collision geometry). Noting that the vertex of a quadratic (
from the previous sections) is locally circular, we model the collision event as a Hertzian contact between two cylinders with parallel axes, assuming linear elasticity.
Following Boresi et al. [
34], the maximum contact pressure
experienced by colliding cylinders is given by
where
is the penetration depth and
is the contact line length observed from the HSV; refer to
Figure 1 for a schematic. The parameter
is a correction factor to account for VF inferior-superior contact bias; we note that this is not included in standard derivations of Equation (
20). This factor is initially assumed to be unity, meaning that there is no bias due to the contact geometry assumption; however, it will be later calibrated as part of the numerical validation.
The parameter
in Equation (
20) is the effective Young’s modulus, defined as
where
E is Young’s modulus,
is Poisson’s ration, and the subscripts 1 and 2 indicate the two VFs, thus allowing consideration of cases wherein the two VFs have different material properties. For the remainder of this study, however, the two VFs are assumed symmetric with regards to tissue properties, that is,
and
, and
is given by the simplified right hand side of the equation. We note that the normalized maximum contact pressure is purely a function of measured quantities. Alternative geometric models for the vocal folds, such as spherical contacting bodies, result in similar expressions for
, though they generally include additional geometric factors, such as the thickness of the VFs, which are not readily measured with HSV. It is also important to note that the result is independent of the cylinder radius in contrast to other shapes (e.g., colliding spheres).
Equation (
20) yields the dimensionless maximum contact pressure. Determination of a dimensional value requires knowledge of the elasticity of the subject’s vocal folds, which is not directly assessable from HSV alone. However, the aim of this project is to develop a tool that allows for simple contact estimations based solely on kinematic data. If quantitative values for the contact pressure are desired, either additional analysis methods must be employed, such as inverse analysis techniques [
35,
36], or population-based values from the literature may be employed. The dimensionless maximum pressure is of a direct value for comparative evaluations performed on a single subject or, using population-based values, as a first cut approximation of the collision forces.
The final stage of CPA consists of extracting the apparent penetration
from the curve representation for each HSV frame. The predicted coefficients
from Equation (
19) are used to calculate the polynomial parameters for each VF. Finally, we take these polynomial curves to compute the next sequence
3. Methods
In this section the CPA method is validated against pressure estimations from other methods. Specifically, we validate quantitatively against self-sustained VF model simulations and silicone models and semi-quantitatively against experimental data from in vivo recordings with laryngeal HSV of a single subject under various conditions.
3.1. Numerical Validation
Synthetic videos were obtained from a numerical model of voice production referred to as the
Modified Body Cover Model (MBCM), which is a modification of existing VF models [
5,
37] to better serve this study. The model features posterior and membranous glottal openings (PGO and MGO) implementations and a triangular (non-plane) intraglottal mass surface representation, which allows for modeling the variations of the contact area and pressure during closure phases in the anterior-posterior direction. The model is fixed on the anterior and posterior VF locations, and the medial portions are considered point masses. The shape of each fold is defined by a linear interpolation between the anterior, medial, and posterior points. When the cover masses are in contact, the resulting overlapping shape has a distributed contact load that is used to calculate the lumped contact pressure interaction between the cover masses. In particular, the contact depth, contact area, and contact pressure values are extracted from the lower cover masses to conform to the benchmark data set. Glottal opening areas are controlled by parameters governing the thyroarytenoid configuration, with the possibility to define incomplete glottal closure scenarios with PGO and MGO gaps. During collision, the MBCM masses overlap as in traditional lumped element VF models [
38]; the penetration depth of the MBCM is observable and serves as a target for analysis of the proposed CPA method.
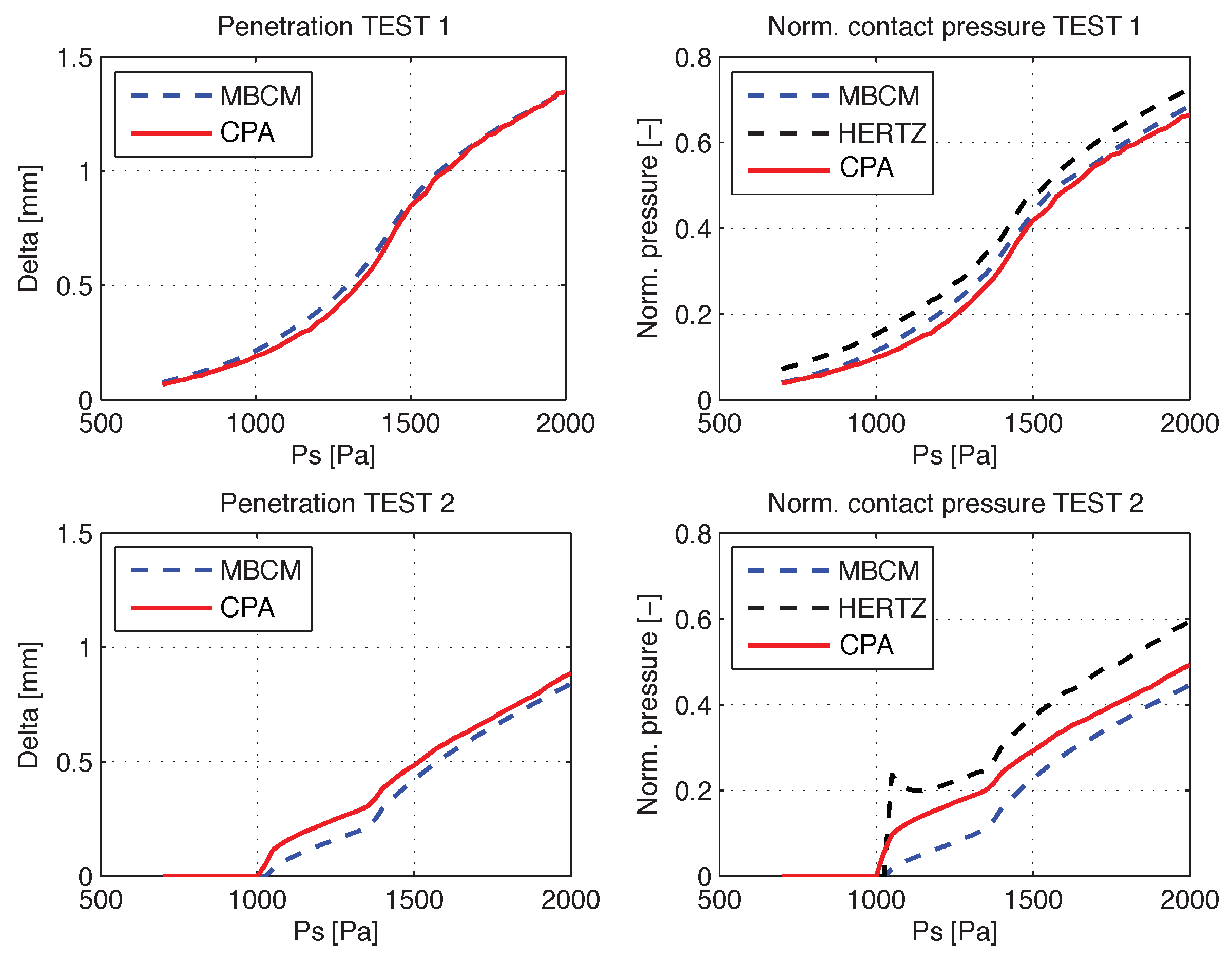
The MBCM model was used to simulate two sets of test cases, one with complete glottal closure phonation (TEST1) and the other with incomplete glottal closure phonation (TEST2). Each test has the same muscle activation, posturing, and vocal tract configurations but differ in the PGO/MGO gaps, which are zero in TEST1 and non-zero in TEST2. For each set, 53 videos with different subglottal pressure values, ranging from 700 to 2000 Pa were obtained. In both test sets, muscular activity was fixed to
(thyroarytenoid),
(cricothyroid), and
(lateral cricoarytenoid) [
39]. Grayscale frame sequences with a transverse view of the MBCM model showing a glottal gap representation were generated. Point locations of each mass were interpolated with parabolic curves to reproduce the glottal gap. Each video frame is
pixels and the frame rate is 8750 fps.
The CPA algorithm is computed on each video with the same configuration setup. The attachment points for these tests are defined by the anterior and posterior rest positions of the MBCM’s low masses, and the video orientation is fixed; as such, the preprocessing stage is not needed. Validation with the synthetic videos consists of comparisons of penetration and collision pressure between the MBCM model and the CPA predictions.
3.2. Silicone Model Experiments for Validation
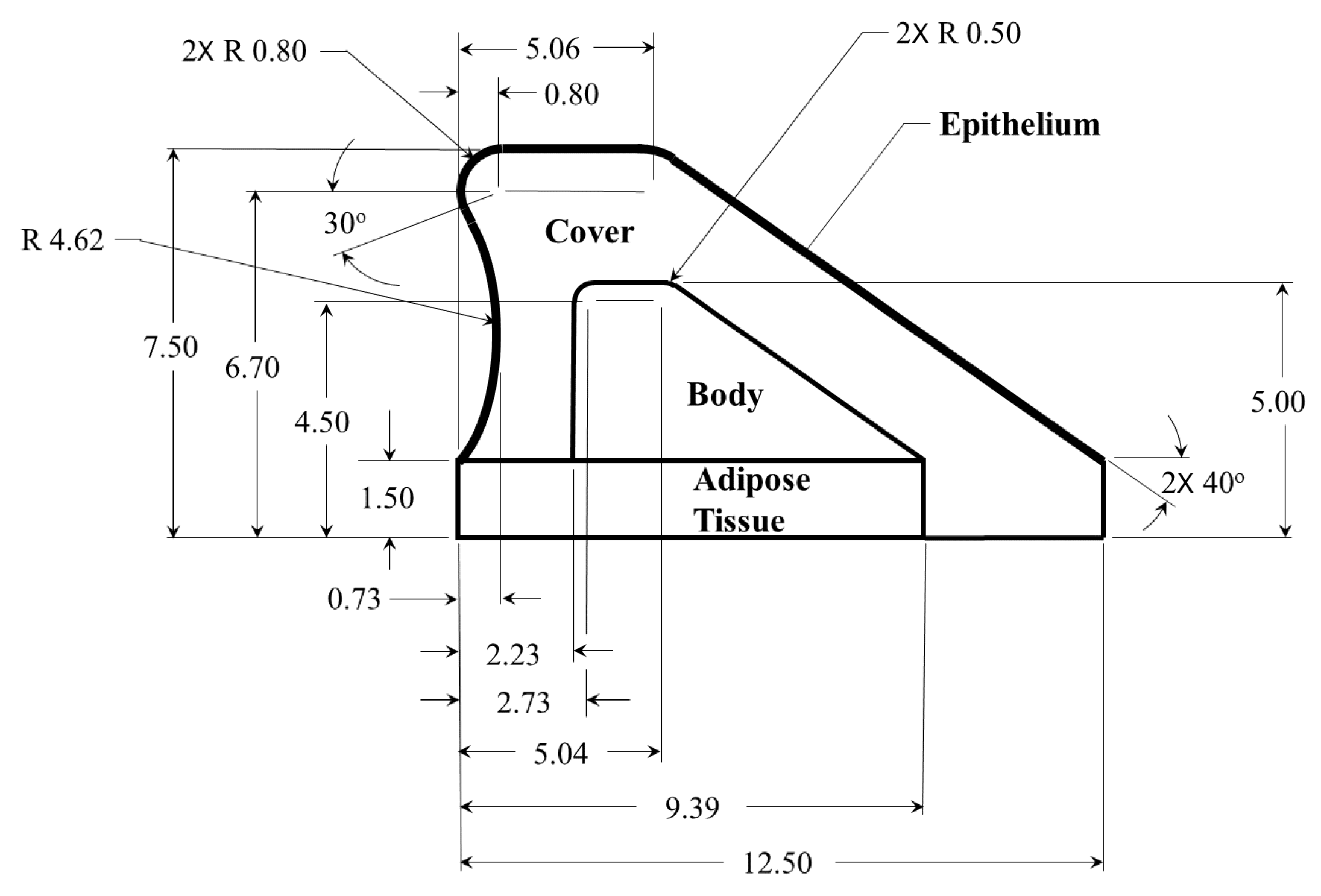
Contact dynamics in silicone, self-oscillating vocal fold models are used for validation of the Hertzian contact approach. The silicone models utilize the same material and follow previously developed approaches for a multi-layer fabrication of silicone vocal fold surrogates [
40,
41,
42,
43]. Details of the geometry utilized for the models are shown in
Figure 5, and the corresponding modulus of elasticity for each layer are presented in
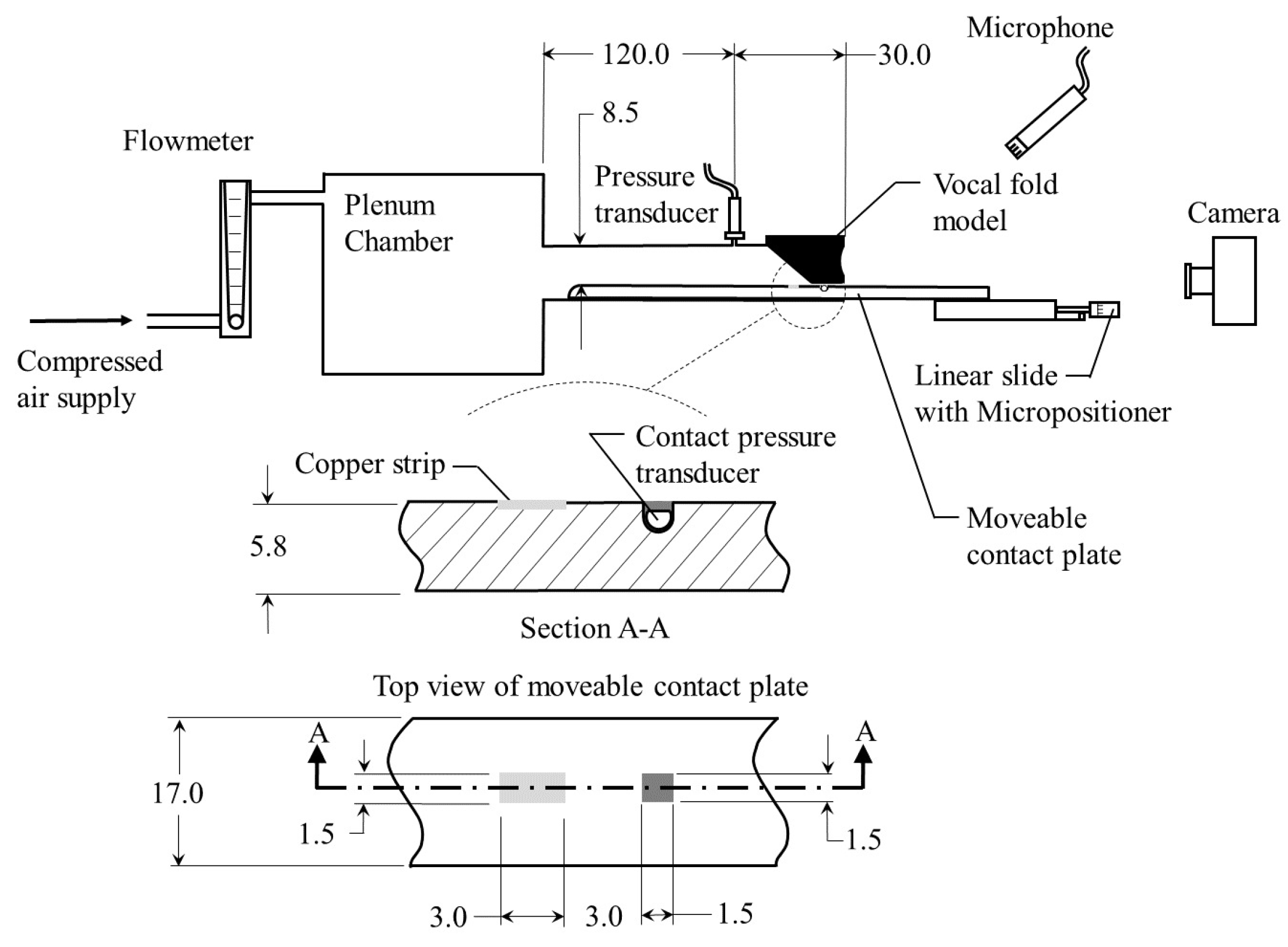
Table 1. The models are inserted into a hemi-laryngeal flow facility, which is driven by regulated, compressed air. Details of the flow facility are presented in
Figure 6. Airflow passes through an in-line Dwyer RMC 103-SSV flow meter before entering the flow facility. The flow facility consists of a lung plenum with a
volume, that has acoustically treated interior walls to minimize acoustic reflections. The plenum exits into a
wide by a
high subglottal channel. The synthetic vocal folds are mounted at the exit of the subglottal tract. A static pressure tap measuring
in diameter is placed upstream of the exit and is connected to a Kulite ET-3DC pressure transducer that monitors the unsteady subglottal pressure. Details of the vocal fold geometry and the stiffness of each corresponding layer are detailed in
Figure 5.
During oscillation, the medial vocal fold surface contacts the lower wall of the subgtlottal tract, which has a movable contact plate insert to enable a direct measurement of the contact pressure and location. The contact pressure is measured by a Millar Mikro–Cath pressure transducer that is flush mounted in the wall of the contact plate and is embedded in silicone such that the upper surface of the tongue remains flat. The pressure transducer is recalibrated while embedded in the silicone via static weight tests that measure the contact force and area of silicone discs resting on the surface of the tongue. In addition, the frequency response of the embedded transducer was measured to be greater than .
To measure the precise location of contact, the procedure first proposed by Reference [
44] is followed. A
wide (anterior-posterior direction) by
long (inferior-superior direction) copper strip is mounted flush to the surface of the tongue and is positioned precisely
inferior to the pressure transducer. The vocal folds models are covered in graphite powder and, together with the copper strip, are wired into one leg of a Wheatsone bridge. Each of the other three legs of the Wheatstone bridge are comprised of a 330 k
resistor. In this manner, when the vocal folds contact the copper strip, the resistance through the VF leg of the circuit, which is determined by monitoring the output voltage from the circuit via LabView
PICe-6321 data acquisition card, decreases, and contact is identified. The movable contact plate extends beyond the exit plane of the vocal folds and is attached to a micropositioner (Thor Labs PT1) so that it can be precisely positioned in the inferior-superior position to determine the contact location. Once the precise position of contact is identified, the plate is adjusted inferiorally/superiorally by
, which corresponds to the offset distance between the copper contact strip and the pressure transducer, thereby ensuring that the contact pressure sensor is centered within the region of contact, where the contact measurements are performed. Contact pressure measurements are acquired at a sampling frequency of
for
and are then sorted and averaged based on the period of oscillation. The peak contact pressure is then identified as an average across all of the acquired cycles.
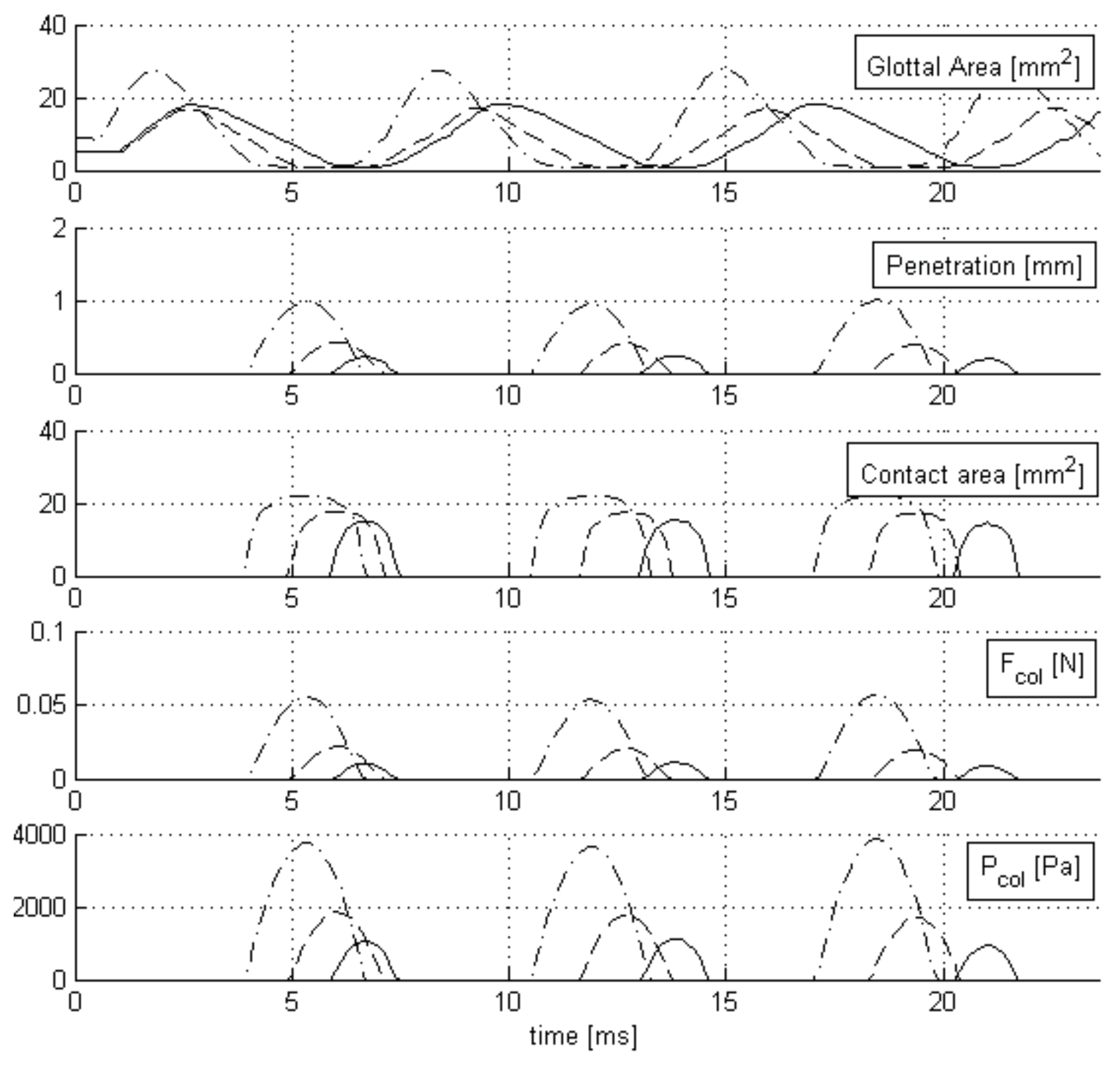
A high-speed video from a superior view of the vocal folds is simultaneously acquired and synchronized with the pressure acquisitions at 20,000 . Data are acquired for three separate moduli of elasticity for the model vocal fold cover: , , and . At the lowest cover value, HSV is captured at a subglottal pressure of . For a cover module of elasticity of , HSV is captured at subgltottal pressures of 2.20–3.40 in increments of . Finally, at the highest value, HSV is acquired for a subglottal pressure of .
3.3. In Vivo Experiment
The HSV recordings are used as a proof of concept for in vivo clinical scenarios. Three phonation gestures with increasing loudness (soft, normal, and loud) in a normal subject were recorded. Each HSV has about 2670 frames of 300 × 300 pixels at 8000 fps, recorded with a high-speed camera (SA-X2, Photron, Tokyo, Japan) connected to a rigid endoscope (9106, KayPentax, Montvale, NJ) using a 35-mm C-mount adapter and a xenon light source (7152B, KayPentax, Montvale, NJ). Each loudness gesture was accompanied with its corresponding
Sound Pressure Level (SPL), obtained with a condenser microphone (ECM8000, Behringer, Willich, Germany) positioned 8 cm away from the mouth and calibrated with a Sound Level Meter (NL-42, Rion, Tokyo, Japan). The procedure was performed under informed consent, following the IRB-approved protocol for the FONDECYT project 1151077. The experiment with these in vivo HSV consists of semi-quantitative comparisons between the contact pressure reached by the patient, taking normal loudness as the reference point. HSV dimensions and CPA configuration parameters are not calibrated; as such, the same CPA values from the synthetic videos in the prior section were used for this experiment. The latter is particularly useful to contrast the proposed Hertz contact output in physical units (e.g., Pa) against the reported data [
16,
20,
21,
22].
All CPA configuration parameters are shown in
Table 2 for both synthetic and in vivo HSV experiments. Note that the material properties are not needed to estimate the normalized pressure but are listed here to allow for a direct comparison with prior studies in the experimental validation.
5. Discussion
The fundamental tenet of CPA is that sufficient information regarding the collision mechanics is embedded in the vocal fold kinematics, which is accessible through high-speed videos to obtain reasonable first-order estimates of contact pressure. That is, CPA is founded on the principle that impact velocity and contact time are sufficient to assess collision pressure magnitudes. Our validation using silicone vocal fold models illustrated that there is an excellent agreement between the mean predicted contact pressure, although with some nonnegligible variability due to image processing difficulties. Agreements with prior numerical studies [
20,
21,
22,
46,
47], experimental measurements in humans [
6,
7,
8], and excised hemilarynx studies [
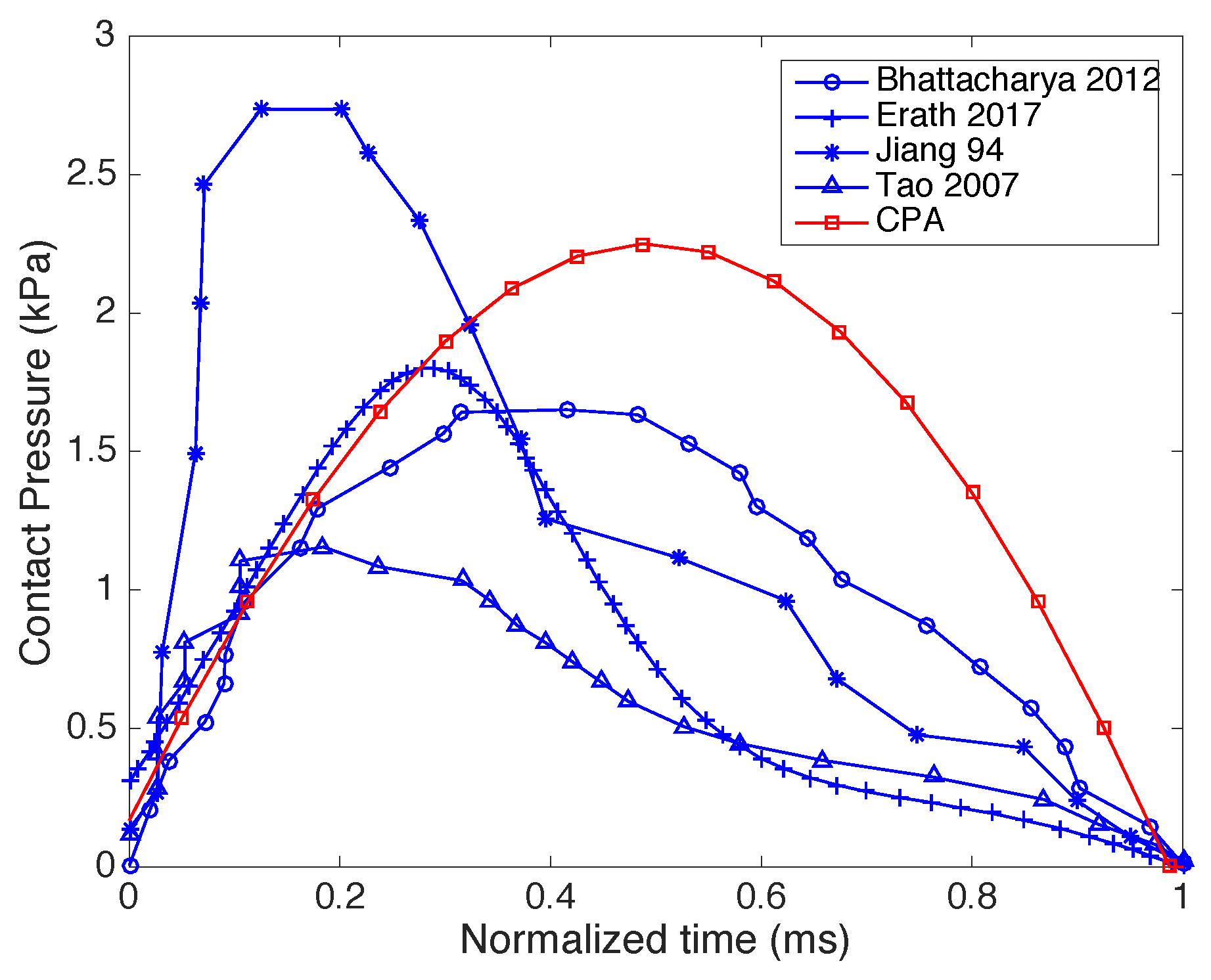
16] also have been found. This supports that the Hertz contact framework is appropriate for the goal of estimating contact pressure directly from the kinematic information, as described in the CPA framework.
There are clinical arguments that suggest that aerodynamic parameters, such as
Maximum Flow Declination Rate (MFDR), are related to collision pressure and stress [
1,
5]. Similar relative changes in aerodynamic-based assessment parameters with loudness for normal subjects have been observed in prior studies [
47] as found with the contact pressure estimates in this study. Numerical models support this relation between MFDR and collision pressure [
5,
37], but the conjecture is still not proven and only theoretical studies that evaluate this are known. That said, our case study supports the idea that CPA is capable of discriminating the increasing effect of collision pressure with loudness in actual in vivo scenarios despite the lack of aerodynamic or other additional information in the recordings.
The proposed Hertz contact model, which, by virtue of employing cylinders, implicitly assumes uniform and simultaneous contact along the thickness of the VFs, has the advantage of not requiring additional subject-specific information in order to estimate the normalized contact pressure. Geometric variations in the inferior-superior direction, however, do influence the contact pressure, as evidenced by the estimated value of
in Equation (
20) differing from one. The value employed in this study was obtained from the numerical validation phase through a comparison with the reduced order model performance. It remains unclear how universal this geometric correction factor may be and requires additional data sets. It is unlikely that the value of
, even if it is not relatively constant between individuals, will change dramatically, however. Similarly, to obtain absolute measures of contact pressure from CPA, one requires additional patient-specific information, namely tissue elasticity. This value can change significantly between subjects or even between vocal gestures. However, even though there could be a bias in the exact magnitude of the collision pressure due to either
or elastic modulus, the relative changes within the same subject are expected to be well-represented. Having access to these simple estimates can be of great interest for clinical practices to easily assess the effectd of therapy or surgical procedures on a given subject, where the unknown tissue and/or geometric parameters remain the same.
There are several parameters that are user-specified when employing CPA: the threshold value for the edge detection of the VFs; identification of the attachment point locations, which dictates the “rest” positions of the folds in model space; and the order of the polynomial used to fit the vocal fold geometry. A performance of the analysis is relatively insensitive to the threshold value in the edge detection, in part due to the averaging employed in those steps, as well as the polynomial fit performed on the extracted points. On the other hand, proper identification of the VF attachment points is critical for a good kinematic representation of the VFs, with inaccurate identification of these points resulting in poor representations of VF trajectories, which, in turn, affects pressure estimations. Higher order polynomials (e.g., or 4) yielded poor and unstable results in the CPA estimation. Good and smooth fits in the registration stage were correctly obtained, but the VF trajectories during the collision phase missed the cinematic coherence. We attribute this issue to the KF model for higher order coefficients in . In these cases, the variability of each is not well-represented with the simple harmonic motion. As such, while the presented framework is derived to enable higher-order polynomial representations, from a practical perspective, we recommend lower-order (i.e., quadratic) fits for optimal performance.
Future efforts will consider additional silicone model validation under more controlled lighting conditions and additional model configurations (multiple elastic moduli and subglottal pressures) as well as in vivo validation where contrast with VF contact pressure is possible. Other avenues of research include exploring this technique in a large pool of subjects, including patients with voice disorders (e.g., nodules and polyps) and adopting the approach for stroboscopic acquisition methods.